The ecology of action selection: insights from artificial life

Abstract

The problem of action selection has two components: what is selected and how is it selected? To understand what is selected, it is necessary to distinguish between behavioural and mechanistic levels of description. Animals do not choose between behaviours per se; rather, behaviour reflects interactions among brains, bodies and environments. To understand what guides selection, it is useful to take a normative perspective that evaluates behaviour in terms of a fitness metric. This perspective, rooted in behavioural ecology, can be especially useful for understanding apparently irrational choice behaviour. This paper describes a series of models that use artificial life (AL) techniques to address the above issues. We show that successful action selection can arise from the joint activity of parallel, loosely coupled sensorimotor processes. We define a class of AL models that help to bridge the ecological approaches of normative modelling and agent- or individual-based modelling (IBM). Finally, we show how an instance of apparently suboptimal decision making, the matching law, can be accounted for by adaptation to competitive foraging environments.

1. Introduction

Real life is all action. Bodies and brains have been shaped by natural selection above all for the ability to produce the right action at the right time. The neural substrates of action selection must therefore be very general, encapsulating mechanisms for perception as well as those supporting motor movements per se, and their operations must be understood in terms of interactions among brains, bodies and structured environments.

How can these complex interactions be modelled? Among biological disciplines, behavioural ecology has a strong tradition of accounting for the role of organism–environment interactions in behaviour (Krebs & Davies 1997). Behavioural ecology and the related field of optimal foraging theory (OFT; Stephens & Krebs 1986) model animal behaviour in terms of optimal adaptation to environmental niches. The goal is not to test whether organisms in fact behave optimally, but to use normative expectations to interpret behavioural data and/or generate testable hypotheses. For example, Richardson and Verbeek explain the observation that crows do not always forage for the largest clams in their environment by noting that eating large clams requires significantly more handling time than eating small clams; the optimal foraging strategy in this case involved selecting a mixture of large and small clams (Richardson & Verbeek 1987). Importantly, while OFT models may suggest ultimate causes for behaviour (i.e. those that derive from evolutionary selective pressures), they are less able to reveal proximate causes (i.e. the underlying agent mechanisms that generate the observed behaviours).

A common method in ecological modelling and OFT has involved the use of state variables, which represent properties of a population as a whole (e.g. size, density, growth rate; Houston & McNamara 1999; Clark & Mangel 2000; McNamara & Houston 2001). Although this approach can preserve mathematical tractability, it makes difficult the incorporation of aspects of adaptive behaviour that depend on the detailed dynamics of agent–agent and agent–environment interactions (Seth 2000, 2002a; Grimm & Railsback 2005). For example, the influence of the spatial aggregation of foragers on resource intake cannot be modelled in the absence of a spatially explicit representation of the environment (Seth 2001b). Partly in response to difficulties of this sort, ecology has increasingly embraced agent-based or individual-based models (ABMs, IBMs; Huston et al. 1988; DeAngelis & Gross 1992; Grimm 1999; Grimm & Railsback 2005). ABMs and IBMs (we use the terms interchangeably) explicitly instantiate individual agents in order to capture the dynamics of their interactions, and they explicitly model the environmental structure that scaffolds these interactions. These features allow ABMs to represent features such as spatial inhomogeneity of resources, which significantly influence behaviour, but which may be difficult to incorporate into state-variable models (e.g. Axtell et al. 2002; Sellers et al. 2007). One important trade-off is that incorporation of such features often comes at the expense of mathematical tractability and another is that ABMs often lack a straightforward normative interpretation as offered by OFT models.

In this paper, we explore how modelling and analysis techniques drawn from artificial life (AL) can complement and extend ABMs, as they relate to action selection. AL is a broad field, encompassing the study of life via the use of human-made analogues of living systems. Here, we focus on a subset of AL methods that have the most relevance to the ecology of action selection. We consider two core features offered by the AL approach, which are as follows.

1. The use of numerical optimization algorithms (e.g. genetic algorithms (GAs); Holland 1992) to optimize patterns of behaviour within the model with respect to some fitness criterion (e.g. maximization of resource intake).

2. The modelling of agent–environment and agent–agent interactions at the level of situated perception and action, via the explicit modelling of sensor input and motor output.

The first of these features provides a natural bridge between OFT models (which incorporate a normative criterion but usually use state variables) and ABMs (which do not rely on state variables but may not incorporate a normative component). The second feature permits the essential distinction between behaviour and mechanism to be realized within the model. Here, behaviour refers to the interactions between an agent and its environment as perceived by an external observer, and mechanism refers, broadly speaking, to the properties of the agent (i.e. body, brain) that underlie these interactions (these definitions will be sharpened in the following section). In this view, the proper mechanistic explanatory targets of action selection are selective mechanisms in both sensory and motor domains that ensure the adaptive coordination of behaviour. Models that do not reach down into the details of sensorimotor interactions run the risk of falsely reifying behaviours by proposing mechanisms that incorporate as components descriptions of the behaviours they are intended to generate (Hallam & Malcolm 1994; Seth 2002a). Of course, this is not to say that models at higher levels of abstraction are necessarily less valuable. With careful interpretation of the relationship between behaviour and mechanism, such models can equally provide useful insights; we will describe one of these models in §6 of this article.

A key challenge for normative models of behaviour lies in accounting for apparently suboptimal (‘irrational’) action selection. For example, many animals behave according to Herrnstein's matching law, in which responses are allocated in proportion to the reward obtained from each response option (Herrnstein 1961). Importantly, while matching behaviour is often optimal, it is not always so (see also Houston et al. 2007). A useful framework for conceiving suboptimal behaviour is ecological rationality, the idea that cognitive mechanisms fit the demands of particular ecological niches and may deliver predictably suboptimal behaviour when operating outside these niches (Gigerenzer et al. 1999). Here, we use the concept of ecological rationality to describe some contributions of AL models to an ecological perspective on action selection. Specifically, we explore the possibility that matching behaviour may result from foraging in a competitive multi-agent environment.

The rest of this article is organized as follows. Section 2 introduces relevant aspects of the field of AL. Section 3 reviews a selection of previous AL models of action selection from the perspective of explicitly distinguishing between behaviour and mechanism. A simple AL model is then described which explores a minimal mechanism for action selection that depends on the continuous and concurrent activity of multiple sensorimotor links (Seth 1998). Using this model as a representative example, §4 explores the methodological potential offered by AL for bridging ABMs and OFT (Seth 2000). Section 5 describes a second AL model which tests the hypothesis that (potentially suboptimal) matching behaviour may reflect foraging behaviour adapted to a competitive group environment (Seth 2001a). Section 6 models matching behaviour at a higher level of description, connecting more closely with optimal foraging models that describe the equilibrium distribution of foragers over patchy resources (Fretwell 1972; Seth 2002b). Finally, §7 summarizes and suggests avenues for future research.

2. Artificial life

Although the roots of AL may be traced as far back as the ‘artificial ducks’ of the eighteenth century automata-maker Jacques de Vaucanson (Fryer & Marshall 1979), the modern field arguably began with John von Neumann's theories of self-replicating automata and cellular automata (von Neumann 1966). However, it was only in the 1980s that AL became a recognizable discipline, distinct from related fields such as artificial intelligence and theoretical biology. Langton coined the term ‘artificial life’ by stating that AL extended ‘the study of life-as-we-know-it into the realm of life-as-it-could-be’ (Langton 1989, p. 1). Presently, AL researchers use a wide variety of computational methods, including ABM (Axelrod & Hamilton 1981), GAs (Holland 1992), swarm intelligence (Bonabeau et al. 1999) and artificial chemistries (Dittrich et al. 2001). There is a prominent strand of AL which explores ‘synthetic ecologies’ (Ray 1991; Adami 1994; Holland 1994; Ofria & Wilke 2004), however, because these models do not focus on decision making by individual agents, they will not be considered further in this article.

In any discussion of AL, it is important to distinguish strong AL, which refers to the position that the products of AL are as alive as their biological inspirations, from weak AL, the view that AL comprises a form of simulation modelling (Sober 1996). In agreement with weak AL, this article assumes that AL models constitute opaque thought experiments, i.e. thought experiments in which the consequences follow from the premises, although possibly in non-obvious ways which may only be revealed via systematic enquiry (Di Paolo et al. 2000). We note that there is a considerable overlap between weak AL and research under the rubric ‘simulation of adaptive behaviour’ (e.g. Meyer & Wilson 1990). Here, no distinction is drawn between the two research areas.

A key feature of AL models is their ability to explicitly distinguish between behaviour and mechanism (Hallam & Malcolm 1994; Hendriks-Jansen 1996; Clark 1997; Seth 2002a). Following from the broad definitions given in §1, behaviour is defined here as observed ongoing agent–environment interactivity, and mechanism is defined as the agent-side structure subserving this interactivity. All behaviours (e.g. eating, swimming, building-a-house) depend on continuous patterns of interaction between agent and environment; there can be no eating without food, no house-building without bricks, no swimming without water. Moreover, it is up to the external observer to decide which segments of agent–environment interactivity warrant which behavioural labels. Different observers may select different junctures in observed activity, or they may label the same segments differently. Therefore, and this is a key point: the agent-side mechanisms underlying the generation of behaviour should not be assumed to consist of internal correlates, or descriptions, of the behaviours themselves.

Another central concept for present purposes is the GA; (Holland 1992; Mitchell 1997). A GA is a search algorithm loosely based on natural selection in which a population of genotypes (e.g. a string of numbers) is decoded into phenotypes (e.g. a neural network controller) which are assessed by a fitness function (e.g. lifespan of the agent). The fittest individuals are selected to go forward into a subsequent generation, and mutation and/or recombination operators are applied to the genotypes of these individuals. In this paper, GAs are used to optimize behaviour within ABMs. While other numerical algorithms may serve this function just as well, we focus on the GA because of its flexibility and success in a wide range of optimization problems (Mitchell 1997).

It bears emphasizing that GAs, being numerical algorithms, cannot guarantee exactly optimal solutions. GAs may fail to find exactly optimal solutions for a number of reasons, including insufficient search time, insufficient genetic diversity in the initial population and overly rugged fitness landscapes in which there exist many local fitness maxima and/or in which genetic operations have widely varying fitness consequences. However, for present purposes, it is not necessary that GAs always find exactly optimal solutions. It is sufficient that GAs instantiate a process of optimization so that the resulting behaviour patterns and agent mechanisms can be interpreted from a normative perspective. Of course, the value of this perspective will depend on the performance of the GA. Therefore, independent criteria should be applied to judge the extent to which the GA has been able to identify solutions of high fitness. While it is beyond the present scope to describe in detail these aspects of the GA methodology, relevant factors include: (i) a satisfactory performance of the behavioural task, (ii) a significant increase in fitness when compared with the initial random population, and (iii) a high fraction of mutations of the fittest individual which lead to the decreases in fitness.

3. AL models of action selection

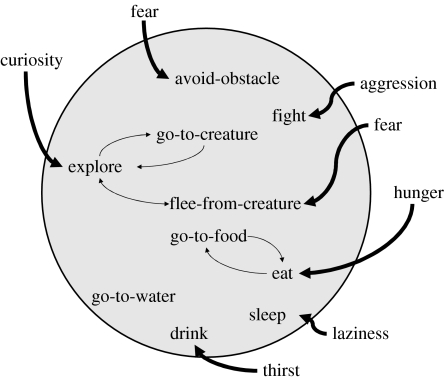
Recent AL models of action selection were pioneered by Brooks' subsumption architecture (Brooks 1986) and Maes' spreading activation control architecture (Maes 1990; figure 1). Brooks decomposed an agent's control structure into a set of task-achieving ‘competences’ organized into layers, with higher layers subsuming the goals of lower layers and with lower layers interrupting higher layers. For Maes, an organism comprises a ‘set of behaviours’ with action selection arising via ‘parallel local interactions among behaviours and between behaviours and the environment’ (Maes 1990, pp. 238–239). These architectures can be related to ethological principles developed more than 50 years ago by Tinbergen and Lorenz, who considered action selection to depend on a combination of environmental ‘sign stimuli’ and ‘action-specific energy’, activating either specific ‘behaviour centres’ (Tinbergen 1950) or ‘fixed action patterns’ (Lorenz 1957). A key issue for these early models was the utility of hierarchical architectures, with some authors viewing hierarchical structure as an essential organizing principle (Dawkins 1976), while others noted that strict hierarchies involve the loss of information at every decision point (Rosenblatt et al. 1989; Maes 1990).

Figure 1.

Decentralized spreading activation action selection architecture adapted from Maes (1990). Agent behaviour is determined by interactions among internal representations of candidate behaviours, modulated by drives (e.g. curiosity). Note that the internal mechanism (within the grey circle) consists of internal correlates of behaviours.

Over the past decade, AL models of action selection have progressively refined the notion of hierarchical control. In a frequently cited thesis, Tyrrell revised Maes' spreading activation architecture to incorporate soft-selection (Rosenblatt et al. 1989) in which competing behaviours expressed preferences rather than entering a winner-takes-all competition (Tyrrell 1993). At around the same time, Blumberg incorporated inhibition and fatigue into a hierarchical model in order to improve the temporal sequencing of behaviour (Blumberg 1994). More recently, Bryson demonstrated that a combination of hierarchical and reactive control outperformed fully parallelized architectures in the action selection task developed by Tyrrell (Bryson 2000). For a current perspective on hierarchical action selection, see Botvinick (2007).

Although space limitations preclude a comprehensive review of alternative modelling approaches to action selection, it is worth noting briefly two currently active directions. One is the incorporation of reinforcement learning (Humphrys 1996; Sutton & Barto 1998), with a recent emphasis on the influences of motivation (Dayan 2002) and uncertainty (Yu & Dayan 2005). The second is the incorporation of neuroanatomical constraints. Notably, Redgrave and colleagues have proposed that the vertebrate basal ganglia implement a winner-take-all competition among inputs with different saliences (Redgrave et al. 1999, see also Hazy et al. 2007). We return to these issues in a discussion of possible extensions to the present approach (see §7).

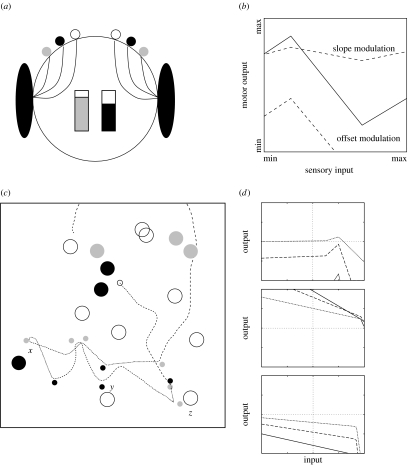
A feature of many AL models of action selection (hierarchical or otherwise) is that mechanisms of action selection are assumed to arbitrate among an internal repertoire of behaviours. We have argued above that this assumption is conceptually wrong-headed in that it confuses behavioural and mechanistic levels of description. What, then, does action selection select? To address this question, we turn now to a simple AL model designed to show that action selection, at least in a simple situation, need not require internal arbitration among explicitly represented behaviours (Seth 1998). The architecture of this model was inspired by Pfeifer's notion of ‘parallel, loosely coupled processes’ (Pfeifer 1996) and Braitenberg's elegant series of thought experiments, which suggest that complex behaviour can arise from surprisingly simple internal mechanisms (Braitenberg 1984). The simulated agent and its environment are shown in figure 2; full details of the implementation are provided in electronic supplementary material, S1. Briefly, the simulated environment contains three varieties of object: two types of food (grey and black) as well as ‘traps’ (open circles, which ‘kill’ the agent upon contact). The closest instance of each object type can be detected by the agent's sensors. The agent contains two ‘batteries’—grey and black—which correspond to the two food types. These batteries diminish at a steady rate and if either becomes empty, then the agent ‘dies’. Encounter with a food item fully replenishes the corresponding battery.

Figure 2.

A minimal model of action selection. (a) Architecture of the simulated agent. Each wheel is connected to three sensors which respond to distance to the nearest food item (grey and black circles) and ‘trap’ (large open circles). The agent has two ‘batteries’ which are replenished by the corresponding food types. (b) The structure of a sensorimotor link (each connection in (a) consists of three of these links). Each link maps a sensory input value into a motor output value via a transfer function (solid line). The ‘slope’ and the ‘offset’ of this function can be modulated by the level of one of the two batteries (dashed lines). The transfer function and the parameters governing modulation are encoded as integer values for evolution using a genetic algorithm. (c) Behaviour of an evolved agent (small circles depict consumed resources). The agent displayed opportunistic behaviour at point x by consuming a nearby grey item even though it had just consumed such an item, and showed backtracking to avoid traps at points y and z. (d) Shapes of three example sensorimotor links following evolution (solid line shows the transfer function; dashed and dotted lines show modulation due to low and very low battery levels, respectively).

Each sensor is connected directly to the motor output via a set of three sensorimotor links (figure 2b). Each link transforms a sensory input signal into a motor output signal via a transfer function, the shape of which can be modulated by the level of one of the two batteries (dashed lines). Left and right wheel speeds are determined by summing motor output signals from all the corresponding links. A GA was used to evolve the shape of each transfer function as well as the parameters governing battery modulation. The fitness function rewarded agents that lived long and maintained a high average level in both batteries.

Figure 2c shows an example of the behaviour of an evolved agent. The agent consumed a series of food items of both types, displayed opportunistic behaviour at point x by consuming a nearby grey item even though it had just consumed another such item, and successfully backtracked to avoid traps at points y and z. Overall agent behaviour was evaluated by a set of behavioural criteria for successful action selection (table 1). Performance on these criteria was evaluated by the analysis of behaviour within the natural environment of the agent (e.g. figure 2c) and of contrived ‘laboratory’ situations designed to test specific criteria. For example, the balance between dithering and persistence was tested by placing an evolved agent in between a group of three grey items and a group of three black items. These analyses demonstrated that the evolved agents satisfied all the relevant criteria (Seth 1998, 2000).

Table 1.

Criteria for successful action selection, drawn from Werner (1994) (see also T. Tyrrell 1993, unpublished data)

1	prioritize behaviour according to current internal requirements
2	allow contiguous behavioural sequences to be strung together
3	exhibit opportunism; for example, by diverting to a nearby ‘grey’ food item even if there is a greater immediate need for ‘black’ food
4	balance dithering and persistence; for example, by drinking until full and then eating until full instead of oscillating between eating and drinking
5	interrupt current behaviour; for example, by changing course to avoid the sudden appearance of a dangerous object
6	privilege consummatory actions (i.e. those that are of immediate benefit to the agent, such as eating) over appetitive actions (i.e. those that set up conditions in which consummatory actions become more probable)
7	use all available information
8	support real-valued sensors and produce directly usable outputs

Examples of evolved transfer functions are shown in figure 2d. Each of these transfer functions showed modulation by a battery level and each set of three functions was influenced by both batteries (e.g. sensorimotor links sensitive to ‘grey’ food were modulated by internal levels of both grey and black batteries). Further analysis of the evolved transfer functions (Seth 2000, unpublished data) showed switching between consummatory and appetitive modes (via a nonlinear response to distance from a food item) and implicit prioritization (via disinhibition of forward movement with low battery levels).

It is important to emphasize that this model is intended as a conceptual exercise in what is selected during action selection. Analysis of the model shows that it is possible for a simple form of action selection to arise from the concurrent activity of multiple sensorimotor processes with no clear distinctions among sensation, internal processing or action, without internal behavioural correlates and without any explicit process of internal arbitration. These observations raise the possibility that mechanisms of action selection may not reflect behavioural categories derived by an external observer, and, as a result, may be less complex than supposed on this basis. They also suggest that perceptual selective mechanisms may be as important as motor mechanisms for successful action selection (Cisek 2007). Having said this, it must be recognized that the particular mechanism implemented in the model is not reflected in biological systems and may not deliver adaptive behaviour in more complex environments. It is possible that action selection in complex environments will be better served by modular mechanisms that may be more readily scalable by virtue of having fewer interdependencies among functional units. Modularity may also enhance evolvability, the facility with which evolution is able to discover adaptive solutions (Wagner & Altenberg 1996; Prescott et al. 1999).

4. Optimal agent-based models

In this section, we generalize the modelling approach of §3 into a novel methodology which integrates ABM with normative optimal foraging modelling (Seth 2000).

OFT assumes that behaviour can be considered to be an optimal solution to the problem posed by an environmental niche. Standard OFT models consist of a decision variable, a currency and a set of constraints (Stephens & Krebs 1986). Consider the redshank Tringa totanus, foraging for worms of different sizes (Goss-Custard 1977). The decision variable captures the type of the choice the animal is assumed to make (e.g. whether a small worm is worth eating), the currency specifies the quantity that the animal is assumed to be maximizing (e.g. rate of energy intake) and the constraints govern the relationship between the decision variable and the currency (e.g. the ‘handling time’ required to eat each worm and the relative densities of different sizes of worm). Given these components, an analytically solvable model can be constructed which predicts how the animal should behave in a particular environment in order to be optimal (i.e. a foraging strategy). Critically, OFT models do not reveal whether or not an animal ‘optimizes’, rather, discrepancies between observed and predicted behaviour are taken to imply, either that relevant constraints have been omitted from the model or that the assumed currency is wrong. We note that OFT is closely related to ‘behavioural economics’ (McFarland & Bosser 1993) in which animals are assumed to allocate behaviour in order to maximize utility.

Importantly, decision variables—and the foraging strategies that depend on them—are often framed in terms of distinct behaviours (i.e. do behaviour X rather than behaviour Y). This carries the assumption that animals make decisions among entities (behaviours) that are in fact the joint products of agents, environments and observers, and which may not be directly reflected in agent-side mechanisms (see §2). A consequence of this assumption is that, since behavioural complexity is not necessarily reflected in the underlying mechanisms, the complexity of an optimal foraging strategy may be overestimated.

The problem of excessive computational and representational demands of optimal foraging strategies has been discussed widely. One potential solution is to consider that animals adopt comparatively simple foraging strategies (‘rules of thumb’) that approximate optimality (e.g. McNamara & Houston 1980; Iwasa et al. 1981; Houston & McNamara 1984, 1999; see also §6). However, as long as these rules of thumb also use decision variables that mediate among distinct behaviours, the possibility of a mismatch between behavioural and mechanistic levels of description remains.

An alternative approach is to dispense with ‘behavioural’ decision variables altogether. The model described in §3 can be thought of as a type of OFT model without a decision variable. It uses an assumed currency (the fitness function), instantiates a set of constraints (the structure of the agent and the environment) and uses an optimization technique (a GA) to generate behaviour. Note, however, that there is no clear analogue of a decision variable. Instead of assuming that the agent must explicitly arbitrate among internally represented behaviours, selective behaviour emerges from the continuous and parallel activity of multiple sensorimotor processes. This example suggests an alternative approach to OFT modelling, via the construction of AL models which explicitly instantiate internal architectures (but not necessarily decision variables) and environmental constraints, and which generate behaviour via the application of optimization techniques such as GAs (Seth 2000). We refer to these models as optimal agent-based models (oABMs). The lower case ‘o’ is intended to reflect a limitation of this approach, which, as we have mentioned, is that GAs do not guarantee exactly optimal solutions (see §2). While such simulation-based models may lack analytical transparency, they supply a number of advantages:

1. The progressive relaxation of constraints is often easier in a simulation model than in an analytically solvable model. For example, representation of non-homogeneous resource distributions can rapidly become intractable for analytic models.

2. There is no need to assume an explicit decision variable (although such variables can be incorporated if deemed appropriate). Construction of oABMs without explicit decision variables broadens the space of possible internal mechanisms for the implementation of foraging strategies, and, in particular, facilitates the generation and evaluation of hypotheses concerning comparatively simple internal mechanisms.

3. oABMs are well suited to incorporate historical or stigmergic constraints that arise from the history of agent–environment interactions, by providing a sufficiently rich medium in which such interactions can create dynamical invariants which constrain, direct, or canalise the future dynamics of the system (Di Paolo 2001). Examples can be found in the construction of termite mounds or in the formation of ant graveyards.

The above features together offer a distinct strategy for pursuing optimality modelling of behaviour. Standard OFT models are usually incrementally complex. Failures in prediction are attributed to inadequate representation of constraints, prompting a revision of the model. However, only certain aspects of standard OFT models—constraints and currencies—can be incrementally revised. Others, such as the presence of a decision variable or the absence of situated perception and action, are much harder to manipulate within an analytically tractable framework. oABMs, being simulation-based, can bring into the focus aspects of OFT models that are either explicit but potentially unnecessary (e.g. decision variables) or implicit and usually ignored (e.g. situated perception and action, historical constraints). Thus, in contrast to an incremental increase in model complexity, oABMs offer the possibility of radically reconfiguring the assumption structure of an optimality model.

It is important to emphasize the different role of GAs within oABMs as compared to related approaches, such as evolutionary simulation models (Wheeler & de Bourcier 1995; Di Paolo et al. 2000) and synthetic ecologies (see §2), in which GAs are themselves the object of analysis insofar as the models aim to provide insight into evolutionary dynamics. In oABMs, GAs are used only to specify behaviour and mechanism; evolutionary dynamics per se are not studied.

5. Probability matching and inter-forager interference

For the rest of this article, we will concentrate on the problem of suboptimal action selection, via an exploration of ‘matching’ behaviour. We first introduce and differentiate two distinct forms of matching: probability matching and the matching law.

In 1961, Herrnstein observed that pigeons match the frequency of their responses to different stimuli in proportion to the rewards obtained from each stimulus type (Herrnstein 1961), a ‘matching law’ subsequently found to generalize to a wide range of species (Davison & McCarthy 1988). By contrast, probability matching describes behaviour in which the distribution of responses is matched to the reward probabilities, i.e. the available reward (Bitterman 1965). The difference between these two forms of matching is well illustrated by the following simple example. Consider two response alternatives A and B which deliver a fixed reward with probabilities 0.7 and 0.3, respectively. Probability matching would predict that the subject chooses A on 70% of trials and B on 30% of trials. This allocation of responses does not satisfy the matching law; the subject would obtain approximately 85% of its reward from A and approximately 15% from B. Moreover, probability matching in this example is suboptimal. Clearly, reward maximization would be achieved by responding exclusively to A. Optimal behaviour does, however, satisfy the matching law, although in a trivial manner: by choosing A on 100% of trials, it is ensured that A is responsible for 100% of the reward obtained. Note that matching does not guarantee optimality: exclusive choice of B would also satisfy the matching law.

Empirical evidence regarding probability matching is mixed. Many studies indicate that both humans and non-human animals show (suboptimal) probability matching in a variety of situations (see Myers 1976; Vulkan 2000; Erev & Barron 2005 for reviews). In human subjects, however, substantial deviations from probability matching have been observed (Gluck & Bower 1988; Silberberg et al. 1991; Friedman & Massaro 1998). According to Shanks and colleagues, probability matching in humans can be reduced by increasing reward incentive, providing explicit feedback about correct responses and allowing extensive training (Shanks et al. 2002). Although a clear consensus is lacking, it remains likely that probability matching, at least in non-human animals, is a robust phenomenon. How can this apparently irrational behaviour be accounted for?

One possibility is that probability matching may result from reinforcement learning (Sutton & Barto 1998) in the context of balancing exploitation and exploration (Niv et al. 2001). Here, we explore the different hypothesis that probability matching can arise, in the absence of lifetime learning, as a result of adaptation to a competitive foraging environment (see also Houston 1986; Houston & Sumida 1987; Houston & McNamara 1988; Thuisjman et al. 1995; Seth 1999, 2001a). The intuition is as follows. In an environment containing resources of different values, foragers in the presence of conspecifics may experience different levels of interference with respect to each resource type, where interference refers to the reduction in resource intake as a result of competition among foragers (Sutherland 1983; Seth 2001b). Maximization of overall intake may therefore require distributing responses across resource types, as opposed to responding exclusively to the richest resource type.

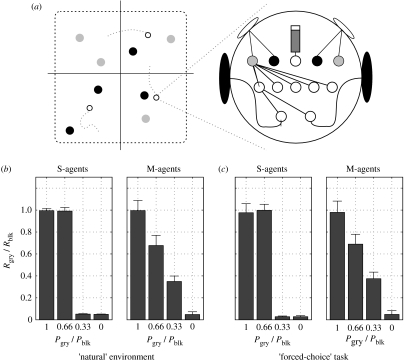
To test this hypothesis, we extended the oABM model described in §3 (Seth 1999, 2001a) (full implementation details are provided in electronic supplementary material, S2). In the extended model, the environment contains two resource types (grey and black) as well as a variable number of agents (figure 3a). Each agent has a single internal ‘battery’ and each resource type is associated with a probability that consumption fully replenishes the battery (P_gry, P_blk). Each agent is controlled by a simple feedforward neural network (figure 3b) in which four input units respond to the nearest resource of each type (grey and black) and a fifth to the internal battery level, and in which the two outputs control the wheels. A GA was used to evolve parameters of the network controller, including the weights of all the connections and the sensitivity of the sensors to the different resource types, in two different conditions. In the first (condition S), there was only one agent in the environment. In the second (condition M), there were three identical agents (i.e. each genotype in the GA was decoded into three ‘clones’). In each condition, agents were evolved in four different environments reflecting different resource distributions. In each environment, black food always replenished the battery (P_blk=1.0), whereas the value of grey food (P_gry) was chosen from the set {1.0, 0.66, 0.33, 0.0}.

Figure 3.

Probability matching. (a) Schematic of the simulated environment, containing multiple agents (open circles) and two types of food (grey and black circles). The expansion shows the internal architecture of an agent, which consists of a feedforward neural network (for clarity only a subset of connections are shown). Four of the five input sensors respond to the two food types; the fifth sensor input responds to the level of an internal ‘battery’ (middle). The outputs control left and right wheel speeds. (b) Summary of behaviour when agents were tested in the environment in which they were evolved. Each column represents a set of 10 evolutionary runs with the abscissa (x-axis) showing the resource distribution, and the ordinate (y-axis) showing the proportion of responses to grey food. Agents evolved in isolation (S-agents) showed either indifference or exclusive choice (zero–one behaviour), whereas agents evolved in competitive foraging environments (M-agents) showed probability matching. (c) Summary of behaviour when evolved agents were tested in a forced-choice task (see text for details), in which probability matching is suboptimal. As in (b), S-agents showed zero–one behaviour, whereas M-agents showed probability matching.

According to the hypothesis, agents evolved in condition S (S-agents) should treat each resource type in an all-or-none manner (zero–one behaviour; see Stephens & Krebs 1986), whereas agents evolved in condition M (M-agents) should match their responses to each resource type according to the value of each resource. Results were supportive of the hypothesis. Figure 3b shows the proportion of responses to grey food as a function of P_gry:S-agents showed zero–one behaviour and M-agents showed probability matching. This suggests that, in the model, zero–one behaviour reflects optimal foraging for an isolated agent, and that probability matching reflects optimal foraging in the competitive foraging environment.

To mimic laboratory tests of probability matching, evolved agents were also tested in a ‘forced-choice’ task in which they were repeatedly placed equidistant from a single grey food item and a single black food item; both S-agents and M-agents were tested in isolation. Figure 3c shows the same pattern of results as in figure 3b, i.e. zero–one behaviour for S-agents and probability matching for M-agents. Importantly, in this case, probability matching is not optimal for P_gry<1 (optimal behaviour would be always to select black food). This result therefore shows that suboptimal probability matching can arise from adaptation to a competitive foraging environment. We also note that matching in the model is generated by simple sensorimotor interactions during foraging, as opposed to by any dedicated decision-making mechanism.

Further analysis of the model (Seth 2001a) showed that probability matching arose as an adaptation to patterns of resource instability (upon consumption, a food item disappeared and reappeared at a different random location). These patterns were generated by sensorimotor interactions among agents and food items during foraging; moreover, they represented historical constraints in the sense that they reflected dynamical invariants that constrained the future dynamics of the system. Both situated agent–environment interactions and rich historical constraints reflect key features of the oABM modelling approach (see §4).

6. Matching and the ideal free distribution

Recall that Herrnstein's formulation of the matching law predicts that organisms match the frequency of their responses to different stimuli in proportion to the rewards obtained from each stimulus type (Herrnstein 1961). In the model described in §5, Herrnstein's law could only be satisfied in the trivial cases of exclusive choice or equal response to both food types. In order to establish a closer correspondence between Herrnstein's matching law and OFT, this section describes a model that abstracts away from the details of situated perception and action.

Herrnstein's matching law can be written as follows:

$$\text{log}\frac{B_{\text{A}}}{B_{\text{B}}}=\text{log}(b)+s\text{log}\frac{R_{\text{A}}}{R_{\text{B}}},$$ (6.1)

where B_A and B_B are the numbers of responses to options A and B, respectively; R_A and R_B are the resources obtained from options A and B, respectively; and b and s are bias and sensitivity parameters, respectively, that can be tuned to account for different data (Herrnstein 1961; Baum 1974). There is robust experimental evidence that in many situations in which matching and reward maximization are incompatible, humans and other animals will behave according to the matching law (Davison & McCarthy 1988). Herrnstein's preferred explanation of matching, melioration, proposes that the distribution of behaviour shifts towards alternatives that have higher immediate value, regardless of the consequences for overall reinforcement (Herrnstein & Vaughan 1980). However, melioration, which echoes Thorndike's ‘law of effect’ (Thorndike 1911), is a general principle and not a specific mechanistic rule.

The mathematical form of the matching law is strikingly similar to that of a central concept in OFT: the ideal free distribution (IFD). The IFD describes the optimal distribution of foragers (such that no forager can profit by moving elsewhere) in a multi-‘patch’ environment, where each patch may offer different resource levels (Fretwell 1972). For a two patch environment, the IFD is written as follows (Fagen 1987):

$$\text{log}\frac{N_{\text{A}}}{N_{\text{B}}}=\frac{1}{m}\text{log}\frac{F_{\text{A}}}{F_{\text{B}}},$$ (6.2)

where N_A and N_B are the number of foragers on patches A and B, respectively; F_A and F_B are the resource densities on patches A and B, respectively; and m is an interference constant [0–1]. Field data suggest that many foraging populations fit the IFD (Weber 1998); an innovative recent study also found that humans approximated the IFD when foraging in a virtual environment implemented by networked computers in a psychology laboratory (Goldstone & Ashpole 2004).

The concept of the IFD allows the hypothesis of §5 to be restated with greater clarity: foraging behaviour that leads a population of agents to the IFD may lead individual agents to obey the matching law.

More than 20 years ago, Harley showed that a relative pay-off sum (RPS) learning rule, according to which the probability of a response is proportional to its pay-off as a fraction of the total pay-off, leads individual agents to match and leads populations to the IFD (Harley 1981; Houston & Sumida 1987). However, it is not surprising that the RPS rule leads to matching since the rule itself directly reflects the matching law; moreover, as Thuisjman et al. (1995) pointed out, the RPS rule is computationally costly because it requires all response probabilities to be recalculated at every moment in time. Here, we explore the properties of an alternative foraging strategy which we have called ω-sampling (Seth 2002b). Unlike the RPS rule, ω-sampling is a moment-to-moment foraging rule (Charnov 1976; Krebs & Kacelnik 1991) which does not require response probabilities to be continually recalculated. In the context of the matching law, ω-sampling is related to strategies based on momentary maximization which specify selection of the best alternative at any given time (Shimp 1966; Hinson & Staddon 1983). In a two patch environment, an ω-sampler initially selects patch A or patch B at random. At each subsequent time-step, the other patch is sampled with probability p, otherwise the estimate of the current patch is compared with that of the unselected patch, and switching occurs if the former is the lower of the two. The estimate of the current patch (or the sampled patch) is updated at each time-step such that more recent rewards are represented more strongly. A formal description of ω-sampling is given in Appendix A, and full details of the model implementation are given in electronic supplementary material, S3.

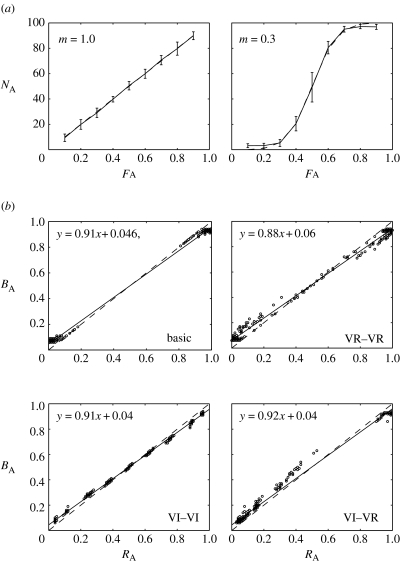
To test the ability of ω-sampling to lead a population of agents to the IFD, we recorded the equilibrium distribution (after 1000 time-steps) of 100 ω-samplers in a two-patch environment in which each patch provided a reward to each agent, at each time-step, as a function of conspecific density, interference (m in equation (6.2)) and a patch-specific resource density. Figure 4a shows equilibrium distributions under various resource density distributions and with two different levels of interference (m=1.0, m=0.3). The equilibrium distributions closely match the IFD, indicating that ω-sampling supports optimal foraging in the model.

Figure 4.

(a) Equilibrium population distributions of 100 ω-sampling agents with high interference (m=1) and low interference (m=0.3) in a two-patch environment (patches A and B). F_A shows the proportion of resources in patch A and N_A shows the percentage of the population on patch A. The distribution predicted by the ideal free distribution (IFD) is indicated by the dashed line. (b) Matching performance in four conditions: basic (reward is directly proportional to response); concurrent variable ratio (VR–VR); concurrent variable interval (VI–VI); and mixed variable interval and variable ratio (VI–VR) (see text for details). R_A shows the reward obtained from patch A and B_A shows proportion of time spent on patch A. Matching to obtained resources is shown by the dashed diagonal line. Equations give lines of best fit.

Figure 4b shows the foraging behaviour of individual (isolated) ω-sampling agents under four different reinforcement schedules which reflect those used in experimental studies of matching. In the basic schedule, reward rate is directly proportional to response rate. Empirical data indicate that animals respond exclusively to the most profitable option under this schedule (Davison & McCarthy 1988), which maximizes reward and which also trivially satisfies the matching law. In line with this data, ω-sampling agents also show exclusive choice.

In the VR–VR (concurrent variable ratio) schedule, each patch must receive a (variable) number of responses before a reward is given. Under this schedule, reward maximization is again achieved by exclusive choice of the most profitable option. Empirical evidence is more equivocal in this case. As noted in the previous section, although probability matching appears to be a robust phenomenon, many examples of maximization have been observed (Davison & McCarthy 1988; Herrnstein 1997). The behaviour of ω-sampling agents reflects this evidence, showing a preponderance of exclusive choice with occasional deviations.

In the VI–VI (concurrent variable interval) schedule, which is widely used in matching experiments, a (variable) time delay for each patch must elapse between consecutive rewards. Under this schedule, reward probabilities are non-stationary, reward rate can be largely independent of response rate and exclusive choice is not optimal. Importantly, matching behaviour can be achieved with a variety of response distributions, including (but not limited to) exclusive choice. The behaviour of ω-samplers is again in line with empirical data in showing matching to obtained reward, in this case without exclusive choice.

The final schedule, VI–VR, is a mixed schedule in which one patch is rewarded according to a variable interval schedule and the other according to a variable ratio schedule. Unlike the previous schedules, matching to obtained reward under VI–VR is not optimal. Nevertheless, both empirical data (Davison & McCarthy 1988; Herrnstein 1997) and the behaviour of ω-sampling agents (figure 4b) accord with the matching law.

Together, the above results show that a foraging strategy (ω-sampling) that leads foragers to the optimal (equilibrium) distribution in a competitive foraging environment (the IFD) also leads individual foragers to obey Herrnstein's matching law. Importantly, ω-samplers obey the matching law even when it is suboptimal to do so. We note that Thuisjman et al. (1995) had made similar claims for a related moment-to-moment strategy (ϵ-sampling), in which foragers retained only a single estimate of environmental quality, as opposed to the multiple estimates required by ω-sampling. Both ϵ- and ω-sampling are related to momentary maximization inasmuch as both specify choosing the best alternative at any given time. However, a detailed comparison of the two strategies revealed that ϵ-sampling failed under certain conditions both in leading populations to the IFD and in ensuring matching behaviour by individual foragers. In particular, ϵ-sampling agents failed to match to obtained reward under the critical VI–VI and VI–VR schedules (Seth 2002b). Interestingly, VI–VI and VI–VR schedules involve a non-stationary component (the VI schedule) that may be a common feature of ecological situations in which resources are depleted by foraging and replenished by abstinence.

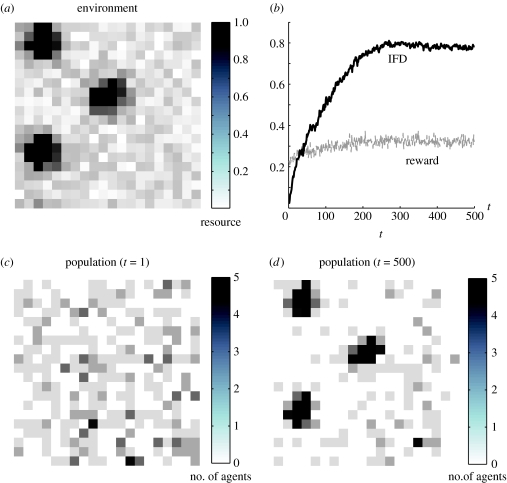
A final analysis shows that the optimal foraging ability of ω-sampling generalizes beyond the two-patch case. Figure 5 shows the distribution of 300 ω-sampling agents in an environment consisting of 400 patches in which resources were distributed so as to create three resource density peaks (figure 5a). Agents maintained estimates of the five most recently visited patches, and were able to move, at each time-step, to any patch within a radius of three patches. Figure 5b–d shows that the distribution of agents, after 500 time-steps, closely mirrored the resource distribution, indicating optimal foraging.

Figure 5.

Foraging behaviour of 300 ω-sampling agents in an environment with 400 patches (interference m=0.5). (a) Distribution of resources, normalized to maximum across all patches. (b) Match between resource distribution and forager distribution (solid line, IFD) and mean reward (grey dashed line, intake) as a function of time. (c) Initial population distribution. (d) Population distribution after 500 time-steps; the population distribution mirrors the resource distribution.

7. Discussion

If ‘all behaviour is choice’ (Herrnstein 1970), then an adequate understanding of action selection will require a broad integration of many disciplines including ecology, psychology and neuroscience. Ecology provides naturalistic behavioural data as well as a normative perspective; neuroscience and psychology provide controlled experimental conditions, as well as insight into internal mechanisms. Successful modelling of action selection will therefore require a computational lingua franca to mediate among these disciplines. In this article, we have shown how the modelling techniques of AL can help provide such a lingua franca. We identified a subset of AL models that help bridge the methods of (normative) OFT and (descriptive) ABMs. These oABMs involve explicitly instantiated agents and structured environments (possibly incorporating situated perception and action), as well as a normative component provided by GAs. We described a series of oABMs showing that (i) successful action selection can arise from the joint activity of parallel, loosely coupled sensorimotor processes and (ii) an instance of apparently suboptimal action selection (matching) can be accounted for by adaptation to a competitive foraging environment.

Ecology has been distinguished by a long tradition of ABM (Huston et al. 1988; DeAngelis & Gross 1992; Judson 1994; Grimm 1999; Grimm & Railsback 2005), and recent attention has been given to theoretical analysis and unifying frameworks for such models (Grimm et al. 2005; Pascual 2005). Within AL, recent attention has been given to methodological practice and interaction with empirical data (Wheeler et al. 2002; Bryson et al. 2007). As a result, there are now many exciting opportunities for productive interactions between AL and ecological modelling. We end with some future challenges in the domain of action selection:

1. What features of functional neuroanatomy support optimal action selection? A useful approach would be to incorporate into oABMs more detailed internal mechanisms based, for example, on models of the basal ganglia (Gurney et al. 2001; Houk et al. 2007).

2. How do historical/stigmergic constraints affect optimal action selection? Incorporation of situated perception and action into oABMs provides a rich medium for the exploration of historical constraints in a variety of action selection situations.

3. How can reinforcement learning be combined with optimality modelling in accounting for both rational, and apparently irrational action selection? This challenge leads into the territory of behavioural economics (Kahneman & Tversky 2000) and neuroeconomics (Glimcher & Rustichini 2004).

4. What role do attentional mechanisms play in action selection? oABMs phrased at the level of situated perception and action allow analysis of the influence of perceptual selective mechanisms on behaviour coordination.

Appendix A. ω-sampling

Let γ ϵ [0,1] (adaptation rate), and ϵ ϵ [0,1] (sampling rate). Let M(t) ϵ {A,B} represent the patch selected, let N(t) ϵ {A,B} represent the unselected patch, and let r(t) be the reward obtained, at time t ϵ {1,2,3,…,T}. Let E_A(t) and E_B(t) represent the estimated values of patches A,B at time t. Define E_A(1)=E_B(1)=0.

For t≥1, if M(t)=A:

$$E_A(t+1)=\gamma E_A(t)+(1-\gamma )r(t),E_B(t+1)=E_B(t),$$

otherwise (if M(t)=B):

$$E_A(t+1)=E_A(t),E_B(t+1)=\gamma E_B(t)+(1-\gamma )r(t).$$

Let Χ ϵ [0,1] be a random number. Let A_ϵ,B_ϵ denote the behaviour of choosing patch (A,B) with probability (1−ϵ). The ω-sampling strategy is then defined by playing:

At t=1 use A_0.5

At t=2 use M(1)_ϵ

At t>2,

if Χ<ϵ or E_M(t−1)<E_N(t−1) choose patch N(t−1),

otherwise choose patch M(t−1).

This strategy has two free parameters: γ and ϵ. In Seth (2002b) a GA was used to specify values for these parameters for each experimental condition separately. Following evolution, mean parameter values were γ=0.427, ϵ=0.052. We note in passing that the use of a GA for parameter setting retains in a limited fashion the normative element of the oABM approach.

Supplementary Material

The Ecology of Action Selection: Insights from Artificial Life

S1: supplementary information regarding the action selection model described in Section 3 of the main text. S2: supplementary information regarding the probability matching model described in Section 5 of the main text. S3: supplementary information regarding the model described in Section 6 of the main text