SCUMBLE: a method for systematic and accurate detection of codon usage bias by maximum likelihood estimation

Abstract

The genetic code is degenerate—most amino acids can be encoded by from two to as many as six different codons. The synonymous codons are not used with equal frequency: not only are some codons favored over others, but also their usage can vary significantly from species to species and between different genes in the same organism. Known causes of codon bias include differences in mutation rates as well as selection pressure related to the expression level of a gene, but the standard analysis methods can account for only a fraction of the observed codon usage variation. We here introduce an explicit model of codon usage bias, inspired by statistical physics. Combining this model with a maximum likelihood approach, we are able to clearly identify different sources of bias in various genomes. We have applied the algorithm to Saccharomyces cerevisiae as well as 325 prokaryote genomes, and in most cases our model explains essentially all observed variance.

The degeneracy of the genetic code affords organisms a wide range of options on how to encode their proteins. Actual codon usage is often far from neutral, and not only are there large variations between species, but also genes within the same organism can exhibit very different patterns of codon usage. In fast-growing organisms, highly expressed genes tend to show a clear preference for a small set of codons, which often correspond to the codons for which the concentration of tRNAs is the highest, or that match their tRNAs well, allowing efficient translation of those codons (1–4). Many genomes also show substantial variation in the nucleotide composition of genes: the GC content can vary considerably (5,6), and in prokaryotes there is often a clear GT versus AC asymmetry between the leading (continuously replicated) strand and the lagging strand (7–9). These variations are particularly evident from the average nucleotide content at the third codon position, which is relatively free of constraints from coding for specific amino acids (5).

A number of indices have been introduced that seek to relate the expression level of a gene to its codon usage (2,3,10,11). The Codon Adaptation Index (CAI) is widely considered the most successful of these (12)—indeed, it has often been used as a substitute for expression data (13–15). However, as CAI is based on the codon usage within a selected set of highly expressed genes, it must be defined separately for each organism, and it only accounts for codon bias directly related to the expression level of a gene.

With the availability of complete genome sequences, a number of unsupervised methods have been presented, which aim to discover patterns in the codon usage within a genome de novo. Most of these algorithms are based on principal component analysis (PCA) or correspondence analysis (CA)—correspondence analysis on relative synonymous codon usage (CA/RSCU) is widely used—and share many of the same limitations (16): they generally do not take into account the length of each gene and most also ignore the number of times each amino acid appears in a gene. Thus, statistically uncertain values are given the same weight as more reliable values, which both limits the accuracy and can give rise to artifacts.

A recent paper (17) introduced an explicit model of codon usage by assigning genes to clusters with different codon usage probabilities. While this approach allows for use of stringent statistical methods, such discrete clustering cannot account for general codon usage biases that affect different genes at different levels, and that may combine in many different ways.

We here introduce a new algorithm for analysis of codon usage that we believe avoids these weaknesses. The algorithm is based on an explicit probabilistic model of codon usage for a genome—or other set of genes—similar to that in ref. (17), but allows for a continuous parameterization of expected codon usage in a low number of dimensions. The dimensions that best explain the observed codon usage of the gene set are determined by maximum likelihood estimation (MLE). While this approach is similar in principle to PCA, our probabilistic model captures expected nonlinearities between expression levels and codon usage, and the use of MLE provides good statistical performance and reduces the risk of artifacts. The algorithm performs well when applied to the yeast genome and to a large number of prokaryote genomes: for every genome, a model with only a few independent biases can explain most of the observed variation in codon usage.

The method of within-block correspondence analysis (WCA) (18,19), although not widely used to analyze codon usage, does appear to overcome many of the problems associated with the common approaches. However, WCA is at some risk for artifacts itself, and it suffers from nonlinearities in the presence of strong biases (see Supplementary Material; below). For ease of comparison, we have included both WCA and CA/RSCU (somewhat different from the version in CodonW; see Supplementary Material) in the implementation of our algorithm, which is available at (NAR website URL).

METHODS AND ALGORITHMS

Probabilistic model of codon usage

We assume that within gene g, each codon is selected independently and randomly from the codons encoding the amino acid a at the corresponding position, with probability P(c|a, g) of selecting codon c. As each codon has nonzero probability only for the correct amino acid, we can specify the model more compactly by p_c(g) = P[c|a(c), g], where a(c) is the amino acid encoded by c.

In analogy with the canonical ensemble of statistical physics, we can express this probability as

1

where E(c, g) is the effective advantage of using codon c in gene g. To model multiple sources of codon usage bias in an organism, or ‘trends’, we further parameterize E(c, g) as

2

The different ‘preference’ functions E_i specify how trend number i favors or disfavors each codon, where E₀ corresponds to the overall codon bias in the whole genome. The ‘offset’ β_i represents to what extent each gene is affected by trend number i. The number of terms in the equation is given by the number of different biases we wish to model. (In the analogy with statistical physics, the Es and βs correspond to energies and inverse temperatures, respectively.)

This parameterization is very natural in the context of codon usage bias: if the only source of bias is selection on the cost of translating all the proteins in the organism, then this exponential form follows directly from the fixation probability given by basic evolutionary theory (20)—Equation (2) would contain a single trend, with E₁ proportional to the cost of translating each codon and β₁(g) proportional to the expression level of gene g. The exponential form also allows us to accurately parameterize varying mutation pressure that acts on individual nucleotides (see Supplementary Material).

The additive form of Equation (2) corresponds to independent biases: a given term will change the relative frequency of two synonymous codons by a fixed factor, independent of any other terms. While our assumptions may not hold exactly in real organisms, they are likely to be good first approximations.

To estimate the parameters of the model—the off sets β_i and the preference functions E_i—we use a customized maximum likelihood approach, SCUMBLE (pseudo-acronym for synonymous codon usage bias maximum likelihood estimation), which is described below. The preference functions are normalized such that the magnitude of an offset corresponds directly to the strength of the bias, and can be compared between different models/species.

MLE of model parameters

According to our model, the probability of using a specific codon is P(c|a, g). Since the amino acid sequence is determined by the real codon sequence, the likelihood of an actual codon is simply P(c|a(c), g) = p_c(g), and the likelihood of a gene is

3

where n_c(g) is the number of times codon c is used in the gene. Similarly, the likelihood for the entire genome—or a given set of genes we wish to consider—is

4

P is here an implicit function of all the parameters of our model—the offsets β_i (g) and the preferences E_i(c). We now apply the principle of MLE (21): we take as our estimate for the βs and Es the values that maximize the total likelihood P. To avoid the risk that the MLE will attempt to tune a probability exactly to zero, we introduce a small additional cost for large offset values: 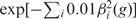. This improves algorithm convergence without affecting results significantly.

There are many different values of the βs and Es that yield the same codon likelihoods p_c(g), and thus the same total likelihood. For instance, setting 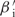(g) = kβ_i(g) for all g and 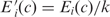for all c leaves all p_c(g) unchanged, for any nonzero value of k. To limit this degeneracy, we require that the E_i are centered:

5

normalized:

6

with the average taken over all codons that have synonymous codons; and orthogonal to each other:

7

Even with these contraints, there are many ways to decompose a given preference function E(c, g) into the different terms of Equation (2)—any rotation between two terms will leave the full preference function unchanged. To specify a unique solution, we use an iterative approach: we first find the best model with a single trend—in this case, there are no other terms to rotate with; thus, the solution is unique up to the overall signs of β₁ and E₁. To find the model with n + 1 terms, we first perform the MLE optimization while keeping the first n preference functions E₁–E_n constant, ensuring a unique solution for E_{n+ 1} (up to the overall sign). We then find the full MLE optimum closest to this constrained optimum.

This approach is very good at assigning different biases to different trends, if the biases have significantly different strength: the strongest bias is assigned to the first trend, then the next strongest is assigned to the next trend, etc. The approach can work well even when there are several biases of similar strength, as the nonlinear properties of the probability function disfavor mixing of biases, unless there are strong correlations.

An alternative approach would be to resolve the degeneracy post factum: once a model with the desired number of trends has been found, one could rotate between the different terms to improve the model. A problem here is to define what constitutes a good versus a bad model—one option is to consider the statistics of the offsets, which should ideally match the statistics of the biases [e.g. selection on codon usage for improved translation is thought to be unidirectional (22)]. However, the statistics of the biases are not well known and are likely different for different types of biases.

When using MLE, one has to be careful not to over-fit the data. Each preference function contains 61 parameters—the number of nonstop codons—and is limited by 20+1 constraints, for a total of 40 free parameters. For a model with T trends, there are T βs per gene, for a total of TN free parameters, where N is the number of genes in the genome.

The data set consists of the codon counts for each gene, i.e. 61 values with 20 constraints (amino acid counts) per gene, for a total of 41N independent data points. As long as the number of data points is much larger than the number of parameters, the risk of overfitting is small. As there are many hundred or thousand genes in most organisms, we can ignore the number of parameters in the preference functions. Thus, overfitting should not be a major problem as long as T is much less than 41.

We use T = 10 as a practical maximum number of terms—this is far more than the number of independent biases we expect to find in any single genome, and it approaches the limit of what is computationally convenient. For genomes with very strong biases, the effective number of independent data points can be far smaller than 41N, and for such genomes we may have to limit the number of trends well below 10.

Model validation and testing

Since we assumed that all codons in a gene are selected independently, we can check the validity of the resulting model through various statistical tests. One particular simple measure of model quality is the normalized variance—the square deviation from the expected codon number, divided by the expected variance:

8

where n_a(g) is the count of amino acid a in gene g. For a true model—with correct preferences E_i and offsets β_i—the normalized variance should average 1 per codon, i.e. 61 total for every gene (when the numerator and denominator are both zero for a codon, we count that as 1). As we fit the model parameters for maximum likelihood, the average variance should be somewhat lower, depending on the number of trends. The normalized variance corrects for the different lengths and amino acid ratios in different genes, thus we can simply compare the distribution of NV (g) for the real genome to the distribution of NV (g) for a genome randomly generated from our model, where we re-estimate the offsets (but not the preference functions) for the randomized genome before we calculate the normalized variance. The excess variance—the difference between the average or median normalized variance of the real genome and the randomized genome—indicates how much variance is not explained by the model, and the reduction in this value upon adding a trend shows how much variance is explained by the new trend.

Another way of evaluating the results is to compare the estimated offsets and preference functions to expected types of bias. For instance, the ‘ideal’ preference function corresponding to GC bias is simply

9

centered and normalized:

10

11

The squared Pearson correlation between E_GC and an estimated preference function 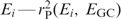—is then a good measure of to what extent the corresponding offset β_i corresponds to GC bias. As each preference function is required to be orthogonal to previous preference functions, except for the constant offset E₀, the cumulative correlation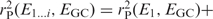 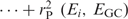is also of interest, as is represents the total fraction of the GC preference signal captured by the first i trends.

For expression-related bias, we can similarly use correlation of an offset with experimentally measured expression levels, or more qualitative measures such as to what extent genes expected to be highly expressed (e.g. ribosomal genes) have offsets distinct from those of the bulk of genes.

Data sets

Data files were downloaded from the GenBank database in GenBank flat file format. The prokaryote genomes analyzed are listed in the Supplementary tables. Only chromosomal genes were used—as plasmids can be inherited independently of the chromosomes, they could potentially exhibit very different codon usage.

We ignore all ORFs that are incomplete, code for less than 100 amino acids, do not have correct start/stop codons (for the specified translation table), contain multiple stop codons, are annotated as having translational exceptions, are annotated as pseudogenes or have excessive repeated nucleotide sequence segments. We also ignore ORFs that contain very few of the 61 possible amino acid-encoding codons—specifically, genes for which the number of different codons minus the number of different amino acids is less than 10—as these would likely suffer from (potentially very severe) overfitting.

We use the Saccharomyces cerevisiae expression data collected by Lu et al. (23), which includes protein expression measurements by western blotting (24), flow cytometry of GFP-tagged fusion proteins (25) and 2D gels (26), and mRNA measurements by single channel DNA microarrays (27), SAGE (28) and microarrays using genomic DNA as reference (29). The 2D-gel data set contains very few data points, and thus correlations with this set have very large error bars.

RESULTS

As detailed in Methods and Algorithms section, our algorithm SCUMBLE finds a codon usage model in which each gene is assigned a given number of ‘offsets’ β_i(g) that indicate to what extent gene g is affected by estimated bias (‘trend’) number i. Each trend is described by a ‘preference function’ E_i(c) that indicates how much trend i favors/disfavors codon c.

Codon usage of budding yeast

We first applied our Algorithm to the genome of the budding yeast S. cerevisiae. The synonymous codon usage of this genome has been extensively studied (3,10–12,14,30). The main bias present in the yeast genome is strongly correlated with expression level (3,10), while a secondary axis identified by CA/RSCU is correlated with GC content (30).

To reduce noise from pseudogenes, we initially used only the named genes in the GenBank data file, but using all the genes gives very similar results. Elimination of genes that were too short or had other problems left 4351 acceptable genes. For this dataset, we used SCUMBLE to find models with from 0 to 10 trends.

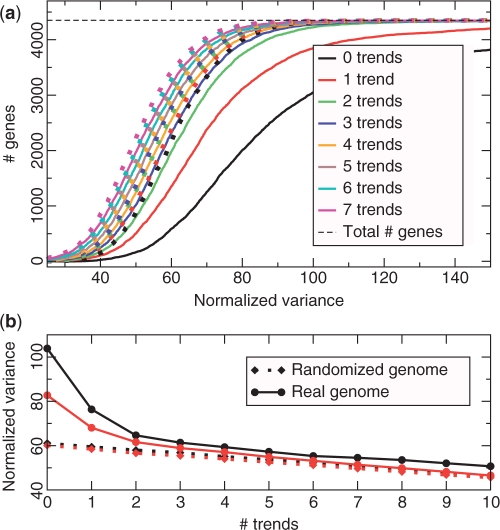
The genes' normalized variance, NV(g), is a good measure of how well a model explains the genome (see Methods and Algorithms section). The cumulative histograms of NV (Figure 1a) indicate that at least two trends are required to explain the data, whereas using more than three trends seems to give little or no improvement. While the first trend only explains about 26.5% of the total variation in codon usage, it explains >60% of the excess variation, compared to the randomized genome (Figure 1b). Together, the two first trends explain an impressive 84% of excess variation.

Figure 1.

(a) Cumulative histogram of the normalized variance for named genes in S. cerevisiae for models with various numbers of trends; actual genome (solid lines) compared to randomized genome (dotted lines). Models with 0 or 1 trend explain the data poorly, as the curve for the real genome is very different from that of a randomized genome, and there are many genes with very high normalized variance. (b) Average (black) and median (red) normalized variance for models with up to 10 trends.

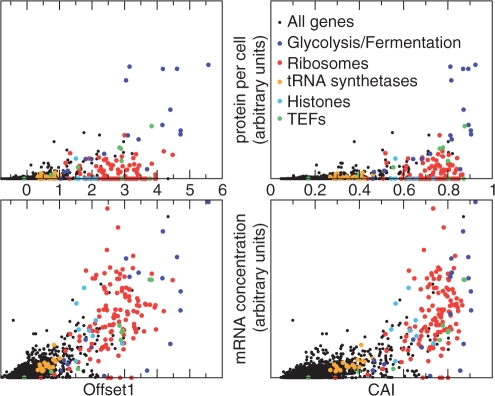
Not surprisingly, the first offset β₁ is strongly correlated with measured expression levels of genes (Figure 2). As there is an abundance of data available for S. cerevisiae, we compared β₁, as well as CAI and the first axes of WCA and CA/RSCU (WCA₁ and RSCU₁), to a number of experimental measurements of cellular mRNA and protein levels (see Methods and Algorithms section). β₁ has significantly higher Pearson correlations with the experimental data than CAI for essentially all the data sets, and even more so compared to WCA₁ or RSCU₁ (Supplementary Figure S1). Notably, β₁ seems to be roughly linearly related to mRNA concentration, whereas there is not a good linear relation between mRNA concentration and the other three descriptors, which tend to saturate for highly expressed genes (Figure 2 and Supplementary Figure S2).

Figure 2.

Experimental values for cellular mRNA/protein levels plotted against the first offset/CAI value of each gene for S. cerevisiae. Several groups of highly expressed genes are plotted in different colors.

To test whether the improved performance is entirely due to correction of nonlinearities, we compared the Spearman rank correlations. Also here, β₁ does have the highest average correlation with experimental data (Supplementary Figure S3), although the differences are much smaller. Figure 2 shows results for the model with four trends, which is the model for which correlations with experiments are maximal, but the models with 1–5 trends all give very similar results. For models with six or more trends, however, β₁ is significantly less correlated with experiments, which is likely a sign of overfitting.

The second trend corresponds to GC content of the codons, as do WCA₂ and RSCU₂. While β₂ correlates well with the fraction of GC in the third codon position within genes—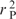 (β₂, GC3) = 0.716—the correspondence is even more clear from the preference function E₂: the correlation between E₂ and the ideal preference function corresponding to GC content, E_GC (see Methods and Algorithms section), is 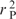(E₂, E_GC) = 0.895. This is even more impressive considering that E₂ is required to be orthogonal to E₁: the cumulative correlation for E₁ and E₂ is 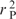(E_1…2, E_GC) = 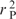(E₁, E_GC)+ 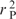(E₂, E_GC) = 0.947. The relatively low correlation between β₂ and GC3 (lower than for WCA₂ and RSCU₂) is due to the nonlinearities in our model and the strong expression-related bias. Removing the 500 genes with the highest values of β₁, the correlation for the remaining genes is 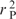(β₂, GC3) = 0.960, which is slightly higher than the correponding correlation for WCA₂ and substantially higher than the correlation for RSCU₂.

The third trend has a significant signal corresponding to the GT content of the codons [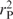 (E₃, E_GT) = 0.552, with cumulative correlation 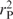(E_1…3, E_GT) = 0.605], and the fourth trend has an even higher signal for CT content of the codons [ 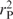(E₄, E_CT) = 0.726, with 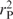(E_1…4, CT) = 0.896].

To check how robust these results are, we applied SCUMBLE to the genes on each individual chromosome and compared the preference functions for the various four-trend models (Supplementary Figure S4). E₀ and E₁ are essentially identical for all the chromosomes, and E₂ only shows minor variations. E₃ and E₄, however, are highly variable—for almost every chromosome there are significant cumulative correlations with E_GT and E_CT, but the exact match between a specific trend and a given nucleotide bias is not well conserved. Most of these differences are probably due to noise.

To determine whether our models can explain not only the variation within a genome, but also the overall codon bias of the yeast genome, we set E₀ to zero for each model and—keeping all the other preference functions the same as before—re-estimate the offsets. Again, the model with two trends explains > 80% of the excess variance (Supplementary Figure S5)—indeed, 62% of the signal in the original E₀ is along E₁ (see E₀ and E₁ in Supplementary Figure S4), with an additional 25% along E₂. Correspondingly, the new offsets 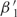and 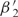differ from the old by almost constant values: 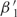(g) ≈ 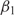(g) + 0.452 and 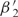(g) ≈ 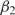(g) − 0.288. As a consequence, 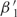is positive for essentially all genes—despite significant statistical noise for short genes—suggesting that all genes experience considerable selection for efficient translation, even if their expression level is low. Although this bias is not always statistically significant for individual genes, the combined statistics of all the genes indicate a bias of β₁ ≈ 0.2 for weakly expressed genes (Supplementary Figure S6). The preferred codons, given by E₁, agree with the known ‘optimal codons’ (4).

Codon usage of prokaryotes

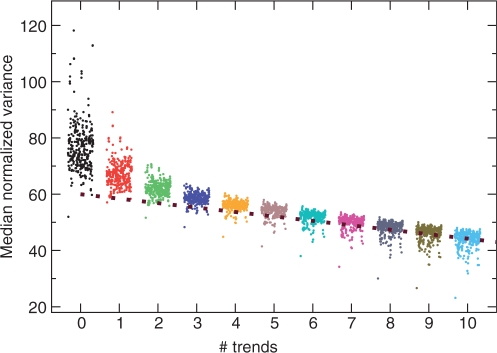
To test how general the results for budding yeast are, we applied SCUMBLE to 325 prokaryote genomes—these include many closely related strains and species, so results should be interpreted with care. For each genome, we found models with from 0 to 10 trends. The normalized variances for these models (Figure 3) indicate that for every prokaryote genome, a model with four trends is sufficient to explain most of the variance in codon usage—the median (average) normalized variance is on average 25% (50%) higher than expected for a genome with no internal biases, and the models with four trends explain >80% of this excess variance. For more than four trends, the variance decreases only slowly with the number of trends. While the variances of most genomes decrease with the same slope, both the observed and expected variance decrease faster for genomes with extremely biased nucleotide content; most of all for Anaeromyxobacter dehalogenans, which has ∼97% G or C at codon position 3.

Figure 3.

Median normalized variance for 325 prokaryote genomes, using models with 0–10 trends. The different genomes are slightly offset along the abscissa, in alphabetical order. The dotted brown line shows approximate median normalized variance for randomized genomes generated from the models (Supplementary Figure S7). Results for the average normalized variance are very similar, except that in rare but not exceptional cases, individual genes dominate the average due to extremely low estimated probabilities of using a specific codon which is, in fact, used.

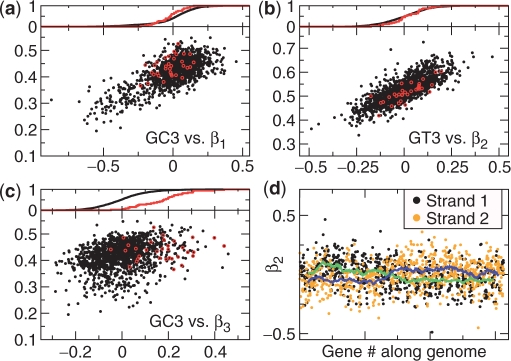
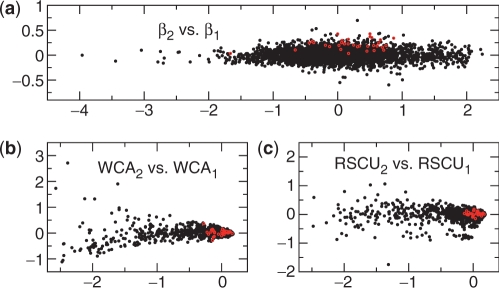
The algorithm's; ability to detect weak biases is well illustrated by the genome of Helicobacter pylori, which has been claimed to contain no codon bias for highly expressed genes (31). SCUMBLE identifies three clear biases (Figure 4). The first two trends correspond to GC content and GT content, respectively. Notably, ribosomal genes have average offsets for both of these trends. For the third trend, however, ribosomal genes are clearly biased towards high offsets, and we identify this trend as a bias related to the expression level of the genes. This bias is not limited to ribosomal genes: of 57 nonribosomal genes from the most abundant proteins in soluble and/or structure-bound fractions (32), 22 of the β₃s are in the top 10%, and only seven are below the median. While the bias is clear, it is indeed quite weak: the average value of β₃ for the ribosomal genes is 0.2, about a 12th of the strength of the expression-level bias in S. cerevisiae. The largest relative preferences are for AUC versus AUA, AUU versus AUA, UUC versus UUU, CCG versus CCC, CUC versus UUA and GGU versus GGG, with magnitudes of about 4 (Supplementary Table S3). For β₃ ≈ 0.2, this corresponds to a change in relative frequency of e^0.24 ≈ 2. Most of these preferred codons are relatively rare even in highly expressed genes, and we cannot say for sure that these are translationally optimal codons—the bias could also be (partially) due to increased mutation rates during transcription.

Figure 4.

A four-trend model of Helicobacter pylori. (a)–(c) GC3 or GT3 plotted against the first three offsets. Genes for ribosomal proteins are circled in red. The cumulative distributionsof the offsets are shown above each graph, for all genes (black) and for ribosomal genes (red). (d) β₂ plotted against the number of the gene along the genome, with genes on different strands in different colors. The green and blue lines are 50-point running averages for strand 1 and 2, respectively.

While CA/RSCU fails to detect the ribosomal codon usage bias in H. pylori, WCA gives very similar results to SCUMBLE (data not shown). However, WCA does not perform as well in the presence of strong nucleotide biases. Figure 5 shows the results from SCUMBLE, WCA and CA/RSCU for the genome of A. dehalogenans. All three methods yield a strong correlation between the first axis and the GC content of the genes, but while β₂ shows a clear bias for ribosomal genes—all 33 ribosomal genes are in the top 35%, which has a P-value of <10⁻¹⁴—WCA₂ and RSCU₂ show no such bias: RSCU₂ depends almost entirely on the codon usage for cysteine, while WCA₂ seems unrelated to any of our indicators. None of the method show any bias for ribosomal genes along the first axis.

Figure 5.

Scatter plot of the first two axes from the four-trend model found by SCUMBLE (a), WCA (b) and CA/RSCU (c) for the genes of Anaeromyxobacter dehalogenans. Genes for ribosomal proteins are circled in red. In (b) and (c), most genes are clustered near the origin; only a small fraction of the genes have significantly negative abscissae.

For both WCA and CA/RSCU, there is a clear correlation between the GC content of the gene (i.e. the first axis) and the magnitude of WCA₂ or RSCU₂. In correspondence analysis, variances are scaled according to the expected variance given by the average codon usage of all genes. In the presence of strong nucleotide bias, the actual nucleotide content of a gene can differ substantially from this average, and this scaling of the variance is then not appropriate. This problem does not occur for SCUMBLE (see Supplementary Material).

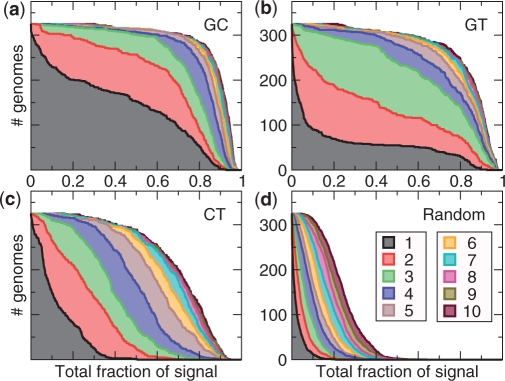
Almost all the 325 prokaryote genomes studied show clear evidence of variable GC bias (Figure 6a): For >90% of the genomes, the first three trends capture more than half the GC preference signal, and for almost half the genomes, the very first trend captures more than half the GC preference signal. GT bias is almost as prevalent as GC bias (Figure 6b), but does not dominate the first trend nearly as often, suggesting that it is usually the weaker bias—indeed, GT bias is found most often at the third trend, while expression bias is more common at the second trend (Supplementary Tables S1 and S2). These signals for GC and GT bias tend to be significantly higher for SCUMBLE than for WCA and CA/RSCU (see Supplementary Figure S8).

Figure 6.

Solid lines: number of prokaryote genomes (out of 325) for which the total fraction of the GC (a), GT (b), CT (c) or random (d) preference signal captured by the first n trends exceeds the abscissa, where n is given by the color. Total shaded area of each color is proportional to the average fraction of signal captured by the corresponding trend.

For both GC and GT bias, the graph for the first trend shows bimodality—both ends have steeper slope than the center—indicating that the algorithm usually separates the biases fairly well. There does not seem to be a strong CT bias in many prokaryote genomes, however (Figure 6c): although there is clearly more signal than expected by random (Figure 6d), it is rarely if ever the dominant signal amongst the first few trends. In most cases, where there is a strong signal for CT bias, this is highly correlated with expression bias, but not always: for Methanopyrus kandleri, each trend in the four-trend model corresponds well to a separate bias—β₁ is GC bias, β₂ is CT bias, β₃ is expression bias and β₄ is GT bias.

DISCUSSION

The standard methods used to analyze the codon usage of genomes are typically only able to account for a small fraction of the total variation (31,33). With our probabilistic model of codon usage, we are able to accurately ascribe a large part of the variation to expected random fluctuations, and we can capture most of the remaining (excess) variation with only a few ‘trends’.

For S. cerevisiae, well above half the excess variation is captured by a single offset β₁, which—due to its high correlation with expression data—we identify as the strength of selection for translational efficiency/accuracy. According to basic evolutionary theory, selection on the overall rate of protein synthesis would cause a selective pressure on codon usage proportional to the expression level of a gene (20). In our model, offsets corresponding to selective pressures are direct estimates of the strengths of these pressures, and we indeed find that β₁ is roughly linearly related to the expression level, unlike WCA₁ and RSCU₁. Given experimental uncertainties of the expression-level measurements, statistical uncertainties of the offsets (see Supplementary Material), and the caveat that expression levels measured in standard experiments may differ from the typical (in nature) levels that affect the codon usage (12), the correspondence is quite good. However, though the relationship is close to linear, it is not proportional: even genes with very low expression level show a substantial bias in codon usage along this trend. This suggests that either this selection can—somehow—be fairly effective even for very weakly expressed genes or there are several causes of this bias, at least one of which does not depend strongly on the expression level.

Our approach to separating the codon usage variation into distinct sources of bias appears to work well for real genomes. SCUMBLE successfully separates different known sources of codon bias for many of the genomes we have analyzed. Additionally, for S. cerevisiae the correlation between β₁ and mRNA expression level—which is higher than the correlation between CAI and expression level even for the model with only one trend—keeps improving as we add up to three additional trends, each of which corresponds to a different mutational bias. Such improvement is all the more remarkable as the third and fourth trends correspond to very weak biases in yeast. This suggests that our model's; nonlinear relationship between codon frequencies and bias strengths is substantially correct, and that different biases affect codon usage fairly independently.

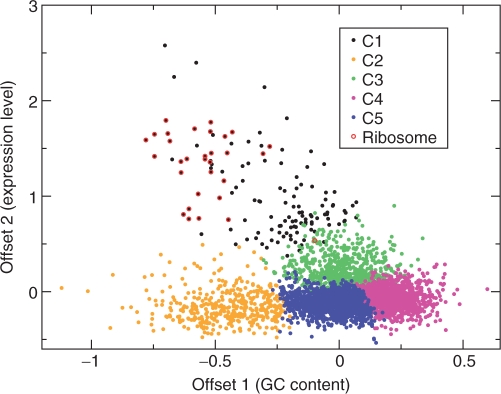
A key feature of our model is that different genes are affected by the same biases but with different strengths. This seems to explain most genomes far better than assigning genes to clusters with different codon usage, as was done in ref. (17): Figure 7 shows a scatter plot of the first two offsets for Bacillus subtilis, color coded according to the cluster identity given in (17). The five clusters correspond almost exactly to compact regions of the two offsets, and we can immediately give the clusters appropriate annotations: Clusters 4, 5 and 2 contain genes with low expression level and respectively high, intermediate and low GC levels, while clusters 3 and 1 contain genes with moderate and high expression levels. There are, however, organisms for which discrete clusters provide a very good description: Codon usage in Borrelia burgdorferi appears to depend only on whether a gene is on the leading or lagging strand during replication, and can thus be described by two clusters (see Supplementary Material).

Figure 7.

Scatter plot of the first two offsets for the four-trend model of B. subtilis, with the genes' colors given by their cluster identity given in ref. (17).

Yeast seems to have a much cleaner GC bias than most prokaryotes: only one of the 325 prokaryote models has a higher combined correlation for the first three preference functions than yeast has for the first two. This is reasonable in light of the different sources of GC bias in prokaryotes and eucaryotes: in prokaryotes, variation of GC content within a genome is related to import of genes from organisms with different natural GC content (34,35). However, the codon usage of such imported genes may also differ from that of the new host organism in other ways, which would be reflected in the preference function estimated for this bias. For yeast, the main source of GC variation is thought to be regional variation in mutation patterns, possibly related to recombination or timing of replication (6,33). Since this is a purely mutational, strand symmetric effect, it is indeed likely to be a pure GC bias. This would also explain why, while models with around four trends tend to explain the vast majority of codon usage variation, there are very few prokaryotes for which the models explain all the variance: import of genes from different species will likely introduce small levels of many different biases that can not all be captured by a simple model. The few prokaryotes for which the models can explain all the codon usage variation are mostly prokaryotes with no significant GC bias, such as B. burgdorferi.

For both Burkholderia mallei and Pseudomonas aeruginosa, genes with relatively low GC content have been claimed to have inhomogeneous codon usage, as they are widely scattered along the second axis of CA/RSCU (15,36). However, as for A. dehalogenans, this appears to be an artifact of the scaling used in CA/RSCU (and in WCA); the results from SCUMBLE do not indicate increased inhomogeneity in this group of genes (Supplementary Material; data not shown).

We found that SCUMBLE performs better than WCA or CA/RSCU in detecting GC or GT biases in prokaryote genomes. SCUMBLE is also able to detect far more biases in prokaryote genomes than a variety of other approaches using PCA (37) (Supplementary Tables S1 and S2). Unlike PCA, SCUMBLE shows a clear signature for the strength of the different biases: GC bias is most often the dominant bias, followed by expression bias and GT bias.

Our model only captures the average codon usage for each gene. While there exist highly localized codon biases, such as for codons used for translational regulation (38), codon bias has also in several cases been shown to increase along the length of the genes (39,40). One possible explanation for this is the effect of codon choice on the rate of nonsense errors (premature termination of translation), as recently modeled in ref. (41). Incorporating such position dependence into SCUMBLE could further improve its ability to accurately detect codon bias.

While we were able to identify codon biases that have been missed by other approaches in those organisms, we did not find any clear cases of codon bias of new or unknown origin: essentially, all codon usage variance could be traced to either selection based on expression level, different mutational patterns, import of genes from other species or statistical fluctuations. It remains to be seen whether any yet unknown biases are present in multicellular organisms.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.