Hospital Quality: A PRIDIT Approach

Abstract

Background

Access to high quality medical care is an important determinant of health outcomes, but the quality of care is difficult to determine.

Objective

To apply the PRIDIT methodology to determine an aggregate relative measure of hospital quality using individual process measures.

Design

Retrospective analysis of Medicare hospital data using the PRIDIT methodology.

Subjects

Four-thousand-two-hundred-seventeen acute care and critical access hospitals that report data to CMS' Hospital Compare database.

Measures

Twenty quality measures reported in four categories: heart attack care, heart failure care, pneumonia care, and surgical infection prevention and five structural measures of hospital type.

Results

Relative hospital quality is tightly distributed, with outliers of both very high and very low quality. The best indicators of hospital quality are patients given assessment of left ventricular function for heart failure and patients given β-blocker at arrival and patients given β-blocker at discharge for heart attack. Additionally, teaching status is an important indicator of higher quality of care.

Conclusions

PRIDIT allows us to rank hospitals with respect to quality of care using process measures and demographic attributes of the hospitals. This method is an alternative to the use of clinical outcome measures in measuring hospital quality. Hospital quality measures should take into account the differential value of different quality indicators, including hospital “demographic” variables.

Measuring and improving hospital quality is an important challenge in any attempt to improve the health care system. It is important because inpatient hospitals provide so much medical care (approximately $500 billion in 2003) (Hippisley-Cox et al. 2006). It is a challenge because medical care does not directly map into health outcomes (Arrow 1963) and because medical care is a credence good (Darby and Karni 1973).1 Therefore, in measuring hospital quality, there are two choices for researchers: measuring inputs to care (process measures) or measuring outputs from care (patient outcomes). Standard examples of inputs include proportion of patients having a blood culture performed before first antibiotic received and proportion of patients who get the most appropriate antibiotic. Widely used output measures include 30-day adjusted mortality and percent of patients readmitted within 1 month after discharge.

The main advantage of outcomes variables is that they directly measure improvements in health. The variable 30-day adjusted mortality, for example, is one that both providers and patients would like to be as low as possible. In addition, they are easy to communicate, both within the health services community and to wider audiences. In the words of Richard Posner, these measures have a low “absorption cost” (Posner 2007).

The imperfect correlation between individual outcome measures and overall health or quality is the biggest disadvantage of outcome variables. Mortality as an outcome measure is subject to a congruence problem, because mortality is a single binary variable that does not fully account for health. One other disadvantage of outcome measures is that they are subject to unconscious manipulation. With the opportunity, indeed the necessity, of eliminating subjects who “did not fit the study specifications,” researchers can unintentionally distort their results in favor of their hypothesis.

The main advantages of process measures are that they are easy to measure and collect. Process measures come from data collected in the course of care, which practitioners record in charts and billing systems. There is therefore a great deal of scope to aggregate process information to use in quality assessment, but little scope for any individual to change or exclude data.

Process measures are even more subject to congruence problems than outcome measures. Additionally, they are difficult to aggregate into single measures of quality. They are also subject to the same sample selection problems as outcome measures, inasmuch as hospitals must still choose to opt in to this data reporting process.

In this study, we will demonstrate that this aggregation process is a feasible solution to the problem of discerning hospital quality, and we will argue that this aggregation, while purely based on circumstantial evidence, is a valid and useful method. Chiefly, it combines low absorption cost, ability to handle high dimension data and absence of extratheoretical assumptions about the connection between process improvements and outcomes in the model.

LITERATURE REVIEW

Prior literature has dealt with the congruity problem in assessing quality of care with standard latent variables techniques on outcomes. A latent variable technique is one in which the dependent variable is assumed to give information about the underlying variable of interest (Greene 2003). An example of work in this area is Sharon-Lise Normand's study using the likelihood of 2-year mortality as the outcome measure and a logit regression (Normand et al. 1995). The advantage of this approach is that she was able to model mortality as well as validate her mortality model with a second sample of individuals. More recently, Landrum, Normand, and Rosenheck compared the use of a Bayesian approach (posterior tail probabilities) to hierarchical modeling (which is a generalized version of logit and similar models). Here, the outcomes data were a report card on the care of patients in VA Medical Centers, which focuses on such outcomes measures as readmission within 180 days and days to first readmission. The research aggregated outcomes measures in a generalized linear model and a Bayesian fashion, finding that there is “… little variation in care at the network level, a goal for the VA” while readmission within 180 days, number of readmissions, number of bed days, and days to first readmission are “… equally correlated with the latent inpatient factor” (Landrum, Normand, and Rosenheck 2003).

There are also studies in the literature that aggregate multiple outcome measures, such as Scanlon et al. (2005) and Dimick, Staiger, and Birkmeyer (2006). Scanlon et al. developed a method for aggregating the performance of HMOs using quality indicators from the HEDIS and CAHPS® databases, which they “… (condensed) into a smaller subset of latent health plan quality domains.” They utilized a Multiple Indicator Multiple Cause model under the assumption that “… each HEDIS and CAHPS measure provides some element of ‘signal’ about an HMO's overall quality …” (Scanlon et al. 2005) assuming, for instance, that level of adolescent immunization and health plan satisfaction convey a positive signal about HMO quality. In contrast, the novel feature of our model is that we do not apply any such assumptions in our aggregation, i.e. we do not assume a priori that an increase in patients given assessment of left ventricular function is necessarily an indicator of a higher quality hospital.

Dimick, Staiger, and Birkmeyer (2006) used a two-level hierarchical model to recover “… the (true) underlying correlations between procedure-specific mortality rates and mortality rates with other procedures, net of the estimation error” from mortality, which is a noisy signal of quality. They concluded that: “Hospitals with low mortality rates for one operation tend to have lower mortality rates for other operations. These relationships suggest that different operations share important structures and processes of care related to performance. Future efforts aimed at predicting procedure-specific performance should consider incorporating data from other operations at that hospital” (Dimick, Staiger, and Birkmeyer 2006). Again, our contribution is that, rather than using mortality, we use only the underlying evidence on process measures to recover quality, a method that is an alternative to using mortality as a measure of quality.

Prior studies that utilize process measures are generally descriptive in nature and focus on practice guidelines. Two examples of this literature are Allison et al. (2000) and Nieuwlaat et al. (2006) Allison et al. addressed the question of quality of care in teaching versus nonteaching hospitals using four process measures, provision of acute reperfusion therapy on admission, administration of aspirin during hospitalization, administration of ACE inhibitors at discharge, and administration of β-blockers at discharge, as well as a measure of mortality. The process measures were utilized separately, so that the result was that: “… admission to a teaching hospital was associated with better quality of care based on three of four quality indicators and lower mortality,” rather than an overall assessment of whether teaching hospitals offer superior quality of care. In their study, it is also the case that “… mortality differences were attenuated by adjustment for patient characteristics and were almost eliminated by additional adjustment for receipt of therapy” (Allison et al. 2000). Nieuwlaat et al. (2006) addressed a different question: what accounts for the differential utilization of a specific intervention (in this case, reperfusion therapy)? Here, the measure was the use of the process itself, and the study used demographics and clinical characteristics of the patient on admission to predict whether a patient received the intervention. They found that hospital-specific factors determined who received the intervention, noting that arrival in a hospital with PCI facilities and participation in a clinical trial were strong predictors of the receipt of reperfusion therapy (Nieuwlaat et al. 2006). While Nieuwlaat et al. predicted whether an individual received the intervention, their study could not infer whether receipt of the intervention indicates higher hospital quality.

One recent study by Werner and Bradlow (2006) uses the Hospital Compare database that we use, but also in order to explain hospital mortality. Using the first 10 measures developed (because they were, and are, the most widely publicized), they found that there is a small, but significant, difference in mortality between the hospitals at the 25th and 75th percentiles of performance (Werner and Bradlow 2006).

METHODS

Objectives

This study's objective is to use the Hospital Compare data to construct a rank ordered measure of hospital quality and best indicators of hospital quality. We also briefly discuss applications of the study design to similar problems.

Design

In this study, we use PRIDIT, an unsupervised, nonparametric aggregation technique. PRIDIT is a nonparametric model in that we do not make any assumptions about the data generating process for the process measures and hospital demographic measures we utilize. This is important because it is not prone to the bias under misspecification problems that affect models such as logit (Goldberger 1991). PRIDIT differs from Bayesian approaches in that PRIDIT is an “unsupervised” method (Brockett et al. 2002). We posit that adherence to practice guidelines in any process measure or hospital demographic variable correlates with quality, but not that it correlates positively. This allows us to test the hypothesis that a quality measure could actually be associated with poorer quality. For example, if we measure hospital emergency rooms by their maximum weight time, a hospital with a superior triage system might also have higher maximum wait times if they are adept at prioritizing cases. In this case, the correlation between maximum waiting time and quality of care might be negative. Therefore, the ability to analyze quality without making assumptions about the direction of the correlation between different measures and quality is an important innovation of this study.

PRIDIT analysis consists of two steps. First, we computed a Ridit score for each hospital, based on the quality indicators and other measures available using the method originally described by Bross (1958). Ridit scoring is a methodology originally developed to deal with difficult to observe dependent variables, such as whether an individual lives in an urban or rural area, and is especially useful when many of the underlying indicator variables which proxy for the dependent variable of interest are binary or, more generally, categorical. This has been the use of Ridit in the medical literature (Donaldson 1998). Using the Ridit score combined with principal component analysis (PCA), we determined a relative quality measure for all hospitals in the study and a relative measure of which quality measures were the best indicators of hospital quality.2 This method of combining PCA with the Ridit score provides the optimal weights for using the proxy variables to determine the dependent variable of interest, which in this case is hospital quality (Brockett et al. 2002). While combining PCA and Ridit in this way to get the PRIDIT score is novel in health outcomes research, similar uses of PCA are not (van der Gaag and Wolfe 1991).

Our use of the Ridit scoring measure is equivalent to treating process measures as ordinal data. If we have two hospitals, where the first reports 83 percent of patients given assessment of left ventricular function and 92 percent of patients given β blocker at arrival, while the second hospital reports 81 and 80 percent, respectively, we say only that the first hospital does better on both measures and do not consider the scale of the difference. By treating the data in this way, we can get an aggregation of the process data that is the most efficient possible. To get the Ridit score, we use the empirical distribution of the ordinal variables to score the hospitals, taking one less the sum of the empirical CDF of hospital performance on any measure and the CDF of the hospital that is ranked one level below (which we denote B_ij=−F_j⁻(i)−(1−F_j(i)) in the Supplementary Material Appendix A, Implementing PRIDIT by Example).

The assumption that allows us to link the PRIDIT scores with quality is that the strongest correlation between the process measures and hospital characteristics is quality of care. In the PCA technique, we describe the space spanned by the variables by 28 orthogonal eigenvectors. The eigenvector with the largest eigenvalue captures more of the variance in the data than any other eigenvector. In other words, the first principle component of the Ridit scores is the “… best linear description of the (data) in the least squares sense” (Theil 1971), just as in linear regression models where the OLS calculation gives us the best linear unbiased estimate of the model. However, we still need to assume that the first principal component is quality rather than some other explanation for the correlation between the various process measures. Mechanisms that could cause between hospital variations on these process measures include number of nurses per 100 beds, IT spending, and so on. We argue that our assumption is valid because of the number of quality measures we use and the number of clinical areas they span.

Data Sources and Variables

Hospital Compare contains 20 quality measures in four categories: heart attack, heart failure, pneumonia, and surgical infection prevention. We list the measures in Table 1, along with their average value (among those hospitals that publicized the measure) and the percent of hospitals that publicized each measure. Here, the percent of hospitals that reported a measure includes hospitals where there were too few patients to justify reporting a statistic, whereas the number of hospitals that publicized a measure refers to reported nonnull values. Hospitals could report a null value for any process measure if “the number of cases is too small (n<25) for purposes of reliably predicting hospital's performance” or “no data are available from the hospital for this measure.” Therefore, when the GAO noted that 98 percent of hospitals submitted data, they were referring to hospitals that participated in the program, not the completeness of the data. The GAO also noted that the completeness of the data could not be verified because Medicare “… has no ongoing process to assess whether hospitals are submitting complete data” (U.S. Government Accountability Office 2006). The major sample selection issue in this data is not which hospitals chose to participate in the program, but whether conditional on participation the data is incomplete in a way that would bias our estimates. If hospital data were all incomplete in the same way or relatively small, it would not bias our estimates because PRIDIT is a relative measure. In order to deal with the possibility of incomplete data, we rely on the fact that the process measures come from charts and billing systems and that, because there is no penalty for low scores, reporting accurate information to CMS is the cheapest option for most hospitals.

Table 1.

Quality Measures in the Hospital Compare Database

Condition	Measure Name	Average (%)	Percent Publicizing (%)
Heart attack	Patients given ACE inhibitor or ARB for left ventricular systolic dysfunction	80	73
Heart attack	Patients given aspirin at arrival	92	87
Heart attack	Patients given aspirin at discharge	89	85
Heart attack	Patients given β-blocker at arrival	85	87
Heart attack	Patients given β-blocker at discharge	87	85
Heart attack	Patients given PCI within 120 minutes of arrival	64	30
Heart attack	Patients given smoking cessation advice/counseling	79	65
Heart attack	Patients given thrombolytic medication within 30 minutes of arrival	30	41
Heart failure	Patients given ACE inhibitor or ARB for left ventricular systolic dysfunction	80	89
Heart failure	Patients given assessment of left ventricular function	80	93
Heart failure	Patients given discharge instructions	52	83
Heart failure	Patients given smoking cessation advice/counseling	74	81
Pneumonia	Patients assessed and given pneumococcal vaccination	56	94
Pneumonia	Patients given initial antibiotic(s) within 4 hours after arrival	77	93
Pneumonia	Patients given oxygenation assessment	99	94
Pneumonia	Patients given smoking cessation advice/counseling	71	83
Pneumonia	Patients given the most appropriate initial antibiotic(s)	78	84
Pneumonia	Patients having a blood culture performed before first antibiotic received in hospital	82	84
Surgical infection prevention	Surgery patients who received preventative antibiotic(s) 1 hour before incision	74	35
Surgical infection prevention	Surgery patients whose preventative antibiotic(s) are stopped within 24 hours after surgery	67	35

An explanation of why CMS selected each measure is available at the Hospital Compare website, http://www.hospitalcompare.hhs.gov. Most of the hospitals that reported data were short-term acute care hospitals, which were then eligible for an incentive payment under the Medicare Modernization Act (MMA). Some critical access hospitals also voluntarily provided data, but were not eligible for MMA payments (Centers for Medicare and Medicaid Services 2006). One aspect of this paper that is different from other analyses is that we used all 20 measures when assessing quality, rather than the 10 originally chosen by MMA. The reason for this is that, despite the fact that fewer hospitals have enough cases to publicize these measures (see Table 1), they increase the discriminatory power of our analysis as measured by the eigenvalue (see Table 2).

Table 2.

Quality Measures and Their PRIDIT Scores

		All Measures			Clinical Measures Only
Condition (1)	Measure Name (2)	Weight (3)	Overall Rank (4)	Importance (5)	Weight (6)	Overall Rank (7)	Importance (8)
Heart attack	Patients given ACE inhibitor or ARB for left ventricular systolic dysfunction	0.34389	16	3	0.38841	13	2
Heart attack	Patients given aspirin at arrival	0.51536	7	2	0.50854	8	1
Heart attack	Patients given aspirin at discharge	0.49976	9	2	0.50363	9	1
Heart attack	Patients given β-blocker at arrival	0.61635	2	1	0.59191	5	1
Heart attack	Patients given β-blocker at discharge	0.58934	3	1	0.59681	4	1
Heart attack	Patients given PCI within 120 minutes of arrival	0.20749	21	4	0.24098	18	3
Heart attack	Patients given smoking cessation advice/counseling	0.45865	11	2	0.49491	11	1
Heart attack	Patients given thrombolytic medication within 30 minutes of arrival	0.06700	28	5	0.08356	20	4
Heart failure	Patients given ACE inhibitor or ARB for left ventricular systolic dysfunction	0.47582	10	2	0.50278	10	1
Heart failure	Patients given assessment of left ventricular function	0.69731	1	1	0.61127	1	1
Heart failure	Patients given discharge instructions	0.58516	4	1	0.61052	2	1
Heart failure	Patients given smoking cessation advice/counseling	0.57617	5	1	0.60126	3	1
Pneumonia	Patients assessed and given pneumococcal vaccination	0.50422	8	2	0.57515	7	1
Pneumonia	Patients given initial antibiotic(s) within 4 hours after arrival	0.16592	24	5	0.29766	17	3
Pneumonia	Patients given oxygenation assessment	0.30895	17	4	0.32813	16	3
Pneumonia	Patients given smoking cessation advice/counseling	0.55314	6	2	0.58126	6	1
Pneumonia	Patients given the most appropriate initial antibiotic(s)	0.38001	12	3	0.38990	12	2
Pneumonia	Patients having a blood culture performed before first antibiotic received in hospital	0.28540	18	4	0.32975	15	3
Surgical infection prevention	Surgery patients who received preventative antibiotic(s) 1 hour before incision	0.34605	15	3	0.34571	14	3
Surgical infection prevention	Surgery patients whose preventative antibiotic(s) are stopped within 24 hours after surgery	0.12399	26	5	0.15318	19	4
Hospital type	Acute care hospital	0.18521	22	5	N/A	N/A	N/A
Hospital ownership	Government hospital	0.17517	23	5	N/A	N/A	N/A
Hospital ownership	Private hospital	0.14241	25	5	N/A	N/A	N/A
	Accredited hospital	0.25435	19	4	N/A	N/A	N/A
	Emergency service available	0.07273	27	5	N/A	N/A	N/A
Academic hospital type	Major teaching	0.24341	20	4	N/A	N/A	N/A
Academic hospital type	Significant teaching	0.34942	14	3	N/A	N/A	N/A
Academic hospital type	Any teaching	0.36509	13	3	N/A	N/A	N/A
Eigenvalues	–	4.51983	–	–	4.30900	–	–

While it is not a perfect correspondence, the most important variables have two characteristics: they are widely publicized and they are less than perfectly adhered to on average. While these process measures may lead to some inappropriate interventions on the margin, all 20 are associated with good clinical practice (Centers for Medicare and Medicaid Services 2006), so the high levels of variation in many of these process measures is informative. In the case of binary variables, it is clearly true that they must be associated with quality (either positively or negatively) because, for example, not-for-profit ownership of a hospital must either be associated with higher or lower hospital quality.

One other critical assumption made with respect to the hospital quality measures deals with how to treat unpublicized quality measures. For example, 203 hospitals in the data set do not publicize data for any of the 20 quality measures. The method we chose to deal with this missing data is to include all quality scores available when calculating the weights for the underlying quality measures. The rationale is that even if hospital A only publicizes patients given aspirin at arrival and reports a null value for all other measures, then setting its result in that one measure against all other hospitals in that measures tells us something about how patients given aspirin at arrival is associated with hospital quality. In particular, it is more informative than excluding hospital A's publication of patients given aspirin at arrival simply because hospital A did not publicize the other measures. The method for coding unpublicized variables is equivalent to assuming that the hospital's performance is precisely average on that measure. Clearly, this assumption is open to question, as it is possible that unpublicized data are associated with lower (or higher) quality.

In addition to the 20 quality measures in the data, there are five structural measures that proxy for hospital quality. The CMS data include whether the hospital is a short-term acute care hospital, the type of organization that owns the hospital, whether the hospital is accredited and whether the hospital provides emergency services. We would generally expect accredited hospitals to be of higher quality than unaccredited hospitals. We might also conjecture that short-term acute care hospitals are of higher quality than critical access hospitals and that those hospitals that provide emergency services are of higher quality than those that do not. There is the continuing debate as to whether government hospitals are better than nongovernment hospitals, whether for-profit hospitals are better and whether teaching hospitals provide better care. In order to answer the latter question, we obtained data on the amount of teaching done by hospitals from the American Hospital Directory (AHD.com 2006).

STATISTICAL ANALYSES3

The statistical analysis in this study is a PRIDIT analysis of the available quality measures. First, we use the Ridit scoring methodology to transform categorical variables, specifically percent given the correct treatment, into scores on the interval [−1,1]. We transform the binary variables for structural characteristics in the same way. We use two different binary measures: whether a hospital was government owned and whether a for-profit entity ran the hospital, to span the three ownership types (nongovernment not-for-profit is the excluded type). Three other binary variables indicate the amount of teaching that a hospital does. All major teaching hospitals (defined by membership in COTH) are coded as being a “major,”“significant,” and “any teaching” hospital. All significant teaching hospitals (defined by membership in ACGME) are coded as being a “significant” and “any teaching” hospital. Finally, hospitals that did any amount of teaching were coded as being “any teaching” hospitals. This has the effect of making the PRIDIT weights cumulative (a major teaching hospital is scored based on being a “major,”“significant,” and “any teaching” hospital).

RESULTS4

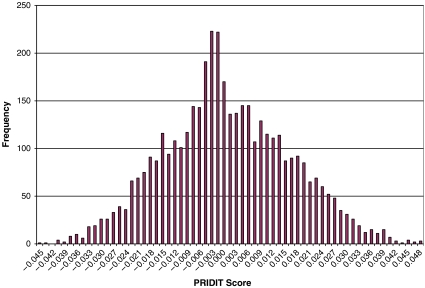
The PRIDIT analysis of hospital quality scores shows that most hospitals are of similar quality and that some of the quality measures are excellent indicators of hospital quality. Looking at Figure 1, we can see that the distribution of hospitals is centered on zero and that the number of hospitals with positive and negative scores (corresponding to better to worse hospitals) is about equal. Additionally, the tails of the distribution are very small, with a kurtosis of −0.23.5 The interpretation of this result is that there are very few hospitals of extreme positive or negative quality. This is broadly consistent, though not directly comparable, with the results of Landrum, Normand, and Rosenheck (2003) and Werner and Bradlow (2006). Using PRIDIT, there is no reason a priori to expect hospitals to be centered on zero6 and tightly distributed rather than, say, positively skewed (as it would be if most hospitals were of high quality and a few were of relatively poor quality). Prior studies using PRIDIT to investigate fraud in individuals found just such a result: most individuals were honest but a few were very likely committing fraud (Brockett et al. 2002). The distribution of hospital scores therefore suggests that most people who have access to a hospital are getting a common quality of treatment.

Figure 1.

Histogram of Hospital PRIDIT Scores Tables

There is, however, a distinction between normal practice and best practice as shown by a small number of the quality measures. We report the weights associated with each measure, as well as their rank in absolute importance (we show ranks on an individual basis and a “binned” basis) in columns (3), (4), and (5) of Table 2. The top six measures are those with weights above 0.575. The PRIDIT weights are multiplicative (Brockett et al. 2002), so that the best measure (patients given assessment of left ventricular function) is twice as good as the 16th best measure (patients given ACE inhibitor or ARB for left ventricular systolic dysfunction) as a quality indicator. This is the most important function for the weights in the PRIDIT analysis: they point to areas where improvement in Hospital Care measures will lead to the greatest improvement in hospital quality, a critical piece of knowledge in a resource-constrained world. The concept of “best practice” is consistent with the literature on high volume hospitals (HVHs) that indicates that these facilities are both much less prevalent than non-HVHs, especially low volume hospitals or LVLs, and that they produce superior outcomes. For instance, Dudley et al. (2002) attributed 602 deaths to the use of LVHs rather than HVHs in California, and showed that LVHs are much more prevalent.

We also find that structural factors, to varying degrees, are important indicators for hospital quality. We find that teaching hospitals are in general of higher quality than nonteaching hospitals, and that the more teaching hospitals do, the higher is their quality, our contribution to the ongoing debate as to whether teaching hospitals' care is of higher quality or whether the effect is monotonic (see, e.g., Papanikolaou, Christidi, and Ioannidis 2006). We also find that privately owned hospitals and government run hospitals are of higher quality. Therefore, the omitted category, not-for-profit hospitals, is associated with lower quality. In contrast, Geweke, Gowrisankaran, and Town (2003) found that “… public hospitals have the lowest quality,” while their finding that “there are no definitive comparisons among ownership categories” is consistent with our finding that ownership type is less important than teaching status and many process measures. In addition, we find that acute care hospitals, accredited hospitals, and those offering emergency services have higher quality, none of which is surprising because achieving any of these characteristics requires significant investment in services.

We also report an alternative specification, where we assess quality using only the clinical measures, in columns (6), (7), and (8). The first numbers to compare are the eigenvalues reported in columns (3) and (6). In PCA, the higher the eigenvalue is, the better the discriminatory power of the measures used, so that when using PRIDIT, a higher eigenvalue corresponds to a higher chance of obtaining the true weights. In this study, using all 28 variables is superior to using the 20 clinical variables alone. The measure with the biggest change, which is a decrease, is patients given initial antibiotic(s) within 4 hours after arrival for pneumonia, which decreases from a weight of 0.298 to a weight of 0.166 and drops in importance from 17th to 24th. The second biggest change is also a decrease for patients given assessment of left ventricular function of 0.086, although that measure continues to be the most important. There must be a correlation between the variation in hospital type, hospital ownership, or academic hospital type and patients given initial antibiotic(s) within 4 hours after arrival and patients given assessment of left ventricular function such that the inclusion of structural characteristics improves our discriminatory power while making these two process measures less important indicators of quality.

COMMENT

The research in this analysis is necessarily imperfect due to the nature of the data used. First, CMS collects and designs all of the quality measures for the Medicare population based on three conditions and surgical practice. While these conditions and surgical practice span a large part of what hospitals do, they are certainly not exhaustive.7 Therefore, conclusions about non-Medicare populations and specialties not covered by the data are less robust than we would like.

One policy implication of this question relates to the prospect for reimbursement based on hospital quality indicators. CMS, or any quality measuring body, would like to use their quality measures to enhance the quality of services provided. One obvious application of this work is for CMS to use the quality weights as a way to reward hospitals differentially for scores on different quality measures. This application, a case of the more general problem of rewarding agents when their performance is difficult to monitor, was an anticipated use of the PRIDIT model (Brockett et al. 2002). Of course, rewarding hospitals in this way has its pitfalls in terms of statistical reliability and true hospital improvement, as the experience of the NHS in England has shown (The Numbers Game 2005). What is clear is that Medicare population individuals who are trying to assess the quality of care in their local hospitals should be looking more closely at higher weighted variables.

CONCLUSION

One important finding of this study is that Medicare quality indicators act as a proxy for hospital quality. This is true even of hospitals that do not publicize quality scores on all measures. This result is important because of the fact that medical care is a good whose quality is generally difficult to assess. Medicare is a monopsonist in the market for medical care for those age 65 and over, as well as for individuals with end stage renal disease. Therefore, it is even more difficult, and thus more important, to develop outside measurements for the quality of services Medicare provides.

The other important finding of this study is that we can aggregate process and structural data in an objective way using PRIDIT. The question of hospitals “gaming” the system, which has been raised with respect to prior studies that used the Hospital Compare data set (Romano 2005), is only problematic if we believe that a substantial number of hospitals are gaming their quality measures in a certain way while others are not. We also get some information about quality from structural measures, where we are sure that misreporting is not a problem. PRIDIT also allows us to combine the positive aspects of process measures (hard to game, easy to measure) and ameliorate the major negative associated with the use of process measures, that they are hard to aggregate. Prior research has applied the PRIDIT methodology to fraud detection and bias detection, but this analysis assesses its usefulness in detecting hospital quality as well. This suggests that we can extend this model to problems such as assessing individual physician quality. This is the type of application that we will explore in future research.

Supplementary material

The following material is available for this article online:

Appendix A

Implementing PRIDIT by Example.

Table S1

Sample Quality Measures and Cumulative Proportions.

Table S2

Ridit Scores and Cumulative Proportions.

Table S3

Principal Component Analysis Calculation Measures—w, Bsq, bsq, b.

Table S4

Principal Component Analysis Calculation Measures—Bnorm.

Table S5

PRIDIT Scores by Quality Measure and in Total.

This material is available as part of the online article from: http://www.blackwell-synergy.com/doi/abs/10.1111/j.1475-6773.2007.00821.x (This link will take you to the article abstract).

Please note: Blackwell Publishing is not responsible for the content or functionality of any supplementary materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.