A physical basis for protein secondary structure

Abstract

A physical theory of protein secondary structure is proposed and tested by performing exceedingly simple Monte Carlo simulations. In essence, secondary structure propensities are predominantly a consequence of two competing local effects, one favoring hydrogen bond formation in helices and turns, the other opposing the attendant reduction in sidechain conformational entropy on helix and turn formation. These sequence specific biases are densely dispersed throughout the unfolded polypeptide chain, where they serve to preorganize the folding process and largely, but imperfectly, anticipate the native secondary structure.

Elements of secondary structure—α-helix, β-sheet, and tight turns—are ubiquitous in proteins (1). What is the physical reason for their pervasive occurrence? Do these patterns arise as a direct consequence of formative interactions within the elements themselves (i.e., locally determined), or are they an indirect consequence of longer range interactions (i.e., globally determined)?

Surprisingly, the field lacks a simple physicochemical theory of secondary structure in peptides and proteins (2, 3). Instead, prediction methods tend to be based on statistical likelihoods (4) or, more recently, on neural nets (5). Alternating patterns of hydrophilic and hydrophobic residues have been noted in amphipathic helices and strands (6, 7), but the interactions they engender are exerted primarily within folded proteins and fail to explain the appearance of corresponding structures in isolated peptides. Statistical mechanical treatments (see, e.g., ref. 8) of secondary structure can be effective (9) but require numerous adjustable, empirical parameters. Surely, the absence of a simple physical theory of secondary structure has contributed to the continuing suspicion that none exists.

Yet, numerous experiments on the kinetics of protein folding show that native-like secondary structure elements form early and rapidly, before substantial tertiary organization. Still, such elements might be statistical accidents that play little or no role in guiding subsequent folding events.

Here, we propose a physical theory for secondary structure based on sterics and local interactions. Our findings demonstrate that local, intrinsic, sequence-dependent biases to be in helix, strand, and turns are densely dispersed throughout the polypeptide chain and are unlikely to be merely accidental (2, 10). At root, these biases are grounded in sterics (11), the most important organizing factor in protein conformation (12). Work in this area began with Sasisekharan (13) and Ramachandran (14), who showed that the conformational space available to amino acids is highly restricted. All residues except glycine and proline are largely constrained to occupy either of two mainchain regions. In one, the polypeptide chain is contracted; in the other, it is extended. Apart from these two, remaining alternatives are disfavored because of steric interference.

In essence, secondary structure bias is largely a consequence of the balance between two opposing local forces that govern the position of equilibrium between these two mainchain states. The competing forces are attractive local interactions vs. sidechain conformational restriction. The former is enthalpic and favorable; the latter is entropic and unfavorable. Contracted conformations are compatible with local hydrogen bonds—both mainchain–mainchain and mainchain–side chain—but the bulky backbone can interfere with sidechain flexibility. Steric interference between mainchain and side chains is relieved in extended conformations, but hydrogen bonds are sacrificed in this state. In some cases, short polar side chains can compensate for loss of conformational freedom by forming hydrogen bonds to the backbone. The equilibrium between these two states—contracted and extended—is sequence-specific because sidechains differ in their steric characteristics and ability to form hydrogen bonds (15–17). Glycine and proline add further complexity to this picture because their backbone geometry differs from that of the other 18 residues, but no additional principles need be invoked.

This physical explanation is applicable to both repetitive and nonrepetitive secondary structure. In repetitive structures—helix and strand—the energetic “tug-of-war” is largely between sidechain conformational entropy and mainchain hydrogen bonding. In nonrepetitive structure—tight turns (18)—the peptide chain is contracted, similar to a single turn of helix, and sidechains may clash with the bulky backbone, but stabilizing sidechain-to-mainchain hydrogen bonds can provide energetic compensation.

Driven primarily by sterics and local hydrogen bonds, these secondary structure biases are expected to emerge in the unfolded state and to preorganize all subsequent folding events. Segments with strong biases are poised to form persisting structure, especially when fortified by additional stabilizing interactions.

We test these ideas by performing short Monte Carlo simulations using linus (19) for a diverse set of experimentally interesting proteins. Computer simulations are an especially effective tool in this regard because, unlike actual experiments, only interactions of interest are included; all others can be eliminated. As described below, we find that sterics and local interactions are sufficient to engender pronounced conformational biases that largely, but imperfectly, anticipate the native secondary structure of the protein.

Methods

Protein conformational space is explored by using a conventional Metropolis Monte Carlo procedure (20). Initially, the starting conformation, C, is set to an extended chain. Progressing from the amino to the carboxy terminus, successive residues, taken three at a time, are perturbed at random, using a predefined move set, to produce a trial conformation, C′. Next, C′ is evaluated: if free of steric clash and if application of the Metropolis criterion leads to acceptance, C is set to C′. Otherwise, C′ is rejected and C is retained. A “cycle” is said to be completed when the chain has been traversed from one end to the other, using this procedure. On completion of every cycle, the structure is saved. All proteins were simulated three times, 1,000 cycles per simulation. Additional details are given below.

Chain Geometry.

Each residue, except glycine, is represented by alanine: specifically, four backbone atoms (N, Cα, C′, O) and the β-carbon (Cβ). Also, each residue, except glycine and alanine, has either one or two side chain pseudoatoms, depending on whether the side chain is β-branched. In particular, valine, threonine, and isoleucine have two additional side chain atoms; others have only one. All relevant geometric parameters for each amino acid are given in Table 5, published as supplemental data on the PNAS web site, www.pnas.org.

Scoring Function.

The scoring function used in the Metropolis criterion consists of four terms, one repulsive and three attractive: steric clashes are penalized and hydrogen bonds, hydrophobic contacts, and salt bridges are all rewarded. To preclude nonlocal effects, attractive forces are limited to nearby chain neighbors. Specifically, the three attractive terms are evaluated only between amino acids separated by no more than five residues in sequence. These four terms are now described explicitly.

Electronic clouds of atoms are not allowed to overlap. Accordingly, all conformations with a steric clash are rejected. Atomic radii are given in the supplemental data.

An H-bond of maximal strength (0.5 units) is assigned to residues i and j when the distance between the amide nitrogen of i and the carbonyl oxygen of j is ≤3.5 Å, and the out-of-plane dihedral O(j) − N(i) − CA(i) − C(i − 1) > 140°. This score scales linearly to 0.0 as the distance between donor and acceptor increases from 3.5 to 5.0 Å. All backbone amide nitrogens (except proline) are considered H-bond donors, and all backbone carbonyl oxygens are considered H-bond acceptors. Additionally, the side chains of Ser, Thr, Asn, Asp, Gln, and Glu are also considered H-bond acceptors, with a maximal score of 1.0 unit. Two additional restrictions also apply: (i) a donor and acceptor must be at least three residues apart in sequence, and (ii) no donor can participate in more than one H-bond.

A hydrophobic contact is assigned between side chain carbon atoms i and j of two residues when

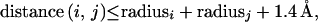where radius_x is the atom’s contact radius. The maximal value is realized when the two atoms are in contact, and it scales linearly to zero as the separation distance increases to 1.4 Å. The maximal value is 0.5 units when both residues are hydrophobic (Cys, Ile, Leu, Met, Phe, Trp, Val), 0.25 units when one residue is hydrophobic and the other is amphipathic (Ala, His, Thr, Tyr), and 0.0 units for all other combinations.

A salt bridge is assigned to contacts between oppositely charged groups (namely, Arg or Lys with Glu or Asp), with a maximal strength of 0.5 units that scales linearly to 0.0 over a separation interval of 1.4 Å.

Move Set.

linus uses a “smart” move set in which three consecutive residues are perturbed simultaneously. Initially, a move consists of choosing one of four equiprobable categories (19) at random: α-helix, β-strand, β-turn, and random coil. Side chain torsion values are chosen at random in the range [0°, 359°]. Both β-turn and random coil moves have multiple subcategories. Four β-turn types are included: types I, I′, II, and II′. A β-turn move defines the conformation of two consecutive residues uniquely, with the third residue set to a randomly chosen value. Specifically, a three residue sequence i-j-k would have either i-j or j-k set to a β-turn conformation, with k or i, respectively, chosen randomly, resulting in eight possibilities.

To extract biases, secondary structure is assigned for all 1,000 saved conformers in a simulation, using the procedure outlined below. This ensemble is evaluated, and for every residue the fraction of conformers in each of the four secondary structures is determined. This fraction is a statistical weight, the probability that the given residue will adopt one of the four secondary structures: helix, strand, turn, or coil. We note in passing that an earlier version of linus enforced biases by “freezing” the chain, an undesirable strategy that abolished reversibility. The current protocol, which uses linus-evolved biases as sample weights, does not suffer from this deficiency.

Helix	j and j + 1 and j + 2 ∈ H	→	j + 1 = helix
Strand	j and j + 1 and j + 2 ∈ S	→	j + 1 = strand
Type I turn	j + 1 ∈ T and j + 2 ∈ T	→	j + 1 = Type I turn (residue i + 1)
	j ∈ T and j + 1 ∈ T	→	j + 1 = Type I turn (residue i + 2)
Type I′ turn	j + 1 ∈ T′ and j + 2 ∈ T′	→	j + 1 = Type I′ turn (residue i + 1)
	j ∈ T′ and j + 1 ∈ T′	→	j + 1 = Type I′ turn (residue i + 2)
Type II turn	j + 1 ∈ U and j + 2 ∈ T′	→	j + 1 = Type II turn (residue i + 1)
	j ∈ U and j + 1 ∈ T′	→	j + 1 = Type II turn (residue i + 2)
Type II′ turn	j + 1 ∈ U′ and j + 2 ∈ T	→	j + 1 = Type II′ turn (residue i + 1)
	j ∈ U′ and j + 1 ∈ T	→	j + 1 = Type II′ turn (residue i + 2)
Coil	None of the above	→	j + 1 = Coil

Secondary Structure Assignment.

Secondary structure is assigned to protein conformation based solely on backbone torsion angles; hydrogen bonding considerations are excluded deliberately. Our assignment criteria are suited to simulations in which only sequentially local interactions between residues are allowed, a restriction that precludes formation of β-sheet or other H-bonded interactions between sequentially distant residues. If an H-bond based method, such as dssp (21), were used to assign secondary structure, then β-strands would evade detection.

Backbone conformation space is partitioned into 36 coarse-grained bins, each represented by a letter code (Table 1). Initially, φ, ψ, and ω values for each residue are computed and mapped into the closest letter code. Conformation codes are then mapped into a secondary structure class. Three codes (M, O, R) belong to two classes; 28 codes belong to no class. Secondary structure classes are S = { A,F,G,L,M,R }; H = { O }; T = { J,O,P }; T′ = { j,o,p }; U = { M,R }; and U′ = { m, r }.

Table 1.

Partition of backbone conformational space into coarse-grained bins

	Secondary structure codes
	−180°	−120°	−60°	0°	60°	120°	180°
180°	A	G	M	S	m	g	a
120°	F	L	R	X	n	h	b
60°	E	K	Q	W	o	i	c
0°	D	J	P	V	p	j	d
−60°	C	I	O	U	q	k	e
−120°	B	H	N	T	r	l	f
−180°	A	G	M	S	m	g	a
	φ

The table partitions φ, ψ space into discrete cells. It should be noted that almost the entire observed population in actual proteins falls within the two cells L and O, corresponding to extended and contracted, respectively. 

Progressing along the sequence, conformation codes for each triple of consecutive residues, 〈 j, j + 1, j + 2 〉, are used to classify the central residue, j + 1, into the first applicable category satisfying one of the following definitions:

Results

The simulation protocol described in Methods has been applied to dozens of proteins, with a similar degree of success in all cases. Twelve molecules were selected for presentation here, based on their perceived interest to the experimental folding community: (i) chymotrypsin inhibitor [3ci2], (ii) intestinal fatty acid binding protein [1ifb], (iii) phage lysozyme [2lzm], (iv) myoglobin [1mbo], (v) myohemerythrin [2hmq], (vi) plastocyanin [6pcy], (vii) protein G [1gb1], (viii) ribonuclease A (7rsa), (ix) ribonuclease S-peptide, (x) ribonuclease H [2rn2], (xi) staphylococcal nuclease [1stg], and (xii) ubiquitin [1ubq]. Protein Data Bank ID codes (22) are given in square brackets. In every case, three sets of simulations were performed, each with uniform sample weights. Little variation was seen in the final sample weights among the three sets. Accordingly, the weights from all three were averaged for presentation (see Fig. 2, published as supplemental data on the PNAS web site, www.pnas.org). In each protein, local biases extracted from simulations suggest the actual secondary structure, though imperfectly.

We seek to compare these simulations to corresponding experimental data. Given the nature of the simulations—local interactions and sterics—perhaps the ideal data for comparison would be the population that emerges in the dead time of most experiments, an elusive quantity. Fragment studies are also revealing, when available. Equilibrium folding studies of partially folded states are useful as well.

Of course, comparison with the native structure is irresistible. Detailed comparisons are given in Table 2. For each secondary structure element in every protein, Table 2 lists the fraction of conformers in helix, strand, turn, and coil. In Table 3, the standard errors for native segments computed from 10 independent simulations are shown for two proteins, myoglobin and GB1. The examples represent worst-case and typical-case linus simulations, respectively; in either case, standard errors are slight.

Table 2.

Population statistics for each secondary structure element

Structure	Residues	H	S	T	C
RNase A
Helix	4–11	58	25	12	6
Helix	25–32	54	23	15	8
*Helix	51–58	23	42	22	13
Strand	39–41	5	74	9	12
Strand	43–47	12	66	13	9
Strand	61–65	26	43	21	11
Strand	72–75	30	37	24	9
Strand	77–87	20	43	25	13
Strand	95–11	17	54	20	10
Strand	114–117	1	87	4	8
Turn	12–12	47	35	12	7
Turn	15–16	44	28	16	13
Turn	23–24	48	26	11	15
Turn	33–33	29	39	15	17
Turn	35–38	18	46	24	13
Turn	59–59	16	60	11	13
Turn	66–67	29	31	23	18
Turn	88–89	13	34	12	41
Hemerythrin
*Helix	19–37	27	44	16	13
Helix	41–64	43	31	12	13
Helix	70–85	54	30	9	7
*Helix	91–103	14	54	22	10
Strand	2–5	0	93	1	6
Strand	9–11	10	71	11	8
Turn	12–14	16	50	24	9
Turn	65–65	72	15	4	9
Turn	68–69	67	8	8	16
Turn	106–111	12	42	26	20
Lysozyme
*Helix	3–10	21	41	26	11
Helix	39–49	65	18	11	6
Helix	60–79	49	24	15	12
*Helix	82–90	15	61	15	10
*Helix	93–105	28	44	18	9
Helix	115–123	51	26	14	9
Helix	126–134	53	26	13	8
*Helix	137–141	21	58	11	10
*Helix	143–154	10	63	17	11
Strand	16–20	24	49	20	8
Strand	24–27	6	58	11	26
Strand	57–59	23	51	7	19
Turn	11–11	17	29	27	26
Turn	21–22	19	30	23	28
Turn	55–56	10	33	12	46
Turn	80–80	28	39	24	9

Structure	Residues	H	S	T	C
Turn	106–106	31	29	26	14
Turn	108–113	13	22	17	48
Turn	155–155	17	36	19	27
Turn	158–163	32	25	30	13
Plastocyanin
Strand	2–5	12	43	19	26
Strand	18–22	2	73	13	13
Strand	25–31	9	70	12	9
Strand	36–42	3	73	14	10
Strand	46–47	3	69	13	15
Strand	56–58	26	44	18	11
*Strand	61–63	38	35	14	13
*Strand	68–74	40	37	14	9
Strand	79–84	7	74	10	9
Strand	93–98	3	55	14	28
Turn	8–9	16	23	24	37
Turn	23–24	5	19	29	47
Turn	43–44	2	62	23	14
Turn	48–49	6	39	16	39
Turn	52–55	21	47	22	10
Turn	59–60	39	21	30	10
Turn	66–67	35	18	17	29
Turn	85–90	16	27	38	19
Staphnase
Helix	55–68	35	33	16	15
Helix	99–106	50	22	17	12
Helix	122–134	74	16	7	4
Strand	8–14	8	73	11	9
Strand	22–27	10	61	20	10
Strand	30–36	5	69	16	10
Strand	39–43	1	80	12	7
Strand	71–77	22	63	10	6
Strand	97–94	24	36	18	23
Strand	109–112	16	48	25	11
Turn	20–21	6	42	12	40
Turn	28–29	4	37	18	41
Turn	37–38	4	68	24	5
Turn	47–48	5	59	23	14
Turn	53–54	7	60	13	21
Turn	84–85	32	25	26	17
Turn	95–96	24	20	15	41
Turn	120–121	59	19	14	7
Turn	135–135	59	30	7	4
Turn	138–140	36	42	13	9
C12
*Helix	32–42	15	00	18	8
Strand	46–52	0	86	7	7

Structure	Residues	H	S	T	C
Strand	55–58	8	71	14	7
Strand	60–62	8	71	12	8
Strand	65–71	18	58	17	8
Strand	78–82	0	45	21	34
Turn	25–29	14	47	18	21
Turn	44–45	1	69	21	9
Turn	53–54	3	53	11	33
Turn	63–64	8	67	12	13
Turn	72–73	20	50	20	10
GB1
Helix	23–36	55	24	13	8
Strand	2–7	4	75	10	11
Strand	12–20	22	43	17	18
Strand	42–45	22	49	14	15
Strand	51–55	4	69	15	12
Turn	10–11	17	34	26	23
Turn	37–37	26	19	16	39
Turn	47–49	22	44	22	12
IFABP
Helix	14–21	69	13	12	6
*Helix	25–32	22	40	20	17
Strand	5–8	6	71	10	13
*Strand	10–12	49	33	10	8
Strand	36–42	15	59	17	9
Strand	46–53	16	55	20	10
Strand	56–63	7	65	17	12
*Strand	66–72	45	23	19	12
Strand	76–84	19	43	13	24
Strand	88–95	32	34	17	17
Strand	100–108	13	58	18	11
Strand	112–119	22	52	17	10
Strand	122–130	30	39	19	13
Turn	33–34	19	46	21	14
Turn	54–55	15	45	26	14
Turn	64–65	9	34	19	39
Turn	86–87	28	24	11	37
Turn	96–98	16	44	13	27
Turn	110–111	17	26	17	40
Turn	120–121	25	24	17	34
Myoglobin
*Helix	5–20	27	43	18	12
*Helix	22–36	12	47	21	20
Helix	52–57	78	12	6	4
Helix	59–77	36	31	17	16
*Helix	92–98	19	53	18	11
*Helix	103–111	17	55	18	9
*Helix	113–119	4	75	11	11

Structure	Residues	H	S	T	C
Helix	127–149	61	19	11	8
*Strand	121–124	31	15	15	39
Turn	38–43	46	32	16	7
Turn	45–49	60	25	7	8
Turn	78–80	40	21	15	24
Turn	99–99	1	92	1	6
Turn	112–112	6	77	10	7
Turn	125–126	58	11	15	15
Rnase H
Helix	44–58	40	31	18	12
*Helix	72–78	31	39	14	16
Helix	101–112	53	22	13	12
Helix	128–142	46	31	14	10
Strand	4–13	3	55	19	23
Strand	17–28	13	28	19	39
Strand	31–39	26	39	15	19
Strand	41–43	21	54	13	12
Strand	61–69	19	60	13	7
Strand	96–98	1	83	6	10
Strand	114–122	19	58	13	10
Turn	29–30	31	26	12	31
Turn	82–90	34	33	18	15
Turn	93–94	13	58	17	12
Turn	99–100	8	74	7	11
Turn	113–113	25	44	13	17
Turn	123–124	12	27	18	43
Turn	149–150	22	17	15	46
Ubiquitin
*Helix	23–32	27	43	20	9
Strand	2–7	12	62	15	11
Strand	11–18	2	80	9	8
Strand	41–45	21	54	17	9
*Strand	48–51	44	26	19	11
Strand	61–62	34	34	24	8
Strand	65–74	18	50	21	11
Turn	8–9	12	33	32	24
Turn	19–20	2	79	8	10
Turn	33–34	15	39	26	20
Turn	38–40	10	61	18	11
Turn	46–47	35	25	15	25
Turn	52–53	27	16	13	44
Turn	56–59	22	46	17	14
Turn	63–64	30	45	18	8

Residue boundaries in each element of secondary structure element and percentage of the ensemble found in helix (H), strand (S), turn (T) and coil (C). 

^*Helix or strand segments in which native bias is not the largest. 

Table 3.

Standard error of the bias toward native secondary structure in 10 independent simulations of myoglobin and GB1

Myoglobin
*Helix	5–20	26.4  ±  1.4
*Helix	22–36	11.5  ±  1.6
Helix	52–57	75.1  ±  4.4
Helix	59–77	35.4  ±  3.9
*Helix	82–98	20.4  ±  1.0
*Helix	103–111	18.8  ±  2.5
*Helix	113–119	5.2  ±  1.1
Helix	127–149	62.9  ±  4.0
*Strand	121–124	29.8  ±  1.6
Turn	38–43	15.3  ±  1.5
Turn	45–49	8.6  ±  1.0
Turn	78–80	14.7  ±  1.4
Turn	99–99	0.7  ±  0.3
Turn	112–112	12.3  ±  2.5
Turn	125–126	13.2  ±  1.9
GB1
Helix	23–36	61.1  ±  4.8
Strand	2–7	73.0  ±  1.8
Strand	12–20	41.4  ±  2.8
Strand	42–45	54.9  ±  4.7
Strand	51–55	67.8  ±  1.2
Turn	10–11	27.8  ±  2.5
Turn	37–37	17.8  ±  3.5
Turn	47–49	25.7  ±  1.8

Percentage of ensemble found in each element of native secondary structure, averaged over 10 independent simulations, together with the standard error. These values differ from corresponding quantities in Table 3, where the weights are averaged over three independent simulations. 

^*Helix or strand segments in which native bias is not the largest. 

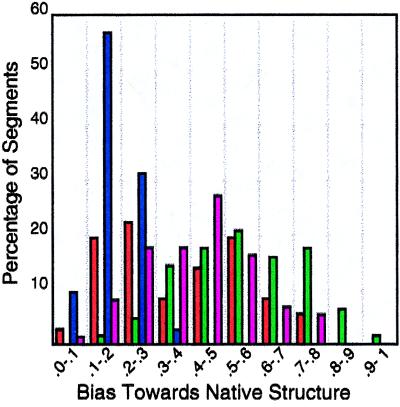
Fig. 1 summarizes these data for the 36 helices, 63 strands, and 74 turns in the total set of proteins. In our simulations, sequences corresponding to actual helices have helical biases that range between 4 and 78%. With one exception, all such sequences populate helical conformers in at least 10% of the ensemble, and half of the sequences populate helical conformers in at least 35% of the ensemble. Sequences corresponding to actual strands have even stronger biases, ranging between 15 and 93%. All but four populate strand conformers in at least one-third of the ensemble. Sequences corresponding to actual turns have turn biases that range between 1 and 38%. Although weaker than both helices and strands, all but eight populate turn conformers in at least 10% of the ensemble.

Figure 1.

Histogram of data from Table 2. The statistical bias toward native secondary structure in helix (red), strand (green), turn (blue), and generalized turn (black) for all segments in Table 2 is parceled into bins, with statistical weights that range from 0.0 to 1.0 in increments of 0.1. The height of each bar corresponds to the percentage of segments in the given bin. For example, 19% of all native helices in the total set of proteins have statistical weights between 0.5 and 0.6 in these simulations, as indicated by the red bar in bin 0.5–0.6. Data for generalized turns are the sum of their turn and helix percentages.

Often, the sum of turn and helix weights is high, indicating a contracted conformation, although not specifically a β-turn or α-helix. In fact, there is only a slight difference in conformation between a turn of helix and a Type I or Type III peptide chain turn. Accordingly, Fig. 1 also plots generalized turns, defined as the sum of contracted conformations (i.e., helix + turn biases). Sequences corresponding to actual turns have generalized turn biases ranging between 2 and 76%; with one exception, all exceed 10%, and all but 12 exceed 25%.

Fig. 1 and Tables 2 and 3 demonstrate that a pronounced bias toward the native conformation is detectable in almost every element of secondary structure, despite the simplicity of these simulations and the absence of all long range attractive interactions. To be sure, the native structure does not necessarily have the highest weights in every case. Segments in which either helix or strand bias toward a non-native conformation exceeds that of the native conformation are annotated with an asterisk in Tables 2 and 3. In this regard, it is important to emphasize that these simulations should not be viewed as a secondary structure prediction algorithm. Rather, they are only intended to test our physical explanation for secondary structure formation based on sterics and short-range attractive interactions, particularly hydrogen-bonding. As seen in Fig. 1, a substantial bias toward the native conformation is present in almost every case. It can happen that segments with locally high helix or strand weights undergo a conformational transition when longer range interactions are included, but this issue is not addressed here.

Chymotrypsin Inhibitor.

Chymotrypsin inhibitor has been studied extensively by Fersht and coworkers (23), who find that the only region with structure before the transition state is near the helix N terminus (namely, residue 16). The simulations reveal such a bias, along with other features of the native protein.

Intestinal Fatty Acid Binding Protein.

Consistent with NMR studies (24), biases for the second helix are weak. However, residues 67–73, a β-strand in the folded protein, have a clear helix/turn bias in the simulations, and, to our knowledge, no other experimental data is available about this site.

T4 Phage Lysozyme.

Using pulsed hydrogen exchange, Lu and Dahlquist (25) find that helices A and E, together with the N-terminal β-sheet, form an early folding intermediate. Although not the most prominent simulated bias, helix E is readily apparent, as is the N-terminal β-sheet. Biases for helix A exhibit considerable turn/helix weights. This N-terminal helix belongs to the C-terminal domain (26), but our simulations are too local to include contributions from such interactions. Both helices D and H have simulated high strand weights; neither appears to be involved in formation of the early intermediate (25).

Myoglobin.

The structure of apomyoglobin has been studied extensively by NMR (27). In equilibrium studies, Wright and coworkers (28) characterized progressively folded states of the molecule. In their hierarchic picture of the folding dynamics, helices A, D, and H are the first to emerge; all have clear helical biases in simulation. In contrast, helical bias is conspicuously absent in the region of the G helix. A peptide fragment corresponding to this region was studied experimentally by Waltho et al., who found “little propensity for helix formation in aqueous solution” (ref. 29, p. 6346).

Myohemerythrin.

This four-helix bundle protein was studied by Dyson et al. (30), who synthesized peptide fragments that cover the molecule and analyzed their conformational preferences by NMR. Fragments corresponding to the native helices exhibit clear preferences for helix-like conformations, which are more pronounced in the A and D helices, and less pronounced in the B and C helices. Simulated biases show the opposite tendency: regions corresponding to the B and C helices have higher helical weights than those corresponding to the A and D helices.

Plastocyanin.

The native structure is a Greek key β-barrel. Barrel staves bracketed by turns are well delineated by the biases, despite a complete absence of interstrand hydrogen bonds, which are precluded by our simulation protocol. The region of non-native turn/helix bias surrounding residue 60 was observed in NMR experiments of Dyson et al. (31), who studied the conformational preferences of peptide fragments that cover the molecule. They noted conspicuous “prepartitioning of the conformational space sampled by the polypeptide backbone” (ref. 31, p. 819) in these isolated peptides.

Protein G B1 Domain.

Fragment studies of Blanco and Serrano (32) confirm a tendency to populate native-like conformations in peptides corresponding to both the initial and final β-hairpins and the central helix. Simulation biases also reflect these tendencies.

Ribonuclease A and S-Peptide.

Ribonuclease S-peptide (33), residues 1–20, is the progenitor of all peptide fragment studies, and the stop signal for the N-terminal helix (residues 3–13) is known to be preserved in the isolated peptide (34). In our simulation, a bias toward helix spans the first two helices but continues through the interconnecting nonhelical region. Puzzled by this result, S-peptide was simulated in isolation; the stop signal is apparent in this case, as shown in Fig. 2 in the supplemental data.

Ribonuclease H.

Summarizing multiple kinetic and equilibrium experiments, Chamberlain and Marqusee (35) find a self-consistent hierarchic folding pathway for the molecule in which helices A and D fold first and are then augmented by helix B and β-strand 4. Each of these regions has pronounced, native-like biases. In fact, the only discrepant region between the native structure and the simulated biases is around residues 78–82, corresponding to an irregular kink between helices B and C.

Staphylococcal Nuclease.

Wang and Shortle (36) synthesized several fragments, one of them corresponding to residues 92–99, which overlap residues 87–93, a β-strand in the x-ray structure with significant helical weights in the simulation (see supplemental data). Unfortunately, no conclusion can be drawn because the region of overlap is slight and the synthesized fragment has a residue substitution (I92G).

Ubiquitin.

Fragment studies of Cox et al. (37) using CD and NMR show a marked tendency toward native-like structure in the molecule’s N-terminal half but not in the C-terminal half. Notably, the N-terminal β-hairpin (residues 1–17) can be detected in the A-state. In another study, Muñoz and Serrano (9) synthesized a fragment (residues 62–76) that includes the final strand of β-sheet (residues 65–71) and found it to have modest (≈8%), non-native helical content by CD. Both studies are consistent with the simulation biases.

Our simulations include additional details not presented here. Among them, regions with high turn weights can be assigned to specific turn types (38) from their backbone dihedral angles. To better understand the physical basis for turns, a separate series of host-guest turn simulations was conducted (see Fig. 3 in the supplemental data).

Turn Simulations.

A 14-residue host sequence (Val₅ -Ala-Pro-Gly-Ala-Val₅) with a central turn-forming sequence (namely, Pro-Gly) was simulated by using the protocol described in Methods. Six guest residues were introduced at position six to probe residue-specific effects: Asp, Asn, Ser, Leu, Glu, and Thr. Relative to the alanyl host, Ser, Asp, Asn, and Leu increase the turn propensity of the Pro-Gly sequence whereas Glu and Thr decrease the turn propensity. For Ser, Asp, and Asn, the preferred turn conformation is Type I or III, either of which enables the guest residue sidechain to form a stabilizing hydrogen bond with the backbone amide of Gly (i + 2) and/or Ala (i + 3). For Leu, Ala, and Glu, which lack side chain to mainchain hydrogen bonds, the preferred turn conformation is Type II. Thr does not show a marked preference. In the case of Leu, a hydrophobic contact (in lieu of an H-bond) can be made with Ala (i + 3) or Val (i + 5). Details are summarized in Table 4 and in the supplemental material.

Table 4.

Population statistics for host–guest turn simulations

Guest residue	Sidechain-backbone H-bond at i + 2, %*	Sidechain-backbone H-bond at i + 3, %*	Percent in turn†
Asp	27.8	9.7	31.8
Asn	27.3	16.7	29.4
Ser	31.8	20.3	30.0
Leu	N/A	N/A	33.7
Glu	<1	1.7	20.1
Thr	26.2	10.4	20.1
Ala	N/A	N/A	26.7

N/A, not applicable. 

^*Percent of the ensemble in which the indicated hydrogen bond is formed. 

^† Percent of the ensemble in which Gly is found at the i + 2 position of a β-turn. Note that turn populations in the supplementary material exceed those listed here because they represent the fraction of the ensemble in which a residue is in either the i + 1 or the i + 2 position of a turn. 

These simulated turn preferences are consistent with the usual turn-formers, namely, Asp, Asn, and Ser (38, 39), and they arise for understandable physical reasons (e.g., hydrogen bonding). linus simulations are sensitive enough to distinguish between Asp, which forms sidechain-backbone H-bonds readily, and Glu, which fails to do so. The simulations also show that even a nonturn former, e.g., Leu, can nonetheless stabilize a turn by using a hydrophobic interaction.

Discussion

Our central purpose in this paper has been to demonstrate that pronounced biases toward protein secondary structure are present in natural protein sequences, that these biases have a discernible physical basis, and that their existence begs reinterpretation of current folding models. Unlike more sophisticated simulations that use a comprehensive potential function—e.g., ref. 40—the biases evident in Tables 2 and 3 are a consequence of sterics and local interactions; longer range interactions were suppressed in the simulation protocol. In every case, these biases largely, albeit imperfectly, anticipate the observed secondary structure of the folded molecule. In several cases in which the linus-evolved biases differ from native secondary structure and in which data describing early folding intermediates are available, the simulations are consistent with these experimental data (e.g., myoglobin, plastocyanin, and ubiquitin).

There has been considerable debate in the literature about whether secondary structure formation is an early folding event (2). The simulations shown here—together with dozens of others that were conducted but not presented—confirm that sterically driven segments of nascent secondary structure can emerge in the unfolded state and preorganize all subsequent folding events.

If these simulations reproduced early folding events reliably, then chain regions with a strong bias toward the “wrong” secondary structure could signal the presence of a non-native intermediate. This need not be true for discrepancies involving weak biases, which may simply have lacked ample opportunity to develop. However, a strong bias toward a discrepant contracted conformation—such as bias toward helix in a known β-strand—would indicate the presence (though not the stability) of an early, non-native intermediate; examples include the non-native helices in intestinal fatty acid-binding protein and plastocyanin, described in the previous section, or those in β-lactoglobulin, described in the review by Baldwin and Rose (3).

Conformational biases arise for several reasons, but the primary factor involves steric interplay between the α- and β-regions of the φ,ψ map. The α-region (near φ = −60°, ψ = −40°) is compatible with the formation of local hydrogen bonds, but in this contracted state, sidechains tend to clash with local backbone, resulting in unfavorable conformational restriction. The price of restriction is measured as loss of sidechain conformational entropy (11, 41). As that price mounts, chain segments are driven toward the remaining alternative, the β-region (near φ = −120°, ψ = +130°), an extended conformation in which steric clash between sidechain and backbone is relieved.

In this physical context, β-strand is appropriately regarded as authentic secondary structure, even in the absence of a hydrogen-bonded partner strand. Accordingly, β-sheet, comprised of two or more H-bonded β-stands, is more appropriately classified as tertiary structure, in that it involves the spatial organization of multiple β-strands, which are often removed from each other in sequence. This distinction—or the lack of it—has spawned continuing confusion about suitable procedures to identify secondary structure from atomic coordinates (42) and motivated our own approach (in Methods), which is based solely on dihedral angles, not hydrogen bonding.

The conformational biases were extracted from Monte Carlo simulations in which all moves are weighted equally. As such, these values almost certainly underestimate the true bias in the protein. A better estimate could have been obtained by using the extracted biases as weights in another round of simulation. In fact, our simulations are typically run by using just such a protocol. However, the simpler protocol was adopted here deliberately because nothing more complicated than that is needed to demonstrate the existence of sharply differentiated, broadly dispersed chain bias.

Many proteins are found to adopt molten globule intermediates (43) at low pH, a state having substantial secondary structure but lacking in specific tertiary interactions. In this regard, the existence of nascent secondary structure segments, as described here, anticipates such states. Sterically driven biases are expected to manifest themselves under essentially all folding conditions, and they would become independently observable whenever specific conditions can be found that destabilize the native protein (relative to the unfolded form) but not some intermediate form.

Conformational Entropy and Protein Folding.

Anfinsen proposed that proteins attain their native state by folding to a global minimum of Gibbs free energy (44). Typically, this hypothesis has been interpreted to mean that the native conformation of individual molecules also corresponds to a global minimum in internal energy because a fully folded protein will have lost its conformational entropy, or almost so. Thus, conformational entropy is thought to play an insignificant role in the thermodynamics of protein folding. Specifically, the Boltzmann-weighted populations of any two states x and y, (g_y/g_x)e^{−(U_y−U_x})/kT (where k = the Boltzmann constant and T = absolute temperature), are thought to depend predominantly on their energy difference, U_y − U_x, and not on the degeneracy of state, g_y/g_x. In contrast, the work presented here reaches the conclusion that conformational entropy, reflected in the degeneracy, is the main factor that discriminates between the two energetically degenerate ground states, α and β, and, in so doing, preorganizes the protein.

The Levinthal Paradox.

The issue of secondary structure bias is intimately related to the Levinthal paradox, which argues that a folding protein does not explore conformational hyperspace freely; otherwise, it would encounter an insoluble search problem (45). For Levinthal, this insight was not a paradox at all, but a convincing demonstration that some intrinsic constraint limits the effective size of conformational space. In this view, proteins solve the “multiple minimum problem” not by an extensive search that identifies the deepest minimum but by a limited search that avoids false minima. The existence of intrinsic bias resolves this paradox by prejudicing the ensemble of available folding trajectories toward the native minimum (46). Thus, a folding protein need not discriminate among an astronomical number of conformations because intrinsic bias “steers” the molecule toward a high degree of preorganization.

“Protein Micelles.”

The prevalence of native-like, stable subdomains (47, 48) in proteins is an expected consequence of intrinsic chain bias. Segments with strong biases are poised to form persisting structure, especially when fortified by additional stabilizing interactions. In this context, it is important to distinguish between stability and specificity (49). Stability is associated with the equilibrium between folded and unfolded forms in a cooperative, two-state folding process. Specificity is associated with conformational particulars of a given folded form (e.g., why does the lysozyme sequence adopt the lysozyme fold and not, for example, the ribonuclease fold?). If the protein’s conformational specificity is established primarily by built-in bias, as this paper has attempted to demonstrate, then stabilizing interactions can be quite nonspecific. Like folding up a carpenter’s rule, the preorganized segments and their interconnecting turns constrain the folding process, which can then be exerted via nonspecific driving forces, such as solvent-squeezing and hydrophobic burial. Thus, a chain segment long enough to adopt conformations with protein-like surface-to-volume ratios (i.e., ≥≈35 residues) (50, 51), and that spans several elements of impending secondary structure with protein-like sequence composition, would be sufficient to engender a stable subdomain. In this view, such subdomains are merely “polypeptide micelles” with an intrinsic chain bias. Indeed, many examples in the literature are consistent with this interpretation (52–55).