Transport of torsional stress in DNA

Abstract

It is well known that transcription can induce torsional stress in DNA, affecting the activity of nearby genes or even inducing structural transitions in the DNA duplex. It has long been assumed that the generation of significant torsional stress requires the DNA to be anchored, forming a limited topological domain, because otherwise it would spin almost freely about its axis. Previous estimates of the rotational drag have, however, neglected the role of small natural bends in the helix backbone. We show how these bends can increase the drag several thousandfold relative to prior estimates, allowing significant torsional stress even in linear unanchored DNA. The model helps explain several puzzling experimental results on structural transitions induced by transcription of DNA.

1. Introduction and Summary

DNA can be regarded as a linear repository of sequence information or as a chemical compound subject to various modifications (e.g., methylation), and each of these viewpoints is important for understanding some aspects of gene function and regulation. However, many other important processes require an appreciation of DNA as a physical elastic object in a viscous environment. For example, the action-at-a-distance between eukaryotic promoters and their enhancers involves an effective concentration of bound enhancer units depending on both torsional and bend rigidity of DNA.

Although the equilibrium statistical mechanics of stiff macromolecules such as DNA is a classical topic (see, e.g., ref. 1), still the nonequilibrium transport properties of such molecules remain incomplete, in part because of the experimental difficulty of probing those properties. In particular, Liu and Wang proposed that the transport of torsional stress (torque) along DNA during transcription could play a role in gene regulation (the “twin-supercoiled domain model”) (2). Transcription causes axial rotation of the transcribed DNA relative to the transcribing polymerase. If free rotation is hindered in some way, a resulting torsional stress will propagate down the DNA, destabilizing (or overstabilizing) the double helix structure at some distant point. The resulting “topological coupling” between nearby genes has been observed in several experiments (see Section 2 below).

Liu and Wang assumed a simple mechanism for the transport of torsional stress, following Levinthal and Crane (3). (Levinthal and Crane’s “speedometer-cable” motion will be called “plumber’s-snake” motion or “spinning” motion in this paper.) In a viscous medium, a straight infinite rod meets a frictional resistance to axial rotation given by:

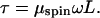1

Here the torque τ (with dimensions of energy) depends on the rotation rate ω (radians/sec) and length L via a friction constant μ_spin. A simple calculation (4) gives μ_spin = 4πηR² ≈1.3⋅10⁻¹⁵ dyn⋅sec, where R ≈ 1 nm is the rod radius, and η = 0.01 erg⋅sec⋅cm⁻³ is the viscosity of water. Other authors give slightly different prefactors (5).

Liu and Wang pointed out that the torsional friction constant μ_spin appearing in Eq. 1 is extremely small because of the factor of R², so they concluded that no significant torsional stress was possible in DNA of reasonable length without some additional physical anchoring. Absent such anchoring, both linear (open) and circular (plasmid) DNA would spin in place, like a plumber’s snake (3). For concreteness, we will consider below the example of a linear DNA of length 3.5 kbp (1,200 nm), rotated at its end with angular frequency ω = 60 radians/sec; a related case is a 7-kbp construct, linear or circular, rotated near its center. In either case, formula 1 gives a maximum torsional stress τ ≈ 9⋅10⁻¹⁸ dyn⋅cm. Because the torque needed to denature DNA locally is several thousand times greater (see below), Liu and Wang’s conclusion seems to be safe.

The analysis of this paper was motivated by several experimental observations, which defy the familiar analysis just summarized (Section 2 below). A variety of assays, both in living cells and in vitro, have found significant torsional stress after transcription at a single promoter on unanchored DNA constructs. All these experiments are sensitive to topoisomerase, pointing to the role of torsional stress. The estimates given above imply that such large stresses are impossible.

To resolve this paradox, the analysis in Sections 3 and 4 below will show that the classical formula 1 can be very misleading: it vastly underestimates the torsional stress on the DNA duplex near the transcribing polymerase. The discussion rests on the observation that DNA is a heteropolymer, i.e., it is naturally bent on length scales longer than its persistence length of about 50 nm. For a curved molecule to spin in place without dragging sideways through the surrounding medium, as assumed in formula 1, requires constant flexing. The natural bends resist this flexing, forcing the molecule to translate through the fluid and greatly increasing the viscous drag through the surrounding water. (Fig. 1d summarizes the model.) This enhanced drag indeed explains the large observed torsional stress near the point of transcription.

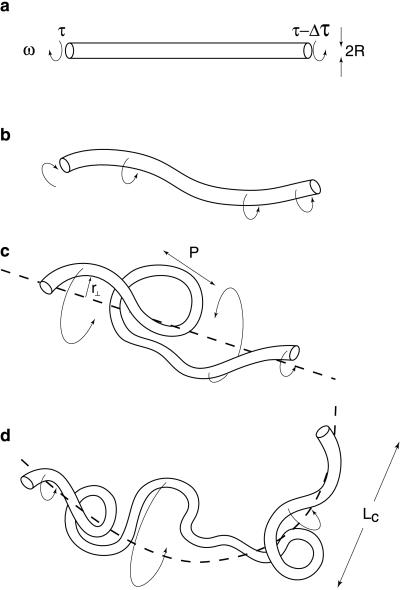
Figure 1.

Four increasingly realistic models of cranked DNA motion. (a) Straight rigid rod, assumed in the derivation of the naïve formula Eq. 1. (b) Naturally straight but thermally bent rod. (c) Naturally bent rigid rod. (d) Hybrid motion of a naturally bent semiflexible rod. The rod rotates rigidly on length scales shorter than L_C while flexing on scales longer than L_C.

2. Experiments

2.1. General.

This section briefly reviews a few of the relevant experimental results, focusing on in vitro assays. Section 3 below describes our physical model. RNA polymerases are efficient motors: for example, Escherichia coli RNA polymerase can generate forces of up to 20 pN against an opposing load (6). When the same mechanical energy is expended against a torsional load, it corresponds to a torque of 20 pN⋅0.34 nm/step divided by 2π radians for every 10.5 steps, or 10⁻¹³ dyn⋅cm, more than enough to induce structural transitions in DNA. The speed of transcription ranges from 50 nt/sec in eukaryotes to twice as great for T7 (7). The corresponding rotational driving rates are then ω = 30 and 60 radians/sec, respectively.

The actual torsional stress during transcription need not, however, attain the maximal value just given. Liu and Wang’s twin-supercoiled domain model rests on the observation that torsional stress will build up only if (a) the polymerase itself is prevented from counterrotating about the DNA template, and (b) a suitable torsional load opposes the rotation of the DNA at a point sufficiently close to the cranking polymerase. The present paper is concerned mainly with point b, but for completeness we first digress to discuss a.

Anchoring at the transcribing polymerase.

A number of effects can prevent counterrotation of the polymerase. For example, in eukaryotes the polymerase may be physically attached to the nuclear matrix. Even without a rigid attachment, the eukaryotic polymerase holoenzyme is physically quite large and thus offers a large hydrodynamic drag to rotation. Similarly, in prokaryotes, the nascent RNA transcript can begin translation before it is fully transcribed, leading effectively to a large complex consisting of polymerase, transcript, and ribosome. Liu and Wang proposed a particularly attractive possibility: if the emerging protein is membrane bound (for example, the tetracycline resistance tet gene product), it can anchor its ribosome to the cell membrane (2). Many experiments have shown that translation of tet greatly increases twin-supercoiled domain effects (see ref. 8 and refs. therein).

The above mechanisms operate only in vivo. Remarkably, twin-supercoiled domain effects have also been observed in a number of in vitro assays, where no cellular machinery exists (see Section 2.2). At least three mechanisms can nevertheless create significant drag opposing counterrotation of the polymerase: (i) polymerase has been found to create a tight loop in the DNA, greatly increasing its effective hydrodynamic radius and hence the drag for counterrotation (9); (ii) the nascent RNA transcript itself will create some hydrodynamic drag to rotation (10); (iii) under the conditions of most experiments (e.g., ref. 10), polymerase is present at concentrations leading to batteries of simultaneously transcribing complexes. To relieve torsional stress, all active complexes would have to counterrotate simultaneously, with a drag proportional to their total number.

Anchoring elsewhere.

Thus, even in vitro, transcription can effectively lead to the cranking of DNA by a nearly immobilized polymerase. As mentioned in point b above, however, cranking at one point still does not suffice to create torsional stress: DNA rotation must be effectively hindered somewhere else as well, because otherwise both linear and circular DNA would simply spin freely in place at the driving rate ω.

As in point a, many mechanisms can anchor DNA in the crowded cellular environment. For example, in eukaryotes a DNA-binding protein could tie the DNA onto some part of the nuclear matrix. Another possibility, envisioned by Liu and Wang and implemented in several experiments, is to bind a second polymerase to the DNA and rely on its resistance to rotation as in a above. The second polymerase can either be stalled or actively transcribing in the opposite (divergent) sense from the first.

Once again, however, the clearest results come from the in vitro assays mentioned earlier, in which only a single promoter is active on a circular (10–14) or even linear (L. B. Rothman-Denes, personal communication; D. Levens, personal communication) template. In these experiments the only known hindrance to free spinning motion is the torsional hydrodynamic drag. If DNA were effectively a simple straight rod of diameter 2 nm, then the estimate in Eq. 1 would apply, and we could confidently predict that transcription would generate negligible torsional stress. Because the experiments contradict this expectation, we must modify the naïve physical picture of the transport of torsional stress in DNA.

2.2. Experimental Results.

In vitro.

Tsao et al. made a circular plasmid with only one promoter actively transcribing (10). They assayed transient torsional stress in the wake of polymerase by allowing topoisomerase I to selectively eliminate negative supercoils, then measuring the remaining degree of positive supercoiling via two-dimensional electrophoresis. They found that transcription induces a degree of supercoiling “much bigger than expected” and concluded that, “It is possible that the degree of supercoiling generated by transcription is underestimated in the theoretical calculation” of ref. 2.

Dröge and Nordheim assayed torsional stress in a 3-kbp circular plasmid using the B–Z structural transition (11). They concluded that, “Interestingly our results suggest that diffusion rate of transcription-induced superhelical twists must be relatively slow compared with their generation, and that under in vitro conditions localized transient supercoiling can reach unexpectedly high levels.” Similarly, Dröge later found that transcription can induce site-specific recombination in vitro (12). Here the conclusion is that transcription created local torsional stress, in turn driving local writhing and bringing recombination sites into synapsis. Wang and Dröge later extended these experiments and called attention to the fact that torsional strain remains localized in a gradient region close to the polymerase, instead of spreading rapidly around the plasmid and canceling at the antipodal point (14).

Drolet, Bi, and Liu studied the reciprocal effects of topoisomerase I and gyrase (13), assaying with one-dimensional electrophoresis. The result of interest to the present paper is that they found that membrane anchoring via the nascent TetA protein was not necessary for transcription-induced supercoiling, in contrast to earlier in vivo studies.

Finally, Rothman-Denes and Levens (personal communications) have used linear (open) 2,300-nm templates including a T7 RNA polymerase promoter near the center. Transcription from this promoter by T7 RNA polymerase generates torsional stress. Rothman-Denes et al. used the activity of a bacteriophage N4 early promoter as a stress reporter. This promoter is inactive in its unstressed state and activated through cruciform extrusion at a superhelical density σ_crit = −0.03 (15), corresponding to a torsional stress of τ_crit ≈ 7⋅10⁻¹⁴ dyn⋅cm, consistent with the estimate given above.† Levens instead used an element of the human c-myc gene, which interacts with single-stranded DNA binding proteins and measured unwinding using potassium permanganate, which reacts with single-stranded tracts. The results of both sets of experiments suggest that structural transitions are induced by T7 RNA polymerase transcription. Thus it again appears that transcription of linear DNA can create torsional stress several thousand times greater than that predicted by the classical formula (1).

In vivo.

As mentioned above, in vivo experiments are harder to interpret, but nevertheless we mention a few illustrative results to show the very general character of the frictional-drag paradox.

Rahmouni and Wells used a circular 6.3-kb plasmid, reporting its torsional stress via the B–Z structural transition (20, 21). They concluded that “the diffusion of supercoils must be slower than was originally predicted” (in ref. 2).

Lilley and collaborators have carried out an extensive series of experiments reviewed in ref. 8. Their conclusion that an “as yet unidentified topological barrier should exist” may point to the same surprisingly large rotational drag argued for in the in vitro experiments above. In later work, they also found that the transcribing polymerase need not be physically anchored, reinforcing the argument in point a of Section 2.1 above (22, 23).

Turning finally to experiments in eukaryotes, we mention only two experiments of Dunaway and coworkers. Dunaway and Ostrander sought to eliminate any anchoring of their DNA template by injecting linear DNA with no subsequences known to associate with the nuclear architecture into Xenopus oocytes (24). They injected an exogenous (bacterial) polymerase into their oocytes and ensured that its promoter was the only spontaneously transcribing promoter on their template. They also used linear templates, reducing the likelihood of any entanglement effects. Using 3.6- to 4.5-kb templates with a ribosomal RNA promoter to report torsional stress, they concluded that “localized, transient domains of supercoiling” could occur in open DNA, trapping significant torsional stress. Similarly, later work by Krebs and Dunaway concluded that, “The viscous drag against a large DNA molecule is apparently sufficient to prevent transcription-generated supercoils from diffusing rapidly off the end of the DNA, so DNA length creates a topological domain” (25). Once again, this conclusion is remarkable in that it contravenes the estimates in Section 1 above.

3. Physical Picture

As described in Section 1, the surprising physical aspect of the experiment is the buildup of torsional stress in the DNA, when nothing seems to prevent the molecule from spinning almost freely in place. Apparently the simple physical model of a uniform elastic rod in a viscous fluid has left out some crucial effect. One may at this point be tempted to abandon simple physical models altogether, pointing to the many specific biochemical features of real DNA which they omit. But the elastic rod model successfully describes many detailed features of DNA stretching and fluorescence-depolarization experiments, including effects of torsional stress (e.g., refs. 17 and 26). Moreover, the surprising observed behavior is generic and robust, not specific to a particular situation, suggesting that the model needs only some simple new ingredient to capture the observed behavior.

In this section, we argue that augmenting the elastic rod model by including the natural bends in the DNA duplex dramatically changes the transport of torsional stress. The strength of these bends has been independently measured; it is not a new free parameter. Their effect on the equilibrium properties of DNA coils has long been recognized. In this section and the next, we instead study their effects far from equilibrium.

3.1. Need for Spin Locking.

Imagine a given segment of an elastic rod (modeling a twist-storing polymer such as DNA) as contained in a black box with only the two ends of the rod accessible. Cranking one end about its axis amounts to injecting a conserved quantity, “linking number” (or Lk), into the rod.‡ We can schematically think of linking number as taking one of five pathways away from the cranking site:

1. Lk can be elastically stored as twist in the rod: the rod segment can rotate about its axis by an amount which depends on position along the rod.

2. Lk can be elastically stored as writhe: the rod can begin to supercoil.

3. Lk can be transported by spinning (plumber’s-snake) motion, emerging at the far end with no net change in the rod state.

4. Lk can be transported by rigid rotation (crankshaft motion) of the whole segment about some axis.

5. Lk can be lost via the action of topoisomerase.

We are interested in steady-state transport, in the absence of topoisomerase, so we consider only the competition between pathways nos. 3 and 4.

This picture allows a more precise summary of the paradox reviewed in Sections 1 and 2 above. The steady transport of injected Lk will meet with resistance in the form of effective frictional constants μ_spin for spinning and μ_rigid for rigid rotation, hence a total frictional constant μ_tot = (μ_spin⁻¹ + μ_rigid⁻¹)⁻¹. But we have seen that experimentally μ_tot is much larger than the theoretically expected value of μ_spin. No matter how large μ_rigid may be, it cannot resolve this paradox. In particular, the well-known coupling between torsional stress and writhing motion (see, e.g., refs. 27 and 28 and refs. therein) is of no help, because the problem is precisely that there is little torsional stress.

What is needed is a way to shut down pathway no. 3, i.e., to lock the spin degree of freedom, at least partially.

The fact that a uniform rod is never actually straight on length scales beyond its bend-persistence length A does not help either.§ Spinning creates no long-range hydrodynamic interaction, because the fluid velocity field falls off on the scale of the rod diameter R = 1 nm (4). Because A is much larger than R, the straight rod approximation is adequate (29). Certainly the spinning in place of a thermally bent but naturally straight rod requires continuous flexing of the rod, because the direction of curvature rotates in the material frame of the rod, but the elastic cost of a bend in a cylindrical rod depends only on the magnitude, not the direction, of the curvature, and this does not change: such a rod has no energetic barrier to spinning.

To summarize, the naïve Eq. 1 will be accurate, and torsional stresses will be small, unless some sort of locking mechanism inhibits free spinning of linear DNA in solution. To find such a mechanism, we must now introduce some new element of realism into our description of DNA.

3.2. Natural Bends.

As mentioned in Section 1, the key ingredient missing so far from our model is the natural curvature of the DNA duplex. Immense effort has been focused on predicting the precise conformation of a DNA tract given its base pair sequence, by using molecular modeling, oligomer crystallography, and NMR, among other techniques. Fortunately, for our problem it suffices to characterize the average effect of curvature over hundreds of base pairs. For such purposes, a very simple phenomenological approach suffices.

Natural DNA is a stack of similar but nonidentical subunits, arranged in an order that is fixed but random for our purposes. It is crucial that even though these bends are random, their effects do not average to zero on length scales much longer than one base pair. Instead, the minimum-energy conformation of such a stack may be regarded as a distorted helix whose backbone follows a random walk, with a structural persistence length P. Note that P is a purely geometrical parameter, having nothing to do with the mechanical bend stiffness κ_bend of DNA nor the thermal energy k_BT. Instead, P reflects the information content in a piece of DNA.

Just as in the straight case, bent (natural) DNA can also be deformed away from its minimum-energy state at some enthalpic cost characterized by a bend stiffness κ_bend, with units energy⋅length. Because fluctuations are controlled by the thermal energy k_BT, we define the bend length A = κ_bend/k_BT. The combined effect of thermal and natural bends then makes DNA a random coil with total persistence length¶ A_tot = (A⁻¹ + P⁻¹)⁻¹ (32). Under physiological conditions, A_tot has the familiar value of 50 nm. Experiments on artificial naturally straight DNA make it possible to determine A and P separately, yielding A ≈ 80 nm and P ≈ 130 nm (33).‖

3.3. Hybrid Motion.

We wish to explore the consequences of the natural bends introduced in the previous subsection for the transport of torsional stress in DNA. Before doing any calculations, it is worthwhile to formulate some intuitive expectations, based on four increasingly realistic cartoons for the steady-state motion of a cranked DNA segment of contour length l (Fig. 1 a–d).

As noted in Section 1, a straight rigid segment (Fig. 1a) would encounter a torsional drag per unit length μ_spinω or a net drop in torsional stress between the ends of μ_spinωl, with friction constant μ_spin given below Eq. 1. We argued in Section 3.1 that the case of a naturally straight but semiflexible segment is similar (Fig. 1b).

Matters change considerably when we introduce natural bends. If the rod were perfectly rigid (Fig. 1c), it would have to execute crankshaft motion; individual rod elements would then drag sideways through the fluid. We will see below that as l increases, the corresponding drag per unit length would increase without bound. On long enough scales, then, we may expect that any realistic molecule cannot be regarded as infinitely stiff.

At the other extreme, we could imagine the naturally bent rod spinning in place. This, however, would mean that every joint periodically bends oppositely to its preferred conformation. The corresponding elastic energy cost creates a barrier to this motion.

We will argue that, in fact, a real semiflexible heteropolymer chooses a compromise between these extremes of motion, selecting a crossover scale L_C and executing a hybrid motion (Fig. 1d). On length scales shorter than L_C, this motion is nearly rigid, because, as just argued, an activation barrier resists flexing. On longer length scales, the motion must cross over to spinning, because as just argued rigid (crankshaft) motion meets a large viscous drag on long scales.

We must now justify these intuitive ideas and obtain a numerical estimate for the crucial crossover scale L_C. Because L_C will turn out to be significantly longer than the base pair step size, we will conclude that the spinning (plumber’s-snake) motion is effectively locked, as we argued was necessary in Section 3.1.

4. Scaling Analysis

We must now justify and quantify the expectations sketched in Section 3.

4.1. Spin Locking.

Consider first the hypothetical case of a perfectly rigid naturally bent rod (Fig. 1c). The viscous force per length f on a straight rod much longer than its radius R, dragged sideways through a viscous medium, is:

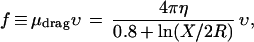2

where υ is the speed and X is the rod length. Our polymer is, of course, not straight on length scales beyond its structural persistence length P, so we substitute P for the long-scale cutoff X in Eq. 2. Because the dependence on X is weak, this is a reasonable approximation.** Taking P = 130 nm and R = 1 nm gives μ_drag ≈ 2.5⋅10⁻² erg⋅sec⋅cm⁻³.

Suppose we crank a rod segment of arc length l, which then rotates rigidly about an axis. Each element of the rod then moves through fluid at a speed υ = r_⊥ω, where r_⊥ is the distance from the rod element to the rotation axis (Fig. 1c). Multiplying the moment arm r_⊥ times the drag force (Eq. 2) and integrating over the curve yields the torque drop Δτ = μ_dragωl〈r_⊥ ²〉 across the segment. Here 〈r_⊥²〉 is the average of r_⊥² along the rod segment.

Each rod segment of course has a different sequence and hence a different preferred shape. Each segment will therefore have a different value of 〈r_⊥²〉. Fortunately, we are interested in the sum of the torque drops across many segments, each with a different random sequence. Thus we may replace 〈r_⊥²〉 by its ensemble average over sequences, which we will call 〈〈r_⊥²〉〉. This average has a simple form: Eq. 7.31 of ref. 1 gives 〈〈r_⊥²〉〉 = lP/9, and hence:

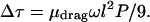3

In the language of Section 3.1, we have just estimated the drag torque μ_rigidωl, finding μ_rigid ≈ μ_draglP/9. Indeed, we see that the drag per unit length grows with l, as suggested in Section 3.3 above. Formula 3 is valid when the segment length l is longer than P, an assumption whose self consistency we will check below.

We can now relax the artificial assumption of a perfectly rigid rod and thus pass from Fig. 1c to the more realistic Fig. 1d. Suppose that a long polymer has been subdivided into segments of length l, each approximately executing rigid rotation about a different axis. The axes will all be different, because we are assuming that l is longer than the structural persistence length P. To join these segments smoothly as they rotate, each segment therefore needs to flex. On average, each segment must periodically bend one end relative to the other by about 90°. The least costly conformational change that accomplishes this is to spread the bending strain uniformly along the entire segment length l; we can then estimate the elastic bending-energy cost as‡‡ lκ_bend/2 (π/2l)². This energy barrier becomes small for large l, just the opposite trend to that of Eq. 3. The physical reason for this behavior is that we do not insist on ironing out every small kink in the rotating rod’s shape; the rod segment can satisfy the imposed conditions on its ends by deforming only a fraction of its many intrinsic bends.

The bending energy needed to crank the segment through an angle θ is roughly the above expression times ½(1 − cos θ); the torque needed to increase θ is then the derivative of this formula, ½ sin θ. Thus the driving torque needed to overcome the bending-energy barrier turn through a complete revolution is just one-half of the above expression. The crossover length L_C is then the value of l at which the viscous torque drop (Eq. 3) just balances this critical value:

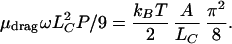4

Substituting the numerical values, we find L_C ≈ 450 nm for T7 RNA polymerase and slightly larger for other slower polymerases.

Our crossover length has indeed proven to be longer than the structural persistence length P, so the assumption l > P made above is self consistent. Indeed, L_C has proven to be about 1.4 kbp. In our illustrative example of a 7-kbp DNA construct cranked at the midpoint, we see that intrinsic bends shut down spinning motion almost completely: the naïve model of Section 1 does not describe the true motion at all. We must now see what this implies for the overall torsional stress on the construct.

4.2. Hydrodynamic Interactions.

In contrast to spinning in place, dragging a thin rod sideways sets up a long-range flow field. Now that we know that spinning is effectively forbidden, we must therefore study the possibility of long-range hydrodynamic interactions between rod segments.

The theory of polymer dynamics tells us that a short random coil dragged through fluid can be viewed as a set of thin-rod elements moving independently in a motionless background (the “free-draining” case), but a long coil instead moves as a solid spherical object because of hydrodynamic interactions (35). The crossover between these two regimes is controlled by the dimensionless parameter Q ≡ 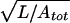μ_drag/η. Free draining corresponds to the case Q ≪ 1. For our illustrative example of a coil of length L = 2,300 nm and total persistence length A_tot = 50 nm, we get Q = 17, interactions are important, and the coil moves as a solid sphere.

The viscous drag torque on such a coil is τ = μ_coilωL, where μ_coil = 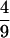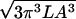·1.26η (see Section 31 of ref. 1). Dividing this torque equally between the upstream and downstream halves of the construct, we find the estimated torsional stress on either side of the cranking point to be ω⋅1.0⋅10⁻¹⁵dyn⋅cm sec. Taking ω = 60 radian/sec then gives a torsional stress of 6⋅10¹⁴ dyn⋅cm, comparable to the value quoted in Section 2 as necessary to induce structural transitions and about seven thousand times greater than the naïve estimate given below Eq. 1.

4.3. Relation to Prior Theoretical Work.

The viewpoint taken in this paper can be regarded as a synthesis of two established threads.

Fluid-mechanics work.

One of these threads studies the deterministic dynamics of externally driven (i.e., far from equilibrium) rods in a viscous environment. For example, Garcia de la Torre and Bloomfield studied the effects of a single permanent large-angle bend on viscous drag (5), obtaining precise versions of some of the formulae given above. Individual large-angle bends caused by DNA-binding factors may well be present in vivo, but our point here is that a statistical distribution of small finite-stiffness bends still leads to dramatic effects.

Several authors have studied the interplay between shape and twist in the dynamics of naturally straight flexible rods in a viscous medium (36–38), again obtaining precise formulae for situations simpler than that studied here. It would be very interesting to incorporate intrinsic bends into their formalism.

Finally, Marko has proposed that the impulsive (jumpy) action of RNA polymerase can lead to transient torsional stresses greater than predicted by the naïve formula (Eq. 1) (39). The range of this enhancement, however, depends on the time scale of each step and may be too short to explain the observed phenomena. Experimental measurement of this time scale will be needed to assess this proposed mechanism.

Simulation work.

A second thread is the extensively studied problem of the equilibrium fluctuations of a polymer, particularly the diffusive torsional motion of DNA as measured in fluorescence experiments. Most of this work used Monte Carlo or Brownian dynamics numerical simulation techniques; most did not introduce long-range hydrodynamic interactions as we did in Section 4.2 above.

Fujimoto and Schurr noted that fitting experimental fluorescence polarization anisotropy data to a model of intrinsically straight DNA yielded an effective hydrodynamic radius that increased with increasing segment length (40). They suggested the possibility that this effect could be caused by permanent or long-lived bends in DNA.

Collini et al. took up the same problem (28), explicitly introducing intrinsic bends. Their physical model, however, was the crankshaft motion of a perfectly rigid zig-zag shape. The zig-zag shape introduces structure on one length scale. A major point of the scaling analysis in Section 4 above, however, was that the minimum-energy conformation of natural DNA is actually a random coil, and random walks have structure on all length scales. A second key point of our analysis was that DNA is not infinitely stiff, leading to the crossover phenomenon found in Section 4.1.

Schurr et al. distinguished between “phase-locked bends,” equivalent to the natural bends in the present work, and “nonphase-locked bends,” including the thermal bends of the present work.†† They verified, using Monte Carlo simulation, that in the absence of natural bends, the torsional drag on a thermally bent rod is the same as that for a straight rod, as argued physically in Section 3.1 above. Schurr et al. went on to anticipate the hybrid motion studied in the present work, proposing that “beyond some length the degree of global phase locking should decrease, as the motion approaches that of a wobbly eccentric speedometer cable, and the effective hydrodynamic radius should reach a plateau value, which is possibly 1.2 nm. The available evidence indicates that this radius is independent of length for L > 60 nm” (29). The authors did not, however, present a model incorporating random natural-bend disorder.

The present work predicts instead that the response of DNA to external cranking is controlled by an effective drag constant that does not saturate until L > L_C. The crossover scale L_C depends on the transcription rate via Eq. 4 and is typically hundreds of nanometers; the saturation value of the effective hydrodynamic radius is then much greater than 1.2 nm. The driven situation of interest here is not, however, the same as the equilibrium situation studied in ref. 29.

Finally, A. Maggs has independently shown that in a naturally straight thermally bent rod, twist relaxation follows the same diffusive law as in a rigid straight rod, out to extremely long scales (over 2 kbp) (A. Maggs, personal communication). Beyond this scale, Maggs found that pathway no. 2 in Section 3.1 above begins to affect twist relaxation, leading to an interesting new scaling relation.

5. Conclusion

The analysis of this paper rests on a surprising fact from slender-body viscous hydrodynamics. The drag torque for spinning a thin rod behaves reasonably as one decreases the rod radius R: it is proportional to R². In surprising contrast, the drag force for pulling such a rod sideways is practically independent of R (Eq. 2 above). The only length scale available to set the rotational drag for rigid crankshaft motion is the radius of curvature of the rod. But a randomly bent rod has structure on every length scale, so the drag torque per length increases without bound for longer segments until the crossover condition, Eq. 4, is met. Because the crossover scale L_C proves to be long, cranked DNA is effectively spin locked on scales shorter than at least 1 kbp. This observation explains why the naïve formula, Eq. 1, is inapplicable, eliminating the paradox described in Section 1.

The transport of torsional stress may enter in many cell processes. Although this paper has stressed its possible role in gene regulation, torsional stress has recently been assigned a role in the disassembly of nucleosomes in front of an advancing polymerase complex (e.g., refs. 41 and 42) in chromatin remodeling (e.g., ref. 43) and in the action of enzymes on DNA (e.g., ref. 44). The ideas of this paper may be relevant to these problems too, although of course in eukaryotes the phenomenon described here may be preempted by the effects of higher-order chromatin structure. Direct manipulation of single DNA molecules sometimes involves cranking as well (e.g., ref. 45).

The simple scaling analysis used in this paper makes some testable predictions. The key claim has been that intrinsic bends can have a huge effect on the transport of torsional stress along DNA. For example, synthetic DNA engineered to be less bent than natural sequences (33) will have longer crossover scale L_C (Eq. 4) and hence should support less torsional stress for a given length. Shortening a linear template below L_C should also sharply reduce the overall drag coefficient. More generally, none of the experimental papers cited earlier made quantitative estimates of the effective torsional friction constant needed to explain their results. One could imagine an in vitro experiment using local stress reporters (e.g., the B–Z structural transition) inserted at various positions to get the full torsional stress profile in space and time, as function of transcription rate. Even a limited subset of this quantitative information would yield insight into the mechanisms of torsional stress transport.