Structure Prediction of Domain Insertion Proteins From Structures of the Individual Domains

Summary

Multi-domain proteins continue to be a major challenge in protein structure prediction. Here, we present a Monte Carlo (MC) algorithm, implemented within Rosetta, to predict the structure of proteins in which one domain is inserted into another. Three new MC moves combine rigid-body and loop movements to search the constrained conformation by structure disruption and subsequent repair of chain breaks. Local searches find that the algorithm samples and recovers near-native structures consistently. Further global searches produced top-ranked structures within 5 Å in 31 of 50 cases in low resolution mode, and refinement of top-ranked low-resolution structures produce models within 2 Å in 21 of 50 cases. Rigid-body orientations were often correctly recovered despite errors in the linker conformation. The algorithm is broadly applicable to de novo structure prediction of both naturally occurring and engineered domain insertion proteins.

Introduction

Over two-thirds of the proteins in the prokaryote and eukaryote proteomes are composed of multiple domains (Ponting and Russell, 2002; Russell, 1994; Vogel et al., 2004). Furthermore, proteins engineered for new functions have been created by combining domains of existing proteins in such a way to link the conformational states of the individual domains. While many natural and engineered domains are joined end-to-end, complex function can arise from the more extensive structural coupling when one domain is inserted within another, creating a domain insertion protein (Baird et al., 1999; Buskirk et al., 2004; Guntas et al., 2005; Ostermeier, 2005; Radley et al., 2003; Russell, 1994; Skretas and Wood, 2005a). Given the difficulties in obtaining structures of large proteins by either x-ray crystallography or NMR, computational protein structure prediction could play an important role for understanding these large proteins. However, while single domains (averaging ∼150 residues per domain (Shen et al., 2005)) can often be predicted to moderate accuracy using de novo or comparative modeling (Rohl et al., 2004a), multidomain proteins are much more challenging due to the higher order organization and increased size (Tress et al., 2007). Complex topology creates additional prediction difficulties due to the interdependence of the degrees of freedom. In this study, we develop and test a method that predicts the overall structure of domain insertion proteins from structures of the individual domains.

The word “domain” has many connotations from evolutionary, structural, and functional contexts. The most common classification in structural biology defines a domain as a compact independently folding unit with structural similarities to other proteins. A number of resources can be used to parse proteins into domains using a structural definition, including the manually curated Structural Classification of Proteins (SCOP (Barton, 1994)) database and the hidden Markov model-based CATH system (Jones et al., 1998; Orengo et al., 1997). The DomIns Database of domain insertion proteins contains 1332 structures, although the number of unique structures is much lower (Selvam and Sasidharan, 2004). For the purpose of this paper, domain insertion proteins are defined by two criteria: 1) they are two-domain proteins and 2) the host domain, A, is non-continuous and thereby made up of two segments, A1 and A2, which are separated in sequence by two linkers and the insert domain, B (Figure 1).

Figure 1. Domain Insertion Protein Structure.

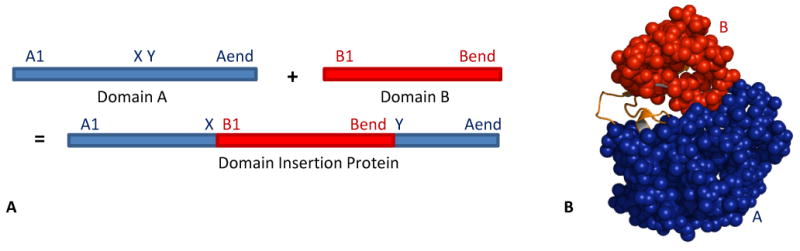
A domain insertion protein consists of two domains, A (blue) and B (red). (A) Primary structure; (B) Tertiary structure. The two 11-residue linkers connecting A to B are orange.

From the structures of domain insertion proteins, a number of observations have been made. First, the inserted domain is most often the smaller of the two domains with the host domain comprising 50-80% of the protein and the insert domain comprising the remaining 20-50% (Aroul-Selvam et al., 2004; Ponting and Russell, 2002). Second, the location of the insertion point is biased such that most insertions occur in the last third of a protein's sequence length. Finally, the ends of the inserted domain are within 8 Å of each other in the crystal structure, allowing insertion to occur more readily (Aroul-Selvam et al., 2004). The reasons for these trends are not clear, but may include evolutionary pressure for easier insertion and correct folding.

Structure prediction experiments, such as the Critical Assessment of Structure Prediction (CASP (Moult et al., 1995)), show that it is very difficult to predict the structure of multidomain proteins, even when homology models of the individual domains are available (Tai et al., 2005; Tress et al., 2005; Venclovas and Margelevicius, 2005). Recently, algorithms have emerged that parse protein sequences into separate domains and use templates matching each piece to create homology models, however most of the time, multidomain proteins are still modeled using a single template for the full length of the protein (Cheng, 2007; Cheng and Baldi, 2006; Clarke et al., 2007; Tress et al., 2007; Zhou et al., 2007). In the domain definition section of CASP, assessors assign official domain definitions by visual inspection using criteria of geometrical separation, symmetry, and recurrence in other structures (Tress et al., 2005). Similarly, predictors use a variety of combined automated and manual inspection algorithms to predict domains (Bradley et al., 2005a; Clarke et al., 2007). In the most recent CASP experiment, CASP7, 16 out of 96 proteins were classified as domain insertion proteins by the assessors (Clarke et al., 2007) using the above criteria, and yet there is no indication that these targets were approached differently than any other structure prediction problem (Zhou et al., 2007); Rhiju Das, Jianlin Cheng, personal communication). Our hypothesis is that increased accuracy can be achieved by using template-based homology modeling for the individual domains (increasing accuracy since these are smaller) and then combining the domains with a domain insertion algorithm. To our knowledge, there is no published study on the systematic prediction of domain insertion proteins from the component domains, and no reliable methods exist to find their structure.

For comparison, there are two general methods for predicting the structure of end-to-end multidomain proteins: the problem can be approached similarly to protein-complex formation by docking two domains (Yuval et al., 2005), or it can be studied with “domain assembly,” where the torsional degrees of freedom of the linkers are sampled, resulting in downstream movement of the second domain relative to the first domain (Wollacott et al., 2007).

Predicting the structure of domain insertion proteins is kinematically more difficult because the domains are connected by two linkers. Compared to a docking approach, the linker torsion angles increase the conformational space, and compared to domain assembly, the second linker and host domain compactness constrains the conformation. The two linkers prevent a domain assembly method from working because any changes made in one linker will move one of the segments of the host domain. Furthermore, since the linkers are often found at the interface between the two domains, a docking approach is insufficient because the linkers must be modeled to provide a full interface region for domain-domain contacts.

In this work we predict structures of domain insertion proteins by simultaneously optimizing the conformation of the linkers and the rigid-body orientation of the host and insert domains. We introduce a Monte Carlo (MC) based algorithm implemented within the Rosetta protein structure modeling suite (Rohl and Baker, 2002) incorporating parts of earlier approaches to both domain assembly and loop modeling. We develop combinations of conformational moves to efficiently search the relevant conformation space and maintain the connectivity constraints of the protein. We test the algorithm in local and global searches in both low- and high-resolution representations.

Results

New move types

At the core of our method are three new MC moves we added to the standard Rosetta move set. These moves simultaneously optimize the linker conformation and rigid-body position, while enforcing the constraints presented by the two linkers. Each move follows a two-step process. The first step applies a perturbation, which is often disruptive, and the second step repairs any disruption caused by the move. Moves are accomplished using a “fold tree” representation of the protein (Bradley and Baker, 2006). A fold tree represents a protein by a graph and allows backbone conformational sampling to be localized without propagation of torsion angle perturbations past specified “cut points.” The structurally continuous segments between cut points are called “edges” and are connected to each other spatially by “jumps,” which encode the rigid-body transformations connecting the edges. Flexible regions, such as the linkers, must be adjacent to at least a single cut point to allow conformational sampling while preventing propagation of backbone torsion angle perturbations far downstream.

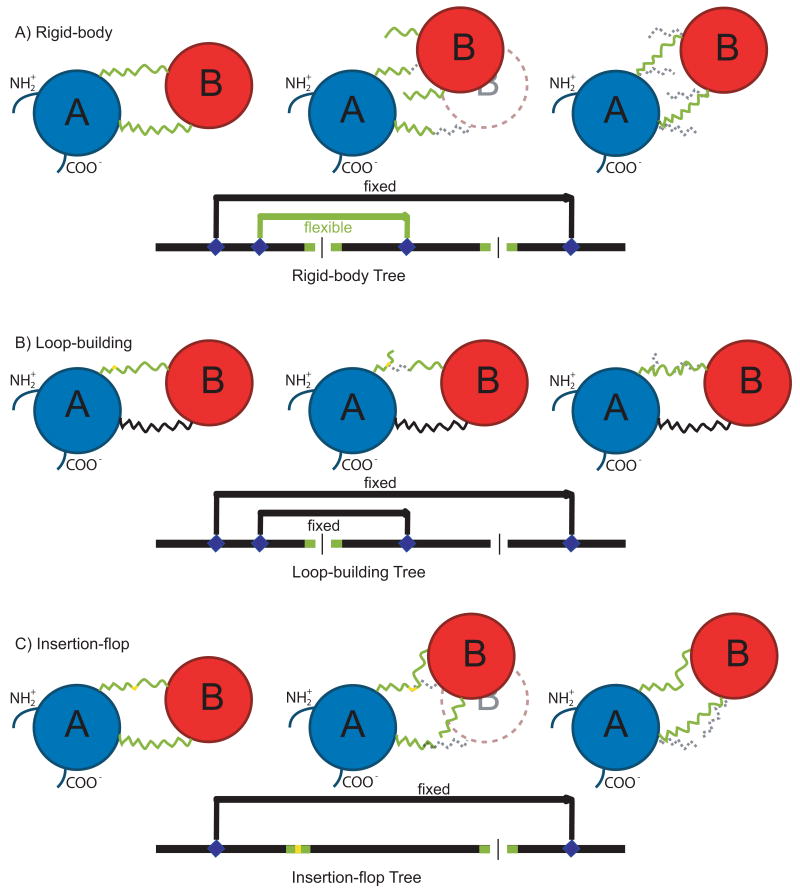
Figure 2 shows the new moves for the low resolution search. Figure 2A describes a rigid-body move wherein domain B is translated and rotated while domain A remains fixed, causing the two linkers connecting the domains to break (Figure 2A, center). The rigid-body fold tree, shown below the cartoon, uses a fixed jump to connect the two halves of domain A so that they move as a single entity. A flexible jump between domain A and domain B is altered to allow B to sample the conformational space around A. The broken chains are later repaired using a loop-building move over two 11-residue linkers, defined as the insertion point residues and five adjacent residues on either side.

Figure 2. Cartoon representation of combination MC moves and their corresponding fold trees.

Each horizontal panel shows an initial position and selected perturbation locations (left), the disrupted structure after a perturbation (center), and the subsequent structural repair (right). In all panels, green represents a flexible region of the protein or the fold tree and a yellow point indicates where a specific φ/ψ angle change occurs.

A: For a rigid-body move, domain A (blue) is kept fixed while domain B (red) samples the conformational space around A, causing the linkers to break. The linkers are repaired using a combination of three-residue fragment insertions and CCD loop closure. The fold tree shows a fixed jump connecting the two parts of domain A in black and the flexible jump connecting domains A and B in green. Both the linkers are flexible so that they can be repaired.

B: For a loop-building move, one linker (green) is built by inserting a three-residue fragment at the point shown in yellow. The insertion of a fragment breaks the linker, and CCD is used to reclose the linker. In the fold tree, only the linker that is being repaired is flexible.

C: For an insertion-flop move, small φ/ψ angle movements are made in one linker (yellow) while allowing the other linker to break. The broken linker is then rebuilt. This “flops” around the insertion domain. In the fold tree, only one jump is used to hold the host domain together.

Connecting linkers between the domains (11 residues each) are built and optimized as a loop-prediction problem through a combination of three-residue fragment insertions (Rohl et al., 2004a) and cyclic coordinate descent (CCD) loop closure (Canutescu and Dunbrack, 2003). CCD iteratively adjusts single dihedral angles to minimize the sum of the squared distances of three backbone atoms across a chain break. As shown in Figure 2B, three consecutive backbone torsion angles are replaced by the insertion of a fragment, causing the linker to break; it is then forced closed using CCD. During the move, the residues in the single linker that is being built and repaired are the only flexible parts of the protein.

The final move type is an “insertion flop” move. Several small φ/ψ torsion angle movements are imposed in one linker, propagating the movement through the insert domain to a chain break in the second linker (Figure 2C). The second linker is subsequently repaired with CCD moves. This process is iterated with the two linkers alternating between the roles of being perturbed or broken-and-repaired. This effectively “flops” around the insert domain, where the linker residues are the only flexible parts.

We tested each move independently to verify the function of the move, to optimize the number of iterations needed, and finally to assess how each move acted on the development set proteins. Finally, we explored combinations of moves to see how they affected each other. Analysis of the effectiveness of each move to lower the score and the computational cost of each move guided us in determining the order of moves and the optimal number of iterations.

Domain insertion algorithm and application

The domain insertion algorithm exploits Rosetta's multi-scale approach combining a low-resolution mode where side chains are represented as pseudo-atom centroids (Simons et al., 1997) and a high-resolution mode with explicit side chains. The low-resolution mode allows for broad and fast exploration of the conformation space, and the new moves are applied in this mode. Starting structures are subjected to five iterations alternating between sets of rigid-body moves and sets of loop-building moves, with Boltzmann criterion checks within each set of moves and after the combined iteration. Thus, the MC search allows for cooperative movement through rigid-body and linker conformation space. Low-resolution structures which are not able to close the chain breaks after the repeated loop-building moves are rejected. The insertion-flop combination moves are less disruptive to structure, therefore they are used after the rigid-body and loop-building moves are complete.

High-resolution refinement allows fine changes in structure to produce the most relevant structure for evaluating the energy for decoy discrimination. Refinement consists of several cycles, wherein each cycle includes φ/ψ perturbations on the backbone of residues in the linkers, minimization of the rigid-body conformation, and CCD to close any chain breaks. Perturbations at this stage are very small to avoid clashes in the highly corrugated all-atom potential function. The interface and surrounding side-chains are periodically repacked using an embedded MC simulated annealing routine to select the best combination of conformations from a discrete rotamer library (Dunbrack and Cohen, 1997; Kuhlman and Baker, 2000).

The low-resolution scoring function derives from the de novo prediction algorithm (Rohl et al., 2004b) except a contact function is added from the docking algorithm (Gray et al., 2003a) to encourage compactness of the domains. The high-resolution scoring function originates from the refinement protocol (Bradley et al., 2005b) and is dominated by van der Waals, solvation, and hydrogen bonding energies. Both scoring functions are supplemented with a penalty function for chain breaks. The full scoring functions for both low- and high-resolution modes are detailed in the Experimental Procedures.

Calculations were performed on a test set of 50 crystal structures of proteins selected from the SCOP database for domain insertion topology and resolution of 2.5 Å or better, removing any multimeric structures and monomeric structures with significant disordered regions. An overlapping development set of seven proteins was used to tune the new moves described above. Computation time is approximately 3 minutes per decoy and varies slightly with protein size. Some targets proved to have high rates of rejection of initial and low-resolution refined decoys due to inability to close linkers, thus increasing total computation time.

Local search with domain insertion is able to discriminate structures

To test whether the energy function recognizes near-native structures as those with minimal energy relative to non-native structures, we performed local structure prediction searches. To ensure sampling near the native crystal structure, initial structures were created from the native structure by perturbing similarly to a local search in docking (Gray et al., 2003a), using a rigid-body transformation and repairing the linkers (Experimental Procedures). In these tests, we used a combined protocol employing both the low- and high-resolution searches, resulting in all-atom decoy structures.

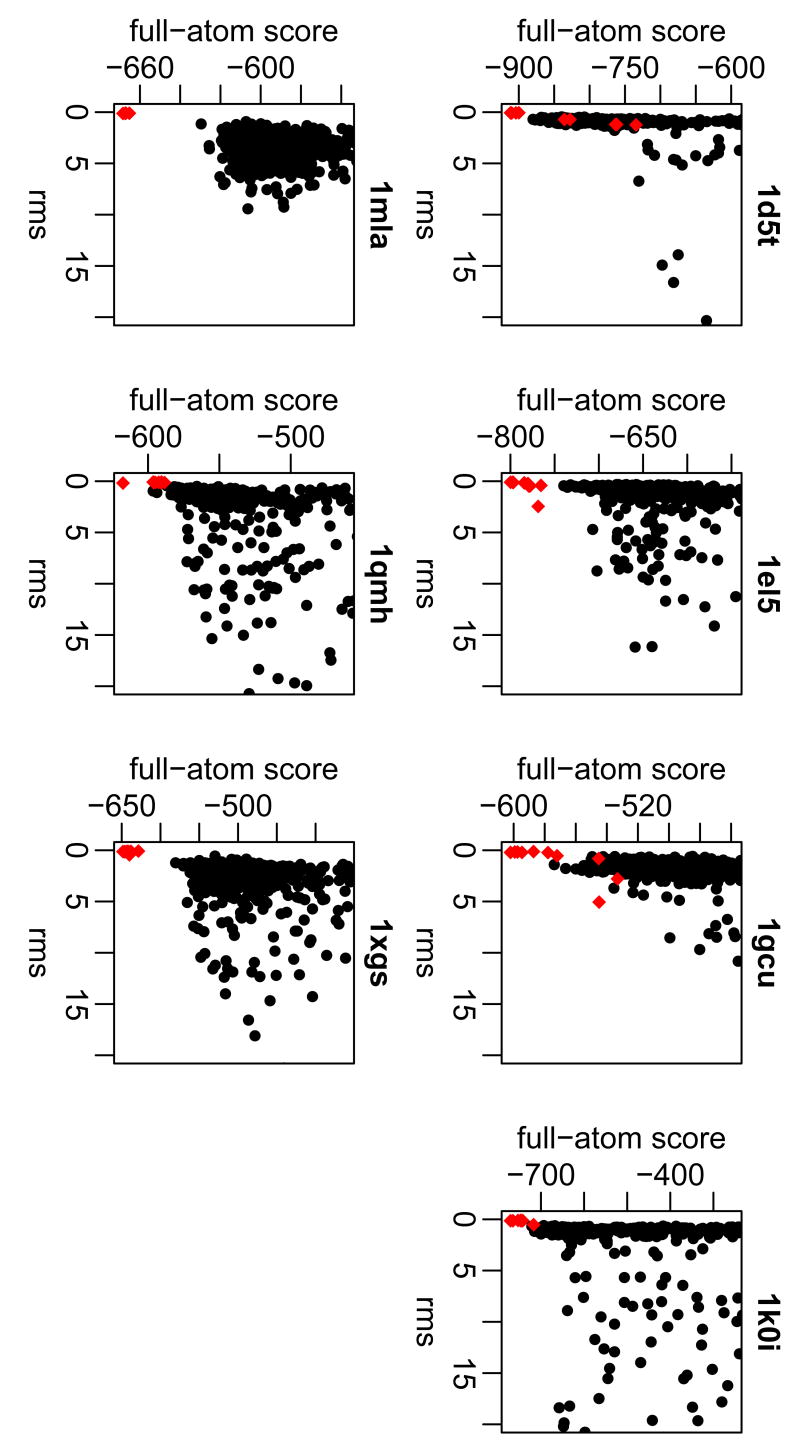
Figure 3 shows the high-resolution score plotted against root-mean squared deviation (rmsd) from the native structure for 500 decoy structures created by the local search for each of the seven proteins in the development set. The funnel-like shape of the plots shows that the minimum energy decoy corresponds to the decoy with the lowest rmsd, indicating that the score function discriminates near-native decoys. The plots also show the score of the native structure after high-resolution refinement to relieve any inherent clashes (red diamonds). These points represent the hypothetical structure that is nearest to the native structure and consistent with the Rosetta energy function. In all seven proteins, the refined native structures are found within 0.1 Å rmsd and are the structures with the lowest score. For the seven proteins presented in Figure 3, all of the plots show that the lowest-scoring decoy is within 1 Å of the native protein structure.

Figure 3. High-resolution energy landscape (score versus rmsd) for the local search on the development set.

Rmsd is calculated over all C_α atoms of the protein. (•) Decoy structures, ( ) refined native structure (using high resolution algorithm).

Global search is successful in most cases tested

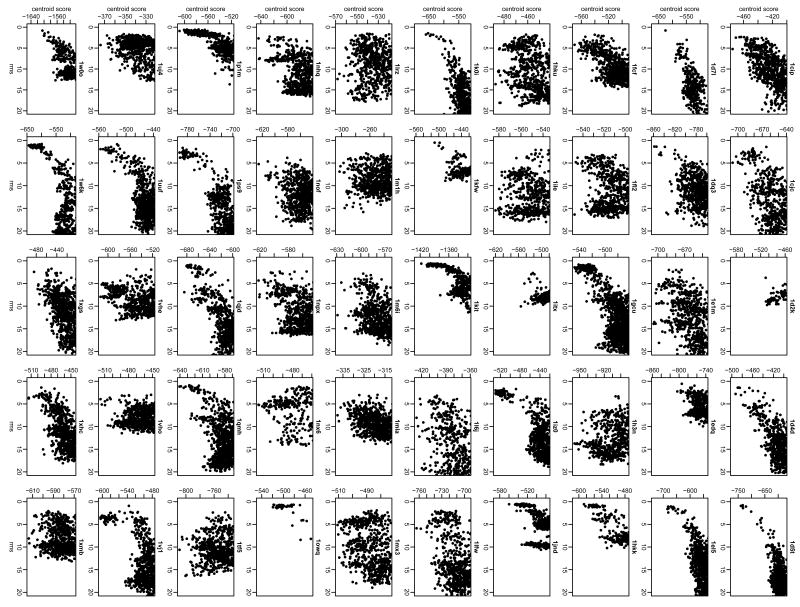
While local searches probe the native energy funnel, a global search with an unbiased starting configuration is a more realistic test of blind prediction ability. To reduce computation time, we first tested the feasibility of using the low-resolution search alone for creating near-native decoy structures. Figure 4 shows plots of the low-resolution score versus rmsd for 800 decoys from global low-resolution searches on each of the 50 proteins in the test set. To our surprise, not only are near-native structures created, but the low-resolution energy function is often able to discriminate near-native structures within a small set of low-scoring decoys. In ∼30 of the targets, funnels are apparent with the lowest scoring decoy within 5 Å of the native structure. These energy funnels reflect more than simple shape-matching of the domain insertion interface: plots of the bump and contact terms of the energy function only occasionally reveal funnels (data not shown); contributions from the residue environment and residue-residue pair scores and other low-resolution terms are necessary to discriminate near-native decoys in a broad range of targets.

Figure 4. Low-resolution energy landscapes (score versus rmsd).

Rmsd is calculated over all C_α atoms of the protein. (•) Decoy structures.

Next, we tested a two-step process where the top-scoring decoys from the global, low-resolution search are retained and used for further refinement in a high-resolution protocol. Ten high-resolution decoys were created from each of the ten top-scoring low-resolution decoys, for a total of 100 high-resolution decoys.

Figure 5 shows plots of the full-atom score versus rmsd for the high-resolution refinement of all of the proteins in the test set. The sparseness of the graph reflects the limited sampling from only top-scoring low-resolution structures, and each low-resolution starting structure produces a small range of rmsds in the ten models created. Several interesting trends can be found when comparing the low-resolution and high-resolution results. In some cases (e.g. 1fl2, 1m1h, 1nhq, 1qjd, and 1xmb), running high-resolution refinement can provide better discrimination and eliminate false-positives structures. Furthermore, the high-resolution refinement sometimes moves a low-rmsd decoy from low-resolution mode closer to the native structure, as is the case for ribose 5-phosphate isomerase (1uj4, moving from ∼4 Å to ∼3 Å) and NADPH-dependent oxidoreductase (1vj1, moving from ∼4 Å to ∼1.5 Å). The fraction of native contacts (f_nat) measure (used in the Critical Assessment of Predicted Interactions, CAPRI (Gray et al., 2003b; Wodak and Mendez, 2004)), and interaction rmsd (iRMSD (Aloy et al., 2003)) show similar trends as the rigid-body rmsd. In several cases (1d4d, 1dq3, 1jnd, 1m1h, 1p1m, and 1xmb), high-resolution refinement improves f_nat and provides better discrimination of near-native decoys (data not shown).

Figure 5. High-resolution energy landscapes (score versus rmsd).

Rmsd is calculated over all C_α atoms of the protein. (•) Decoy structures, ( ) refined native structure (using high resolution algorithm), ( ) ten refined structures for the lowest rmsd structure from the low-resolution search (only shown for cases where the lowest-rmsd structure from the low-resolution search provides a high-resolution final prediction that is closer to the native structure and lower in energy than any of the refined structures from the ten top-scoring low-resolution decoys.)

In a couple cases, high-resolution refinement does not improve the structure at all, but rather creates an increase in false positives, as can be seen in isoleucyl-tRNA synthetase (1ile) and the translocase seca subunit (1tf5). The plots in Figure 5 for these two proteins show the lowest scoring decoys (black) with lower scores than the refined native structure (red diamonds), indicating that the scoring function does not discriminate accurately. Note that the high-resolution search typically perturbs the decoy by only a few Ångstroms from the starting structure. Thus, the high-resolution refinement can only save a low-resolution search which provides top-scoring decoys within a moderate range of the native structure (3-5 Å). In fact, when the 100 top-scoring low-resolution decoys are refined for C-terminal binding protein 3 (1hku), the lowest-scoring decoys are within 2 Å versus 18 Å using only the 10 top-scoring low-resolution decoys (data not shown), indicating that additional computing time can improve some cases by probing deeper in the list of low-resolution decoys.

The funnels seen in Figures 4 and 5 can be quantified by counting the number of low-scoring decoys that have rmsd less than a threshold. Table 1 summarizes the results for both the low-resolution search and the high-resolution refinement. For the complete set of 50 proteins, the low-resolution search is successful to 2 Å rmsd for 17 proteins and to 5 Å rmsd for 31 proteins. The high-resolution refinement leads to an improvement in the number of successes with 21 proteins less than 2 Å rmsd and 33 with less than 5 Å rmsd. Therefore, the high-resolution search helps find a conformation that is closer to the native and increases the number of decoys in these low rmsd conformations. Other measures of accuracy show similar trends, with 27 proteins resulting in an f_nat greater than 30% and 27 with an iRMSD less than 3 Å. Table 1 also shows the best rmsd for the five top-scoring decoys and for all decoys in low- and high-resolution searches. The best rmsds are below 1 Å in several cases, and in about 30 cases, the best-rmsd of the top-five structures is within an Ångstrom of the best-rmsd of the whole decoy set.

Table 1. Results of the global search on the test set.

PDB	Low Resolution				High Resolution
	N2	N5	RMSbest	RMSscore	N2	N5	RMSbest	RMSscore
1kfw	5•	5•	0.51 (0.51)	0.51	5•	5•	0.47 (0.40)	0.48
1hkk†	5•	5•	0.56 (0.56)	0.56	5•	5•	1.1 (0.58)	1.1
1jnd	5•	5•	0.49 (0.42)	0.56	5•	5•	1.6 (0.76)	1.6
1kit	5•	5•	0.61 (0.59)	0.61	5•	5•	0.69 (0.58)	0.88
1w0o	2•	5•	0.81 (0.81)	0.81	3•	5•	0.82 (0.68)	1.0
1p1m	5•	5•	0.65 (0.54)	0.9	5•	5•	0.63 (0.61)	0.64
1d5t*	5•	5•	0.77 (0.77)	0.91	1	1	0.98 (0.98)	0.98
1w6k†	5•	5•	1.1 (0.80)	1.1	1	5•	1.1 (0.95)	2.2
1owq	5•	5•	0.66 (0.66)	1.2	5•	5•	0.65 (0.48)	0.7
1qmh*	5•	5•	1.1 (0.88)	1.2	5•	5•	0.83 (0.44)	0.94
1dq3	2•	5•	1.4 (1.4)	1.4	5•	5•	0.48 (0.47)	0.48
1gcu*	4•	5•	1.4 (0.79)	1.4	5•	5•	0.88 (0.62)	0.88
1el5*	4•	5•	1.1 (1.1)	1.6	5•	5•	1.3 (1.1)	1.4
1k0i*	4•	5•	1.4 (1.4)	1.7	5•	5•	1.1 (0.84)	1.1
1uuf	3•	5•	1.6 (0.87)	1.9	5•	5•	0.50 (0.39)	1.3
1iz0	1	5•	2.0 (1.6)	2.0	5•	5•	0.62 (0.61)	0.69
1edq	1	5•	0.57 (0.57)	2.2	1	5•	0.98 (0.92)	2.5
1ps9	0	5•	2.6 (1.7)	2.7	1	4•	1.4 (1.4)	3.7
1d4d	3•	5•	1.4 (1.4)	2.8	4•	5•	1.9 (1.3)	1.9
1vj1	0	5•	3.1 (0.91)	3.5	5•	5•	0.55 (0.55)	0.6
1xhc	0	5•	3.2 (1.4)	3.8	5•	5•	1.0 (0.81)	1.1
1uj4	1	5•	2.0 (1.7)	4.3	0	5•	3.0 (1.7)	3.0
1cjc	0	5•	3.6 (1.4)	4.9	0	3•	4.2 (2.2)	4.2
1qjd	4•	4•	0.99 (0.89)	6.9	5•	5•	0.62 (0.61)	0.7
1vho	0	3•	4.0 (3.0)	4.0	0	0	5.1 (2.1)	5.4
1fcf	0	3•	3.8 (1.8)	4.2	0	3•	3.7 (3.7)	3.7
1npx	0	3•	4.2 (2.4)	4.3	0	4•	3.3 (2.6)	3.4
1cip	0	3•	2.4 (2.4)	5.2	2•	5•	1.9 (1.4)	3.6
1d7l	1	2•	0.79 (0.79)	0.79	5•	5•	0.79 (0.79)	0.79
1mx3	0	2•	4.3 (1.9)	5.1	0	0	13.5 (3.4)	13.6
1fl2	0	2•	3.8 (3.2)	16.4	0	5•	3.0 (2.7)	3.0
1xgs*	0	1	2.5 (1.8)	2.5	5•	5•	1.2 (1.2)	1.2
1nhq	0	1	2.7 (2.3)	2.7	0	5•	2.9 (2.2)	3.0
1d2k†	0	1	3.8 (3.8)	3.8	0	0	8.9 (3.8)	9.0
1nof	0	1	4.7 (3.9)	5.2	0	0	6.6 (2.5)	7.5
1m1h	0	1	5.0 (2.9)	6.9	0	5•	3.4 (3.4)	3.7
1mla*	0	1	4.9 (3.0)	7.5	0	0	7.6 (4.9)	7.9
1vhe	0	1	4.9 (1.9)	8.0	0	0	5.3 (3.4)	5.4
1l6j	0	1	3.9 (3.2)	8.1	0	0	7.0 (3.2)	7.1
1itx†	0	1	4.0 (2.7)	10.1	0	0	5.1 (3.3)	5.1
1m6i	0	1	4.8 (2.8)	12.0	0	0	11.1 (4.2)	11.2
1lrz	0	1	4.9 (1.6)	12.4	0	0	10.1 (3.0)	10.2
1nx6	0	0	5.1 (1.2)	5.2	0	3•	3.7 (3.7)	3.7
1lfw	0	0	5.3 (2.0)	5.9	0	0	6.4 (3.1)	6.4
1xmb	0	0	6.3 (2.1)	8.1	0	5•	5.5 (2.1)	5.5
1tf5	0	0	7.8 (2.4)	10.6	0	0	8.4 (6.9)	8.4
1hku	0	0	5.3 (1.8)	13.6	0	0	18.4 (3.3)	18.8
1h3n	0	0	13.7 (3.0)	13.8	0	0	13.2 (7.9)	13.4
1e1m	0	0	7.1 (2.0)	13.9	0	0	8.6 (5.4)	8.7
1ile	0	0	10.7 (2.1)	15.4	0	0	11.0 (10.9)	15.0
Total	17/50	31/50			21/50	33/50

N2 – number of the five top-scoring decoy structures that are within 2Å rmsd of the native structure

N5 – number of the five top-scoring decoy structures that are within 5Å rmsd of the native structure

RMS_best – rmsd of the lowest-rmsd decoy among the five top-scoring decoys; number in parentheses is the lowest rmsd among all 800 decoys.

RMS_score – rmsd of the lowest scoring decoy.

For totals, a success indicates that two or more of the five top-scoring decoys being within a certain rmsd cutoff, denoted by a dot (•).

^*Protein is part of the development set

^†Less than 800 decoy structures were created due to run time limitations

Successes

Successful predictions can identify approaches to modeling that are working correctly. Figure 6 shows the best-scoring decoy superimposed on the native structure for a signal processing protein (1owq), hypothetical protein TM0936 (1p1m), flavocytochrome C3 (1qjd), and NADPH-dependent oxidoreductase (1vj1). For the signal processing protein and hypothetical protein TM0936 (Figure 6A-B), not only is the algorithm able to identify the correct insert domain orientation, but it can also find the correct rotamer positions for most of the side chains at the interface and in the linkers. For flavocytochrome C3 and NADPH-dependent oxidoreductase (Figure 6C-D), the insert domain is in the correct conformation, but there is some variation in the linker regions. A higher variability in the rmsd of the linkers than that of the domain orientation is commonly observed.

Figure 6. Examples of accurate predictions with native-like insert domain orientation and side-chain packing.

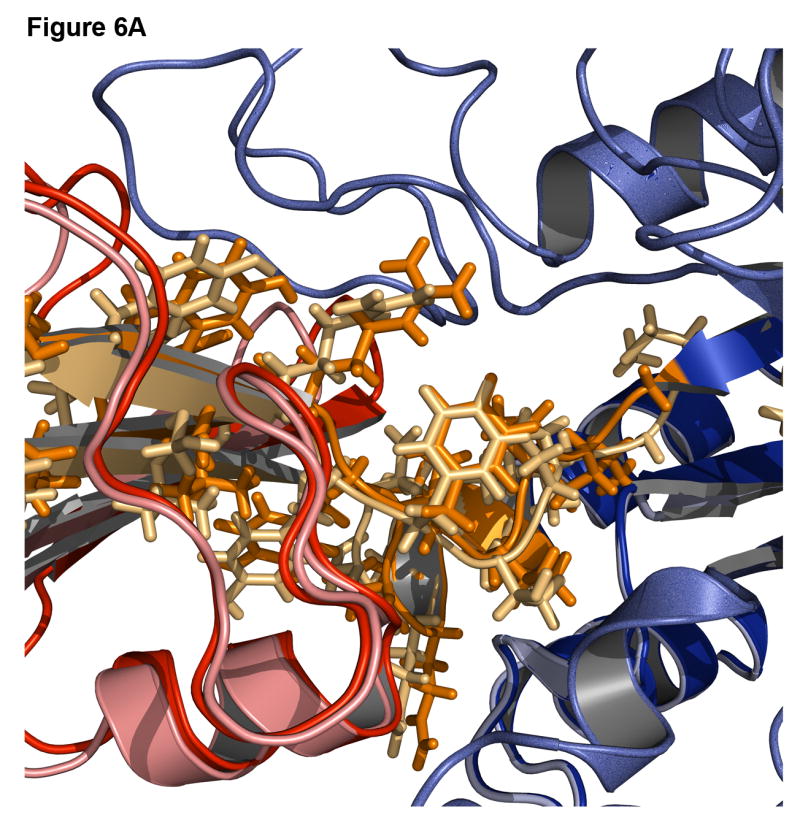
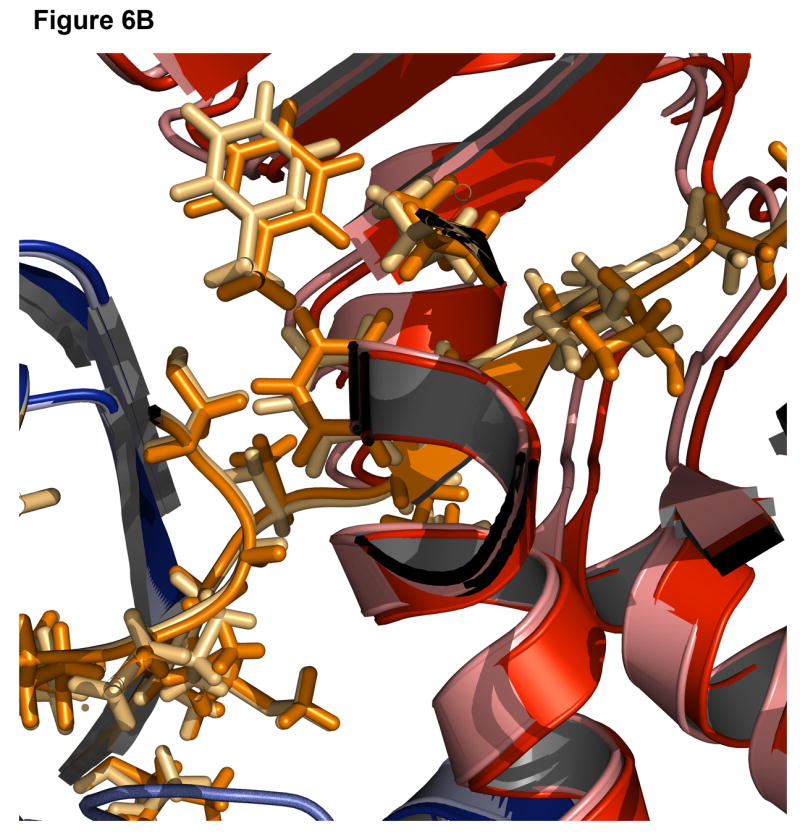
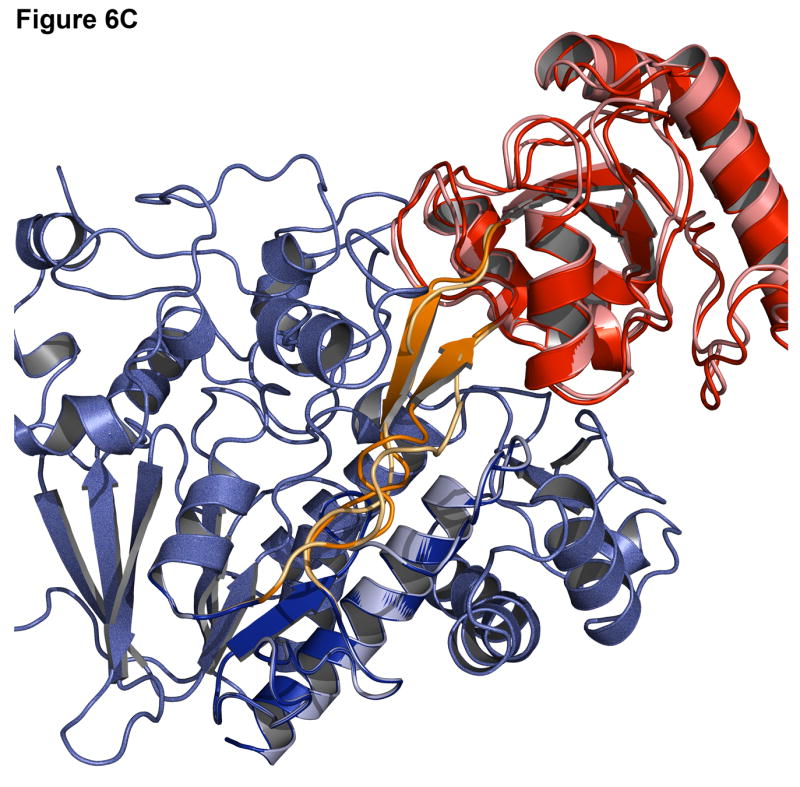
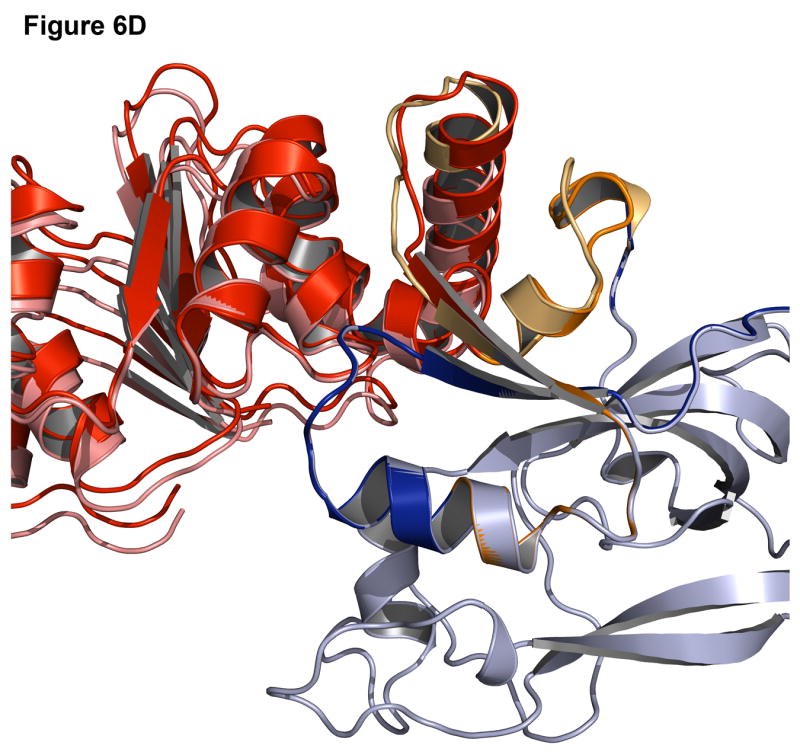
(A) Signal processing protein (1owq, C_α rmsd = 0.70Å). (B) Hypothetical protein TM0936 (1p1m, C_α rmsd = 0.64Å). (C) Flavocytochrome C3 (1qjd, C_α rmsd = 0.70Å). (D) NADPH-dependent oxidoreductase (1vj1, C_α rmsd = 0.60Å). The native structures are in dark shades with the host domain in blue, insert domain in red, linkers in orange. Structures were superimposed using only the host domain coordinates.

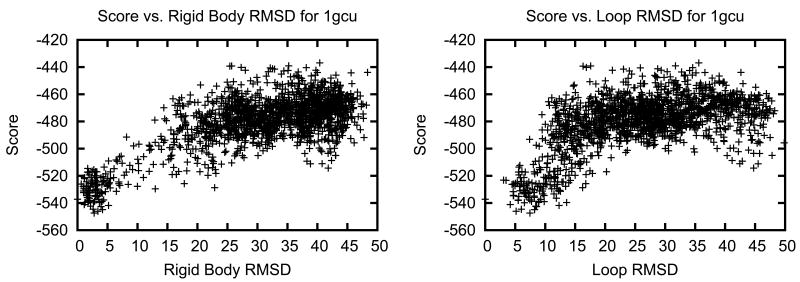
To illustrate the variability of linker conformations among decoys, Figure 7 shows low-resolution score plotted versus two types of rmsd for the case of biliverdin reductase A (1gcu). On the left is a plot of the score vs. rmsd of the insert domain C_α atoms after each decoy is superimposed onto the native structure using the host domain C_α coordinates. The right plot shows the score vs. the rmsd of the linker residue C_α atoms after superposition using only the linker C_α coordinates. In rigid-body space, the lowest scoring decoys are ∼2.5 Å from the native with ample sampling below 5 Å (Figure 7, left). However, there are no structures created with a linker rmsd less than 4 Å and the lowest scoring decoy has a linker rmsd near 5 Å (Figure 7, right). Therefore, the linkers account for the highest amount of inaccuracy in the models.

Figure 7. Low-resolution energy landscape using different rmsd measurements for biliverdin reductase A (1gcu).

Left: Score vs. rmsd over all C_α atoms of the insert domain after superimposing the host domain; Right: Score vs. rmsd over C_α atoms of only the linker residues after superimposing the linkers.

Failures

Failures can often be more instructive than successes since they point out problems in the modeling methods. One common cause for a failure is a small interface between the two domains. In the case of leucyl-tRNA synthetase (1h3n, Figure 8A-B), the insert domain is relatively small compared to the host domain and there are many alternate interfaces where the insert domain is likely to find a conformation that is compact, improving the low-resolution contact score and the van der Waals energy in the high-resolution score. Indeed, in the lowest energy structure (pink, Figure 8A) the insert domain fills a cavity in the host domain (red, Figure 8B), resulting in a shift of the insert domain away from the native conformation. Similarly, the lowest scoring model for C-terminal binding protein 3 (1hku) shows a 180° rotation of the insert domain towards the host domain, resulting in a more compact, though incorrect, structure (Figure 8C-D).

Figure 8. Examples of challenging complexes where prediction failed.

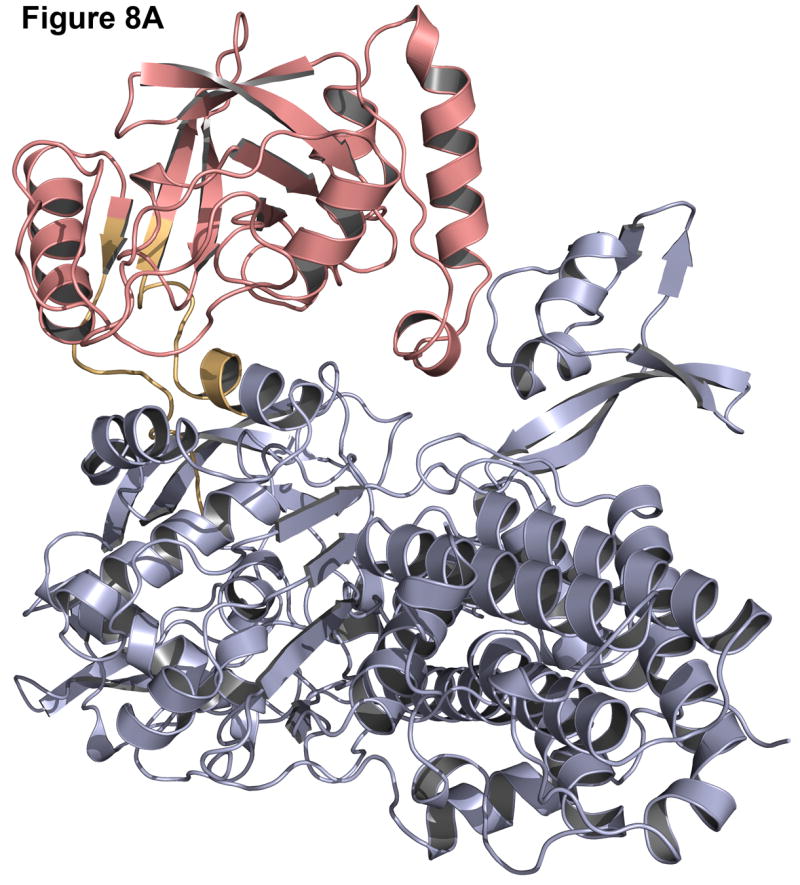
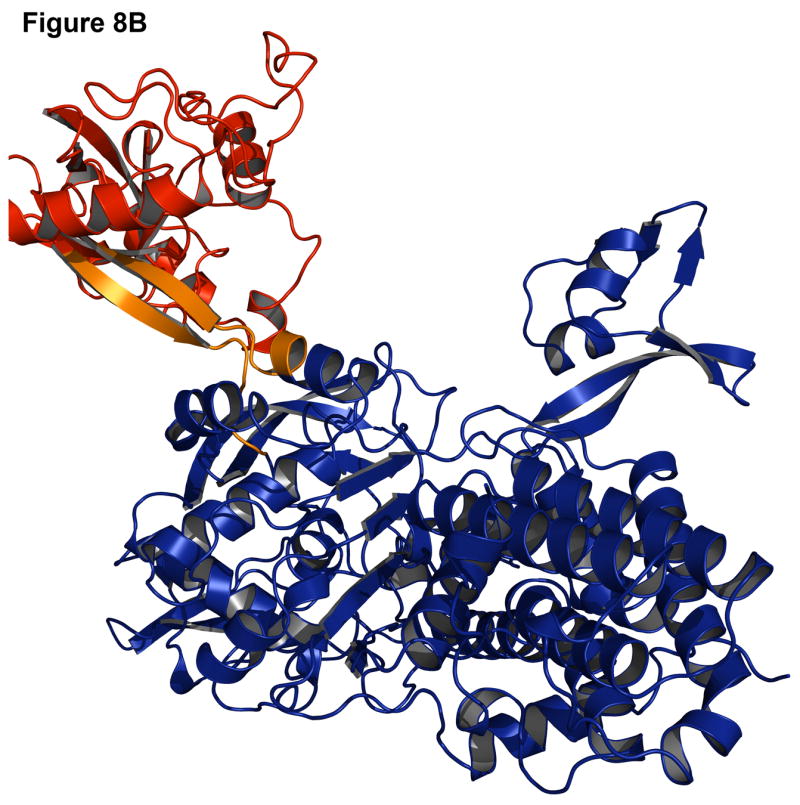
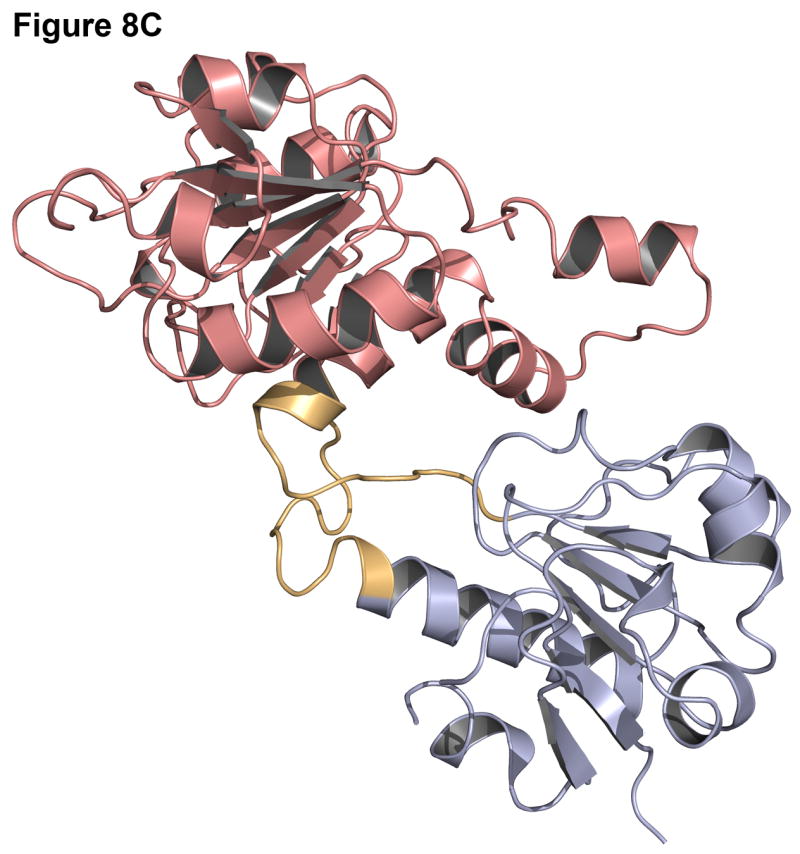
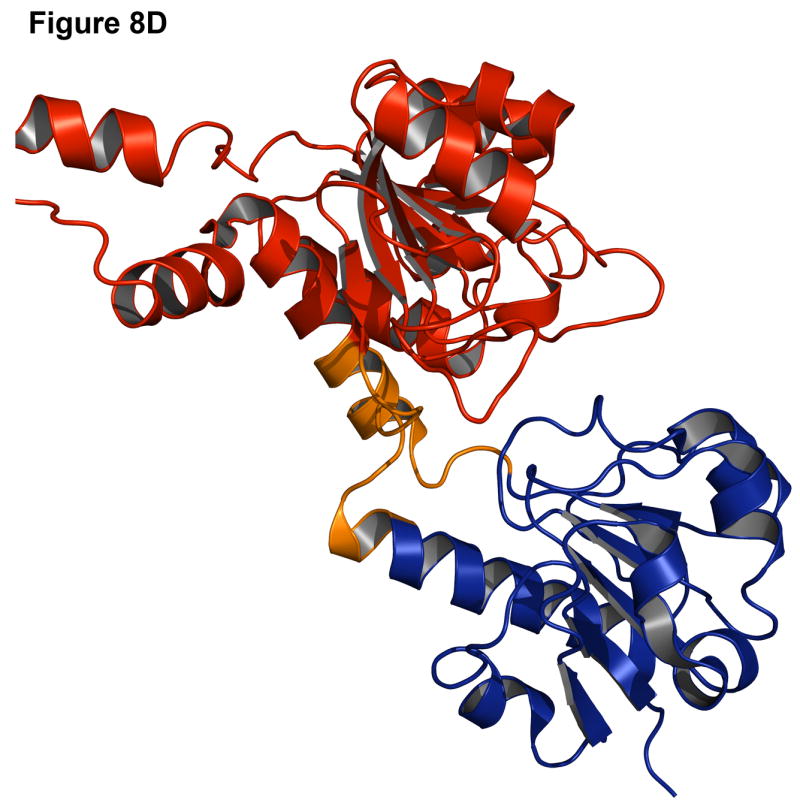
Native structure and best scoring decoy structures for leucyl-tRNA synthetase (1h3n) and C-terminal binding protein 3 (1hku) with the host domain in blue, insert domain in red, and linkers in orange, with the native structure in darker shades. (A) The best scoring decoy structure for leucyl-tRNA synthetase creates a more compact structure than the native structure (B). (C) In the best scoring decoy structure for C-terminal binding protein 3, more contacts occur when the insert domain is rotated 180° from the native structure (D).

These failures may indicate deficiencies in the energy calculation for the backbone and an overemphasis on van der Waals (contact) energies. Alternatively, the protein domains may be loosely connected in solution with flexible rigid-body orientations, one of which is stabilized by crystal contacts in the x-ray structure, making structure prediction difficult.

A second, rarer reason for failure is the inability of the scoring function to discriminate near-native decoys. On the high-resolution plot for isoleucyl-tRNA synthetase (1ile, Figure 5), several decoys at an rmsd of 15 Å (black points) have a score well below the lowest score of the refined native structures (red diamonds). Similarly for translocase seca subunit (1tf5), several decoys near 10-15 Å have scores below those of the refined native structures. To test whether these predictions could have been improved by refinement of all low-resolution decoys, rather than only the ten top-scoring low-resolution decoys, scores for ten structures refined from each of the lowest-rmsd decoys in the low-resolution set are also shown (green points). In the cases of translocase seca subunit and isoleucyl-tRNA synthetase, the near-native decoys are still are not the lowest-scoring, thus a correct prediction is still not possible. However, in several other cases (1d2k, 1edq, 1el5, 1hku, 1l6j, and 1w0o), refining the lowest-rmsd structure results in a low-scoring, near-native structure which is not sampled using only the lowest-scoring decoys from the low-resolution mode.

Discussion and Conclusions

Combinations of domains into multidomain architectures create diverse and complex functions, but few approaches are available to predict their superstructure. Many domains are linked end-to-end, but a significant fraction are joined through domain insertion, creating an intimate association between the sequences of the individual domains and a coupled folding problem. In this article, we have presented and tested one algorithm to predict the structure of domain insertion proteins. The domain insertion problem is unique in that there are multiple degrees of freedom which are interdependent on each other, thus our algorithm simultaneously optimizes the conformation of the joining linkers and the rigid-body displacement of the domains. Such an interdependent problem is also encountered in other protein structure prediction problems such as motif grafting for vaccine design (Bill Schief, personal communication) or folding using docking type approaches with connected secondary structures (Haspel et al., 2007).

To achieve predictions in light of the constraints, we exploited the fold tree graph to propagate conformational changes (Bradley and Baker, 2006) and created new Monte Carlo moves based on combinations of simpler moves which disrupt and then restore chain continuity. Similar to the introduction of combination moves for simulating dense polymer melts with configurational bias techniques (Escobedo and de Pablo, 1995), these moves proved to be efficient and capable of solving the coupled domain insertion structure prediction problem.

The results in Table 1 and Figures 4-8 indicate that the Rosetta domain insertion algorithm is capable of recovering the native structure of naturally occurring domain insertion proteins with an overall success rate of ∼65%. The high success rate may be due to the fact that the two linkers create constraints not present in pure docking problems, reducing the conformational space such that even a low-resolution approach is successful in a moderate fraction of targets. On the other hand, the linker prediction, which was typically the least accurate part of the models, is harder than a standard loop-modeling problem since the stems of the linkers are not fixed relative to each other and the environments surrounding the linkers are not constant. Nevertheless, the failure of a simple docking algorithm to predict domain insertion protein structure shows that linkers are critical for occupying sufficient space. Finally, it is important to remember that the tests performed here included an unfair advantage by using crystal structures of the individual domains, similar to the ‘bound’ protein-protein docking problem.

In the cases where there is a failure in recovering the native structure, there is often a larger volume available to the insert domain around the host domain and linkers with less secondary structure and more exposure to solvent. Several of these cases fail in low-resolution but are successful upon high-resolution refinement due to the more accurate energy function. More of the failures might be turned into successes through improvements in the scoring function to better include effects of protein conformational entropy, explicit waters, backbone torsional potentials, and electrostatics (which are more important at the protein surface). In addition to the scoring function, the number of low-resolution decoy structures used in refinement may be limiting. Greater sampling could be achieved by going deeper into the list of top-ranked, low-resolution structures at the expense of increased computer time. Alternatively, crystal contacts may be needed to position the domains to match the x-ray conformation of a dynamic protein. Crystal contacts have been found to be helpful for high-resolution prediction of loop conformations (Jacobson et al., 2002; Jacobson et al., 2004).

The results of CASP7 (http://predictioncenter.org/casp7) on domain insertion proteins show that the prediction groups were often able to predict the separate domains to moderate accuracy using algorithms that search for templates matching the entire protein's length. Thus, individual domain structures typically serve as good starting points for multidomain structure prediction. In many cases, a template matching the host domain was used to predict the full protein and led to moderately accurate predictions. By using a separate template for the host and insert domains, a more accurate model might be predicted using a domain insertion algorithm to combine the separately predicted domains. Domain insertion proteins have not been considered as a multidomain protein problem before this study, and we plan to test the algorithm in CASP8.

The current study focused on the recovery of known protein structures using native structures for the individual domains. In the consideration of using domain insertion prediction in blind predictions from sequence alone, several additional steps are required. First, a method is required for predicting the number of domains in a protein and identifying whether it is a domain insertion protein. Domain prediction is an old problem (Taylor, 1999), and there are several promising methods developed recently (Clarke et al., 2007; Tress et al., 2005) which are overcoming problems such as differing definitions of domains (Bryson et al., 2007; Veretnik et al., 2004). To exploit our domain insertion prediction method, domain identification methods need to be extended to allow domain-size gaps. Second, homology modeling can be used on the separate domains (Melo and Sali, 2007; Rohl et al., 2004a), with the benefit that each domain may be modeled more accurately when using two small templates in the absence of a single large template. The homology-modeled domains can then be used in the domain insertion algorithm to provide a model of the complete protein structure. Inserting domains using homology structures will be more challenging than the native-backbone tests presented in this paper due to the uncertainties in the homology structures. Furthermore, to accommodate intra-domain structural changes due to the combination of the domains, refinement of the final structure, including sampling of small backbone torsion angle changes, may be helpful (Bradley et al., 2005b). Due to the size of these multidomain proteins, such refinement will be computationally challenging and thus beyond the scope of the current study. Alternatively, domain insertion modeling might be valuable to find the structure of new proteins by crystallography using a molecular replacement strategy (Rossmann, 1990, 2001).

Beyond prediction of wild-type biological proteins, the algorithm is promising for understanding and designing new proteins with combined function. For example, Guntas et al. have used experimental domain insertion techniques to combine the functions of maltodextrin binding protein (MBP) with TEM-1 β-lactamase in a switch whose catalysis activity is dependent on the concentration of maltose (Guntas et al., 2005; Guntas et al., 2004). The switching activity in the insert domain may arise from backbone changes induced by the presence of the fused host domain as it undergoes a hinge motion. Structural models can guide experiments to test such hypotheses. Other targets are inteins, such as Mycobacterium tuberculosis RecA, in which inserted domains are capable of self-excision upon activation (Buskirk et al., 2004; Skretas and Wood, 2005b). As in the blind prediction problem, in order to model the domain motions from which the functional coupling is likely to arise, the current domain insertion algorithm is likely to need supplementation by a backbone refinement algorithm. The combination of these algorithms will be a valuable tool for engineering new proteins with complex function arising from the combination of domains.

Experimental Procedures

Test set

We curated a comprehensive set of 50 domain insertion proteins with known structures from the Structural Classification of Proteins (SCOP) database (Barton, 1994). The set of all SCOP structures (27599 structures) was reduced as follows: 1) single-domain proteins and those without a discontinuous domain were deleted (1118 structures remaining); 2) multimeric proteins were removed (216 structures remaining); 3) redundant proteins with matching names (which always indicated high sequence identity) were eliminated (80 structures remaining); and 4) proteins with resolution > 2.5 Å were removed (50 structures remaining). Proteins in the resulting set range from 186-821 residues with domains of 70-300 residues. In several cases (1d4d, 1edq, 1h3n, 1ile, 1kit, 1l6j, 1ps9, 1qjd, 1tf5, and 1w0o) the host definition includes more than one structural domain, creating “host domains” of 300-600 residues. Proteins in the test set represent prokaryotes and eukaryotes and include functions from protein transport and transcription to antibiotic inhibition.

Development set

The development set, used to tune the MC moves and global and local protocols, consists of a subset of seven proteins from the test set that we selected by searching through proteins in the DomIns database (www.domins.org, (Selvam and Sasidharan, 2004)). The set was created as follows: 1) all non-redundant proteins from DomIns were downloaded (1167 structures); 2) proteins were selected with single split domains (134 structures), eliminating those with multiple insertions; 3) proteins with resolution > 2.5Å were deleted, leaving 65 structures; 4) oligomeric proteins for which linkers were located at the interface between the monomers were removed since symmetry was not modeled in this study (11 structures remaining); and 5) four of the 11 remaining structures had significant missing density or other anomalies and were eliminated, leaving seven structures. The resulting development set, marked in Table 2 with asterisks, includes enzymes, inhibitors, and a secretory protein.

Table 2. Description of proteins in the test set.

PDB	Resolution (Å)	Protein name	Classification	Protein size (AA)	Host Domain	Insert Domain
1cip	1.5	Guanine nucleotide-binding protein α-1	Hydrolase	347	32-60; 182-347	61-181
1cjc	1.7	Adrenodoxin reductase	Oxidoreductase	460	6-106; 332-460	107-331
1d2k	2.2	Chitinase 1	Hydrolase	427	36-292; 355-427	291-354
1d4d†	2.5	Flavocytochrome C fumarate reductase	Oxidoreductase	569	4-359; 506-569	360-505
1d5t*	1.04	Guanine nucleotide dissociation inhibitor	Hydrolase inhibitor	431	2-291; 389-431	292-388
1d7l	2.2	P-hydroxybenzoate hydroxylase	Oxidoreductase	394	1-173; 276-394	174-275
1dq3	2.1	Endonuclease	Hydrolase	454	1-128; 415-454	129-416
1e1m	1.85	Adrenodoxin reductase	Oxidoreductase	460	6-106; 332-460	107-331
1edq†	1.55	Chitinase A	Hydrolase	563	24-443; 517-563	444-516
1el5*	1.8	Sarcosine oxidase	Oxidoreductase	385	1-217; 322-385	218-321
1fcf	2.1	Photosystem II D1 protease	Hydrolase	463	77-156; 249-463	157-248
1fl2	1.9	Alkyl hydroperoxide reductase subunit F	Oxidoreductase	521	212-325; 452-521	326-451
1gcu*	1.4	Biliverdin reductase A	Oxidoreductase	292	1-128; 247-292	129-246
1h3n†	2	Leucyl-tRNA synthetase	Aminoacyl-trna synthetase	813	1-225; 418-813	226-417
1hkk	1.85	Chitotriosidase	Hydrolase	385	22-266; 335-385	267-334
1hku	2.3	C-Terminal binding protein 3	Transcription co-repressor	345	15-114; 308-345	115-307
1ile†	2.5	Isoleucyl-tRNA synthetase	Aminoacyl-trna synthetase	821	1-197; 387-821	198-386
1itx	1.1	Glycosyl hydrolase	Hydrolase	451	33-337; 410-451	338-409
1iz0	2.3	Quinone oxidoreductase	Oxidoreductase	301	2-98; 270-302	99-269
1jnd	1.3	Imaginal disc growth factor-2	Hormone/growth factor	420	2-278; 371-420	279-370
1k0i*	1.8	P-Hydroxybenzoate hydroxylase	Hydrolase	394	1-173; 276-394	174-275
1kfw	1.74	Chitinase B	Hydrolase	444	10-327; 389-444	328-388
1kit†	2.3	Sialidase	Hydrolase	781	25-216; 347-781	217-346
1l6j†	2.5	Matrix metalloproteinase-9	Hydrolase	444	29-215; 391-444	216-390
1lfw	1.8	PepV	Hydrolase	468	1-186; 383-468	187-382
1lrz	2.1	Factor essential for expression of methicillin	Antibiotic inhibitor	412	1-244; 310-412	245-309
1m1h	1.95	Transcription antitermination protein NusG	Transcription	186	5-50; 132-186	51-131
1m6i	1.8	Programmed cell death protein 8	Oxidoreductase	608	128-263; 401-477	264-400
1mla*	1.5	Malonyl-coenzyme A acyl carrier protein	Acyltransferase	307	3-127; 198-307	128-198
1mx3	1.95	C-terminal binding protein 1	Transcription repressor	352	27-125; 319-352	126-318
1nhq	2	C-terminal binding protein 1	Oxidoreductase	321	1-119; 243-321	120-242
1nof	1.42	Xylanase	Hydrolase	413	31-43; 321-413	44-320
1npx	2.16	Xylanase	Oxidoreductase	321	1-119; 243-321	120-242
1nx6	2.15	Aspartate-semialdehyde dehydrogenase	Oxidoreductase	371	1-133; 358-371	134-357
1owq	2	Signal processing protein	Signaling protein	361	1-239; 308-361	240-307
1p1m	1.5	Hypothetical protein TM0936	Unkown function	404	1-49; 331-404	50-330
1ps9†	2.2	2,4-dienoyl-CoA reductase	Oxidoreductase	671	1-465; 628-671	466-627
1qjd†	1.8	Flavocytochrome C3	Fumarate reductase	568	1-359; 506-568	360-505
1qmh*	2.1	Rna 3′-terminal phosphate cyclase	Phosphate cyclase	338	5-184; 280-338	185-279
1tf5†	2.18	Preprotein translocase seca subunit	Protein transport	780	1-226; 349-780	227-348
1uj4	1.8	Ribose 5-phosphate isomerase	Isomerase	227	3-131; 206-227	132-205
1uuf	1.76	Zinc-type alcohol dehydrogenase-like protein	Oxidoreductase	348	3-144; 313-348	145-312
1vhe	1.9	Aminopeptidase/glucanase homolog	Unkown function	367	3-72; 163-367	73-162
1vho	1.86	Endoglucanase	Unkown function	333	3-69; 153-333	70-152
1vj1	2.1	Putative NADPH-dependent oxidoreductase	Unknown function	351	1-124; 312-351	125-311
1w0o†	1.9	Sialidase	Hydrolase	777	25-216; 347-777	217-346
1w6k	2.1	Lanosterol synthase	Isomerase	732	6-99; 379-732	100-378
1xgs*	1.75	Methionine aminopeptidase	Aminopeptidase	295	1-194; 272-295	195-271
1xhc	2.35	NADH oxidase /Nitrite reductase	Oxidoreductase	289	1-103; 226-289	104-225
1xmb	2	IAA-amino acid hydrolase homolog 2	Hydrolase	407	16-194; 314-407	195-313

^*Indicates a protein is part of the development set

^†Indicates the “host domain” includes more than one structural domain. Additional domains are as follows: 1d4d, 4-102; 1edq, 24-132; 1h3n, 687-814; 1ile, 682-821; 1kit, 544-781; 1l6j, 29-105; 1ps9, 1-330; 1qjd, 1-102; 1tf5, 571-780; 1w0o, 544-777.

Domain insertion problem

The domain insertion algorithm requires the protein's sequence and structures of the individual component domains. Component domains maintain a fixed backbone to reduce the conformational search space. The low-resolution problem is

$$\text{min }G(T,R,\{{\varphi }_{\text{i}}\},\{{\psi }_{\text{i}}\})$$

where G is a function approximating the free energy of the folded protein subject to connectivity constraints, T and R are vectors describing the relative location and orientation of the host and insert domains by six translational and rotational degrees of freedom, and {φ_i} and {ψ_i} represent the 44 backbone torsional angles of the linker segments. For the high-resolution problem, the set of all side-chain torsion angles {χ_ij} must also be determined for all residues in the protein.

Initial conditions

Local searches probe the energy landscape near the native structure; therefore each simulation begins with a different local perturbation of the native structure as follows. Similar to the local starting position in docking (Gray et al., 2003a), a rigid-body perturbation translates the insert domain by Gaussian random distances of 3 Å perpendicular to the plane of contact between the domains and 8 Å standard deviation in the parallel directions, spins the insert domain around the line of domain centers by a Gaussian random angle of 8° standard deviation, and tilts off the line of centers by a Gaussian random angle of 8° standard deviation around a center of rotation located at the midpoint of the linkers.

A global search emulates a blind prediction and thus requires an unbiased starting structure. Therefore, a script arbitrarily randomizes the positions and orientations of the domains, and then they are systematically positioned by defining a vector for each domain pointing from the domain center to the centroid of the domain linker residues. The insert domain is rotated and translated until the two vectors are collinear and of opposite direction, and the insert domain is rotated around the collinear vectors until the four ends of the linkers are as close to co-planar as possible. The resulting structure is stored for repeated input. For each independent decoy, this structure is perturbed by randomly rotating the insert domain around the centroid of the linker residues.

For both local and global searches, to avoid searching impossible conformations, any starting structures with significant clashes are immediately rejected. Finally, linkers are initially built using a single iteration of the loop building protocol.

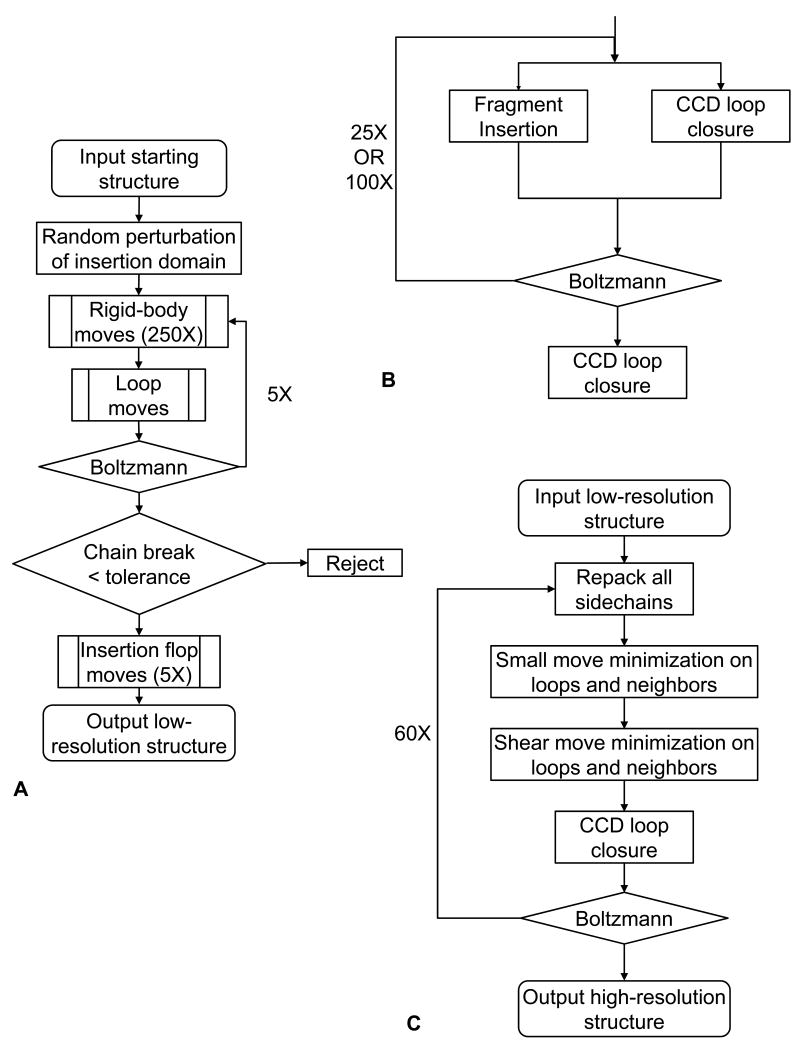
Low-resolution search

After the initial perturbation, the low-resolution search algorithm (Figure 10A) starts with an outer loop of five cycles of rigid-body and loop moves. Each set of rigid body moves consists of 250 rigid-body perturbations (∼2 Å and/or 5°) each followed by a Metropolis test of move acceptance,

Figure 10. Algorithm flow charts.

(A) Low-resolution mode; (B) Details of the loop-building algorithm for low-resolution mode; (C) High-resolution mode.

$$P=\{\begin{array}{cc}\text{exp}(-\Delta G/kT)& \text{for}\Delta G>0\\ 1& \text{for}\Delta G\le 0,\end{array}$$

where P is the probability of acceptance of a move, k is the Boltzmann constant, T is temperature, and ΔG is the change in score resulting from the move. Rigid-body step sizes are adjusted every 50 moves to maintain a move acceptance rate near 50%.

Rigid body moves are followed by a set of loop building moves (Figure 10B) which alternate between a random 3-residue fragment insertion (3mers) and CCD (Canutescu and Dunbrack, 2003) loop closure, followed by the Metropolis criterion to accept or reject trial configurations. Fragment insertions and CCD are repeated 25 times during the first three outer iterations and 100 times in the later iterations, and the chain-break score weight is increased geometrically every 10 cycles from 0.02 to 1.0.

After rigid-body and loop building cycles are completed (Figure 10A), a final CCD procedure is applied. If the chain-break score is not within the tolerance of 0.02 Å, the decoy is rejected. Otherwise, to complete the low-resolution stage with a finer optimization, five sets of insertion flop moves are performed, where each set consists of 10 perturbations of linker backbone torsion angles followed CCD and a Metropolis test.

High resolution search

The high-resolution search (Figure 10C) first places an all-atom side-chain at every residue position and repacks them using a rotamer library (Dunbrack and Cohen, 1997) and gradient-based minimization (Wang et al., 2005). Next, a random small perturbation of a φ or ψ angle (“small move”) and a pair of φ/ψ angles (“shear move”, (Rohl et al., 2004b)) are used to perturb the backbone of the linkers using a fold tree as shown in Figure 2A-B. After each backbone torsion angle change, the structure undergoes gradient-based minimization with the linker backbone torsion angles and the rigid-body transformation as independent variables, then CCD loop closure on both linkers and a Metropolis test. The cycle is repeated 60 times starting each time with side-chain packing of the residues which have increased energy since the last cycle, or a full repack of all residues every 10 cycles.

Energy function

Rosetta's multi-scale algorithm is based on two scoring functions. At low-resolution, a fast energy function is used that accounts for the backbone heavy atoms and a pseudo-atom representing the centroid of the side-chain atoms. The scores, developed for and tested on folding, loop building, and docking problems, include bumps, contacts, knowledge-based residue environment and residue-residue pair propensities, a loop-closure measure, and a Ramachandran score (Gray et al., 2003a; Rohl et al., 2004b; Simons et al., 1999).

At high resolution, Rosetta uses an all-atom potential to capture atomic scale physical forces. For the domain insertion application, this includes van der Waals interactions (Gray et al., 2003a), implicit solvation (Lazaridis and Karplus, 1999), orientation dependent hydrogen bonding (Kortemme et al., 2003; Morozov and Kortemme, 2005; Morozov et al., 2004), and a rotamer probability to capture side-chain internal energies (Dunbrack and Cohen, 1997; Kuhlman and Baker, 2000). Both low and high-resolution score functions include a score to penalize the chain breaks calculated as the square-root of the difference between the square of the N-C distance across the chain break and the square of the ideal N-C distance. The energy function implicitly includes entropic contributions from the solvent, but it neglects the conformational entropy of the protein itself. Parameters and weights have been published previously (Bradley et al., 2005b; Kuhlman et al., 2003).

Algorithm Availability

The full domain insertion protocol is freely available for academic and non-profit use as part of the Rosetta structure prediction suite at www.rosettacommons.org. The distribution includes supporting scripts, documentation, and full source code.