Geometric constraints on neuronal connectivity facilitate a concise synaptic adhesive code

Abstract

The nervous system contains trillions of neurons, each forming thousands of synaptic connections. It has been suggested that this complex connectivity is determined by a synaptic “adhesive code,” where connections are dictated by a variable set of cell surface proteins, combinations of which form neuronal addresses. The estimated number of neuronal addresses is orders of magnitude smaller than the number of neurons. Here, we show that the limited number of addresses dictates constraints on the possible neuronal network topologies. We show that to encode arbitrary networks, in which each neuron can potentially connect to any other neuron, the number of neuronal addresses needed scales linearly with network size. In contrast, the number of addresses needed to encode the wiring of geometric networks grows only as the square root of network size. The more efficient encoding in geometric networks is achieved through the reutilization of the same addresses in physically independent portions of the network. We also find that ordered geometric networks, in which the same connectivity patterns are iterated throughout the network, further reduce the required number of addresses. We demonstrate our findings using simulated networks and the C. elegans neuronal network. Geometric neuronal connectivity with recurring connectivity patterns have been suggested to confer an evolutionary advantage by saving biochemical resources on the one hand and reutilizing functionally efficient neuronal circuits. Our study suggests an additional advantage of these prominent topological features—the facilitation of the ability to genetically encode neuronal networks given constraints on the number of addresses.

Much of the complexity of neuronal networks lies in the pattern of synaptic connections between neurons (1). The human brain contains ≈10¹¹ neurons, each forming ≈10⁴ synaptic connections (2). How do neurons know how to make the right connections? Roger Sperry's “chemoaffinity hypothesis” postulates that neurons select their targets by recognizing distinct molecular markers displayed on the neuronal surfaces (3). The implication of this hypothesis is that neuronal connectivity is genetically encoded. Candidate genetic loci for the synaptic connectivity code have been found in several organisms including Caenorhabditis elegans (4, 5), Drosophila (6), and vertebrates (7). Recent work has suggested that in vertebrates, protocadherins—cell adhesion proteins of the cadherin superfamily may constitute this adhesive code (7–13). Protocadherins are localized to the synaptic junctions, where they form contacts with similar proteins on neighboring neurons (13, 14).

A naïve design for genetically encoding neuronal networks would assign each neuron a unique address and a list of addresses that it should connect to. This design potentially permits the genetic encoding of any arbitrary network but poses the problem of requiring diversity of the markers constituting the neuronal addresses. Although the genomic architecture of the protocadherin proteins resembles that of T cell receptors, with a variable extracellular portion of the protein spliced to a constant intracellular domain (8), mechanisms such as somatic recombination and hypermutation, which generate diversity in the immune system have not been observed in the protocadherin loci. Rather, the distinct number of protocadherin proteins in the mammalian brain is currently estimated to be ≈50 (7) and does not seem to increase from mouse to human. The marker diversity needed could be obtained by a combinatorial expression of a set of markers. With a set of m markers one could potentially achieve 2^m different neuronal addresses, enough to implement any connectivity pattern even with 50 proteins. However, such an elaborate combinatorial expression by a neuron has not yet been observed. Rather, individual neurons usually express only a small subset of protocadherin proteins, and the number of possible distinct combinations on a single neuron has been estimated at ≈10⁵ (9). Thus, the orders-of-magnitude differences between the number of available combinations of molecular markers and the size of the neuronal network seem to represent a paradox as to how the resulting connectivity can be achieved.

Here, we suggest that this paradox can be resolved if the design of neuronal networks is not random but rather displays unique topological features—a geometric layout with recurring connectivity patterns. We find that the vast complexity of neuronal wiring can be genetically encoded by a concise set of neuronal addresses if neurons are physically limited in space so that they can potentially form connections not with the entire network but, rather, with a limited set of targets in their physical neighborhood. This geometric network design allows the reutilization of the same set of markers in different, physically separated regions of the networks.

We also find that the appearance of recurring connectivity patterns that effectively create a more ordered network can further reduce the number of required neuronal addresses. In our simulations, we generate geometric networks with different levels of order and show that the extent at which the same connectivity patterns are reutilized inversely correlates with the minimal number of neuronal addresses required. We further demonstrate these results by showing that the number of neuronal addresses needed to wire the C. elegans neuronal network is significantly lower than in randomized networks with the same geometric constraints and the same symmetry.

Geometric architecture of neuronal networks has been suggested to be optimal in the sense of minimizing wire length (15, 16), thus saving biochemical resources and minimizing signal delay and attenuation. Our study highlights an additional potential evolutionary advantage of geometric constraints—allowing network wiring with a concise limited set of molecular markers. Our results further predict that a constraint on the number of molecular markers may select for ordered network topologies containing recurring connectivity patterns.

Results

Number of Neuronal Addresses in Geometric Networks Scales Sublinearly with Network Size.

We first sought to compare the minimal number of addresses required to genetically encode arbitrary networks with no geometry to the number required to encode networks with geometric constraints. We generated arbitrary directed geometric networks with N nodes arranged on a d-dimensional Euclidean lattice with toroidal (continuous) boundary conditions (17). Among every pair of nodes within a range of R lattice units, an edge in each direction is set with probability p = k/D, where D = (2R + 1)^d is the neighborhood size. and k is the average number of edges per node (Fig. 1b). Arbitrary networks without geometric constraints were created according to the Erdős–Rényi model (18) by connecting any pair of nodes with probability p = k/N in each direction (Fig. 1a).

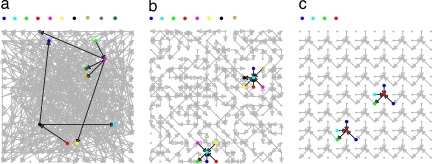
Fig. 1.

The number of addresses required to wire geometric networks is smaller than the number required to wire arbitrary networks. All networks have 225 nodes and a mean connectivity of two edges per node. Addresses are depicted by colors. The addresses of the two highlighted nodes and their connected neighbors in each figure are shown above each image. (a) An arbitrary Erdős–Rényi network in which all nodes can connect to each other requires 218 addresses. (b) A 2D geometric network with a neighborhood size of D = 9 nodes requires only 38 addresses. (c) An ordered geometric network in which the same connectivity pattern in a neighborhood of size D = 9 is iterated throughout the network. The network requires 12 addresses. The geometric networks shown have noncontinuous boundary conditions for clarity.

We consider a neuronal wiring code in which each neuron is identified uniquely by an address, a protein or a set of proteins expressed on its surface. A neuron X will form a synapse with neuron Y if the pattern of proteins on Y's dendrites corresponds to that on X's axon. We do not assume any mechanism of interaction or internal computation here, only that neurons are uniquely identified by a set of proteins on their surface and that a deterministic intracellular logic determines whether the addresses will connect or not [neurons can display different sets of proteins on their axons and dendrites, but for simplicity, we define a neuronal address as the union of these two sets]. The results that follow are invariant to such an extension of the model (see Methods)]. A pattern of connectivity between any two neuronal addresses A, B (a directed edge, edges in both directions, or no edge) requires that all neuronal pairs in the network that have these addresses and are physically close enough to connect will connect similarly. We computed the minimal number of addresses compatible with a given network using a heuristic optimization algorithm (Methods). Hereafter, the number of addresses and the minimal number of addresses will be used synonymously.

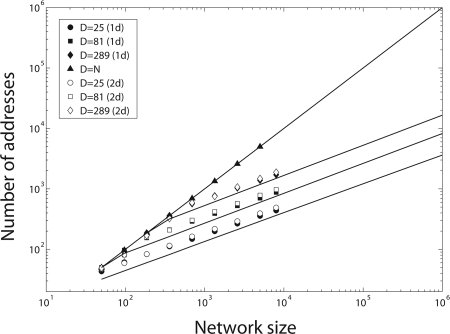
A crucial difference between arbitrary networks and geometric networks is in the set of nodes to which any given node can connect. Whereas in arbitrary networks, this set includes the entire network, in geometric networks this set includes only nodes within a volume of size D = (2R + 1)^d (Fig. 1). We find that the minimal number of neuronal addresses scales linearly with network size N in arbitrary networks without geometric constraints (Fig. 2). In contrast, in geometric networks in which D is larger than log(N), the number of addresses scales approximately as $\sqrt{DN}$, the square root of the network size and the neighborhood size (see Methods for analytical derivation). Thus, increasing the network size while maintaining the same geometric constraints (same D) results in a substantial decrease in the number of required addresses relative to arbitrary networks with no geometry. As the local connectivity neighborhood size D approaches N, the geometric constraints are alleviated, and the number of addresses scales linearly with network size N. Thus, the smaller the target size allowed for each neuron, the smaller the number of addresses required. In geometric networks in which the neighborhood size D is smaller than log(N), the number of neuronal addresses is asymptotically independent of network size (Methods).

Fig. 2.

Number of addresses in geometric networks scales sublinearly with network size. Shown is a log–log plot of minimal number of addresses vs. network size. In arbitrary networks with no geometric constraints, the number of addresses scales linearly with network size N (filled triangles). In geometric networks, the minimal number of addresses scales approximately as the square root of network size N and of the neighborhood size D. Filled symbols are simulation results for 1D geometric networks, open symbols are for 2D networks. The number of addresses is independent of dimensionality and depends only on the neighborhood size. Lines show the analytical approximation obtained by numerically solving Eq. 3. All networks have a mean connectivity k = 5 (standard errors smaller than marker size).

The scaling exponent of the number of neuronal addresses versus network size depends slightly on the mean connectivity of each neuron k. It peaks at ≈1/2 (that is, the number of addresses scales as N^α, where α = 1/2) for k = D/2 and becomes smaller for both smaller and larger mean connectivity [see supporting information (SI) Fig. S1]. The number of neuronal addresses required to encode the wiring of a fully connected neighborhood (k = D) and an empty network (k → 0) approaches zero.

Many real world networks are often modeled not with the Erdős–Rényi model, which result in a Poissonian degree distribution, but rather with networks with heavy tailed degree distributions (19, 20). To study the effect of heavy tailed degree distributions on the minimal number of neuronal addresses, we simulated geometric networks with power law out degrees (p(k) ≈ k^−γ) (19, 20). Such networks have been suggested to better represent neuronal networks such as that of the worm C. elegans (17). Interestingly, the more skewed the connectivity distribution (the smaller the power exponent γ), the smaller the number of addresses needed. This can be understood when considering the limit of γ = 2. In this limit, a condensation effect occurs, where each local neighborhood resembles a star-like network (21), with a central hub connecting to all reachable targets. Such a topology contains only two addresses in each neighborhood—one for the hub and another for all other nodes.

The scaling behavior of the number of addresses with neighborhood size is obtained for 1D and 2D (Fig. 2) as well as for 3D geometric networks (data not shown). It depends only on the size of the neighborhood and not on the dimension. In addition, our results can be generalized to other network models such as topographic mappings and small-world networks (22) (SI Text). The significant reduction in the required number of neuronal addresses is achieved whenever neurons are constrained to potentially connect only to a subset of neurons rather than to any other neuron in the network (Fig. S2).

Our model assumes that neurons are capable of arbitrarily complex calculations on the addresses displayed on their surfaces. The attainable calculations performed by a neuron may be limited by biochemical mechanisms. For example, one can consider a more mechanistically detailed code in which synapses form only if the source and target neurons display a common surface protein on their axons and dendrites respectively. Such a limitation will increase the number of addresses required to encode the same network topology (thus our calculations provide a lower bound).

In summary, we find that a geometric network design in which connections for each neuron are arbitrarily placed not with the entire network but only within a limited physical neighborhood substantially reduces the required number of neuronal addresses. The minimal number of neuronal addresses scales approximately as the square root of the network size rather than a linear scaling in arbitrary networks with no geometry.

Geometric Networks Containing Recurring Connectivity Patterns Require Fewer Addresses than Arbitrary Geometric Networks.

Thus far, we compared random networks with geometric constraints to arbitrary networks without geometric constraints and found that geometric networks facilitate connectivity with far fewer neuronal addresses. The human neuronal network is ≈1,000 times larger than the mouse neuronal network. Arbitrary geometric neuronal wiring would thus require only ≈30 times as many addresses in human relative to mouse, rather than 1,000 times in networks without geometric constraints. However, the estimated number of protocadherin addresses (10⁵) is still orders of magnitude smaller than the square root law prediction (assuming n = 10¹¹ and D > 10⁴, the required number of addresses should exceed 10⁷). We next attempt to solve this discrepancy.

An important characteristic of real neuronal networks that we have thus far ignored is that they are not random but, rather, display recurring connectivity patterns (17, 23–27). These patterns, often termed “network motifs,” have been suggested to serve as functional building blocks in information processing networks (28). We next studied whether such nonrandomness in the network topology further reduces the required minimal number of neuronal addresses relative to random geometric networks.

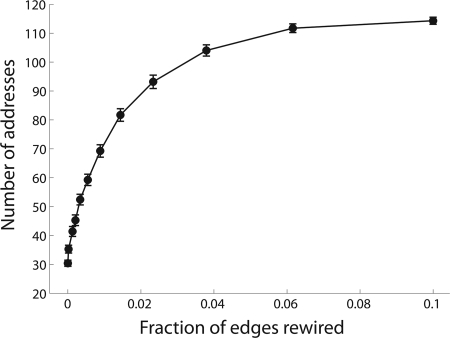
We started out with an ordered geometric network, in which the same connectivity pattern was repeated in each neighborhood (Fig. 1c). We then randomized the network by successively removing and adding edges at random within each local neighborhood and recalculated the minimal number of addresses.

We find that the more ordered the networks, the fewer the number of addresses required to encode it (Fig. 3). In the extreme case of a fully ordered network, the number of addresses becomes invariant to network size. In this case, increasing the network size involves adding neighborhoods with the same connectivity and the same set of addresses (Fig. 1c). Thus, increasing the size of the network, while repeating existing connectivity patterns, can facilitate encoding neuronal networks with substantially fewer addresses than random geometric networks.

Fig. 3.

Ordered geometric networks require fewer addresses than random geometric networks. One-dimensional geometric ordered networks with n = 1,000 nodes and k = 2 edges per node with a neighborhood size of D = 25 were generated by replicating the connections in one random neighborhood throughout the network. The network was then randomized by shuffling edges within each neighborhood. The number of addresses increases as the geometric networks become less ordered. x axis is the fraction of edges rewired; y axis is the number of addresses. Standard deviations are across 100 repetitions.

Number of Addresses in C. elegans Neuronal Network Is Significantly Smaller than Randomized Networks with the Same Degree Sequences and the Same Geometric Constraints.

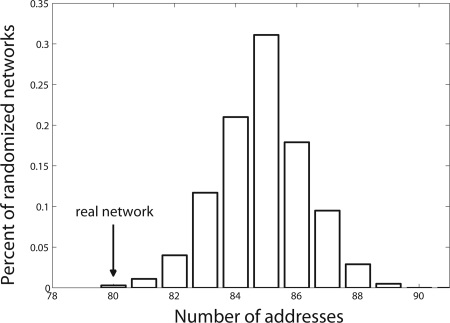
We have shown that in simulated ordered geometric networks containing recurring connectivity patterns, the number of neuronal addresses is substantially lower compared with random geometric networks. We next asked whether this order-related reduction occurs in real neuronal networks. To answer this, we computed the minimal number of addresses in the C. elegans neuronal network, the only one to date whose connections have been fully mapped (24). We then generated 1,000 randomized networks with the same degree sequences as the real network (same number of incoming and outgoing edges at each node), and with the same geometric constraints, and computed the minimal number of addresses for each network. Lacking detailed coordinates and physical span of the neurons, we used the pattern of connection to estimate a measure of physical proximity (Methods).

We find that the real neuronal network, with 281 nodes and >2,000 edges can be encoded by 80 neuronal addresses. This means that it can potentially be wired with 80 different combinations of surface proteins. The randomized networks could be encoded by 85 ± 1.5 neuronal addresses (P = 0.003) (Fig. 4). Indeed, the C. elegans neuronal network has been shown to contain a large set of highly significant network motifs that cannot be explained solely by geometry (17, 26, 28). This result holds even when controlling for all right–left and ventral–dorsal symmetries in the network (SI Text).

Fig. 4.

Number of addresses required to wire the C. elegans neuronal network is significantly smaller than the number required to wire randomized networks with the same degree of connectivity and the same geometric constraints (P = 0.003). Shown is the distribution of addresses for the randomized networks. Arrow denotes the number of addresses required to wire the real network, 80 addresses.

Discussion

Understanding how the patterns of neuronal connections are genetically encoded is a formidable challenge. Here, we studied the relation between the topologies of neuronal networks and the minimal number of genetically encoded addresses required to wire them. We found that the number of neuronal addresses required to wire arbitrary Erdős–Rényi networks, in which any two neurons can potentially form a synaptic connection is on the order of the number of neurons in the network. In contrast, arbitrary networks with geometric constraints require a significantly smaller number of addresses that scales approximately only as the square root of the network size. We also found that within the class of geometric networks, the minimal number of addresses is further reduced in ordered network topologies in which a connectivity pattern is replicated throughout the network. The more “order” there is in the network, the lower the number of addresses needed to encode it.

The existence of geometric patterns of connectivity in neuronal networks in which neurons are constrained to connect to a limited physical neighborhood have been realized for a long time and attributed to a wire-length minimization principle, saving biochemical resources and minimizing signal delay and attenuation (15, 16). Here, we suggest a different evolutionary force that may select for a geometric network design. We find that geometric networks can be wired with a substantially smaller number of neuronal addresses compared with arbitrary networks without geometry. Because physically separated parts of the network cannot form connections, the same set of addresses (e.g., surface proteins) can be reused again and again. Thus, if neuronal wiring is to be genetically encoded by a limited set of addresses, a geometric network might be the only way to realize this goal.

The optimality of the geometric design of neuronal networks has an analogy in the technological world. In radio broadcasting, a limited frequency band is used to accommodate different information channels, each using a limited bandwidth around a carrier frequency (29). By limiting the transmission power of antennas, the same carrier frequencies can be used to transmit different information in spatially remote areas. As in the genetically encoded addresses, the information conveyed in the radio transmission has a limited resource—frequency band, and by restricting communication to a local region, the resource can be reused. A high-power transmission of an antenna would preclude the reuse of the same carrier frequencies in neighboring regions for transmitting different information.

Neuronal networks are far from random, displaying highly overrepresented connectivity patterns termed network motifs (17, 23–27). Network motifs in neuronal networks have been suggested to be selected as recurring functional building blocks, performing efficient calculations (23, 25, 28). Here, we found that within the class of geometric networks, ordered networks in which the same connectivity pattern is replicated throughout the network facilitate an additional reduction in the minimal number of neuronal addresses. Thus, this study suggests that recurring network patterns in neuronal networks confer an additional advantage: they allow the wiring of these networks with a concise set of genetically encoded addresses.

To study whether the connectivity patterns of real neuronal networks may facilitate a reduction in the number of genetically encoded addresses, we compared the minimal number of neuronal addresses required to encode the neuronal network of C. elegans to randomized versions with the same degree sequences and the same geometric constraints. We found that the number of addresses in the real network is significantly smaller than in the randomized networks. This result holds even when controlling for all right–left and ventral–dorsal symmetries in the network and may be linked to the abundance of recurring connectivity patterns found in this network (17, 28). It is important to note that the numerical difference between the number of addresses in the C. elegans network and the average number in the randomized versions, although statistically significant, is quite small. Modern high-resolution techniques for probing neuronal connectivity (30) may soon provide detailed large-scale data of neuronal connectivity in mammalian brains. It will be interesting to apply the comparison introduced here to these networks.

In mammals, an estimate of the available different expression patterns of protocadherins, the proteins suggested to act as neuronal molecular markers (7–13), is 10⁵ (9), orders of magnitude lower than the number of neurons (10⁸ in mouse and 10¹¹ in human). This discrepancy represents an apparent paradox. This study suggests that the paradox can be resolved if neuronal networks are wired, not in an arbitrary manner, but are instead geometrically constrained and contain recurring connectivity patterns.

What are the constraints that limit the number of surface proteins encoded in the genome and their combinations on individual neurons? The immune system, often compared in complexity to the nervous system (31), has achieved an astounding genetic diversity of 10¹⁶ different T cell receptor types (32). Why then does the nervous system not use parallel mechanisms to generate comparable marker diversity? One possibility is that the stochastic diversity-generating mechanism of somatic recombination and hypermutation used by T cells is not suitable for the deterministic expression required for a genetically encoded neuronal connectivity.

Another possible limitation on the number of different surface proteins could be their inherent nonspecificity (13, 14). For example cadherin proteins generally bind in a homophilic manner, but heterophilic nonspecific binding is very common. It might be postulated that the number and molecular identity of the protocadherins would be chosen so that they are maximally dissimilar, thus minimizing nonspecific binding. A similar constraint of avoiding nonspecific binding has been suggested to limit the number of transcription factors (33). An additional constraint on the number of combinations of molecular markers on a single neuron might be the elaborate internal computation needed to decode these biochemical addresses.

A prediction of our analysis is that the genetically encoded addresses should be expressed in a ubiquitous manner throughout the brain. Indeed, unlike other proteins from the cadherin superfamily in which expression is limited to specific brain regions or subsets of neurons, protocadherins are broadly expressed throughout the central nervous system (10, 12, 34, 35).

The human neuronal network is three orders of magnitude larger than the mouse neuronal network, although the number of protocadherins in their genomes is the same. This study predicts that either the number of combinations of different protocadherins on a single neuron is larger in human, resulting in more addresses obtained in a combinatorial fashion, or that the human neuronal network is more ordered, containing more repetitive connectivity patterns compared with mouse. Modern high-resolution techniques for probing neuronal connectivity (30) and for exploring expression patterns on single neurons (9, 36) will allow testing these predictions.

This study touched on only one layer of neuronal complexity—that of the pattern of synaptic connections. Much of the complexity of neuronal networks lies in the synaptic weights, which are dynamically modified in an activity-dependent manner during processes such as learning (1, 37). Activity-dependent mechanisms cannot only affect synaptic weights but can completely rewire synapses (37). Thus, the model presented here that considered solely genetically encoded neuronal wiring is only an approximation. Another layer of complexity is the intracellular molecular mechanism by which neurons recognize the neuronal addresses of neighboring neurons to decide whether to form a synaptic connection or not. Unraveling this decoding mechanism is an exciting field for future research.

The conclusions of this study, namely that geometric networks with recurring connectivity patterns facilitate connectivity with a concise set of addresses, do not depend on the precise identity of the neuronal addresses or on the biochemical details of the synaptic adhesive code. In fact, these conclusions may apply to other biological networks in which connectivity is determined by genetically encoded addresses. In transcriptional networks, for example, where edges represent binding of transcription factor proteins to the promoters of target genes, the genetically encoded addresses are amino acid sequences on the surface of the transcription factors and short DNA sequences on the promoters of the target genes. The diversity of these addresses is limited, e.g., by coding constraints (33). It would be interesting to investigate whether such constraints dictate distinct topologies for these and other biological networks.

Although biological systems are tuned to optimality by evolution, the performance criteria for which these systems are optimized are often elusive. This study suggests that the genetically encoded geometric neuronal connectivity exemplify this phenomenon. We suggest an evolutionary advantage for geometric constraints and network motifs in neuronal networks. Not only do these topological features of connectivity allow a more efficient transmission between neurons and efficient computation but also facilitate the genetic encoding of these networks with a concise set of genetically encoded addresses.

Methods

Network Generation.

We generated arbitrary directed geometric networks G with N nodes arranged on a d-dimensional Euclidean lattice with toroidal (continuous) boundary conditions, as in ref. 17. Among each pair of nodes with distance r ≤ R lattice units, an edge is set in each direction with probability p = k/D, where D = (2R + 1)^d is the neighborhood size, and k is the average number of edges per node. We used the L-infinity norm: the distance r between each pair of nodes X,Y with coordinates {X_i}_i=1..d and {Y_i}_i=1..d is r(X,Y) = max∣X_i − Y_i∣. Erdős–Rényi networks (18) were created by connecting any pair of nodes with probability p = k/N in each direction.

Minimal Number of Addresses.

Given a directed network G(V,E) with nodes V and edges E and a nondirected neighborhood network G′(V,E′) in which any two nodes are connected by a link if they are physically close enough to be able to connect, we seek a mapping f from V to a set of addresses C and a corresponding directed network GC(C,E″), where the nodes are the addresses, and the edges represent the relations between them. A solution S = {f,GC} is admissible if for every pair of nodes (u,v)∈E′ so that f(u) = A and f(v) = B, (u,v)∈E iff (A,B)∈E″. In other words, the connectivity pattern between any two addresses, as defined by GC (the presence or absence of an edge) must be replicated for all nodes with these addresses that are within physical reach of each other. We sought to compute the admissible mapping with minimal size ∣C∣. This problem is nondeterministic polynomial time complete (NP-complete) (Fig. S4). When the neighborhood network is the complete graph (that is, the geometric constraints are alleviated), the problem of finding addresses and their relation GC is similar to block model methods in social network analysis (38, 39).

Heuristic Algorithm for Finding the Minimal Number of Addresses.

We applied a heuristic greedy search algorithm to compute the minimal number of addresses. A similar algorithm has been applied for graph coloring problems (40). The greedy search begins with an empty assignment of addresses to nodes and an empty directed graph GC. It scans the nodes according to some predefined order and successively assigns addresses and updates GC. The first node is assigned address 1. Thereafter, at node i, we check whether any of the previously assigned c addresses is consistent with the connections of i. If none of the addresses are consistent, a new address is added. If one or more previously used address is consistent, node i is assigned one of the consistent address according to one of four rules (see below). In both cases, GC is updated appropriately. An address assignment c_i to node i is consistent if two conditions are met: (i) The connections between i and all other nodes in its neighborhood that have already been assigned an address are congruent with GC. (ii) For each node j that has already been assigned address c_i, we list the set of common reachable nodes between i and j, {S_ij}—nodes that are in the neighborhood of both i and j. Consistency means that for each u in S_ij i → u iff j → u and u → i iff u → j. Although the second condition is not necessary to reach an admissible solution, without it the fraction of admissible solutions reached decreases substantially. The greedy search is evoked many times, each time with different node orders and choices between consistent addresses. The node orders used are in-order, increasing degree, decreasing degree, and random order. The address choices are according to the address with the most assigned nodes, the least assigned nodes, according to the order at which they have been created, and at random. We ran the algorithm with all combinations, including 10 different random address choices for each node order and output the minimal number of addresses found.

Scaling Formula for the Number of Neuronal Addresses.

Here, we show analytically that under biologically relevant network and neighborhood sizes, the minimal number of neuronal addresses scales as the square root of both network and neighborhood sizes. We first calculate the number of admissible solution with c addresses:

This formula can be understood as follows: There are c^N possible mapping of nodes to addresses (f) and for each mapping 2^c2 possible directed networks GC representing the relations between addresses (we neglect a c! term in the denominator that corrects for isomorphic solutions because its effect on the bound below is negligible). We next consider the probability that an arbitrary network G will be admissible given one solution (a predefined S = {f,GC}). There are DN ordered pairs of nodes that should be consistent with the solution S. This means that, given a node v and another node in its neighborhood u, the presence or absence of an edge v → u should match the presence or absence of an edge in GC between f(v) and f(u). Given an arbitrary solution S, the probability that all these pairs will be consistent with the solution is (1/2)^ND. This will generally be extremely small; however, Eq. 1 indicates that there are many possible solutions. The probability that any solution with c addresses will be admissible is:

An estimate for the minimal number of addresses c can be obtained by setting p = 1:

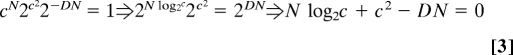The minimal number of addresses can be obtained by numerically testing increasing values of c, from 1 up to the maximum possible number of addresses N, until Eq. 3 is satisfied. If c > 2^D, the term c^N dominates in Eq. 3 and the minimal number of addresses is independent of network size N:

For N ≪ 2^D, the quadratic term in c in Eq. 3 dominates, and the scaling of the minimal number of addresses is:

This is the power-law observed in this study (Fig. 2). See Fig. S3 for detailed analysis of the scaling regimes of Eq. 3.

Eq. 3 can also be interpreted as follows: The minimal number of addresses c is the smallest for which the number of realizable networks (given by Eq. 1) is equal to the number of arbitrary geometric networks, which is ≈2^DN:

If the neighborhood size D is smaller than log₂N (or equivalently N > 2^D), an upper bound of c = 2^D will be sufficient to wire any network, regardless of N, because the left side of Eq. 6 is always larger than c^N. Thus, in this regime, the number of addresses becomes independent of network size. However, for neighborhood sizes larger than log₂N (N < 2^D), the maximal value of c^N that is obtained when each node has a different address (c = N) is not enough to cover the geometric network space. In this regime, the term 2^{c^2} dominates, and we derive the square-root scaling law. In networks without geometry, D ≈ N, and Eq. 6 indicates that the minimal number of addresses c is also on the order of the number of nodes N (2^{c^2} ≈ 2^N2).

Note that the analysis here did not require designating the precise geometric constraints, e.g., Euclidean lattice. In fact, the analysis is valid for any network in which nodes are limited so that they can potentially connect only to a part of the network D rather than to any other node. Such limitations also include topographic mappings in which nodes connect to a limited set of targets at a large distance and small-world networks (SI Text).

The square root scaling remains intact when considering a more elaborate code in which each neuron is assigned two addresses, one representing the set of proteins expressed on its axon and one for the set of proteins expressed on the dendrites. In this model, the number of possible solutions will be n(c) = c^2N2^c2 instead of n(c) = c^N2^c2, which leads to a negligible effect on the scaling of minimal number of addresses with network size, as long as N² ≪ 2^D, the regime in which all biologically relevant networks reside.

Relation Between Network Order and the Number of Neuronal Addresses.

We generated maximally ordered networks in which each neighborhood contains exactly the same connectivity pattern, an arbitrary Erdős–Rényi network of size D. We then rewired these networks by successively deleting an edge and adding a new edge within the same local neighborhood. This creates networks with the same geometric constraints with decreasing levels of order. The minimal number of neuronal addresses for each level of order was calculated (Fig. 3).

C. elegans Neuronal Network.

The C. elegans neuronal network was downloaded from www.wormatlas.org/handbook/nshandbook.htm/nswiring.htm. The network includes 281 nodes, 2,194 chemical synapse connections and 1,031 gap junction connections. The minimal number of addresses was computed as in the simulated geometric networks. Because we do not have precise information on the neuronal physical location, specifically on the physical span of neuronal processes, we used a different measure of geometric proximity based on the neuronal connectivity. We define the proximal targets of a neuron X as the set of all nodes that send a directed synaptic connection to X, receive a directed synaptic connection from X, or connect to X via a gap junction. This definition is only an approximation and may miss neuronal pairs that are in physical proximity but do not have any connection.

C. elegans Neuronal Network Randomization.

Randomized versions of the C. elegans neuronal network were generated as follows: starting from the original network, we performed the following Markov chain Monte Carlo algorithm: For 50,000 iterations, we chose pairs of nodes (s1, t1), and (s2, t2), such that s1 → t1, s2 → t2, s1 ↛ t2, s2 ↛ t1 and (s1, t2) and (s2, t1) are within physical reach of each other. We then switched them so that s1 → t2, s2 → t1. The algorithm produces random networks that have the same degree sequence as the real network. It is similar to the network randomization algorithm used in ref. 28 but, in addition, preserves the geometric constraints of the real network.