Currents in Response to Rapid Concentration Jumps of Amphetamine Uncover Novel Aspects of Human Dopamine Transporter Function

Abstract

Amphetamine (AMPH) is a widely abused psychostimulant that acts as a substrate for the human dopamine transporter (hDAT). Using a piezoelectric rapid application system, we measured AMPH-induced currents mediated by hDAT. Whole-cell patch-clamp recordings in a heterologous expression system reveal that AMPH induces a rapidly activating and subsequently decaying inward current mediated by hDAT. We hypothesize that this transient inward current reflects a conformational change associated with substrate translocation. The AMPH-induced current strictly depends on extracellular Na⁺. Elevated intracellular Na⁺ has no effect on the peak AMPH-induced current amplitude but inhibits the steady-state current. In addition, elevated intracellular Na⁺ causes an overshoot outward current upon washout of AMPH that reflects hDAT locked in a Na⁺-exchange mode. Furthermore, elevated intracellular Na⁺ dramatically accelerates the recovery time from desensitization of the AMPH-induced current, revealing a new role for intracellular Na⁺ in promoting the transition to the hDAT “outward-facing” conformation. Ion substitution suggests that both extracellular and intracellular Cl⁻ facilitate transporter turnover in contrast to the classical model of Cl⁻ as a cotransported ion. We present an alternating-access model of hDAT function that accurately fits the main features of the experimental data. The model predicts that translocation of substrate occurs within milliseconds of substrate binding but that slow reorientation of the empty transporter is the rate-limiting factor for turnover. The model provides a framework for interpreting perturbations of hDAT activity.

Introduction

Neurotransmitter reuptake by transport proteins is a major mechanism for terminating synaptic transmission. High-affinity transport systems have been identified for the neurotransmitters dopamine (DA), norepinephrine, serotonin, GABA, glutamate, and glycine (for review, see Masson et al., 1999; Torres et al., 2003). These transporters function by coupling the movement of sodium ions down their electrochemical gradient to the transmembrane translocation of substrate. The dopamine transporter (DAT) is the plasmalemmal membrane protein that mediates the inactivation of released DA through its reuptake. DAT is also the major molecular target responsible for the rewarding properties and abuse potential of amphetamine (AMPH), cocaine, and related psychostimulants (Koob and Bloom, 1988; Nestler, 1992; Chen et al., 2006).

Limited information is available regarding the conformational changes that accompany neurotransmitter transport. In the alternating access model, an external and an internal gate alternately allow access to the binding site and permeation pathway from the extracellular and intracellular milieu (Jardetzky, 1966). DA uptake is dependent on both sodium and chloride ions, and two sodium ions and one chloride ion are hypothesized to be cotransported with each DA molecule (Amara and Kuhar, 1993; Rudnick and Clark, 1993).

This stoichiometry predicts that the transport process should be electrogenic. Consistent with this prediction, when DAT is expressed in oocytes or in mammalian expression systems, an inward current results from the extracellular application of DA or other substrates such as AMPH or 1-methyl-4-phenylpyridium (MPP⁺) (Sonders et al., 1997; Sitte et al., 1998; Khoshbouei et al., 2003; Pifl et al., 2004). Although valuable in exploring the molecular mechanisms for transporter function, these previous studies were limited in temporal resolution of substrate-induced currents because of the fact that measurements were made at steady state or with relatively slow substrate application.

Rapid solution exchange coupled with patch-clamp recording is a routine method for investigation of ligand-gated ion channels (Breitinger, 2001) and has also been used to study charge movement mediated by transporters for the neurotransmitters glutamate (Bergles et al., 1997; Otis et al., 1997; Otis and Jahr, 1998; Grewer et al., 2000; Otis and Kavanaugh, 2000; Bergles et al., 2002; Mim et al., 2005), GABA (Cammack and Schwartz, 1996; Bicho and Grewer, 2005), and glycine (Aubrey et al., 2005). This experimental approach provides real-time measurement of the molecular events initiated immediately after substrate binding to the transporter. Here, we characterize substrate-induced currents with high temporal resolution for the human DAT (hDAT).

Materials and Methods

Whole-cell patch-clamp recording.

EM4 cells, human embryonic kidney 293 (HEK-293) cells stably transfected with a macrophage scavenger receptor to promote adherence, were stably transfected with an N-terminal yellow fluorescent protein (YFP)-tagged human dopamine transporter [“hDAT cells” (Kahlig et al., 2004)] and cultured in DMEM (#10–017-CV; Invitrogen, Carlsbad, CA) supplemented with 10% fetal bovine serum, 100 U/ml penicillin, 100 μg/ml streptomycin, and 2 mm glutamine (37C; 5% CO₂). Addition of the N-terminal YFP tag to DAT did not significantly alter [³H]DA uptake and did not perturb the ability of the transporter to produce AMPH-induced steady-state currents (Saunders et al., 2000; Khoshbouei et al., 2003; Kahlig et al., 2004). Cells were cultured on 12 mm round glass coverslips (CS-12R; Warner, Hamden, CT) for 1–2 d before recording. Patch-clamp recording (at 23°C) was performed using an Axopatch 200B amplifier (Molecular Devices, Union City, CA), and currents were acquired using Clampex9 software (Molecular Devices). The voltage was −60 mV unless otherwise noted. Currents were filtered at 1 kHz using an 8-pole Bessel filter (model 4302; Ithico, Ithica, NY) and sampled at a rate of 2 kHz. Recording pipettes were fabricated from quartz glass (#Q100-70-7.5; Sutter Instruments, Novato, CA) with a typical resistance of 2–5 MΩ. Whole-cell series resistance was uncompensated and was typically 4–10 MΩ. Unless otherwise noted, the intracellular solution consisted of the following (in mm): 120 KCl, 0.1 CaCl₂, 2 MgCl₂, 1.1 EGTA, 10 HEPES, 30 dextrose, pH 7.35. Unless otherwise noted, the extracellular solution consisted of the following (in mm): 130 NaCl, 1.5 CaCl₂, 0.5 MgSO₄, 1.3 KH₂PO₄, 10 HEPES, 34 dextrose, pH 7.35. All chemicals were purchased from Sigma (St. Louis, MO) unless otherwise noted. Dextrose, HEPES, MgSO₄, and KOH were purchased from EMD Chemical (Gibbstown, NJ). EGTA, potassium acetate, and NaOH were purchased from Fisher Scientific (Fair Lawn, NJ). Solution exchange was achieved by a piezoelectric translator (PZ-150M; Burleigh, Plano, TX) moving a theta glass (#1407201; Hilgenberg, Malsfeld, Germany) with control solution flowing continuously through one barrel and AMPH (or DA) solution through the other barrel. The piezoelectric translator was driven through Clampex9 with a voltage step or ramp (5–10 ms) filtered at 25–250 Hz (Ithico 4302). The speed of solution exchange around the cell was calculated from the current recorded upon substituting KCl for NaCl in the external solution (see Fig. 1B). The current was fit to a single exponential function. The time constant for the current rise was 5.2 ± 0.7 ms, and the time constant for the washout was 5.6 ± 1.0 ms (n = 7). The interface between solutions was visualized by the difference in refractive index of the two solutions after adding 5 mm dextrose to either the control or drug side of the solution flow. The time between consecutive substrate applications was at least 5 s for control conditions and at least 2 s for experiments with elevated intracellular Na⁺, unless the paired-pulse recovery time was measured. Current traces plotted in all figures represent the mean current for at least 10 sweeps.

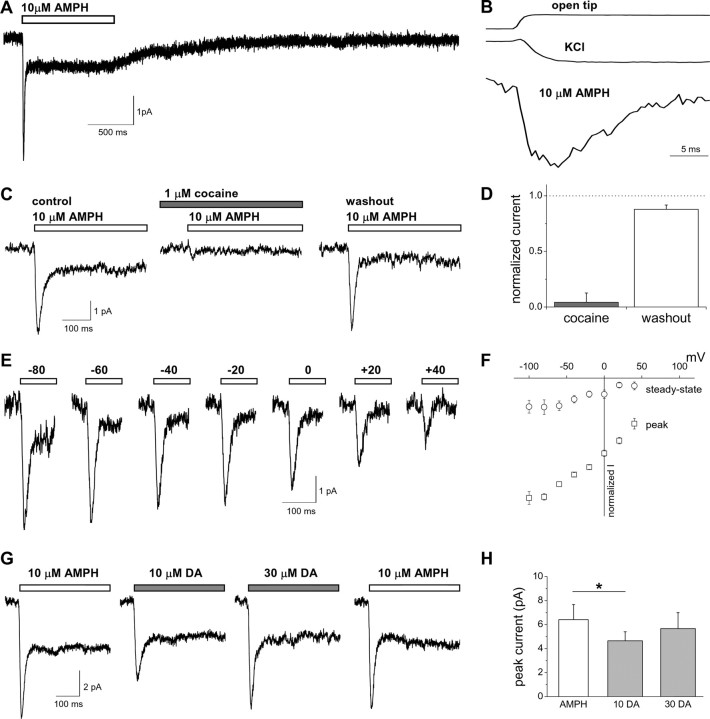
Figure 1.

Characterization of the AMPH-induced peak and steady-state currents mediated by hDAT. A, AMPH (10 μm) was applied for 1 s to hDAT cells under whole-cell voltage clamp (−60 mV). The mean current of 10 consecutive sweeps is plotted. B, The AMPH-induced current is plotted aligned with current obtained in response to switching from NaCl to KCl external (see Materials and Methods) to measure the time course of solution exchange around the cell (KCl). The current for the open pipette tip in response to switching from 1× to 0.5× external solution is plotted for comparison. All three currents were normalized to the maximal current recorded. C, The inward current induced by AMPH and obtained from a representative cell was blocked by the DAT inhibitor cocaine. The current recovers after washout of cocaine. D, The AMPH-induced peak current recorded during cocaine application or washout was normalized to the initial AMPH control response (n = 4). E, Representative currents recorded at different voltages in response to a 1 s application of AMPH. F, Current–voltage relationships of the AMPH-induced currents normalized to the peak current obtained at −60 mV (n = 4–6). G, hDAT-mediated currents induced by a 1 s application of AMPH or DA to the same cell at −60 mV. H, The peak current amplitude recorded either with 10 μm AMPH or with two different DA concentrations (n = 3; *p < 0.05, repeated-measures ANOVA).

Data analysis.

Currents were analyzed using Clampfit9 or Channelab (Synaptosoft, Decatur, GA). Curve fitting was performed with Origin 6 (Microcal, Northampton, MA).

The time course for recovery from desensitization was fit to the following equation:

where τ is the time constant, and A is the relative amplitude of the decay, fixed to the degree of desensitization at the end of the first pulse (1 − I_steady-state/I_peak).

The dose–response relationships for AMPH or Na⁺ were fit to the two-component equation:

where [X] is the concentration of AMPH or Na⁺, A1 is relative amplitude of component 1, A2 is fixed to be 1 − A1, E1 and E2 are the EC₅₀ values of the respective components, and p is the Hill slope and was fixed to be equivalent for both components.

Integration of current traces (see Fig. 5) to determine charge transfer was performed in Clampfit9. The peak current was integrated using the steady-state current level as the baseline.

Figure 5.

Elevated intracellular Na⁺ regulates the AMPH-induced current. A, Representative current traces at different voltages with substitution of 90 mm Na⁺ for intracellular K⁺. The internal solution contained either 90 mm Na⁺ plus 30 mm K⁺ or control 120 mm K⁺. B, The I–V relationship for the peak current is not altered significantly by the presence of 90 mm intracellular Na⁺ (n = 6; p > 0.05, two-way ANOVA). The steady-state currents are significantly reduced by high intracellular Na⁺ (*p < 0.05, two-way ANOVA). C, Representative current evoked by a 1 s application of 10 μm AMPH with 90 mm Na⁺ internal solution. Inset, The amplitude of the overshoot current is voltage independent. The peak and overshoot currents are plotted as a function of voltage normalized to the peak current at −60 mV for each cell (n = 6). D, Charge transfer is quantified by integrating the inward peak current (Q peak) or the outward overshoot current (Q overshoot) at either 0 or −60 mV. The slope of the linear fit is 0.998 at 0 mV and 0.677 at −60 mV. E, F, The kinetic properties of the AMPH-induced current at −60 mV (rise time and decay time constant of the peak current) are plotted as a function of internal Na⁺ concentration (n = 5–10 for each Na⁺ concentration; ANOVA, *p < 0.05). G, H, The steady-state and overshoot currents, normalized to the peak current, are plotted against concentration of internal Na⁺ (n = 5–10 for each Na⁺ concentration; *p < 0.05).

Statistical analysis was performed in Prism 3 or Prism 4 (GraphPad software, San Diego, CA). A Student's t test was used for pair-wise comparisons unless otherwise noted. ANOVA followed by Tukey's post hoc test was used for multiple comparisons. All data are expressed as mean ± SEM.

Modeling.

Modeling was performed as described previously (Bicho and Grewer, 2005; Mim et al., 2005). Briefly, the time-dependent population of individual states, P_i, in response to AMPH concentration jumps was calculated by numerically integrating the system of coupled differential rate equations describing the kinetic scheme in Figure 9A, using Berkeley Madonna software. The voltage dependence of individual rate coefficients, k_i, in the reaction scheme was introduced according to transition state theory with symmetric barriers (Laeuger, 1991):

Here, k_ij⁰ is the rate coefficient of the individual transporter reaction, transitioning from state i to j, at a voltage, V, of 0 mV. z_Q,ij is the apparent valence of the transition, and F, R, and T have their usual meaning. Currents per mole of transporter, I, were then calculated using the following relationship:

Currents were subsequently normalized to fit the experimental data. Solution exchange time was explicitly modeled with an exponential time constant of 5 ms. Modeling was performed at −60 mV, unless stated otherwise, and parameters were restricted by detailed balancing at 0 mV. The kinetic parameters were varied manually, until a satisfactory representation of the key experimental data were achieved.

Figure 9.

An explicit alternating access model fit to the hDAT currents can recapitulate major features of experimental data. A, Alternating access model of hDAT function (rate constants are given for the rates at 0 mV) (see Materials and Methods). The kinetic parameters shown were used to fit the data for B–H as described below. In each case, the model simulation (color) is superimposed on the experimental data (gray). B, hDAT currents at −60 mV in response to a 1 s application of 10 μm AMPH under control conditions were normalized, aligned to the time of the peak, and averaged among cells (n = 49). C, Mean pooled experimental data for representative cells (n = 4) and model simulations for a 1 s application of 10 μm AMPH in the presence of 90 mm intracellular Na⁺. D, For control conditions, paired-pulse responses to 100 ms applications of 10 μm AMPH at a variable interval were normalized, aligned, and averaged among cells and compared with model simulations (n = 5). E, Mean pooled experimental data for representative cells (n = 3) and model simulations for paired-pulse responses to 100 ms applications of 10 μm AMPH in the presence of 90 mm intracellular Na⁺. F, Experimental and simulated dose–response relationship for AMPH-induced peak (squares) and steady-state currents (circles). G, Experimental and simulated dose–response relationship of AMPH-induced peak (squares) and steady-state currents (circles) as a function of extracellular Na⁺. H, Experimental and simulated voltage dependence of AMPH-induced peak (squares) and steady-state (circles) currents for the indicated internal solutions. Currents are normalized to the peak value at −60 mV.

Results

Rapid application of substrate induces an inward current through hDAT

hDAT cells (HEK cells stably expressing hDAT) were voltage clamped using the whole-cell patch configuration (V_m, −60 mV, unless otherwise noted). Rapid application of the substrate AMPH (10 μm) was achieved using a piezoelectric translator to move a double-barrel glass application pipette (Fig. 1A). Application of 10 μm AMPH to hDAT cells resulted in a rapidly rising and decaying current (peak amplitude, 6.5 ± 0.5 pA; n = 93). The time for the current to increase during the rising phase from 10 to 90% of the amplitude of the peak current (10–90% rise time) was 7.4 ± 0.3 ms (n = 93). This current decayed in the continued presence of AMPH to a steady-state level smaller than the peak (time constant, τ, of decay, 17.2 ± 0.7 ms; steady-state to peak ratio, 0.24 ± 0.01; n = 93). Upon washout of AMPH, the steady-state current decayed to the baseline with a time constant of 528 ± 43 ms (n = 71).

The time course of solution exchange around the cell was calculated from the current obtained in response to switching from normal external Na⁺ to a solution in which K⁺ was substituted for Na⁺. Figure 1B shows the solution exchange time course aligned to the AMPH-induced current. The current in response to switching the external solution from 1× to 0.5× with the open pipette tip was recorded and plotted for comparison (Fig. 1B). The time course for solution exchange was the same for the addition and removal of the activating solution. The AMPH-induced current activates with a time course similar to the time for solution exchange. This solution exchange time course is explicitly included in the modeling of hDAT function (see Fig. 9).

To establish that hDAT mediates the AMPH-induced currents, we verified the sensitivity to cocaine, a DAT inhibitor. Cocaine reversibly blocked the AMPH-induced peak and steady-state currents (Fig. 1C,D). Measurements of the voltage dependence of the AMPH-induced currents were performed (Fig. 1E,F). The decay time constant for the peak current and the steady-state to peak current ratio were independent of voltage (p > 0.05, by one-way ANOVA; n = 4–6). Over a range of voltages (from −100 to +40 mV), the AMPH-induced current was inward under our control ionic conditions of a predominantly NaCl external solution and KCl internal solution. Currents did not reverse within the voltage range tested, as expected from the zero-trans ionic conditions used for Na⁺ and AMPH and from the hDAT transport stoichiometry. Both the peak and steady-state currents appear to saturate at hyperpolarized voltages. However, in the oocyte preparation, Sonders et al. (1997) demonstrated that substrate-induced DAT currents do not saturate up to a voltage of −120 mV. At extreme negative potentials, the currents in our preparation are less stable and more variable, which may account for the observed differences.

Although these results suggest that AMPH induces a peak current, which rapidly decays, and a steady-state current mediated by hDAT, it is unclear whether this characteristic time dependence is generally associated with the action of DAT substrates or specifically associated with the effect of AMPH on hDAT. To address this question, we compared in the same cell the currents evoked by AMPH to those induced by the endogenous DAT substrate DA (Fig. 1G,H). Similarly to AMPH, application of DA to hDAT cells resulted in a peak and a steady-state current (Fig. 1G). Perfusion of hDAT cells with DA (10 μm) resulted in peak currents significantly smaller than those recorded with 10 μm AMPH (Fig. 1H) (n = 3; p < 0.05, repeated-measures ANOVA). However, the peak currents recorded in the presence of a higher concentration of DA (30 μm) were not significantly different from those recorded with 10 μm AMPH, which is a saturating concentration (see Fig. 3B). Therefore, substrate-induced peak and steady-state currents after substrate binding are a general feature of hDAT function.

Figure 3.

The amplitude and properties of the AMPH-induced current are concentration dependent. A, hDAT current evoked by a 1 s application of the indicated concentrations of AMPH to the same cell. B, The steady-state and peak currents for each AMPH concentration were normalized to the peak current obtained with 10 μm AMPH (n = 4–13 for each concentration). The dose–response relationship for the dependence of the peak current on the AMPH concentration exhibits two components with different apparent affinities for AMPH. The high apparent affinity component has an EC₅₀ value of 0.036 μm and accounts for 38% of the current amplitude. The lower apparent affinity component has an EC₅₀ value of 1.38 μm and accounts for 62% of the current amplitude. C, D, The kinetic properties (rise time and decay time constant) of the AMPH-induced current are plotted as a function of AMPH concentration.

To assess whether exposure to AMPH regulates the amplitude of the peak current in response to a subsequent AMPH application, we used a paired-pulse protocol (Fig. 2A,B). AMPH (10 μm) was applied twice for a duration of 100 ms at a variable interstimulus interval. At short interstimulus intervals, the peak current was diminished, indicating that the transporter was in a refractory or desensitized state for current induction by AMPH. As the interstimulus interval was increased, the amplitude of the current response recovered back to the full control (first pulse) response (Fig. 2A,B). The time course of recovery averaged from six cells was fitted to a single exponential function with a time constant of 700 ms (Eq. 1). The mean recovery time constant from fits to individual cells was 710 ± 91 ms (n = 6). The paired-pulse recovery rate is an indicator of the maximal transporter turnover rate in the limit of a saturating concentration of the substrate and reflects the mean time required to complete one transport cycle, as demonstrated previously for glutamate transporters (Otis and Jahr, 1998; Otis and Kavanaugh, 2000). The paired-pulse protocol was also used to measure the turnover rate with DA as the substrate (Fig. 2C,D). The time course of recovery averaged from four cells was fitted to a single exponential function with a time constant of 703 ms. The mean recovery time constant from fits to individual cells was 730 ± 210 ms (n = 4). The turnover rate of hDAT is therefore the same for AMPH and DA, within experimental error.

Figure 2.

Paired pulses of substrate indicate the turnover rate of hDAT. A, AMPH (10 μm) was applied for 100 ms with a paired-pulse protocol at a variable interval to monitor recovery from desensitization of the AMPH-induced peak current. Representative mean current of each interval is plotted normalized to the amplitude of the peak current obtained with the first AMPH application (dotted line). The lines above the current indicate the times of AMPH application. B, The normalized peak current is plotted as a function of time between AMPH applications to evaluate the recovery time from desensitization. The recovery time course is fitted to a single exponential function with a time constant of 700 ms (n = 6). C, DA (100 μm) was applied for 100 ms with a paired-pulse protocol at a variable interval to monitor recovery from desensitization of the DA-induced peak current. Representative mean current of each interval normalized to the amplitude of the peak current obtained with the first DA application (dotted line). D, The normalized peak current is plotted as a function of time between DA applications. The recovery time course is fitted to a single exponential function with a time constant of 703 ms (n = 4).

To characterize the concentration dependence of the substrate-induced currents, we applied AMPH over a range of concentrations from 0.03 to 30 μm (Fig. 3). Representative current traces are shown in Figure 3A. The currents were normalized to the peak current obtained with 10 μm AMPH for each cell (Fig. 3B, open squares). The AMPH concentration dependence of the peak current exhibited two components with different apparent affinities (Eq. 2). The higher apparent affinity component exhibited an EC₅₀ value of 0.036 μm and accounted for 38% of the peak current amplitude. The lower apparent affinity component exhibited an EC₅₀ value of 1.38 μm and accounted for 62% of the peak current amplitude. The two components of the dose–response relationship for the peak current could reflect multiple binding sites or cooperativity among subunits in a multimeric complex. However, they can also be explained with a single binding site model with the two components reflecting the nonequilibrium nature of the peak current (see Fig. 9F). The concentration dependence of the AMPH-induced steady-state current differed from that of the peak current (Fig. 3B, open circles), saturating at a lower AMPH concentration (EC₅₀, 0.03 μm).

Figure 3C shows that at low AMPH concentrations, the rise to the peak current response became slower, suggesting that at a low concentration, AMPH binding may be rate limiting. Similarly, at low AMPH concentrations, the time constant for the peak current decay slowed (Fig. 3D). This slower decay is possibly caused by asynchronous activation at low substrate concentrations.

Ion dependence of the AMPH-induced current

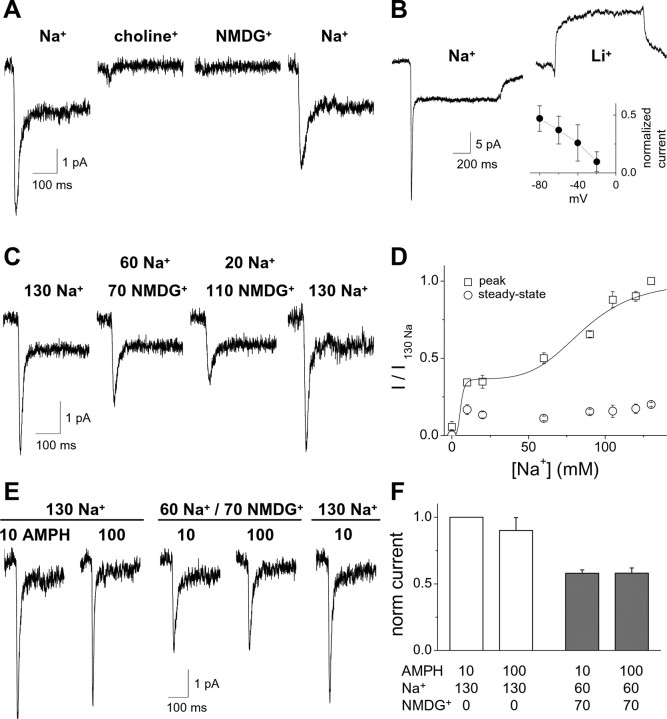
We next measured AMPH-induced currents under different ionic conditions (Fig. 4). Substitution of external Na⁺ with either NMDG⁺ (N-methyl-d-glucamine) or choline⁺ abolished the AMPH-induced current (Fig. 4A). The current was partially restored after reperfusion of the cell with the control Na⁺ solution. To test further the dependence of the AMPH-induced current on extracellular cations, we substituted Li⁺ for Na⁺ (Fig. 4B). In the presence of Li⁺, application of 10 μm AMPH did not cause an inward current but rather induced an apparent outward current that was 32 ± 2% of the inward peak current recorded in the presence of Na⁺ (n = 6). This outward current likely reflects inhibition of a leak current by AMPH, as shown previously by Sonders et al. (1997). Consistent with this hypothesis, the current–voltage relationship for the AMPH-induced current in Li⁺ exhibited a negative slope (Fig. 4B, inset), indicative of an inhibition rather than an activation of a conductance.

Figure 4.

The AMPH-induced inward current depends on extracellular Na⁺. A, Substituting external Na⁺ with choline⁺ or NMDG⁺ abolishes the current induced by AMPH (10 μm, 1 s). B, After substitution of Na⁺ by Li⁺, AMPH does not induce a desensitizing inward current but does induce an apparent outward current that may reflect inhibition of a Li⁺ leak current by AMPH (n = 6). Inset, The I–V relationship for the AMPH-induced current in Li⁺ normalized to the peak AMPH-induced current in Na⁺ (n = 4). C, Partial substitution of Na⁺ by NMDG⁺ results in a partial inhibition of the AMPH-induced current (concentrations are given in mm). D, The amplitude of the AMPH-induced current is shown as a function of Na⁺ with substitution by NMDG⁺ (n = 6–15). The dose–response relationship for the dependence of the peak current on the Na⁺ concentration exhibits two components with different apparent affinities for Na⁺. The high apparent affinity component accounts for 37% of the current amplitude and was saturated at the lowest Na⁺ concentration tested. For fitting the data, the EC₅₀ value of the high apparent affinity component was set at 5 mm as an upper limit. The lower apparent affinity component exhibits an EC₅₀ value of 86 mm and accounts for 63% of the current amplitude. E, F, Substitution of Na⁺ by NMDG⁺ reduces the peak current in response to 10 μm AMPH and 100 μm AMPH to a similar extent (n = 5). μm, AMPH concentration; mm, Na⁺ and NMDG⁺ concentrations.

Partial substitution of Na⁺ with NMDG⁺ reduced the amplitude of the AMPH-induced peak current but not of the steady-state current in the range of Na⁺ concentrations studied (from 10 to 130 mm) (Fig. 4C). The time constant for the decay of the peak current was not dependent on the concentration of Na⁺ (ANOVA, p > 0.05; n = 6–15) (data not shown). The dependence of the peak current on the Na⁺ concentration exhibited two components with different apparent affinities for Na⁺ (Fig. 4D) (Eq. 2). The high apparent affinity component accounted for 37% of the current amplitude and was saturated at the lowest Na⁺ concentration tested. The lower apparent affinity component exhibited an EC₅₀ value of 86 mm and accounted for 63% of the current amplitude. The two components of the Na⁺ dose–response might reflect multiple binding sites, although a model with a single Na⁺ binding event accounts for a dose–response relationship with two distinct apparent affinity components (Fig. 9G).

To determine whether the reduction of the AMPH (10 μm) induced peak current by partial substitution of Na⁺ with NMDG⁺ results from a shift in the dose–response relationship for AMPH, we applied 10 μm AMPH or 100 μm AMPH in 130 mm Na⁺ external control solution or 60 mm Na⁺/70 mm NMDG⁺ external solution (Fig. 4E,F). Under partial substitution of Na⁺ with NMDG⁺, the current induced by 100 μm AMPH was not significantly different from 10 μm AMPH. These data suggest that this decrease in the AMPH-induced peak current is not caused by a decrease in the apparent affinity for AMPH.

We hypothesized that the current may be mediated by inward Na⁺ flux. To test this hypothesis, we substituted Na⁺ for K⁺ as the major intracellular cation (Fig. 5A). This internal solution contained 90 mm Na⁺ and 30 mm K⁺. There was no significant difference in the amplitude of the peak current recorded with a 90 mm Na⁺ internal solution at −60 mV (4.8 ± 0.7 pA; n = 9) compared with control conditions (0 mm Na⁺ internal solution). If the AMPH-induced peak current was predominantly caused by an uncoupled Na⁺ conductance, then under these internal ionic conditions, the current–voltage relationship would be predicted to shift leftward. The current–voltage relationship is not markedly shifted leftward by substitution of internal Na⁺ for K⁺ as the predominant intracellular cation (Fig. 5B). Furthermore, the peak current remained inward even at a voltage of +40 mV. These data indicate that the AMPH-induced hDAT peak current is not simply a result of uncoupled Na⁺ conductance. Although there is no change in the current–voltage relationship for the peak current, elevated intracellular Na⁺ concentration eliminated the AMPH-induced steady-state current (Fig. 5A,B). Thus, the steady-state current depends on the transmembrane Na⁺ concentration gradient, whereas the peak current depends only on extracellular Na⁺ concentration.

Elevated intracellular Na⁺ modulates AMPH-induced current

In the presence of elevated intracellular Na⁺ concentrations, washout of AMPH results in an outward “overshoot” current (Fig. 5C). This is in contrast to the current recorded after washout of AMPH in control conditions (0 mm intracellular Na⁺) (Fig. 1A). The overshoot current (Fig. 5C) had an amplitude of 25 ± 2% of the peak current and decayed with a time constant of 46 ± 9 ms (n = 10). Although the amplitude of the peak current was voltage dependent, the overshoot current did not change with voltage (Fig. 5C, inset). To compare the inward charge movement during the peak current with the outward charge movement during the overshoot current, we integrated the area under the overshoot current and plotted this integral against the area under the peak current (Fig. 5D). The charge carried by the inward peak current was greater than the charge carried by the outward overshoot current at −60 mV (filled squares), whereas the charges were nearly identical at 0 mV (Fig. 5D, open squares).

To characterize the dependence of the peak and overshoot currents on intracellular Na⁺ (from 0 to 120 mm), we substituted intracellular Na⁺ for K⁺ (Fig. 5E–H). Intracellular Na⁺ did not change the rise time of the peak current (Fig. 5E) (p > 0.05, ANOVA followed by Tukey's post hoc test; n = 5–93) but did accelerate the rate of decay of the peak current at 90 or 120 mm Na⁺ (Fig. 5F) (*p < 0.05, compared with control 0 mm Na⁺; ANOVA followed by Tukey's post hoc test; n = 5–93). Although the peak current amplitude was not altered by increasing intracellular Na⁺ concentration, the ratio of the steady-state current to the peak current significantly decreased above 30 mm intracellular Na⁺ (Fig. 5G) (*p < 0.05, ANOVA followed by Tukey's post hoc test; n = 5–93). In contrast, under the same conditions, the overshoot current increased with increasing intracellular Na⁺ concentration (Fig. 5H) (*p < 0.05, Kruskal–Wallis test with Dunn's multiple comparison test).

Thus, intracellular Na⁺ regulates the rate of transitions between conformational states of the transporter. We hypothesized that elevated intracellular Na⁺ would also regulate the rate of recovery from desensitization to pair pulses of AMPH (Fig. 6). This recovery rate reflects the rate for a transporter transitioning to an outward-facing conformation ready to bind the substrate. In the presence of 90 mm internal Na⁺, the rate of recovery of the peak current was accelerated more than 10-fold compared with 0 mm Na⁺ control (Fig. 6A, compare top and bottom). These rates of recovery obtained from multiple experiments were plotted in Figure 6B (n = 6–9). The rate of recovery from desensitization depended on the intracellular Na⁺ concentration (Fig. 6C) and correlated directly with the amplitude of the overshoot current observed upon washout of AMPH (Fig. 6C, inset). These data suggest that increasing intracellular Na⁺ facilitates the transition of the transporter to the “outward-facing” state. This is because the rate at which the transporter becomes ready to subsequently bind AMPH after the first AMPH application is accelerated with high intracellular Na⁺. The accelerated recovery rate and the outward overshoot current suggest that high intracellular Na⁺ may prevent intracellular substrate release and lock the substrate to the transporter in an “Na⁺-exchange” mode.

Figure 6.

Elevated intracellular Na⁺ accelerates recovery from desensitization to paired pulses of AMPH. A, AMPH (10 μm) was applied for 100 ms with a paired-pulse protocol at a variable interval to monitor recovery from desensitization. One representative cell is shown for 90 mm Na⁺ or 0 Na⁺ internal. B, The current in response to the second AMPH application, normalized to the current in response to the first application, is plotted against the time between the applications for 0 mm (open squares) and 90 mm (closed circle) internal Na⁺ (n = 6–9). The time constant (τ) for recovery from desensitization for each Na⁺ concentration was determined by fitting to a single exponential function. C, The time constants are plotted as a function of intracellular Na⁺ concentration (n = 5–9). Inset, The rate of recovery from desensitization (1/τ) correlates with the amplitude of the overshoot current across different intracellular Na⁺ concentrations.

An overshoot current was reported for the glycine transporter GLYT1 upon washout of the substrate (Aubrey et al., 2005). Aubrey et al. (2005) observed that the size of the overshoot current for GLYT1 increased with increased duration of substrate application, supporting the hypothesis that the overshoot current reflects reverse transport through GLYT1 of internal substrate accumulated in the cell by prolonged forward transport. We performed an analogous experiment in hDAT cells recording the overshoot current upon washout of AMPH 100 ms and 1 s after AMPH application under conditions of elevated intracellular Na⁺ (Fig. 7A,B). In contrast to the behavior observed for GLYT1, the hDAT overshoot current did not increase with increasing duration of AMPH application. We also tested whether the presence of high intracellular substrate concentration along with high Na⁺ modified the amplitude of the AMPH-induced current (Fig. 7C). Neither the presence of 10 μm AMPH nor 2 mm DA had a significant effect on the amplitude of the peak AMPH-induced current (p > 0.05; n = 7–9) (data not shown) or the amplitude of the overshoot current (Fig. 7C,D) (p > 0.05; n = 7–9). Together, these data suggest that the overshoot current for hDAT is generated by the failure of occupied carrier to release substrate intracellularly and the return of the transporter to an outward-facing conformation upon washout of AMPH. This failure to release intracellular substrate is a result of the presence of high intracellular Na⁺.

Figure 7.

In the presence of elevated intracellular Na⁺, intracellular substrate does not alter the overshoot current nor the recovery time from desensitization. A, B, At saturating intracellular Na⁺ concentrations (90 or 120 mm internal Na⁺), application of 10 μm AMPH to the same cell for either 100 ms or 1 s produces similar outward overshoot currents upon washout of AMPH (n = 9). In B, the overshoot current was normalized to the peak current. C, Washout of 10 μm AMPH upon a 1 s application produces an outward overshoot current in the presence of intracellular substrate (either AMPH or DA) and elevated intracellular Na⁺ (90 mm Na⁺). Representative traces from two different cells are displayed. D, With 90 mm intracellular Na⁺ (control), the presence of either 10 μm AMPH or 2 mm DA in the internal solution did not affect significantly the overshoot current recorded after washout of externally applied AMPH (p > 0.05, ANOVA; n = 7–10). E, AMPH was applied for 100 ms with a paired-pulse protocol at a variable interval to monitor recovery from desensitization. One representative cell is shown for 2 mm DA/90 mm Na⁺ internal. The time course is similar to that observed with high intracellular Na⁺ in the absence of intracellular substrate (see Fig. 7 for comparison). F, The current in response to the second AMPH application, normalized to the current in response to the first application, is plotted against the time between the applications in the presence or absence of the intracellular substrates (90 mm intracellular Na⁺; n = 6–9). G, The presence of internal substrate has no effect on recovery from desensitization in the presence of 90 mm intracellular Na⁺ (n = 6–9). AMPH, 10 μm AMPH; DA, 2 mm DA in the internal solution.

In addition to the overshoot current, the high intracellular Na⁺ concentration affects the rate of recovery from desensitization to a second pulse of AMPH (Fig. 6). This rate may be limited by at least two factors: (1) the time for the substrate to unbind from the transporter; and (2) the time for the transporter to return to an outward-facing state. To test whether substrate unbinding from the intracellular side is rate limiting for recovery, we measured the recovery rate from desensitization to AMPH in the presence of intracellular substrate (compare Figs. 7E and 6A). Neither intracellular AMPH (10 μm) nor DA (2 mm) had an effect on the recovery rate (Fig. 7F,G), suggesting that in the presence of elevated intracellular Na⁺, hDAT can return to a competent state to rebind extracellular AMPH without first releasing substrate from the cytoplasmic side.

hDAT function is facilitated by both extracellular and intracellular Cl⁻

To assess the regulation of hDAT function by Cl⁻, we measured AMPH-induced currents in the presence of varied concentrations of extracellular or intracellular Cl⁻ (Fig. 8). Figure 8, A and B, shows that reducing extracellular Cl⁻ from 130 to 15 mm by acetate⁻ (Ac⁻) substitution dramatically reduced the peak current but had no effect on the steady-state current. Nominally complete substitution of Cl⁻ by Ac⁻ reduced both the peak and steady-state currents.

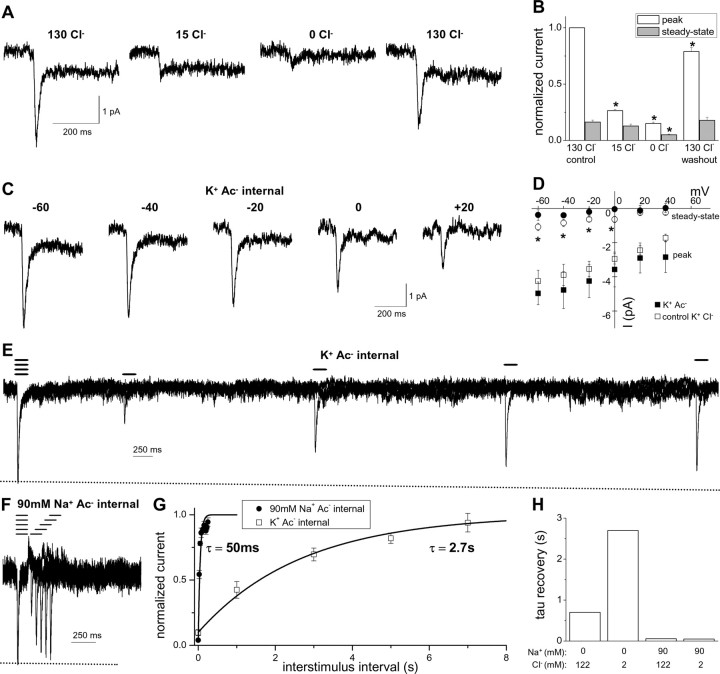
Figure 8.

The AMPH-induced current depends on both external and internal Cl⁻. A, Current traces in response to a 1 s application of 10 μm AMPH recorded in the presence of the indicated extracellular concentration of Cl⁻ substituted by Ac⁻. B, The current for each condition was normalized to the control 130 mm Cl⁻ peak current for each cell (*p < 0.05, repeated measures ANOVA; n = 6). C, Current traces in response to a 1 s application of 10 μm AMPH recorded at different voltages with substitution of Ac⁻ for Cl⁻ as the predominant intracellular ion. The pipette solution (internal solution) contained 120 mm Ac⁻ plus 2 mm Cl⁻ (K⁺ Ac⁻ internal). D, The I–V relationship for the peak current is not significantly different for K⁺ Ac⁻ internal and control K⁺ Cl⁻ internal (n = 4–6; *p < 0.05, two-way ANOVA). The steady-state current is reduced by K⁺ Ac⁻ internal. The pipette solution (internal solution) contained either 120 mm Ac⁻ plus 2 mm Cl⁻ (K⁺ Ac⁻ internal) or 122 mm Cl⁻ (K⁺ Cl⁻ internal). E, AMPH (10 μm) was applied for 100 ms with a paired-pulse protocol at a variable interval to monitor recovery from desensitization in the presence of K⁺ Ac⁻ internal. F, A paired-pulse protocol with 90 mm Na⁺ Ac⁻ internal (90 mm Na⁺, 30 mm K⁺, 120 mm Ac⁻, 2 mm Cl⁻). G, The normalized peak current is plotted as a function of time between AMPH applications to evaluate the recovery time from desensitization (n = 4). H, The fitted paired-pulse recovery time is shown for the indicated intracellular concentrations of Na⁺ and Cl⁻ (n = 4–9).

Next, we substituted Cl⁻ with Ac⁻ as the dominant internal anion (Fig. 8C,D). The peak currents measured under these conditions showed similar properties to those recorded under control internal Cl⁻ conditions (compare Figs. 8C and 1E). The amplitude of the peak current (5.4 ± 0.9 pA), the rise time of the peak current (7.3 ± 0.9 ms), and the time constant for peak decay (19 ± 2 ms) with Ac⁻ internal solution (n = 13) were not significantly different from the control Cl⁻ internal solution (n = 93) at −60 mV. In addition, the current–voltage relationship for the peak current with Ac⁻ internal solution is similar to that for the control Cl⁻ internal solution (Fig. 8D). Therefore, these data suggest that Cl⁻ flux makes little if any contribution to the peak hDAT current induced by AMPH. In contrast, there was a statistically significant reduction in the steady-state current when Ac⁻ was substituted for Cl⁻ (steady-state to peak current ratio, 0.11 ± 0.04 for Ac⁻ internal compared with 0.24 ± 0.01 for control Cl⁻ internal; p < 0.05; n = 13–93).

The observation that substitution of intracellular Cl⁻ by Ac⁻ reduced the steady-state current suggested that this substitution slowed the turnover rate for the transporter. Consistent with this hypothesis, the time constant for recovery from desensitization to paired pulses of AMPH was 2.7 s with K⁺ Ac⁻ internal (Fig. 8E,G) compared with 0.7 s with K⁺ Cl⁻ internal (compare Figs. 8G and 2B). Based on the classically hypothesized coupled Cl⁻ cotransport, by decreasing intracellular Cl⁻, the transporter turnover rate would be expected to be faster, because trans-inhibition by intracellular Cl⁻ would be relieved. In contrast to this expectation, we observed that intracellular Cl⁻ binding to the transporter facilitates rather than inhibits transporter turnover.

Elevated intracellular Na⁺ induces an overshoot current upon AMPH washout and a rapid paired pulse recovery even under substitution of intracellular Cl⁻ by Ac⁻ (Figs. 8F–H, 5, 6). These data provide further support for the hypothesis that elevated intracellular Na⁺ inhibits intracellular substrate release and places the transporter in a Na⁺-exchange mode. Furthermore, this implies that Na⁺ unbinding must precede Cl⁻ unbinding from the inside of the transporter.

Modeling of hDAT function

We developed a simplified model of transporter function that is consistent with our experimental data (Fig. 9A). This model can account for the major properties of the electrical currents recorded under both control conditions (Fig. 9B) and elevated intracellular Na⁺ (Fig. 9C). To account for the dependence of AMPH-induced currents on both intracellular and extracellular Cl⁻, we modeled a Cl⁻ binding step as a prerequisite for both Na⁺ and substrate binding and the transitions between inward and outward facing conformations of the transporter. The basic premise of our alternating access model is that the binding of Na⁺ and AMPH occurs in a “first-in, first-out” manner. Thus, Na⁺ binds to the transporter before AMPH and must unbind from the intracellular side before AMPH. Once Na⁺ and AMPH are bound, the transporter rapidly moves the cargo to the intracellular side. This translocation transition (T°■Cl■Na■AMPH ↔ Tⁱ■Cl■Na ■AMPH) is electrogenic (total valence, z_Q, 0.20) and mediates the majority of the peak current. After unloading the Na⁺ and substrate, the empty transporter slowly converts back to an outward facing conformation. This reorientation of the empty transporter (transition Tⁱ■Cl ↔ T°■Cl) is electrogenic (total valence, z_Q, 0.80) and mediates the majority of the steady-state current. The relatively slow Tⁱ■Cl ↔ T°■Cl transition is the rate-limiting step for transporter turnover and deactivation of the steady-state current after substrate removal. Therefore, the recovery rate of the peak current from desensitization is slow under control conditions in the presence of intracellular K⁺ and absence of intracellular Na⁺ (Fig. 9D). However, the presence of high intracellular Na⁺ prevents release of intracellular AMPH from the transporter and places the transporter in a Na⁺-exchange mode. In this mode, the recovery from desensitization is rapid (Fig. 9E), because the occupied carrier rearranges to the outward-facing conformation more rapidly than the empty carrier. When AMPH is washed out of the extracellular solution, as the occupied carrier returns to an outward-facing conformation in the Na⁺-exchange mode, the charges associated with translocation are moved outward causing the overshoot current observed in the presence of high intracellular Na⁺. The rapid exchange of the Na⁺ and AMPH-occupied transporter and the unbinding of AMPH from the extracellular side of the transporter explain why the transporter exhibits rapid recovery from desensitization in the presence of high intracellular Na⁺ (Fig. 9E). This model also accounts for the changes in steady-state and peak currents induced over a range of different substrate and Na⁺ concentrations (Fig. 9F,G). Furthermore, the model accounts for the voltage dependence of the peak and steady-state currents in the presence of different concentrations of intracellular Na⁺ and Cl⁻ (Fig. 9H).

Figure 8 shows that both extracellular and intracellular Cl⁻ are required for efficient transporter turnover. In our model, we account for these observations with a Cl⁻ binding step as permissive for transporter binding of Na⁺ and substrate as well as for transporter turnover. This model accounts well for the experimental data, including substitution of extracellular and intracellular Cl⁻ (Fig. 10). The requirement for both extracellular and intracellular Cl⁻ is inconsistent with coupled Cl⁻ influx being required for substrate uptake. If Cl⁻ influx was required for DAT turnover, then high intracellular Cl⁻ should slow turnover, as has been shown recently for the GABA transporter (Zomot et al., 2007). In contrast, here, we show that intracellular Cl⁻ positively regulates DAT turnover rate [compare Figs. 2B (high Cl⁻) and 8G (low Cl⁻)].

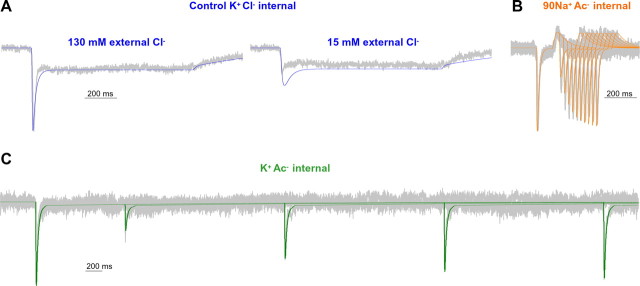
Figure 10.

An explicit alternating access model can account for the regulation of AMPH-induced currents by Cl⁻. The model simulation (color) is superimposed on the experimental data (gray). A, hDAT currents at −60 mV in response to a 1 s application of 10 μm AMPH with control (K⁺Cl⁻) internal solution were normalized, aligned to the time of the peak, and averaged among cells (n = 3). External Cl⁻ was substituted by Ac⁻ to reduce [Cl⁻] to 15 mm. B, C, Mean pooled experimental data for representative cells (n = 4) and model simulations for paired-pulse responses to 100 ms applications of 10 μm AMPH at a variable interval. The external solution was Na⁺Cl⁻. The internal solution was 90 mm Na⁺ Ac⁻ (90 mm Na⁺, 30 mm K⁺, 120 mm Ac⁻, 2 mm Cl⁻) or K⁺ Ac⁻ (120 mm K⁺, 120 mm Ac⁻, 2 mm Cl⁻).

In addition to the model presented in Figures 9 and 10, we evaluated other potential models. In one of the variants, we placed the Na⁺ dissociation step after the AMPH dissociation step (first-in, last-out sequence). This model was unable to account for the data obtained in the presence of high intracellular Na⁺, because no exchange activity should be observed in the absence of intracellular AMPH (intracellular AMPH dissociation would always drive the transporter into the fully dissociated state, preventing reverse translocation). In other variants of the model, we assigned electrogenicity to different steps in the transport cycle. Placing electrogenicity on the extracellular Na⁺ binding step led to an oscillation in the AMPH-induced current, which is not observed in the experimental data (see Discussion). Assigning voltage dependence to the AMPH binding reaction also resulted in a less than optimal model, because in this case, the peak current is expected to increase linearly with [AMPH]. This behavior is not consistent with the experimental data (Fig. 3B). Finally, we tested models with all steps electroneutral, except the relocation of the empty carrier. In this case, no peak current should be observed, in contrast to the experimental data (Fig. 1A). This last argument also holds for rate-limiting extracellular Na⁺ binding being the only electrogenic step in the transport cycle. To summarize, our model describes the data reasonably well, in contrast to other tested models. However, the possibility cannot be excluded that other more complex models can be generated that describe the data equally well, or better. This conclusion should not be surprising, given the complexity of the multistep dopamine transport process.

Discussion

Molecular mechanism of AMPH-induced inward current

Here, we report the first characterization with high temporal resolution of substrate-induced currents for a mammalian monoamine transporter. The AMPH-induced currents we describe have similar activation kinetics to the serotonin transport current recorded in the Retzius-P cell synapse of the leech (Bruns et al., 1993). We interpret the decay of the peak current after AMPH application to reflect the transition from synchronized to desynchronized operation of the population of transporters (Bruns et al., 1993; Bergles et al., 1997; Otis et al., 1997). Our model predicts that translocation of substrate is rapid and that the turnover of the transporter is rate limited by the transition of the empty transporter from an inward- to an outward-facing conformation. Consistent with this hypothesis, the recovery rate from desensitization to a second substrate application (an index of turnover rate) was the same for two different substrates, AMPH and DA (Fig. 2).

The rapid AMPH-induced peak current is dependent on extracellular Na⁺ (Fig. 4). However, the presence of high intracellular Na⁺, which reduces the transmembrane Na⁺ gradient, does not inhibit the amplitude of the peak current, nor does it shift its voltage dependence (Fig. 5A,B). Therefore, the peak current does not depend on net transport of Na⁺. We hypothesize that the peak current is mediated primarily by charge movement associated with the translocation of ions/substrate in the presence of Na⁺ (Kanai et al., 1995; Watzke et al., 2001). This charge movement may represent a combination of the translocation of ions and substrate through the transporter and/or a fixed charge on the transporter that moves through the membrane electric field. We cannot unequivocally rule out a contribution of voltage-dependent Na⁺ binding to the peak current, although our attempts to assign a weak voltage dependence to the Na⁺ binding step did not account for the time course and relative amplitudes of the peak and steady-state currents. Also, if the Na⁺ binding is electrogenic, then it is not associated with a large valence, because this would lead to a significant voltage dependence and [Na⁺] dependence of the peak current decay rate, which were not found experimentally. In contrast to the peak current, the steady-state current was abolished by raising intracellular Na⁺ and significantly reduced by lowering intracellular Cl⁻. These data are consistent with the steady-state current in hDAT being dependent upon the Na⁺ concentration gradient and also dependent on both intracellular and extracellular Cl⁻.

Regulation of hDAT function by intracellular Na⁺

Elevated intracellular Na⁺ dramatically accelerates the rate of recovery of the peak current from desensitization (Fig. 6). Thus, in contrast to the slow recovery of empty transporter, the presence of Na⁺ on both sides of the transporter may result in a rapid cycling “Na⁺-exchange” mode of function. Under control conditions, the substrate binds along with Na⁺ and is translocated to the cytoplasm by the conformational change that moves the substrate binding site from an outward-facing to an inward-facing conformation. Na⁺ and the accompanying substrate molecule may then unbind from the inward-facing binding site and, in the rate limiting step of transport, the empty carrier must transition to an outward-facing conformation. In contrast, in the presence of elevated intracellular Na⁺, the inward-facing Na⁺ binding site is occupied, and there is no net Na⁺ translocation, consistent with the absence of steady-state current. We hypothesize that elevating intracellular Na⁺ prevents substrate unbinding from the inward face of the transporter and places the transporter in a rapid Na⁺-exchange mode between inward- and outward-facing conformations. When extracellular substrate is rapidly removed, we record an outwardly directed overshoot current that represents the reorientation of occupied transporter and the release of substrate to the extracellular milieu. Therefore, similar to the glycine transporter, the overshoot current does reflect the reverse transport of substrate bound to the transporter, but under our experimental conditions, this reverse transport is of a substrate molecule that never dissociates from the inside of the transporter.

Regulation of hDAT function by Cl⁻

DA transport requires extracellular Cl⁻, and the structural basis for Cl⁻ dependence of transport has been elucidated recently (Forrest et al., 2007; Zomot et al., 2007). Cl⁻ functions to counterbalance the charge of a Na⁺ ion and appears to be necessary for Na⁺ binding and subsequent substrate binding. Although the function of hDAT is clearly dependent on extracellular Cl⁻, the role of Cl⁻ regulation of transport and the movement of Cl⁻ through the transporter are complex and poorly understood. The classically hypothesized stoichiometry of DAT transport suggests influx of Cl⁻ induced by substrate (Rudnick and Clark, 1993). In contrast, a substrate-induced uncoupled Cl⁻ conductance mediating a positive inward current has been reported at physiological voltage, suggesting efflux of Cl⁻ induced by substrate (Ingram et al., 2002). Additionally, there is little information in the literature about the regulation of DAT by intracellular Cl⁻. Here, we show that both extracellular Cl⁻ and intracellular Cl⁻ facilitate transporter turnover, consistent with a modulatory role of Cl⁻ in substrate translocation (Loo et al., 2000). Our data suggest that internal Cl⁻ facilitates hDAT turnover. This Cl⁻-mediated process is different than the inhibition of turnover by internal Cl⁻ reported for GABA transporter GAT-1 reconstituted in liposomes. This may reflect a distinction between the fundamental mechanisms of GABA and DA transporters (Zomot et al., 2007).

Modeling of hDAT function

We postulate a first-in, first-out mechanism for the interactions of Na⁺ and substrate with the transporter with the binding of Na⁺ before substrate. The unbinding of Na⁺ before the substrate from the cytoplasmic face of the transporter provides a mechanistic explanation for the effects of intracellular Na⁺ on substrate-induced currents (Fig. 5–7). Such a mechanism is also consistent with high intracellular Na⁺ promoting reverse transport of substrate through hDAT (Liang and Rutledge, 1982, 1983; Khoshbouei et al., 2003).

In addition to the kinetic features described in the preceding paragraphs, the model allows the prediction of some other kinetic parameters that are important for the physiological function of the transporter. First, from the model, we can obtain a direct estimate of the theoretical hDAT maximal turnover rate of 1.9 s⁻¹ at −60 mV, similar to the experimentally determined value of 1.4 s⁻¹ (Fig. 2). This value compares well with that determined for DA transport in a previous report from combining uptake and binding experiments (Sonders et al., 1997). Our data show that the recovery time from desensitization to a second pulse of substrate is the same for AMPH and DA (Fig. 2), as expected if the turnover rate is mainly determined by the substrate-independent rearrangement of the empty transporter but not by substrate translocation (Nelson and Rudnick, 1979). Second, we can estimate the bimolecular rate constant of AMPH binding to hDAT as 3 × 10⁸ m⁻¹s⁻¹. This value is in the typical range of small molecule–protein interactions (Fersht, 1999) and indicates that AMPH access to its binding site in the presence of bound Na⁺ is not associated with large energy barriers. Third, the model places the main electrogenicity onto the Tⁱ■Cl to T°■Cl transition of the empty (no substrate or Na⁺ bound) carrier (Fig. 9), similar to a model hypothesized for the glucose transporter (Parent et al., 1992; Mackenzie et al., 1996; Loo et al., 2006). The charge movement associated with this transition may be caused by a combination of movement of intrinsic charges of the transporter within the membrane and/or outward movement of a bound Cl⁻ ion. Transitions of the Na⁺ and AMPH-loaded transporter are only weakly electrogenic, in agreement with data available for the GABA transporter (Lu and Hilgemann, 1999; Bicho and Grewer, 2005). We hypothesize that a Cl⁻ ion and/or intrinsic charges on the transporter may counterbalance part of the inward charge movement associated with substrate and Na⁺ translocation and that the outward movement of this net negative charge, after substrate and Na⁺ unbinding from the inside of the transporter, provides the major electrogenic basis for the steady-state current.

Previous reports have described a channel-like mode of conduction for monoamine transporters (Galli et al., 1996, 1998; Kahlig et al., 2005). Under control conditions, this uncoupled conductance is extremely rare (open probability, <1%) (Kahlig et al., 2005). Importantly, we also showed that AMPH exposure (on the time scale of minutes) activates kinases such as calcium calmodulin-dependent protein kinase II, which sustains DAT uncoupled conductance (Fog et al., 2006; Wei et al., 2007). In our rapid application experiments, we define steady-state DAT current using a brief (1 s) application of AMPH. Therefore, it is possible that longer exposure to AMPH may be required to sustain channel-like activity through DAT depending on activation of signaling pathways.

In this paper, we present an alternating access model that can primarily account for a wide range of data characterizing substrate-induced currents with a stoichiometric transport model. The model provides a framework to interpret future studies on regulation of monoamine transporters. For example, we now have an opportunity to evaluate the specific effects on the transitions of the transporter cycle by phosphorylation of the hDAT N terminus, which has been shown to regulate dopamine efflux (Khoshbouei et al., 2004).