Abstract
A statistical mechanical model is presented which explicitly accounts for the fluctuations, the electrostatic, and the excluded volume correlations for ions bound to a polyelectrolyte such as DNA. The method can be employed to treat a wide range of ionic conditions including multivalent ions. The microscopic framework of the theory permits the use of realistic finite length and grooved structural model for the polyelectrolyte and modeling of the finite size of the bound ions. Test against Monte Carlo simulations suggests that the theory can give accurate predictions for the ion distribution and the thermodynamic properties. For multivalent ions, the theory makes improved predictions as compared with the mean-field approach. Moreover, for long polyelectrolyte and dilute salt concentration, the theory predicts ion binding properties that agree with the counterion condensation theory.
I. INTRODUCTION
Polyelectrolyte folding requires the proper ionic solution condition. It is essential to understand how the ionic condition, such as ion concentration, ion size, and ion charges, determines the polyelectrolyte folding stability and cooperativity. The ion-polyelectrolyte interaction is crucial to the distribution of the ions in the close proximity of the polyelectrolyte surface. The closely bound ions reside within a short distance of 1~2 hydrated ionic radii from the polyelectrolyte surface, so the discrete properties of the bound ions can be very important.
The local ion concentrations near the polyelectrolyte surface, especially around the charged groups, can be high.1,2 The condensed distribution of the bound ions causes strong correlations between the ions, as are characterized by a large correlation parameter Γ=q2/(εawskBT),3–7 where q is the ionic charge, kB is the Boltzmann constant, T is the temperature, ε is the dielectric constant, and aws is the Wigner-Seitz radius. Multivalent ions carry high charges q and generally involve very strong correlations. In fact, the electrostatic correctional force may be responsible for the attraction between like-charged polyelectrolytes,3,8–10 and may also contribute to the folding driving force for nucleic acids.11–15
In addition, fluctuations in the ion binding will affect the mechanical and thermodynamic properties of the polyelectrolyte. For example, fluctuations in ion distribution can reduce bending rigidity for randomly charged polymer.16,17 Moreover, the ion fluctuation is closely related to the stability of the system. Most previous models on ion fluctuation are based on simplified models.16–21 In the present study, we address detailed polyelectrolyte structures and ion sizes in addition to the ion-ion correlations due to both Coulombic and excluded volume interactions.
Classical approaches, including the counterion condensation (CC) theory22 and the Poisson-Boltzmann equation (PB) theory,23–29 have enabled quantitative predictions for the thermodynamic properties of proteins, DNAs, RNAs, and other polyelectrolytes. The CC theory assumes a two-state ion distribution and assumes an average uniform distribution of the bound ions, while neglecting the direct interactions between the bound ions and the polyelectrolyte backbone charges. PB is a mean-field theory which neglects the correlation effects. Both CC and PB ignore the fluctuations in counterion distributions and assume a mean distribution of counterions. Monte Carlo (MC) and molecular dynamics simulations30,31 and the hypernetted chain theory32,33 can account for the ion size, excluded volume, and inter-ion correlations, but require random sampling of the ionic configurations or through convoluted integral equation solutions.
In this paper, we present a statistical thermodynamics model for a rigid polyelectrolyte of finite length immersed in a salt solution. The purpose here is to provide an analytical treatment for the ion-polyelectrolyte binding by considering the detailed geometry of the polyelectrolyte and the finite size of the ions. In contrast to the previous CC- or PB-based studies, the present study considers electrostatic correlations and fluctuations for the bound ions. Moreover, compared with the previous simplified salt-free models,3,20 we consider the contributions from the added salt ions in the supporting solution. The current form of the theory is developed for rigid polyelectrolyte. This is a first step towards a theory that can treat the interactions between multiple polyelectrolyte chains and the folding of a flexible polyelectrolyte, which involves an ensemble of chain conformations.
II. POLYELECTROLYTE STRUCTURE
In the present study, we use the double-helical B-DNA as a paradigm for the polyelectrolyte. Previous studies have shown that the detailed grooved structure, and the positions of the phosphate groups are important for the distribution of the bound ions.1,34 All-atom models can give the details for the polyelectrolyte structure, but are intractably complex for a rigorous statistical mechanical theory developed in the present study. Therefore, we employ a coarse-grained semi-realistic polyelectrolyte model while retaining the key structural features.
First, the model should provide the major and minor grooves. The groove structures, which have been neglected in many previous simplified models, are important because the interactions of the bound ions are dependent on the detailed geometry of the polyelectrolyte surface. Second, the model should properly account for the sizes and the positions of the negatively charged phosphate groups as well as other neutral groups on the nucleotide backbone. Previous simulations based on realistic polyelectrolyte structures have shown that the thermodynamic results are quite sensitive to the backbone charge distribution.34,35 This is different from the simplified cylindrical polyelectrolyte model, where the uniform and discrete charge distributions give similar results.
We use a previously reported grooved DNA helix model to describe the polyelectrolyte structure.34 The model, which retains a high degree of realism for the polyelectrolyte structure, is tractable for our statistical mechanical calculations. Previous detailed molecular simulations have validated the grooved model through the computation of the detailed ion distribution.34 Figure 1 shows the grooved model. We represent a B-form DNA structure of L nucleotide units as two helical strands, each with L/2 nucleotide units, around a central cylindrical rod of radius rcore=3.9 Å. The central cylindrical rod represents the space occupied by the base pairs and is assumed to be inaccessible to the salt ions. We use two hard spheres to represent the chemical groups in a nucleotide unit: a charged sphere with a point charge −e (e=protonic charge) at the center to represent the phosphate group and a neutral sphere to represent the rest of the group in the nucleotide. The phosphate sphere is placed at the center of the phosphate group of the nucleotide and the neutral sphere lies between the phosphate sphere and the cylindrical rod, as shown in Fig. 1. Both spheres are assumed to have radius of r0=2.1 Å. The radii of the spheres are chosen to best simulate the more realistic soft potential (a smooth distance-dependent potential functions).34 For a B-DNA, the phosphate charge positions are given by the following equation:36
FIG. 1.
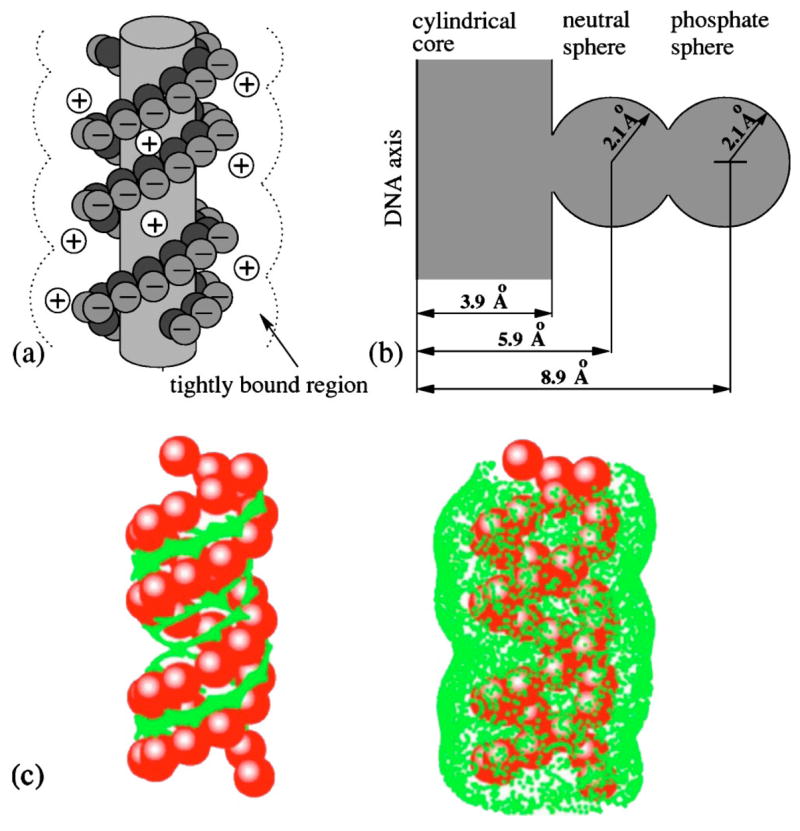
(a) The B-DNA grooved primitive model (Ref. 34). In our theory, the region around DNA molecule is divided into two parts: (i) the tightly bound region, where counterions are trapped by the strong electrostatic field and are strongly correlated; (ii) the diffusively bound region (outside the dotted lines), where ions are diffusive and can be described by the Poisson-Boltzmann theory. The boundary between the two regions is determined by Fig. 1(c). (b) The cross section of the B-DNA grooved model shows the position of cylindrical core, intermediate neutral sphere, and phosphate sphere. (c) The tightly bound regions around a B-DNA of length L=40 in Na+ (left) and Mg2+ (right) solutions at bulk concentration c0=0.1M. The red spheres represent the phosphate groups and the green dots represent the points on the boundaries of the tightly bound regions.
| (1) |
where s (=1,2) denotes the two strands and i (=1,2,…, L/2) denotes the nucleotides on each strand. The initial position parameters and are 0° and 0 Å for the first strand, and 154.4° and 0.78 Å for the second strand.
III. TIGHTLY BOUND IONS AND BINDING MODES
We assume that ions are hydrated, i.e., the model does not treat the desolvated ions binding to (often deeply penetrated) specific sites of the polyelectrolyte. We use ionic radii 3.5, 4.5, and 3.5 Å for the hydrated Na+, Mg2+, and Cl− ions,37 respectively. The positively charged counterions tend to bind to the polyelectrolyte (polyanion in our model) in the solution. We classify the bound counterions into two types: “the tightly bound ions” and “the diffusively bound ions.” The tightly bound ions are trapped in the strong electrostatic field on the polyelectrolyte surface. They lose, to a considerable extent, the radial degree of freedom, though they may diffuse on the polyelectrolyte surface. On the other hand, the diffusively bound ions are more mobile and are diffusively distributed in the solution around the polyelectrolyte.
We can use the fluid model to describe the diffusively bound ions. In the mean-field approximation, the local concentration cα(x) at position x for ions of species α obeys the Boltzmann distribution, as determined by the electrostatic potential ψ(x),
| (2) |
where zαe is the charge of the ion and is the bulk concentration. The electric potential ψ(x) is given by the solution of the PB,
| (3) |
where ρf is the charge density of the fixed charges and ε0 is the permittivity of free space.
Since ψ(x) decreases rapidly as x approaches the polyelectrolyte surface, which, according to Eq. (2), causes an abrupt increase in the counterion concentration cα(x). There may exist a region of x sufficiently close to the polyelectrolyte surface where ions are sufficiently condensed so that ions become strongly correlated. We call the strongly correlated ions as the tightly bound ions, and the corresponding region as the tightly bound region. How to quantitatively and unambiguously define the tightly bound region? We use the following criteria.
-
Strong electrostatic correlation can be characterized by a large correlation parameter:
(4) Here we use ε≃78 (=bulk solvent) for inter-ion distance d≥2rc≥7Å (rc=ion radius) for Na+ or Mg2+. Previous computer simulations suggest that Γc≃2.6 for the liquid to gaseous phase transition for ion system.5–7 To measure the (excess) electrostatic correlation induced by the polyelectrolyte, we use the Wigner-Seitz radius aws(x) for counterion concentration in excess of the bulk solvent concentration:3
(5) -
Ions of finite size in the high concentration region become crowded and can frequently bump into each other, causing the excluded volume correlation between the ions. A strong excluded volume correlation induced by the polyelectrolyte can be characterized by a small mean inter-ion distance d,
(6) where rc is the ion radius, Δr is the mean displacement of ions from the equilibrium positions, and 2(rc+Δr) is the closest distance between two ions before they overlap. From Lindermann’s melting theory, we choose Δr/d≃0.1 as the melting point for the correlated structure.38–40
From the counterion concentration cα(x) in Eq. (2) and the corresponding aws in Eq. (5), we can quantitatively map out the tightly bound region, from either Eq. (4) or Eq. (6)—whichever is first satisfied as the ion position x approaches the polyelectrolyte surface. In fact, we find that for Na+ solutions, Eq. (6) gives the tightly bound region, while for Mg2+ solutions, which involve stronger electrostatic interactions, Eq. (4) determines the tightly bound region. In Fig. 1(c), we show the tightly bound region for a double stranded oligomeric B-DNA in Na+ and Mg2+ solutions, respectively. As shown in the figure, the tightly bound region is roughly a thin layer (or patches of thin layers) on the polyelectrolyte surface, and the tightly bound region covers a wide area from the surface of the phosphate groups to the major or minor grooves, depending on the size and the charge of the counterions. We call the tightly bound region for each nucleotide (=monomer of the DNA polyelectrolyte) as a tightly bound cell. A tightly bound ion in the tightly bound cell can either reside in the major or minor groove or bound to the respective phosphate group.
As described above, according to the inter-ion correlation strength, we can classify two types of ions: the tightly bound and the diffusive ions for counterions inside and outside the tightly bound region, respectively. For the (strongly correlated) tightly bound ions, we need a theory that goes beyond the PB to account for the strong correlation and fluctuation. In the following sections, we develop such a theory. The main points of the theory include the following.
To consider the fluctuation of the tightly bound ions, we introduce binding modes. A binding mode M is defined by the ion occupation numbers mi in the tightly bound cells (i=1,2,…,N; N=the number of the tightly bound cells in the polyelectrolyte): M={m1,m2,…,mi,…,mN}.
The use of the discrete modes makes it possible to fully account for the m-particle (ion) electrostatic correlation ( is the number of the tightly bound ions).
For a given tightly bound mode, the tightly bound ions have freedom to move around in their respective tightly bound cells. For each mode, we perform the statistical average over the possible positions of the tightly bound ions to determine the potential of mean force (free energy) of the bound ions. The finite size of the ions, the polyelectrolyte structure, and the electrostatic and steric correlations are fully accounted for in the calculation.
For each mode (charge distribution) of the tightly bound ions, we use the mean-field PB theory to describe the distribution of the (weakly correlated) diffusive ions. From the ion distribution, we can determine the free energies of the system, including the interaction between the tightly bound ions and the diffusive ions. We can also determine the dominant binding modes, the fluctuations, and the radial distribution of the bound ions, etc.
IV. STATISTICAL MECHANICS MODEL
Consider an L-mer polyelectrolyte immersed in a solution of N+ cations and N− anions. The total partition function of the system is the sum of the partition functions ZM (M=the binding mode) for all the possible binding modes:
| (7) |
From the mode partition function ZM we obtain the probability pM for the binding mode and the mean distribution {m̄1,m̄2,…,m̄L} of the tightly bound ions:
| (8) |
At the center of the theory is the mode partition function ZM. We consider a mode M with Nb tightly bound ions (and Nd=N+ + N− − Nb diffusive ions). We use Ri (i = 1,2,…,Nb) and rj (j =1,2,…,Nd) to denote the coordinates of the ith tightly bound ion and the jth diffusive ion, respectively. The total interaction energy for a given configuration (R,r) can be decomposed as Ub(R) for the electrostatic interactions between the tightly bound charges (=charges of the tightly bound ions and the phosphate charges), Us(R,r) for the interactions between the diffusive ions, and Uint(R,r) for the interactions between the tightly bound charges and the diffusive ions.
For a given mode, Ri can distribute within the volume of the respective tightly bound cell and rj can distribute in the volume V of the solution. Averaging over the possible ion distributions gives the free energies ΔGb and ΔGd for the tightly bound and for the diffusive ions, respectively,
| (9) |
| (10) |
Strictly speaking, for a given mode M, the diffusive ion free energy ΔGd is dependent on the spatial coordinates R of the tightly bound ions in the tightly bound cells. However, assuming the dependence of ΔGd on the tightly bound ions is mainly through the net tightly bound charge, which is fixed for a given mode, we can ignore the R dependence of ΔGd. In practice, we approximate ΔGd by ΔGd(R̄), where R̄ is the mean value of R.
The decoupling of R and ΔGd results in the separation of the R and the r variables in the configurational integral for ZM,
| (11) |
where c+=N+/V denotes the total cation concentration, and Z(id) is the partition function for an ideal solution without the insertion of the polyelectrolyte:
The excluded volume and the electrostatic interactions are inherently coupled. In our calculation, the excluded volume effect is considered not only for the configurational integral ( ) in Eq. (11) (see Sec. B below), but also for the electrostatic integral in Eq. (9) for ΔGb (see Sec. A below). From the above expression for ZM and the total partition function Z [see Eq. (7)], we can compute the electrostatic free energy ΔGel:
| (12) |
Physically, ΔGel is the free energy change upon the insertion of the polyelectrolyte.
A. Free energy of the tightly bound ions
The interaction energy Ub in Eq. (9) for a given configuration R of the tightly bound ions can be decomposed as two parts: the Coulomb interactions uij between charges in the ith and the jth (j≠i) tightly bound cells and uii between the tightly bound charges in the same (ith) cell,
| (13) |
| (14) |
where, as shown in Fig. 2(a), (i′,i″), and (j′, j″) denote the tightly bound ions in the ith and the jth tightly bound cells, respectively. ze is the electric charge of the corresponding ion, r and ε represent the distance and the effective dielectric constant for the electrostatic interaction between the respective charges, and mi and mj are the occupancies of the tightly bound ions in the ith and the jth cell, respectively.
FIG. 2.
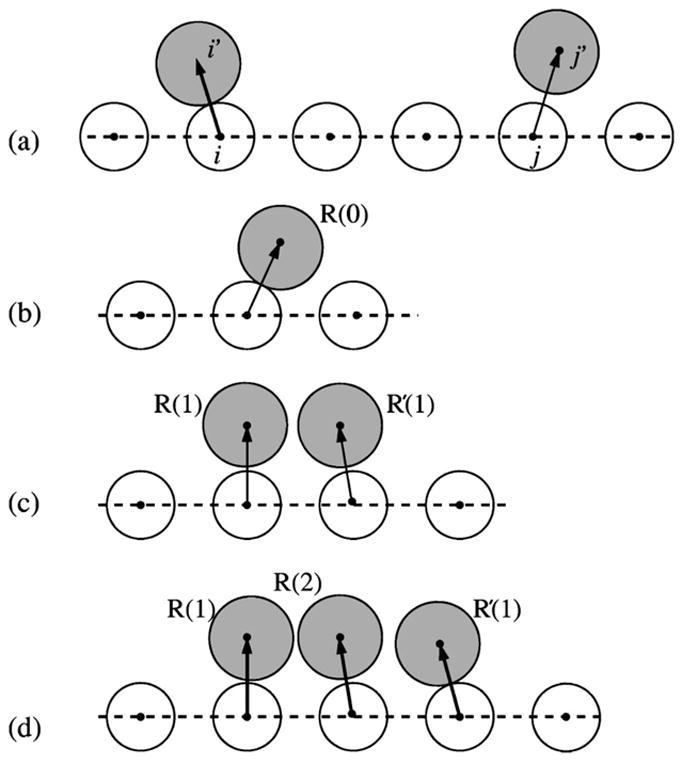
Illustration of (a) the electrostatic and (b)–(d) the excluded volume interactions between charges in the tightly bound region. Empty circles represent phosphate groups and the shaded circles represent the tightly bound ions.
We simplify the calculation for ΔGb by assuming
| (15) |
where the pairwise potential of mean force arises from the averaging over the possible coordinates of the tightly bound ions in the respective cells:
| (16) |
Here νi and νj denote the volumes of the respective tightly bound cells. In the evaluation of the electrostatic integrals in Eq. (16), the excluded volume interactions between ions i and j are rigorously accounted for. In fact, the excluded volume effect plays a significant role because the steric conflict is quite severe between ions distributed in the neighboring tightly bound cells.
We define two potentials of mean force: Φ1(m) for the intracell interactions uii, where m is the occupancy of the tightly bound ions in the cell, and Φ2(i,j,mi,mj) for the intercell interaction uij, where mi and mj are the occupancies of the tightly bound ions in the cells:
| (17) |
Φ1 and Φ2 can be precalculated and tabulated for different parameters. For a given mode M=(m1,m2,…,mL), the sum of the potentials of mean force gives the free energy ΔGb:
| (18) |
The potential of mean force Φ2(i, j,1,1) for a DNA of length L=30 is plotted in Fig. 3. From the figure, it is clear that the dominant interactions come from ions distributed in spatially neighboring phosphate cells: |i−j|=1 for the nearest neighbors along the sequence, |i−j|=10 for the spatial neighbors separated by an exact helical turn (=10-nt in sequence), and |i−j|=11 and 21 for phosphates (on separate strands) in the closest spatial proximity in the minor and major grooves, respectively.
FIG. 3.
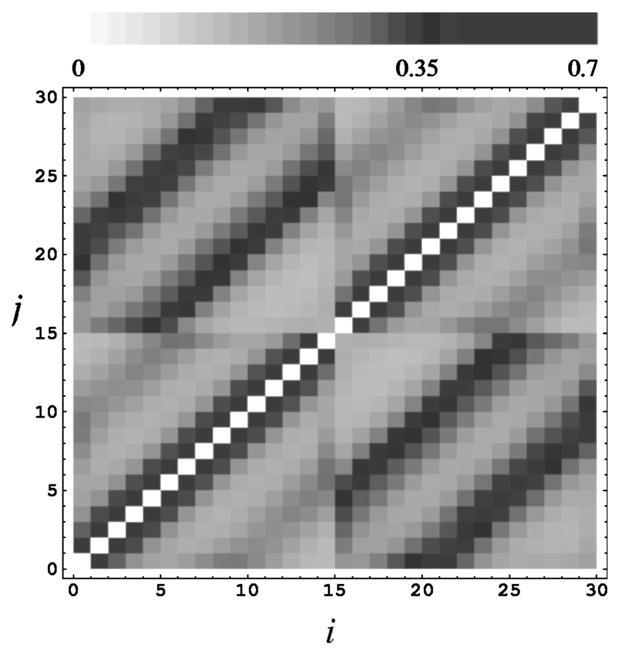
The pairwise potential of mean force Φ2(i, j,1,1) (in kBT) between two phosphate cells (i and j) with a Mg2+ ion in each cell [see Eqs.(16) and (17)], for a DNA oligomer of length L=30 in a 0.01M [Mg2+] solution. The phosphates 1≤i, j≤15 reside in strand 1 and 16≤i, j≤30 in the other strand of DNA.
B. Excluded volume correlations between the tightly bound ions
The volume integral in Eq. (11) provides a measure for the free accessible space of the Nb tightly bound ions in the tightly bound region. Since an exact treatment for the full excluded volume correlations between all the Nb tightly bound ions is intractable, we decompose the Nb-ion correlation into pairwise correlations between ions in adjacent tightly bound cells. This leads to a factorable excluded volume for the Nb ions,
| (19) |
where the excluded volume interferences between the ions in adjacent cells are accounted for by the single ion volume integral νi=∫ dRi:
νb(0) if there exists no tightly bound counterion in the neighboring tightly bound cells;
νi=νb(1) if there exists a bound ion in one of the neighboring tightly bound cells;
νb(2) if there exist bound ions in both neighboring tightly bound cells.
Physically, the finite volume of the ions in the neighboring cells restrict the viable space of the ion, causing νb(2)<νb(1)<νb(0). We apply Eq. (19) to the one-, two-, and three-ion systems in Figs. 2(b)–2(d), and compute νb(n) (n=0,1,2) through the following equations for the three model systems:
| (20) |
| (21) |
| (22) |
Here the (multiple-ion) excluded volume interactions are fully considered when evaluating the above integrals.
Because the geometry of the tightly bound regions are quite irregular, the multidimensional integrations over the tightly bound region for Φ1 and Φ2 and for the free volume νb(n) are time consuming. However, since the tightly bound region is mainly a thin layer on the surface of the polyelectrolyte, we can approximate the tightly bound region as a uniform thin layer of thickness δ. The thickness of the layer represents the maximum displacement of the tightly bound ion away from the polyelectrolyte surface. Multivalent ions usually have a thicker layer of the tightly bound region because ions are confined by a stronger electrostatic force. δ can be obtained from the volume νb(0),
| (23) |
Where is the mean distance to the center of the respective phosphate sphere [see Fig. 2(b)] and Ω(0) is the solid angle of the surface of the tightly bound cell measured from the center of the phosphate sphere. Since a tightly bound cell covers most of (or all of) the nucleotide surface, we can take Ω(0) as the solid angle that covers the full surface of a nucleotide unit.
C. Free energy of the diffusively bound ions
The free energy ΔGd accounts for the electrostatic interactions between the diffusive ions and between the diffusive ions and the tightly bound ions. We use the mean-field theory (PB) to describe the diffusively bound ions and make the following approximation for ΔGd:
where the averaging is for both the spatial configuration R of the tightly bound ions and the configuration r of the diffusive ions. The above approximation results in an additive sum for ΔGd,
where ΔGs is the free energy of the diffusive ion solution, and ΔGint is the free energy for the interaction between the diffusive and the tightly bound ions (and the fixed charges on the polyelectrolyte backbone):
We make use of the mean-field results for ΔGint and ΔGs (Refs. 41 and 42) and have 1
| (24) |
where the first integral gives ΔGint and the enthalpic part of ΔGs, and the second integral gives the entropic part of ΔGs. ψ(x) and ψ′(x) are the electrostatic potentials with and without the diffusive salt ions, respectively. ψ′(x) is introduced because ψ(x)−ψ′(x) gives the electrostatic potential from the diffusive ions. α denotes the ion species, zαe is the charge of the ion, is the bulk ion concentration, and cα(x) is the local ion concentration determined from the electrostatic potential ψ(x) [see Eq. (2)] and ψ(x) is obtained from PB [Eq. (3)].
D. Electrostatic potential for the diffusive ions in the solution
For a zc:1 salt, the general PB in Eq. (3) for the diffusive ions has the following form:
| (25) |
Here φ=eψ/kBT is the reduced electrostatic potential in the diffusive solution and is the Debye-Hückel screening parameter. c0 is the bulk salt concentration and NA is the Avagadro’s number. The charge density ρf of the fixed charges includes the phosphate charges and the tightly bound ions. Using the aforementioned approximation for the decoupling of the diffusive ion distribution and the tightly bound ion configuration R, we fix the tightly bound ions in a tightly bound cell to the center of the respective phosphate spheres. As a result, the ith tightly bound cell with mi tightly bound ions would contribute a fixed charge of (mizαe−e) at the center of the phosphate sphere, where zαe is the charge of a tightly bound ion. Though the coordinates of the tightly bound ions are approximated as being fixed here, no such approximation is made in the calculations for the tightly bound ions. In fact, the averaging over all the possible coordinates inside the tightly bound region yields the potentials of mean force Φ1 and Φ2 and the free energy ΔGb for the tightly bound ions.
Existing PB solvers23–29,43 have been successful in predicting the electrostatic interactions for complex protein and nucleic acid structures. In the present study, based on the algorithms used in the PB solvers,23,43–45 we develop a three-dimensional (3D) finite-difference algorithm that is convenient to use for our present model. The algorithm of solving the nonlinear PB is divided into two parts: the assignment of the physical quantities and the outer boundary conditions onto the grid points, and the actual iterative process of solving PB.
We first assign the grid charges inside the tightly bound region by partitioning a charge onto the eight nearest grid points, weighted by a trilinear function:43 (1−dx)(1−dy) × (1−dz), where dx, dy, dz are the distances of the charge from the grid point in the x,y,z directions, respectively. We then assign dielectric constants ε at the midpoints between grid points. We assign ε=2 inside and ε=78 outside the polyelectrolyte molecule.23–25 We also assign the Debye-Hückel parameter κ for each grid point. Specifically, we assign κ=0 inside the tightly bound region because of the absence of the diffusive ions, and κ=κ0 for grid points in the diffusive ion region.23 We use the screened Debye-Hückel potential as the boundary condition for the potential on the outer boundary.43
To solve the nonlinear PB equation iteratively, we use a simple method proposed in Ref. 46. If there is a good trial solution φa for the exact solution φ for PB, Δ φ (=φ− φa) would be a small quantity. We substitute φ (=φa+Δφ) into PB equation and perform Taylor expansion about the small quantity Δφ. Keeping only the linear terms of φ−φa in PB, we have the following linearized PB:
Starting from an initial trial φa, we can solve PB iteratively over all the grid points by applying the above equation, until an appropriate convergence condition is satisfied. In this way, φ at all grid points can be obtained. In our algorithm, the iteration is truncated at |φ−φa|≤10−4.
In addition, we employ the focusing operation23 in order to obtain the detailed electrostatic field near the molecule. Specifically, we use the three-step focusing process.47 In the first run, PB is solved on a large-scale grid. The size of the (cubic) cell of the first run relies on the salt concentration used. Generally, we keep it larger than six times of the Debye length of salt solution in order to properly account for the salt effects and to diminish the boundary effect. In the second run, a smaller area near the polyelectrolyte is selected and PB is solved based on a smaller grid. The outer boundary conditions of the second run are interpolated from the potentials of the first run using trilinear interpolation. For the second and the third run, the sizes of the cubic cells are kept at 102 and 51 Å, respectively, and the corresponding resolutions are kept at 0.85 Å per grid and 0.425 Å per grid, respectively. The corresponding number of grid points is 1213 for both the second and the third run. High resolution is used for the region near the polyelectrolyte surface because the most important potential change occurs in that region. To test our numerical algorithm, different resolutions are used, and the results are stable.
E. Effects of dielectric discontinuity
The dielectric discontinuity (low ε in DNA and high ε in solvent) is partially accounted for by the effective dielectric constants for the charge-charge interactions [see Eqs. (13) and (14)]. Previous studies use a distance-dependent dielectric function to account for the dielectric effects.48–54 Although the studies appeared to be successful, the treatments are physically oversimplified for the molecules with arbitrary shapes.1,55 Physically, the charge-induced reaction field of the low dielectric DNA molecule causes an increase in the phosphate-counterion attraction,1,55 a repulsive force on the counterion due to its self-image, and an increased (decreased) Coulomb forces between ions on the same (opposite) side of the DNA.1,55–58 The former two effects are considered to play roles in the ion distribution,1 and the third effect may not be significant because counterions tend to repel each other and inter-ion distance are generally large,1 especially for hydrated ions. In this section, we examine the dielectric effects for the specific grooved DNA model employed in the present study. We use εsol=78 for the solvent and εDNA=2 for the DNA (including the cylindrical core, the neutral and the phosphate sphere; see Fig. 1).
First, we calculated the effective dielectric constant ε pi-pj for the interactions between phosphates at pi and pj: εp-p=εsolφ0/φ, where φ and φ 0 are the electric potential at pj due to a charge at pi with and without the presence of the DNA (as a dielectric medium of εDNA=2) in the solution. Figure 4 shows εpi-pj as a function of the angular distance between pi and pj. Our results are in quantitative agreement with those obtained from all-atom calculations:58 for different pi and pj, the effective dielectric constant is around the value of εsol=78. ε pi-pj can be as low as about 70 if the two phosphates are located at the same side of DNA, and can be as high as 100 when they are on the opposite sides, in which case the charge-charge interaction is weak.
FIG. 4.
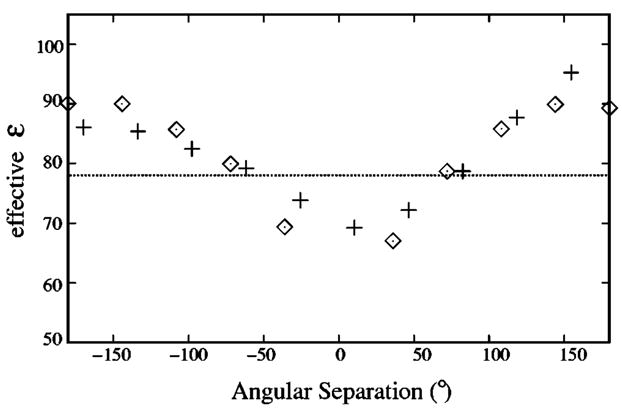
The effective dielectric constant εp-p for the electrostatic interactions between two phosphates in B-DNA as functions of the angular separation with respect to the helical axis. ⋄ denotes εp-p between two phosphates on the same strand, and + represents εp-p between phosphates on the different strands.
Second, we evaluated the change of self-energy ΔEs(r) of a test ion at r due to the ion-induced reaction field of DNA,
| (26) |
where zce is the ion charge, and φi(r) and are the electric potentials due to the presence of the test charge at r, with and without the presence of the DNA (as a dielectric medium of εDNA=2), respectively. Theoretically, the self-energy of point charge is infinity. In our numerical calculation, it is a large finite value in the finite-difference method. ΔEs(r) is given by the difference of two large self-energies zce φi(r) and . The results of ΔEs(r) have been tested to be quite stable against different grid sizes. Figures 5(a) and 5(b) show the results for ΔEs for Na+ and Mg2+. It is clear that ΔEs is positive due to the interaction with the self-image of the ion. ΔEs(r) in general obeys the following order: in the minor groove > in the major groove>near the phosphates. Moreover, ΔEs(r) decays rapidly away from the DNA surface, which agrees with the previous experimental results on a clay DNA model.1,55 Quantitatively, our ΔEs is slightly smaller than that measured in the experiment, which may be attributed to the different dielectric DNA models used.1,55 Since ΔEs(r) is proportional to the square of the valency, Mg2+ ions in general have larger ΔEs(r) value. On the other hand, Mg2+ ions have larger excluded volume than Na+ ions because of the larger hydrated radius, and thus Mg2+ ions are distributed further away from the DNA.
FIG. 5.
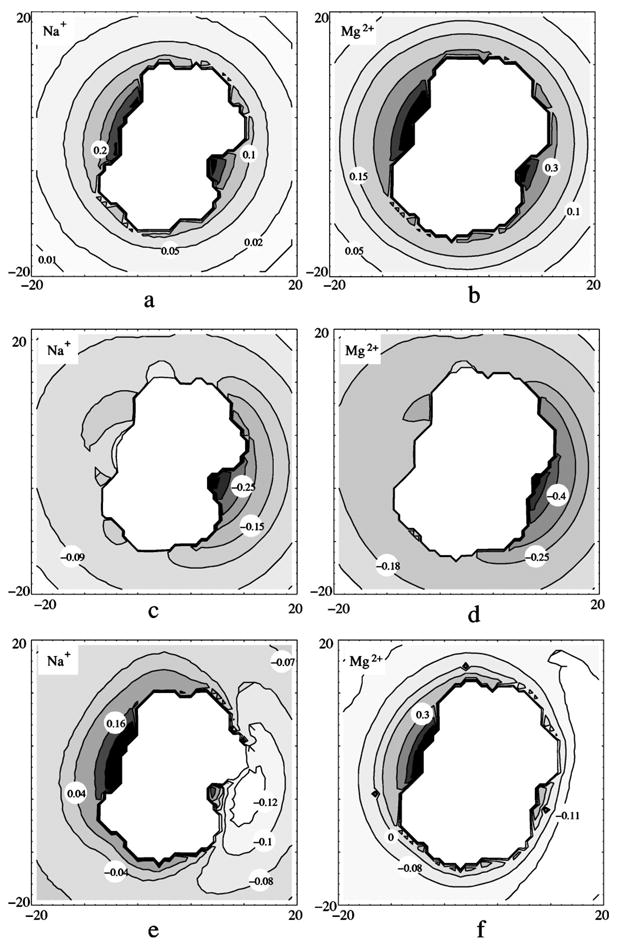
The two-dimensional contours in a plane perpendicular to the B-DNA helix for the energy change (in kBT) due to dielectric discontinuity (ε=2 in DNA and ε=78 in solvent): the change of self-energy ΔEs for Na+ (a) and Mg2+ (b) ions; the change of the interaction from phosphates ΔEp for Na+ (c) and Mg2+ (d) ions; and the total change of energy ΔE (=ΔEs + ΔEp) for Na+ (e) and Mg2+ (f) ions. The central blank spaces are the inaccessible volumes for the hydrated ions (DNA helix plus a excluded volume layer with one ion radius).
Third, we computed the change of the interaction energy ΔEp(r) between a (test) ion and the phosphates in the phosphate-induced reaction field of DNA,
| (27) |
where φp(r) and are the potentials at r due to the phosphate charges on DNA of εDNA=2 and εDNA=εsol =78, respectively. Figures 5(c) and 5(d) show the ΔEp(r) for the Na+ and Mg2+ ions. ΔEp(r) is negative due to the (negative) image charges of the phosphates. The strength of the attractive ΔEp(r) obeys the following order: in the minor groove>near the phosphates>in the major groove. This is because an ion in the minor groove can be much closer to the phosphate charges than one in the major groove.
Because ΔEs(r) is positive (repulsive) while ΔEp(r) is negative (attractive), ΔEs(r) and ΔEp(r) can compensate and cancel each other. We plot the net effect ΔE(r)=ΔEs(r)+ΔEp(r) in Figs. 5(e) and 5(f). The figures show that inside the major groove, ΔE(r) is positive and contributes a destabilizing free energy to the ion binding. Moreover, for both Na+ and Mg2+ ions, ΔE(r)<0 near the phosphates, which means that the reaction field is stabilizing for ion binding near the phosphates. For Na+ ions, ΔE(r) is small [see Fig. 5(e)]. For Mg2+ ions, ΔE(r) is larger than that for the Na+ ion in the major groove. In the minor groove and near the phosphates, ΔE(r) is small too. For example, at a radial distance of 10.2 Å in the minor groove (minimum accessible distance for a hydrated Mg2+ in the minor groove), ΔE(r) is −0.1kBT for Na+ and 0.3kBT for Mg2+. For a larger radial distance, ΔE(r) of Mg2+ becomes negative too. For example, at radial distance 14 Å, ΔE is about −0.15kBT. The different behavior between Na+ and Mg2+ ions comes from their different valencies. Since, and ΔEp(r)∞zc, ΔEs(r) is dominant for multivalent zc ions (larger zc) near DNA surface (e.g., deep in grooves), and ΔEp(r) becomes important when ions are away from the deep groove positions. For both Na+ and Mg2+ ions, ΔE(r) is small as compared with the Coulombic energy. Therefore, the effect of dielectric discontinuity due to DNA on ions’ distribution does not appear to be significant.59,60 Furthermore, previous studies suggested that the dielectric constant of nucleic acids (and protein) might be much larger than 2,61–64 and consequently the effects of dielectric discontinuity become even smaller. Therefore, in the present study, for simplicity, we neglect the effects (the reaction field) arising from the dielectric discontinuity.
As a caveat, we note that the reaction field is nonadditive, thus the above decomposition for the contributions from different charges is a simplification for a complex problem. A major approximation in the above test charge calculation is to neglect the effect from the ion cloud surrounding the DNA and the interactions between the ion cloud and the DNA (and the phosphates). With such an approximation, ΔEs(r) and ΔEp(r) can be solved from the linear Poisson equation (rather than the nonlinear PB), and they are additive. As a result, ΔEs(r)+ΔEp(r) can give the total energy from the DNA reaction field. However, rigorously speaking, the energy of the reaction field is nonadditive, and the different components of the reaction field and the self-energy are inherently coupled due to the ion-DNA and ion-ion interactions. Therefore, the results given above can only provide a crude estimation for the self-energy (and the reaction field energy). Nevertheless, the ΔEs(r) and ΔEp(r) may provide some insights in the effects of DNA dielectric discontinuity.
V. DYNAMICS OF THE TIGHTLY BOUND IONS AND THE ION-BINDING MODES
A. Monte Carlo simulation
Since MC simulation is independent of the analytical statistical mechanical theory, it can provide a test and validation for the statistical mechanical theory. In addition, we can employ MC simulations to obtain the kinetic information for the tightly bound ions. We use the grooved model for the polyelectrolyte structure, and use hard spheres for ions with charges placed at the centers of the spheres. We use a cell model by placing the polyelectrolyte at the center of a cubic cell and placing ions in the cell and in the neighboring image cells.30,65–67 We also impose charge neutrality for the system, so the net charge of the simulation cell is zero. The size of the cubic cell is always kept six times larger than the Debye length of the solution to diminish the boundary effect. The numbers of different ions in the simulation depend on the cell size, salt concentration, and polyelectrolyte length. The concentration of polyelectrolyte is assumed to be very dilute so that interactions between different polyelectrolytes can be ignored. In the simulation, we keep the polyelectrolyte fixed and allow the ions to move. The aqueous solvent is modeled as continuous medium with dielectric constant 78.
The electrostatic energy for a given ion distribution of the system is evaluated as the sum of the Coulombic interactions65,66
where i denotes ions in the cell, j(≠i) denotes ions in the cell and in the image cells, l denotes the phosphate groups, and zie,zje, and zle are the charges of the respective ions and the phosphate groups. The first double summation accounts for the interactions between ions in the cell and all other ions (in the cell and the adjacent image cells). The second double summation accounts for the interactions between ions in the cell and the phosphate charges on the polyelectrolyte backbone. Following the simulational algorithm,66 we consider only the nearest adjacent image cells.
For each Monte Carlo move of the ions, we compute the energy change ΔE of the system, and the probability exp (−ΔE/kBT) for the particular move to be accepted. The ions are simulated to move with the acceptable probabilities. Such process of stochastic move continues until the system reaches thermal equilibrium from which the equilibrium distribution of the ions can be obtained.
To validate our MC simulation method, we run MC simulations for three different DNA lengths L=20, 40, and 80 in both the 1:1 (NaCl) and 2:1 (MgCl2) salt solutions at ionic strength 0.022M, and compare the ion distribution with that obtained from the simulations in Ref. 68 for infinitely long DNA. In order to make direct comparisons, we use the same set of parameters as those used in Ref. 68: ε=78, and ion radius=2.1 and 3 Å for counterions and coions, respectively. The comparison with Ref. 68 shows that the predicted distribution for the fractional excess charge Qtot(R) for large L is indeed very close to the known result for infinitely long chain. Here the fractional excess charge per nucleotide Qtot(R) is defined as the net charge per nucleotide within radial distance R around the polyelectrolyte. In fact, the result for L=80 is already very close to the infinite-length results, which confirms the previous finding that the counter-ion concentration near the middle of oligomer for L≥40 closely approaches that of the infinite-length polyelectrolyte.66
B. Dynamics of the tightly bound ions
All-atom molecular dynamics69,70 and Brownian dynamics71 simulations show that (i) the majority of bound counterions keep hydrated,72,73 (ii) most ions are not bound to specific sites, (iii) the mobility of bound counterions is less than ions in bulk solvent,74 and (iv) the diffusion of the bound counterions in the grooves is local.71 For the present groove model of DNA, we use Monte Carlo simulation to investigate the ensemble averaged statistical properties as well the single ion trajectory for a bound ion.
We first compute the mean residence time averaged over all the ions in the region immediately surrounding the polyelectrolyte: the mean time τp(δ) for a tightly bound ion to stay within a distance of rc+δ (rc=ion radius) from the surface of the respective phosphate group and time τ⊥(δ) for a tightly bound ion to stay within a radial distance of rc+δ from the polyelectrolyte surface. Physically, τp is a result of the radial motion as well as the motion parallel to the polyelectrolyte surface. Clearly τp(δ)<τ⊥(δ) for any δ. Figures 6(a) and 6(b) show the Monte Carlo results for τ⊥ and τp for different bulk salt concentration c0 and different δ. Mg2+ has longer residence time than Na+, because Mg2+ is electrostatically more strongly attracted to the anionic polyelectrolyte.
FIG. 6.
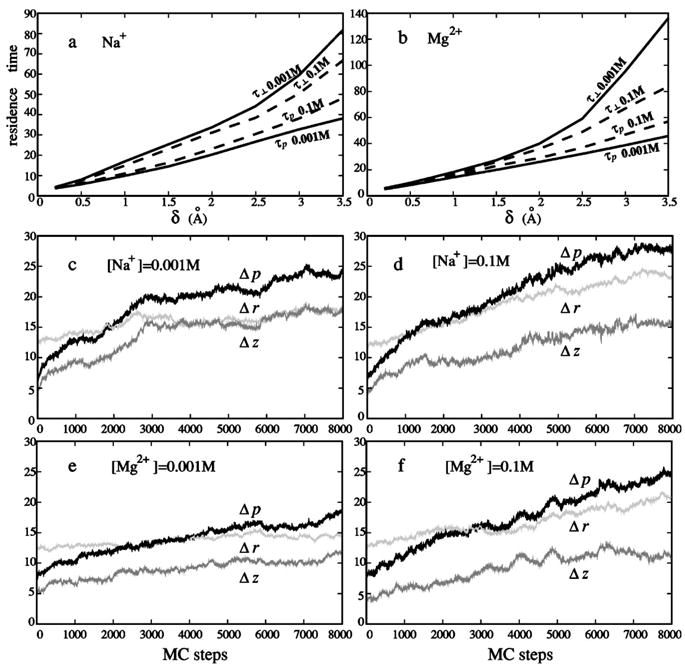
(a,b) The mean residence time τp (bottom two lines) for a counterion to stay within a distance of rc +δ (rc=counterion radius) from the surface of the respective phosphate group, and the mean residence time τ⊥ (upper two lines) for a counterion to stay within a radial distance of rc+δ from the polyelectrolyte surface. Solution conditions are (a) Na+ and (b) Mg2+, with salt concentrations c0=0.001M (solid lines) and 0.1M (dashed lines). Both τ⊥ and τp are scaled as number of Monte Carlo steps. (c–f) Three characteristic distances of counterions (in unit of angstrom): the distance Δp of tightly bound counterions from the respective phosphate sphere centers (black lines); the distance Δz in the axis direction (gray lines); and the radial distance Δr of counterions from DNA axis (light gray lines). (c) [Na+]=0.001M; (d) [Na+]=0.1M; (e) [Mg2+]=0.001M; (f) [Mg2+]=0.1M. The counterions, which reside in the layer with thickness δ=2 Å, are tracked in the simulations, and the tracking process is performed after the system reaches thermal equilibrium.
As the ion concentration c0 is increased, more ions are bound. The increase in the number of the bound ions causes several notable changes in the dynamic properties of the bound ions, which are follows.
A larger number of the tightly bound ions would provide more effective charge neutralization of the polyelectrolyte and hence a weaker radial electrostatic field around the polyelectrolyte. As a result, the radial motion of the ion becomes less restricted, causing shorter radial residence time τ⊥.
A larger number of the bound ions means increased Coulombic and excluded volume repulsion between the bound ions. The increased inter-ion repulsion would suppress and restrict the parallel motion of the tightly bound ions, causing a reduction in the displacement parallel to the polyelectrolyte surface. Indeed, as shown in Figs. 6(c)–6(f), higher ion concentrations correspond to smaller axial displacement Δz.
As the parallel motion “shrinks,” the difference between τ⊥ and τp(<τ⊥) decreases. In the limiting case when there is no parallel motion, τ⊥ becomes equal to τp. In fact, the Brownian dynamics simulation71 for infinite long polyelectrolyte estimated that τp/τ⊥~1/8 for salt free solution (with monovalent ions added to neutralize the system). Our MC simulation for a finite length polyelectrolyte L=24 gives that τp/τ⊥ decreases from 1/1.2 to about 1/2 as [Na+] decreases from 0.1M to 0.001M. Here, we choose δ=3 Å when evaluating τ⊥ and τp. As [Na+] decreases and L increases, τp/τ⊥ is expected to approach the value predicted from the Brownian dynamics simulation.
We also track the trajectories for single bound counterions. We find that, for ions inside the bound region, the parallel diffusion is localized to the nearest neighbor or the next nearest neighbor tightly bound cells. The result agrees with a previous study.71 Moreover, as shown in Figs. 6(c)–6(f), higher c0 results in more mobile ions outside the bound region, because of the stronger charge neutralization on the polyelectrolyte and thus a weaker electric field nearby. This effect is more pronounced for multivalent ions because of the stronger charge neutralization.
C. Equilibration kinetics of the binding modes
Different binding modes (=configurations of the tightly bound ions) result in different electric fields around the polyelectrolyte, causing different distribution of the diffusive ions. We would like to understand the kinetics for the coupling between the diffusive ions and the binding modes.
A change in the binding mode can arise either from the radial diffusion, causing the binding or dissociation of an ion, or from the parallel diffusion (hopping) across the different tightly bound cells, which conserves Nb. The radial diffusion changes the total number of the tightly bound ions Nb and the parallel diffusion conserves Nb. Ion diffusion around DNA has been investigated using all-atom simulation74 and from continuous-medium simulation.71 It was found that D⊥≤D||≤ D0 for the diffusion coefficients D⊥ and D|| for the bound counterions in the radial (⊥) and parallel (||) directions and for the ions in the bulk D0 solvent.71,74 D⊥ and D|| increase and approach D0 with the increase of radial distance from the DNA surface. Moreover, different types of counterions can have very different diffusion coefficients, for example, Li+ diffuses much slower than Na+ near the DNA surface,70 though they both are monovalent ions. Furthermore, the diffusion near DNA is dependent on the geometry as well as the charge distribution on the polyelectrolyte. In general, D⊥≪D0 due to the electrostatic attraction from the phosphate groups, and D||, depending on the ion and the polyelectrolyte structure, could be comparable to D0 or D⊥.
Preequilibrium case
If D||~D0 and D⊥≪D0, the mode change due to the parallel diffusion is much faster than that due to the radial diffusion. This would cause the modes with the same total number Nb of the tightly bound ions to preequilibrate through the fast parallel diffusion before conversion into a mode of different Nb. As a result, the diffusive ions in the solution would “see” an approximately preequilibrated ensemble of modes with the same Nb and a preequilibrated distribution of the tightly bound ions {m̄1,m̄2, …,m̄L}:
| (28) |
where the sums are for all the modes with Nb tightly bound ions. In this case, we need to solve PB and the free energy ΔGd of the diffusive ions for each Nb, not for each mode. Note that for an L-mer polyelectrolyte, there are 2L+1 possible Nb values (Nb=0,1,2,…,2L). Because 2L+1 ≪the number of the binding modes, the preequilibration results in a great reduction in the computational time.
Non-preequilibrium case
If D||≪D0 and D⊥≪D0, since the mode conversion is much slower than the relaxation of the diffusive ions in solution, preequilibration does not occur. As a result, the calculation of ΔGd requires to solve the PB for each tightly bound mode separately. Given the large number of the modes, this is a formidable computational problem. To circumvent the problem, we use the following two approaches.
We first make the preequilibrium assumption, and compute the mode probability pM [see Eq. (28)] for each mode M. We then regard the modes of large pM as the “important” modes, and recompute ΔGd (and ZM and pM) rigorously without the preequilibration assumption for the important modes. In our calculation, we choose pM>10−3 as the criteria for the important modes. The approach is validated because different cutoff values (around 10−3) result in consistent thermodynamic results.
We note that, as shown in Fig. 7, for a given Nb, there exists an overall correlation between ΔGd and ΔGb. In general, modes of low ΔGb have high ΔGd, vice versa. This is because the tightly bound ions in the low ΔGb modes tend to be uniformly partitioned among the different tightly bound cells so that they can maximally avoid each other to lower the electrostatic potential energy. Such “dispersed” charge distribution gives a weaker electric field around the polyelectrolyte and thus a higher ΔGd as compared with an aggregated charge distribution. The relationship between ΔGd and ΔGb provides a simple way to obtain ΔGd from ΔGb without solving the PB equation.
FIG. 7.
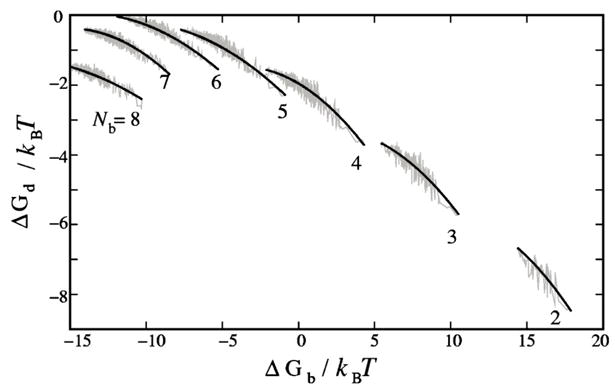
The correlation between free energy ΔGd and ΔGb for the different number of the tightly bound ions Nb. The zigzag (gray) lines represent the results from the Poisson-Boltzmann equation for each individual tightly bound mode (nonequilibration case). The spline (black) lines are from the three-point fitting. Here, L=12 and [Mg2+]=0.01M.
To obtain the functional relationship between ΔGd and ΔGb for a given Nb, we select the modes with the maximum, minimum, and intermediate values of ΔGb, and calculate ΔGd for the three modes by solving the PB for each mode. We then construct a spline function by fitting the three data points. This simplified treatment significantly reduces the computational time, because we only need to solve PB for three times for each Nb. Our tests for short polyelectrolytes show that the algorithm can give very good estimates for the free energy ΔGd (except for small fluctuations); see Fig. 7.
The actual dynamic properties of the ions may lie closer to either of the above preequilibrium and non-preequilibrium cases. We consider both cases in this work. We present the results for the preequilibration case, followed by a separate section to discuss the differences between the two cases. Therefore, in the following sections, we assume preequilibration except in the section where non-preequilibration is explicitly stated.
VI. ION DISTRIBUTION AND THE ELECTROSTATIC FREE ENERGY
To validate our PB solver, we first calculate the electrostatic potential around an charged cylinder of infinite length, and compare the results with the known results obtained in previous studies.24,75,76 We use the two-step dielectric model (ε=2 and 78 inside and outside the polyelectrolyte, respectively). We employ the periodic boundary condition to model the infinitely long polyelectrolyte cylinder.24 The comparison shows that, the electric potentials given by our PB solver are in good accord with the previous results.
A. Quantitative characterization of the tightly bound layer
From Eqs. (20) and (23), we can obtain the volume νb(0) of the tightly bound region and the mean thickness δ of tightly bound layer. Table I gives the values of δ for DNA with different length L in the Na+ and Mg2+ solutions of different concentration. δ for [Mg2+] solution is much larger than that in [Na+] solution. This is because Mg2+ ions have much stronger inter-ion correlations than the Na+ ions and thus have a larger tightly bound region. Moreover, δ increases as the bulk ion concentration increases, because higher bulk salt concentration leads to a higher bound ion concentration and thus stronger correlation for bound ions. We can also compute the free volume νb(1) and νb(2) from Eqs. (21) and (22).
TABLE I.
Mean thickness δ of the tightly bound region for B-DNA of different length L in solutions with different [Na+] or [Mg2+].
| Width δ (Å)
|
||||||||
|---|---|---|---|---|---|---|---|---|
| [Na+]
|
[Mg2+]
|
|||||||
| L | 1M | 0.1M | 0.01M | 0.001M | 0.1M | 0.01M | 0.001M | 0.0001M |
| 40 | 0.14 | 0.06 | 0.03 | 0.02 | 2.5 | 2.4 | 2.1 | 2.0 |
| 30 | 0.12 | 0.04 | 0.02 | 0.01 | 2.4 | 2.1 | 2.0 | 1.9 |
| 20 | 0.08 | 0.01 | 0.0 | 0.0 | 2.2 | 1.9 | 1.7 | 1.5 |
| 10 | 0.01 | 0.0 | 0.0 | 0.0 | 1.8 | 1.3 | 1.0 | 0.8 |
B. Electrostatic free energy ΔGel
Figure 8 shows the electrostatic free energy ΔGel [see Eq. (12)] as a function of the bulk salt concentration c0 for the Na+ and Mg2+ solutions. As a comparison, we also show the results from a pure Poisson-Boltzmann calculation (without considering the tightly bound ions) for low bulk salt concentrations, for which PB can give an accurate description for the system in a Na+ solution.77 In the pure Poisson-Boltzmann calculation, in order to account for the ion size, we have added an excluded volume (charge-free) layer on the polyelectrolyte surface.78,79 The thickness of the charge-free layer is equal to the ion radius rc. We find that both our theory and PB predict that ΔGel decreases as c0 increases. This is because higher salt concentration causes stronger electrostatic screening and stronger charge neutralization for the polyelectrolyte, and consequently lowers the electrostatic repulsion between the polyelectrolyte charges.
FIG. 8.
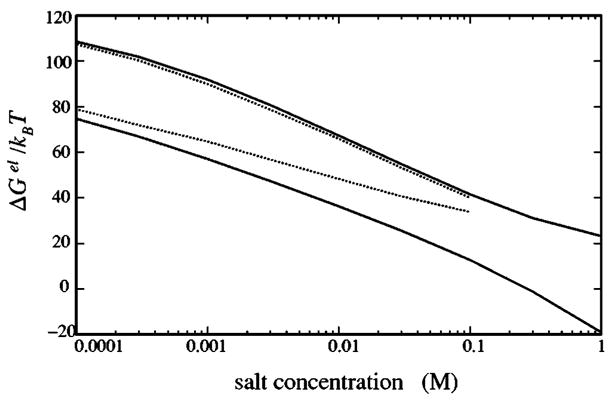
Electrostatic free energy of B-DNA oligomer with length L=24 in Na+ (upper two lines) and Mg2+ (bottom two lines) salt solutions at room temperature. Solid lines, from the present model; dotted lines, from Poisson-Boltzmann equation.
As shown in Fig. 8, ΔGel predicted from our theory for a Na+ solution is very close to that predicted from PB. For a Mg2+ solution, however, our theory predicts a lower free energy ΔGel than PB. This is because the correlated distribution of the tightly bound ions can have lower energies than the mean-field configuration. Moreover, ΔGel for a Mg2+ solution is much lower than that of a Na+ salt solution, because of the much stronger attraction between Mg2+ and the phosphate groups.
C. Ion radial distribution
The mean net charge Qb of the tightly bound ions per nucleotide unit and the total charge of the diffusively bound ions Qd(R) per nucleotide unit can be calculated from the following equations:
| (29) |
where the sum over α is for all the ion species, and and are the mean number of the tightly bound counterions and the mean diffusive ion concentration averaged over all the possible binding modes.
We compute the total bound charge Qtot(R) within a cylindrical region of radius R. Since a binding mode only specifies the number (not the spatial distribution) of the tightly bound ions in each tightly bound cell, the model cannot give the continuous R dependence of Qb. Thus we cannot obtain a continuous R dependence of Qtot(R). We define a stepwise R dependence of Qtot(R),
| (30) |
where the step function is defined as θ(x)=0 for x<0 and θ(x)=1 for x≥0, and R*=8.9Å+2.1Å+δ+ rc (rc =counterion radius) is the outermost radial distance on the contour of the tightly bound region (simplified as a thin layer of thickness δ); see Fig. 1.
In Fig. 9, we test the theory predictions against the MC simulation. For Na+ solutions, both our theory and the PB can make accurate predictions for Qtot(R). For Mg2+ solutions, however, our theory makes better predictions than PB. Because PB ignores the low energy correlated configurations of the tightly bound ions and thus under-estimates the bound ion charge.80,81
FIG. 9.
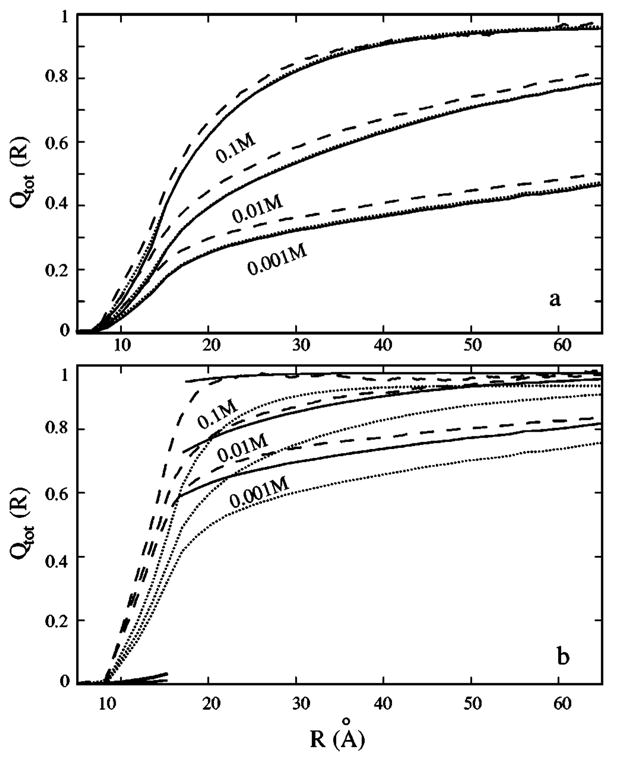
The spatial distribution of the total charge (per nucleotide) Qtot(R) within a cylindrical region of radius R around the a B-DNA helix of length L=24 in (a) [Na+] and (b) [Mg2+] solutions at room temperature. c0 =0.1M, 0.01M, and 0.001M from top to bottom. Dashed lines, Monte Carlo simulations; dotted lines, Poisson Boltzmann equation; solid lines, the present model.
D. Tightly bound counterions
In Fig. 10(a), we plot the charge Qb of the tightly bound ions as a function of the bulk salt concentration c0 for both the Na+ and Mg2+ solutions. We find that our theory generally gives quite accurate predictions (as tested against the MC simulation results) over a wide range of c0. As c0 increases, the entropic cost for ion binding decreases. Consequently, the binding of the tightly bound ions becomes more favorable, resulting in more tightly bound ions and hence a larger ions are more Qb. Moreover, because Mg2+ strongly attracted to the polyelectrolyte than Na+ ions, Qb for Mg2+ is much larger than that for Na+. In fact, for a Na+ solution, the electrostatic correlation is weak and only very few ions are tightly bound.
FIG. 10.
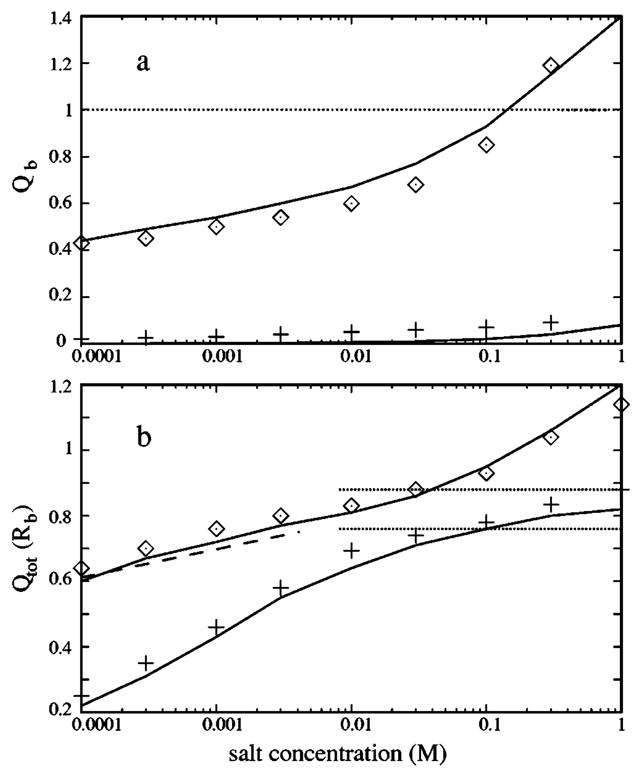
(a) The salt concentration dependence of the charge Qb of the tightly bound counterions (per nucleotide) for a B-DNA oligomer of length L=24 in [Mg2+] (upper line) and in [Na+] (bottom line) solutions. Lines, from the present model; symbols, from the Monte Carlo simulation. (b) The salt concentration dependence of the total charge Qtot(Rb) of the bound ions per nucleotide for a B-DNA oligomer of length L=24 in [Mg2+] (upper lines) and [Na+] (bottom lines) solutions. Solid lines, from the present model; dotted lines, from the counterion condensation theory for an infinite-length DNA in [Mg2+] (upper line) and in [Na+] (bottom line) (Ref. 22); dashed line, from the counterion condensation theory for an oligomer in monovalent ionic solution (Ref. 88); symbols, from the Monte Carlo simulation.
From Fig. 10(a), we note that Qb exceeds unity at high Mg2+ concentrations. This means that negatively charged DNA molecule is “overneutralized” by Mg2+ ions. We note that such overcharging34,82 or charge inversion83 phenomena cannot be predicted by the mean field theories. In fact, the overcharging may be related to the attraction between two like-charged macroions.84
E. Total bound ions and comparisons with the counterion condensation theory
The tightly bound counterions in our theory are different from the “bound counterions” or “condensed counterions” defined in the CC theory.22 The bound ions in PB or CC include both the tightly bound ions and the diffusively bound ions defined in our theory. Therefore, the total charge of the condensed ions in the CC theory corresponds to the total charge of all the ions within a properly defined bound radius Rb>R*:
Various methods have been used to define Rb.75,82,85–87 Here we define Rb through the following equation:87 , where is the total charge of the counterions within a radial distance R. can be computed in the same way as Qtot(R) from Eqs. (29) and (30), except that the sum for ion species α in Eq. (29) is for the counterions only. The number of bound ions from the definition agrees with that of CC theory for infinite-length cylinder polyelectrolyte.87
For an infinite-length DNA, CC predicts that the condensed counterions have total charge of 0.76e per nucleotide for Na+ and 0.88e per nucleotide for Mg2+.22 For an L-mer DNA (finite-length) in a 1:1 salt solution, a modified CC theory88 gives that, the total condensed counterion charge is equal to (1−1/ξ) for L≥λD/b and (1−ξcri/ξ) for L≪λD/b. Here ξcri=ln(λD/b)/ln(L), ξ=lB/b is the Manning parameter, λD is the Debye length and b=1.7 Å is the longitudinal spacing of the charges on the polyelectrolyte backbone.
We use MC simulation to obtain the radial distribution function , from which the bound radius Qtot Rb is calculated. In Fig. 10(b), we plot Qtot(Rb) predicted from the MC simulation, from the present theory, and from the CC theory for infinite- and finite-length polyelectrolytes. Figure 10(b) shows that Qtot(Rb) from our theory is in good agreement with that from the MC simulation. For a finite-length polyelectrolyte, our theory and the CC theory predict qualitatively the same c0 dependence for the bound ions. Moreover, as we expected, higher the c0 gives larger bound charge Qtot(Rb). For c0≤0.01M, the CC theory overestimates the bound ion charges Qtot(Rb) because the CC results used here are for line charge polyelectrolyte, and the line charge can enhance the counterion condensation.
F. Dependence of the polyelectrolyte length
Figure 11(a) shows the charge Qb of tightly bound ions as a function of the DNA length L. From the figure, we find that for a broad range of the polyelectrolyte length L, Qb predicted from the present theory is in good agreement with that given by the MC simulation. Moreover, as we expected, the longer the length L, the stronger the electrostatic field near the polyelectrolyte surface, and thus the more counterions (i.e., the larger Qb) trapped on the polyelectrolyte surface.
FIG. 11.
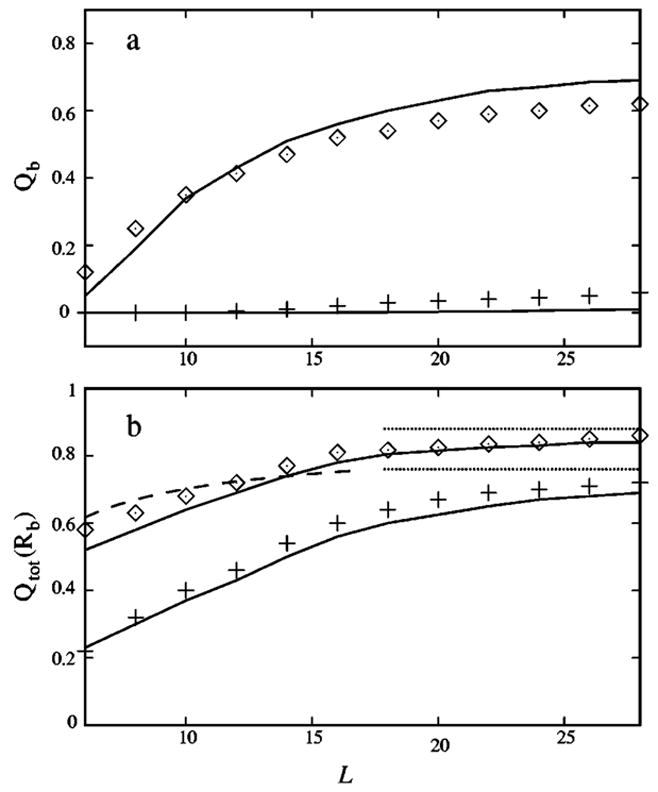
(a) The polyelectrolyte length L dependence of the charge Qb of the tightly bound counterions per nucleotide in [Mg2+] (upper line) and [Na+] (bottom line) solutions at bulk salt concentration 0.01M. Solid lines, from the present model; symbols, from the Monte Carlo simulation. (b) The polyelectrolyte length L dependence of the total charge Qtot(Rb) of the bound ions per nucleotide for a B-DNA oligomer in [Mg2+] (upper two lines) and [Na+] (bottom two lines) solutions at bulk salt concentration 0.01M. Solid lines, from the present model; dotted lines, from the counterion condensation theory for the DNA of infinite length in [Na+] (bottom line) and [Mg2+] (upper line) solutions (Ref. 22); dashed line, from the counterion condensation theory for ionic oligomer in monovalent ionic solution (Ref. 88); symbols, from the Monte Carlo simulation.
Plotted in Fig. 11(b) is the L dependence of the total charge Qtot(Rb) for the bound counterions. The figure shows that the results for Qtot(Rb) from the present theory are in accord with the results from the MC simulation. Furthermore, the present theory and the CC theory give the same qualitative L dependence of Qtot(Rb). As L increases, our predicted Qtot(Rb) monotonically approaches the CC result for an infinitely long DNA.
VII. STATISTICAL THERMODYNAMICS IN THE NON-PREEQUILIBRATION CASE
The results presented above are based on the preequilibrium assumption: different binding modes of the same number Nb of the tightly bound ions can quickly preequilibrate, so the diffusive ion distribution is determined by the preequilibrated charge distribution of the tightly bound ions. However, if the dynamics of the bound ions is slow so that the preequilibration cannot occur, the diffusive ions would “see” discrete binding modes (rather than the averaged preequilibrium distribution). As a result, we should consider the diffusive ion distribution (and the free energy ΔGd) for each individual mode separately.
For a given mode M, the preequilibrium and non-preequilibrium cases have the same free energy ΔGb for the tightly bound ions. The difference between the two cases arises from the different ΔGd for the diffusive ions. In the preequilibrium case, ΔGd is based on an ensemble of modes (with the same number Nb of the tightly bound ions), while in the non-preequilibrium case, ΔGd is based on each individual mode. However, as shown in Fig. 7, for a given Nb, the majority of the modes are distributed within a narrow range of ΔGd, which means ΔGd for an individual mode is not very different from that for the equilibrium ensemble of all the modes. Therefore, the preequilibrium and non-preequilibrium cases have similar thermodynamic properties.
In addition, for modes with proper occupancy of the tightly bound ions, since the tightly bound ions involve much stronger electrostatic interactions than the diffusive ions, we have |ΔGb|≫|ΔGd|. As a result, the main behavior of the mode probability pM∞e−(ΔGb+ΔGd)/kBT [see Eqs. (8) and (11)] and the thermodynamic properties are dominated by ΔGb. Therefore, the preequilibrium and non-preequilibrium cases, which have the same free energy ΔGb for the tightly bound ions for any given mode M, would have very similar thermodynamic properties.
Indeed, we find that for both the Na+ and the Mg2+ solutions of low salt concentration, the theory gives very close results for ΔGel, Qtot(R), and the c0 dependence of Qb and Qtot(Rb) for the two cases (results not shown).
However, for high salt concentrations, especially for multivalent ion solutions, due to the strong ionpolyelectrolyte interaction, ΔGd would sensitively depend on the charge distribution (=mode) of the tightly bound ions, causing the pronounced differences between the preequilibrium and non-preequilibrium cases. For example, at [Mg2+]=1M, Qb and ΔGel are equal to 1.4 and −19.1kBT, respectively, for the preequilibration case, and equal to 1.3 and −21.8kBT, respectively, for the non-preequilibration case.
In addition, even though the preequilibrium and the non-preequilibrium cases can have quite similar average statistical thermodynamic properties, they can have different distributions for the tightly bound ions . Figure 12 shows the distribution of the tightly bound ions. For the preequilibration case, in a [Na+] solution or a dilute [Mg2+] solution, the tightly bound counterions tend to reside in the middle portion of the polyelectrolyte. This is because the middle portion has the strongest electric field and is thus the most favorable binding region for the counterions. For Mg2+ of higher concentrations, the counterions tend to bind to the two ends of the polyelectrolyte, because in this case there would be a large number of the tightly bound Mg2+ ions, and the significant inter-ion repulsion makes the end positions more favorable for ion binding.
FIG. 12.
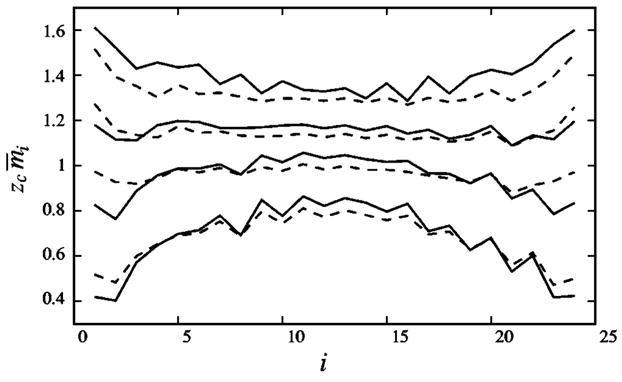
Distribution of the tightly bound counterions along a B-DNA oligomers of length L=24 in [Mg2+] solutions with different salt concentrations c0. mi is the number of the tightly bound ions within ith (i = 1,2,…,L) tightly bound cell and zce is the charge of the counterion. From top to bottom: c0=1M, 0.3M, 0.1M, and 0.01M, respectively. Solid lines are for the preequilibration case and the dashed lines are for the non-preequilibration case. The phosphates (the tightly bound cells) are labeled according to their z coordinates along the DNA axis [see Eq. (1)].
The distributions of the tightly bound ions in the non-preequilibrium case are more uniform than the preequilibrium case, due to the following reason. Consider all the modes with the same number of the tightly bound ions Nb. The free energy ΔGb for the tightly bound ions is large and varies sharply for different modes. Therefore, for the preequilibrium case, we expect that , which is determined by ΔGb only [see Eq. (28)], would have a bumpy distribution for different i’s. For the non-preequilibrium case, however, is determined by ΔGb+ΔGd through the mode probability distribution pM∞e−(ΔGb+ΔGd)/kBT. Because ΔGd tends to compensate the change of ΔGb (see Fig. 7), pM is less bumpy, and the distribution for the tightly bound ions is expected to be more smooth.
As the polyelectrolyte length L increases, the tightly bound ions tend to be more uniformly distributed for both the preequilibrium and the non-preequilibrium cases.
VIII. CONCLUSION AND DISCUSSIONS
According to the inter-ion correlations, we can unambiguously distinguish two types of bound counterions around a polyelectrolyte: the (strongly correlated) tightly bound ions and the (weakly correlated) diffusively bound ions. For the tightly bound ions, we consider the discrete properties of the ions and the full electrostatic correlations and fluctuations, while for the diffusively bound ions, we use the mean-field fluid model to describe the ion distribution. The theory predicts all the important properties of the ion distributions, the number of the bound ions, and the electrostatic free energies. The predicted results quantitatively agree with those from the MC simulations. For multivalent ions, which have strong correlation effects, the theory makes improved predictions than the mean-field theory, which neglects the inter-ion correlations. The present form of the theory is based on a semi-realistic model for the polyelectrolyte structure. It can be directly used to predict the statistical thermodynamics, including the correlated distributions of the tightly bound ions, the most stable binding modes, and the electrostatic free energies, for rigid double-helical polyelectrolytes. Further development of the theory would enable the treatment for more complex polyelectrolyte structures and for multipolyelectrolytes complexes.
The present theory differs from the previous models (e.g., the counterion condensation theory) in several aspects. The theory is based on a more realistic structural representation for the polyelectrolyte, rather than a simple cylindrical or line-charge model. Moreover, the tightly bound ions in our theory are different from the condensed ions in the counterion condensation theory. In fact, the condensed ions in the counterion condensation theory contain both the tightly bound ions and the diffusively bound ions in our theory. Also, we consider the discrete distributions and the full correlated Coulomb interactions for the tightly bound ions. Unlike the counterion condensation theory, which assumes the uniform averaged charge neutralization, the present theory can treat fluctuations in the bound ion distribution. In addition, the present theory accounts for the direct Coulomb interactions between the tightly bound ions and the phosphate charges on the polyelectrolyte. The present theory allows the tightly bound ions in a given binding mode, to move around within the respective tightly bound cells, i.e., in the minor and major grooves and in the space around the phosphate groups. The averaging over all the possible positions of the tightly bounds ions within the respective tightly bound cell gives the potentials of mean force in the model.
Further development of the model should include the desolvation effect for the dehydrated bound ions, and the more detailed spatial distribution of the tightly bound ions within the tightly bound cells. Nevertheless, the present theory is a first step toward a more realistic model to include the atomic details. The combination of the rigorous statistical mechanical treatment for the correlations and fluctuations and the semirealistic structural models for the ions and the polyelectrolyte has enabled predictions beyond the mean-field models, especially for multivalent ions of which the correlation effects can be important.
Acknowledgments
The authors are grateful to Dr. Dirk Stigter and Dr. Gerald Manning for stimulating communications. This research was supported by NIH/NIGMS through Grant No. GM063732 and by the Molecular Biology Program at the University of Missouri-Columbia.
References
- 1.Conrad J, Troll M, Zimm BH. Biopolymers. 1988;27:1711. doi: 10.1002/bip.360271103. [DOI] [PubMed] [Google Scholar]
- 2.Guéron M, Weisbuch G. Biopolymers. 1980;19:353. [Google Scholar]
- 3.Rouzina I, Bloomfield VA. J Phys Chem. 1996;100:9977. [Google Scholar]
- 4.Rouzina I, Bloomfield VA. Biophys J. 1998;74:3152. doi: 10.1016/S0006-3495(98)78021-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pollock EL, Hansen JP. Phys Rev A. 1973;8:3110. [Google Scholar]
- 6.Slattery W, Doolen G, Dewitt H. Phys Rev A. 1980;21:2087. [Google Scholar]
- 7.Ichimaru S, Iyetomi H, Tanaka S. Phys Rep. 1987;149:91. [Google Scholar]
- 8.He SQ, Arscott PG, Bloomfield VA. Biopolymers. 2000;53:329. doi: 10.1002/(SICI)1097-0282(20000405)53:4<329::AID-BIP5>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 9.Bloomfield VA. Biopolymers. 1997;44:269. doi: 10.1002/(SICI)1097-0282(1997)44:3<269::AID-BIP6>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 10.Levin Y, Arenzon JJ, Stilck JF. Phys Rev Lett. 1999;83:2680. [Google Scholar]
- 11.Das R, Kwok LW, Millett IS, et al. J Mol Biol. 2003;332:311. doi: 10.1016/s0022-2836(03)00854-4. [DOI] [PubMed] [Google Scholar]
- 12.Fang X, Pan T, Sosnick TR. Biochemistry. 1999;38:16840. doi: 10.1021/bi991700n. [DOI] [PubMed] [Google Scholar]
- 13.Heilman-Miller SL, Thirumalai D, Woodson SA. J Mol Biol. 2001;306:1157. doi: 10.1006/jmbi.2001.4437. [DOI] [PubMed] [Google Scholar]
- 14.Heilman-Miller SL, Pan J, Thirumalai D, Woodson SA. J Mol Biol. 2001;309:57. doi: 10.1006/jmbi.2001.4660. [DOI] [PubMed] [Google Scholar]
- 15.Rook MS, Treiber DK, Williamson JR. Proc Natl Acad Sci USA. 1999;96:12471. doi: 10.1073/pnas.96.22.12471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ha BY, Thirumalai D. J Phys II. 1997;7:887. [Google Scholar]
- 17.Ha BY, Thirumalai D. Macromolecules. 2003;36:9658. [Google Scholar]
- 18.Ha BY, Liu AJ. Phys Rev Lett. 1997;79:1289. [Google Scholar]
- 19.De la Cruz MO, Benolli L, Delsanti M, Daliez JP, Spalla O, Driford M. J Chem Phys. 1995;103:5781. [Google Scholar]
- 20.Arenzon JJ, Stilck JF, Levin Y. Eur Phys J B. 1999;12:79. [Google Scholar]
- 21.Muthukumar M. J Chem Phys. 2004;120:9343. doi: 10.1063/1.1701839. [DOI] [PubMed] [Google Scholar]
- 22.Manning GS. Q Rev Biophys. 1978;2:179. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- 23.Gilson MK, Sharp KA, Honig B. J Comput Chem. 1987;9:327. [Google Scholar]
- 24.Sharp KA, Honig B. J Phys Chem. 1990;94:7684. [Google Scholar]
- 25.Nicholls A, Honig BJ. J Comput Chem. 1991;12:435. [Google Scholar]
- 26.Grant JA, Pickup BT, Nicholls A. J Comput Chem. 2001;22:608. [Google Scholar]
- 27.You TJ, Harvey SC. J Comput Chem. 1993;14:484. [Google Scholar]
- 28.Sept D, Baker NA, McCammon JA. Protein Sci. 2003;12:2257. doi: 10.1110/ps.03187503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Proc Natl Acad Sci USA. 2000;98:10037. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mills P, Anderson CF, Record MT., Jr J Phys Chem. 1985;89:3984. [Google Scholar]
- 31.Ermak DH, McCammon JA. J Chem Phys. 1978;69:1352. [Google Scholar]
- 32.Bacquet R, Rossky PJ. J Phys Chem. 1984;88:2660. [Google Scholar]
- 33.Vlachy V. Annu Rev Phys Chem. 1999;50:145. doi: 10.1146/annurev.physchem.50.1.145. [DOI] [PubMed] [Google Scholar]
- 34.Montoro JCG, Abascal JLF. J Chem Phys. 1995;103:8273. [Google Scholar]
- 35.Allahyarov E, Löwen H, Gompper G. Phys Rev E. 2003;68:061903. doi: 10.1103/PhysRevE.68.061903. [DOI] [PubMed] [Google Scholar]
- 36.Arnott S, Hukins DWL. Biochem Biophys Res Commun. 1972;47:1504. doi: 10.1016/0006-291X(72)90243-4. [DOI] [PubMed] [Google Scholar]
- 37.Marcus M. Ion Solvation. Wiley; Great Britain: 1985. [Google Scholar]
- 38.Lindemann FA. Z Phys. 1910;11:609. [Google Scholar]
- 39.Zhou Y, Karplus M, Ball KD, Berry RS. J Chem Phys. 2002;116:2323. [Google Scholar]
- 40.Truskett TM, Torquato S, Sastry S, Debenedetti PG, Stillinger FH. Phys Rev E. 1998;58:3083. [Google Scholar]
- 41.Overbeek JThG. Colloids Surf. 1990;51:61. [Google Scholar]
- 42.Stigter D. Biophys J. 1995;69:380. doi: 10.1016/S0006-3495(95)79910-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Klapper I, Hagstrom R, Fine R, Sharp K, Honig B. Proteins. 1986;1:47. doi: 10.1002/prot.340010109. [DOI] [PubMed] [Google Scholar]
- 44.Lamm G, Pack GR. J Phys Chem B. 1997;101:959. [Google Scholar]
- 45.Lamm G, Pack GR. Int J Quantum Chem. 1997;65:1087. [Google Scholar]
- 46.Xiang Z, Shi Y, Xu Y. J Comput Chem. 1995;16:200. [Google Scholar]
- 47.Chen SW, Honig B. J Phys Chem B. 1997;101:9113. [Google Scholar]
- 48.Hingerty BE, Ritchie RH, Ferrell TL, Turner JE. Biopolymers. 1985;24:427. [Google Scholar]
- 49.Young MA, Jayaram B, Beveridge DL. J Phys Chem B. 1998;102:7666. [Google Scholar]
- 50.Ramstein J, Lavery R. Proc Natl Acad Sci USA. 1988;85:7231. doi: 10.1073/pnas.85.19.7231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Fenley MO, Manning GS, Olson WK. Biopolymers. 1990;30:1191. doi: 10.1002/bip.360301305. [DOI] [PubMed] [Google Scholar]
- 52.Wang L, Hingerty BE, Srinivasan AR, Olson WK, Broyde S. Biophys J. 2002;83:382. doi: 10.1016/S0006-3495(02)75177-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ehrenson S. J Comput Chem. 1989;10:77. [Google Scholar]
- 54.Hassan SA, Guarnieri F, Mehler EL. J Phys Chem B. 2000;104:6478. [Google Scholar]
- 55.Troll MT, Roitman D, Conrad J, Zimm BH. Macromolecules. 1986;19:1186. [Google Scholar]
- 56.Skolnick J, Fixman M. Macromolecules. 1978;11:867. [Google Scholar]
- 57.Stigter D. Biopolymers. 1998;46:503. [Google Scholar]
- 58.Jayaram B, Sharp KA, Honig B. Biopolymers. 1989;28:975. doi: 10.1002/bip.360280506. [DOI] [PubMed] [Google Scholar]
- 59.Gavryushov S, Zielenkiewicz P. J Phys Chem B. 1997;101:792. [Google Scholar]
- 60.Gavryushov S, Zielenkiewicz P. Biophys J. 1998;575:2732. doi: 10.1016/S0006-3495(98)77717-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Dwyer JJ, Gittis AG, Karp DA, Lattman EE, Spencer DS, Stites WE, García-Moreno B. Biophys J. 2000;79:1610. doi: 10.1016/S0006-3495(00)76411-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lee KK, Fitch CA, García-Moren B. Protein Sci. 2002;11:1004. doi: 10.1110/ps.4700102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Cerutti DS, Wong CF, McCammon JA. Biopolymers. 2003;70:391. doi: 10.1002/bip.10498. [DOI] [PubMed] [Google Scholar]
- 64.Antosiewicz J, McCammon JA, Gilson MK. J Mol Biol. 1994;238:415. doi: 10.1006/jmbi.1994.1301. [DOI] [PubMed] [Google Scholar]
- 65.Le Bret M, Zimm BH. Biopolymers. 1984;23:271. doi: 10.1002/bip.360230208. [DOI] [PubMed] [Google Scholar]
- 66.Olmsted MC, Anderson CF, Record MT., Jr Proc Natl Acad Sci USA. 1989;86:7766. doi: 10.1073/pnas.86.20.7766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Jayaram B, Swaminathan S, Beveridge DL, Sharp K, Honig B. Macromolecules. 1990;23:3156. [Google Scholar]
- 68.Abascal JLF, Montoro JCG. J Chem Phys. 2001;114:4277. [Google Scholar]
- 69.Feig M, Pettitt BM. Biophys J. 1999;77:1769. doi: 10.1016/S0006-3495(99)77023-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lyubartsev AP, Laaksonen A. J Biomol Struct Dyn. 1998;16:579. doi: 10.1080/07391102.1998.10508271. [DOI] [PubMed] [Google Scholar]
- 71.Guldbrand LE, Forester TR, Lynden-Bell RM. Mol Phys. 1989;67:473. [Google Scholar]
- 72.MacKerell AD., Jr J Phys Chem B. 1997;101:646. [Google Scholar]
- 73.Hud NV, Polak M. Curr Opin Struct Biol. 2001;11:293. doi: 10.1016/s0959-440x(00)00205-0. [DOI] [PubMed] [Google Scholar]
- 74.Makarov VA, Feig M, Andrews BK, Pettitt BM. Biophys J. 1998;75:150. doi: 10.1016/S0006-3495(98)77502-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Kotin L, Nagasawa M. J Chem Phys. 1962;36:873. [Google Scholar]
- 76.Shkel IA, Tsodikov OV, Record MT., Jr J Phys Chem B. 2000;104:5161. [Google Scholar]
- 77.Fixman M. J Chem Phys. 1979;70:4995. [Google Scholar]
- 78.Misra VK, Draper DE. J Mol Biol. 2000;299:813. doi: 10.1006/jmbi.2000.3769. [DOI] [PubMed] [Google Scholar]
- 79.Misra VK, Draper DE. Proc Natl Acad Sci USA. 2001;98:12456. doi: 10.1073/pnas.221234598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Bhuiyan LB, Outhwaite CW, Bratko D. Chem Phys Lett. 1992;193:203. [Google Scholar]
- 81.Bratko D, Vlachy V. Chem Phys Lett. 1982;90:434. [Google Scholar]
- 82.Deserno M, Holm C, May S. Macromolecules. 2000;33:199. [Google Scholar]
- 83.Grosberg AY, Nguyen TT, Shklovskii BI. Rev Mod Phys. 2002;74:329. [Google Scholar]
- 84.Messina R, Holm C, Kremer K. Phys Rev Lett. 2000;85:872. doi: 10.1103/PhysRevLett.85.872. [DOI] [PubMed] [Google Scholar]
- 85.Le Bret M, Zimm BH. Biopolymers. 1984;23:287. doi: 10.1002/bip.360230208. [DOI] [PubMed] [Google Scholar]
- 86.Pack GR, Wong L, Lamm G. Biopolymers. 1999;49:575. doi: 10.1002/(SICI)1097-0282(199906)49:7<575::AID-BIP4>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- 87.Qian H, Schellman JA. J Phys Chem B. 2000;104:11528. [Google Scholar]
- 88.Manning GS, Mohanty U. Physica A. 1997;247:196. [Google Scholar]


