Assessment of Detective Quantum Efficiency: Intercomparison of a Recently Introduced International Standard with Prior Methods

Abstract

Purpose

To prospectively evaluate the recently introduced international standard method for measurement of the detective quantum efficiency (DQE) of digital radiography systems, in comparison with representative prior methods.

Materials and Methods

A recently introduced international standard method (International Electrotechnical Commission [IEC] 62220-1, 2003) for DQE measurement and two previously described DQE evaluation methods were considered. In addition to an overall comparison, evaluations of the following method factors were performed: beam quality, beam-limiting devices (apertures or collimators), noise power spectrum (NPS) analysis algorithms and parameters (area, region of interest size, background detrending), and modulation transfer function (MTF) test devices and methods.

Results

Overall, at low to middle frequencies, the IEC method yielded DQE estimates that were 3.3% and 6.5% lower than the values yielded by the two previous methods. Averaged over the frequency range of 1.5–2.5 mm⁻¹, the DQE estimate derived by using the IEC method was 7.1% lower and 12.4% higher than the estimates derived by using the other two methods. Results obtained with the two previous DQE evaluation methods agreed well (within 2.0%) in the low- to middle-frequency range but diverged by up to 10% at higher frequencies. When the DQE method factors were evaluated separately, the largest percentage deviations in DQE were associated with (in order of decreasing influence) the MTF analysis method (~11%), the beam limitation (about 7%–10%), the beam quality (~9%), and the NPS analysis method (~3%).

Conclusion

Comparison of DQE estimates obtained by using the recently introduced international standard technique with those obtained by using prior methods revealed that the overall measurement method can affect the DQE estimate by as much as 12%. Findings further suggest that both beam limitation achieved by means of internal collimation (rather than external apertures) and use of a radio-opaque edge MTF device yield a more accurate estimation of the DQE.

Detective quantum efficiency (DQE) historically has been the most commonly used metric of the overall image quality of radiographic systems (1). Defined as the ratio of the squared image signal-to-noise ratio to the number of incident x-ray photons, the DQE describes how efficiently a system translates incident x-ray photons into useful signal (relative to noise) within an image. With the introduction of digital radiographic imaging systems, the DQE has continued to be regarded as a convenient, reasonably accurate, and widely accepted metric of image quality (2,3).

Although the DQE is almost universally regarded as the best overall indicator of the image quality of digital radiography systems, until recently there was no universally accepted standard for the measurement of this parameter. In 2003, the International Electrotechnical Commission (IEC) published a standard method (4) for measurement of the DQE that also included specifications for the measurement of two associated metrics: the modulation transfer function (MTF) and the noise power spectrum (NPS). Given the large amount of literature on DQE measurements, the introduction of the standard has created the need for insight into how the results acquired by using the standard technique compare with the results obtained by using prior methods (5,6). Thus, the purpose of our study was to prospectively evaluate the recently introduced international standard method for measurement of the DQE of digital radiography systems, in comparison with representative prior methods (7–13).

Advances in Knowledge

• Comparison of detective quantum efficiency (DQE) estimates obtained by using the recently introduced international standard technique with estimates obtained by using prior methods revealed that the overall measurement method can affect the DQE estimate by as much as 12%.

• The DQE method factors that had the greatest effect on the DQE estimate were (in order of decreasing influence) MTF analysis method (~11%), beam limitation (about 7%–10%), beam quality (~9%), and NPS analysis method (~3%).

• Findings suggest the use of both beam limitation achieved by means of internal collimation and a radio-opaque edge MTF device for more accurate estimation of the DQE.

Materials and Methods

Imaging System

The prototype flat-panel detector used in this study was provided by GE Healthcare (Milwaukee, Wis) through a research agreement. To compare DQE measurement methods specifically—as opposed to the performance of specific imaging systems—all measurements were obtained (N.T.R.) by using a single representative flat-panel imaging device. This device has a 0.2-mm pixel pitch and an amorphous silicon–cesium iodide flat-panel detector equivalent to that in a commercially available system (Revolution XQ/i; GE Healthcare) (5,6,14). The detector was calibrated before the acquisition of imaging data according to manufacturer guidelines.

Beam Conditions

Each of the three DQE measurement methods involves the use of an enhanced x-ray beam quality that is based on a combination of specified tube voltage and external beam–hardening filtration (Table 1). Furthermore, the three DQE techniques differ in terms of the method and extent of beam limitation used. The DQE measurement methods of both Dobbins et al (8) and Samei and Flynn (13) involved the use of the internal collimator of the tube to restrict the beam extent to the outer edge of the detector, whereas the IEC method (4) involves the use of a specified set of external lead apertures (Fig 1) to restrict the area of the beam to 16 × 16 cm.

Table 1.

X-ray Beam Conditions for Measurement of DQE

Beam Quality*	Beam Limitation	Tube Voltage (kV)	Beam Filtration	Measured HVL (mm Al)†	Exposure Estimate at Detector Surface (mR)‡			q Value (mm−2 mR−1)§
					Enl/3.2	Enl	3.2Enl
Dobbins et al (8)	None	70	0.5 mm Cu||	6.7	0.187	0.494	1.270	271 500
Samei and Flynn (13)	None	70	19 mm Al†	6.6	0.195	0.400	1.308	255 855
IEC RQA5 with no aperture	None	74	21 mm Al†	7.1	NA	0.555	NA	264 626
IEC RQA5 with external aperture	External (16 × 16 cm)	74	21 mm Al†	7.1	0.197	0.526	1.339	264 626
IEC RQA5 with internal aperture	Internal collimator (16 × 16 cm)	74	21 mm Al†	7.1	NA	NA	NA	264 626

^*The IEC-specified RQA5 beam quality was evaluated with full detector irradiation—that is, with no apertures; with IEC-specified external lead apertures restricting the field of view to 16 × 16 cm; and with the device’s internal collimator adjusted to simulate the effect of the IEC-specified external apertures. Numbers in parentheses are reference numbers.

^†Aluminum (Al) type 1100 alloy (99.0% purity) was used for historical reasons and because of the nonuniformity of aluminum filtration with greater than 99.9% purity, as reported previously (15). HVL = half-value layer.

^‡E_nl = IEC-defined normal exposure (~0.4 mR). NA = not applicable; no exposure or NPS measurement was performed under this condition. 1 R = 2.58 × 10⁻⁴ C/kg.

^§q = number of incident x-ray photons per unit area per unit of exposure incident on the detector. 1 R = 2.58 × 10⁻⁴ C/kg.

^||Cu = copper.

Figure 1.

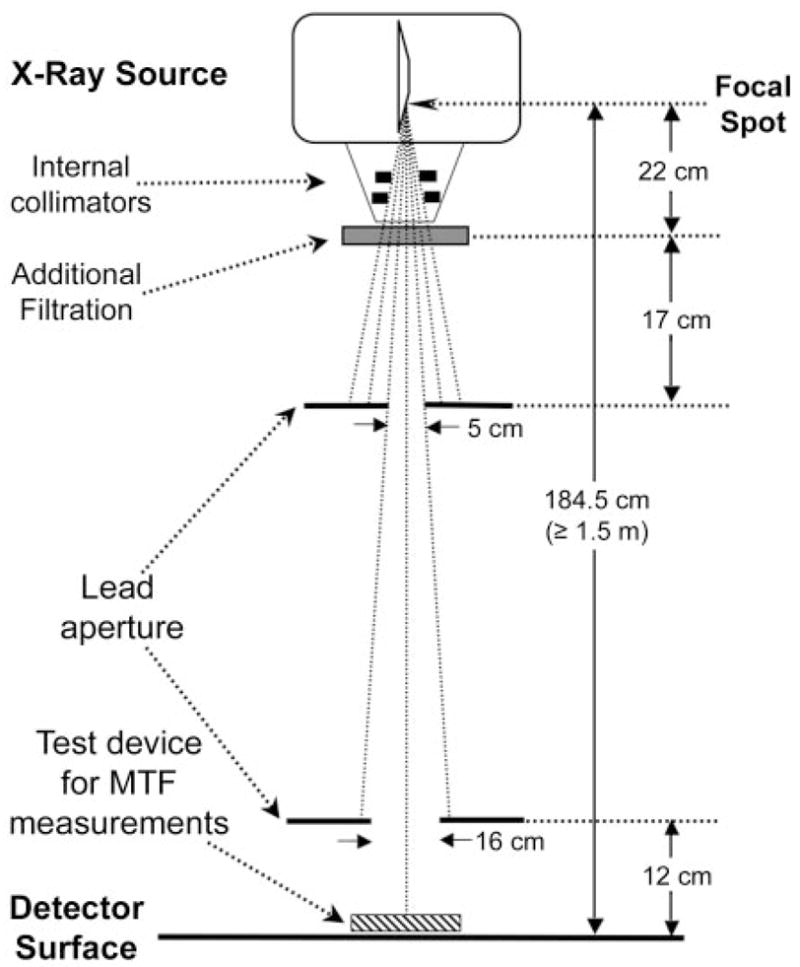
DQE test geometry, compliant with the IEC 62220-1 standard. For the RQA5 beam quality, additional filtration with 21 mm of aluminum is used to simulate the spectral quality of radiation incident on the detector during a typical clinical examination. The detector is positioned at a source-to-image distance of 1.5 m or greater. The internal collimator of the device and external beam–limiting lead apertures are adjusted to achieve a radiation field of approximately 16 × 16 cm at the detector surface. The IEC standard specifies the exact position and size of only the aperture closest to the detector. The radio-opaque MTF device is placed adjacent to the detector as shown.

The effect of beam quality in the absence of beam limitation was evaluated by using the IEC DQE method with each of three beam qualities (Table 1). In addition, the effect of the beam limitation independent of beam quality was assessed by using the IEC-specified RQA5 beam quality (16) in three configurations: without beam limitation, with the IEC-specified external apertures, and with the internal tube collimators configured to achieve beam limitation comparable to that of the IEC-specified external apertures (5,6). It should be noted that the aluminum filtration used to achieve the RQA5 beam quality was type 1100 (99.0% purity) rather than the higher-purity (>99.9%) aluminum specified in the standard because of the highly visible structured image nonuniformities associated with the use of very-high-purity (≥99.9%) aluminum filtration (15).

Determination of MTF

As the first component of DQE assessment, the MTF was measured according to the prescribed MTF measurement device of each method—specifically, (a) a radiopaque edge (IEC [4]), (b) a slit (Dobbins et al [8]), and (c) a radiolucent edge (Samei and Flynn [13])—by using acquisition and analysis algorithms specific to each method. To isolate the effect of the MTF measurement method from all other factors, all MTF devices were imaged by using the same beam quality (RQA5 beam quality at exposure of 1.03 × 10⁻⁶ C/kg [4.0 mR]). Additional images were acquired at exposures of 2.0 × 10⁻⁶ C/kg (7.7 mR) (slit) and 9.5 × 10⁻⁷ C/kg (3.7 mR) (radiolucent edge) by using the beam qualities associated with the Dobbins et al and Samei et al methods, respectively (Table 1). All MTF images were analyzed by using basic Fourier analysis techniques tailored to each method. The images of the slit device were analyzed with a slit MTF algorithm developed by Fujita et al (17) and adapted by Dobbins (7) and Dobbins et al (7,8). The radiolucent edge and radio-opaque edge images were analyzed according to the Samei et al and IEC methods by using an algorithm developed by Samei et al (9–13). Further details of the MTF data acquisition and analysis component of the current study are described elsewhere (5).

Determination of NPS

The second component of the DQE evaluation involved acquiring NPS estimates—derived from flat-field images—by using the three methods. The image acquisition and analysis details for these measurements were described previously (6). Flat-field images were acquired at approximate exposures of E_nl/3.2, E_nl, and 3.2E_nl, where E_nl (Table 1) is approximately 1.03 × 10⁻⁷ C/kg (0.4 mR), according to the manufacturer of the detector used in this study. NPS estimates were derived from the images by using algorithms and parameters specific to each of the three methods. The three techniques involved similar processing parameters, with the exception of the area of the detector evaluated, the size and number of the regions of interest (ROIs) used for analysis, the background subtraction method (detrending), and the inclusion of on-axis data in the reported NPS results (Table 2). In addition, the images acquired by using the IEC beam quality and beam limitation were analyzed with each of the three NPS algorithms to assess the effect of computational technique alone. Further details of the NPS data acquisition and analysis component of the current study are reported elsewhere (6).

Table 2.

Summary of Measurement Parameters for Evaluated DQE Methods

Overall DQE Method	IEC Apertures	Beam Quality*	MTF Device	MTF Analysis Method	NPS Analysis Method	NPS Analysis Area†	ROI Size and Type‡	NPS Band Size§	NPS Detrending
Dobbins et al	None	70 kV 0.5 mm Cu	Slit	Dobbins et al	Dobbins et al	640 × 640 Pixels (10)	128 Pixels, NOL	±4	Two-dimensional (first order)
						1024 × 1024 Pixels (1)
Samei and Flynn	None	70 kV 19 mm Al	Radiolucent edge	Samei and Flynn	Samei and Flynn
Historical						640 × 640 Pixels (10)	128 Pixels, NOL	±7 With on-axis data	Two-dimensional (second order)
						1280 × 1280 Pixels (1)
Current						640 × 640 Pixels (3)	128 Pixels, OL
						1280 × 1280 Pixels (1)
IEC||	External	RQA5	Radiopaque edge	IEC	IEC	640 × 640 Pixels (3)	256 Pixels, OL	±7	Two-dimensional (second order)
						640 × 640 Pixels (10)

Note.—Parameters used in the Dobbins et al (8), Samei and Flynn (13), and IEC (4) methods are given.

^*Cu = copper, Al = aluminum.

^†The first set of parameters corresponds to the parameters employed for the evaluation of the NPS and combined NPS plus MTF dependence on the DQE estimate. Comparable statistical quality in the NPS estimates was achieved by varying the relative number of images analyzed with each method (5). The second set of parameters corresponds to results regarding the effect of the overall DQE method. The number of images analyzed was indicated by the specifications of each image, or in the case of the IEC method, by the requirement to use a total of at least 4 million independent image pixels in the NPS analysis. The number of images used is in parentheses.

^‡NOL = nonoverlapping (one pass) ROIs, OL = overlapping (four passes) ROIs.

^§Number of rows of data averaged in two-dimensional NPS to produce a one-dimensional NPS curve.

^||The IEC method requires the use of 256 × 256-pixel ROIs for NPS analysis involving the use of an overlapping placement scheme achieved with four successive analysis passes with ROIs offset as follows: (x, y); x + 128, y; x, y + 128; and x + 128, y + 128. x And y are the reference coordinates for the top left-most corner of the analysis area.

Determination of Incident Exposure and q Value

An essential step in determining the DQE is estimating the incident exposure (E) associated with each NPS measurement (Table 1). The incident exposure at the detector was estimated (N.T.R.) by using the system (linearity) response function (5) to convert the mean pixel value to an exposure value.

Another element required to compute the DQE is the q value (Table 1), which was estimated by means of computer spectrum modeling for each of the beam conditions evaluated. For the IEC method, a q value of 264 626 mm⁻² mR⁻¹ was obtained by multiplying the IEC-specified q value (4) of 30 174 mm⁻² μGy⁻¹ by the conversion factor of 8.77 μGy mR⁻¹ air kerma per unit exposure. For the Dobbins et al and Samei et al beam qualities, q values were computed (E.S. and J.T.D.) by using the DXSPEC (18) and xSpect (13) computational models and were 271 500 mm⁻² mR⁻¹ and 255 855 mm⁻² mR⁻¹, respectively, which correspond to the values used historically (7–13).

Computation of DQE

The frequency-dependent DQE, DQE(f), was computed (N.T.R.) by using the estimated MTF, NPS, q, and E values:

$$\begin{array}{ll}\text{DQE}(f)& ={\text{S}}^2\frac{{\text{MTF}}^2(f)}{\text{NPS}(f)\times q\times E}\\ & =\frac{{\text{MTF}}^2(f)}{\text{NNPS}(f)\times q\times E},\end{array}$$

where MTF(f) is the frequency-dependent MTF; NPS(f) is the frequency-dependent NPS; and NNPS(f) is the frequency-dependent normalized NPS (3,6), calculated as [NPS(f)]/S², where S² is the square of the large-area signal intensity (assuming the detector is linear with respect to exposure). The DQE estimates were computed with the quantities specific to each method or condition. For these computations, in adherence with the IEC specification and to facilitate comparisons, all of the MTF and NPS results were averaged into frequency-sampling intervals of 0.05 mm⁻¹. The DQE estimates derived by using each of the three methods were compared (N.T.R., E.S., J.T.D.). Additional comparisons were made to elucidate the isolated effects of beam quality, beam limitation, MTF analysis method, and NPS analysis method on the DQE estimate. DQE curves were then compared by computing the relative difference (expressed as a percentage) between one curve and another at each 0.05 mm⁻¹ frequency bin and averaging over the frequency ranges of interest (N.T.R.). Error estimates for the DQE results were derived (N.T.R., E.S., and J.T.D.) from the reported MTF (5) and NPS (6) values and the error estimate in the computed exposure.

Results

Effect of Beam Limitation

With all other factors constant, across the entire frequency range, the measured DQE estimate without external beam–limiting apertures—that is, with full detector irradiation—was generally lower than that obtained when the IEC-specified external beam–limiting apertures were used. The results indicated a mean relative difference of 6.8% (standard deviation, 0.9) between the DQE estimates obtained with and those obtained without external apertures over spatial frequencies 0.5 mm⁻¹ and greater (Fig 2). Within the same frequency range, the mean relative difference in the measured DQE estimate with use of the device’s internal collimators for beam collimation compared with the DQE estimate obtained with use of the IEC-specified external apertures was 9.6% (standard deviation, 0.9).

Figure 2.

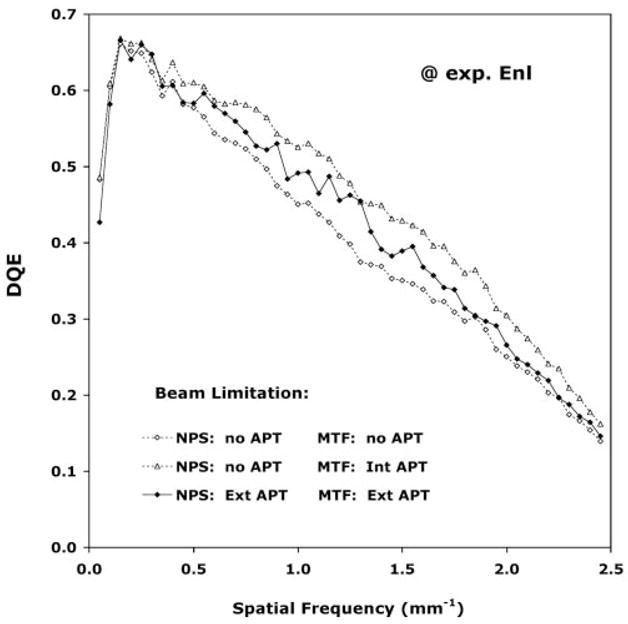
Graph illustrates effects of various beam-limiting conditions on DQE estimates: full detector irradiation with no external apertures (NPS: no APT, MTF: no APT), limited 16 × 16-cm detector irradiation for MTF measurement with internal collimators and no additional external apertures (NPS: no APT, MTF: Int APT), and limited 16 × 16-cm detector irradiation with external apertures (NPS: Ext APT, MTF: Ext APT). Data were collected by using the IEC RQA5 beam quality and the IEC standard acquisition and processing method. Ten images acquired at a detector exposure level corresponding to E_nl (Table 1) were analyzed by using a total of 160 overlapping 256 × 256-pixel ROIs for the NPS component of the DQE measurements. Error bars less than ±2.5%.

Effect of Beam Quality

Regarding the effect of beam quality on the DQE estimate (Fig 3), all other factors except q—the effect of which was removed by evaluating the results in terms of the product of q · DQE—were kept constant. When the full detector was irradiated, the DQE estimate obtained by using the beam quality for the Samei et al method (70 kV, 19 mm of aluminum) was only slightly lower than that obtained by using the IEC RQA5 beam quality (74 kV, 21 mm aluminum) (mean relative difference, 2.2%; standard deviation, 1.4%; over spatial frequencies of 0.5 mm⁻¹ and greater). In comparison, over the same frequency range, the mean relative difference in the DQE estimate obtained by using the beam quality for the Dobbins et al method (70 kV, 0.5 mm of copper) was 8.7% (standard deviation, 1.4%) higher than that obtained by using the IEC RQA5 beam quality without apertures.

Figure 3.

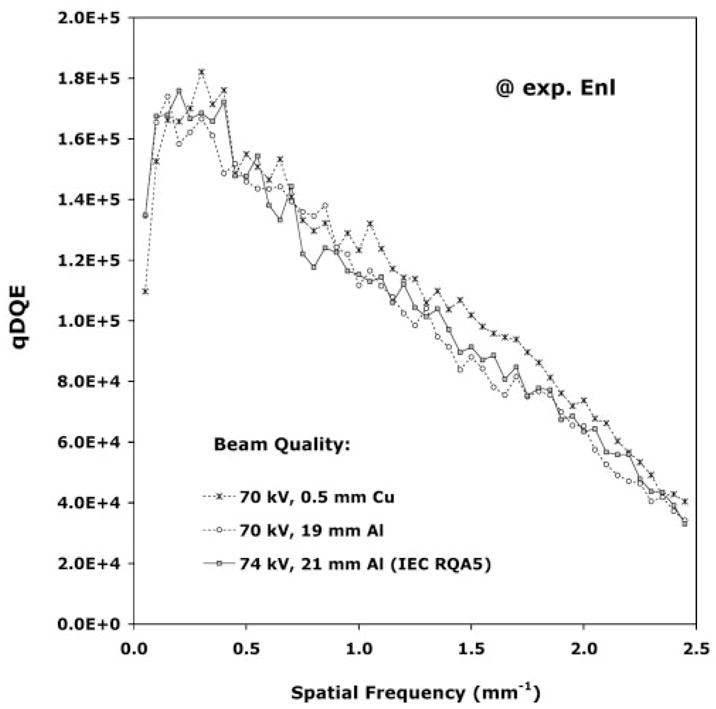
Graph illustrates DQE dependence on beam quality. The q · DQE products obtained with the following beam qualities are plotted: 70 kV, 0.5 mm of copper filtration (used by Dobbins et al); 70 kV, 19 mm of aluminum filtration (used by Samei et al); and 74 kV, 21 mm of aluminum filtration (IEC RQA5) with no added apertures. Excluding beam quality, in all other respects the acquisition and processing method complied with the IEC standard. Three images acquired at a detector exposure level corresponding to E_nl (Table 1) were analyzed by using a total of 48 overlapping 256 × 256-pixel ROIs for the NPS component of the DQE measurements. Error bars less than ±4.3%.

Effect of NPS Analysis Method

Isolating the effect of the NPS analysis approach, we evaluated the DQE estimate with each of the three NPS methods by using a common data set of flat-field images acquired according to the IEC protocol. With the effect of differences in q value between methods eliminated, the q · DQE products (Fig 4) for incident exposures of E_nl/3.2, E_nl, and 3.2E_nl indicated consistent results at all three exposure levels and excellent agreement among the different methods, except at the lowest spatial frequencies (≤0.15 mm⁻¹), at which the q · DQE product derived by using the IEC-NPS method decreased precipitously. The mean relative difference in the estimated q · DQE products over spatial frequencies of 0.5 mm⁻¹ and greater derived by using the methods of Dobbins et al (8), Samei and Flynn (historical) (13), and Samei et al (current) (Table 2) were, respectively, 0.3%, 2.8%, and 2.0% (standard deviation, ≤1.2) higher than the product derived by using the IEC standard method.

Figure 4.

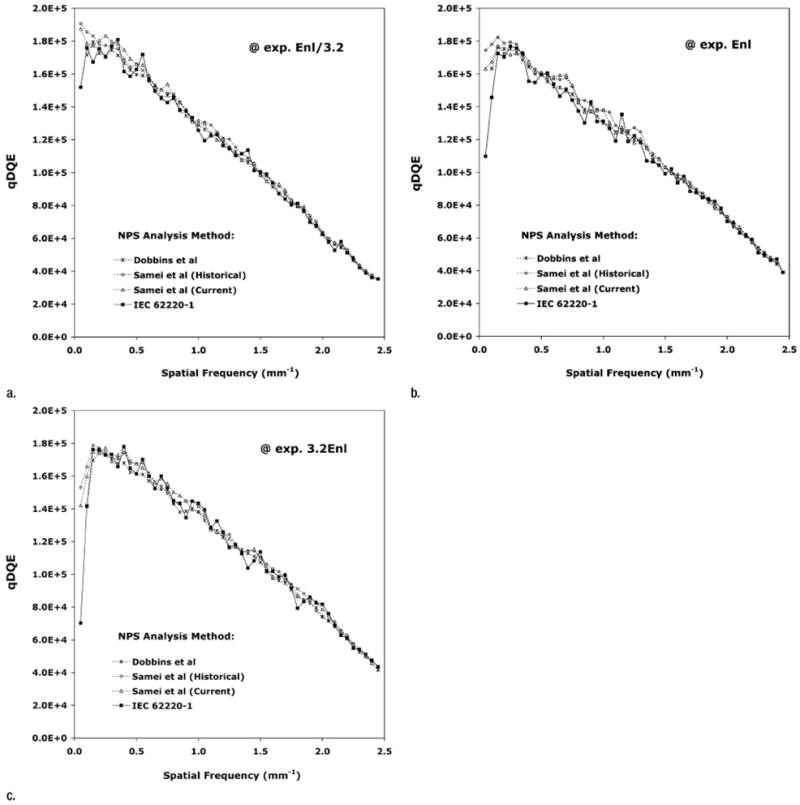
Graphs illustrate DQE dependence on NPS analysis method. The q · DQE products corresponding to detector exposures of (a) E_nl/3.2, (b) E_nl, and (c) 3.2E_nl are plotted. IEC beam quality with external apertures, the IEC radio-opaque edge MTF method, and a common NPS data set acquired according to the IEC standard method were used. The Dobbins et al, Samei and Flynn (historical), Samei et al (current), and IEC 62220-1 NPS analysis methods were evaluated with use of a central 640 × 640-pixel area of analysis for the NPS estimate on 10 images containing 250 nonoverlapping 128 × 128-pixel ROIs (Dobbins et al method), 10 images containing 250 nonoverlapping 128 × 128-pixel ROIs (Samei and Flynn historical method), three images containing 219 overlapping 128 × 128-pixel ROIs (Samei et al current method), and three images containing 48 overlapping 256 × 256-pixel ROIs (IEC 62220-1 method). Error bars less than ±2.2%, less than ±2.5%, less than ±2.5%, and less than ±4.3% for the Dobbins et al, Samei and Flynn (historical), Samei et al (current), and IEC 62220-1 methods, respectively.

Combined Effect of NPS and MTF Methods

Qualitatively, the results obtained at different incident exposures with each method were consistent except at very low spatial frequencies. For the NPS-MTF methods of Dobbins et al and Samei et al, the q · DQE product estimates were higher than those obtained by using the IEC standard method, except at the highest spatial frequencies (Fig 5). Furthermore, within the limits of uncertainty there appeared to be close agreement (within 2% on average) between the results obtained by using the Dobbins et al and those obtained by using the Samei et al method in the low to middle range of spatial frequencies (0.15–1.00 mm⁻¹). However, the results obtained by using the historical and current methods of Samei et al, which did not differ by a mean of more than 1.5% (standard deviation, 0.8) over the frequency range of 0.5–2.5 mm⁻¹, began to diverge from those obtained by using the method of Dobbins et al at spatial frequencies of 1.0 mm⁻¹ and greater and approached the results obtained by using the IEC method at spatial frequencies of 2.0 mm⁻¹ and greater. When averaged over spatial frequencies of 0.5 mm⁻¹ and greater, the mean relative differences in the q · DQE product estimates derived by using the methods of Dobbins et al, Samei et al (historical), and Samei et al (current) were, respectively, 13.3%, 7.5%, and 6.7% (standard deviation, ≤1.2) higher than the product obtained by using the IEC standard method. From these results, the effects of MTF analysis (5) alone were estimated to be 11.0%, 4.4%, and 4.4% (standard deviation, ≤0.4), respectively.

Figure 5.

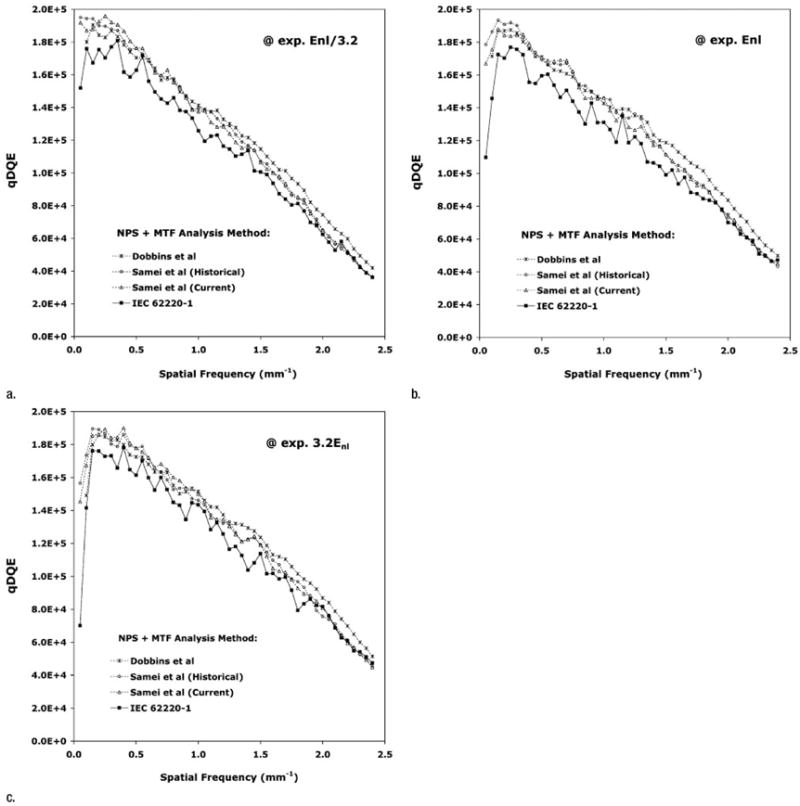
Graphs illustrate DQE dependence on combined NPS and MTF analysis methods. The q · DQE products corresponding to detector exposures of (a) E_nl/3.2, (b) E_nl, and (c) 3.2E_nl are plotted. Results were obtained by using the IEC beam quality condition with external apertures, a common NPS image data set acquired by using the IEC standard method, and MTF data acquired according to the Dobbins et al (slit), Samei et al (radiolucent edge), and IEC 62220-1 (radiopaque edge) methods. For the NPS estimates, the area of analysis, number of images, and ROIs for each method are those specified in Figure 2. Error bars less than ±2.2%, less than ±2.5%, less than ±2.5%, and less than ±4.3% for the Dobbins et al, Samei and Flynn (historical), Samei et al (current), and IEC 62220-1 methods, respectively.

Comparison of Overall Methods

Overall comparison of the DQE estimates obtained by using each method (Fig 6a) revealed that when the effect of variations in q were excluded, use of the DQE method of Dobbins et al, as compared with use of the IEC DQE method, resulted in a higher q · DQE product estimate over the full frequency range but yielded results that approached those obtained by using the IEC method at the cutoff frequency. The results derived by using the historical and current methods of Samei et al agreed with each other quite well at all spatial frequencies. Within the 0.15–0.75 mm⁻¹ range, use of the Samei et al method resulted in q · DQE products that were qualitatively greater than those obtained by using the IEC method and essentially equivalent to those obtained by using the Dobbins et al method. In the spatial frequency range of 0.8–1.1 mm⁻¹, the Samei et al method yielded q · DQE product estimates that were roughly equivalent to those obtained by using the IEC method. However, beyond this range, the Samei et al method yielded product estimates that were lower than those obtained by using the Dobbins et al and IEC standard methods.

Figure 6.

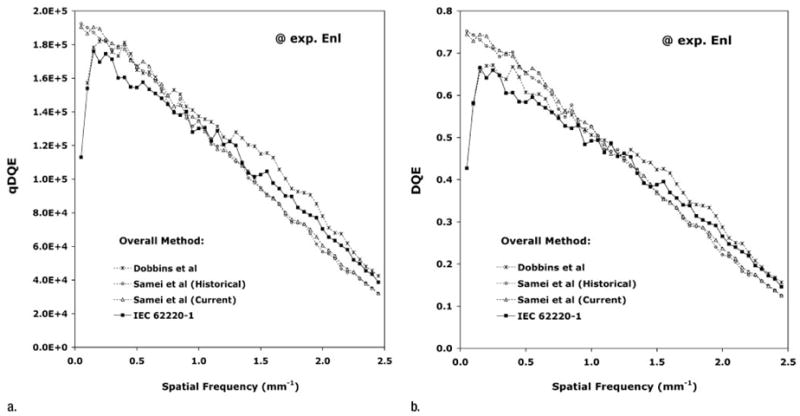
Graphs illustrate comparison of overall DQE methods, including beam quality and limitation, NPS analysis method, and MTF analysis method (a) without and (b) with q value variations taken into consideration at detector exposure levels corresponding to E_nl. For the Dobbins et al overall method, the following parameters were used: 70 kV with 0.5 mm of copper filtration (no beam limitation), the slit MTF method, a 1024 × 1024-pixel analysis area on one image with 64 nonoverlapping 128 × 128-pixel ROIs for NPS analysis, and a q value of 271 500 mm⁻² mR⁻¹. For the Samei and Flynn historical method, the following parameters were used: 70 kV with 19 mm of aluminum filtration (no beam limitation), the radiolucent edge MTF method, a 1280 × 1280-pixel analysis area on one image with 100 nonoverlapping 128 × 128-pixel ROIs for NPS analysis, and a q value of 255 855 mm⁻² mR⁻¹. For the Samei et al current method, the historical method parameters were used, with the exception that 343 overlapping 128 × 128-pixel ROIs were used for NPS analysis. For the IEC 62220-1 method, the following parameters were used: 74 kV with 21 mm of aluminum filtration, IEC-specified external apertures, the IEC radiopaque edge MTF method, a 640 × 640-pixel analysis area on 10 images with 160 overlapping 256 × 256-pixel ROIs for NPS estimates, and a q value of 264 626 mm⁻² mR⁻¹. Error bars less than ±4.0%, less than ±3.8%, less than ±2.2%, and less than ±2.5% for the Dobbins et al, Samei and Flynn (historical), Samei et al (current), and IEC 62220-1 methods, respectively.

The DQE estimates (with q value dependence included) derived by using the Dobbins et al and IEC methods (Fig 6b) were in the closest agreement in the frequency range of 0.25–1.25 mm⁻¹, with the IEC method yielding DQE estimates that were comparatively lower (mean relative difference, 5.7%; standard deviation, 0.8%; over frequencies greater than 0.5 mm⁻¹). The historical and current methods of Samei et al agreed well with one another over the full range of frequencies (mean relative difference, 1.5%; standard deviation, 0.9%; over frequencies of greater than 0.5 mm⁻¹), and both techniques yielded DQE estimates that were higher (at low frequencies) and lower (at high frequencies) than those derived by using the Dobbins et al and IEC methods (Table 3). The crossover point at which all methods yielded equivalent DQE estimates was approximately 1.0 mm⁻¹.

Table 3.

Relative Differences in DQE Estimates between the Three DQE Measurement Methods

Spatial Frequency Range	Samei and Flynn (historical) vs IEC Method	Samei et al (current) vs IEC Method	Dobbins et al vs IEC Method	Samei and Flynn (historical) vs Dobbins et al Method
0.5–2.5 mm−1	−4.3 ± 0.9	− 2.9 ± 0.8	5.7 ± 0.8	−5.2 ± 1.0
0.25–1.25 mm−1	6.5 ± 1.0	7.5 ± 0.8	3.3 ± 1.1	1.5 ± 1.3
1.5–2.5 mm−1	−12.4 ± 1.3	−10.8 ± 1.1	7.1 ± 1.1	−10.0 ± 1.4

Note.—Data are mean relative differences, cited as percentages, ±standard deviations.

Discussion

Our study results show that moderate differences in estimated DQE that result from methodologic differences do exist. With publication of the recently introduced international standard for DQE measurement (IEC 62220-1), a consensus as to the “best practice” method for DQE evaluations has been reached that will facilitate future intercomparisons. Nevertheless, there is still a broad body of published literature on existing imaging devices, and the results obtained by using the international standard method cannot be easily compared with the previously published results obtained by using the other methods.

We found that the values obtained by using the IEC method were lower than those obtained by using the established methods of Dobbins et al (8) and Samei and Flynn (13) at low frequencies and intermediate between the Dobbins et al and Samei et al results at frequencies of greater than 1.5 mm⁻¹. At the very lowest frequencies, the results obtained by using the IEC method (4) diverged substantially from those obtained by using the Samei et al methods. In the IEC-reporting range (≥0.5 mm⁻¹) and relative to the IEC method, the greatest differences were seen in the middle to high frequency range, corresponding to mean relative differences of approximately 7% (Dobbins et al vs IEC method) and approximately 12% (Samei et al vs IEC method).

Our two prior reports (5,6) describe in detail the comparison of specific MTF and NPS results. In terms of NPS analysis, all three methods agreed exceptionally well (mean relative difference, <1.6%; standard deviation, 0.6%; over the frequency range of 0.15 mm⁻¹ to cutoff). Since none of the measurement parameters had a substantial effect on the measured NPS, we can infer that the observed differences between the DQE measurement methods were not due in any substantial way to differences in the NPS technique, except at the very lowest spatial frequencies (<0.2 mm⁻¹), at which the differences were due to a combination of the detrending method and the size of the ROIs used for NPS measurement (6). It should be noted tangentially that although beam limitation had no measurable effect on the NPS estimates, the use of beam limitation had the disadvantage of increasing the number of images required to achieve the same number of independent image pixels and a comparable level of precision in the NPS and DQE estimates.

In terms of MTF analysis, we noted differences in the measured MTF as a function of the applied method in our recent report (5). Although the differences were relatively modest, because the MTF term in the expression for DQE is squared, the MTF method accounted for the majority of the noted differences in the DQE estimates. Primarily related to the MTF, beam quality and beam limitation each were found to individually affect the DQE estimate by 7%–10%. Results from a related study (5) demonstrated that in the presence of device misalignment and image glare (1), the MTF estimate measured by using a slit (Dobbins et al method) was less accurate than the MTF estimate measured by using an edge (Samei et al and IEC methods). In that study, it was concluded that the radiopaque edge method recommended by the IEC and the beam limitation achieved by using the device’s internal collimators yield the most accurate estimate of overall MTF in the presence of glare and therefore constitute the preferred approach for characterizing the MTF for DQE measurement.

An important element of DQE evaluation is estimation of the level of exposure associated with the NPS measurement used to compute the DQE estimate. Direct single-exposure measurements generally have a precision of 5%–10%. In our study, we used an average of a large number of individual exposure measurements (6) to improve precision to within about 0.6% at high exposure values but only achieved a precision of within about 6.4% at low exposures. However, our use of the system transfer function in the exposure estimation process (5) resulted in further precision, yielding an overall exposure uncertainty of about 0.2% across the exposure range. This improvement in precision had a favorable influence on the precision of DQE estimates, enabling a more statistically rigorous comparison of the methods.

Notwithstanding the findings, the present investigation was limited in a number of respects. First, the study was aimed at comparing the recently introduced international standard with only two other methods. Other DQE assessment methods would probably compare differently. Second, the comparisons were made at only a single—although typical—range of x-ray spectra based on a tube voltage of about 70 kVp. The evaluated methods might compare differently at other beam qualities. Finally, the study was based on evaluation involving the use of only one image receptor—namely, an indirect flat-panel detector. This limitation resulted from the intended focus of the study, which was the intercomparison of methods rather than of systems. Nevertheless, the findings of this study are generalizable (with caveats), because the relative differences between the DQE estimates observed in this work are likely to be reflective of the relative magnitude of expected differences due to varying measurement methods for other classes of digital radiographic imaging systems. Furthermore, for studies in which the same type of flat-panel device is used, a quantitative correction could be applied to relate the DQE measurement to any of the three DQE measurement methods described herein.

In summary, we found that the choice of overall measurement method can affect the DQE results by as much as 12%; therefore, careful attention to the details of the DQE measurement method is necessary to ensure reliable estimation of the DQE and comparison with previously published results. The DQE results obtained by using the Dobbins et al and Samei et al methods agreed well at low to middle frequencies (mean relative difference, 2.0%; standard deviation, 1.3; over frequency range of 0.25–1.25 mm⁻¹) but deviated substantially at higher frequencies (mean relative difference, 10.0%; standard deviation, 1.4; over frequency range of 1.5–2.5 mm⁻¹). The IEC technique yielded lower DQE estimates than either of these methods in the 0.25–1.25 mm⁻¹ range (mean relative differences, 3.3% and 6.5%, respectively; standard deviations, 1.1 and 1.0, respectively), whereas at frequencies of greater than 1.5 mm⁻¹, the IEC method yielded estimates intermediate between the Dobbins et al and Samei et al (historical) values (mean relative differences, 7.1% and 12.4%, respectively; standard deviations, 1.1 and 1.3, respectively). We have the following recommendations regarding DQE measurements, which are based on our study results and consistent with the findings reported in associated publications (5,6):

1. Using the IEC RQA5 spectrum (based on an iteratively achieved target half-value layer with type 1100 aluminum filtration for improved image uniformity [15]) yields a calibrated spectrum, but for well-calibrated radiographic systems it probably has little advantage over using a specific target voltage and filtration (as in the Samei et al and Dobbins et al methods).

2. Use of internal collimation instead of the IEC-specified external beam apertures yields better estimates of the MTF and the DQE while diminishing the complexity of image acquisition (5).

3. Use of a more conventional (larger) field of view (as in the Samei et al and Dobbins et al methods), as opposed to the beam limitation specified by the IEC, reduces the number of images required to achieve low variance in NPS and DQE results (6).

4. Using a radiopaque edge (as in the IEC standard method) to measure the MTF component of the DQE permits relatively easy alignment compared with using a slit and yields a more accurate measurement of the MTF in the presence of image glare than either the slit method or the radiolucent edge method (5).

5. In NPS analysis, use of 128 × 128-pixel ROIs, coupled with second-order polynomial background detrending (as in the Samei et al method), improves estimation of the DQE at low frequencies (6).

Abbreviations

DQE

detective quantum efficiency

E_nl

IEC-defined normal exposure

IEC

International Electrotechnical Commission

MTF

modulation transfer function

NPS

noise power spectrum

q

number of incident x-ray photons per unit area per unit of exposure incident on the detector

ROI

region of interest