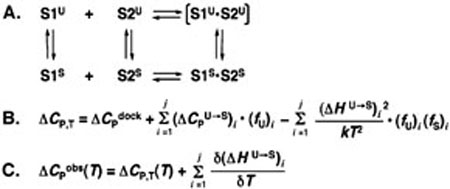Heat Capacity Changes Associated with DNA Duplex Formation: Salt- and Sequence-Dependent Effects

Abstract

Duplexes are the most fundamental elements of nucleic acid folding. Although it has become increasingly clear that duplex formation can be associated with a significant change in heat capacity (ΔC_p), this parameter is typically overlooked in thermodynamic studies of nucleic acid folding. Analogy to protein folding suggests that base stacking events coupled to duplex formation should give rise to a ΔC_p due to the release of waters solvating aromatic surfaces of nucleotide bases. In previous work, we showed that the ΔC_p observed by isothermal titration calorimetry (ITC) for RNA duplex formation depended on salt and sequence. In the present work, we apply calorimetric and spectroscopic techniques to a series of designed DNA duplexes to demonstrate that both the salt dependence and sequence dependence of ΔC_ps observed by ITC reflect perturbations to the same fundamental phenomenon: stacking in the single-stranded state. By measuring the thermodynamics of single strand melting, one can accurately predict the ΔC_ps observed for duplex formation by ITC at high and low ionic strength. We discuss our results in light of the larger issue of contributions to ΔC_p from coupled equilibria and conclude that observed ΔC_ps can be useful indicators of intermediate states in nucleic acid folding phenomena.

Phase transitions within systems of many weak interactions are generally associated with a significant change in heat capacity (1–3). Macromolecular folding events are examples of such transitions, and heat capacity changes (ΔC_ps) have been measured for folding in many proteins (summarized in ref 4) and an increasing number of nucleic acids (5). When ΔC_p is large relative to ΔS for the same transition, the ΔC_p can significantly perturb fold stability (ΔG) as a function of temperature (6). Large ΔC_ps can result in the phenomenon of cold denaturation, as observed for proteins (7–9) and recently for RNA (10, 11). Usually, ΔC_p is thought to arise from solvent effects that accompany the burial of hydro-phobic and/or aromatic surfaces upon folding. In nucleic acids, residual stacking in the single-stranded state is also temperature dependent (Figure 1 and refs 12–22) and may reduce the amount of aromatic surface exposed in the unfolded state under some conditions, thus complicating the interpretation of observed ΔC_ps. While ΔC_ps associated with protein folding have been investigated in great detail (e.g., ref 23 and references cited therein), there have been fewer systematic studies of the ΔC_p of nucleic acid folding (6, 11, 12, 20, 21, 24–30).

FIGURE 1.

Coupling of single strand stacking equilibria to nucleic acid duplex formation. (A) Schematic depicting the formation of duplex from component strands S1 and S2. Each strand participates in an equilibrium between unstacked (U) and stacked (S) states. Strand stacking is coupled to duplex formation, so duplex composed of unstacked strands is bracketed to indicate that it is a virtual state. (B) Equation showing the components of ΔC_p observed for duplex formation at a given temperature. ΔC_p^dock refers to the intrinsic ΔC_p for helix formation from stacked strands; the second term refers to the intrinsic ΔC_p for conversion of single strands from unstacked to stacked states weighted by the fraction of unstacked strands. Here, ΔC_p^U→S is summed over contributions from both S1 and S2; the third term refers to the contribution to ΔC_p arising from the linkage of fluctuating intermediates that shift in fractional population as a function of duplex formation and is also summed over contributions from both strands. (C) Equation showing the dependence of the observed ΔC_p on temperature in the case of coupling to temperature-dependent equilibria. In addition to the phenomena shown in (B), fractional unfolding of single strands results in further temperature dependence of measured ΔHs that contribute to the observed ΔC_p.

The origin of ΔC_ps associated with protein folding has been thoroughly examined (4, 23, 31, 32). Empirically, the ΔC_p has been found to be proportional to the amount of hydrophobic surface area buried during folding (23). Methodes employing solute transfer data for small molecule model compounds (and an assumption of group additivity) can largely account for ΔC_ps of protein folding based on solvent exposure of nonpolar versus polar surfaces (33); these approaches do not directly transfer to nucleic acid systems (27, 34, 35). Whereas ΔC_p has been correlated with changes in solvent-exposed hydrophobic surface area, the underlying physical basis of this correlation lies in changes in the fluctuations of hydrogen-bonding patterns among solvating waters (36–38). More generally, the heat capacity of any macroscopic state arises from a balance between the extent of fluctuations among microscopic substates and the enthalpic/entropic differences between those substates (32). With regard to macromolecular folding processes, fluctuations can occur not only among solvating waters but also between intermediate folding states within an ensemble. In fact, when folding is coupled to such equilibria, one component of the total observed ΔC_p at any given temperature derives from the mere presence of fluctuation between linked intermediates of different enthalpy (32, 39). As shown in Figure 1B, this contribution exists above and beyond the intrinsic ΔC_ps associated with moving between intermediate states. Furthermore, temperature-dependent coupled equilibria (e.g., single strand unstacking in nucleic acids) may result in temperature dependence of measured ΔH values, as well as those for ΔS and ΔG, for a nominal folding transition (such as duplex formation). This temperature dependence in ΔH contributes to estimates of ΔC_p deriving from measurements of ΔH at different temperatures (Figure 1C). Contributions to the observed ΔC_p deriving from coupled equilibria may be prominent in the case of nucleic acid duplex folding at physiological temperatures (25–37 °C), where partially structured intermediates may be abundant (20). Even for the seemingly simple process of duplex folding, experimentally observed ΔC_ps may therefore arise from a combination of intrinsic effects and those deriving from the linkage and temperature dependence of intermediate states. Measuring and understanding all such contributions is essential to accurately predicting the thermodynamics of duplex formation at physiological temperature.

Although the physical origins of ΔC_ps in nucleic acid folding have been far less studied, they certainly overlap with those that apply to proteins. Since duplex formation is typically coupled to some amount of base stacking (i.e., net stacking is greater in the folded duplex than in the unfolded single strands), one would therefore expect to observe duplex folding ΔC_ps that correspond to the release of waters solvating the aromatic surfaces of unstacked bases. ΔC_p effects are nevertheless frequently ignored in nucleic acid studies (40).

The polyanionic nature of DNA and RNA phosphodiester backbones may add further complexity to the relationship of nucleic acid ΔC_ps with solution conditions. The highly negative backbones attract a dense atmosphere of condensed counterions. These ions are typically necessary for higher order folding (41) and have a major impact on the thermodynamics of folding (42, 43). Theoretical treatments applying counterion condensation and Poisson–Boltzmann theories to the issue of duplex folding ΔC_ps have disagreed about the extent to which electrostatic effects contribute to the ΔC_p (6, 35, 44, 45). We recently observed that the ΔC_ps observed by isothermal titration calorimetry (ITC)¹ for the formation of a pair of RNA duplexes strongly depended on solution ionic strength (46). Furthermore, the magnitude of the ΔC_p per base pair differed substantially between the two duplexes, suggesting a marked sequence dependence and challenging the convention of applying a constant per base pair approximation of ΔC_p (6, 20, 29). As supported by differential scanning calorimetry (DSC) measurements, these ITC results could be interpreted on the basis of salt-dependent changes in residual structure of the single strands, consistent with ΔC_p contributions from temperature-dependent coupled equilibria and linkage effects.

Here, we report the results of a more thorough investigation of the contribution of salt- and sequence-dependent effects on single strand structure to ΔC_ps observed by ITC. We have applied ITC, DSC, circular dichroism (CD), and optical melting methods to a series of five DNA duplexes. The duplexes were designed to exhibit varying degrees of single-stranded stacking. We found that ΔC_ps observed by ITC could be accounted for entirely by progressive melting of the single strands; in fact, by measuring the thermodynamics of single strand melting, we could quantitatively predict the ΔC_p observed by ITC. Thus, both salt- and sequence-dependent effects on ΔC_p were tied to the phenomenon of single-stranded stacking. We discuss our results in light of recent theoretical descriptions of the molecular basis for changes in ΔC_p and consider the implications for thermodynamically based structure prediction algorithms.

MATERIALS AND METHODS

Preparation of Oligonucleotides

RNAs were chemically synthesized (Dharmacon, Inc.), deprotected according to the manufacturer's protocol, and resuspended in water. DNAs were also chemically synthesized (Integrated DNA Technologies, Inc.), deprotected and desalted by the manufacturer, and resuspended in water. The purity of the deprotected RNA and DNA oligonucleotides was assessed by denaturing PAGE and MALDI-TOF and deemed ≥95%. Concentrations of stock and sample solutions were determined from the absorbance at 260 nm using extinction coefficients calculated from the sequences (47).

Circular Dichroism Spectroscopy

CD spectra were collected on a Jasco J-715 spectropolarimeter using a 0.1 cm path length quartz cuvette and a Peltier device for temperature control. Accumulations of 10 spectra were averaged, collecting from 200 to 300 nm at 100 nm min⁻¹, 1 nm bandwidth, and 0.5 s response time. DNA samples were prepared at 100 μM strand concentration in 10 mM sodium cacodylate, pH 6.6, and 0.1 or 1.0 M added NaCl. Prior to data collection at 25 °C, samples were heated at 95 °C for 2 min, cooled ambiently for 30 min, and then preequilibrated at 25 °C for 10 min.

Isothermal Titration Calorimetry

A VP-ITC titration calorimeter (MicroCal, Inc.) was used for all measurements. Samples were prepared by diluting a small volume of stock into 10 mM NaHEPES, pH 7.5, and 0.1, 0.4, or 1.0 M added NaCl. The syringe and sample cell DNAs were prepared in matched buffers to minimize background heats of dilution. All buffers were prepared from stock solutions on the day of use and extensively degassed under vacuum. Samples were heated at 95 °C for 2 min and cooled ambiently at least 30 min prior to data collection. After an initial 2 μL injection to counteract backlash in the autotitrator (48), ITC experiments consisted of eleven 10 μL injections followed by approximately fifteen 15 μL injections of oligonucleotide at 75 μM into 1.4 mL of the complementary strand at 5 μM. This variable injection method ensured good data coverage of the critical lower baseline and transition regions while saving time during collection of the long, linear upper baseline. Sample stirring was set at 310 rpm for all measurements. All samples pertaining to a given temperature series (i.e., used to calculate a given ΔC_p) were split from one larger sample. By using this method, small errors in sample concentration would contribute only to the absolute ΔH but not substantially to the variation in ΔH with temperature. Reported data reflect titration of duplex S2 strands into their S1 counterparts. Control experiments inverting the direction of titration revealed no significant differences. Titration data were collected at 15, 25, 35, and 45 °C.

ITC data were analyzed with ORIGIN software (MicroCal Inc., version 7.0). The raw thermogram data were integrated and normalized, resulting in a plot of ΔH (mol of injectant)⁻¹ versus molar ratio. In each experiment, a long upper baseline was collected after the binding transition of the duplexes had been saturated. The terminal ~10 points (i.e., the clearly linear portion) of the upper baseline in each experiment were fit to a straight line, which was subsequently subtracted from the entire data set to remove contributions from background heats of mixing and dilution. A total ΔH for each reaction was obtained by nonlinear least-squares fitting of the plot of ΔH (mol of injectant)⁻¹ versus molar ratio to a single site binding model (49) to obtain ΔH, K_A, and the reaction stoichiometry, n, for duplex formation under each condition. For simple duplex formation, the expected n = 1. Across all of the ITC experiments, n = 0.98 ± 0.06. Experiments were designed such that the c-value (c = K_A[nucleic acid]n) lay in the preferred range, between 1 and 1000 (49). Observed ΔC_ps were calculated by fitting plots of observed ΔH versus T to a line (Kaleidagraph; Synergy Software, Inc.), where the fitted slope corresponded to a linear approximation of ΔC_p. Errors in observed ΔC_ps were estimated both from fitting error and from estimated upper limits on error in spectroscopically measured sample concentrations.

Differential Scanning Calorimetry

An ETR-VP-DSC differential scanning calorimeter (MicroCal, Inc.) was used for all of the DSC experiments. The DSC samples at 50 μM duplex were loaded into a 0.513 mL sample cell. Oligo-nucleotides used in DSC experiments were prepared from stocks originally resuspended in the buffer to be used for the experiment. Complementary oligonucleotides were diluted into buffer (10 mM NaHEPES and 0.1 or 1.0 M added NaCl) and heated 2 min at 95 °C. The samples were cooled ambiently and then allowed to equilibrate at 20 °C. All samples were degassed under vacuum. The DSC reference cell contained a buffer matched to the one in which the sample was dissolved. After an initial cycle against buffer to establish thermal history, thermal scan data were collected on buffer blanks and on nucleic acid samples. Thermal scans were measured from 2 to 90 °C (duplexes at 0.1 M added NaCl) or from 2 to 100 °C (duplexes at 1.0 M added NaCl), scanning at a rate of 90 °C h⁻¹ with a 15 min preequilibration prior to each thermal cycle. Samples, preequilibrated at 20 °C, were loaded in cycle between 25 and 15 °C. Data were collected only for cycles of increasing temperature. Data were analyzed using ORIGIN software (MicroCal Inc., version 7.0). Raw data were corrected by subtraction of a buffer blank scan and then normalized by the molar concentration of the duplex. Multiple scans were compared by normalizing pretransition baselines to zero C_p. Thermal scans were further analyzed by nonlinear least-squares fitting to a two-transition, two-state model where the first transition accommodated a lower temperature, lower enthalpy “premelting” event evident as a premelting tail in the observed peaks. Such premelting transitions have been previously observed and analyzed in DSC studies of similar DNA duplexes (21, 50). The second transition included a ΔC_p fitting parameter.

Optical Melting

Samples were prepared by dilution of stock solutions into buffers containing 10 mM NaHEPES, pH 7.5, and 0.1 or 1.0 M added NaCl. All samples were heated at 95 °C for 2 min and cooled ambiently for at least 30 min prior to data collection. Duplex samples (consisting of equimolar mixtures of strands S1 and S2 for a given duplex) were collected at 0.5–15 μM total strand concentration. Single strand samples were collected at 2.5 μM strand concentration. Samples were housed in 1 cm path length quartz cuvettes. Thermal melting data were collected on a Varian Cary 100 Bio UV/visible spectrometer with temperature controlled by a Peltier device. Sample absorbance was monitored at 260 nm while temperature was ramped at 1 °C min⁻¹, typically between 2 and 90 °C for duplexes or 2 and 70 °C for single strands. All melt data were collected in duplicate or triplicate.

Melting curves were directly fit to a double-baseline, two-state model for van't Hoff estimates of ΔH and T_M:

A260=(miT+bi)(1−α)+(mfT+bf)α 1

where A₂₆₀ is the optical absorbance at 260 nm, m and b are slope and baseline parameters, and α is the fraction folded:

α=exp⁡(ΔHR(1TM−1T))1+exp⁡(ΔHR(1TM−1T)) 2

For single strands, subsequent analysis was conducted using the directly fit van't Hoff ΔH and T_M. For duplexes, the fitted T_Ms corresponding to melts done at 0.5–15 μM total strand concentration were used to generate a plot of T_M⁻¹ versus ln(C_T/4), where C_T is the total strand concentration. The plots were fit to a line by least-squares analysis, and the van't Hoff ΔH and ΔS were extracted from the slope and intercept of the line according to the relationship (43, 51):

1TM=RΔHln⁡(CT/4)+ΔSΔH 3

The extracted parameters could be used to predict T_M at arbitrary strand concentrations by substituting the desired C_T into eq 3 and solving for T_M. Errors on reported values were based on propagated fitting error and/or reproducibility over replicate measurements.

Prediction of ΔC_ps Observed by ITC Using Fractional Enthalpies of Single Strand Melting

Estimates of temperature-dependent enthalpic contributions based on unfolding of single strands were made by using van't Hoff values for ΔH and T_M acquired from direct curve fitting of thermal melt data for the strands. Fitted van't Hoff parameters were substituted into eq 2 to obtain the fraction unfolded (f^unfold, which is equivalent to 1 – α) at a given temperature. The fractional extent of unfolding was multiplied by the van't Hoff molar ΔH for unfolding to obtain the fractional enthalpic contribution as a function of temperature:

funfold(T)ΔH=fΔH(T) 4

Profiles of fractional enthalpic contributions relevant to any given ITC experiment were generated by summing the contributions of the two component strands as calculated from eq 4, using van't Hoff parameters for single strand melting collected under buffer conditions identical to those used in the ITC experiment. Although such profiles were sufficient to predict ΔC_p, it was useful to add to the profile for fractional single strand unfolding a constant parameter for helix formation from completely stacked single strands, ΔH^dock. In this way, individual ΔH values observed by ITC could be compared directly to the predicted ΔHs:

ΔHpredicted(T)=ΔHdock+fΔH(T) 5

Appropriate values for ΔH^dock were estimated by subtracting f^ΔH(15 °C) from the ΔH observed by ITC at 15 °C and correcting for the small difference in f^ΔH at 15 °C versus its low-temperature asymptote.

RESULTS

Design of DNA Duplexes with Strands of Varying Stacking Propensity

We previously found that the observed ΔC_p for formation of RNA duplexes was significantly dependent on solution ionic strength and varied considerably (per base pair) as a function of sequence (46). These results prompted us to explore in more detail the underlying physical basis for the salt- and sequence-dependent heat capacity changes. As previously suggested by others (20, 21), we noted that the observed ΔC_ps could possibly be accounted for by changes in single strand stacking across the temperature range probed by ITC. We therefore hypothesized that the dependence of ITC-detected ΔC_ps on ionic strength and on sequence reflected changes in single-stranded stacking in each case. To quantitatively explore this phenomenon, we designed a series of 13-mer DNA duplexes and subjected them to analysis by CD, ITC, DSC, and optical melting.

The five DNA duplexes used in this study are shown in Figure 2. Each duplex possesses identical GC content as a percentage of total base pair composition, and the predicted T_Ms all lie within about 1.5 °C of one another. Furthermore, all duplexes feature identical three base pair GC termini (indicated by gray boxes in Figure 2) to minimize possible differences in “fraying” behavior. Imposed on this background of similarity, however, we intended to compose the duplexes of single strands that systematically differed in stacking propensity. To modulate the stacking propensity, we varied the number and contiguity of purines (boldfaced in Figure 2) in the strands to create “purine islands” that might serve as nucleation centers for single strand stacking. We predicted little stacking propensity for strand S2 in any of the duplexes. Our design is most clearly evident in S1 strands across the series. Thus, strand D-I S1 contains seven contiguous purines within its variable region, whereas strand D-V S1 contains four discontiguous purines, precluding purine–purine stacking. Intermediate cases raised interesting questions. For example, whereas strands D-III S1 and D-IV S1 both possess islands of three purines, D-III S1 also features two additional flanking purines within the variable region, just beyond single pyrimidine interruptions. Would any stacking engendered by a stretch of three contiguous purines be sufficient to bridge the pyrimidine interruptions to form a more extensive stack and thereby affect duplex folding thermodynamics? Finally, to test for effects that might be due to duplex helical geometry (i.e., A-form versus B-form), we included an RNA version of duplex D-I, called R(D-I).

FIGURE 2.

Duplexes used in these studies. DNA duplexes are denoted D-I through D-V. An RNA version of D-I is denoted R(D-I). The component strands of each duplex are labeled S1 and S2. Invariant terminal regions of the DNA duplexes and R(D-I) are indicated by gray boxes. Purines are indicated by boldfaced nucleotides. As one moves from D-I to D-V in the series of DNA duplexes, purines decrease in number and/or contiguity within the variable region of S1 in each duplex, a design feature intended to systematically reduce stacking propensity within those strands. These variations in purine content were made such that the total GC content of all duplexes remained constant, as did the overall stability; all duplexes exhibit experimental T_Ms within a few degrees of one another

CD of Single Strands Suggests That Designed Purine Islands Confer Salt-Dependent Stacking

To assess the amount of salt-dependent, single strand structure actually conferred by our approach, we subjected each strand to CD at 25 °C and 0.1 or 1.0 M added NaCl. As shown in Figure 3A, strand D-I S1 (containing an island of seven contiguous purines) shows a large response to added NaCl, whereas strand D-V S1 exhibits a much smaller salt-dependent change. Like strand D-V S1, S2 strands of the same two duplexes appear much less structurally responsive to added NaCl (Figure 3B). These spectra were entirely consistent with our hypothesis and intended design. Other strands showed intermediate behavior, also consistent with our design.

FIGURE 3.

Structural response of DNA strands to added NaCl as observed by CD. (A) Spectra for D-I S1 at 0.1 and 1.0 M added NaCl (thick dashed and solid lines, respectively) and for D-V S1 at 0.1 and 1.0 M added NaCl (thin dashed and solid lines, respectively). Strand D-I S1 responds more to added NaCl, consistent with the greater stacking propensity conferred by a contiguous stretch of purines. (B) Spectra for D-I S2 at 0.1 and 1.0 M added NaCl (thick dashed and solid lines, respectively) and for D-V S2 at 0.1 and 1.0 M added NaCl (thin dashed and solid lines, respectively). Neither strand shows significant response to added salt, consistent with a lack of stacking propensity conferred by the absence of contiguous purines within those strands. All samples in (A) and (B) contained 10 mM sodium cacodylate, pH 6.6. Strand concentrations were 100 μM, and spectra were collected at 25 °C.

ITC of Designed Duplexes Reveals Salt- and Sequence-Dependent ΔC_ps

We used ITC to measure the ΔH associated with formation of duplexes D-I through D-V at temperatures between 15 and 45 °C and at 0.1, 0.4, and 1.0 M added NaCl (Figure 4 and Table 1). For all duplexes, observed ΔC_ps varied to some degree as a function of added NaCl (though not clearly so in the case of duplex D-V), in line with our previous results for RNA duplexes (46). Significant differences in observed ΔC_ps became apparent between duplexes as a function of added NaCl. Differences were most evident at 1.0 M added NaCl, where the rank ordering of observed ΔC_ps matched that predicted from our single strand stacking hypothesis, as reflected in our duplex design. Notably, despite the fact that all five DNA duplexes shared identical GC content and virtually identical stability, the per base pair ΔC_ps observed at 1.0 M added NaCl varied 2-fold, from 60 to 120 cal mol⁻¹ K⁻¹ bp⁻¹. These per base pair values are similar to those previously reported for DNA duplexes (6) but underscore the potential danger of assigning a constant per base pair ΔC_p to the duplex folding process. Titrations of an RNA version of duplex D-I [listed as R(D-I) in Table 1] showed similar results to those observed for D-I, supporting the idea that salt-dependent changes in observed ΔC_p derive in general from single strand effects, as opposed to the specifics of helical geometry or other such parameters.

FIGURE 4.

(A) Representative data for ITC of DNA duplexes. A 75 μM solution of D-I S2 was titrated into 1.4 mL of a 5 μM solution of D-I S1. Solutions were equilibrated at 45 °C. Both DNAs were in 10 mM NaHEPES, pH 7.5, and 1 M added NaCl. The upper panel shows the raw thermogram. The lower panel shows integrated injection data (solid squares) and a least-squares fit of the data to a one-site binding model (solid line), yielding the following parameters: ΔH = −84.4 kcal mol⁻¹; ΔS = −128 cal mol⁻¹ K⁻¹; K_A = 1.1 × 10⁸ M⁻¹; n = 0.95; c = 522. Values of K_A and ΔS have relatively large errors due to the high c-value. Data collection parameters were designed to optimize the accuracy of ΔH and ΔC_p to facilitate the comparisons relevant to this study. (B) Plot of ΔH values observed by ITC for formation of duplex D-I at 0.1 M added NaCl (solid circles), 0.4 M added NaCl (solid squares), and 1.0 M added NaCl (solid triangles). Dashed lines represent linear least-squares fits of each data series; the slope of each fit corresponds to a linear approximation of the observed ΔC_p. (C) Plot of ΔH values observed by ITC for formation of duplex D-V. All conventions are the same as in (B).

Table 1.

Summary of Thermodynamic Data^a,^b for Duplexes D-I through D-V and R(D-I) from ITC,^c DSC,^d and Optical Melting^e

duplex	parameter	0.1 M NaCl	0.4 M NaCl	1 M NaCl
D-I	ΔHITC(15 °C)	59	48	41
	ΔHITC(25 °C)	67	64	54
	ΔHITC(35 °C)	77	79	74
	ΔHITC(45 °C)	85	85	84
	ΔCpITC(15–45 °C)	0.9 ± 0.1	1.3 ± 0.2	1.5 ± 0.1
	ΔHDSC(TM)	111 ± 2 (63 °C)		97 ± 2 (69 °C)
	ΔCpDSC (TM)	0.88 ± 0.02		1.14 ± 0.02
	ΔHUV(vH)	105 ± 12		112 ± 11
	ΔSUV(vH)	291 ± 30		303 ± 30
	TMvH at 10, 100 μM CT	58, 62 ± 1 °C		66, 71 ± 1 °C
	ΔΔHDSC-ITC(TMDSC)f	10 ± 4 (63 °C)		−23 ± 5 (69 °C)
	ΔΔHDSC-ITC(35 °C)g	≈9		≈−16
	ΔΔHUV-ITC(TMUV)h	8 ± 13 (58 °C)		−4 ± 12 (66 °C)
D-II	ΔHITC(15 °C)	50	48	42
	ΔHITC(25 °C)	63	61	52
	ΔHITC(35 °C)	72	77	69
	ΔHITC(45 °C)	78	86	82
	ΔCpITC(15–45 °C)	0.9 ± 0.1	1.3 ± 0.1	1.4 ± 0.1
	ΔHUV(vH)	119 ± 17		105 ± 7
	ΔSUV(vH)	337 ± 50		285 ± 20
	TMvH at 10, 100 μM CT	55, 60 ± 1 °C		66, 71 ± 1 °C
	ΔΔHUV-ITC(TMUV)h	32 ± 18 (55 °C)		−6 ± 8 (66 °C)
D-III	ΔHITC(15 °C)	56	50	46
	ΔHITC(25 °C)	68	62	58
	ΔHITC(35 °C)	82	75	74
	ΔHITC(45 °C)	89	89	84
	ΔCpITC(15–45 °C)	1.1 ± 0.1	1.3 ± 0.1	1.3 ± 0.1
	ΔHUV(vH)	114 ± 12		112 ± 11
	ΔSUV(vH)	320 ± 30		305 ± 30
	TMvH at 10, 100 μM CT	58, 62 ± 1 °C		66, 71 ± 1 °C
	ΔΔHUV-ITC(TMUV)h	11 ± 13 (58 °C)		1 ± 12 (66 °C)
D-IV	ΔHITC(15 °C)	68	67	60
	ΔHITC(25 °C)	81	75	70
	ΔHITC(35 °C)	91	86	82
	ΔHITC(45 °C)	96	96	93
	ΔCpITC(15–45 °C)	0.9 ± 0.1	1.0 ± 0.1	1.1 ± 0.1
	ΔHUV(vH)	102 ± 9		103 ± 9
	ΔSUV(vH)	283 ± 20		276 ± 20
	TMvH at 10, 100 μM CT	59, 64 ± 1 °C		68, 74 ± 1 °C
	ΔΔHUV-ITC(TMUV)h	−7 ± 10 (59 °C)		−15 ± 11 (68 °C)
D-V	ΔHITC(15 °C)	62	58	44
	ΔHITC(25 °C)	75	64	50
	ΔHITC(35 °C)	86	72	56
	ΔHITC(45 °C)	95	80	67
	ΔCpITC(15–45 °C)	1.1 ± 0.1	0.8 ± 0.1	0.8 ± 0.1
	ΔHDSC(TM)	113 ± 2 (64 °C)		111 ± 2 (71 °C)
	ΔCpDSC(TM)	1.08 ± 0.02		0.89 ± 0.02
	ΔHUV(vH)	108 ± 22		104 ± 10
	ΔSUV(vH)	301 ± 60		280 ± 30
	TMvH at 10, 100 μM CT	59, 64 ± 1 °C		68, 73 ± 1 °C
	ΔΔHDSC-ITC(TMDSC)f	−3 ± 3 (64 °C)		23 ± 3 (71 °C)
	ΔΔHDSC-ITC(35 °C)g	≈−4		≈23
	ΔΔHUV-ITC(TM UV) h	−2 ± 23 (59 °C)		19 ± 12 (68 °C)
R(D-I)	ΔHITC(15 °C)	54		54
	ΔHITC(25 °C)	62		67
	ΔHITC(35 °C)	71		79
	ΔHITC(45 °C)	81		92
	ΔCpITC(15–45 °C)	0.9 ± 0.1		1.3 ± 0.1

^aAll values are reported for the duplex unfolding transition.

^bΔHs are reported as kcal mol ⁻¹, ΔC_ps are reported as kcal mol⁻¹ K⁻¹ , and ΔSs are reported as cal mol⁻¹ K⁻¹ .

^cThe estimated error for all individual ΔH^ITC data points is ±2 kcal mol⁻¹, based on replicate measurements inverting the direction of titration.

^dThe reported error for ΔC_p^DSC is the least-squares fitting error, which is certainly a gross underestimate of the actual error deriving from uncertainty in the subjective selection of pre- and posttransition baselines. The actual error in ΔC_p^DSC is more realistically on the order of 30%, based on the variation of that fitted parameter across multiple fits employing different baseline selections.

^eΔH^vH and ΔS^vH values were obtained from plots of TM ⁻¹ versus ln(C_T/4) for optical melts of duplexes, where ΔH^vH and ΔS^vH are extracted from the slope and intercept of linear fits to the data (see Materials and Methods); errors for these parameters were assigned on the basis of the least-squares fitting error for the slope and intercept. Whereas errors in ΔH^vH and ΔS^vH can be quite large, they are also correlated with one another such that errors in TMs predicted from ΔH^vH and ΔS^vH are much smaller.

^fΔΔH^DSC-ITC (T_M^DSC) values were calculated by taking the difference between ΔH^DSC and ΔH^ITC extrapolated to the DSC T_M using ΔC_p^ITC.

^gΔΔH^DSC-ITC (35 °C) values were calculated by taking the difference between ΔH^DSC extrapolated to 35 °C using ΔC_p^DSC and the actual experimental value of ΔH^ITC at 35 °C. Due to the significant error actually associated with fitted ΔC_p^DSC parameters, ΔΔH^DSC-ITC (35 °C) values are simply reported as approximate quantities.

^hΔΔH^UV-ITC (T_M^UV) values were calculated by taking the difference between ΔH^UV and ΔH^ITC extrapolated to the UV T_M (at 10 μM C_T) using ΔC_p^ITC.

DSC Analysis of Duplexes D-I and D-V Is Largely Consistent with the Salt and Sequence Dependence of ITC-Detected ΔC_ps

Whereas ITC-derived thermodynamic parameters are relevant to temperatures selected by the experimenter during data collection, parameters determined by DSC analysis are relevant at the observed T_Ms, which typically occur at much higher temperature. We therefore subjected duplexes D-I and D-V to DSC at 0.1 and 1.0 M added NaCl in order to compare the results with those obtained in the lower temperature ITC experiments. Results are shown in Figure 5 and Table 1.

FIGURE 5.

DSC data for duplexes D-I and D-V at 0.1 and 1.0 M added NaCl. (A) Duplex D-I in 0.1 M added NaCl; (B) duplex D-I in 1.0 M added NaCl; (C) duplex D-V in 0.1 M added NaCl; (D) duplex D-V in 1.0 M added NaCl. All samples contained 50 μM duplex and 10 mM NaHEPES, pH 7.5. In each panel, the solid line represents actual melting data that has been background corrected and normalized for sample concentration; the dashed line represents a nonlinear least-squares fit of the data to a two-transition, two-state model as described in Materials and Methods.

The duplex melting transitions were amenable to fitting by a two-transition model, involving a lower temperature “premelting” transition and a major, “melting” transition. Previous DSC studies of short DNA duplexes observed similar behavior, a phenomenon attributed to premelting transitions involving either duplex bending (50) or a combination of fraying and twisting (21). We therefore fit the data to two transitions, allowing for a ΔC_p only in the second transition. Fitting ΔC_ps for both transitions revealed strong covariation between ΔC_p 1 and ΔC_p 2, typically summing to the same quantity observed for fitting to a single ΔC_p assigned to the second transition. Reasonable fits were obtained as indicated by dotted lines in Figure 5. Both duplexes exhibited an expected increase in T_M at higher NaCl concentration. The total ΔH summed over both transitions was higher in all cases than those observed at the lower temperatures probed by ITC (15–45 °C), consistent with the presence of a ΔC_p for duplex formation. Fitted DSC ΔC_ps all fell within the range of 0.8–1.1 kcal mol⁻¹ K⁻¹, values that are essentially the same within uncertainty. At low NaCl concentrations and for sequences with low single-stranded stacking propensity, the ΔC_p observed by DSC was similar to the corresponding one measured by ITC. In the case of duplex D-I at 1.0 M added NaCl, however, the ΔC_p observed by DSC is substantially smaller than that measured by ITC, possibly indicating that the single strand stacking equilibria which were hypothesized to contribute heavily to the ΔC_p at lower temperatures are less influential at higher temperature. If the strands were largely unstacked at the T_M, then coupled stacking equilibria would contribute less significantly to the observed ΔC_p. One consequence of this situation is that extrapolations of ΔH to lower temperature, using the ΔC_p observed by DSC, would not reflect the increased stacking interactions actually present. We note that ΔC_ps deriving from fits to DSC data are heavily dependent on somewhat subjective selections of pre- and posttransition baselines. Therefore, we hesitate to excessively interpret the DSC data. Our DSC results are, however, consistent with those previously obtained for similar DNA duplexes (20, 21).

Optical Melting of Duplexes Yields T_Ms and ΔHs in Agreement with DSC

By far the most common method for obtaining thermodynamic parameters for duplex melting is optical melting (43, 51). We subjected duplexes D-I through D-V to optical melting across a 30-fold range of strand concentrations. Representative melting data for duplexes D-I and D-V (along with melting data for their component strands) are shown in Figure 6A,B. We fit observed duplex transitions in order to obtain the T_M at each strand concentration. From the resulting data set (and as described in Materials and Methods), we generated plots of T_M⁻¹ versus ln(C_T/4) to obtain van't Hoff measurements of the ΔH and ΔS associated with duplex melting (Figure 6C,D and Table 1). Within error, the van't Hoff estimates of ΔH agreed with those obtained by DSC. In addition, the T_Ms predicted by the van't Hoff analysis for strand concentrations used in the DSC experiments agreed within 2 °C (typically less) of those actually observed. Therefore, DSC and optical melting measurements of duplex melting appear to report consistent thermodynamic parameters relevant to observed T_Ms but at odds with those observed at lower temperatures by ITC.

FIGURE 6.

Representative optical melting data at 260 nm and van't Hoff analysis, shown for duplexes D-I and D-V. Samples are in 10 mM NaHEPES, pH 7.5, and 1.0 M added NaCl. Melting data (circles) in (A) and (B) have been normalized for direct comparison and shown with two-state fits (solid line). (A) Data for thermal melting of 2.5 μM duplex D-I and for component strands D-I S1 and D-I S2, each at 2.5 μM. (B) Data for thermal melting of 2.5 μM duplex D-V and for component strands D-V S1 and D-V S2, each at 2.5 μM. (C) Plot of T_M⁻¹ versus ln(C_T/4) for duplex D-I, reflecting thermal melts conducted at 0.5–15 μM C_T, where solid circles represent individual melting experiments. The solid line represents a linear least-squares fit of the data to a van't Hoff model, as described in Materials and Methods, van't Hoff estimates of ΔH and ΔS for duplex melting are extracted from the fitted slope and intercept and reported in Table 1. (D) Plot of T_M⁻¹ versus ln(C_T/4) for duplex D-V. All conventions are the same as in (C).

Single Strand Optical Melting Parameters Allow Accurate Prediction of ΔC_ps Observed by ITC

To assess the contributions of salt- and sequence-dependent stacking equilibria on the ΔH and ΔC_p observed by ITC, we directly curve-fit single strand melting profiles collected by optical melting to a van't Hoff model for a unimolecular transition. Since ITC-detected reaction stoichiometries were all 1:1 and reported similar enthalpies of duplex formation regardless of the direction of titration, we were confident that neither single strand formed homomeric complexes at even the highest concentrations used in the study. The fitting produced a series of T_Ms and van't Hoff ΔH values for the single strands melting at 0.1 and 1.0 M added NaCl (Table 2). From the fitted parameters, we calculated the fractional extents of single strand melting as a function of temperature and, therefore, could extract the enthalpic contribution of coupled single strand equilibria at any given temperature. From this information we obtained the contributions to ΔH from single strand structural rearrangements at the temperatures explicitly probed in the ITC experiments (15, 25, 35, and 45 °C). Remarkably, the temperature dependence of observed ΔHs predicted solely from the fractional extent of single strand melting accurately predicted the ΔC_ps observed by ITC for all duplexes at both high and low concentrations of NaCl (Table 3 and Figure 7). Such close agreement strongly supports our hypothesis that the salt and sequence dependence of ΔC_ps observed by ITC derive from perturbations to the same fundamental phenomenon: stacking propensity within single strands.

Table 2.

vant Hoff Measurements of ΔH and T_M for Single Strand Melting of Component Strands^a

	0.1 M NaCl		1.0 M NaCl
strand	ΔHvH (kcal mol−1)	TM(°C)	ΔHvH (kcal mol−1)	TM(°C)
D-I S1	36.5 ± 0.7	9.0 ± 0.4	40.1 ± 0.7	25.7 ± 0.3
D-I S2	23.4 ± 0.5	34.9 ± 0.2	21 ± 2	45.6 ± 0.9
D-II S1	31.0 ± 0.5	14.8 ± 0.3	29 ± 1	28.8 ± 0.5
D-II S2	24.8 ± 0.2	44.5 ± 0.2	31 ± 1	44.1 ± 0.3
D-III S1	35 ± 5	10 ± 2	30 ± 2	26 ± 1
D-III S2	26.0 ± 0.2	39.6 ± 0.1	27.0 ± 0.7	44.0 ± 0.2
D-IV S1	NDb	NDb	30 ± 4	42 ± 1
D-IV S2	18.6 ± 0.5	37.5 ± 0.3	24 ± 1	43.5 ± 0.4
D-V S1	19 ± 5	27 ± 3	18 ± 2	32 ± 3
D-V S2	28.9 ± 0.7	41.0 ± 0.3	25 ± 1	46.7 ± 0.3

^aParameters derive from direct curve fitting of optical melting profiles. All samples contained 2.5 μM strand, 10 mM NaHEPES, pH 7.5, and 0.1 or 1.0 M added NaCl.

^bND: not determined due to the small Δє and low temperature of the single strand melting transition.

Table 3.

Comparison of ΔC_ps Observed by ITC with Those Predicted from Single Strand Melting^a

	0.1 M NaCl		1.0 M NaClM
duplex	ΔCpITC	fΔHΔCppredict	ΔCpITC	fΔHΔCppredict
D-I	0.9 ± 0.1	0.8 ± 0.1	1.5 ± 0.1	1.6 ± 0.2
D-II	0.9 ± 0.1	0.9 ± 0.1	1.4 ± 0.1	1.4 ± 0.1
D-III	1.1 ± 0.1	0.8 ± 0.2	1.3 ± 0.1	1.3 ± 0.1
D-IV	0.9 ± 0.1	ND	1.1 ± 0.1	1.0 ± 0.2
D-V	1.1 ± 0.1	1.0 ± 0.2	0.8 ± 0.1	0.7 ± 0.2

^aValues are presented for the unfolding reaction in kcal mol⁻¹ K⁻¹

FIGURE 7.

Comparison of ΔHs for duplex formation observed by ITC, DSC, and optical melting with those predicted from single strand melting alone. (A) Schematic of the calculation of ΔH^prcdict(T) from ΔH^dockand f^ΔH(T) as described in Materials and Methods; (B) duplex D-I at 1.0 M NaCl; (C) duplex D-V at 1.0 M added NaCl; (D) duplex D-I at 0.1 M added NaCl. In each case, the solid black line represents ΔH^prcdict = ΔH^dock + f^ΔH and turns into a dashed line at higher temperatures to indicate that reliable ITC data cannot be collected close to the T_M. Solid shapes represent experimental ΔHs from ITC (circles), optical melting (diamonds), or DSC (squares). Dotted lines represent extrapolations of ΔH(T) based on various estimates of ΔC_p: ITC ΔHs were extrapolated using ΔC_p^ITC; DSC ΔHs were extrapolated using ΔC_p^DSC; optical melting (UV) ΔHs were extrapolated using a constant 60 cal mol⁻¹ K⁻¹ bp⁻¹ estimate of ΔC_p.

Our results also highlight the potential for linear approximations of ΔC_p based on ITC data to yield values idiosyncratic to the temperature window chosen for study. Figure 8 simulates the change in observed ΔC_p for duplex D-I in 1.0 M added NaCl as a 30° experimental window (like those employed in our ITC studies of D-I through D-V) moves across the melting transitions of the component single strands.

FIGURE 8.

Model of the variation in observed values of ΔC_p^ITC as the center of a 30° experimental window moves across temperature. The model is based on single strand melting data for the component strands of duplex D-I in 10 mM NaHEPES, pH 7.5, and 1.0 M added NaCl. Dashed lines show the pronounced contribution of single strand melting to the observed ΔC_p within the temperature range usually targeted for structure prediction, 25–37 °C.

Coupled single strand unstacking events result in a strong nonlinear temperature dependence of the observed ΔC_p. Other temperature-dependent phenomena must contribute to the observed ΔC_p at higher temperatures (i.e., after the UV-detected single strand melting transitions are essentially complete) to explain the values derived from the thermal melting methods (DSC and UV). For example, progressive unstacking of single strands could continue at high temperature, consistent with the linearly sloping upper baselines evident in our single strand optical melting experiments (Figure 6A,B). Another possibility is that, at high temperature, the single-stranded species sample a very large number of alternate conformations, resulting in a significant increase in fluctuations in the unfolded state relative to the duplex. Since heat capacity ultimately derives from energetic fluctuation, such a situation is consistent with the presence of a high-temperature contribution to ΔC_p.

Our data support the idea of a component of ΔC_p that grows in at high temperature and becomes the dominant contribution to ΔC_p in thermal melting studies but which is negligible at low temperature. For example, ΔHs observed at the T_M (i.e., those measured by DSC and optical melting) are most often larger than those predicted from the lower temperature single strand melting transitions or observed by ITC (Figure 7 and Table 1). Furthermore, we observe significant ΔC_ps at the T_M for duplexes D-I and D-V by DSC. Since a high-temperature contribution to ΔC_p was physically plausible and supported by our data, we attempted to model the effects of a ΔC_p component that grows in at higher temperature (Figure 9). We globally fit our ITC, DSC, and UV data to a simple sigmoidal transition in ΔC_p (Figure 9 A) that would sum with the contribution made by fractional melting of the single strands. As seen in Figure 9B, a high-temperature ΔC_p component could explain the large ΔHs observed at the T_M without significantly affecting the close correspondence we observe between ΔH^predict and ΔC_p^ITC at lower temperatures.

FIGURE 9.

Results of global fitting analysis of a hypothetical increase in ΔC_p at higher temperatures, shown for duplex D-V in 10 mM NaHEPES, pH 7.5, and 1.0 M added NaCl. High-temperature ΔHs measured by optical melting and DSC cannot be accounted for by contributions from single strand melting. Some other, undefined factor(s) must contribute to the temperature dependence of ΔH (i.e., the observed ΔC_p). (A) To model the effects of such an undefined contributor to ΔC_p^obs, nonlinear least-squares minimization was used to optimize a sigmoidal increase with temperature in ΔC_p (triangles). The sigmoidal increase was added to the observed ΔC_p arising from single strand melting (circles), yielding ΔC_p^obs(T) (solid line). (B) To observe the effects of the modeled ΔC_p on the temperature dependence of ΔH, ΔC_p^obs(T) was integrated to obtain the corresponding profile of observed ΔH(T) (dotted line). Within this framework, we used global fitting to optimize the sigmoidal transition (panel A, triangles) for amplitude, width, and midpoint, constraining for the best fit with four parameters: ΔC_p^DSC (panel A, square), ΔH^DSC (panel B, square), ΔH^UV (panel B, diamond), and all ΔH^ITC points (panel B, circles). Although the model is certainly an oversimplification, clearly a high-temperature contribution to ΔC_p must exist in order to explain ΔC_p^DSC and to reconcile the disparity between observed ΔH^DSC/ΔH^UV values and the much smaller high-temperature ΔHs attributable to coupled single strand melting (panel B, solid/dashed line).

DISCUSSION

We have investigated the molecular basis for ΔC_ps associated with nucleic acid duplex formation. Spurred by an initial observation that ITC-detected ΔC_ps for a pair of RNA duplexes differed as a function of salt and sequence (46), we undertook a more extensive study with a series of designed DNA duplexes. This study was driven by the hypothesis that both ionic strength and sequence-dependent effects on observed ΔC_ps arose from modulation of the stacking propensity for single strands. This hypothesis was strongly supported by data from ITC, DSC, optical melting, and CD analysis of the duplexes and their component strands. Our results are consistent with the long-held notion that coupled single strand equilibria are major contributors to the overall thermodynamics of duplex formation. We show that such coupled equilibria so dominate the temperature dependence of the ΔH associated with strand association that parameters measured for melting of single strands quantitatively predict ΔC_ps, which also vary with temperature, observed by ITC for duplex formation in the 15–45 °C temperature range. Further, our results highlight the important challenge of refining thermodynamic models of nucleic acid structure so as to incorporate a realistic description of intermediate folding states at relevant temperatures.

Many studies have concluded that coupled equilibria of single strands can significantly perturb the observed thermodynamics of duplex formation (12–16, 19–21, 52–54). Structural equilibria of single strands will typically be more prominent at lower temperatures. As a function of coupled equilibria, observed ΔC_ps will therefore be temperature dependent and highly nonlinear, as shown in Figures 8 and 9A. At least in the case of the short DNA strands examined in this study, the single strand T_Ms produce a maximum in the observed ΔC_p very near the usual target temperature range for structure prediction. The maximum is coincident with the overall midpoint of the summed melting transitions for the single strands and is consistent with a physical picture wherein C_p derives from fluctuations between states (32, 39). As noted by Holbrook et al. (20), the large enthalpic contributions of temperature-dependent coupled equilibria make it desirable to reference thermodynamic parameters reported for nucleic acid association reactions to specific states of the component strands (e.g., stacked, unstacked). The impact of coupled equilibria is especially pronounced when attempting to calculate hybridization thermodynamics in the context of heterogeneous ensembles of strands (54), as is typically the case in microarray and PCR applications. Markham and Zuker have begun to address these issues by calculating hybridization thermodynamics from Boltz-mann distributions that explicitly consider coupled uni-molecular and bimolecular equilibria within a system (55).

The ability of fractional enthalpies associated with single strand melting to quantitatively predict ITC-detected ΔC_ps suggests that, within the temperature range probed by ITC, the intrinsic ΔC_p associated with docking of stacked strands is negligible. This result agrees with the previous analysis of Holbrook et al. for a 14-mer DNA duplex (20). For the most part, therefore, ΔC_ps for duplex formation measured at lower temperatures by ITC reflect the heat capacities of single strand melting transitions as opposed to differences in the intrinsic heat capacities of folded and unfolded states at those temperatures. This situation implies that, for the prediction of hybridization energies at 25 or 37 °C, one might be able to effectively use single-stranded melting behavior to account for the nonlinear temperature dependence of duplex ΔHs.

We observe substantial ΔC_ps by DSC for duplexes D-I and D-V, where the ΔC_ps pertained to T_Ms well above fitted single strand melting transitions. In the study mentioned above (20), ΔC_ps observed by DSC were attributed to high-temperature unstacking events inferred from the difference in UV absorbance seen for melted single strands versus that seen for the monomeric component nucleotides for each strand. Single strand melting transitions occurring at high temperatures (i.e., ≥60 °C) may therefore contribute to the ΔC_ps we observe by DSC. In addition, the extent of fluctuation between microscopic substates may be enhanced at higher temperatures, thereby increasing the contribution of linked enthalpy fluctuation (Figure 1B) to the total observed ΔC_p.

Regardless of the technique used to measure ΔC_p, establishing the exact molecular nature of nominal endstates can be extremely difficult. One line of thinking would suggest that thermal scanning methods should be preferred because the measured parameters pertain to the T_M, a temperature often high enough that single strands may be safely considered “unstacked”. At least two problems attend this approach. First, the actual degree of unstacking at the T_M will vary from system to system. Second, thermodynamically based structure prediction algorithms [e.g., mfold (56)] are typically used to assign stability to nucleic acid structures at 25–37 °C; extrapolations of ΔG from T_M-based measurements (employing either no ΔC_p or a T_M-based ΔC_p) will systematically neglect the effects of single strand stacking actually present at the target temperature. Figure 7B clearly illustrates how simple extrapolations to lower temperature from parameters measured at the T_M can badly miss the mark. The ΔH for duplex melting measured by van't Hoff analysis of optical melting data was extrapolated to lower temperatures using a constant per base pair ΔC_p that reflects the literature consensus value. This seemingly reasonable practice nevertheless dramatically overestimates the actual ΔH at lower temperatures because it fails to reflect the magnitude and temperature dependence of ΔC_p. As shown by the extrapolations of UV- and DSC-detected ΔHs in Figure 7B–D, all linear extrapolations from high temperature are likely to fail in this respect due to their inability to capture the enthalpic effects of single strand equilibria. ITC therefore emerges as an interesting alternative. Whereas parameters measured by ITC will often report on duplex association transitions from a complicated ensemble of unfolded end states, those measured values nevertheless provide an accurate description of the temperature-dependent process of duplex formation as it actually occurs at relevant, lower temperatures.

At the same time, our results make abundantly clear that one must be careful with ΔC_ps measured by ITC. In the five DNA duplexes studied, the observed ΔC_p was predominantly a function of (1) the placement of the experimental ITC temperature window relative to the summed single strand melting transitions (Figure 8) and (2) the specific positions of ITC data points within the window (compare panels B and D of Figure 7). In other words, ΔC_ps observed by ITC could be quite variable for a given duplex depending on the exact temperature range chosen for study and the points within that range actually sampled. It therefore seems wise to collect optical melting curves for component single strands in order to intelligently guide the design of ITC studies of duplex formation. Ultimately, of course, the most complete thermodynamic description of any given duplex will arise from the combined results of several methods, sampling a wide range of temperatures.

Incorporation of sequence-dependent ΔC_ps into nearest-neighbor models for secondary structure prediction may prove problematic. Our data suggest that the minimal effective “island” for nucleation of single strand stacking is probably about three or four nucleotides in length, and the effects are not necessarily additive. Further and more finely grained investigation of the sequence requirements for stacking and the resulting contributions to the observed ΔC_p will be necessary to decide how best to handle this problem.

As predictive models make strides toward three-dimensional structure prediction, the challenge of accurately modeling intermediate states (as exemplified by partially stacked strands in this study) will likely assume even greater importance. Unpaired regions of nucleic acids are likely sources of intermediate folding behavior, and observed ΔC_ps may serve as telling indicators for the presence of such intermediates. This is one area where the ability of ITC to detect the temperature-dependent enthalpic contributions of single-stranded species may prove especially valuable. For example, systematic thermodynamic studies of RNA helical junctions have observed a wide range of ΔC_ps for three- and four-way junctions (57, 58). Both the rules for tertiary folding of such junctions and the molecular details accounting for the observed ΔC_ps in these systems remain obscure. Moreover, a recent, large-scale bioinformatic study concluded that inadequate prediction of helical junction regions was a major bottleneck to improving the accuracy of RNA secondary structure prediction algorithms (59). Finally, work by Fang et al. on the catalytic domain of RNase P RNAs (C-domain) has produced an example where biology has adaptively exploited intermediate folding transitions associated with distinct ΔC_ps (60). The thermophilic version of C-domain achieved enhanced thermal stability via the presence of a highly unstable intermediate folding state. Moreover, the ΔC_p associated with folding from the intermediate to the native state was 5-fold greater in the thermophilic RNA than in a mesophilic counterpart. Hence, accurate assignment of stability to the native state required explicit consideration of an intermediate state, and critical differences between intermediates were associated with a major change in ΔC_p. Only through the measurement and understanding of heat capacity changes in nucleic acid structural transitions (secondary or tertiary) can we peer into the realm of these ensemble states.