Abstract
We construct and analyze a model network of the pyloric rhythm of the crustacean stomatogastric ganglion consisting of an oscillator neuron that inhibits two reciprocally inhibitory follower neurons. We derive analytic expressions that determine the phase of firing of the follower neurons with respect to the oscillator. An important aspect of the model is the inclusion of synapses that exhibit short-term synaptic depression. We show that these type of synapses allow there to be a complicated relationship between the intrinsic properties of the neurons and the synapses between them in determining phase relationships. Our analysis reveals the circumstances and ranges of cycle periods under which these properties work in concert with or independently from one another. In particular, we show that phase maintenance over a range of oscillator periods can be enhanced through the interplay of the two follower neurons if the synapses between these neurons are depressing. Since our model represents the core of the oscillatory pyloric network, the results of our analysis can be compared to experimental data and used to make predictions about the biological network.
Keywords: oscillator, phase plane, central pattern generator, synaptic depression
1 Introduction
Neuronal networks responsible for the generation of rhythmic motor activity often operate over a broad range of frequencies [18]. In many such oscillatory central pattern generating (CPG) networks the relative activity phase between groups of neurons remains fixed despite large variations in network frequency [6, 10, 11, 13, 14, 25]. Hence, in face of changes in network frequency, the time delay between the active states of these neuron groups must be adjusted proportionally with the network cycle period. Yet, the biological mechanisms underlying such adjustments are largely unknown. Previous modeling studies have addressed the question of phase determination in neuronal networks. There is a large literature on weakly coupled oscillators (see [8] for example) in which the phase relationship between neurons is obtained through methods of averaging. In studies of the lamprey CPG, the phase between neurons is explicitly constrained within the model [5], allowing the authors to investigate what mechanisms are consistent with the constraint. Work on understanding the inter-segmental lag in the crayfish CPG has focused on the interaction between weak and strong coupling [15, 30].
In previous work, we have suggested that short-term synaptic depression helps promote phase maintenance in feed-forward networks. We showed that depression in the feed-forward inhibitory synapse from an oscillator to a follower neuron allows the phase to be fairly constant over a large range of cycle periods [17] and that intrinsic ionic currents such as the transient potassium A current can act synergistically with synaptic depression to extend the range of phase maintenance [4]. In the current study, we focus on a CPG neuronal network to examine phase maintenance of follower neurons in a three-cell network in which a pacemaker neuron imposes the network oscillations on two follower neurons coupled with reciprocally inhibitory synapses (inset of Fig. 1). The questions of interest center on the synaptic and intrinsic mechanisms that control the activity phase of the follower neurons and their dependence on cycle frequency. This network is modeled after the pyloric network of the crustacean stomatogastric ganglion which consists of an oscillatory pacemaker group of neurons AB and PD and four sets of follower neurons [20]. The pacemaker AB and PD neurons are always co-active, due to strong electrical coupling, and inhibit all follower neurons which, in turn, become active in two distinct (but sometimes overlapping) intervals in each cycle, thus producing a tri-phasic rhythm (Fig. 1A). Previous experimental studies have shown that the activity phases of all neurons in this network are relatively well maintained, despite large variations (0.5–2 Hz) in cycle frequency [13, 14].
Fig. 1.
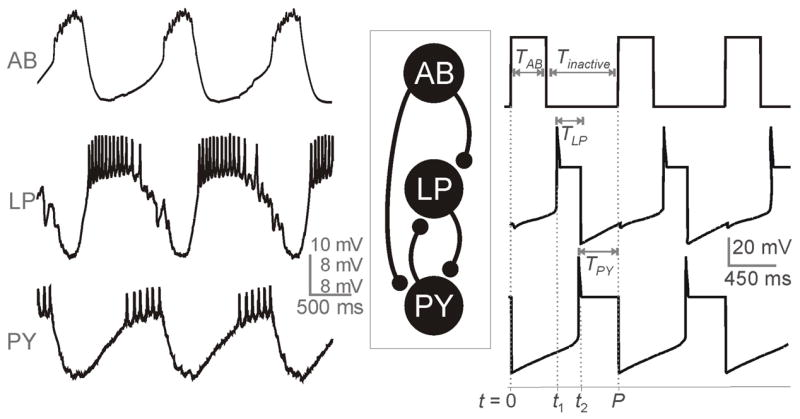
Voltage traces of a typical ongoing tri-phasic pyloric rhythmic activity involving the pacemaker neuron AB and follower neurons LP and PY. Left traces show experimental recordings (Nadim, unpublished data) and the traces on the right are the simulation of our model which provides an approximation to the envelope of oscillations observed in the experimental traces. The temporal parameters are marked in the model traces. The middle panel is a reduced schematic diagram of the pyloric network, showing the cells and synapses used in the model.
In this study, we use the AB neuron as the representative of the pacemaker group and the follower neurons LP and PY as representatives of the follower neurons active in two distinct phases. The other pacemaker neuron type PD two follower neuron types IC and V D, which are co-active with LP and PY, respectively, are not included in our model. Thus, in our model, AB sends feed-forward inhibition to LP and PY while the latter two neurons reciprocally inhibit one another.
We use phase-plane analysis to derive a set of equations that can be numerically solved at any value of the period to determine the phase relationship between AB and the follower neurons. As we vary the cycle period of AB, we investigate how the activity phases of LP and PY changes. The analysis allows us to determine the role of each of the neurons and the synapses between them in setting their activity phases. In particular, we show that when all synapses exhibit short-term depression, there are multiple control mechanisms for setting the phases. These control mechanisms may work in concert or be completely independent from one another. We show that as the cycle period changes, the control of the network phase relationships shifts between different sets of parameters associated with the neurons and their synapses. Our results, therefore, indicate that synaptic depression within the pyloric network provides a natural mechanism to help the network maintain the observed phase relationships among its different neurons despite large changes in the cycle period.
The mathematical techniques that we employ are motivated by geometric singular perturbation theory in which a difference in time scales is exploited to reduce a high-dimensional model to low-dimensional sub-systems that are more amenable to analysis [21]. We utilize this idea to project the dynamics of the neurons in their silent state onto a two- or three-dimensional phase space. Analyzing the ensuing dynamics in these phase spaces then makes it possible to analytically determine how long each neuron spends in its silent state, thereby allowing us to calculate the phase of each neuron. In parallel, we numerically solve the full set of model equations to see how these numerical solutions compare with those obtained from the analytic reduction method.
The paper is organized as follows. In section 2, we derive the model set of equations and describe the dynamics of synaptic depression. Section 3 contains results with section 3.1 containing the derivation of the firing times and subsequent subsections discussing the role of each of the synapses within the network. Section 4 contains a Discussion in which we address some of the modeling assumptions and implications for the biological network.
2 Model
The network we are studying consists of three neurons, AB, LP, and PY. A schematic of the network architecture is shown in Fig. 1 together with biological and simulation voltage traces of these neurons. AB is the pacemaker neuron of the pyloric network. It oscillates at frequencies that lie between 0.5 and 2.0 Hz [24]. The activity of the pacemaker AB neuron is taken for simplicity to be a square-wave. In particular, we denote the time that AB is active by TAB and the time it is inactive by Tinactive. Therefore the period of AB satisfies P = TAB + Tinactive. LP and PY are the follower neurons of the pyloric network. We are mostly interested in the burst envelope of these neurons so we use Morris-Lecar type equations to model their activity [22]. The equations to describe the activity of LP and PY without synaptic connectivity are:
| (1) |
| (2) |
where x is PY or LP. vx is the voltage of neuron x, Ix in an applied current, gleak,x is the conductance of the leak current, Eleak,x is the reversal potential of the leak current, and wx is the recovery variable of K+. The functions m∞, w∞, and τ∞ are sigmoidal functions of voltage and are given in the Appendix. Recent experiments by Rabbah et al [27] showed that the delay in firing of PY relative to firing of LP is due to intrinsic properties of the neurons. Thus, in the silent state, we choose τw,LP (vLP ) < τw,PY (vPY ) so that PY has a a slower intrinsic decay rate than LP.
We denote the right-hand side of (1) by f(vx, wx). The vx- and wx-nullclines associated with (1) and (2) are the set of points {(vx, wx): f (vx, wx = 0} and {(vx, wx): wx = w∞(vx)}. The former is cubic shaped, the latter is sigmoidal. We assume that for both LP and PY, these nullclines intersect at a stable fixed point along the right branch of the cubic nullcline. Thus in the absence of input, both LP and PY tend to a high-voltage fixed point.
LP and PY receive inhibitory synaptic inputs from AB and also from one another. The synapses are modeled to be depressing meaning that the strength of the synapse weakens as the frequency of the pre-synaptic neuron increases. The equations to model the activity of LP and PY are:
| (3) |
| (4) |
| (5) |
| (6) |
In the above equations, ḡAB, ḡPY and ḡLP are the maximal conductances of the AB, PY and LP synapses, respectively, while sAB, sPY and sLP are the associated gating variables. Einh is the reversal potential of the synapses that is chosen so that all synapses are inhibitory.
Our model for the synapses is similar to that in [17] where each synapse has a gating variable sx and another variable dx that measures the extent of synaptic depression of the synapse. Both variables follow piecewise continuous linear kinetics. They are coupled at discrete moments of time whenever a pre-synaptic cell becomes active. When this occurs, sx is set equal to the current value of dx; see Fig. 2. At all other times the equations for the each of the synaptic variables are:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
Fig. 2.
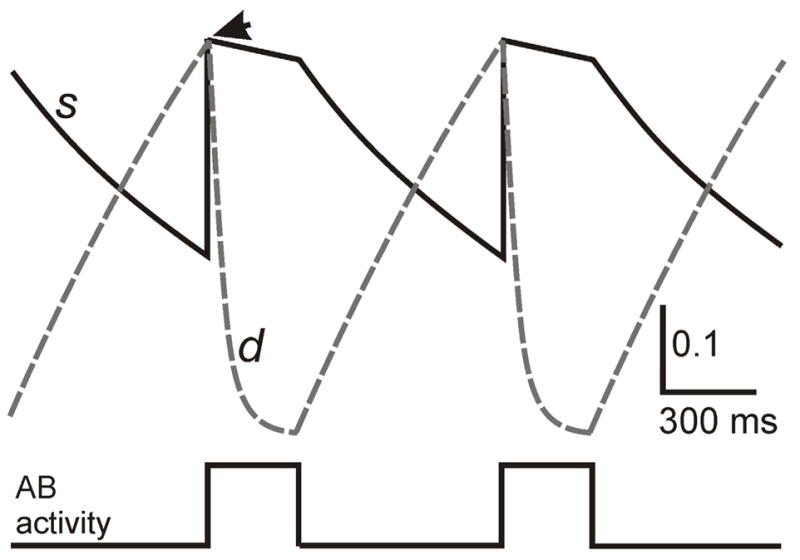
Dynamics of the synaptic and depression variables. A schematic associated with the AB synapse is shown. At the moment (marked by arrow) AB becomes active, the s variable (solid) is reset to the current value of d (dashed). At all other times, the two variables are decoupled and governed by distinct sets of equations. During the time AB is active, s decays at a slow rate and d depresses. Once AB becomes inactive, s decays at a different rate, while d recovers. The s and d variables for the LP and PY synapses behave in a similar manner.
For example, when AB enters its active state, we set sAB = dAB and then let dAB and sAB evolve according to (7) and (8). vT is the activation threshold of the synapses. When vAB < vT, dAB increases to d̂AB(Tinactive) (recovery from depression) with rate 1/τα where d̂AB(Tinactive) is an increasing function of Tinactive given by
| (13) |
In this equation, P1 determines the half-activation time of d̂AB and x1 determines the steepness of d̂AB. This relationship models the dependency of recovery from depression on the cycle period of activity and is used to provide a better approximation of the two time scales of recovery observed in the pyloric synapses [3]. Once vAB goes above threshold (AB becomes active), sAB is set to dAB and then decreases at a rate of 1/τζ where τζ is a large parameter. While vAB remains above threshold, dAB decreases towards 0 with time constant 1/τβ representing the depression of the AB synapse. Once vAB goes below threshold, sAB decreases to 0 with rate 1/τκ. As the inactive phase of AB increases, the synapse has more time to recover from depression and thus dAB has more time to increase towards d̂AB(Tinactive).
Similarly, we let
| (14) |
where TLP refers to the length of time LP is active. Note that TLP is a priori unknown, but will be determined below. d̂PY (P; TPY ) can also be modeled using a sigmoid similar to d̂AB where TPY refers to the length of time that PY is active. For simplicity, however, we set d̂PY = 1.
In some cases that we will examine, the synapses from AB to LP and PY will be non-depressing. In these cases, the strength of the AB synapses will be independent of period. Whenever AB becomes active, we will set sAB = 1 instead of dAB.
The mathematical effect of inhibition is to lower the vx–nullcline of the post-synaptic cell in the (vx; wx) phase space. Consider LP for example. Before it receives inhibition from the pacemaker AB, LP lies at a high-voltage fixed point. The inhibition from AB turns on quickly and causes this fixed point to disappear, thereby allowing LP to return to its silent state. Depending on the strength of the AB inhibition (which due to depression is period dependent), the vLP - and wLP -nullclines may intersect either on the middle or left branch of the cubic. In the former case, LP will be able to leave the silent state due to its intrinsic properties, while in the latter LP will remain in the silent state until the AB inhibition decays; Fig. 3. The general effect of PY inhibition on LP and of AB and LP inhibition on PY is similar.
Fig. 3.
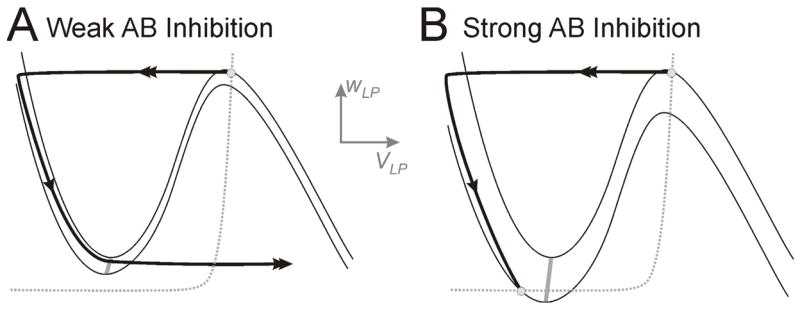
The influence of AB inhibition on the dynamics of LP.A. The inhibition from AB to LP causes LP to return to the silent state, but is too weak to affect the time that LP spends in this state. Note the lack of intersection of the v- (solid) and w-nullclines (dotted) along the left branches. B. The inhibition from AB is strong and creates a fixed point on the left branch of the v-nullcline. In this case LP must wait for AB inhibition to decay, thereby allowing the stable fixed point (lower white circle) to disappear before it can jump to the active state. White circles indicate stable fixed points. The two v-nullclines in each case indicate no (upper) or maximal (lower) inhibition from AB to LP. The gray curve is the LP jump curve.
We will not carry out a formal singular perturbation analysis in this paper. Instead, we will assume that the wx, sx and dx variables evolve more slowly than the vx variables while the trajectory is away from the branches of a cubic nullcline. This can be achieved by taking the time constants associated with those variables to be large and will allow us to project the dynamics of the neurons while they are near the left branch of a cubic onto a lower dimensional phase space; see [1, 4] for related examples. Simulations of our model are done using the software package XPPAUT [9]. Numerical solutions of equations (25) and (26), below, were obtained using MATLAB. Parameter values are given in the Appendix.
3 Results
We describe the tri-phasic pyloric rhythm starting with the onset of AB activity at t = 0 as shown in Fig. 1. AB remains active for time TAB during which time both LP and PY are silent. At t = t1, LP becomes active for a time length TLP. During this time, it inhibits PY. At t = t2, PY becomes active and inhibits LP enough to return LP to the silent state. PY stays active for a time length TPY. After one period P = TAB + Tinactive, AB again becomes active, inhibiting PY and LP and the cycle continues. We define φLP = t1/P and φPY = t2/P as the phase at which LP and PY fire with respect to the onset of AB activity. The main goal of this paper is to determine these two quantities as a function of P, and to show what effect synaptic depression has on these two phases. Throughout this paper, we shall change P by changing the time Tinactive while keeping TAB fixed; see the Discussion for comments on how changing period in different ways affects the results.
To determine φLP and φPY, we must determine t1, t2, TLP and TPY. However the latter two quantities obey TLP = t2 − t1 and TPY = P − t2. Thus we need only determine two equations for the remaining unknowns t1 and t2. To calculate these times we first must understand how LP and PY evolve in their silent state, and what causes them to have a chance to jump to the active state. Consider first LP in the case where only AB inhibition is present. In the vLP – wLP phase plane, inhibition lowers the vLP –cubic nullcline. As LP evolves in the silent state, the synapse from AB decays, causing the cubic nullcline to rise slowly back toward its original location. LP can jump to the active state when it reaches a local minimum of any of the slowly rising cubics. These local minima form a one-dimensional LP-jump curve in (vLP, wLP ) space; labeled j.c. in Fig. 4A.
Fig. 4.
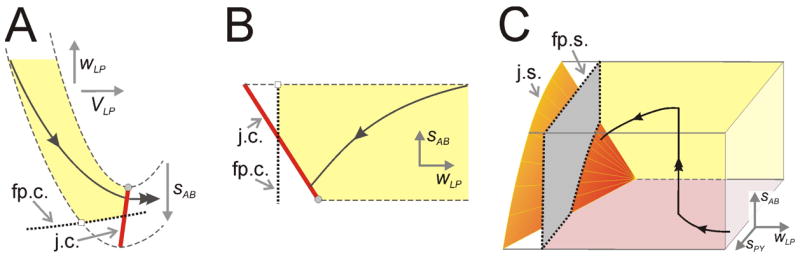
Jump curves and surfaces. A. The dynamics of LP activity in response to AB inhibition alone. The set of local minima of the v-nullclines forms a one-dimensional jump curve j.c. The v-nullclines for different values of AB inhibition (sAB) form a surface (shaded) that is bounded by two extremes (dashed) in each case indicate no (upper) or maximal (lower) inhibition from AB to LP. The w-nullcline is the dotted curve. The trajectory is shown as a solid curve. Additionally, the intersection of the w-nullcline with different v-nullclines forms a curve of fixed points, fp.c. B. The projection of the slow manifold (shaded) depicted in panel A onto the wLP-sAB phase space. C. The projection of the LP trajectory onto the wLP-sAB-sPY phase space. The jump and fixed point surfaces, j.s. and fp.s., are now both two-dimensional. The trajectory begins toward the front of the box with a high value of sPY, but a low value of sAB, and moves down, to the left, and into the box (sAB, sPY and wLP all decay). When AB becomes active, the trajectory is reset vertically to a higher value of sAB. The trajectory then moves in the same way as before but for the time AB is active, sAB decays very slowly. The trajectory escapes when it reaches j.s. (orange surface).
Another way to visualize this is in the (wLP, sAB) phase space; Fig. 4B. When projected into this phase space, the trajectory moves down and to the left. In addition to the LP-jump curve, there exists a curve of fixed points, labeled fp.c.. These points are not true fixed points of the system, but rather are points along which the vLP – and wLP –nullclines intersect , but where . A typical trajectory in this phase space will transition to the active state when it reaches the jump curve. Let us now add in the PY inhibition to LP. In this case, LP must potentially wait for both the AB and PY inhibitions to decay in order to jump to the active state. The local minima of the associated cubics now form a two-dimensional jump surface (j.s.) and the fixed points form a two-dimensional surface (fp.s.) as shown in the (wLP, sAB, sPY ) phase space in Fig. 4C. Similarly, there exists a two-dimensional PY -jump surface resulting from the slow decay of the AB and LP synapses to PY and a two-dimensional surface of fixed points.
Let us assume that AB becomes active at t = 0 and that both LP and PY are in their silent state. LP is the first to reach its jump surface, primarily because of the assumption that when the neurons are below threshold, τw,LP (vLP ) < τw,PY (vPY ). Assume that the jump surface is a plane and can be expressed by the linear relationship:
| (15) |
Note that if ḡPY = 0, (15) reduces to the equation for a one-dimensional linear jump curve as in [4]. The constants M1 and are both positive and can be determined from the ḡPY = 0 case. The former is related to the slope of the LP-jump curve; the latter is related to the level of inhibitory synaptic input needed to make the vLP -nullcline tangent to the wLP -nullcline; see figure 4B. We now calculate the value at time t1 of the three dynamic variables explicitly represented in (15). The first is the easiest. Since AB is taken to be a periodic square wave function (with period P = TAB + Tinactive), the value of the depression variable dAB will also be periodic. Using this fact, it is straightforward to find from (7) that the maximal value of dAB occurs at the onset of AB activity and is given by
| (16) |
Note that dmax,AB(P ) is an increasing function of Tinactive. At the time that AB becomes active sAB is set equal to dmax,AB and then decays according to (8). Thus sAB(TAB) = dmax,AB(P)e−TAB/τζ. During the time that AB is silent, sAB decays with time constant τκ, so
| (17) |
Note that the case when AB is not depressing can be considered by simply setting dmax,AB ≡ 1. We next calculate sPY (t1). Since the tri-phasic rhythm is assumed to be periodic, we similarly find that
| (18) |
This maximum occurs at the onset of the PY burst. Note that dmax,PY depends on TPY where this term is to be determined by t2 (TPY = P − t2). Utilizing the activity of the previous cycle of a periodic solution, t = 0 corresponds to the end of a PY burst. Therefore sPY (0) = dmax,PY e−TPYτ2 and at time t1
| (19) |
Finally, we determine wLP (t1). When PY becomes active (during the previous cycle) assuming ḡPY > 0, LP returns to the silent state with a value we denote wLP.LP stays in the silent state for time TPY + t1 = P − (t2 − t1). Assuming that w∞(LP ) ≈ 0 near the left branches of the vLP nullcline and that τw,LP (vLP ) is a constant denoted by τw,LP, we find
| (20) |
We can now substitute equations (17)–(20) into (15). Note however that if ḡPY = 0, then LP stays in the active state until AB becomes active and (20) is replaced by wLP (t1) = ŵLP e−t1/τw,LP.
To find a second equation relating the times t1 and t2, we use a linear approximation for the PY -jump surface:
| (21) |
Similar to before,
| (22) |
To calculate sLP (t2), we note that LP becomes active at t = t1. Thus independent of the value of sLP prior to t1, sLP (t1) = dmax,LP, where
| (23) |
LP remains active until time t2 which implies
| (24) |
Similar to before wPY (t2) = ŵPY exp(−t2/τw,PY ) where τw,PY is the time constant for PY activity in its silent state. We can now substitute into (21) to obtain the following two equations for t1 and t2:
| (25) |
| (26) |
Note that TPY = P − t2, and if ḡPY = 0 then TLP = P − t1, while if ḡPY > 0 then TLP = t2 − t1.
Equations (25) and (26) can be solved numerically to obtain t1 and t2. In specific parameter regimes, certain terms on the left-hand side of the above equations become small and an analytic estimate for t1 and t2 becomes possible. Our goal for the remainder of the paper is to use (25) and (26) to understand how φLP = t1/P and φPY = t2/P depend on the parameters in these equations. We shall check this for several cases; when the LP and PY inhibition is absent (section 3.1), when LP to PY inhibition is added (section 3.2), when PY to LP inhibition is present (section 3.3), and when both reciprocal synapses are present (section 3.4).
3.1 Phase determination with no synapses between LP and PY
When the synapses between LP and PY are removed, we set ḡLP = 0 and ḡPY = 0 in equations (25) and (26). Then t1 and t2 (and, therefore φLP and φPY ) are determined by the properties of the AB synapses and the intrinsic properties of the neurons. In this case, the dependence of φLP on P has been previously shown by Manor et al [17], and that of φPY is similar.
If the AB synapses onto LP and PY are not depressing, then φLP and φPY both decay like 1/P since (25) and (26) are no longer period dependent. For each cell, this decay is controlled either by τκ the time constant of decay of the AB synapses and ḡAB the maximal conductance of the synapse or by the cell’s own intrinsic time constant of decay in the silent state, τw,LP or τw,PY. The situation changes dramatically when the AB synapses are depressing. Following the results of Manor et al [17], with an appropriate choice of parameters, both sets of parameters can control the phase curves, each doing so at different ranges of periods. In particular, when τκ is large enough so that the synaptic decay is slower than the rate at which wPY and wLP decay on the left branches of their respective nullclines, phase maintenance is enhanced. In Fig. 5A, we can see that for 500 < P < 650, φLP and φPY decrease. In this range of periods, the synapses from AB to LP and PY are largely depressed and, consequently, do not significantly contribute to the time at which LP and PY fire. Here the first terms on the left-hand sides of (25) and (26) are close to zero, the second terms are absent (ḡPY = ḡLP = 0) and therefore the third terms alone determine t1 and t2. Thus in this range, phase is mostly determined by the intrinsic dynamics of LP and PY. In the range 650 < P < 1000, the AB synapse increasingly recovers from depression (dmax,AB gets larger; Fig 5B). As a result the synaptic properties take over control for setting φLP and φPY in this range. For P > 1000, the AB synapse has maximally recovered from depression causing dmax,AB to saturate. Now the first terms on the left-hand sides of (25) and (26) take longer to decay then the third terms (since τκ is large enough). Thus the synapses from AB determine the firing times. However, as the period increases, the phase decreases like 1/P since the value of dmax,AB in the first terms will eventually saturate; dmax,AB →1 as P →∞ [17]. These three regimes combine together to cause the phase curve to be cubic in shape. Thus, although a constant phase is not perfectly achieved, phase-maintenance is better than when the AB synapse is non-depressing where φLP and φPY decay like 1/P.
Fig. 5.
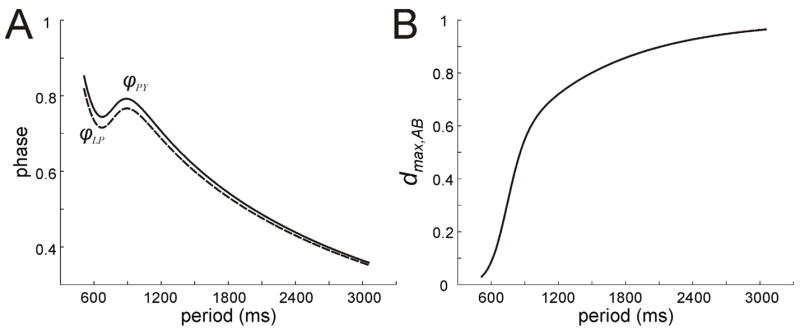
Behavior of LP and PY when only AB inhibition is present. A. Phase curves for LP and PY show a stereotypical cubic shape indicating that different mechanisms and parameters control phase at different periods. B. The value of dAB,max increases with period. The strengthening of the feed-forward AB synapses for P > 600 causes the control of phase (as shown in panel A) to switch from the LP and PY intrinsic mechanisms to the AB synapses.
3.2 The effect of LP to PY inhibition on φPY
We now explore how the presence of the LP to PY synapse affects φPY. We show that the inclusion of the LP to PY synapse leads to another way to control the phase of PY activity. In (25) and (26), we let ḡPY = 0 while setting ḡLP to a positive value. When the synapse from LP to PY is present, each time LP is active, it provides further inhibition to PY. In order for PY to fire, the LP inhibition must also decay. Therefore, the additional time it now takes for PY to fire is determined, in part, by the the size of ḡLP sLP and the rate at which sLP decays. Using equation (26), we can determine over which parameter regimes the LP to PY synapse significantly contributes to φPY. For example, suppose τ4, the time constant of decay of the sLP synapse when LP is active, is small enough, or that ḡLP, the maximal conductance of this synapse is small. Then the term ḡLP sLP is insignificant and, therefore the LP to PY synapse does not significantly affect t2. However, if τ4 is not so small compared with τK and τw,PY, and if ḡLP is big enough, then the LP inhibition will more significantly contribute to φPY
The period dependence of the LP synapse and the rates of depression and recovery also play a role in setting phase. For example if the time constant of recovery from depression of the LP synapse (τc) is very small, then the synapse will recover quickly and will largely be period independent. Similarly, if the depression time constant τd is small, then the synapse will be ineffective at suppressing its post-synaptic target. More interestingly, depending on the value of parameters, the the LP to PY synapse can work in concert with or independently of the AB synapse to effect PY firing. Figure 6A shows graphs of the φLP, φPY and dmax,LP for different choices of the parameter P2, the half activation of the strength of the LP to PY. The dashed line traces show the case when P2 = 570 (note the half-activation of the AB synapse P1 = 870 in all cases), the dotted line traces when P2 = 870 and the solid traces when P2 = 1770. In the latter case, the length of the LP interburst (t1 = P − TLP ) never becomes large enough to cause the LP to PY synapse to gain strength. Thus dmax,LP = 0 (Fig. 6B) and φPY looks as it would if ḡLP = 0. When the parameter P2 is lowered to 870, then the LP to PY synapse does strengthen around P = 1380 (dotted traces) because P − TLP becomes larger than P2. Here, the synapse becomes strong in a range of periods for which the AB synapse is already saturated. Thus it controls φPY quite independently of the AB to PY synapse. When, P2 = 190 (dashed traces), the LP to PY synapse works in concert with the AB to PY synapse to delay PY firing. Here the phase curve has a single local maximum that is larger in value than when the LP to PY synapse is absent. Numerical simulations of the full set of equations using XPPAUT yield similar results (not shown). As P → ∞, the value of dmax,LP tends to d ^LP [1 − exp(− (P − TLP )= τc)] since TLP → ∞ as can be seen from equations (14) and (23). Thus dmax,LP is bounded away from one and thus the LP to PY synapse never fully recovers.
Fig. 6.
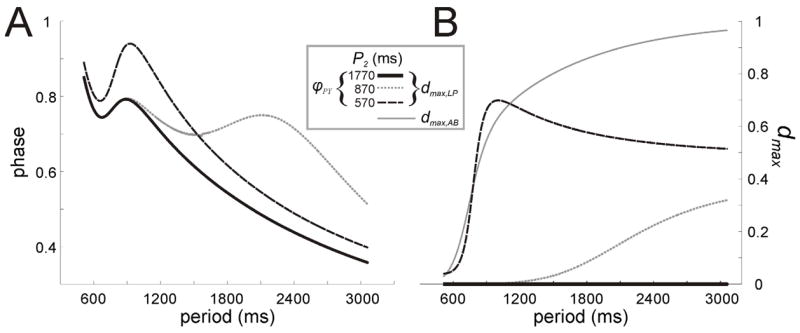
Behavior of PY under AB and LP inhibition. A. The PY phase curves shown in three conditions indicate how the half-activation period (P2) of the LP to PY synapse affects its ability to change the phase of PY. B. The behavior of dLP,max for the three cases shown in panel A. The value dAB,max (grey solid curve) is also shown to illustrate the relationship between the two synapses.
3.3 The role of PY to LP inhibition on φLP and φPY
Next we address what effect the synapse from PY to LP has on the phase of LP and PY. Again depending on the parameters, there are many possibilities that can be considered. However we shall take a cue from the biological system and study one important subcase. It is known that the PY to LP synapse is initially strong, depresses very quickly and also decays very quickly once PY becomes silent [16]. From these results, we conclude that the primary role of the PY to LP synapse is to end the firing of LP and return it to its active state. This simple role, however, has a dramatic affect on both φLP and φPY. First, the knocking down of LP to its silent state by PY means that at small periods, φLP decreases. In particular, for small values of P, the AB synapse is weak and does not play a big role in setting t1, which is set mainly by the intrinsic properties of LP. Once LP is on the left branches of its vLP nullcline, wLP begins to decay before AB becomes active. Thus when AB next becomes active, LP is much closer to the jump surface than it would have been had it been knocked down to the silent state by AB, Fig. 7. Thus the remaining time that LP must now spend evolving toward the jump surface is much smaller in the presence of the PY synapse than in its absence. Therefore t1 is significantly smaller and φLP decreases. At large P, however, the AB synapse is stronger and continues to dominate the determination of t1. This is especially true if we choose τ1, the time constant of decay of the PY to LP inhibition to be small.
Fig. 7.
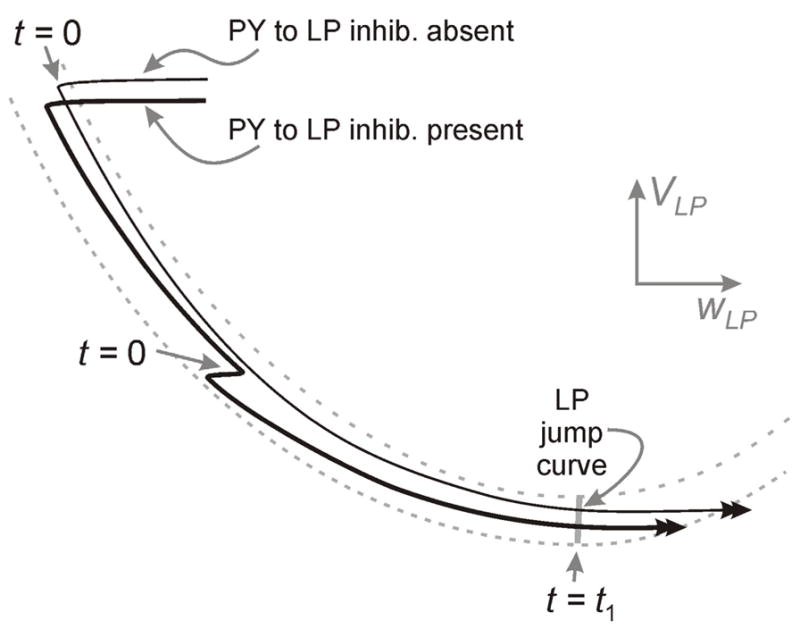
The behavior of LP in the presence and absence of PY inhibition. Without PY inhibition, the time t1 is calculated from the moment LP falls back to the silent state, associated with the onset of AB activity (t=0; top arrow) to the jump point. When PY inhibition is present (the bold trajectory), the onset of AB activity occurs at a lower point on the left branch of the vLP nullcline (t=0; middle arrow) and t1 is calculated from this moment to the jump point and is therefore much smaller.
The second effect of the presence of the PY to LP synapse is to strengthen the LP to PY synapse. This is because the presence of the PY to LP synapse causes LP to have a shorter active duration than when this synapse is absent. Note that when ḡPY = 0 (the PY to LP inhibition is absent), TLP = P − t1, whereas when ḡPY > 0 (the PY to LP inhibition is present), TLP = t2 − t1 because the PY inhibition ends the LP burst. Thus LP spends a larger fraction of its period in the silent state, which, in turn increases both terms of equation (23) allowing dmax,LP to increase with P, Fig. 8. Moreover, since TLP is bounded as P → ∞, dmax,LP→ 1 in this limit. Therefore independent of the value of P2, the LP to PY synapse will play a role in setting the PY phase. Thus, the effect of PY inhibition is to strengthen the inhibition that it itself receives! The ramifications of this are explored in the next section.
Fig. 8.
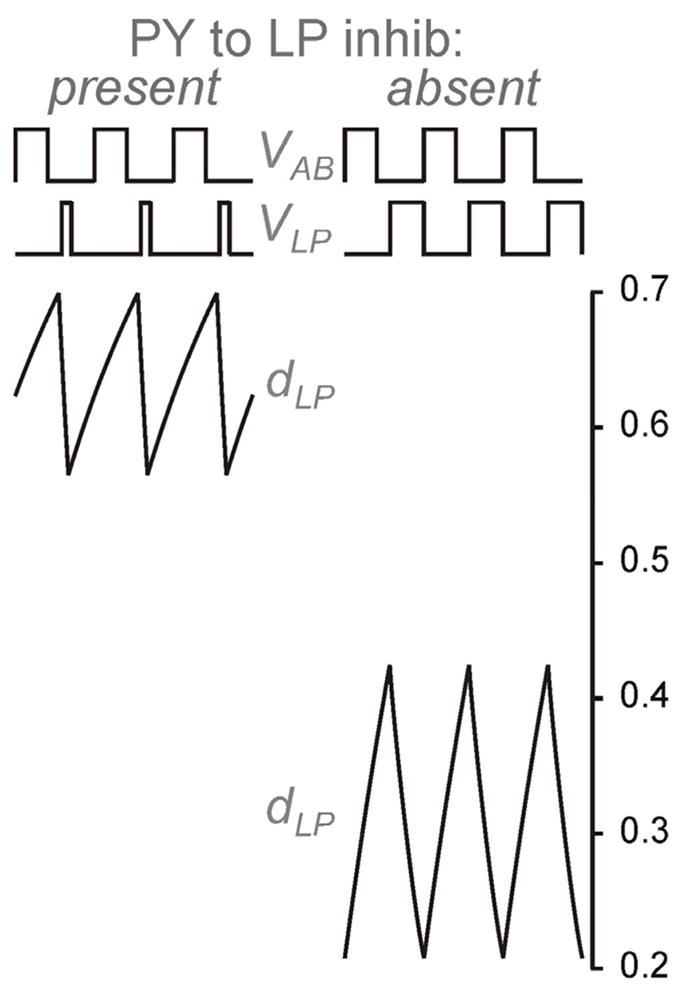
The effect of PY inhibition on dLP. When PY inhibition is present, LP inhibition strengthens independently of the half activation (P2) of the synapse since LP spends more time in the silent state. When the PY inhibition is absent, the LP inhibition can only strengthen if P2 is sufficiently small as LP spends relatively little time in the silent state.
3.4 Reciprocal inhibition between LP and PY
The above results indicate that the inhibitory synapses between the two pyloric neurons LP and PY can play a role in enhancing the ability of the neurons to achieve phase maintenance. Indeed, we have seen that the LP to PY synapse can control PY phase in a range of periods for which the AB synapses to LP and PY are already saturated, and thus are no longer period dependent. Therefore, it is natural to consider cases in which the AB inhibition is both non-depressing and depressing.
When the AB synapse is non-depressing (dmax,AB ≡ 1), and the inhibition between LP and PY is absent, φLP and φPY decrease like 1/P. In order for the synapse from LP to PY to be able to create a range of periods over which φPY increases, dLP must increase as the period increases. Similarly, dPY must increase as the period increases in order to create a range of periods over which φLP increases. Let us first consider dmax,LP as given by equation (23). This term will increase as period increases so long as LP spends increasingly longer times in the silent state. As P increases, even though the time t1 need not increase the time P − TLP will. To understand this, recall that one role of the PY inhibition to LP is to return the latter to the silent state at an earlier stage than AB would have. This is independent of depression of either the AB or PY synapses. Thus the LP to PY synapse will have a chance to recover for more time and thereby will strengthen. A stronger LP to PY synapse delays PY firing and thus increases φPY. In Fig 9A, we show an example of this; panel A1 is obtained by solving the full set of equations numerically with XPPAUT, while panel A2 is obtained by solving (25) and (26) with MATLAB. In particular, the LP to PY synapse becomes strong when P − TLP > P2(= 1140). In this range, the value of the synaptic and depression time constants associated with the LP synapse play an increasingly larger role in setting PY phase. If the time constant of LP to PY synaptic decay is chosen to be large relative to the time constant of decay of the AB synapse, then the LP synapse can increase the phase of PY for a range of periods larger than P2. For very large values of P, the LP synapse will fully recover from depression and will not be able to further increase the delay of PY firing. Thus for large P, we expect φPY to decay like 1/P as shown in the figure.
Fig. 9.
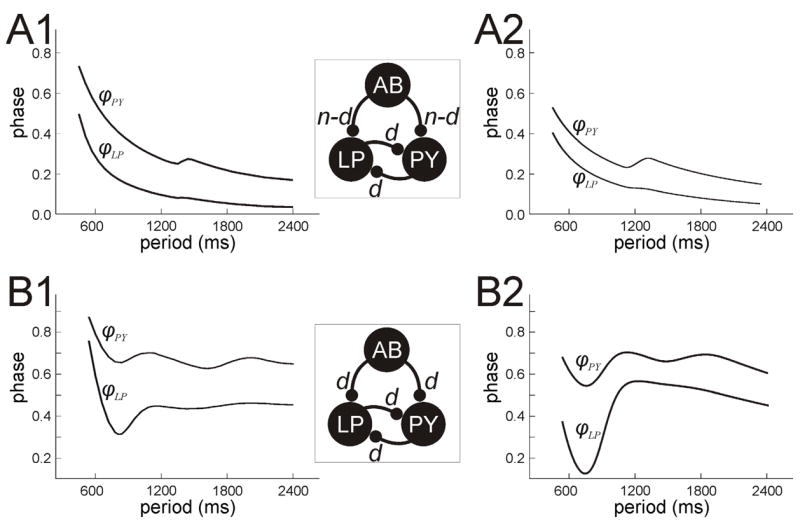
LP and PY phase curves when reciprocal inhibition between the two is present. A. When the AB synapses are non-depressing, the PY phase can still be better than 1/P if the LP inhibition to PY is depressing. The local maxima of ϕPY are due to the strengthening of the LP to PY synapse. Also note the small increase in ϕLP near these periods. B. When the AB synapses are depressing, ϕPY and ϕLP can both have multiple local extrema. Panels A1 and B1 were obtained by numerically solving the full set of equations for their respective cases. Panels A2 and B2, obtained by solving equations (25) and (26), show good qualitative agreement with these numerical results.
A delay in PY firing has the added effect of strengthening the PY to LP synapse provided that this synapse is also depressing, as PY spends more time in the silent phase. This can have a very subtle effect on the LP phase. At first glance, the PY to LP synapse does not appear to do much to help LP phase be constant, instead almost all of this work falls on AB. However PY does put LP in a position so that at small periods, the intrinsic controlled LP phase is much closer to the larger period AB-synaptically controlled LP phase. Moreover at these larger periods where the AB synapse is strengthening, increases in strength of the PY to LP synapse can induce changes in the LP phase. This is because this synapse can now complement the AB to LP synapse to keep the LP neuron near the jump surface for a longer time, thereby delaying LP firing. This subtle effect, however, does not dramatically affect the LP phase since the time constant of decay of the PY to LP synapse is small. Thus its effect will have worn off by the next LP cycle. This is consistent with the biological system where the PY to LP synapse is a strong, short lasting one whose main effect is to terminate LP firing [16].
In summary, when the AB input is non-depressing, the depression of the LP to PY synapse can still be utilized to improve phase maintenance of PY. However the phase of LP is still mostly determined by the AB synapse and basically decays like 1=P.
When the reciprocal inhibition between LP and PY is present and the AB synapses are depressing, the complexity of the network is increased. However, the dynamics of LP and PY can be understood based on the results of sections 3.1–3.3. As discussed above, depending on parameters, various synaptic or intrinsic parameters play a role in setting phase at different intervals of period. Let us focus on the case where P2 > P1 (P2 = 1470 and P1 = 870). In this case, both φLP and φPY can have several local maxima and minima and, in particular, can have good phase maintenance over a large range of periods. Figure 9B shows one such case where φLP varies between .35 and .45 and φPY varies between .6 and .7 for P 2 [500; 2400]. These curves can be parsed into three distinct intervals. At small periods, the AB, LP and PY synapses are weak and play little role in setting phase. Here intrinsic parameters of LP and PY, namely τw,LP and τw,PY, are more important; only the last term of the left hand side of equations (25) and (26) is large. At intermediate periods, the AB synapse strengthens while the LP and PY synapses remain weak. Here, the time constant of AB synaptic decay, τk, is the most important parameter in setting phase. The first term on the left hand side of (25) and (26) is dominant. Finally, at larger P, the AB synapse has saturated and plays no additional role in setting phase. Instead, at these periods the LP and PY synapses have strengthened enough to be important. In particular, the inhibition from PY to LP allows LP to spend more time in the silent state, thereby strengthening the LP to PY synapse. This strengthened synapse in turn delays PY firing, increasing its phase, and strengthening the PY to LP synapse. The time constants of decay between the LP and PY reciprocal synapses play the most important role of setting phase for large P. In this case, the first and second terms on the left hand side of (25) and (26) are large, but the first terms decay more quickly then the second terms. Thus the control of phase for large P is most strongly controlled by time constants associated with the reciprocal LP and PY synapses.
The importance of the PY to LP synapse in redirecting the role of the LP to PY synapse can not be overstated. In particular, when the PY to LP synapse is absent, the LP to PY synapse strengthens only as a result of the effect of the delay to firing induced by the AB to LP synapse. The LP to PY synapse is only effective in a range of periods that depends closely on the AB to LP synapse; see section 3.2 and the relationship between the parameters P1 and P2. However, when the PY to LP synapse is present, the LP to PY synapse can act much more independently. Namely, it can strengthen in a range of periods that is largely independent of any effects of the AB induced delay, and therefore can affect the PY phase curve in a range of periods that is different than the AB synapse does. In particular, in order for the LP synapse to strengthen, the value of P2, the half-activation of the depression and recovery term associated with dLP need not be related to P1, the half-activation associated with dAB.
4 Discussion
Central pattern generating (CPG) networks are often driven by pacemaker neurons that set the network frequency and the influence the firing times of follower neurons via feed-forward synapses [7]. Nonetheless, the dynamics of these networks are often modulated or controlled by mechanisms that are downstream from the feed-forward inputs. Even in small networks, the dynamics resulting from the interactions among the rhythmically active neurons can be surprisingly complicated. We have analyzed a simplified network, modeling the pyloric CPG of the crustacean stomatogastric ganglion. Our results build on our previous studies that examined the effect of short-term synaptic depression, a common property of many synapses, on the activity phase of a follower neuron in a two-cell feed-forward network [4, 17].
In this study we focused on a three-cell network, consisting of a pacemaker neuron AB that produces feed-forward inhibitory synapses on two follower neurons LP and PY. The follower neurons also have reciprocally-inhibitory synaptic connections thus producing feedback interactions in the network. We examined the mechanisms that determine the activity phase of LP and PY in face of changes in network frequency. Our analysis demonstrates that phase constancy is enhanced when the synapses between neurons are depressing. As a result, the PY and LP neurons can keep a relatively constant phase over a four-fold change in the network cycle period, consistent with the experimental findings of Hooper [13].
Mathematical analysis carried out in lower dimensional phase spaces allowed us to understand how different combinations of parameters can affect the activity phase of follower neurons in different ranges of the cycle period. It also revealed a number of interesting facts about how the dynamics of the network evolve. For example, it has traditionally been thought that the primary role of the PY to LP synapse is simply to return LP to its silent state [27]. Our analysis now demonstrates that an additional effect of this synapse is to strengthen the LP to PY synapse by causing LP to spend more time in its silent state, allowing for recovery from short-term depression. This effect occurs whether or not the PY to LP synapse is depressing, thus indicating that the plasticity of this synapse may not be so critical to the proper functioning of the network.
4.1 Role of synaptic depression
Many synaptic connections in CPGs exhibit short-term depression [19, 23, 26]. Our results show that synaptic depression can play a variety of potential roles in setting the phases of the follower LP and PY neurons. First, the feed-forward synapses from AB to both LP and PY allow the intrinsic properties of these follower neurons to determine phase at small periods where the AB synapses are weak. At intermediate cycle periods, these same synapses strengthen and become more effective in the control of the activity phases. Second, the depression in the LP to PY synapse allows the PY phase to be determined by this synapse in different ranges of periods. If the LP synapse strengthens in the same range of periods as the AB synapses, then these two work in concert to determine PY phase. If not, the LP to PY synapse can work independently of the AB to PY synapse to influence the phase of PY activity. As a consequence, even if the AB synapse is non-depressing, the LP to PY synapse can still promote phase constancy of φPY (to be better than 1/P) in some range of periods. Third, as shown in section 3.4, depression in the PY to LP synapse can also have a small but subtle effect on the LP phase. Thus, changes in the cycle period of the pacemaker neuron AB may not directly affect AB’s synapses, yet result in changes in downstream synapses that the pacemaker does not directly target. This provides another set of candidate mechanisms that can affect the phase of the follower neurons.
4.2 Consequences of model assumptions
The primary modeling assumption made here is that the individual spikes within a burst are not of large relevance in determining the phase relationships of neurons. Synapses in the stomatogastric ganglion have both a spike-mediated and a non-spike-mediated (graded) component whose strength depends on the slow oscillatory waveforms of the presynaptic neuron [12]. When action potentials, and therefore spike-mediated transmission, is blocked by bath application of tetrodotoxin, a tri-phasic rhythm characteristic of the pyloric network activity can be generated by applying various modulatory substances [2]. Thus, the simplified Morris-Lecar type models and graded synapses used provide a good first-order approximation of the activity of the pyloric network, in particular the envelope of the slow oscillations (as in Fig. 1) and its underlying synaptic mechanisms. We note that our model of short-term depression was chosen to match known biological results. In particular, equations (13) and (14) are used specifically to model the longer time scale associated with recovery of pyloric synapses [3, 28]. The specific form of these synapses is important to our results in that changes to parameters associated with these equations (as in Fig 6) may lead to deterioration of phase maintenance. We also chose the time constants of the various synaptic connections to mimic known biological facts. For example, the time constants associated with the PY to LP synapse were chosen to make it strong, fast decaying and fast depressing consistent with published experimental results [16].
The other major modeling assumption is that the jump surfaces in the silent states of LP and PY are planes. This assumption allowed us to analytically derive (25) and (26). The results shown in Fig. 9 validate this assumption as they show a very good qualitative agreement between phase curves obtained from (25) and (26) with those obtained by numerically solving the full set of equations. This qualitative agreement occurs despite the fact that our analytic reduction effectively ignores the behavior of the neurons when they are active and only records their w values at the moment they return to the silent state.
In our earlier work [17], we considered cases where P was varied either by increasing TAB while keeping Tinactive fixed or by increasing both TAB and Tinactive but keeping the duty cycle (TAB/P ) constant. We showed that changing the period in the feedforward AB – LP network in either of these ways still allows the phase of LP to be controlled by either synaptic or intrinsic parameters at different ranges of periods. In the current model, our derived formulas (25) and (26) allow us to again consider either of those two possibilities. The same qualitative behavior exists in both cases, namely that there are distinct ranges of period over which one set of parameters or the other would dominate phase determination. However, the shapes of the phase curves and their dependence on various parameters are quantitatively different in the two cases.
4.3 Conclusions
Many neural networks maintain a constant relative phase in the activity patterns of participating neurons despite changes in network frequency [6, 25]. In CPGs this constraint on phase is of special importance because the underlying neural patterns are commanded to muscles that often have to be activated at precise phases of each cycle in order to produce meaningful behavior, for example, locomotion [29, 30]. We have built on our previous modeling results to propose mechanisms through which synaptic dynamics, such as short-term depression, can contribute to phase maintenance in face of changes in network frequency. Our most important findings are that synaptic interactions among follower neurons may affect their phase in each cycle of oscillation and that these interactions may extend the range of cycle periods for which there is phase maintenance beyond those made possible by the dynamics of the feed-forward synapses from the pacemaker neurons. These predictions are potentially important for understanding mechanisms underlying phase maintenance in the pyloric network and can be experimentally tested by manipulating the strength and dynamics of the synapses in this network using pharmacological agents or the dynamic clamp technique.
Acknowledgments
This work was supported, in part, by a grant from The City University of New York PSC-CUNY Research Award Program (CM), the National Science Foundation DMS-0315862 (AB, CM) and DMS-0615168 (AB) and the National Institutes of Health MH-60605 (FN).
5 Appendix
We numerically solved equations (1)–(14) to obtain our results. In these equations m∞(vx) =0.5(1+tanh((vx +1.2)/18)), w∞(vx) = 0.5(1+ tanh((vx −15)/5)), and τw(vx) = mx(40 − 30w∞(vx)). For both LP and PY, Ix = 75, gleak = 2, Eleak = −60, Einh = −80, gCa = 4, ECa = 120, gK = 8, and EK = −84. In all simulations, TAB = 300, τα = 1800, and τβ = 15.
In the case of the depressing synaptic AB input, mLP = 8.1, mPY = 8.4 and ḡAB = 1.8. When the LP and PY synaptic inputs were present, we set ḡLP = 1 and ḡPY = 2. However, when these synapses were not present, ḡLP and ḡPY were set equal to 0. The remaining parameter values were as follows : τk = 1650, τc = 3300, τd = 990, τa = 2700, τb = 150, τ1 = 60, τ2 = 600, τ3 = 210, τ4 = 300, x1 = 55, x2 = 35, P1 = 570 and P2 = 1470.
When the AB synapses were not depressing, we simply set dAB ≡ 0.38. We changed mLP = 2.55, mPY = 3.15, ḡAB = 1.4, ḡLP = 13, ḡPY = 11, τk = 1200, τc = 60, τd = 60, τa = 1350, τb = 240, τ1 = 60, τ2 = 1350, τ3 = 330, τ4 = 60, P2 = 1140 and x2 = 10.
We solved equations (25) and (26) using MATLAB. We used the same set of parameter values as we did when using XPPAUT. There are a few parameters in these equations that do not explicitly appear in (1)–(14) that can be estimated from the geometry of the nullclines. We set M1 = M2 = 3.12, ŵLP = ŵPY = 1. For the non-depressing case Fig. 9 A1 and A2, , τw, LP = 102, τw,PY = 126, and for the depressing case Fig. 9, B1 and B2, , τw, LP = 240, τw,PY = 255.
References
- 1.Ambrosio-Mouser C, Nadim F, Bose A. The effects of varying the timing of inputs on a neural oscillator. SIAM J Appl Dyn Syst. 2006;5:108–139. doi: 10.1137/050625795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Anderson WW, Barker DL. Synaptic mechanisms that generate network oscillations in the absence of discrete postsynaptic potentials. J Exp Zool. 1981;216:187–191. doi: 10.1002/jez.1402160121. [DOI] [PubMed] [Google Scholar]
- 3.Birmingham JT, Manor Y, Nadim F, Abbott LF, Marder E. An empirical model describing the dynamics of graded synaptic transmission in the lobster pyloric network. In: Bower James M., editor. Computational Neuroscience: Trends in Research. Plenum Press; NY: 1998. [Google Scholar]
- 4.Bose A, Manor Y, Nadim F. The activity phase of postsynaptic neurons in a simplified rhythmic network. J Comput Neurosci. 2004;17:245–261. doi: 10.1023/B:JCNS.0000037685.71759.1a. [DOI] [PubMed] [Google Scholar]
- 5.Cohen A, Ermentrout GB, Kiemel T, Kopell N, Sigvardt K, Williams T. Modelling of intersegmental coordination in the lamprey central pattern generator for locomotion. TINS. 1992;15:434–438. doi: 10.1016/0166-2236(92)90006-t. [DOI] [PubMed] [Google Scholar]
- 6.DiCaprio RA, Jordan G, Hampton T. Maintenance of motor pattern phase relationships in the ventilatory system of the crab. J Exp Biol. 1997;200:963–974. doi: 10.1242/jeb.200.6.963. [DOI] [PubMed] [Google Scholar]
- 7.Dickinson PS. Neuromodulation of central pattern generators in invertebrates and vertebrates. Curr Opin Neurobiol. 2006;16:604–614. doi: 10.1016/j.conb.2006.10.007. [DOI] [PubMed] [Google Scholar]
- 8.Ermentrout GB. n:m phase-locking of weakly coupled oscillators. J Math Biol. 1981;12:327–342. [Google Scholar]
- 9.Ermentrout GB. Simulating, analyzing, and animating dynamical systems: A guide to XPPAUT for researchers and students. SIAM. 2002 [Google Scholar]
- 10.Friesen WO, Pearce RA. Mechanisms of intersegmental coordination in leech locomotion. Sem Neurosci. 1993;5:41–47. [Google Scholar]
- 11.Grillner S. Control of locomotion in bipeds, tetrapods and fish. In: VBB, editor. Handbook of Physiology, section 1, The Nervous system. II. Maryland: Waverly Press; 1981. pp. 1179–1236. [Google Scholar]
- 12.Graubard K, Raper JA, Hartline DK. Graded synaptic transmission between identified spiking neurons. J Neurophysiol. 1983;50:508–521. doi: 10.1152/jn.1983.50.2.508. [DOI] [PubMed] [Google Scholar]
- 13.Hooper S. Phase maintenance in the pyloric pattern of the lobster (Panulirus interruptus) stomato-gastric ganglion. J Comput Neurosci. 1997;4:191–205. doi: 10.1023/a:1008822218061. [DOI] [PubMed] [Google Scholar]
- 14.Hooper S. The pyloric pattern of the lobster (Panulirus interruptus) stomatogastric ganglion comprises two phase-maintaining subsets. J Comput Neurosci. 1997;4:207–219. doi: 10.1023/a:1008867702131. [DOI] [PubMed] [Google Scholar]
- 15.Jones S, Kopell N. Local network parameters can affect inter-network phase lags in central pattern generators. J Math Biol. 2006;52:115–40. doi: 10.1007/s00285-005-0348-0. [DOI] [PubMed] [Google Scholar]
- 16.Mamiya A, Manor Y, Nadim F. Short-term dynamics of a mixed chemical and electrical synapse in a rhythmic network. J Neurosci. 2003;23:9957–9564. doi: 10.1523/JNEUROSCI.23-29-09557.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Manor Y, Bose A, Booth V, Nadim F. Contribution of synaptic depression to phase maintenance in a model rhythmic network. J Neurophysiol. 2003;90:3513–3528. doi: 10.1152/jn.00411.2003. [DOI] [PubMed] [Google Scholar]
- 18.Marder E, Calabrese R. Principles of rhythmic motor pattern generation. Physiol Rev. 1996;76:687–717. doi: 10.1152/physrev.1996.76.3.687. [DOI] [PubMed] [Google Scholar]
- 19.Marder E. From biophysics to models of network function. Annu Rev Neurosci. 1998;21:25–45. doi: 10.1146/annurev.neuro.21.1.25. [DOI] [PubMed] [Google Scholar]
- 20.Marder E, Bucher D. Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu Rev Physiol. 2006;69:291–316. doi: 10.1146/annurev.physiol.69.031905.161516. [DOI] [PubMed] [Google Scholar]
- 21.Mishchenko EF, Rozov NK. Differential Equations with Small Parameters and Relaxation Oscillators. New York: Plenum Press; 1980. [Google Scholar]
- 22.Morris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J. 1981;35:193–213. doi: 10.1016/S0006-3495(81)84782-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nadim F, Manor Y, Kopell N, Marder E. Synaptic depression creates a switch that controls the frequency of an oscillatory circuit. PNAS. 1999;96:8206–8211. doi: 10.1073/pnas.96.14.8206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nusbaum MP, Beenhakker MP. A small-systems approach to motor pattern generation. Nature. 2002;417:343–50. doi: 10.1038/417343a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.O’Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 1993;3:317–330. doi: 10.1002/hipo.450030307. [DOI] [PubMed] [Google Scholar]
- 26.Parker D, Grillner S. Activity-dependent metaplasticity of inhibitory and excitatory synaptic transmission in the lamprey spinal cord locomotor network. J Neurosci. 1999;19:1647–1656. doi: 10.1523/JNEUROSCI.19-05-01647.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rabbah P, Nadim F. Synaptic dynamics do not determine proper phase of activity in a central pattern generator. J Neurosci. 2005;25:11269–11278. doi: 10.1523/JNEUROSCI.3284-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rabbah P, Nadim F. Distinct synaptic dynamics of heterogeneous pacemaker neurons in an oscillatory network. J Neurophsyiol. 2007;97:2239–2253. doi: 10.1152/jn.01161.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sigvardt KA. Spinal mechanisms in the control of lamprey swimming. Am Zool. 1981;29:19–35. [Google Scholar]
- 30.Skinner F, Mulloney B. Intersegmental coordination of limb movements during locomotion: Mathematical models predict circuits that drive swimmeret beating. J Neurosci. 1998;18:3831–3842. doi: 10.1523/JNEUROSCI.18-10-03831.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]


