Antigen-driven CD4+ T cell and HIV-1 dynamics: Residual viral replication under highly active antiretroviral therapy

Abstract

Antigen-induced stimulation of the immune system can generate heterogeneity in CD4+ T cell division rates capable of explaining the temporal patterns seen in the decay of HIV-1 plasma RNA levels during highly active antiretroviral therapy. Posttreatment increases in peripheral CD4+ T cell counts are consistent with a mathematical model in which host cell redistribution between lymph nodes and peripheral blood is a function of viral burden. Model fits to patient data suggest that, although therapy reduces HIV replication below replacement levels, substantial residual replication continues. This residual replication has important consequences for long-term therapy and the evolution of drug resistance and represents a challenge for future treatment strategies.

The advent of highly active antiretroviral therapy (HAART) has provided a wealth of information on the interaction between HIV and the human immune system and is continuing to stimulate the debate on the basic mechanisms of viral pathogenesis (1–3). Posttherapy patterns of viral load decline, and changes in CD4+ T cell population structure inform our knowledge of heterogeneity in within-host viral replication and immune system reconstitution. A central paradox remains, however. How does HIV cause immune system failure while infecting only a small overall proportion of CD4+ T cells? We address this question by placing the within-host dynamics of HIV replication within the context of an immune system that is heterogeneously structured in terms of the distribution of cell turnover rates by diverse and repeated antigenic stimulation. We use a model of antigen-driven T cell proliferation (4–8) to show that HIV infection can reduce the ability of a single antigen-specific activated CD4+ T cell subpopulation to help antigen clearance. The proliferation rate distribution of the entire CD4+ T cell population then emerges naturally from a consideration of the effect of constant immune system stimulation by multiple antigens. Inclusion of such population heterogeneity within a model of HIV replication in the lymph nodes is then shown to provide a conceptual framework capable of explaining the following key observations: a rapid multiphase decline in HIV RNA levels after treatment (9–15); a rapid initial rise in CD4+ T cells after treatment, followed by a phase of slower recovery (16–18); a low prevalence of HIV-infected CD4+ T cells in the peripheral blood and lymph nodes, as measured by HIV DNA levels (19–24); an increase in viral load after antigenic stimulation induced by vaccination (25–30); and faster CD4+ T cell replication after therapy than before treatment (31).

One key point arising from this framework is that the CD4+ T cell population itself—not other cell classes—can provide the main reservoir (32–35) of long-lived infected cells, which have been shown by earlier models (36, 37) to be necessary to describe the observed multiphase posttreatment decline in HIV RNA levels. The hypothesis that long-lived CD4+ T cells are the dominant infected cell reservoir has recently received support from the results of studies (35, 38–40) of the effect of IL-6, tumor necrosis factor-α, and IL-2 on infected cell populations. Other cells (3, 36, 41, 42), such as macrophages (32) and follicular dendritic cells (24), are not precluded from playing a role, but for simplicity are ignored in the analyses described below.

We assume that CD4+ T cell susceptibility to HIV infection, infected cell life time, and viral production rates increase as a function of cell proliferation rate, an assumption supported by observations that CD4+ T cells are most susceptible to viral entry when dividing and that progress via the postinfection virus life cycle is slowed within resting cells (5–7, 43). The proportion of resting CD4+ T lymphocytes with integrated HIV DNA (some of which can produce infectious virus) is reported to be limited, but their numbers are higher than the number of infected macrophages (32). Furthermore, although the precise role of CD4+ T cells with unintegrated HIV DNA remains unclear, such cells may also provide another slowly replicating HIV reservoir.

Unlike earlier work (36, 37, 41, 44), our analysis does not assume that drug treatment regimens prevent all viral replication, thus allowing for comparisons between different treatment protocols. We illustrate how estimation of the absolute degree to which drugs inhibit viral replication is complicated by the dependence of the posttreatment rate of viral decay on the pretreatment reproductive potential of HIV. Another distinct aspect of our analysis is that parameters are estimated by simultaneously fitting the model to observed posttreatment measures of viral load and CD4+ T cell counts from a number of patients.

We start with the description of a simple model of T cell proliferation via antigenic stimulation, before turning to the dynamics of cell infection and death. The complexity of explicitly modeling quiescent and activated naïve and memory cell pools is avoided by describing all cells in an antigen-specific CD4+ T cell population, x_i (using dimensionless state variables), in terms of their mean activity (proportional to proliferation rate), ɛ(a_i). This variable is assumed to be a simple logistic function of antigen density, a_i, such that

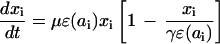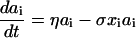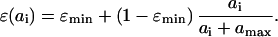1

The form of relationship between ɛ and a_i is chosen such that activity increases linearly at low antigen densities but saturates to one for high antigen densities, giving a maximum proliferation rate of μ per day. The population size of the antigen-specific T cell population is regulated through a logistic death rate such that the maximum population size increases proportionally with activity, ɛ(a_i), up to a maximum size of γ (typically up to 1% of the total T cell population size, ignoring cases of superantigens such as cytomegalovirus). This formulation captures the rapid die-away of activated proliferating cells after antigen clearance (45) without the need to explicitly model apoptotic mechanisms and memory/effector cell type differentiation. Antigen clearance occurs at a rate proportional to the density of antigen-specific CD4+ T cells. The model has three types of behavior depending on the replication rate, η, of the antigen (i.e., a pathogen). If η < σγɛ_min, antigen will eventually be eliminated completely, and the antigen-specific memory cell population size will fall to the baseline (quiescent memory cell) level of γɛ_min, maintained by a “quiescent” proliferation rate μɛ_min. For σγɛ_min ≤ η < σγ, antigen will be controlled but not eliminated, and the memory cell population size will reach an equilibrium somewhat above the baseline level. If η > σγ, then the immune system is unable to control antigen growth (i.e., immune failure); thus, σγ represents the threshold replication rate for immune escape.

When HIV is introduced into the system, this threshold is lowered proportionately to the viral burden induced. More precisely, if the susceptibility of a maximally active cell to infection is β (see Eq. 2 below), then the threshold replication rate for immune escape is reduced by a factor of approximately 1 − 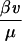, where v is the viral load. The model therefore captures a key aspect of HIV pathogenesis as well as progressively decreasing immunocompetence with increasing viral load (46).

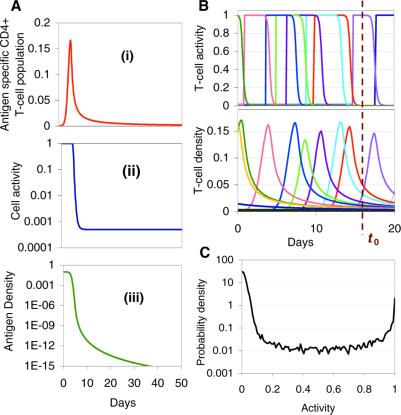
Fig. 1A shows the simulated CD4+ T cell proliferation response (in the absence of HIV) to antigenic stimulation for the case when antigen can be cleared completely. The activity of the antigen-specific CD4+ T cells remains high while the population expands during the process of antigen clearance, before decaying (along with the population size) to the slow turnover rate characteristic of quiescent memory T cells. Fig. 1 B and C shows how extending this framework to simulate specific CD4+ T cell responses against random exposures to multiple antigens gives rise to heterogeneity in the proliferation rates of the antigen-specific CD4+ T cell populations, depending on when in the past they were last challenged by antigen. All CD4+ T cells outside the actively replicating memory populations are assumed to turnover at the low baseline rate of quiescent cells. By averaging over all possible antigen-challenge event times, a continuous distribution can be obtained for the proliferation rate of nonnaïve CD4+ T cells. Interestingly, this distribution is bimodal, with the great majority of cells being quiescent (lowest proliferation rate) and most of the rest being highly active (highest proliferation rate). Hence, the model—without explicitly modeling CD4+ T cell activation processes (47)—effectively generates quiescent (memory/naïve) and active T cell pools.

Figure 1.

(A) Model response of antigen-specific CD4+ T cell population to stimulation by a nonreplicating antigen (η = 0; e.g., tetanus toxoid). (i) T cell population size; (ii) changing population proliferation rates during antigen clearance; (iii) antigen density. Parameter values: Initial dose = 0.1; σ = 50 per day; μ = 2 per day; γ = 10⁻⁴; a_max = 10⁻⁶; ɛ_min = 0.0005. (B) Schematic illustration calculated by using stochastic model of how constant random exposure to multiple antigens leads to a cross-sectional distribution of antigen-specific subpopulation activities at a given time t₀, which consists of large numbers of low activity memory cells (from past antigen exposures) and a few highly active cells aiding clearance of recently acquired antigens. Curves shown are from a random multiple antigenic stimulation of a CD4+ T cell population consisting of 1,000 antigen-specific subpopulations with dynamics described by Eq. 1, assuming that random antigen replication rates are drawn from an exponential distribution with mean of 0.1 per day. (C) An example of such a dynamically generated distribution calculated by averaging over 10,000 realizations of the simulation model. The finite width of the low activity side of the distribution reflects the range of equilibrium memory cell activity levels required to control replicating antigen. The bimodality of such distributions can be proved analytically. Other parameters are as described for A.

The effect of this heterogeneity in CD4+ proliferation rates on overall HIV dynamics can be assessed by introducing HIV into a system consisting of thousands of such antigenic-specific populations. However, although such an approach may be necessary to model long-term HIV pathogenesis, a reasonable description of short-term posttherapy dynamics can be obtained by neglecting individual antigen responses and activation/deactivation processes and approximating the dynamically generated proliferation distribution described above with a static bimodal parametric form, f(ɛ). Denoting the density of uninfected cells with activity ɛ (which varies from ɛ_min to 1) by x(ɛ) and the proportion of infected cells by y(ɛ), our model becomes

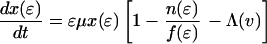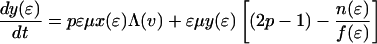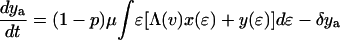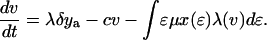2

The model incorporates density-dependent proliferation of CD4+ T cell populations, with the equilibrium population size, n(ɛ) = x(ɛ) + y(ɛ), of cells with proliferation rate ɛμ being proportional to f(ɛ). Infection occurs at a rate proportional to cell turnover, with the saturating form of Λ(v) = v/(v + μ/β) corresponding to a situation in which the great majority of cell infection (and consequent viral production) occurs only when a cell is actively dividing (nonquiescent). This functional form of Λ(v) (≈βv/μ for v ≪ μ/β) can be analytically derived from more complex models that explicitly describe the quiescent and active phases of the cell cycle. Once a cell is infected, we assume either that it immediately starts producing large amounts of virus (burst size λ) and is cleared without further division (the cell class y_a) or that, with a low probability (32), P, it survives the cell replication cycle and enters a longer-lived pool of “latently” infected cells producing little or no virus until cell replication occurs once more. For simplicity, we assume here that such infected cells produce no virus while quiescent, and then reenter the virus-producing infected cell pool, y_a, on next dividing, again with probability 1 − P. We are therefore effectively neglecting the effect of any permanently nonproductive pool of infected cells (32), because it does not contribute to viral dynamics. Also, we ignore the nonproductive eclipse period (which might be as long as 1 day) after cell infection, because this period has little effect on dynamics occurring on the time scale of weeks to months. Lastly, note that the population variables in Eq. 2 are normalized such that the total equilibrium CD4+ T cell population size is one in the absence of HIV; thus, all state variables need to be multiplied by N, the (quasi)equilibrium number of CD4+ T cells in 1 μl of plasma, to be compared with data.

The clearance rates of actively infected cells and free virus are denoted δ and c, respectively. We would emphasize that precise estimation of these parameters from posttherapy declines in viral load is extremely problematic, because both contribute in similar ways to the overall decay rate of virus after initiation of HAART. Furthermore, in fitting to a single patient alone, both parameters cannot be readily distinguished from the drug efficacy, unless the crude assumption that drugs inhibit 100% of viral replication is made. However, if data from multiple patients are fitted simultaneously, drug efficacy can be somewhat better resolved, under the assumption that the considerable variation between patients in the rate of decline of viral load is caused by differences in drug effect. We here model reverse transcriptase inhibitor (RTI) action through a multiplicative reduction factor affecting the transmission coefficient, β, and protease inhibitor action by a reduction in the production rate of infectious virus, λ, and the addition of a class of noninfectious virus.

Redistribution between the lymph nodes and peripheral blood is one explanation for the observed increases in peripheral CD4+ T cell numbers in the first 3–4 weeks of HAART (16–18), the suggestion being that HIV-induced cell retention in lymphoid tissues is reduced as viral load declines. We model these transport processes by denoting the total CD4+ T cell populations in these compartments as T_L and T_P respectively. Then,

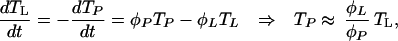3

where, φ_L and φ_P are, respectively, the transport rates from lymphoid tissues to the peripheral blood and vice versa, and the second equality holds so long as these rates are large compared with those of other dynamical processes. HIV-induced cell retention can be modeled by expressing φ_L as a decreasing function of viral load. A simple suitable functional form is φ_L/φ_P = 0.02/[1 + (b − 1)/(1 + d log(v/10⁶)], where b measures the degree of cell retention in the lymph induced by a viral load of 10⁶ per ml, and d determines how retention declines with viral load. When v = 0, φ_L/φ_P ≈ 0.02, corresponding to an assumption that 2% of CD4+ T cells reside in the peripheral blood for an uninfected individual. In this context, Eq. 2 then reflects HIV dynamics in the lymph, with N being the equilibrium number of CD4+ T cells in 0.02 μl of lymph. This model of adherence empirically captures trends in CD4+ T cell numbers well but offers little insight into the processes controlling adherence. More mechanistic models are therefore one topic of ongoing research.

For model validation and parameter estimation, we used maximum likelihood methods to fit to posttherapy peripheral blood HIV RNA levels and CD4+ T cell numbers from nine patients—three in each of three HAART treatment groups (see Appendix). Furthermore, we coupled the model to a single antigen-specific CD4+ T cell population with dynamics as described by Eq. 1 (but with the addition of HIV), to allow fitting to averaged viral load data from 10 patients who were given a booster dose of tetanus toxoid (30). The model was fitted to results from the nine patients and the averaged viral load data after immunization simultaneously, allowing most parameters to be common to all patients and only a few to vary between patients. The results presented here use a discrete form of the model with two proliferation rate classes corresponding to the two peaks of the dynamically generated proliferation rate distribution (Fig. 1B). Better fits can be obtained with finer stratification of the cell activity spectrum but at a high computational cost.

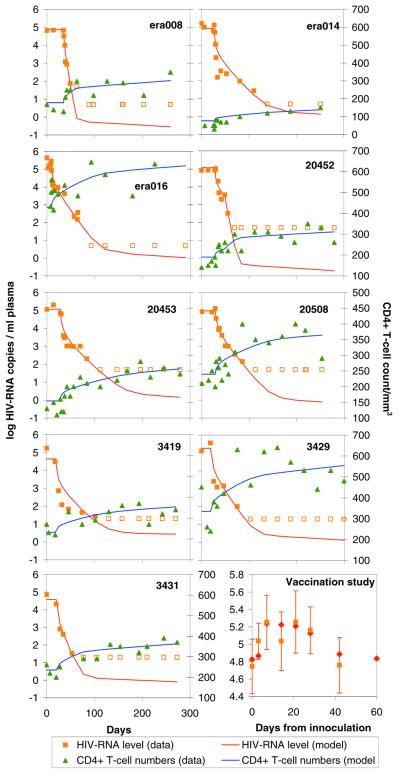
Fig. 2 shows the good correspondence between model fits and posttherapy viral load and CD4+ data obtained, and Tables 1–3 give the corresponding maximum likelihood parameter estimates (e.g., viral half-life and infected cell half-lives). The figure should be regarded as demonstrating model validation rather than being the primary goal of this work, but Tables 1–3 present the key numerical results arising from the conceptual framework developed. For all patients, between 1.5 and 3.5% of CD4+ T cells are estimated to be proliferating at the fastest rate of one division per 16 h. The infected fraction of this population is responsible for over 99% of virus production at the start of therapy, and its clearance occurs during the first rapid phase of viral load decline. Constraining model fits to give the low proportion of cells infected suggested by measured HIV DNA levels (under 0.1%; refs. 20, 21, and 39) gives parameter estimates indicating that such cells produce hundreds of virions (24, 31) before dying in under a day (net clearance rate of >3 per day). Our estimates of infected cell clearance rates for highly productive cells differ significantly from previous estimates (9, 10, 41), largely because earlier work has always assumed that antiretroviral therapy prevents 100% of viral replication in vivo. The great majority of CD4+ T cells are estimated to be quiescent (with an interdivision time of approximately 500 days), and the small proportion of these cells that are infected are estimated to produce the very small amounts of virus responsible for the second, slower phase of viral load decline. Free virus clearance rates are estimated to be very large (<2-h lifetime), but the lack of high temporal resolution data on primary viral load decline means that we had limited information with which to estimate this parameter. The model fit to postimmunization data illustrates how a relatively small antigen-induced, highly activated cell population can increase the susceptible target cell pool sufficiently to reproduce the sizeable postvaccination fluctuations in viral load seen in many studies (25–30), providing further support for this conceptual framework.

Figure 2.

Best fit of within-host HIV replication model to observed post-HAART changes in HIV RNA levels and CD4+ T cell counts in 9 patients in three therapy studies (see text) and to observed postimmunization viral load fluctuations averaged over 10 patients who received tetanus toxoid. Maximum likelihood methods were used to simultaneously fit the model to these data, allowing only a few parameters to vary between patients. Note that, for HIV RNA measurements, closed and open squares represent measurements above and below the detectability threshold of the assay.

Table 1.

Patient-Specific Fitted Parameters

Patient	Proportion of cells in most active state	Fraction of viral replication prevented by drug	β	N
Vaccination	0.016  (0.007, 0.028)	N/A	5.11  (2.93, 12.76)	1,089  (668, 1602)
era008	0.015  (0.004, 0.034)	0.63  (0.23, 0.98)	9.95  (3.36, 208.71)	652  (294, 1677)
era014	0.030  (0.007, 0.035)	0.76  (0.24, 0.95)	8.71  (2.46, 58.07)	364  (124, 734)
era016	0.034  (0.008, 0.034)	0.36  (0.14, 0.78)	2.84  (1.98, 11.53)	1,161  (742, 1711)
20452d	0.034  (0.006, 0.035)	0.47  (0.16, 0.83)	3.19  (1.86, 22.05)	587  (323, 858)
20453e	0.031  (0.009, 0.034)	0.54  (0.16, 0.87)	4.39  (2.38, 28.85)	538  (278, 859)
20508e	0.032  (0.006, 0.034)	0.32  (0.08, 0.80)	2.82  (2.09, 30.13)	672  (417, 1019)
3419	0.008  (0.004, 0.034)	0.50  (0.47, 0.52)	13.95  (5.27, 24.52)	744  (389, 1025)
3429	0.027  (0.009, 0.035)	0.52  (0.47, 0.54)	4.36  (2.36, 10.32)	1,108  (753, 1375)
3431	0.007  (0.004, 0.034)	0.50  (0.43, 0.53)	15.97  (3.29, 30.69)	745  (394, 1020)

Parameter estimates and approximate 95% multivariate confidence bounds, together with transmission variables derived from fitted parameters. Most parameters were fitted to have common values for all patients, with only a few being patient-specific. Parameter estimates quoted refer to the dimensionless equations given in the text; all state variables from these equations need to be multiplied by N to give population size corresponding to 0.02 μl of lymphoid tissue (assuming lymphoid and peripheral blood compartments are of equal volume). 

Table 3.

Transmission variables calculated from fitted parameters

Patient	Pretreatment R0	Posttreatment k	Ratio of pretreatment to posttreatment k
Vaccination	1.34 (1.16, 2.52)	0.034 (0.015, 0.059)	0.86 (0.63, 0.93)
era008	2.46 (1.17, 26.67)	0.032 (0.010, 0.070)	0.64 (0.19, 0.92)
era014	4.11 (1.30, 21.70)	0.062 (0.015, 0.070)	0.49 (0.20, 0.88)
era016	1.54 (1.13, 4.40)	0.070 (0.017, 0.070)	0.81 (0.48, 0.94)
20452d	1.72 (1.09, 5.49)	0.070 (0.015, 0.070)	0.76 (0.43, 0.96)
20453e	2.18 (1.18, 7.67)	0.065 (0.020, 0.070)	0.68 (0.36, 0.92)
20508e	1.44 (1.07, 4.68)	0.066 (0.013, 0.070)	0.83 (0.46, 0.97)
3419	2.01 (1.83, 2.03)	0.019 (0.010, 0.069)	0.70 (0.70, 0.74)
3429	1.88 (1.79, 1.91)	0.056 (0.019, 0.070)	0.73 (0.72, 0.75)
3431	1.98 (1.72, 2.03)	0.016 (0.010, 0.070)	0.71 (0.70, 0.76)

See legend to Table 1. Note that posttreatment k is restricted to be in the range of 0.015–0.07 per day; δ is restricted to be in the range of 0–4 per day; and μ is restricted to be in the range of 1–2 per day. 

Model results are consistent with the view that initial posttherapy CD4+ T cell increases are largely due to cell redistribution (16–18) between lymph nodes and peripheral blood, though proliferation can also play some role, particularly if a wider range of T cell activities are modeled. Changing proliferation rates certainly do play an important role in CD4+ T cell kinetics after the initiation of therapy. As HIV RNA levels decline, so does the proportion of rapidly proliferating (highly activated) cells that are infected, allowing that population to increase in size significantly within a few weeks—though while remaining a small proportion of the entire CD4+ T cell population. An increase in the mean rate of CD4+ T cell replication is therefore induced by the initiation of HAART, in line with recent observations of CD4+ T cell kinetics (31). However, redistribution may explain part of this effect, given that HIV-induced retention/adherence of activated CD4+ T cells in the lymphoid tissues is greater than it is for quiescent cells.

Of key clinical importance is the potential of this mathematical framework to give insight into the degree to which different drug regimes inhibit viral replication. For all the patients considered here, drug action is estimated to be effective in the sense of reducing the basic reproduction number (average number of infected cells produced by one initially infected cell), R₀, of HIV (44, 48) within the host to below the critical threshold of one required for sustained viral persistence (49). However, our estimates indicate that the effect of drugs is often to push R₀ only slightly below this critical threshold, perhaps reflecting the implicit use of this criterion in defining the minimum inhibitory concentration and hence in determining dosage. These estimates imply that significant residual viral replication does occur under HAART (50, 51), with steeper and deeper first-phase declines indicating lower levels of replication. Caution is required; estimates of drug effect are confounded with the death rate of virus-producing cells and somewhat depend on the detail with which the CD4+ T cell activity distribution is modeled (such that assigning more activity levels can increase drug inhibition estimates). However, even allowing for structural and parameter uncertainty, residual viral replication still has important consequences for the evolution of drug resistance. Because the key factor determining the frequency of emergence of de novo resistance is the posttherapy value of R₀ (44), our results suggest that clinical treatment should not only be aimed at reducing viral load to below detectable limits but at doing so as rapidly as possible so as to minimize residual replication.

Some caution should also be exercised in interpreting the estimates of pretherapy viral β, because the model (although capturing many aspects of pathogenesis) has been constructed to equilibrate at the values of viral load and CD4+ count corresponding to patient measurements before the initiation of therapy. In reality, these estimates may therefore more reflect the stage of pathogenesis reached by the patient than differences in viral virulence between patients.

Model predictions and their agreement with observed pattern give insight into the possible effects of drug-induced activation of CD4+ T cell populations (35, 38) as a therapeutic intervention for eliminating otherwise long-lived reservoirs of infected cells. By activating a large proportion of all CD4+ T cells, such treatment would be expected to result in a short burst of viral production where the previously quiescent and long-lived infected cells are eliminated in a matter of days (39). Repeated courses of drugs that stimulate CD4+ T cell activation should therefore enhance the likelihood of viral elimination from the host. However, we predict that the outcome of such therapy critically depends on the level of residual viral replication under the accompanying antiretroviral therapy. If R₀ is just under one before this kind of treatment, the effect of massively increased cell activation may push R₀ above one during treatment, thereby potentially maintaining (or even increasing) the proportion or number of cells infected with HIV (52). Ongoing clinical studies together with increasing experimental data on the relationships between HIV infection, antigen responses, and T cell kinetics will allow testing of both these predictions and many of the basic immunological and virological assumptions underlying our model framework.

In this article, we have developed a simple conceptual framework that explains changes in viral load and CD4+ T cell abundance in patients undergoing HAART and viral load fluctuations after immunization. This framework is consistent with recent observations of CD4+ T cell dynamics. Extensions of this framework that explicitly model multiple antigen and HIV-specific responses together with CD8+ T cell dynamics also have the potential to give greater insight into the population processes underlying long-term HIV pathogenesis. Key to the approach is the incorporation of activation heterogeneity within CD4+ T cell subpopulations caused by past and present exposure to a diverse array of antigens. A simple model of T cell proliferation under repeated and diverse antigenic exposure predicts a bimodal distribution in division rates. Thus, the CD4+ T cell population essentially consists of one group of fast dividing cells and one group of slowly replicating cells. The latter provides a reservoir for HIV-1, whereas the former harbors the majority of the viral population. By using sophisticated parameter estimation techniques based on fitting to many patients simultaneously, viral turnover rates are in reasonable agreement with earlier estimates (9, 10, 41), but estimates of infected cell lifetime and of the impact of HAART on viral replication rates differ significantly, with the apparent precision of earlier estimates having been shown to be largely due to restrictive model assumptions. Of particular clinical significance is the prediction that HAART may leave a residue of viral replication (51) that may be important with respect to the evolution of resistance. Antiretroviral therapy should therefore aim to reduce viral burden, and hence the net replication rate, as rapidly as possible.

Table 2.

Parameters common to all patients

Parameter	Estimate
μ	2.00  (1.00, 2.00)
ɛmin	0.0011  (0.0003, 0.0022)
λ	185.80  (110, 296)
δ	4.00  (0.97, 4.00)
c	11.94  (2.20, 17.80)
p	0.000026  (10−6, 0.0006)
b	1.74  (1.38, 2.01)
d	0.11  (0.05, 0.18)
γ	0.0075  (0.0004, 0.024)
amax	5.34 × 10−4 (10−10, 0.036)

See legend to Table 1. Certain parameters are assigned assumed values: η (replication rate of tetanus toxoid) = 0; s = 50 per day, x₀ (initial size of tetanus-specific CD4 + pool) = γɛ_min. 

Abbreviations

HAART

highly active antiretroviral therapy

RTI

reverse transcriptase inhibitor

AZT

3′-azido-3′-deoxythymidine

Appendix

All nine patients were initially naïve to antiretroviral agents. Three patients (20508, 20453, and 20452) were treated with a combination of RTIs [Zidovudine (AZT) and Lanivudine] and one protease inhibitor (Ritonavir; ref. 15). Blood was sampled at 0, 2, 7, 10, and 14 days, then weekly until week 4, and then monthly from week 6, with HIV RNA being measured by reverse transcription–PCR (Amplicor HIV monitor, Roche Molecular Biochemicals) in a standard protocol with an input of 200 μl of plasma resulting in a lower detection limit of, on average, 234 (99–670) copies per ml. Two patients (3431 and 3429) were treated with a combination of three RTIs (Nevirapine, AZT, and Didanosine), and one (3419) was treated with two RTIs (AZT and Didanosine; ref. 53). Blood was collected at the start of treatment, at weeks 1, 2, and 4, then every 4 weeks until week 60, and subsequently at 2-monthly intervals, with the same HIV RNA assay described above, except that ultracentrifuging was used to obtain a lower detection limit of 20 copies per ml. The remaining three patients (era008, era014, and era016) received a combination of five drugs: four RTIs (AZT, 3TC, Abacavir, and Nevirapine) and one protease inhibitor (Indinavir; ref. 13). HIV RNA was measured by using the nucleic acid sequence-based RNA amplification method (NucliSens HIV-1, Organon Teknika–Cappel) in a protocol with 2 ml of plasma input and a 10-fold RNA-input increase in the amplification step, resulting in a lower detection limit of five copies per ml. In all nine patients, CD4+ T cells were enumerated by using immunostaining and flow cytometry.

HIV RNA and CD4+ count data and corresponding model outputs were scaled to the approximate plasma volumes used for measurement. The data were assumed to arise from negative binomial distributions, where the variance was calculated as the Poisson sampling variance for the sample volume plus measurement errors estimated from earlier studies (0.5 log for RNA and 50 for CD4; refs. 54 and 55). The best fitting maximum likelihood parameter set is that which minimizes −2 log(likelihood). Nonlinear minimization algorithms were used (56), with the model being numerically integrated by using Burlisch–Stoer methods for each point sampled in parameter space. Approximate univariate 95% confidence bounds were calculated by random Latin-Hypercube sampling of the multidimensional maximum likelihood confidence region in the vicinity of the best fit point, together with extensive sensitivity analysis and systematic exploration of parameter interdependencies. However, some caution should still be exercised in interpreting these bounds, given that the exact confidence region may be highly disconnected.