Abstract
Nonelectrolyte polymers of poly(ethylene glycol) (PEG) were used to estimate the diameter of the ion channel formed by the Bacillus anthracis protective antigen 63 (PA63). Based on the ability of different molecular weight PEGs to partition into the pore and reduce channel conductance, the pore appears to be narrower than the one formed by Staphylococcus aureus α-hemolysin. Numerical integration of the PEG sample mass spectra and the channel conductance data were used to refine the estimate of the pore's PEG molecular mass cutoff (∼1400 g/mol). The results suggest that the limiting diameter of the PA63 pore is <2 nm, which is consistent with an all-atom model of the PA63 channel and previous experiments using large ions.
INTRODUCTION
Bacillus anthracis secretes three proteins whose concerted action causes late-stage anthrax toxicity. Some of the physical properties of these toxins, and the steps leading to cell death, were outlined elsewhere (1–5). Briefly, protective antigen 83 (PA83, 83 kg/mol) binds to target cells, is cleaved by furin-like proteases, and the 63-kg/mol fragment (PA63) that remains bound to the membrane oligomerizes into a heptameric prepore complex, pre-(PA63)7. Lethal factor (LF, 90 kg/mol) and edema factor (EF, 89 kg/mol) bind to pre-(PA63)7, and the two complexes, LF:pre-(PA63)7 and EF:pre-(PA63)7, become associated with endocytotic vesicle membranes. Acidification of the endosome interior is thought to cause the prepore to form a functional transmembrane ion channel (PA63)7, which facilitates the entry of LF and EF into the cytoplasm. Once inside the cell, LF interferes with mitogen-activated protein kinase kinase (MAPKK) signaling proteins and EF-increased cAMP production, which can lead to cell death.
The process by which (PA63)7 catalyzes LF and EF transport into the cytosol remains in question. Recent electrophysiology studies demonstrated the ability of full-length LF (6,7) and EF (6,8,9) and the N-terminal domains of LF and EF (LFN and EFN) (8,10) to interact with (PA63)7 channels in planar bilayer membranes. Based on the pattern of (PA63)7 channel ionic current blockades caused by LFN, EFN, and LF as a function of transmembrane pH gradient and the applied potential, others suggested that the proteins and their fragments are driven completely through the channel (8,10), reminiscent of protein-conducting channels in the endoplasmic reticulum (11,12). Although compelling, these experiments did not directly demonstrate the translocation of LF or the toxin fragments through the (PA63)7 channel, as was shown for single-stranded DNA translocation through the Staphylococcus aureus α-hemolysin (αHL) channel (13).
Understanding the size of the (PA63)7 channel is important for placing constraints on the mechanism(s) by which the two anthrax toxins LF and EF are transported into the cytoplasm. An earlier key study estimated the effective (PA63)7 channel pore diameter using tetraalkylammonium ions (14,15). The results suggested that the narrowest part of the channel is ∼1.1 nm in diameter (14), and the cis entrance diameter is ∼1.2 nm (15,16), which is significantly smaller than LF or EF in their native conformations (e.g., Fig. 1) (17,18). Another approach, which estimates the channel pore diameter from conductance measurements and assumes that the channel is a uniform right circular cylinder (19), is not appropriate for sizing the (PA63)7 channel because its conductance is not proportional to the bulk electrolyte conductivity (20), and a model suggests that the pore is lined extensively with negative charges (21).
FIGURE 1.
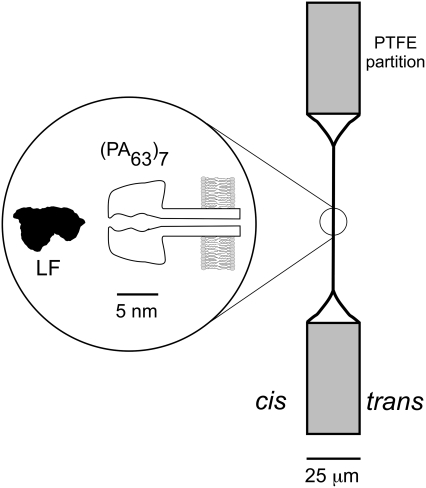
Schematic view of the experimental system. Bacillus anthracis PA63 protein, added to one side (cis) of a planar bilayer membrane formed on a small hole in a PTFE Teflon partition, spontaneously binds to the membrane and forms a heptameric ion channel (PA63)7. The illustration of the channel is based on a theoretical model (21). A cross section of Bacillus anthracis lethal factor (LF) is shown to scale. The LF binds strongly to the (PA63)7 ion channel (6,7,20).
Here, we estimate the diameter of the (PA63)7 channel pore, using differently sized nonelectrolyte poly(ethylene glycol) (PEG) molecules. The PEGs reduce the bulk conductivity of electrolyte solutions. Therefore, polymers that are small enough to partition into the pore reduce the channel's conductance (22). Thus, the channel PEG molecular mass cutoff and the hydrodynamic radii of the polymers (23) provide a measure of pore diameter. Although no theory accurately accounts for the partitioning of PEGs into channels (22,24–28), these polymers were used for estimating the lumen diameters of several channels (22,25,27,29–33) and the porosity of cell walls (29,34,35). This method avoids the potentially strong coulombic interactions that occur between ionic probes and ion channels decorated with fixed charges (21,36).
MATERIALS AND METHODS
PEG and PEG-free electrolyte solutions
The PEG-free electrolyte solution consisted of 0.1 M KCl, 5 mM MES (FLUKA, Ronkonkoma, NY), pH 6.6, with a bulk conductivity of 12.6 mS/cm. The desired solution pH value was set with KOH (J.T. Baker, Phillipsburg, NJ). Stock PEG solutions were made with 25 g of PEG in 55 mL of 0.1 M KCl, 5 mM MES, at pH 6.6. The mean molecular masses of PEG400 to PEG20000 (FLUKA, Sigma-Aldrich, St. Louis, MO) ranged from 400–20,000 g/mol. The final PEG concentration was sufficiently small to avoid the polymer-polymer repulsion that could increase PEG partitioning into the channel (26). In addition, the solution conductivity with a similar weight percent PEG is independent of the PEG molecular mass (37,38).
Channel reconstitution in planar lipid bilayer membranes
The method of membrane formation was described previously (39). Briefly, lipid bilayer membranes were formed on a ∼100-μm-diameter hole in a 25-μm-thick Teflon partition that divided a Teflon chamber. For bulk PEG partitioning experiments, the membrane-forming lipid solution was DiPhyPC (1,2-diphytanoyl-sn-glycero-3-phosphocholine) dissolved in pentane (Burdick and Jackson, Muskegon, MI) at 10 mg/mL. Initially, electrolyte solutions partially filled each half-chamber (volume, ∼2 mL; surface area, ∼1.2 cm2). Approximately 15 μL of lipid in pentane was applied at the air-solution interfaces when the fluid levels were below the hole in the partition. Using the method of Montal and Mueller (40), the fluid levels were slowly raised above the hole to form a lipid bilayer that was bathed on both sides with electrolyte solution. Before raising the fluid levels, the rim of the hole was lightly coated with hexadecane in pentane (1:100 v/v).
After formation of the membrane, single (PA63)7 channels were created by adding ∼0.3 μL of ∼0.2 mg/mL PA63 (List Biological Laboratories, Campbell, CA) in 10 mM bis Tris propane, pH 8.5, to one half-chamber (the cis compartment). Fig. 1 indicates the nomenclature, and provides a depiction of the channel and membrane geometry. Two Ag/AgCl electrodes (In-Vivo Metrics, Healdsburg, CA) were used to apply a potential across the partition and membrane. During data acquisition, the membrane potential was applied to the cis end of the channel, with the trans end held at virtual ground. A positive potential drove cations from the cis to the trans chamber. All experiments were performed at room temperature, i.e., 22.5 ± 1°C.
For experiments that used PEG tethered to lipid head groups, we used asymmetric membranes comprised of DiPhyPC and DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine) at a ∼1:1 mol ratio on the trans side, and a ∼1:1 mol ratio mixture of DiPhyPC and either DOPE-PEG350 (1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(poly(ethylene glycol))-350]) or DOPE-PEG3000 (1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(poly(ethylene glycol))-3000]). The stock solutions of DOPC, DOPE-PEG350, and DOPE-PEG3000 were dissolved in chloroform (J.T. Baker, Phillipsburg, NJ). All lipids were obtained from Avanti Polar Lipids (Alabaster, AL).
Channel size estimated with PEGs
The diameter of the (PA63)7 channel was estimated from the size of the PEG molecules that partitioned into the pore from the bulk aqueous phase. The ionic current of single (PA63)7 channels reconstituted in a membrane was initially recorded in buffer without PEG, I(−PEG). Poly(ethylene glycol) was introduced to both reservoirs by the addition of concentrated PEG stock solutions. The ionic current in the presence of PEG, I(+PEG), was then measured to determine the ratio I(+PEG)/I(−PEG). Instantaneous current-voltage (I/V) relationships of (PA63)7 channels in the absence and presence of PEG were measured with V = +200 mV to −200 mV in 10-mV steps. The duration of each voltage step and the voltage-off period between steps were 1 s each.
Matrix-assisted laser desorption ionization–time-of-flight analysis of PEG samples
Because commercially available PEGs are polydisperse in molecular mass, we characterized their mass distributions using a Voyager DE-STR (PerSeptive Biosystems, Framingham, MA) matrix-assisted laser desorption ionization (MALDI) mass spectrometer in reflectron mode. Desorption/ionization was produced by irradiation with pulsed ultraviolet light (337 nm) from a nitrogen laser. Samples were prepared as 1% w/w solutions in distilled water, and were mixed 1:1 with a matrix solution consisting of 1:1 acetonitrile:water saturated with 2-(4-hydroxyphenylazo) benzoic acid (Sigma, St. Louis, MO), with 0.1% fluoroacetic acid added. The instrument was operated at 20 kV in the negative ion mode, using an extraction delay time set at 200 ns. The final spectra were averaged from 100 shots with the laser power set slightly over the threshold for the spectral appearance, to limit decomposition and reduce background levels.
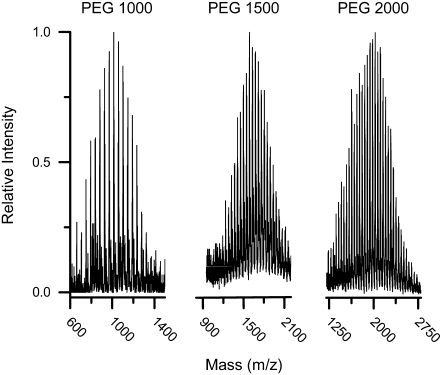
The MALDI–time-of-flight (TOF) spectra of several PEG samples used in this study are shown in Fig. 2. The full widths at half-maximum of the PEG mass distributions were proportional to the square root of the peak mass, which indicates a Poisson distribution in the polymerization. A spectrum of a PEG sample that shows a distribution of molecular weights indicates that the yields of individual n-mers are independent of each other, and that the sensitivity of the detector to PEG mass can be ignored over a single molecular mass distribution: the instrumental sensitivity variation is <20% over the range 1000 g/mol to 10,000 g/mol.
FIGURE 2.
The MALDI-TOF mass spectra of three polydisperse PEG samples used in this study (PEG1000, PEG1500, and PEG2000 g/mol mean molecular masses).
RESULTS AND DISCUSSION
The goal of this study was to estimate the diameter of the limiting (i.e., smallest) aperture of the Bacillus anthracis (PA63)7 ion channel, using differently sized nonelectrolyte PEG polymers (22,25,31,32,36,41,42). The largest PEG molecule that partitions into the pore was determined, and the channel size was then inferred from the PEG hydrodynamic radii (22,23). Because the limiting aperture diameter can only be determined if the polymer is transported through the channel, we performed control experiments to test whether the results obtained with soluble PEGs provide sufficient proof for PEG translocation this possibility.
Effects of PEGs on (PA63)7 single-channel conductance
The PEGs smaller than the pore diameter should enter the pore and reduce the channel conductance, whereas larger PEGs that cannot enter the pore should have little or no effect on the ionic current (22,25,31,32,36,41,42). A typical response of the (PA63)7 single-channel current to PEGs with different molecular masses is shown in Fig. 3. Relatively small polymers (e.g., PEG400) markedly decreased the current, whereas larger ones (e.g., PEG 4000) did not. Thus, PEG400, but not PEG4000, partitions into the channel pore. The small but perceptible decrease in current caused by PEG1500 suggests that PEGs in the lower molecular mass fraction of that polymer dispersion (Fig. 2, center) are small enough to enter the pore (see below).
FIGURE 3.
Single (PA63)7 channel ionic current response to PEG. The electrolyte solution contained 0.1 M KCl, pH 6.6, and 1.2% (w/w) PEG. The applied potential was V = +100 mV.
The effects of different concentrations of PEGs on the (PA63)7 mean single-channel current at −70 mV applied potential, normalized to that in the absence of the polymer, is shown in Fig. 4. As expected, the relatively small polymers that partition into the pore decreased the current monotonically over a wide range of PEG concentration (Fig. 4, open symbols). This conductance decrease can be described by a simple model in which one PEG molecule reacts reversibly with a single (PA63)7 pore with a dissociation constant, KD = 9 mM (Fig. 4, solid line). If we assume that the equilibrium constant and the rate constants for the dissociation and association of the polymer with the pore (i.e., koff and kon, respectively) are defined as KD = koff/kon, that the reaction is diffusion-controlled, and kon ≈ 108 M−1s−1, as estimated from the Smoluchowski treatment of diffusion (43), then koff ≈ 106 s−1. Thus, the mean time that a PEG molecule would be associated with the pore is τ = 1/koff ≈ 10−6 s. Under the experimental conditions used here, τ would need to be ∼20-fold greater to see individual PEG-induced blockades. Indeed, single-channel recordings at a 10-kHz bandwidth with [KCl] = 0.1 M, 1 M, and 4 M demonstrated that none of the PEGs cause transient current blockades that last long enough to be detected (data not shown). In contrast, the mean residence time for small PEGs in the αHL channel is ∼100 μs for 1 M NaCl (25,44), and ∼10 ms for 4 M KCl (45).
FIGURE 4.
The PEG molecular mass and concentration dependence for the (PA63)7 ionic current. The results obtained with five differently sized PEG samples (PEG400 (open squares); PEG1000 (open circles); PEG1500 (solid triangles); PEG2000 (solid down triangles); and PEG4000 (solid diamonds) are shown. The solid line is the prediction of a model for PEG partitioning, assuming a 1:1 (PEG:pore) equilibrium constant KD = 9 mM. (Inset) The effect of Dextran 4900 on the (PA63)7 channel ionic current. The applied potential was V = −70 mV.
Surprisingly, for [PEG] > 10 mM, even the larger polymers that are presumably pore-impermeant decreased the (PA63)7 channel conductance (Fig. 4, solid symbols). The decrease in current caused by the larger PEGs for 10 mM < [PEG] < 100 mM was essentially independent of the PEG molecular mass. The steeper dependence on the concentration of PEG caused by the larger polymers rules out a 1:1 (PEG:pore) equilibrium reaction scheme. If we assume that N molecules of the larger PEGs bind simultaneously to the pore and reduce the channel conductance, the data can be fit with N = 2 (not shown). However, we observed essentially the same effect with a chemically different polymer, dextran 4900 (Fig. 4, inset), which suggests that the conductance decrease caused by the larger PEGs is not solely attributable to highly specific chemical interactions between the polymer and the channel.
It was shown that PEGs that are too large to partition into a relatively large ion channel (e.g., αHL) at low polymer concentration can do so when the PEG concentration is very high because of interactions (i.e., entropic repulsion) between the polymers in the bulk (26,46). The “free energy of confinement” for the larger PEGs in the αHL pore was estimated to be ΔF ≈ 9 kT (26). By applying this treatment (Eq. 9 and Fig. 3B of Krasilnikov and Bezrukov (26)), the value of the free energy cost for the partitioning of large PEGs into the (PA63)7 pore is ΔF = 3 kT.
This analysis may not be applicable to the results shown here for the (PA63)7 channel for several reasons. First, using the same formalism leads to the conclusion that the “free energy of confinement” for PEG3400 in the (PA63)7 channel is less than that for the same polymer in the αHL channel. However, that is not consistent with the pore-size estimates of the two channels, based on conductance measurements and the ability of smaller PEGs to partition into the pores. Second, although even large PEGs reduce the (PA63)7 channel conductance, they do so at relatively small PEG concentrations (i.e., [PEG] < 13% w/w), compared with the entropic regime discussed by Krasilnikov and Bezrukov (26) (i.e., [PEG] >15% w/w). Moreover, the entropic repulsion model ignores the fact that PEG interacts with the αHL pore walls (24,25,45).
For the voltage-dependent ion channel (VDAC), pore-impermeant PEGs osmotically remove water molecules from the pore, and gate the channel to a more closed conformation at a given value of the applied potential (44). This mechanism might account for the effects of relatively high concentrations of PEGs (with molecular masses >1500 g/mol) on the (PA63)7 channel conductance. However, to avoid complications in interpreting estimates of the (PA63)7 pore size based on the effects of PEG on the channel conductance, we used positive applied potentials (see below) and [PEG] < 10 mM.
(PA63)7 channel pore size estimation
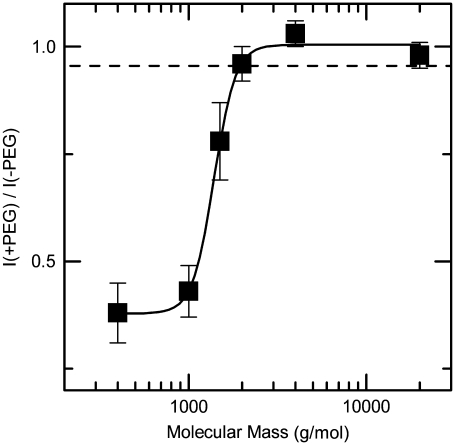
The ratio of the single-channel current in the presence of PEG to that in the absence of the polymer is shown in Fig. 5 for PEG400 to PEG20,000 and V = +70 mV. The results suggest that PEGs with a mean molecular mass ≤1500 g/mol enter the pore. Interestingly, the smaller PEGs decreased the (PA63)7 channel conductance to a greater extent (i.e., ∼60%) than they decreased the bulk conductivity (∼4%, Fig. 5, dashed line). This result suggests that either the PEG concentration in the (PA63)7 channel is much higher than in the bulk or that the aqueous solution confined within the channel is not bulk-like.
FIGURE 5.
The molecular mass cutoff of the (PA63)7 channel estimated from the effect of differently sized PEG molecules on the single-channel current. The PEG concentration was 1.2% (w/w), and the applied potential was V = +70 mV. The PEGs with nominal molecular masses <2000 g/mol partitioned into the channel and thereby decreased the current. The dashed line represents the ratio of the bulk conductivities in the presence and absence of 1.2% (w/w) PEG. Each point represents the mean (± SD) of 3–5 independent experiments.
Poly(ethylene glycol) could be much more effective at reducing (PA63)7 channel conductance than expected because the water in that pore may be organized differently than in either the bulk or the αHL channel pore. Alternatively, the (PA63)7 channel may be so narrow that a single PEG molecule may block the ion-conducting pathway in a manner analogous to that of a critical percolation threshold mechanism (47).
A refined estimate of the pore diameter was obtained from both the PEG MALDI-TOF spectra (Fig. 2) and the PEG partitioning data (Fig. 5). For simplicity, we assume that: 1) all polymers in the PEG400 sample can enter the pore, 2) all of the polymers in the PEGs with mean molecular masses >4000 g/mol are excluded from the pore, and 3) within a polydisperse population, polymers that are small enough to enter the pore reduce the conductance, independent of the polymer mass. The relative decreases in I(+PEG)/I(−PEG) caused by PEG1000, PEG1500 and PEG2000 (0.95, 0.35, and 0.015, respectively) were used to determine the partitioning fraction of each polydisperse PEG mixture. Specifically, the MALDI-TOF spectra (Fig. 2) were numerically integrated from a smaller to a larger PEG molecular mass to determine the fractional area equal to the relative current decrease caused by the PEGs. The PEG molecular mass cutoff estimated in this manner is ∼1400 g/mol (i.e., ∼32 ethylene glycol repeat units). PEG1408 has a mean hydrodynamic radius R ≈ 1 nm (22,23,31). Therefore, the (PA63)7 channel pore polymer-accessible aperture diameter is ≤2 nm. The PEG pore-sizing method may overestimate the (PA63)7 channel-limiting aperture diameter, because the pore-permeant PEGs may not be transported completely through the limiting pore aperture.
The PEGs that enter the (PA63)7 pore not only reduce the mean channel conductance, but also change the shape of the I/V relationship from nonlinear and slightly rectifying to superlinear (Fig. 6, A and B, PEG400 and PEG1000). Blaustein and Finkelstein observed a similar superlinear I/V relationship when they used ionic probes to estimate the size of the (PA63)7 channel (14,15). They concluded that the charged probes were lodged in the pore at low applied potential, and then were forced completely through the channel at higher voltages. Because the physical and chemical properties of the ionic probes and PEGs are different, the mechanism that causes qualitatively similar I/V line shapes may also differ. Nevertheless, the PEG-induced I/V relationship superlinearity may be caused by the expulsion of polymer from the side of the channel opposite to the one it entered. At relatively small positive values of the applied potentials, PEG400 and PEG1000 could enter the pore and become weakly bound to it. Because of the high (PA63)7 channel cation selectivity (∼20:1) (48), K+ ions and water molecules traveling in the cis to trans direction might dislodge the PEGs at higher voltages. Positive applied potentials would favor the complete transport of PEG from the cis side to the trans side because of momentum transfer during the collision process. For negative applied potentials, the direction of PEG transport would be reversed.
FIGURE 6.
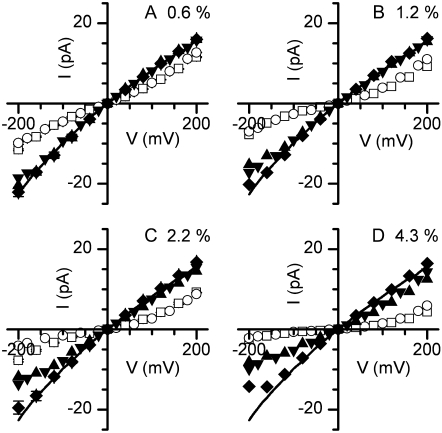
The effect of differently sized PEGs on the (PA63)7 single channel I/V relationship. In each plot, data were obtained in the absence of PEG (solid line), or in the presence of PEG400 (open squares), PEG1000 (open circles), PEG1500 (solid up triangles), PEG2000 (solid down triangles), and PEG 4000 (solid diamonds). The effects caused by PEGs at 4 polymer concentrations (w/w) (A, 0.6%; B, 1.2%; C, 2.2%; and D, 4.3%) are shown.
PEG1500 had a slight effect on the I/V relationship for negative applied potential, which again suggests that only the lower molecular mass fraction of the polydisperse PEG1500 sample enters the pore. Of the PEGs investigated here, those with mean molecular masses >1500 g/mol cause negligible effects on the (PA63)7 single-channel I/V relationship at concentrations ≤1.2% w/w (Fig. 6, A and B). At PEG concentrations exceeding 2% w/w, even the larger PEGs decreased the single-channel current for negative applied potentials (Fig. 6, C and D), as discussed above (Fig. 4).
Is the observed I/V relationship line-shape change (Fig. 6, open symbols) a sufficient condition to conclude that the smaller PEGs transport through the channel? To address this question, we formed (PA63)7 channels in membranes containing DiPhyPC:DOPC (1:1 mol ratio) on the trans side and DiPhyPC:PEG-tethered lipid (i.e., DOPE-PEG350 or DOPE-PEG3000 in a 1:1 mol ratio with DiPhyPC) on the cis side. Assuming there was no phase separation of the non-PEGylated and PEGylated lipids, the latter's concentration was sufficiently great to induce entropic repulsion between the surface-bound polymers, thereby extending and uncoiling the polymers from the membrane-solution interface (49,50). For membranes containing many (PA63)7 channels, the I/V relationships showed that PEG350-tethered lipid had no effect on the line shape, but that the PEG3000-tethered lipid did (Fig. 7). These results suggest that the free end of the longer tethered PEG molecules can enter the pore, and that PEG need not completely transport through the pore to cause an I/V relationship that is qualitatively similar to that obtained with PEG400 or PEG1000 in the bulk (Fig. 6). Thus, the (PA63)7 channel pore diameter, d ≈ 2 nm, obtained here using PEGs is likely to be an overestimate of the limiting aperture.
FIGURE 7.
The I/V relationship of (PA63)7 channel reconstituted into membranes containing PEG-tethered lipids. Shown are multi-(PA63)7 channel I/V relationships for membranes containing DiPhyPC:DOPC on the trans side and DiPhyPC with either DOPE-PEG350 (open squares) or DOPE-PEG3000 (solid diamonds) on the cis side. The ionic currents for membranes containing DOPE-350 were divided by 15. The illustrations depict how the longer PEG3000-tethered lipid might reduce the channel (bottom right), and why the shorter PEG350-lipids cannot.
CONCLUSION
We used differently sized nonelectrolyte PEG polymers to estimate the diameter of the Bacillus anthracis (PA63)7 ion channel. This value, d ≈ 2 nm, is greater than that determined with ions as sizing probes (d ≈ 1.1 nm) (14,15) for the same electrolyte solution conditions. This value may be an overestimate for three reasons. First, PEG may not be completely transported through the pore. Second, similar PEG partitioning experiments with the αHL channel demonstrated that the PEG molecular mass cutoff for that pore was greater (i.e., ∼2250 g/mol, which corresponds to a diameter d ≈ 2.5 nm) (25,51), but the αHL channel crystal structure suggests that the smallest diameter inside that pore is d ≈ 1.6 nm (52). Apparently, in the case of αHL, PEGs either overestimate or do not probe the diameter of this part of the pore. The question of whether they do so for the (PA63)7 channel is still open. Third, the PEG molecules in the pore may not be spherical (45).
Other experimental evidence suggests that the (PA63)7 channel pore is smaller than that of the αHL channel. First, at a given concentration of 1:1 electrolyte in solution, the (PA63)7 single-channel conductance is ∼10-fold less that that of the αHL channel. Second, the (PA63)7 single-channel conductance does not scale with the bulk KCl conductivity (20). Third, the degree to which pore-permeant PEGs decrease the bulk conductivity and the single-channel currents of (PA63)7 (Fig. 5) and αHL (25,31,36,41) suggests that, unlike the αHL channel (25,53), the interior of the (PA63)7 pore is not predominately filled with a bulk-like aqueous solution. Finally, the (PA63)7 pore may be so narrow that the ionic conduction pathway is markedly interrupted by a single PEG molecule.
Fig. 8 illustrates a cross-sectional view of the (PA63)7 channel model (21) and spherical representations of PEG 400, 1000, and 1500 molecules. If none of the PEGs used here completely transport through the (PA63)7 pore, then our value for the limiting pore diameter is an overestimate. To address this issue, we are performing experiments to determine whether other types of small molecules can transport completely through the (PA63)7 channel.
FIGURE 8.
Scaled illustration of a theoretical model for the (PA63)7 channel (21) and PEGs. The idealized illustrated spheres represent molecules of PEG400, PEG1000, and PEG1500, based on PEG hydrodynamic radius data (23). The numbers inside the pore indicate the diameter, in angstroms, at those locations, based on a model for the channel (21).
Acknowledgments
We acknowledge the National Cancer Institute for providing the compounds and for the allocation of computing time and for staff support at the Advanced Biomedical Computing Center. We thank Dr. Kenneth A. Rubinson for measuring the mass spectra of PEG samples, the National Institute of Standards and Technology (NIST) Center for Advanced Research in Biotechnology for the use of a mass spectrometer, and Vincent M. Stanford (Information Technology Laboratory, NIST) for helpful suggestions regarding numerical methods.
This work was supported in part with funds from the NIST Office of Law Enforcement Standards (J.J.K.), the NIST Single Molecule Manipulation and Measurement Program (J.J.K.), NSF (CTS-0555201, J.J.K.), the NIST-National Research Council Research Associateship Program (B.J.N. and J.W.F.R.), the Conselhno Nacional de Desenvolvimento Cientifico e Tecnologico of Brazil (O.V.K.), the Rede de Nanotecnologia Molecular e de Interfaces of Brazil (O.V.K.), and the Instituto do Milenio de Materiais Complexos of Brazil (O.V.K). This project was also funded in part with federal funds from the National Cancer Institute, National Institutes of Health, under contract N01-CO-12400.
The identification of commercial materials and their sources is given in describing the experimental results. In no case does this identification imply recommendation by the National Institute of Standards and Technology, nor does it imply that the material is the best available. The content of this publication does not necessarily reflect the views or policies of the Department of Health and Human Services, nor does the mention of trade names, commercial products, or organizations imply endorsement by the U.S. Government.
Editor: Francisco Bezanilla.
References
- 1.Ascenzi, P., P. Visca, G. Ippolito, A. Spallarossa, M. Bolognesi, and C. Montecucco. 2002. Anthrax toxin: a tripartite lethal combination. FEBS Lett. 531:384–388. [DOI] [PubMed] [Google Scholar]
- 2.Benson, E. L., P. D. Huynh, A. Finkelstein, and R. J. Collier. 1998. Identification of residues lining the anthrax protective antigen channel. Biochemistry. 37:3941–3948. [DOI] [PubMed] [Google Scholar]
- 3.Petosa, C., R. J. Collier, K. R. Klimpel, S. H. Leppla, and R. C. Liddington. 1997. Crystal structure of the anthrax toxin protective antigen. Nature. 385:833–838. [DOI] [PubMed] [Google Scholar]
- 4.Wang, X. M., R. Wattiez, M. Mock, P. Falmagne, J. M. Ruysschaert, and V. Cabiaux. 1997. Structure and interaction of PA63 and EF (edema toxin) of Bacillus anthracis with lipid membrane. Biochemistry. 36:14906–14913. [DOI] [PubMed] [Google Scholar]
- 5.Wesche, J., J. L. Elliott, P. O. Falnes, S. Olsnes, and R. J. Collier. 1998. Characterization of membrane translocation by anthrax protective antigen. Biochemistry. 37:15737–15746. [DOI] [PubMed] [Google Scholar]
- 6.Halverson, K. M., R. G. Panchal, T. L. Nguyen, R. Gussio, S. F. Little, M. Misakian, S. Bavari, and J. J. Kasianowicz. 2005. Anthrax biosensor, protective antigen ion channel asymmetric blockade. J. Biol. Chem. 280:34056–34062. [DOI] [PubMed] [Google Scholar]
- 7.Panchal, R. G., K. M. Halverson, W. Ribot, D. Lane, T. Kenny, T. G. Abshire, J. W. Ezzell, T. A. Hoover, B. Powell, S. Little, J. J. Kasianowicz, and S. Bavari. 2005. Purified Bacillus anthracis lethal toxin complex formed in vitro and during infection exhibits functional and biological activity. J. Biol. Chem. 280:10834–10839. [DOI] [PubMed] [Google Scholar]
- 8.Krantz, B. A., R. A. Melnyk, S. Zhang, S. J. Juris, D. B. Lacy, Z. Y. Wu, A. Finkelstein, and R. J. Collier. 2005. A phenylalanine clamp catalyzes protein translocation through the anthrax toxin pore. Science. 309:777–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Neumeyer, T., F. Tonello, F. Dal Molin, B. Schiffler, and R. Benz. 2006. Anthrax edema factor, voltage-dependent binding to the protective antigen ion channel and comparison to LF binding. J. Biol. Chem. 281:32335–32343. [DOI] [PubMed] [Google Scholar]
- 10.Zhang, S., E. Udho, Z. Y. Wu, R. J. Collier, and A. Finkelstein. 2004. Protein translocation through anthrax toxin channels formed in planar lipid bilayers. Biophys. J. 87:3842–3849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Simon, S. M., and G. Blobel. 1991. A protein-conducting channel in the endoplasmic-reticulum. Cell. 65:371–380. [DOI] [PubMed] [Google Scholar]
- 12.Simon, S. M., and G. Blobel. 1992. Signal peptides open protein-conducting channels in Escherichia coli. Cell. 69:677–684. [DOI] [PubMed] [Google Scholar]
- 13.Kasianowicz, J. J., E. Brandin, D. Branton, and D. W. Deamer. 1996. Characterization of individual polynucleotide molecules using a membrane channel. Proc. Natl. Acad. Sci. USA. 93:13770–13773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Blaustein, R. O., and A. Finkelstein. 1990. Voltage-dependent block of anthrax toxin channels in planar phospholipid-bilayer membranes by symmetrical tetraalkylammonium ions—effects on macroscopic conductance. J. Gen. Physiol. 96:905–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Blaustein, R. O., and A. Finkelstein. 1990. Diffusion limitation in the block by symmetrical tetraalkylammonium ions of anthrax toxin channels in planar phospholipid-bilayer membranes. J. Gen. Physiol. 96:943–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Finkelstein, A. 1994. The channel formed in planar lipid bilayers by the protective antigen component of anthrax toxin. Toxicology. 87:29–41. [DOI] [PubMed] [Google Scholar]
- 17.Drum, C. L., S. Z. Yan, J. Bard, Y. Q. Shen, D. Lu, S. Soelalman, Z. Grabarek, A. Bohm, and W. J. Tang. 2002. Structural basis for the activation of anthrax adenylyl cyclase exotoxin by calmodulin. Nature. 415:396–402. [DOI] [PubMed] [Google Scholar]
- 18.Pannifer, A. D., T. Y. Wong, R. Schwarzenbacher, M. Renatus, C. Petosa, J. Bienkowska, D. B. Lacy, R. J. Collier, S. Park, S. H. Leppla, P. Hanna, and R. C. Liddington. 2001. Crystal structure of the anthrax lethal factor. Nature. 414:229–233. [DOI] [PubMed] [Google Scholar]
- 19.Hille, B. 1992. Ionic Channels of Excitable Membranes, 2nd ed. Sinauer Associates, Sunderland, MA.
- 20.Orlik, F., B. Schiffler, and R. Benz. 2005. Anthrax toxin protective antigen: Inhibition of channel function by chloroquine and related compounds and study of binding kinetics using the current noise analysis. Biophys. J. 88:1715–1724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nguyen, T. L. 2004. Three-dimensional model of the pore form of anthrax protective antigen. Structure and biological implications. J. Biomol. Struct. Dyn. 22:253–265. [DOI] [PubMed] [Google Scholar]
- 22.Krasilnikov, O. V. 2002. Sizing of channels with neutral polymers. In NATO Advanced Research Workshop. Structure and Dynamics of Confined Polymers. J. J. Kasianowicz, M. S. Z. Kellermayer, and D. W. Deamer, editors. Kluwer Press, Dordrecht, Netherlands. 97–115.
- 23.Kuga, S. 1981. Pore-size distribution analysis of gel substances by size exclusion chromatography. J. Chromatogr. 206:449–461. [Google Scholar]
- 24.Bezrukov, S. M., and J. J. Kasianowicz. 2002. Dynamic partitioning of neutral polymers into a single ion channel. In NATO Advanced Research Workshop. Structure and Dynamics of Confined Polymers. J. J. Kasianowicz, M. S. Z. Kellermayer, and D. W. Deamer, editors. Kluwer, Dordrecht, Netherlands. 117–130.
- 25.Bezrukov, S. M., I. Vodyanoy, R. A. Brutyan, and J. J. Kasianowicz. 1996. Dynamics and free energy of polymers partitioning into a nanoscale pore. Macromolecules. 29:8517–8522. [Google Scholar]
- 26.Krasilnikov, O. V., and S. M. Bezrukov. 2004. Polymer partitioning from nonideal solutions into protein voids. Macromolecules. 37:2650–2657. [Google Scholar]
- 27.Rostovtseva, T. K., E. M. Nestorovich, and S. M. Bezrukov. 2002. Partitioning of differently sized poly(ethylene glycol)s into OmpF porin. Biophys. J. 82:160–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Krasilnikov, O. V., C. G. Rodrigues, and S. M. Bezrukov. 2006. Single polymer molecules in a protein nanopore in the limit of a strong polymer-pore attraction. Phys. Rev. Lett. 97:018301-1–018301-4. [DOI] [PubMed] [Google Scholar]
- 29.Berestovsky, G. N., V. I. Ternovsky, and A. A. Kataev. 2001. Through pore diameter in the cell wall of Chara corallina. J. Exp. Bot. 52:1173–1177. [PubMed] [Google Scholar]
- 30.Kaulin, Y. A., L. V. Schagina, S. M. Bezrukov, V. V. Malev, A. M. Feigin, J. Y. Takemoto, J. H. Teeter, and J. G. Brand. 1998. Cluster organization of ion channels formed by the antibiotic syringomycin E in bilayer lipid membranes. Biophys. J. 74:2918–2925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sabirov, R. Z., O. V. Krasilnikov, V. I. Ternovsky, and P. G. Merzliak. 1991. Influence of some nonelectrolytes on conductance of bulk solution and conductivity of ion channel—determination of pore radius from electric measurements. Biol. Mem. 8:280–291. [Google Scholar]
- 32.Sabirov, R. Z., and Y. Okada. 2004. Wide nanoscopic pore of maxi-anion channel suits its function as an ATP-conductive pathway. Biophys. J. 87:1672–1685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ternovsky, V. I., Y. Okada, and R. Z. Sabirov. 2004. Sizing the pore of the volume-sensitive anion channel by differential polymer partitioning. FEBS Lett. 576:433–436. [DOI] [PubMed] [Google Scholar]
- 34.Scherrer, R., T. C. Beaman, and P. Gerhardt. 1971. Macromolecular sieving by the dormant spore of Bacillus cereus. J. Bacteriol. 108:868–873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Scherrer, R., L. Loudon, and P. Gerhardt. 1974. Porosity of the yeast cell wall and membrane. J. Bacteriol. 118:537–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bezrukov, S. M., and J. J. Kasianowicz. 1997. The charge state of an ion channel controls neutral polymer entry into its pore. Eur. Biophys. J. 26:471–476. [DOI] [PubMed] [Google Scholar]
- 37.Sabirov, R. Z., N. A. Yulchibaeva, and O. V. Krasilnikov. 1993. Blocking of latrotoxin channels by cadmium ions. Biofizika. 38:168–171. [PubMed] [Google Scholar]
- 38.Stojilkovic, K. S., A. M. Berezhkovskii, V. Y. Zitserman, and S. M. Bezrukov. 2003. Conductivity and microviscosity of electrolyte solutions containing polyethylene glycols. J. Chem. Phys. 119:6973–6978. [Google Scholar]
- 39.Bezrukov, S. M., and J. J. Kasianowicz. 1993. Current noise reveals protonation kinetics and number of ionizable sites in an open protein ion channel. Phys. Rev. Lett. 70:2352–2355. [DOI] [PubMed] [Google Scholar]
- 40.Montal, M., and P. Mueller. 1972. Formation of bimolecular membranes from lipid monolayers and a study of their electrical properties. Proc. Natl. Acad. Sci. USA. 69:3561–3566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Krasilnikov, O. V., R. Z. Sabirov, V. I. Ternovsky, P. G. Merzliak, and B. A. Tashmukhamedov. 1988. The structure of Staphylococcus aureus alpha-toxin-induced ionic channel. Gen. Physiol. Biophys. 7:467–473. [PubMed] [Google Scholar]
- 42.Sabirov, R. Z., O. V. Krasilnikov, V. I. Ternovsky, and P. G. Merzliak. 1993. Relation between ionic channel conductance and conductivity of media containing different nonelectrolytes—a novel method of pore-size determination. Gen. Physiol. Biophys. 12:95–111. [PubMed] [Google Scholar]
- 43.Berg, H. C., and E. M. Purcell. 1977. Physics of chemoreception. Biophys. J. 20:193–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zimmerberg, J., and V. A. Parsegian. 1986. Polymer inaccessible volume changes during opening and closing of a voltage-dependent ionic channel. Nature. 323:36–39. [DOI] [PubMed] [Google Scholar]
- 45.Robertson, J. W. F., C. G. Rodrigues, V. M. Stanford, K. Rubinson, O. V. Krasilnikov, and J. J. Kasianowicz. 2007. Single molecule mass spectrometry in solution using solitary nanopores. Proc. Natl. Acad. Sci. USA. 104:8207–8211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zitserman, V. Y., A. M. Berezhkovskii, V. A. Parsegian, and S. M. Bezrukov. 2005. Nonideality of polymer solutions in the pore and concentration-dependent partitioning. J. Chem. Phys. 123:146101–146102. [DOI] [PubMed] [Google Scholar]
- 47.Stauffer, D., and A. Aharony. 1994. Introduction to Percolation Theory. Taylor & Francis, New York.
- 48.Blaustein, R. O., T. M. Koehler, R. J. Collier, and A. Finkelstein. 1989. Anthrax toxin: channel-forming activity of protective antigen in planar phospholipid-bilayers. Proc. Natl. Acad. Sci. USA. 86:2209–2213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hansen, P. L., J. A. Cohen, R. Podgornik, and V. A. Parsegian. 2003. Osmotic properties of poly(ethylene glycols): quantitative features of brush and bulk scaling laws. Biophys. J. 84:350–355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Majewski, J., T. L. Kuhl, M. C. Gerstenberg, J. N. Israelachvili, and G. S. Smith. 1997. Structure of phospholipid monolayers containing poly(ethylene glycol) lipids at the air-water interface. J. Phys. Chem. B. 101:3122–3129. [Google Scholar]
- 51.Krasilnikov, O. V., R. Z. Sabirov, V. I. Ternovsky, P. G. Merzliak, and J. N. Muratkhodjaev. 1992. A simple method for the determination of the pore radius of ion channels in planar lipid bilayer-membranes. FEMS Microbiol. Immunol. 105:93–100. [DOI] [PubMed] [Google Scholar]
- 52.Song, L. Z., M. R. Hobaugh, C. Shustak, S. Cheley, H. Bayley, and J. E. Gouaux. 1996. Structure of staphylococcal alpha-hemolysin, a heptameric transmembrane pore. Science. 274:1859–1866. [DOI] [PubMed] [Google Scholar]
- 53.Kasianowicz, J. J., and S. M. Bezrukov. 1995. Protonation dynamics of the alpha-toxin ion-channel from spectral-analysis of pH-dependent current fluctuations. Biophys. J. 69:94–105. [DOI] [PMC free article] [PubMed] [Google Scholar]