Ejection Dynamics of Polymeric Chains from Viral Capsids: Effect of Solvent Quality

Abstract

We present simulations investigating the effects of solvent quality on the dynamics of flexible (RNA-like) and semiflexible (DNA-like) polymers ejecting from spherical viral capsids. We find that the mean ejection time increases and the ejection time distributions are broadened as the solvent quality decreases. Our results thus suggest that DNA ejection may be very efficiently controlled by tuning the salt concentration in the environment, in agreement with recent experimental findings. We also observe random pauses in the ejection. These become extremely long for semiflexible polymers at lower solvent quality, and we interpret this as a signature of a low driving force for ejection. We find that, for most polymers, ejection is an all-or-nothing process at the solvent conditions we investigated: polymers normally completely eject once the process is initiated.

INTRODUCTION

A crucial early step in the bacterial infection cycle is the ejection of the packaged genome into the host cell. Bacteriophages, such as φ29, exploit the enormous capsid pressure, typically approximately tens of atmospheres, to release their genome in the bacterium which they infect. This large pressure is due to the narrow capsid dimensions—of the order of the persistence length of the packaged double-stranded DNA. Such a close confinement gives rise to both a large entropic penalty and to strong repulsive interactions among the various DNA segments.

The DNA or polymer ejection in such highly pressurized systems has recently attracted considerable theoretical (1–4) and experimental (5–9) attention. The ejection process is not trivial and it appears to depend strongly on the experimental conditions and the particular phage considered. For example, Mangenot et al. (8) have recently performed single molecule experiments to characterize ejection from the T5 phage. They found ∼25% of ejecting capsids released their genome completely within the first minute. Interestingly, the rest ejected the DNA in three or two discrete steps, which appeared to be correlated to the positions of “nicks” in the DNA sequence.

Such steps, or pauses, were also indirectly observed by de Frutos et al. (9). They suggested that pauses are short during the early ejection stages when the capsid pressure is highest, but become longer as the last DNA sections are released. These authors also found that decreasing the temperature delayed ejection and greatly reduced its rate. Moreover, the ejection became less efficient when the solvent quality was degraded by changing the salt concentration of the buffer (both inside and outside the viral capsid). These experiments could not distinguish whether this was due to partial ejection from all capsids or total ejection from fewer capsids.

Evilevitch et al. (5,6) described rather different results for the λ-phage. They found no obvious pauses in the DNA ejection. They also reported that increasing the salt concentration outside the capsid leads to an osmotic pressure difference which stops the ejection when a given fraction of DNA had been emitted. They argued that this occurred when the excess pressure acting on the DNA inside the capsid balanced the osmotic pressure resisting ejection.

In a very recent article, Inamdar et al. (2) have discussed the possibility of chaperones aiding ejection. These are proteins that bind reversibly to the ejected DNA, lowering its energy.

In related single molecule experiments on φ29, Smith et al. (10) considered packaging rather than ejection. They observed random pauses during the loading process which slowed as the capsid became fuller. They estimated the internal force on the capsid exerted by the packaged genome as 50 pN, sufficient for pressure-driven injection into the host cell to be a viable mechanism.

Although experiments are becoming increasingly sophisticated, there are still gaps in our understanding of pressure-driven, viral ejection. Models are needed to clarify the generic features of the process and to help guide experiments. We have recently developed such a model (3,11), which gives rate curves that are consistent with those reported by Smith et al. (10) and which reproduces the random pauses during packing seen in those experiments. The approach was used to explore the dependence of the ejection rate on both polymer flexibility and on capsid shape.

The model is based on the stochastic rotation dynamics algorithm (12), which couples a coarse-grained molecular dynamics description of the polymer to a mesoscopic model for the solvent. Importantly, this approach includes the effects of hydrodynamic interactions, and, in particular, the flow field set up in the fluid during the ejection process.

Our aim here is to use this approach to investigate the effect of solvent conditions on the pressure-driven ejection of semiflexible (DNA-like) and flexible (RNA-like) polymers. (We note that most RNA viruses may be organized with the genome only occupying a shell close to the capsid wall (13). However, artificial or longer RNA sequences may be designed or found to fill more of the capsid.) We explicitly simulate the kinetics of ejection from spherical capsids, thereby modeling phages like T7, λ, and HK97. We measure ejection time distributions for flexible and semiflexible polymers and find that solvent conditions broaden these distributions and slow the ejection rates. We observe random pauses in the ejection process whose duration increases as the solvent quality decreases and which, for semiflexible polymers in a poor solvent, are longest when approximately half the polymer is ejected. We argue that the pause distribution gives information about the force driving the ejection.

We first briefly describe the simulation model and then present and interpret our results and discuss them in the context of recent experiments on DNA ejection.

SIMULATION MODEL

The polymer is represented by a coarse-grained chain of N = 100 beads joined by finitely extensible nonlinear elastic (FENE) springs. The spring potential, acting between two consecutive beads at a distance d, is

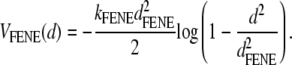(1)

The beads also interact via a Lennard-Jones potential, which has the form

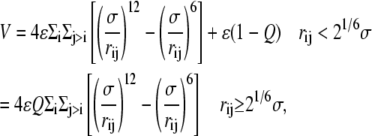(2)

where r_i is the position of the i^th bead and 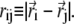Finally, there is a bending rigidity term,

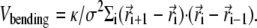(3)

The potential parameters are chosen to be σ = 2.5 nm and ɛ = k_BT. We take k_FENE and d_FENE to be 30 k_BT/σ² and 1.5σ, respectively. The bond length is approximately equal to σ. The value κ in Eq. 3 is a bending rigidity which sets the persistence length l ∼ κσ/k_BT. We set l = 0 for a flexible polymer and l = 10σ for a semiflexible polymer where 10 σ is a compromise between reaching typical genomic stiffness (20 σ under physiological conditions for double-stranded DNA (10)) and feasible length and timescales in the simulations.

The parameter Q ≥ 0 controls the effective solubility of the polymer. For Q = 0, only the repulsive part of the Lennard-Jones potential remains, resulting in a good solvent. (Note that this force field, for the good solvent, is different from the one in (3), which is why the ejection force curves are also different (Fig. 4) (14).) For Q > 0, the attractive part of the potential is turned on, equivalent to degrading the solvent quality. Here we use Q = 0, 0.6, and 0.8 to keep the simulations within a manageable time. A positive value of Q may qualitatively be realized physically via a buffer containing multivalent counterions, such as spermidine or spermine. The updating of the beads' positions and velocities is performed using the velocity-Verlet molecular dynamics algorithm.

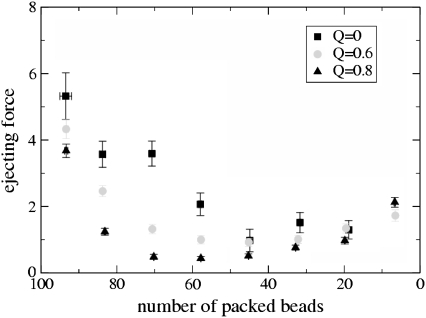
FIGURE 4.

Plot of the force (in units of k_BT/σ, note that k_BT/σ is equal to 1.64 pN with the values used here) acting on the bead closest to the capsid entrance (and hence pushing the polymer out of the capsid) as a function of number of beads remaining inside the capsid for a semiflexible polymer in a solvent of variable quality parameterized by Q. The force at 5% packing at Q = 0 is not shown for visibility, as it would be large on the scale used here.

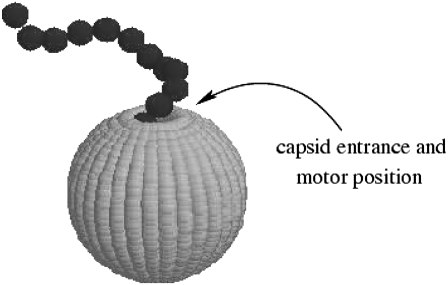
The capsid shape, illustrated in Fig. 1, is

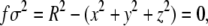(4)

with R = 3.02σ. This choice of geometry leads to an internal volume ∼86σ ³. Correspondingly, the filling fraction of the polymer inside the capsid is then ∼0.4, close to the values typically achieved by double-stranded DNA in phages. The capsid is modeled as a hard shell with a hole that permits the entrance of one bead at a time. A repulsive force of the form k_BT/(σ f ⁴) is applied to any bead which is at a point for which | f | ≤ 0.2.

FIGURE 1.

A polymer ejecting from a spherical capsid as modeled in our simulations. The capsid entrance (from which the polymer ejects) is also shown.

The motor that feeds the polymer into the capsid, before ejecting it, is, in reality, extremely complex (15). Here we use a simple model aimed at capturing the basic physics. Essentially the motor has to 1), capture a bead; and 2), feed it into the capsid. This is accomplished by requiring the motor to apply a radial force (of magnitude 5 k_BT/σ), together with a constant force toward the center of the capsid (of magnitude 10 k_BT/σ), if the bead enters a cylinder of radius 0.7σ and length σ with origin at the capsid entrance. The details of this mechanism do not affect the results.

The polymer is initially configured randomly except for the requirement that the first bead lies within the capsid and the rest outside. The polymer is equilibrated in this position (for ∼500 simulation time steps) before opening the bead entrance and applying the feeding force. A single bead is left out to initiate ejection once the motor force is set to zero. This is done after leaving time for the polymer to relax within the capsid (for ∼5000 simulation time steps).

The polymer is coupled to a coarse-grained solvent model, stochastic rotation dynamics. This acts as a hydrodynamic thermostat allowing momentum transfer between beads and allowing flows to be set up in the surrounding fluid as a consequence of the bead motion.

Briefly, the stochastic rotation dynamics algorithm solves the equation of motion of the solvent by considering particles which move with continuous positions and velocities but at discrete time intervals. The simulation has two steps. In the first one, the streaming step, the position vectors of the solvent particles are simultaneously updated by advecting them according to their instantaneous velocity vectors. In the second step, named the collision step, momentum is transferred between the particles. This is achieved by partitioning the simulation box into a grid of cubic cells of σ−length sides (the average density of solvent particles is five per σ ³). The particles in each cell undergo stochastic multiparticle collisions by rotating each particle's velocity with respect to the center of mass velocity of the cell, through a fixed angle α about a random axis (different from cell to cell). The coupling of the polymer bead with the solvent is a momentum transfer, which occurs by including any bead within a given cell in the collision step. To ensure Galilean invariance, it has been shown (16) that the grid has to be randomly shifted at each collision step. For more details on the stochastic rotation dynamics algorithm, and its application in polymer hydrodynamics, we refer the reader to the literature (11,12,16,17).

Parameters are chosen so that the solvent has a viscosity ∼5 cP, which is comparable to that of cytosol. The capsid is permeable to the solvent, which is the physical situation for phage capsids. Note that we measure time and force in simulation units: one simulation unit can be mapped onto 3 ns (assuming room temperature and given the viscosity above) and 1.64 pN, respectively. (This mapping yields an ejection time of several microseconds for our short DNA chains. If we assume that the ejection timescales with length, L, as L^3ν, with ν = 0.588 for self-avoiding chains, when we scale our ejection times to, e.g., λ DNA lengths, we get a value in line with other predictions for nick-free DNA (2).)

RESULTS

Ejection is slower in a poor solvent

We first consider the effect of solvent quality on the ejection process. Degrading the solvent quality is tantamount to making the attractive interactions between polymer beads stronger. This is accomplished by choosing Q > 0 in Eq. 1. In experiments this effect can be realized by adding spermidine or other multivalent counterions which are known to lead to DNA condensation.

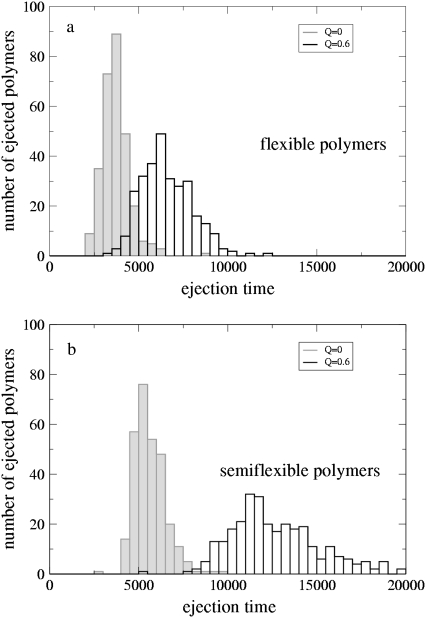
Fig. 2 compares the ejection time distributions for the semiflexible and flexible polymers at Q = 0 (good solvent) and Q = 0.6 (bad solvent). Each distribution comprises results for at least 290 chains. For both flexible and semiflexible polymers the mean ejection time is increased by a factor ∼2 for the poor solvent and the distributions are broadened. This is because attractive interactions tend to condense the DNA which reduces the free energy penalty of confinement in the capsid (or equivalently the pressure inside the capsid) and hence the ejection force. Moreover, the entropic gain from being outside the capsid is less for a collapsed polymer—again reducing the driving force for ejection.

FIGURE 2.

Ejection time distributions for (a) flexible and (b) semiflexible polymers at different solvent qualities. Time is measured in simulation units.

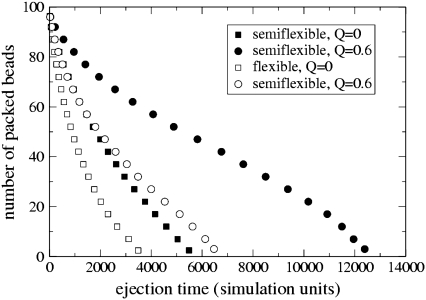
To explore this further, Fig. 3 shows the number of packed beads inside the capsid versus time averaged over many polymers. In a good solvent, both flexible (open symbols) and semiflexible (solid symbols) chains eject at a rate which decreases as the number of packed beads decreases reflecting the reduced internal capsid pressure. For the flexible chain this behavior persists as the solvent quality is reduced. The semiflexible chain, however, shows a qualitatively different behavior in the poor solvent. The rate of ejection decreases until approximately half the chain lies outside the capsid and then increases again to complete ejection.

FIGURE 3.

Number of packed beads versus ejection time for flexible (open symbols) and semiflexible (solid symbols) polymers at different solvent qualities.

This can be understood by thinking about the free-energy landscape for a very strongly collapsed polymer (large Q). The polymer will lie in free-energy minima when it is fully collapsed either inside or outside the capsid. There will be a free-energy barrier, with height that increases with Q, between these minima, corresponding to the DNA having to partially unwind as it ejects. If, as for Q = 0.6, the pressure inside the capsid is sufficient to overcome this barrier, the polymer will eject increasingly slowly until approximately half its length is out. The propensity of the polymer to condense outside the capsid will then aid the ejection and the ejection rate will increase again. (We note that in simulations for larger Q = 1, no DNA is ejected on the timescale of the simulation.)

For a flexible polymer, one expects the same behavior, but ejection will only be inhibited at a larger Q, because the pressure is larger, and therefore the effect of the energy barrier is less important.

Force curves in a poor solvent

That ejection is less efficient in a poor solvent may also be quantified by examining the curves in Fig. 4, which show how the force pushing the bead closest to the capsid entrance (see Fig. 1) depends on the number of beads remaining in the capsid. This force is maximal when the polymer is all inside the capsid and decreases for a given filling percentage as the solvent quality decreases (or equivalently as the concentration of polyvalent counterions increases). Interestingly, for larger Q, the minimal force is not found at the end of ejection but near the middle of the process, in agreement with the beginning of the formation of a free-energy barrier as discussed above.

The fact that the force is nonmonotonic may be testable with single molecule experiments which map out the force curves for different ionic strengths when, e.g., the buffer contains spermidine. Another possible signature of our results may be looked for in experiments with crowding agents (such as dextran or poly-ethylene-glycol), which are free to diffuse outside the capsid but not to enter it, and which exert an osmotic pressure at the capsid entrance. In this case the force exerted by the crowding solution may balance the force ejecting the polymer. For a given range of poly-ethylene-glycol concentrations (and a force of a few pN magnitude, see Fig. 4), we predict that there will be two values of the fraction of packaged genome for which a balance holds.

Pause distribution in a poor solvent

The data we have presented so far has been averaged over many ejecting polymers. It is also interesting to look at the behavior of individual polymers where we find random pauses in the ejection. We note that these are not correlated with any chemical features on the chain as suggested by experiments on T5 (8), but rather result from the random occurrence of DNA configurations near the hole which are unfavorable to ejection in agreement with the experiments of Smith et al. (10) on φ29.

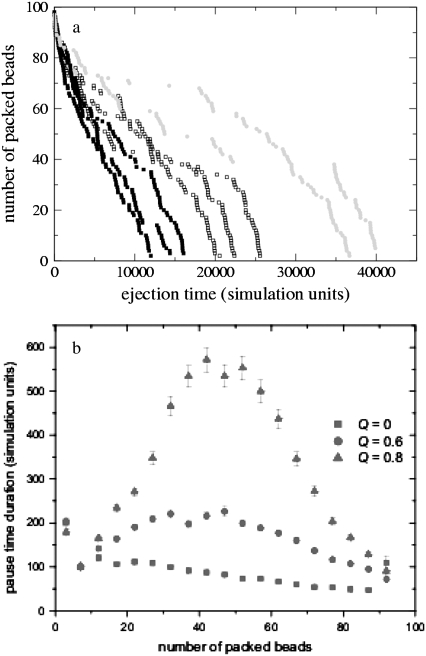
Fig. 5 a shows the number of packed beads versus ejection time for a representative sample of single chain ejection events. Fig. 5 b presents the pause duration data averaged over 515 chains as a function of the number of packed beads for Q = 0, 0.6, and 0.8 for the semiflexible chains. As the solvent quality is degraded, a clear peak forms at the point when ∼50% of the polymer length has been ejected. This corresponds to the chain length where ejection is slowest. Pauses occur due to transient jamming at the exit. When the driving force for ejection is lower, it takes longer for the chain to reorganize into a configuration favorable for ejection. Thus, the pause distribution is a measure of the driving force for ejection.

FIGURE 5.

(a) Number of packed beads versus ejection time for representative ejection events for semiflexible polymers. Several different runs are shown, to give an idea of the spread due to fluctuations. (b) Average duration of pauses versus number of packed beads for different solvent qualities.

Chains which fail to eject

For Q = 0.8, ∼10% of the chains failed to completely eject within the simulation time. The number of beads left within the capsid varied from 11 to 66, with an average of 33 and standard deviation of 14. Given that it is possible for chains to fully eject at this value of Q, we expect that these chains would eventually escape if it was possible to run the simulation for longer. For Q = 1.0, however, no chain ejected; in fact, the bead left outside the capsid to initiate ejection was readsorbed. This signals that the excess pressure inside the capsid was very small and unable to overcome any change to the collapsed configuration. We do not see a situation where the DNA partially ejects and comes to equilibrium with a tail of a given length outside the capsid, as seen in Evilevitch et al. (5). It would be of interest to try to find simulation conditions for which this occurs.

Hydrodynamic flow speeds up the ejection

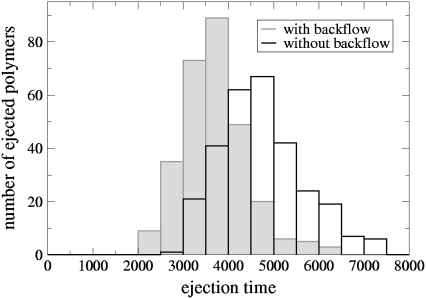
We finally assess the importance of hydrodynamic flow in controlling the ejection time distributions in a good solvent (Q = 0) for flexible polymers. Fig. 6 compares these distributions with and without hydrodynamics (which can be turned off by setting the velocity of every solvent particle to a value drawn from a Maxwell-Boltzmann distribution at each time step (19)). This figure highlights a significant effect on the ejection. Without backflow, the time distribution is wider and is peaked at a later time. This is because the polymer beads are, on average, trying to move in the same direction. The flow set up by a given bead is felt by its neighbors and helps them to do this. Similar behavior is seen for polymers translocating through a hole (19).

FIGURE 6.

Ejection time distributions for flexible chains in a good solvent (Q = 0) when backflow is considered (solid histogram) and when it is neglected (open histogram). Time is measured in simulation units.

DISCUSSIONS AND CONCLUSIONS

In summary, we have presented coarse-grained molecular dynamics simulations of the ejection of a polymer of variable flexibility from a spherical hull, as a model for DNA ejection from a capsid in presence of multivalent counterions. In agreement with experiments, we have seen that degrading the solvent quality leads to a slower ejection, so that it is possible in principle to stop DNA ejection from a phage by controlling the salt composition of the solvent of the host into which the phage DNA is ejected.

Our results provide evidence for the following picture of ejection:

1. The driving force for ejection decreases as pressure inside the capsid decreases.

2. The driving force decreases as the solvent quality decreases. This is because the DNA is less constrained within the capsid, and because there is less entropic advantage in its lying outside the capsid.

3. There is a free-energy barrier to ejection because, to eject, the DNA has to unwind and form two coils, one inside and one outside the capsid. This acts to slow the ejection rate in the first half of the process and to speed it up in the second half.

We see pauses in the ejection rate, which are random and, as expected for our simple, translationally invariant, model of DNA, not linked to a particular position on the chain. We interpret these pauses as arising from temporary blockages due to the polymer taking up a configuration at the exit to the capsid from which it is difficult for a bead to escape. The pauses are longer when the driving force for escape is smaller or, equivalently, the ejection rate is lowest. In our simulations, this is most apparent in a poor solvent, when approximately half the DNA has been ejected. This interpretation agrees with experiments by de Frutos et al. (9), who report that (for good solvent conditions) pauses are longest during the later stages of ejection when the capsid pressure is lowest.

We find that for very poor solvents the DNA does not eject but remains fully packed within the capsid. It is interesting that this is a different behavior to that seen in experiments by Evilevitch et al. (5), where ejection stopped after a finite and rather reproducible length of DNA lay outside. It would be interesting to explore whether similar behavior can be observed in the simulations, perhaps by restricting the counterions to lie outside the capsid or by applying an external, e.g., osmotic, force at the capsid entrance. It will also be interesting to investigate the effects of temperature and of chaperones or other DNA binding proteins (2,20) on the ejection process. Finally, it would be worthwhile to apply the model proposed here to the study of ejection dynamics in the case of different genomic organization; for example, viruses with small single-stranded RNA and DNA, which is absorbed on the capsid surface (13,21).