Empirical laws of survival and evolution: Their universality and implications

Abstract

Presented analysis of human and fly life tables proves that with the specified accuracy their entire survival and mortality curves are uniquely determined by a single point (e.g., by the birth mortality q₀), according to the law, which is universal for species as remote as humans and flies. Mortality at any age decreases with the birth mortality q₀. According to life tables, in the narrow vicinity of a certain q₀ value (which is the same for all animals of a given species, independent of their living conditions), the curves change very rapidly and nearly simultaneously for an entire population of different ages. The change is the largest in old age. Because probability to survive to the mean reproductive age quantifies biological fitness and evolution, its universal rapid change with q₀ (which changes with living conditions) manifests a new kind of an evolutionary spurt of an entire population. Agreement between theoretical and life table data is explicitly seen in the figures. Analysis of the data on basic metabolism reduces it to the maximal mean lifespan (for animals from invertebrates to mammals), or to the maximal mean fission time (for bacteria), and universally scales them with the total number of body atoms only. Phenomenological origin of this unification and universality of metabolism, survival, and evolution is suggested. Their implications and challenges are discussed.

Empirical Laws

Human mortality is arguably the best quantified phenomenon in biology, which is extensively studied (1–5). During the last century it decreased 40-fold for newborns, but only 3-fold for 80-year-olds. Not surprisingly, the factors that affect the mortality of newborns and 80-year-olds depend on their different life histories and living conditions and are clearly different. Yet, there is a strong correlation between mortality rates at different ages (3, 6–9), while the next section demonstrates that according to life tables (10–13) the birth mortality (or the survival probability at a single given age) determines entire survival and mortality curves according to the law, which is valid at any age and universal for species as remote as humans and flies. Statistical accuracy of this law quantifies the “mortality robustness” with respect to age and prehistory. Mortality at any age decreases, together with the birth mortality q₀. In the narrow vicinity of a certain q₀ = q^*₀ the decrease rate changes very rapidly and nearly simultaneously for an entire population of different ages. The rate jump is significantly larger in old age and is maximal at 83 years. The crossover q^*₀ is the same for all humans, independent of their race, sex, country, living conditions, and history. Such universality of q^*₀ implies (see the next section) that if a population consists of subpopulations with different q₀ values, then with the specified accuracy all of these subpopulations have either q₀ < q^*₀, or q₀ > q^*₀ only. A formal “mixture” of different populations for the same calendar year (to improve statistics and mortality calculation accuracy) may obscure the picture and be misleading, especially in the vicinity of the crossover.

Analysis (see below) of fly life tables (14–17) yields for flies the same universal survival law (with quasi-singularities at certain q^*₀) as for humans. Because the probability to survive to the mean reproductive age quantifies biological fitness, the universal survival dependence on the birth mortality (which changes with time and living conditions) quantitatively describes evolution, while its quasi-singularities manifest unusual Gould-Eldridge spurts for an entire population.

Survival probability scales with the mean lifespan. The maximal mean lifespan of all animals from invertebrates to mammals, and the maximal mean fission time for bacteria (both denoted by x̄_max thereafter), universally scale with the total number of body atoms (18), which changes by 20 orders of magnitude. Metabolism per body atom also reduces to x̄_max only (18).

I argue that quantitative universality of metabolism, survival, and evolution implies that all evolutionary changes during billions of years are subject to fundamental biological constraints and that the laws of biological and nonbiological dynamics may be as different as the laws of quantum and classical mechanics. A phenomenological origin of these laws is considered; their computer simulations, implications, and challenges are discussed.

Human Mortality

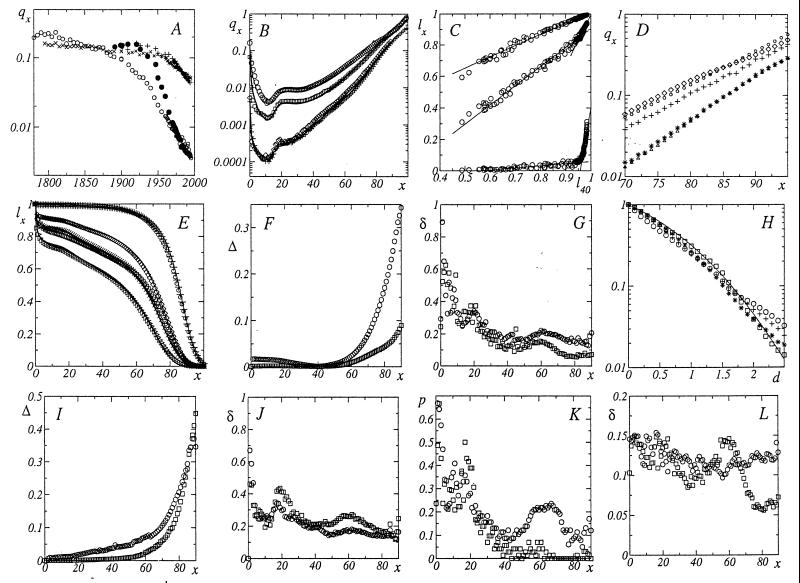
Human mortality rate significantly changes with time and country (10–13) (see, e.g. Fig. 1A). The change is very different at different times and ages: the mortality rates at birth and at 80 years were close in 1900, but they are 13-fold different in 1994. As a result, the mortality curve shape considerably changes with time (e.g., mortality quasiplateau all but disappeared, see Fig. 1B). Consequently, only the most stable Gompertz region (1) of advanced and old age was extensively studied. To determine the probability ℓ_x to survive to any age x (i.e., the relative number of survivors to x), quantify all changes in the population and its living conditions (with time, race, sex, country, and its history), with, e.g., ℓ₄₀ or the birth mortality. Start with the dependence of ℓ_x on ℓ₄₀ (for a given x) according to life tables (10–13) of Japan, Sweden, and Germany. Fig. 1C yields the universal (for all humans) dependence, which at any age rapidly changes in the narrow vicinity of ℓ₄₀ = 0.97. The change is most pronounced in old age. The corresponding evolution of the mortality rate q_x is clearly seen in Fig. 1D. Beyond 70 years, q_x is almost the same for a 1947 Japanese female (ℓ₄₀ = 0.709) and 1960 Japanese male (ℓ₄₀ = 0.897) despite the increase in ℓ₄₀ by ∼0.19. It slightly changes when ℓ₄₀ further increases by 0.06 to 0.959 (for 1980 Swedish male); then significantly decreases when ℓ₄₀ increases by a mere 0.024 to 0.983 (for 1990 Japanese female) or to 0.985 (for 1995 Swedish female).

Figure 1.

(A) Evolution of mortality rate (at birth, q₀ and at 80 years, q₈₀) with chronological year for Swedish (q₀, O, q₈₀, x) and Japanese (q₀, ●; q₈₀, +) females. (B) Agreement between theoretical and lifetable mortality rates q_x (in all cases the age x is in years) for 1891/1898 Japanese (O, q₀ = 0.1612), and 1926/1930 Swedish (□, ℓ₄₀ = 0.81) males; 1992/1994 German (⋄, q₀ = 0.0515), and 1990 Japanese (+, ℓ₄₀ = 0.983) females. The calculations according to the data in brackets are presented by thick lines for Eqs. 1–3 and thin lines for Eqs. 3–5. (C) Evolution of the survival probability ℓ_x with ℓ₄₀ for 1891–1995 Swedish (10, 11), 1891–1990 Japanese (10), and 1871–1992 German (13) males and females. The ages x = 20, 60, and 90 yield upper, middle, and lower curves, respectively. Solid lines are linear approximations. Note a rapid and nearly simultaneous, for different ages, change in the slope at ℓ₄₀ ≅ 0.97. (D) Evolution of the mortality curve in the vicinity of ℓ₄₀ ≅ 0.97: 1947 Japanese female (O, ℓ₄₀ = 0.709); 1960 Japanese (⋄, ℓ₄₀ = 0.897) and 1980 Swedish (+, ℓ₄₀ = 0.959) males; 1995 Swedish (∗, ℓ₄₀ = 0.897), and 1990 Japanese (Δ, ℓ₄₀ = 0.983) females. (E) Agreement between theoretical and life table survival probabilities ℓ₄₀ for 1891/1898 Japanese males (▹, ℓ₄₀ = 0.582); 1891/1900 Swedish (□, ℓ₄₀ = 0.695), and 1947 Japanese (X, ℓ₄₀ = 0.709) females; 1926/1930 Swedish males (⋄, q₀ = 0.0668); 1990 Japanese (+, q₀ = 0.00418), and 1995 Swedish (O, q₀ = 0.00358) females. Calculations according to Eqs. 1 and 2 and 3–5 are presented by thick lines for Eqs. 1-3 and thin lines for Eqs. 3–5. (F) Accuracy of the universal survival law: mean square deviations Δ₁(O), and Δ₂ (□) of Eqs. 1 and 2 from experimental data (10-13). (G) Accuracy of the universal survival law: mean square deviations δ₁ (O) and δ₂ (□) of Eqs. 1–3 from experimental data. (H) Accuracy of the universal survival law: probability (on a semilogarithmic scale) of relative (with respect to their mean quadratic values) deviations exceeding d for Eqs. 1–3 (O for ℓ_x + for q_x) and for Eqs. 3–5 (□ for ℓ_x, ∗ for q_x). The probability of random fluctuations is presented by the solid line. (I) Same as in F, but for Eqs. 4 and 5. (J) Same as in G, but for Eqs. 3–5. (K) Probability P of |q̃_x − q_x|/q_x > 0.25 for Eqs. 1 and 3 (O) and Eqs. 2 and 3 (□) vs x. (L) Same as in G, but for life tables with |q̃_x − q_x|/q_x < 0.25 only.

In agreement with Fig. 1C, at any x the dependence of ℓ_x on ℓ₄₀ may be approximated with two linear ℓ̃_x beyond ℓ₄₀ = 0.6 (ℓ₄₀ < 0.6 is discussed later). The least mean square value Δ of Λ_x = |ℓ̃_x − ℓ_x|/ℓ_x for each x is provided by

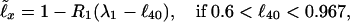1

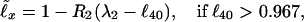2

where the slopes R₁, R₂ and (upper) level values λ₁, λ₂(ℓ̃_x = 1 when ℓ₄₀ = λ₁, λ₂) are presented in Table 1 (x = 0 is missing, since, by the definition, ℓ₀ ≡ 1. The interval ℓ₄₀ > 0.967 is narrow in ℓ₄₀, but it yields a broad interval in, e.g., ℓ₉₀, see Fig. 1C). Eqs. 1 and 2 allow one to calculate the survival probability ℓ̃_x. For instance, 1990 (here and on such number is the calendar year) Japanese females have (12) ℓ₄₀ = 0.98292, and thus yield Eq. 2. So, e.g., their ℓ̃₆₀, with R₂(60) and λ₂(60) from Table 1, equals 0.93654, while the life table (12) value is ℓ₆₀ = 0.93991. The survival probability determines the mortality rate (experimental q_x and theoretical q̃_x); according to ref. 19,

3

For instance, 1990 Japanese females, by Eqs. 2 and 3 and Table 1, have q̃₆₀ = ℓn(0.93654/0.93162) = 0.00527, while, by ref. 12, q_x = ℓn(0.93991/0.93539) = 0.00482.

Table 1.

Evolution rates R₁, R₂ and level parameters λ₁, λ₂

Age	R1	λ1	R2	λ2	Age	R1	λ1	R2	λ2
1	0.38985	0.98371	0.25418	1.0005
2	0.48224	0.97923	0.27272	1.0012
3	0.52646	0.97789	0.28633	1.0014
4	0.55528	0.97742	0.29846	1.0014
5	0.57564	0.97733	0.31114	1.0012
6	0.59005	0.97749	0.32302	1.001
7	0.60134	0.97773	0.3348	1.0007
8	0.61076	0.97798	0.34617	1.0005
9	0.61884	0.97821	0.35489	1.0003
10	0.62632	0.97842	0.36105	1.0003
11	0.63266	0.97864	0.36628	1.0004
12	0.63902	0.97884	0.37109	1.0005
13	0.64567	0.97902	0.37824	1.0004
14	0.65267	0.97923	0.38431	1.0004
15	0.66079	0.97946	0.39169	1.0005
16	0.67019	0.97985	0.40282	1.0004
17	0.68125	0.98031	0.41787	1.0003
18	0.69395	0.98084	0.43744	0.99996
19	0.70755	0.98155	0.45969	0.9997
20	0.72242	0.98226	0.48342	0.99942
21	0.738	0.98297	0.50645	0.9992
22	0.75392	0.98366	0.53037	0.99898
23	0.76979	0.98434	0.55315	0.99883
24	0.78551	0.98502	0.57803	0.99863
25	0.8011	0.98568	0.602	0.99848
26	0.81638	0.98634	0.62385	0.99843
27	0.83116	0.98705	0.64419	0.99848
28	0.84548	0.98777	0.66676	0.99847
29	0.85936	0.98852	0.68531	0.99864
30	0.87291	0.98931	0.70685	0.9987
31	0.88616	0.99014	0.72999	0.99878
32	0.89933	0.99097	0.7504	0.99897
33	0.91234	0.99184	0.77616	0.99901
34	0.92515	0.99277	0.8023	0.99913
35	0.9378	0.99378	0.83152	0.9992
36	0.95044	0.99484	0.86258	0.9993
37	0.9629	0.99599	0.89167	0.9995
38	0.97532	0.9972	0.92669	0.99963
39	0.98771	0.99858	0.96237	0.99981
40	1	1	1	1
41	1.0121	1.0016	1.0447	1.0001
42	1.0247	1.0032	1.0875	1.0004
43	1.036	1.0051	1.1353	1.0006
44	1.0476	1.0071	1.1926	1.0008
45	1.0591	1.0093	1.2514	1.001
46	1.0702	1.0118	1.311	1.0012

47	1.0812	1.0144	1.3807	1.0015
48	1.0921	1.0173	1.4579	1.0017
49	1.1031	1.0204	1.5378	1.0019
50	1.1139	1.0239	1.6223	1.0022
51	1.125	1.0275	1.7143	1.0025
52	1.1356	1.0315	1.8222	1.0027
53	1.1461	1.0359	1.9484	1.0027
54	1.1567	1.0406	2.0916	1.0027
55	1.1669	1.0457	2.2469	1.0026
56	1.1768	1.0513	2.407	1.0027
57	1.1862	1.0574	2.6021	1.0025
58	1.1952	1.064	2.8108	1.0024
59	1.2041	1.0712	3.0411	1.0023
60	1.2143	1.0788	3.2744	1.0023
61	1.2192	1.0878	3.5286	1.0023
62	1.2255	1.0973	3.8072	1.0023
63	1.2315	1.1076	4.1191	1.0023
64	1.2351	1.1192	4.4614	1.0022
65	1.2369	1.1321	4.8115	1.0023
66	1.2368	1.1463	5.1963	1.0023
67	1.2337	1.1623	5.6221	1.0023
68	1.2276	1.1802	6.0755	1.0024
69	1.2183	1.2003	6.5628	1.0025
70	1.2051	1.223	7.0902	1.0026
71	1.1879	1.2486	7.6596	1.0028
72	1.1655	1.278	8.2643	1.003
73	1.1383	1.3117	8.9137	1.0032
74	1.1052	1.3508	9.5862	1.0035
75	1.0663	1.3962	10.268	1.004
76	1.0215	1.4494	10.968	1.0045
77	0.97125	1.5119	11.561	1.0054
78	0.91377	1.5875	12.221	1.0063
79	0.85517	1.6749	12.824	1.0074
80	0.78647	1.7861	13.375	1.0087
81	0.71478	1.9224	13.742	1.0105
82	0.64169	2.0907	13.998	1.0126
83	0.56723	2.3036	14.16	1.015
84	0.49384	2.5738	14.071	1.0181
85	0.42166	2.9278	13.84	1.0218
86	0.35469	3.3826	13.58	1.0258
87	0.29127	4.0027	12.774	1.0322
88	0.23341	4.8591	11.921	1.0394
89	0.18324	6.0344	10.825	1.0493
90	0.13644	7.9011	9.5889	1.0624
91	0.1123	9.5129	8.5906	1.076
92	0.0825	12.725	7.2659	1.0981

Eqs. 1 and 2 and Table 1 allow one to relate ℓ₄₀, and thus ℓ_x, to the survival probability at any fixed age, e.g., to ℓ₁ (and thus, by Eq. 3, to the birth mortality q₀ = −ℓnℓ₁ ≅ 1 − ℓ₁):

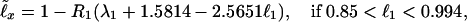4

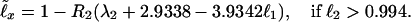5

Examples of entire survival and mortality curves according to the life tables (10–13) and to Eqs. 1–5 complemented with Table 1, are presented in Fig. 1 B and E. The figure demonstrates the accuracy and sensitivity of the universal law to the exact value of ℓ₄₀ and ℓ₁ − cf. the mortality curves of 1990 Japanese (ℓ₄₀ = 0.98292) and 1994 German (ℓ₄₀ = 0.97938) female, with very close values of ℓ₄₀.

Statistically, the accuracy of Eqs. 1 and 2 is quantified in Fig. 1 F and G with the mean square values Δ (of Λ = |ℓ̃_x − ℓ_x|/ℓ_x) and δ (of D = |q̃_x − q_x|/q_x), and in Fig. 1H with the probabilities of relative survival and mortality fluctuations, exceeding a given value d (i.e. of Λ/Δ > d and D/δ > d). By Fig. 1F, the survival mean square deviation does not exceed 10% until 75 for Eq. 1 and 90 years for Eq. 2. By Fig. 1G, the mean mortality fluctuation is always ⪝20% beyond 25 years. By Fig. 1H, the probability of fluctuations significantly deviates from and is higher than that of random ones for large (d > 2) fluctuations in Eq. 1 only. Elsewhere it may be calculated according to the normal distribution, with Δ and δ from Fig. 1 F and G. Mortality fluctuations increase in young (Fig. 1G) age. (Then statistics in developed countries are low, e.g., six girls died in their ninth year in 1995 Sweden.) Consequently, Eqs. 4 and 5 are less accurate than Eqs. 1 and 2. Their survival fluctuations (Fig. 1I) do not exceed 10% until 60 for Eq. 4 and 70 for Eq. 5; thereafter they increase to 30% at 80 years. Mortality fluctuations (Fig. 1J) do not exceed 30% beyond 25 years. Relative to the mortality change (with time and country), the inaccuracy is less than 20% at any age. For instance, Fig. 1 G and J yield δ ∼ 0.5, while the birth mortality q₀ changes 15-fold in Eqs. 1 and 4 and 2.5-fold in Eqs. 2 and 5 intervals. With the accuracy specified above, Table 1 replaces hundreds of human life tables. This accuracy statistically quantifies also the survival and mortality robustness with respect to the q₀ and ℓ₄₀ fluctuations. Elucidate the impact of relatively large mortality fluctuations. By Fig. 1K, beyond 20 years the probability of |q̃_x − q_x|/q_x > 0.25 in Eqs. 1 and 2 is ⪝20%. The elimination of the corresponding life tables decreases the maximal and the mean (Fig. 1L) mortality fluctuations to 25% and less than 15% correspondingly, and yields the fluctuation distribution, which is similar to the one presented in Fig. 1H, but with the lower probability of d > 2.

Consider the implications and challenges of the above results. With the specified accuracy, survival and mortality at any age are statistically predetermined by the (same calendar year) survival at a fixed age or birth mortality, independent of time, previous history, race, country, sex, and fluctuations. In particular, close values of, e.g., ℓ₄₀ imply close survival and mortality curves. Indeed, 1896 Swedish (ℓ₄₀ = 0.69599) and 1947 Japanese female (0.70945) survival curves of different races in different countries at different (not even overlapping for the majority of population) periods in their different history (Fig. 1E); 1994 German (0.97938), 1990 Japanese (0.98292), and 1995 Swedish (0.9853) female mortality curves (Fig. 1 B and D) are nearly identical. Even in the same country in the same year, the factors, which affect the birth mortality, are clearly different from those affecting the mortality of 80- or 40-year-olds during their different lifespans. So, the validity of Eqs. 1–5 implies that human living conditions change sufficiently little and/or slowly‡ for relatively accurate adaptation, and that Fig. 1 E-G statistically quantify the impact and age dependence of prehistory and premature mortality combined. Eqs. 1 and 2 describe the universal (for all humans) evolution of the survival probability ℓ_x with ℓ₄₀ (and via ℓ₄₀ with time, race, sex, country, its history, and living conditions). For a given age, its rate dℓ_x/dℓ₄₀, i.e., the slope in Fig. 1C, rapidly changes from one constant value R₁ to another R₂, in the narrow vicinity of the crossover ℓ₄₀ = 0.967. There, by Table 1, it decreases before x = 40 years (the maximal decrease equals 0.335 at 12 years) and increases thereafter (the maximal increase equals 14.9 at 83 years). As functions of age, R₁ and R₂ are maximal at 63 years (R₁ = 1.19) and 83 years (R₂ = 15.345) correspondingly. Thus, the survival evolution rate and its crossover increase are the highest in old age under better conditions (which yield higher ℓ₄₀).

The rates of ℓ_x evolution with ℓ₁ and q₀ = −ℓnℓ₁ ≅ 1 − ℓ₁ are proportional to R: e.g., by Eq. 4, dℓ_x/dℓ₁ = 2.5651 R₁; dℓ_x/dq₀ = −ℓ₁dℓ_x/dℓ₁ ≅ −dℓ_x/dℓ₁. Universal Eqs. 1–3 for ℓ̃_x(ℓ₄₀) and Table 1 allow one to reconstruct the past and to predict the future change of human survival and mortality, including inevitability of evolution crossovers. Suppose, e.g., that Eq. 1 is established in the interval 0.7 ≤ ℓ₄₀ ≤ 0.85 only. Its extrapolation to smaller ℓ₄₀ yields ℓ_x = 0 when ℓ₄₀ = λ₁ − (1/R₁). The largest ℓ₄₀, which yields ℓ_x = 0, equals, by Table 1, 0.608 (at x = 91). Because humans do not die out at 91 years, this means that earlier, at ℓ₄₀ ⪝ 0.6, the slope of ℓ̃₉₁(ℓ₄₀) was smaller. Indeed, Fig. 1C suggests a change at ℓ₄₀ ≅ 0.6 (but provides only few experimental points there, which are insufficient for approximation). The extrapolation of Eq. 1 to larger ℓ₄₀ yields ℓ_x = 1 when ℓ₄₀ = λ₁. The smallest ℓ₄₀, which yields ℓ_x = 1, is, by Table 1, 0.977 (at x = 5). But humans do not stop dying until 5 years. This predicts the future decrease of the ℓ̃₅ slope at ℓ₄₀ ⪞ 0.977, in agreement with Fig. 1C. Similar reasoning for Eq. 2 yields its invalidity at ℓ₄₀ < 0.96 and at ℓ₄₀ > 0.998. The proximity of the “invalidity limits” 0.977 and 0.96 in Eqs. 1 and 2 proves a narrow crossover region there, in agreement with Fig. 1C. (The predicted region ℓ₄₀ ≅ 0.998 is still beyond experimental reach).

Consider a population with ℓ₄₀ = ℓ̄₄₀. Suppose it consists of the subpopulations with the ℓ₄₀ values ℓ₄₀⁽¹⁾ < 0.967 and ℓ₄₀⁽²⁾ > 0.967 and the concentrations c⁽¹⁾ and c⁽²⁾(c⁽¹⁾ + c⁽²⁾ = 1, c⁽¹⁾ℓ₄₀⁽¹⁾ + c⁽²⁾ℓ₄₉⁽²⁾ = ℓ̄₄₀). The population ℓ̃_x = c⁽¹⁾ (1 − R₁λ₁ + R₁ℓ₄₀⁽¹⁾) + c⁽²⁾(1 − R₂λ₂ + R₂ℓ₄₀⁽²⁾) is linear in ℓ̄₄₀ and yields Eqs. 1 and 2 with the accuracy ∼c⁽²⁾ and ∼c⁽¹⁾ correspondingly. Thus, before the crossover c⁽²⁾ is relatively small (i.e., almost all phenotypes are in the “phase”§ where c⁽¹⁾ ≅ 1, and their ℓ₄₀ ≤ 0.967). Then, rapidly and nearly simultaneously, an entire population of different ages changes its “phase” to c⁽²⁾ ≅ 1 (where almost all phenotypes have ℓ₄₀ ≳ 0.967) in the narrow vicinity of the “phase transition point” ℓ₄₀ ≅ 0.967. Population migration that mixes phases smears the transition. In a given country, the accuracy of Eqs. 1 and 2 and 4 and 5 and the transition width between them quantify the stationarity and phase homogeneity of the population. The latter are high in countries as different as Japan and Sweden. In Sweden, the sharpness of the transition suggests a true singularity (21). To improve statistics, one may mix up populations with very close (especially when ℓ₄₀ ≅ 0.97) values of ℓ₄₀ only.

Universality of Mortality, Metabolism, and Evolution

In the last decade nonhuman mortality was studied in populations of 1.2 millions medflies (14, 17) and up to 5,000 genetically homogeneous fruitflies (15, 16) in different conditions (overcrowded cages with more than 7,000 medflies in a cage, individual cells, cups, and vials), which may change during the medfly lifespan (because medflies die out and their population density in a cage drastically decreases). Theoretical study (19) demonstrated for species as remote as humans and flies the same survival dependence on the mean life expectancy at birth x̄:

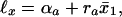6

where a = 1 when x̄ < x* and a = 2 when x̄ > x*; x* = 75 years for humans and x* = 32 days for flies. Presumably, Eq. 6, and thus Eqs. 1 and 2 and 4 and 5, are universal for all animals. The universality of the survival ℓ_x microevolution with x̄ for humans and flies, complemented with its explicit relation to fly genotypes (19), suggests that Eq. 6 describes evolution at large and quantifies fitness with the survival probability. Remarkably, the evolutionary rate dℓ_x/dx̄ dependence on x̄ and x for humans and flies is similar (19) (for humans it is proportional to R); in particular, the rate is maximal in old age. The rate crossover at x̄ = x* quantifies a new kind of the Gould-Eldridge (22) spurt. It separates subpopulations within the same species, which belong to one of the x̄ intervals (phases) only, and thus quantitatively distinguishes genetically very close populations. According to ref. 19 and the previous section, the spurts are unusual. An entire population, which yields Eqs. 1–5, from newborns to elderly (whose birth is thus separated by the whole lifespan), very rapidly and nearly simultaneously (at x̄ ≅ x*) changes its evolutionary rate. Such phase transitions may be consistent with very unusual latent [possibly adaptive (refs. 23–25), but see ref. 26] mutations accumulated and switched on at the crossover x̄ = x* simultaneously for almost all genotypes and ages by some kind of “evolvability” (27) and selection mechanism. For different (e.g., Swedish and Japanese) populations the crossover x̄(t) = x* is reached at different calendar times t. So, their dependence ℓ_x(t) = ℓ_x[x̄(t)] yields bifurcations (cf. ref. 28). It may be described (21) by the three-dimensional “evolutionary landscape” function E = E(x, t) = −ℓnℓ_x[x̄(t)].

By Eq. 6, survival and evolution universally reduce to the mean life expectancy at birth x̄. The latter may change for a given species by a factor of three (10–13), while for different animals x̄ may change by more than 2 orders of magnitude (18). Its maximal value x̄_max for any animal from invertebrates to mammals scales (18) with the mean animal volume V

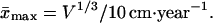7

This formula also is valid for the bacteria fission time (18). It was suggested (18) that the power of V in Eq. 7 may be somewhat decreased by fractality; the corresponding decrease in Ṅ₀ was calculated (29) to be 1/12 (i.e. on the edge of experimental accuracy, (ref. 18). Following ref. 18, I refine Eq. 7 to

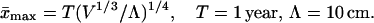8

(Numerically, Λ ∼ the Brownian walk of an oxygen atom over the time T.) The value of x̄_max determines metabolism also (18): on average 10 oxygen molecules are consumed per body atom per maximal mean lifespan (for any animal from invertebrates to mammals) or per maximal mean fission time (for any oxygen-consuming bacteria). Thus, if the total number of consumed oxygen molecules is N₀ and of body atoms is N_A, then

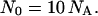9

Because N₀ = Ṅ₀x̄_max, the average oxygen consumption rate per body atom ṅ₀ = Ṅ₀/N_A is related to ẋ_max:

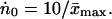10

Mutation rate also universally reduces (21) to x̄.

Phenomenology of Universality

Dynamics of any closed macroscopic system is related to the entropy increase (20). Life, in contrast, is well known (30) to be related to the entropy decrease of an animal (which therefore is never a closed system). A necessary condition of entropy decrease (20) is an energy supply (metabolism), whose destructive byproduct is a lethal irreparable molecular damage, which limits the maximal lifespan. So, individual death is an inevitable implication of life, and metabolism is related to the maximal (in the absence of all other factors) mean lifespan. The calculation and analysis of the consumed and destructive energies (18) yields Eq. 9.

Individual death leads to equilibrium and entropy increase. Thus, a necessary condition for the preservation of entropy decrease is the population reproduction. To further decrease the entropy, i.e. to increase genetic information, the population must change and adapt to changing conditions. Variability is provided by mutations. Maximally rapid genetic adaptation to changing conditions implies that all causes of mortality must most efficiently reduce to genetics. This means that although individual survival is highly accidental, the statistical probability of a cohort to survive to a given age under given living conditions universally depends on its (genetic) polymorphism and on parameters, which are strongly correlated with genetics (e.g., via immunity and thus the chances to survive illness; physical fitness and thus the chances to escape predators, capture prey, survive war). Indeed, by Eq. 6, for species as remote as humans and flies the survival probability ℓ_x(x̄) depends on age x and, e.g., the mean life expectancy at birth x̄ (19), independent of calendar year, country, race, and sex for humans; of family (medflies or fruitflies), conditions (overcrowded cages or individual cells), genetic composition for flies. So, all changes in polymorphism and living conditions reduce to the change in x̄. Thus, ℓ_x(x̄) describes also the universal law of evolution, quantifying “fitness” with the survival probability.

So, life is related to entropy decrease, which inevitably leads to individual death; death implies reproduction and evolution; evolution is related to mutations and death, which eliminates deleterious mutations and thus less fit individuals. (Truly, the role of death is multifaceted!) Because natural selection is related to survival, the latter quantifies macroevolution. Eq. 6 quantitatively reduces a three-dimensional evolutionary bush (21) to the survival probability, which allows for computer simulations (similar to those presented in refs. 31–34).

Natural evolution is hereditary and individual (the elimination of less-fit individuals is beneficial for the species). It selects populations, whose better chances to survive are verified over many generations. At a certain stage evolutionary genetic adaptation may be complemented with individual learning. Inductive learning is relatively recent (on an evolutionary scale). So, according to the molecular scale of evolution (25), the latter corresponds to a relatively small genome change. One wonders whether inductive reasoning emerges at every evolutionary summit. There are no immediate benefits, and thus no incentives, for an individual to invest time and effort in the preservation of the results of inductive learning for future generations. So, a breakthrough discovery of a nongenetic information transfer from generation to generation is little probable. Different from genetic evolution, it allows for a long-range information transfer to many individuals over many generations, thus providing a possibility for long-range correlations and time-space nonlocality in interactions between individuals (postevolution). The latter might lead to technology, thus to nonlinear (e.g., in population density) interactions between individuals and to absolute instability of a civilization (21). In a technological society destructive (e.g., bacteriological) power, available to an individual or a small group (a microscopic fluctuation) may rapidly become lethal for the population at large (absolute instability of life), lead to a near-instantaneous entropy increase and to the return to an equilibrium lifeless state. The reasoning is not limited to terrestrials and may resolve the Fermi-Hart (35–38) paradox: if extraterrestrial intelligence exists, why can it not be contacted? Presumably, it is either not sufficiently developed, or almost certainly already extinct.

Universality and Its Challenge

The previous section considers why evolution leads to universal laws of survival, evolution, and metabolism; why, e.g., Eq. 9, which relates metabolism and lifespan, is universal for all animals from bacteria to mammals, with no dimensional or dimensionless adjustable parameters. The problem of how this happens, despite different evolution (over billions of years), diversity (for ṅ₀ and x̄_max over millions of species from bacteria to mammals, with 10²⁰-fold body mass change) and living conditions (e.g., from hot water to cold air), is a true challenge. The situation, whose comprehensive description includes an enormous number of variables, but macroscopically reduces to few variables only, is well known in thermodynamics, where many billions of billions of variables, which describe individual atoms, reduce to pressure and temperature only. Universal laws are typical in the vicinity of critical points (20). Per Bak (32) demonstrated self-organized criticality. Yet, the universality of biological dynamics of all animals is unprecedented (no dynamic universality class in physics is even remotely as broad) and suggests that biology does not reduce to physics, just as irreversible turbulence does not reduce to reversible mechanics of atoms in liquids. Essentially, the situation resembles the emergence of quantum mechanics. In 1911 Rutherford suggested that an atom is similar to the solar system: its electrons rotate around the nucleus. Bohr noticed that this model does not explain an amazing stability of an atom (39). No planetary system returns to its initial state after a collision with another one, while the stationary state of an atom is universal with respect to its prehistory (e.g., its collisions or prior chemical bonds with other atoms. Imagine cars that self-repair themselves precisely to the initial state after millions of head-on high speed collisions!) This observation ultimately led to quantum mechanics. Empirical laws of heat radiation, photoeffect, and atomic spectra yielded its microscopic equations. Universal, self-reproducing during the evolution, biological laws (for animals, which are macroscopic as cars rather than microscopic as atoms) may lead to underlying “biological” equations and their microscopic implications (e.g., for DNA sequences).

Uniqueness of biological systems may be related to the uniqueness of natural evolution. Natural evolution is extraordinary rapid: the evolution from the first fishes to humans occurred in about 100 million generations, while it takes a million times more collisions (generations) for a given molecule to traverse 1 mm of water. Such speed is related to mortality, which extinguishes less-fit offsprings. Indeed, suppose there are on average Q offsprings per animal (survival implies Q > 1). If the population is stationary, i.e., only one of them survives, then the probability of survival is 1/Q in each generation and the probability of survival in G generations is (1/Q)^G. If, e.g., Q = 1.1, then after 100,000,000 generations each survivor is chosen from 10^4,000,000 a priori options. This unimaginably huge number demonstrates the uniqueness of a biological system. (The reasoning is readily generalized to a nonstationary population.)

Genetic evolution may be elucidated by a cartoon. Prepare 10 million copies of nursery rhymes books (bacteria). Randomly change, add or delete one letter in each of the books. Shred (kill) all copies with meaningless portions, and multiply surviving copies to restore the original (10,000,000) number. Repeat the procedure until it yields the Shakespeare level books (humans). The cartoon may be generalized to account for sexual reproduction with dominant and recessive alleles and to model natural evolution. The bottleneck in a computer simulation of this model is a computer that can identify a meaningless text, i.e., to formally define meaning. The mathematical challenge is related to high statistical proximity of a meaningful system to a disordered one that increases (40) together with the amount of information in the former. (Try to statistically distinguish an encyclopedia from Hamlet if both are presented in a binary code).