Environmental regulation in a network of simulated microbial ecosystems

Abstract

The Earth possesses a number of regulatory feedback mechanisms involving life. In the absence of a population of competing biospheres, it has proved hard to find a robust evolutionary mechanism that would generate environmental regulation. It has been suggested that regulation must require altruistic environmental alterations by organisms and, therefore, would be evolutionarily unstable. This need not be the case if organisms alter the environment as a selectively neutral by-product of their metabolism, as in the majority of biogeochemical reactions, but a question then arises: Why should the combined by-product effects of the biota have a stabilizing, rather than destabilizing, influence on the environment? Under certain conditions, selection acting above the level of the individual can be an effective adaptive force. Here we present an evolutionary simulation model in which environmental regulation involving higher-level selection robustly emerges in a network of interconnected microbial ecosystems. Spatial structure creates conditions for a limited form of higher-level selection to act on the collective environment-altering properties of local communities. Local communities that improve their environmental conditions achieve larger populations and are better colonizers of available space, whereas local communities that degrade their environment shrink and become susceptible to invasion. The spread of environment-improving communities alters the global environment toward the optimal conditions for growth and tends to regulate against external perturbations. This work suggests a mechanism for environmental regulation that is consistent with evolutionary theory.

The Gaia theory postulates that life is part of a global system that tends to self-regulate the abiotic environment in a habitable state (1, 2). Evolutionary biologists have long criticized Gaia theory for the lack of an evolutionary mechanism by which organisms that contribute to regulating the planetary environment would leave the most descendants (2–4). The Daisyworld model (5–7) showed that self-regulation need not imply teleology and could involve natural selection, but it is a special case in that traits selected for at the individual level always contribute to global regulation (2). The Guild model (8) of environmental regulation and nutrient cycling in an evolving ecosystem shares the same limiting assumption, that individuals can benefit only from those local environmental alterations that also act to stabilize the global environment in habitable conditions. Thus, neither model can adequately address the problem of “cheats” that profit from regulation but save the energy of contributing to it. The problem of cheats is avoided if environmental alteration is based on metabolic by-products that are selectively neutral at an individual level (2, 9, 10). This is the case with the majority of biogeochemically significant metabolic reactions.

The absence of individual-level selection pressures for traits that contribute to environmental regulation poses the question of why stabilizing negative feedbacks should dominate over destabilizing positive feedbacks at the global scale (11). However, selection pressures above the level of the individual can, in some circumstances, drive adaptation (12–19) and may provide a stabilizing influence on biogeochemical cycles. We assume metabolic by-product effects on the environment in the Flask model (19–21). Flask is an individual-based simulation model of microbial evolution that simulates an evolutionary process involving model organisms that each have a genetic code (22, 23). Populations of microbes are suspended in flasks of liquid. Individual microbes grow by consuming nutrients, reproduce and mutate, and alter their environment as a cost-free by-product of their metabolism. Ecological dynamics and selection pressures are not prescribed but instead emerge from the interactions of individual microbes with their shared environment. In a single well mixed flask, nutrient-recycling loops (8, 9) robustly emerge, which leads to an increase in population size (21). However, population crashes and endogenous extinctions can be caused by “rebel” mutants that grow rapidly but, in doing so, alter the abiotic environment away from the state to which the community is adapted (21). Artificial selection of flask ecosystems based on properties of the abiotic environment produces an adaptive community-level response that in some cases involves interactions between multiple “species” and in other cases can be explained purely by individual-level adaptation (19).

Here we develop a spatially structured version of the Flask model with multiple interconnected flasks in a ring topology. We use this model to test for the emergence of environmental regulation in an evolutionary system in which environmental alteration by organisms occurs solely as a by-product of metabolism. The environment within each flask is well mixed, and all organisms share the same environmental preferences, so individuals within a local community cannot benefit differentially from environmental alteration. However, imperfect mixing between flasks allows the metabolic actions of local communities to create environmental heterogeneity in the global system. When environmental conditions are good, populations expand to consume all available nutrients, and nutrient limitation creates the main selection pressure. When environmental conditions are harsh enough to constrain metabolism and restrict growth, higher-level selection acts on traits that affect the environment. Communities that improve their local environment out-compete communities that degrade their environment. The spread of improving communities leads to global environmental stabilization and regulation against external perturbations. Our findings suggest a mechanism to help reconcile Gaia theory and natural selection (2).

Model Description

The spatial Flask model [see supporting information (SI) Appendix 1 for full model description] consists of F (= 10) flasks connected in a ring topology. Each flask contains a neutral liquid matrix in which is suspended a microbial population. The composition of the liquid medium determines the environment of the microbes. Some of the chemicals present are nutrients [meaning, specifically, different compounds of a particular nutrient element (e.g., nitrogen)] that may be consumed as food and converted to biomass, whereas others are nonconsumable and form part of the abiotic environment. The environment is assumed to have properties such as temperature, pH, salinity, etc. that both affect and can be affected by microbial activity. Nonconsumable chemicals and physical properties of the flask environment are collectively referred to as abiotic factors to distinguish them from nutrients. There is a flow of liquid medium through each flask that occurs continuously at a prescribed rate. The inflow brings with it influxes of nutrients at fixed concentrations and steady inputs to abiotic factors, whereas the outflow removes fixed proportions of stored nutrients and abiotic factors. The liquid medium in each flask is assumed to be well mixed so that, in the absence of external perturbation, the composition of the medium in each flask will reach a homogeneous steady state. In the spatial model, each flask has the same volume and has the same imposed fluxes of nutrients and abiotic factors. “Diffusive” between-flask mixing is implemented by exchanging a constant volume of liquid between each neighboring pair of flasks at each time step. Hence, when concentrations of microbes or nutrients vary between neighboring flasks, there is a net transfer that reduces any gradient. Transport of microbes carries genetic information that can qualitatively change local community compositions.

Microbes are modeled as simple organisms that consume and excrete nutrients and affect the levels of abiotic factors in their environment as a by-product of metabolism. The model microbes have genetic traits that specify their patterns of uptake and excretion of nutrients and their effects on their abiotic environment. Microbes grow by converting consumed nutrients to biomass and reproduce by splitting when their biomass reaches a fixed threshold. Mutation occurs with low probability during each reproductive event. Microbes affect their abiotic environment in proportion to the amount of biomass created during growth. Growth is constrained by nutrient availability, by a universal maximum consumption rate, and by the fit between the current state of the abiotic environment and each microbe's “optimal” preferred abiotic conditions. The abiotic constraint on microbe growth is defined so that metabolic rates decline smoothly with distance from an optimum environmental state in which the metabolic rate is maximized. Each microbe pays a fixed “maintenance cost” at each time step to represent the inevitable thermodynamic inefficiency of metabolism and the cost of maintaining cellular machinery. The combination of these constraints defines boundaries on the environmental axes at which metabolism exactly compensates for microbe maintenance demands (so that net growth is zero). Within these boundaries lies the “habitable region” in which metabolic rates are high enough to support net growth; outside the boundary, the harsh abiotic environment reduces metabolic rates such that microbes would eventually starve.

We test for environmental regulation by considering the fit between organisms and environment in the presence of external perturbations. If the biota maintains the environment in a habitable condition in the presence of perturbations that would otherwise render it uninhabitable, then we say that the biota are regulating their environment. To quantify the goodness of fit between the organisms and their environment, we introduce an “environmental error” metric (Γ) that is measured as the absolute resultant distance of the actual abiotic environmental state from the microbes' preferred conditions for growth, that is, 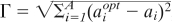, where a_i is the actual level and a_i^opt is the ideal level of the ith abiotic factor. There are two mechanisms by which the fit between organisms and environment might be improved over time: (i) organisms might alter the environment toward their preferences, or (ii) organism preferences might adapt to suit prevailing conditions. Here, to isolate the effects of environmental alteration, we impose a universal environmental preference for all microbes, which also prevents any individual from gaining a differential advantage by altering the environment. We have also run the model with adaptation of environmental preferences and observe qualitatively similar results, but in that scenario it is difficult to separate out the contributions of adaptation and environmental alteration to improving the fit between organisms and their environment.

Results

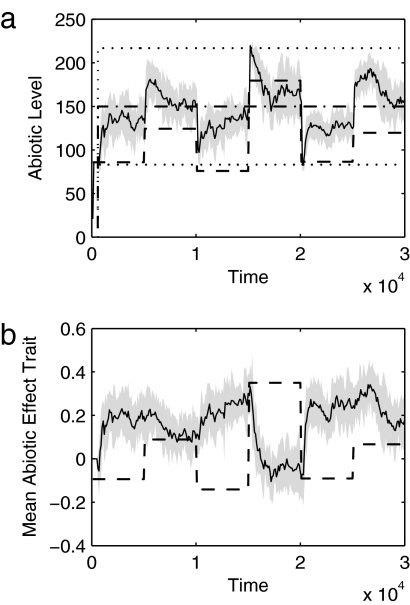
The model organisms collectively alter their environment toward their preference (Fig. 1; further examples are shown in Fig. S1). The spatial model was seeded with an inoculum of randomly generated microbe species and then observed for an extended period, during which perturbations were applied by periodically reassigning external abiotic fluxes (see Methods). In a typical run (Fig. 1a), there is an early period in which seed species unsuited to the initial environmental conditions go extinct, after which those species that survive multiply and diversify. Nutrient-recycling loops are formed (21) that allow larger populations to be supported through more efficient use of supplied resources. The abiotic environment shows a tendency to move toward the growth optimum after perturbation and remains within the habitable region even after a perturbation that would take the “dead” state outside it. Changes to external abiotic fluxes can initially cause the abiotic environment to move outside the limits of the habitable region, because the net environmental effect of the community is not adapted to the new external forcing. This excursion is followed by a period of adaptation as the composition of the community alters to compensate for the changed external flux levels. The average allele value (across all organisms) for genes determining abiotic effect traits changes in a manner that generally counteracts changes in external forcing (Fig. 1b).

Fig. 1.

The environment is constrained to habitable conditions and external forcing is counteracted by genetic change. Data are shown for a typical run (F = 10 flasks, R_D = 1% diffusive between-flask mixing per time step) with random reassignment of external abiotic influx every 5,000 time steps. (a) The state of the abiotic environment (solid line gives mean value; shaded area is ±1 SD measured across all flasks) remains close to the ideal growth conditions (dash-dot line) and within the boundaries of the habitable region (dotted lines). The distance between the actual abiotic state and ideal conditions provides the environmental error Γ. The “dead” abiotic state (dashed line) shows the state of the environment if no organisms were present and demonstrates the perturbing effect of changes in external forcing. (b) The mean allele value (solid line gives mean value; shaded area is ±1 SD measured across the whole community) for genes controlling the metabolic by-product effects of organisms on the abiotic environment. The mean allele value changes in response to external forcing (dashed line, not to scale; shown for illustration only).

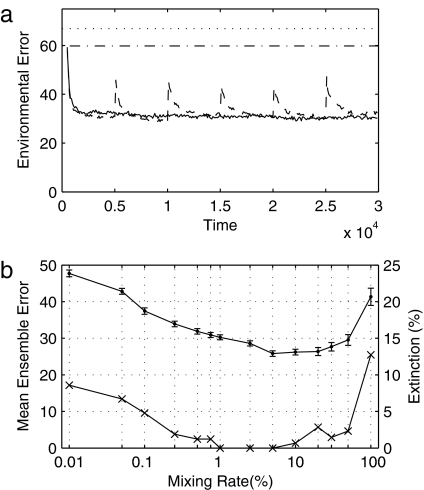
We ran ensembles of both unperturbed and perturbed runs (Fig. 2; see Methods). Mean environmental error across each ensemble (Fig. 2a) declines over time before reaching an asymptote value that is slightly lower than the error that would be expected if individual runs were distributed evenly across the habitable region. Inspection of individual runs from the ensemble confirms this distribution, with a skew toward the optimum conditions for growth (i.e., in the direction of decreasing error). In the perturbed ensemble, error is rapidly reduced following a spike after each perturbation. This trend is robust to changing the frequency of perturbation (Fig. S2). Extreme perturbations can cause global extinction by pushing the environment too far from the habitable region for any organisms to survive, but such events are rare within the range of perturbations used here. The extinction rate is not affected significantly by perturbation frequency (Fig. S2). Regulation of multiple environmental variables poses a greater challenge than regulation of a single variable, but error reduction over time is still observed to be robust when the model is run with two or three abiotic factors (Fig. S3). In the standard form of the model, organisms are assumed to feed continuously and simultaneously. To verify that no artifacts are introduced by the simultaneous update algorithm (such as unintended potential for altruism), we also ran the model with a randomized sequential update algorithm and found the results to be robust (Fig. S4).

Fig. 2.

Ensemble results show error reduction over time and the effect of the diffusive mixing rate on regulation and extinctions. (a) Mean environmental error (Γ) in unperturbed/perturbed ensembles of 200 runs with F = 10 and R_D = 1%. In the unperturbed ensemble (solid line), error decreases over time to an asymptote level. In the perturbed ensemble (dashed line), error is rapidly reduced from a spike after each perturbation. Data are plotted together with habitability bound (dotted line) and predicted environmental error in absence of life (dash-dot line). (b) Effect of mixing rate (R_D, logarithmic scaling) on the final (asymptote) ensemble error value (dot markers, left ordinate; ensemble mean ± 1 SE) and the frequency of global extinction events (cross markers, right ordinate) after life has initially been established [F = 10, ensembles of 200 unperturbed runs for each mixing rate value in {0.01, 0.05, 0.1, 0.25, 0.5, 0.75, 1, 2.5, 5, 10, 20, 30, 50, 100} (%)]. Intermediate mixing rates provide the greatest error reduction and least frequency of global extinction. Runs in which initial seed did not become established are omitted.

Because all organisms have the same fixed environmental preferences, any error reduction observed must be a result of environmental alteration by the biota rather than adaptation toward prevailing conditions. To examine the effect of spatial connectivity, we varied the rate of diffusive mixing (R_D, percentage of flask volume mixed per time step) between the flasks from close to zero (almost disconnected flasks) to perfect mixing (which creates a homogeneous global system). When there is an intermediate level of mixing between the flask ecosystems, there is a marked reduction in the environmental error relative to the case with either very high or very low mixing rates (Fig. 2b). Mixing rate also affects the likelihood of a global extinction (Fig. 2b). In unperturbed runs, most extinctions occur during the initial seeding phase, when the inoculum is unsuited to its initial environment (these extinctions are factored out of Fig. 2), but it is also possible for an established community to go extinct by degrading its environment to a point at which growth is prevented and starvation occurs (21). Intermediate mixing rates prevent global extinction by allowing refugia-recolonization dynamics (24) to occur; such mixing rates are high enough to allow effective reseeding after local extinction but low enough to maintain environmental heterogeneity and, thus, make simultaneous global extinction unlikely. For any given mixing rate, the likelihood of global extinction is reduced by increasing the number of flasks in the spatial system, which increases environmental heterogeneity and the likelihood of refugia.

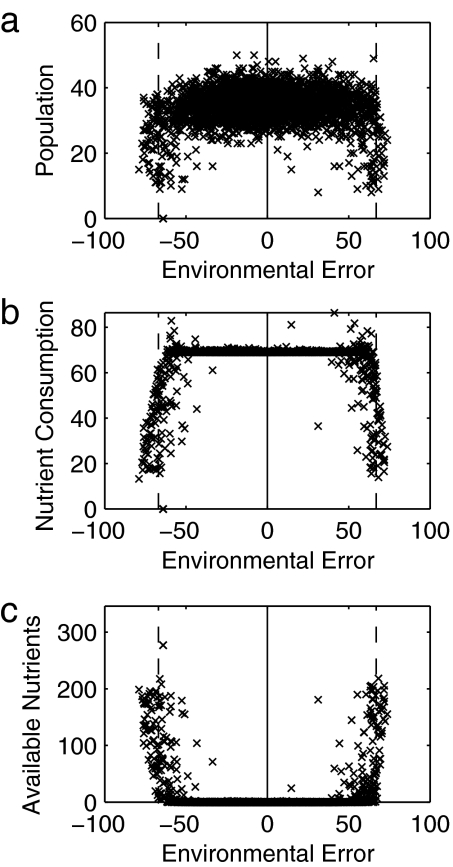
Once life is established in the system, environmental error is broadly constrained to habitable levels. Inside the habitable region, “biotic plunder” (25) occurs; populations expand to carrying capacity (Fig. 3a), and all available nutrients are consumed (Fig. 3b) so that no stored nutrients are available in the environment (Fig. 3c). At the boundaries of the habitable region this situation changes as abiotic constraints on metabolism affect growth; the consumption rate decreases, nutrients build up in the environment, and populations shrink.

Fig. 3.

System behavior falls into two characteristic regimes depending on environmental error. Data are shown from the same example run as shown in Fig. 1. Different system metrics are scatter-plotted against environmental error over the course of the run: (a) population size; (b) nutrient-consumption rate (a proxy for productivity); (c) available nutrient levels in the environment. The solid vertical lines show the ideal abiotic conditions for growth (the zero-error state), and the dashed vertical lines show the boundaries of the habitable region. Within the habitable region, population size is typically at the carrying-capacity level determined by nutrient supply, consumption rates and growth are both high, and levels of stored nutrients in the environment are minimal. At (and outside) the boundaries of the habitable region, population sizes decrease, consumption/growth rates decrease, and nutrients build up in the environment.

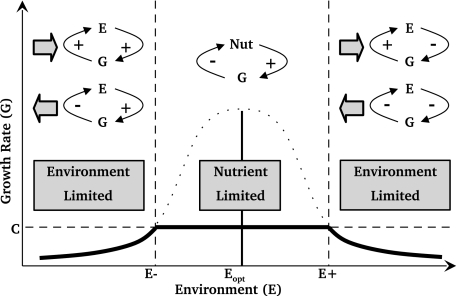
Thus, there are two identifiable regimes for the system (Fig. 4). In the nutrient-limited regime, abiotic conditions are good and theoretically allow fast metabolic rates, but the actual growth rates achieved are limited by nutrient availability. Nutrient availability increases growth, which decreases nutrient availability. This negative-feedback loop stabilizes the system in a state of nutrient scarcity (25). Traits that determine metabolic by-product effects on the abiotic environment are selectively neutral, because nutrient constraints mean that changes to the environment that do not move the system out of the habitable region make no difference to growth rates. Nutrient-consumption traits are strongly selected, because nutrient scarcity gives consumption patterns a strong impact on growth rates.

Fig. 4.

Schematic of nutrient-limited and environment-limited feedback regimes in relation to the growth response of microbes to the state of the abiotic environment. The boundaries between regimes occur at the boundaries of the habitable region, that is, at the states of the abiotic environment at which microbe growth rate (dotted line) exactly balances maintenance cost (C, horizontal dashed line). This relation provides upper (E⁺) and lower (E⁻) habitability bounds (vertical dashed lines) on the abiotic environmental variable (E) on either side of the growth optimum (E_opt, vertical solid line). The dotted line shows the hypothetical growth rate of microbes permitted by abiotic conditions if there were no nutrient limitation. The actual microbe growth rate (solid black line) takes into account both nutrient and environmental constraints. In the nutrient-limited regime (between E⁻ and E⁺), negative feedback on growth occurs in which nutrient availability increases growth, which decreases nutrient availability. In the environment-limited regimes (above E⁺ or below E⁻), there is a symmetrical difference between the feedback structures above and below the growth optimum. When population growth causes net increase in E (right arrows), there is positive feedback on growth below E⁻ (where growth improves the environment and increases growth rate) and negative feedback on growth above E⁺ (where growth degrades the environment and decreases growth rate). When population growth causes net decrease in E (left arrows), there is negative feedback on growth below E⁻ and positive feedback on growth above E⁺.

In the environment-limited regime, abiotic conditions are poor enough to have a detrimental impact on microbial growth rates. Abiotic effect traits are selected, because the environment is the key determinant of growth rates. Nutrient-consumption traits are selectively neutral, because nutrients are abundant and nonlimiting; not all supplied nutrients are being consumed at each time step. Feedback loops between abiotic environmental state and growth rates (2) may be positive (where growth improves the environment and increases growth) or negative (where growth degrades the environment and decreases growth) (Fig. 4). The sign of the feedback loop depends on the net collective effect of the community on the abiotic environment and whether the current abiotic environmental state is above or below the optimum; positive feedback on growth occurs when the community moves the environment toward the optimum state, whereas negative feedback on growth occurs when the community moves the environment away from the optimum. Populations that degrade their environment reduce in size, but complete extinctions are rare, because (in addition to refugia-recolonization processes) negative feedbacks on growth (2) usually prevent a community from driving itself extinct by its own actions.

The truncated shape of the schematic growth curve (Fig. 4) results from the combination of the feedback loops between nutrient availability and growth and between the abiotic environment and growth. This truncated shape is in qualitative agreement with observed data (Fig. 3).

Feedbacks on growth alone cannot explain the systematic trend in error reduction over time or its sensitivity to mixing rate (Fig. 2). The consistent genetic response that counteracts changes in external forcing (Fig. 1b, Fig. S1) shows that selection is active on traits that determine metabolic by-product effects on the abiotic environment. These traits are selectively neutral within a flask, because shared environmental preferences and the well mixed local environment prevent any individual from gaining an advantage over its competitors by environmental alteration. However, between-flask environmental heterogeneity resulting from imperfect mixing allows a higher-level selection mechanism to operate. The genetic composition of local communities determines their environmental impact and, thus, affects their viability. Larger (and therefore denser) populations export more individuals (via the diffusive mixing process) than smaller populations, which makes them more successful at colonizing or invading neighboring locations. In the environment-limited regime, any local community that chances on (by random mutation or mixing of individuals between flasks) a species composition that has an improving effect on its abiotic environment will increase its growth rate and expand in size, amplified by positive feedbacks on growth (2). Such environment-improving communities will spread and colonize neighboring locations, whereas local communities that have a degrading effect on their environment will shrink and become more susceptible to invasion (because of reduced competition for resources). Thus, in the environment-limited regime, with abundant stored nutrients to support growth, differential proliferation of adjacent ecosystems leads to selection on collective environment-altering traits. This selection pressure favors environment-improving communities, and the spread of these communities across the global system brings the abiotic environment back toward habitable conditions.

Discussion

The spatial Flask model shows how environmental regulation can emerge from the collective metabolic by-product effects of the biota in a manner consistent with evolutionary theory. This work complements previous models (5–8) in which environmental regulation depends on a direct individual-level selective benefit for “regulating” environmental alterations. Our model relaxes this limiting assumption and, without positing any form of altruism, shows that higher-level selection can shape the collective environment-altering properties of local communities.

It is theoretically possible for higher-level selection to favor the presence of a single species or trait value that alone can cause the observed environmental alteration (19), but in this study this is not the case. Within each local community there is always high diversity in abiotic effect-trait values, although the net balance of values consistently adapts in response to environmental perturbations. Therefore, community-level adaptation results from a change in the distribution of trait values and not from the emergence of a single well adapted species. The high diversity observed in abiotic effect-trait values confirms the lack of individual-level selection pressure on these traits, emphasized by comparison with the low diversity in nutrient-consumption traits, which are strongly selected at the individual level (21).

The higher-level selection mechanism does not imply long-term higher-level adaptation. Communities are not transmitted intact from one location to another, and accurate reassembly of a colonizing community is uncertain. Mutations and microbe transport continually alter local community composition. Thus, the higher-level selection process acts on differential rates of proliferation created by transient “phenotypic” traits, and we observe selection without accurate inheritance or reliable transmission. Despite these weaknesses, there is sufficient persistence of community composition for the intercommunity selection mechanism to operate. The spread of environment-improving communities is sufficient to steer the global system away from the environment-limited regime and back into the nutrient-limited regime. When the system re-enters the nutrient-limited regime, the environment is no longer limiting and the environment-altering properties of local communities become selectively neutral.

The regulatory system we propose is not a universal or infallible mechanism. Some perturbations will be accommodated easily, whereas others will cause system-wide extinction. In our model system, higher-level selection for environmental improvement creates a regulatory mechanism that is reasonably robust, but it still may be overcome by extremely severe or very frequent perturbations. In other scenarios, there may be competing selection pressures that outweigh the selection pressure for environmental improvement and thereby destabilize the system. However, the occasional failure of regulation does not imply its absence, just as the remarkable homeostasis of living organisms is not negated by the possibility of fatal disturbance.

In our model, a level of spatial structure is imposed that is necessary for higher-level selection to occur (26). However, tests that varied the level of spatial structure by distributing the same overall volume of liquid among different numbers of flasks (including an approximation of continuous spatial structure by a large number of very small flasks) showed that the regulatory mechanism is robust. This finding increases our confidence in the results. In principle, our predicted mechanism for environmental regulation could be tested in a system of real interconnected microbial ecosystems under laboratory conditions [see, e.g., recent work that linked migration and dispersal to evolutionary/ecological dynamics in spatially structured microbial metacommunities (27, 28)]. This is a topic for future work.

For now we speculate that the mechanism we have identified could operate, in principle, in natural ecosystems. The real world contains spatial structure, albeit less uniform than that in our model. Consider, for example, ecosystems in different lakes, in soil, or in peat bogs on different hilltops. Equally, in the ocean, eddies and gyres provide a degree of spatial structure that restricts exchange of organisms with other regions. Microbial consortia are known to display a variety of interesting spatial dynamics, whereas the spatial association of diverse microbial species living in biofilms is known to aid their survival (29). Our model may be particularly relevant to the early Earth. After its origin, life may have been distributed in different “ponds” [e.g., abundant meteorite craters (30)]. Exchange of organisms and material between these ponds could occur through airborne transport or flooding events. In such a system, perhaps the first successful ecosystems could have come to dominate and regulate the global environment through the mechanism we propose.

Methods

Model description can be found in SI Appendix 1. For simplicity here, we use just N (= 2) nutrients and A (= 1) abiotic environmental variables, which gives (2N + A) (= 5) genetic loci; sensitivity testing on N and A (Fig. S3) shows that the results reported are robust. Each run updated a ring of F = 10 interconnected flasks for T_run = 30,000 time steps. The system was seeded after 500 time steps with a diverse inoculum of K_m = 100 randomly generated individuals in each flask. Each flask received a different inoculum. Mutation occurred during reproduction with a P_mut (= 1%) chance of a new allele value at each offspring locus. Flux parameters were initialized randomly at the start of each run with values randomly sampled from a constrained range. The same flux parameters were applied to all flasks in the spatially coupled system. Ensemble data were collected from 200 runs that were identical except for the random initialization of microbial inocula and flux parameters, which were drawn from identical distributions across each ensemble. Perturbations were applied by random reassignment of external fluxes to abiotic variables every 5,000 time steps (different perturbation frequencies were tested; see Fig. S2). Ensembles were analyzed to test sensitivity to various other parameters including F, T_run, P_mut, K_m, τ (the severity of the abiotic constraint on growth), seed population diversity, and flux sizes (I^min, I^max, O^min, O^max). No qualitative sensitivity in system dynamics relevant to the results reported was observed. We tested for finite size effects caused by the ring topology, but none were found for the ranges of parameters used. Here we impose on all microbes a preference of a^opt = 150 for the single abiotic variable used in standard runs. Different target vectors were used when A was varied (Fig. S3). We also tested the effect of a different model update algorithm in which organisms feed sequentially rather than simultaneously (the standard model formulation), which gave qualitatively similar results (Fig. S4).