Protecting residential care facilities from pandemic influenza

Abstract

It is widely believed that protecting health care facilities against outbreaks of pandemic influenza requires pharmaceutical resources such as antivirals and vaccines. However, early in a pandemic, vaccines will not likely be available and antivirals will probably be of limited supply. The containment of pandemic influenza within acute-care hospitals anywhere is problematic because of open connections with communities. However, other health care institutions, especially those providing care for the disabled, can potentially control community access. We modeled a residential care facility by using a stochastic compartmental model to address the question of whether conditions exist under which nonpharmaceutical interventions (NPIs) alone might prevent the introduction of a pandemic virus. The model projected that with currently recommended staff–visitor interactions and social distancing practices, virus introductions are inevitable in all pandemics, accompanied by rapid internal propagation. The model identified staff reentry as the critical pathway of contagion, and provided estimates of the reduction in risk required to minimize the probability of a virus introduction. By using information on latency for historical and candidate pandemic viruses, we developed NPIs that simulated notions of protective isolation for staff away from the facility that reduced the probability of bringing the pandemic infection back to the facility to levels providing protection over a large range of projected pandemic severities. The proposed form of protective isolation was evaluated for social plausibility by collaborators who operate residential facilities. It appears unavoidable that NPI combinations effective against pandemics more severe than mild imply social disruption that increases with severity.

It has been nearly 40 years since the last influenza pandemic in 1968. A sporadic, but steadily larger series of human cases of H5N1 avian influenza with a case fatality rate >50% stands as a harbinger of the devastating potential a novel influenza virus might pose. To validate estimates of mortality and morbidity, and to explore options for the control of an influenza pandemic, several researchers have modeled both the process of influenza transmission and various intervention measures aimed at mitigating its consequences (1–7). Many of these studies suggest that antiviral pharmaceutical agents and vaccines would be the most effective interventions, with nonpharmaceutical interventions (NPIs) relegated to a subordinate, incremental role. However, it is also clear that the levels of antivirals and vaccines needed for effective control are not likely to be available at the start of a pandemic, even in the most affluent societies, and should resistance to current antivirals emerge, NPIs would be thrust to the fore.

Recognizing the potentially critical importance of delays of a few weeks or months after the demonstration of human-to-human transmissibility of a new influenza virus, the current global strategy is focused initially on containment of outbreaks (8). Although it is uncertain whether sufficient antiviral and vaccine resources will be available to provide effective pandemic control in economically developed countries, it is certain that the bulk of control efforts will rely on NPIs in less economically developed settings in which most of the world's population now lives. Mathematical models (2, 3, 7) used together with historical studies of the 1918–1919 influenza pandemic in the United States (9, 10) suggest that the timely implementation of NPIs at the community level may have been somewhat effective in curtailing pandemic influenza. However, these studies conclude that most implementations began too late and were halted too soon. A comprehensive review of NPI containment strategies used by U.S. communities during the 1918–1919 pandemic concluded that the timely and continuous implementation of NPIs seemed to have curtailed the outbreak (11–13).

A recent study (7) focused on the application of NPIs for pandemic control within both the social community and acute-care hospitals. The dynamical model used in that study revealed that the tight coupling between acute-care hospitals and the community within which they are embedded limits the extent to which NPI measures can effectively control pandemic spread within the hospital itself. The essential finding was that for a pandemic of moderate severity (e.g., ℛ₀ ≈ 2.1) or greater, there was no practical level of within-hospital transmission control that could protect the institution from being overwhelmed.

The open nature of community access makes containment in acute-care hospital settings nearly impossible. However, other health care and social institutions have the potential to restrict community access to a greater degree. These include ≈16,000 institutions within the United States that care for individuals who require assistance with activities of daily living, such as the disabled (mostly elderly) and the mentally and developmentally challenged (14). The aim of this modeling study was to estimate the levels of NPIs that would be required to protect any residential care facility (with the capability of controlling community access) against the introduction of a pandemic virus. We chose an extension of a Susceptible–Exposed–Infected–Recovered (SEIR) stochastic compartmental model to represent a facility providing residential care to disabled persons. The objective of this work was threefold: (i) to determine whether an intrinsic ability to control access to these facilities provided a basis for protection against pandemic influenza, (ii) to identify specific NPIs and combinations thereof that could achieve community access control, and (iii) to develop practical implementations of these NPI combinations sufficient for protection over the full range of projected pandemic categories.

Results

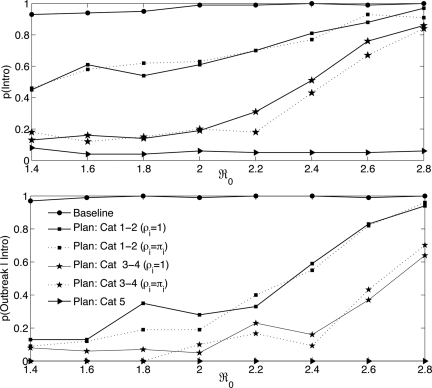
Although no formal sensitivity analyses were performed in this study to explore the effects of uncertainty in parameter estimation, we did examine the bounds of effects of one portion of our model, the portion involving the applicability of NPIs to individuals who appear asymptomatic but are, in fact, infected with the pandemic virus. It is not uncommon in epidemics of seasonal influenza for persons to become infected with the circulating virus yet remain entirely without symptoms throughout the course of the infection. This is considered very unlikely for infection with a virus completely novel to human immune systems (R. Belshe, R. Couch, and P. Glezen, personal communications). Furthermore, because an asymptomatic state for a pandemic infection is likely to be associated with a very low level of replication and/or a high level of immunological efficacy, shedding and transmission are likely to be both short in duration and low in magnitude. Nevertheless, because this is widely considered the linchpin to the efficacy of NPIs, we simulated both the case in which NPIs had no effect in further reducing the transmission of virus for asymptomatic persons (Fig. 1, solid lines), and the case in which the transmission-reducing effects of NPIs were the same for both infected and asymptomatic persons (Fig. 1, dashed lines). Some types of NPIs (e.g., isolation) can by their nature be applied only to symptomatic persons, whereas other NPI types would require exceptional rigor to be applied even approximately as stringently to asymptomatic persons. In what follows, we have provided the results for simulations assuming equal efficacy in transmission reduction for asymptomatic and infectious persons and no efficacy for asymptomatic persons.

Fig. 1.

p(Intro) and p(Outbreak|Intro) denote the probabilities of a virus introduction and a pandemic outbreak given a virus introduction in a facility, respectively. These results are based on 100 realizations for each of severity scenarios described by ℛ₀ ε (1.4, 2.8). Results depicted by solid and dashed lines assumed ρ_i = 1 and ρ_i = π_i, respectively.

We simulated a baseline scenario and three plans that included NPIs for a range of pandemic severities (4, 6, 15) represented by the basic reproduction number, ℛ₀ (Fig. 1, all values displayed in the figure are listed together with 95% confidence intervals in supporting information (SI) Tables S1 and S2). Although cases of infection are reported throughout, corresponding cases of mortality from each of the intervention plans simulated can be easily obtained from Table 1 by multiplying the final epidemic size by the case fatality proportion (CFP) in Table 2. Simulations were scored as resulting in the emergence of an outbreak when the clinical attack rate exceeded 5% of the facility population size (10 infections in a resident population of 200). We set the duration of a pandemic wave to 180 days and presumed a virus introduction if a case arose within this time in the simulations. The parameter estimates assumed in these simulations are provided in Table 2 (see also Table S3).

Table 1.

The final epidemic size is denoted by Episize_i, where i marks its maximum, mean, and median value

ℛ0	Episizemax	Episizemean	Episizemedian
Baseline :: Plan Category 1–2
1.4	(143 :: 20)	(71 :: 2)	(78 :: 0)
1.6	(160 :: 22)	(106 :: 3)	(122 :: 1)
1.8	(177 :: 86)	(132 :: 7)	(142 :: 1)
2.0	(176 :: 91)	(148 :: 8)	(153 :: 1)
2.2	(183:: 104)	(161 :: 11)	(164 :: 2)
2.4	(185 :: 143)	(170 :: 26)	(171 :: 9)
2.6	(192 :: 125)	(173 :: 45)	(177 :: 45)
2.8	(194 :: 159)	(178 :: 81)	(179 :: 88)
Plan Category 3–4 :: Plan Category 5
1.4	(13 :: 1)	(0 :: 0)	(0 :: 0)
1.6	(16 :: 1)	(1 :: 0)	(0 :: 0)
1.9	(29 :: 1)	(1 :: 0)	(0 :: 0)
2.0	(34 :: 1)	(1 :: 0)	(0 :: 0)
2.2	(39 :: 1)	(2 :: 0)	(0 :: 0)
2.4	(88 :: 1)	(3 :: 0)	(1 :: 0)
2.6	(104 :: 1)	(12 :: 0)	(2 :: 0)
2.8	(118 :: 2)	(26 :: 0)	(12 :: 0)

Results for the baseline and intervention plans simulated (punctuation mark :: separates these outcomes). These findings assumed that interventions had no effect on asymptomatic persons (ρ_i = 1). Mortality cases corresponding to these simulations may be obtained by multiplying Episize_i by the case fatality proportion (CFP) in Table 2.

Table 2.

Variables, parameter definitions, and values assumed in the numerical simulation of a resident facility

Variables	Parameters	Values	References
ℛ0	Basic reproduction number	1.4–2.8	4, 6, 15
m	Fraction of exposed that progress to infection	0.667	16
1/φ i*	Average latency period, days	1.9	5, 6
1/γA	Average recovery period for asymptomatic, days	5	4, 17
1/γI	Average recovery period for infected, days	5	4, 17
CFP	Case fatality proportion	0.03–0.15	18
δI	Resident mortality rate, δI = (CFP/1 − CFP) γI (day−1)	0.0062–0.035	16
πi*	Transmission reduction parameter when applied to infected	0.05–1	4
ρi*	Transmission reduction parameter when applied to asymptomatic	0.05–1	4
ηi*	Infectiousness of asymptomatics relative to symptomatics	0.02	16
1/ξVF; 1/ξVC	Average time spent between locations by visitors, hours; days	0–2; 7	14
1/ξSF; 1/ξSC	Average time spent between locations by staff, hours; hours	8–12; 12–16	14
pA	Probability of having asymptomatics escape monitoring efforts	1	Estimated
pE	Probability of having exposed escape monitoring efforts	0.14–1	Estimated
pI	Probability of having infecteds escape monitoring efforts	0.1–1	Estimated

*i = R, SF, VF, SC, VC.

Baseline Scenario.

The baseline scenario assumed that no interventions were incorporated. Our results showed that the median epidemic size (Table 1, baseline :: plan category 1–2) inside a facility was significantly lower for relatively mild outbreaks (ℛ₀ = 1.4; 78 cases) than for severe outbreaks (ℛ₀ = 2.8; 179 cases). The relatively high attack rates predicted by the model for a resident facility could be attributed to the expected high contact levels among individuals circulating within such a facility. For the baseline scenario, a virus introduction (Intro) into a residential facility was highly probable (Fig. 1 Upper) and occurred rapidly. Note also that, given a virus introduction, an outbreak was almost inevitable [p(Outbreak|Intro) ≥ 0.97] for all values of ℛ₀ (Fig. 1 Lower).

Assessing the Role of NPIs.

We chose three levels of NPI intervention strategies to conform to the category classification scheme for pandemic influenza proposed by the Centers for Disease Control and Prevention (CDC). Generally speaking, we found that conventional NPIs sufficed to curtail only mild outbreaks, and that higher levels of NPIs, requiring greater social restriction and higher levels of cooperation, were needed to manage more severe outbreaks.

Plan: Category 1–2.

The preparedness plan for category 1–2 pandemics was designed to simulate the implementation of various NPIs discussed in most U.S. state plans. We assumed that these plans would produce a 50% reduction in transmission. This level of effect reduced the epidemic size (median) from 171 to 9 cases for ℛ₀ = 2.4 (Table 1, baseline :: plan category 1–2) for the case in which the NPIs were assumed not to apply to asymptomatic persons. Results for simulations of the case in which NPIs were assumed to apply to asymptomatic persons with an effect comparable to that on infected persons are virtually indistinguishable in Fig. 1. This is because, for pandemic viruses, our information is that the asymptomatic class is likely to be both very much smaller and much less infectious than for seasonal influenza (see Discussion). Although the probability of a virus introduction remained significant [p(Intro) ≥ 0.5, ℛ₀ > 1.4], Fig. 1 Lower shows that, if a 50% reduction in transmission can be achieved, the probability of an outbreak would be reduced by at least twofold for most pandemics (ℛ₀ < 2.4); and that varying the impact of the asymptomatic class over the full range did not demonstrably change the simulation result.

Plan: Category 3–4.

The simulations for category 1–2 pandemics revealed that employee entry–reentry was the most important element in the control of influenza introductions into a facility. Further revealed was that approximately a 10-fold reduction in the probability of an introduction was required to provide substantive protection against more severe pandemics. This could be accomplished by increasing employee commitments to 10 or more days in continuous residence at the facility, but this was considered socially unworkable. However, any attempt to reduce the number of days on-site (from 10) necessarily required a mechanism for a corresponding reduction in the probability of reintroduction of the pandemic virus to compensate for the increased frequency of reentry. By using data on time from infection to symptomatic illness for A(H3N2) and A(H5N1) viruses (P. Glezen, R. Couch, and R. Belshe, personal communications), we simulated the effects of scenarios in which employees, together with all with whom they shared their domicile, entered isolation from the community within their own homes during the last portion of off-time away from a residential facility.

The consequences of a 4-days-on/4-days-off/2.3-days isolation period lowered the probability of reintroduction of the virus by approximately a 16-fold (at ℛ₀ = 2) compared with daily 12-h shifts; and was considered socially acceptable by collaborators working closely with residential care facilities. Except for the introduction of employee off-shift isolation periods and increased restrictions on visitors, both of which are accounted for explicitly in the dynamical model, the NPIs for this plan were similar to those of plan category 1–2. Therefore, we again assumed an overall reduction in transmission of 50%. With this assumption, the estimated probability of virus introduction was reduced to <50% for ℛ₀ < 2; and the probability of an outbreak was reduced by >50% from baseline for all but the most severe simulated pandemic (ℛ₀ = 2.8) (see Fig. 1 Lower). Again, the impact of excluding the small and relatively noninfectious asymptomatic class from the reduction of transmission (ρ_i = 1; solid curves in Fig. 1) produced no discernible difference in the simulations.

Plan: Category 5.

This plan simulated virtually complete facility isolation and assumed an overall 95% reduction in transmission. Clearly, such levels of NPI could reduce the possibility of pandemic virus introduction to very low levels (Fig. 1).

Discussion

The model developed in this study suggests that it is indeed possible for residential care facilities (nursing homes and the like) to protect residents and staff from pandemic viruses even without access to vaccine and antiviral resources. However, protection from severe pandemics requires significant social changes and a high degree of motivation and cooperation in the staff of such facilities. Nearly all earlier studies evaluating interventions for mitigating the impact of pandemic influenza have agreed that, barring the emergence of resistance, pharmaceutical agents (antivirals and vaccines) will be the most effective interventions possible. These studies also noted, however, that adequate supplies of both antivirals and vaccines are unlikely to be available at the start of any pandemic. Therefore, even in developed countries, the brunt of pandemic mitigation will be borne initially by community agencies using largely or solely NPIs. Outside economically developed countries, NPIs will most likely be the only intervention methods available. Further unfortunately, previous analyses indicated that NPIs, as previously conceptualized, will be modest in efficacy. Our baseline and category 1–2 scenarios suggest that conventional NPIs should be expected to protect facilities that can control community access only in pandemics of, at most, moderate severity. Models and discussions of the use of NPIs have included measures such as closures of social gathering places (e.g., school, churches, and stadiums), social distancing techniques for interpersonal interactions, isolation of infected persons, quarantine of persons exposed to infection, and other behavioral changes aimed at delaying the propagation of a pandemic. Mathematical models, used together with historical studies of data on the 1918 flu pandemic in the United States, have advanced the proposition that community-wide application of NPIs may have been the main factor responsible for the varying degrees of impact experienced by U.S. municipalities in the 1918 pandemic. These studies also suggested that NPI effectiveness was contingent on timely implementation and consistent compliance (7, 9, 10), and that early relaxation of these measures may have been responsible for re-ignition of pandemic waves. Perhaps the most germane and compelling study is the work of Markel et al. (11–13), which concluded that nothing except protective isolation measures worked in containing the second wave of the 1918 pandemic in the United States. Seeking pragmatic protection against even severe pandemics, we conceptualized and evaluated the consequences of a combination of NPIs that incorporated notions of transmission control measures, and protective isolation for both facilities themselves and for employees off-site.

Our results indicate that, in the absence of interventions, the introduction of a pandemic virus into residential facilities is inevitable. In our simulations, introductions occurred rapidly and resulted in outbreaks with attack rates that increased sharply with increasing pandemic severities, particularly for intervention levels below those of plan category 5. In several U.S. states, current recommendations for managing absenteeism because of pandemic illness suggest identifying, ahead of the pandemic, temporary workers to take the place of any facility staff afflicted. It is critical that commitments to/from temporary workers include a full understanding that multiple day shifts may be required and that multiday intervals with isolation precautions will be required between work shifts. Our simulations indicate that off-site intervals shorter than ≈3 days provide insufficient protection against introduction of the pandemic virus on reentry. Restricting access to facilities is critical in reducing the risk of introduction.

Our plan for pandemics of category 1–2 shows that even a level of NPIs that seems easily implementable and involves only minor social disruption can significantly reduce the impact of most pandemics in these facilities. In our simulations, the projected effect of this plan reduced the probability of a pandemic introduction by 5-fold (ℛ₀ = 1.4) and dramatically reduced the size of an epidemic (mean: 71 to 2 cases; median: 78 to 0 cases). Implementation of a successful plan for category 3–4 pandemics requires employee commitments to multiday continuous presence at the facility, to behaviors designed to reduce the probability of becoming infected during time away from a facility, and isolation for the latter portion of multiday off-work periods. Simulations based on this plan project >80% reductions in the probability of an outbreak, a reduction in the maximum size of any epidemic by >50% for all but the two most severe pandemics evaluated (ℛ₀ = 2.6, 2.8), and a decrease in the number of cases (median size of epidemics) by >90% for all pandemics simulated. The NPI measures proposed in this plan were judged to be implementable by managers of such facilities who have incorporated the results of this study into a training program and video for their institution and other residential facilities (see Acknowledgments). Asymptomatic carriers of infection are often considered to be the weakest point in epidemic control. However, direct information on pandemic viruses led us to low estimates for the size and level of infectiousness of the asymptomatic class. These estimates, in turn, led to simulation results that suggest that the degree to which NPI measures are actually applied to asymptomatic persons will not be consequential in a pandemic.

The most effective plan simulated (category 5) required virtually complete facility isolation, complete visitor restriction, expanded isolation periods for employee reentry, and high levels of viral mitigation imposed on all goods and high-priority services entering a facility to reduce transmission. The effectiveness of such a plan would require rigorous and unfailing implementation of the simulated NPI measures, but our study shows that these facilities do have a viable opportunity to prevent the introduction of the pandemic virus at almost any severity level. These results seem reassuring, may provide an attainable alternative for facilities that care for these highly vulnerable populations, and may prove to be the only alternative should resistance to available antiviral agents emerge in a pandemic virus.

This study has demonstrated that something previously considered implausible, the protection of a health care institution against pandemic influenza by using only nonpharmaceutical measures, may be possible and practical. This work will succeed if it stimulates individuals concerned with mitigating the impact of pandemic influenza in such facilities to evaluate and consider implementation of the recommendations implicit here. It is apparent that, although surviving a pandemic may be possible, its effective control will not be easy. At levels of severity above mild, social disruption is inevitable and must increase further with severity. The activities of daily life will be altered for all, and commitment from every person in the facility community is essential if the facility, its residents, and staff are to withstand what could be humankind's most severe test.

We have identified that the effectiveness of NPIs depends strongly on a timely implementation and full compliance. We have further emphasized that great risks are associated with premature relaxation of these control measures. This model assumes that social disruption implicit in most of the plans proposed will not inhibit implementation of these plans. A limitation of our approach is the lack of a comprehensive sensitivity and uncertainty analysis to define both the role of individual NPI elements and the degree to which lack of compliance will degrade protection. This would greatly clarify the role that asymptomatic-but-infected persons may play in propagating pandemics. The most important limitation of this study, however, is the absence of a modeling approach that captures the level of detail in the various control measures proposed, and validates the level of transmission reduction assumed. Our model simulated the estimated consequences of these interventions rather than simulating the actions themselves at the individual level.

Methods

Mathematical Model.

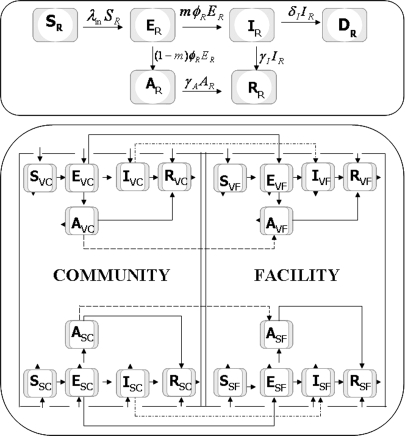
The dynamics of residents in a facility and staff and visitors circulating between the community and a facility were simulated stochastically by using a compartmental model depicted in Fig. 2. These dynamics were simulated for a facility housing 200 residents and 75 on-site staff. The model assumed that each resident received an average of 3 h of care daily and that staff members worked an average of 8 h/day shifts (5 day/week schedules). The model assumed an initial population size of 40 visitors who had contact with residents (only 1 resident in 5 receives any visitors at all), visitations averaging 2 h, and homogenous mixing of the effect of visitation on all residents. Table 3 provides the population sizes assumed in these simulations. Residents were classified according to the epidemiological classes: susceptible (S_R), exposed (E_R), asymptomatic (A_R), infectious (I_R), recovered (R_R), and deceased (D_R). Susceptible individuals became exposed at rate β_R. A fraction m of exposed persons became symptomatic and progressed to infection (I_R) at rate φ_R, whereas the remaining 1 − m remained asymptomatic and infectious at a reduced level (A_R). Infected individuals recovered at rate γ_I or succumbed to disease at rate δ_I. Asymptomatic individuals recovered at rate γ_A. Mortality rates (δ_I) for infected residents were estimated from the case-fatality proportion of residents (CFP), as δ_I = ((CFP/(1 − CFP)))γ_I. Case fatality rates attributable to infection by pandemic influenza will likely vary from pandemic wave to wave in a manner that cannot be known a priori. Our results assume a constant relationship between attack rates and mortality rates both within and between pandemic waves. Mortality projected by our models can be obtained by multiplying the total estimated number of cases for all scenarios by the CFP that appears in Table 2.

Fig. 2.

Compartmental epidemic model for residents in a facility (Upper) and visitors and staff in the community and in a resident facility (Lower).

Table 3.

Initial conditions assumed in the numerical simulation of a resident facility

Epidemiological classes	Initial population size	Reference
SC, SR, SVC, SVF, SSC, SSF	50,000, 200, 27, 13, 8, 75	14
EC, ER, EVC, EVF, ESC, ESF	1, 0, 1, 0, 1, 0	14
IC, IR, IVC, IVF, ISC, ISF	1, 0, 1, 0, 1, 0	14
Ai, Ri, Di	0, 0, 0	14

The circulation dynamics of visitors and staff between a facility and the community are depicted in Fig. 2. These populations were defined according to their immediately current location (e.g., community or facility) and the epidemiological states: susceptible (S), exposed (E), asymptomatic (A), infected (I), and recovered (R). Visitors located in the community or in the facility were indexed by VC and VF, respectively. Similarly, staff located in the community or a facility were indexed by SC and SF, respectively. We indexed individuals in the general community by C. We let 1/ξ_i denote the average time that visitors (i = VF, VC) and staff (i = SF, SC) spent in the facility and the community (Table 2) (see also Table S4). For simplicity, we have assumed that the time spent by staff and visitors in the community/facility was exponentially distributed.

The total population was given by N_tot = N_in + N_out, where N_in and N_out describe the total population size inside and outside a facility, respectively. The per capita rates at which susceptible individuals acquired infection inside and outside the facility were denoted by λ_in and λ_out, respectively. The rate λ_in is also called the force of infection for individuals inside the facility. It included the contribution of all individuals that circulate within a facility (residents, staff, and vsitors). λ_in = [Σ_i=R,SF,VF β_i(π_iI_i + ρ_iη_iA_i)]/N_in, where β_i represents the disease transmission of both populations and η_i represents the relative lack of infectiousness of the A_i population. Efforts to reduce disease transmission were accounted via the parameters π_i and ρ_i. We considered two cases, ρ_i = 1 (NPIs not applicable to asymptomatic persons) and ρ_i = π_i (NPIs equally applicable to infected and asymptomatic persons). Similarly, λ_out is the force of infection for individuals outside a facility. It included contributions from contacts among staff off-duty (indexed by SC), visitors in the community (indexed by VC), and general community members (indexed by C). λ_out = Σ_i=SC,VC,C β_i(π_iI_i + ρ_iη_iA_i)/N_out. Further details on the model formulation, the force of infection, simulation approach, and the calculation of the basic reproduction number are provided in the SI Text.

Baseline.

This scenario assumed that staff spent 8 h (per day) caring for residents, and visitors spent, on average, 2 h (per week) in the facility without restrictions. Our information was that only one resident in five receives visitors, and these were assumed not to modify their visiting behavior on the basis of their own infectious state. Because of our assumption of homogeneous mixing within each model compartment, we treated this situation as equivalent to a reduction in overall visitation effect by a factor of 1/5. Staff and visitors did not apply social distancing measures during the time spent outside the facility, and in-facility monitoring was not implemented. Intervention plans scenarios considered included the baseline above and plans that simulated the consequences of implementing the following nonpharmaceutical interventions: (i) Restrictions on visitors and staff entering the facility, (ii) social distancing measures for staff and visitors, (iii) monitoring of staff returning to the facility, and (iv) isolation of symptomatic residents and immediate removal from the premises of symptomatic staff. The range of visitor restrictions considered included reducing average visiting periods to a single hour and complete restriction of all visitor–resident contact. Social distancing practices implemented by visitors and staff involved both those directed to the community (e.g., abstaining from social gatherings and public places such as schools, churches, and theaters) and those directed to intrafacility interactions (e.g., maintaining 3-foot distances for other than required direct contact and eliminating meetings and resident gatherings). In-facility monitoring of staff returning to work was conceptualized to involve assessment of oral temperature and evaluation of stated history.

Plan: Category 1–2.

Control measures in this plan increased staff shifts from five 8-h shifts per week to four 12-h shifts per week, assumed social distancing practices for staff and visitors that directly reduced a resident's risk of infection by 50%, and reduced the average duration of visits in the facility from 2 to 1 h. We considered both the case in which ρ_i = π_i (NPIs fully applicable to persons without symptoms) and ρ_i = 1 (NPIs inapplicable to asymptomatic persons).

Plan: Category 3–4.

In addition to the array of NPIs delineated in plan category 1–2, the category 3–4 plan further assumed the following: complete visitor restrictions, temperature monitoring and history assessment of returning staff. Visitor restrictions involved communication via electronic devices and/or from behind transparent impermeable barriers with airflow control. Most importantly, plan category 3–4 introduced an employee work schedule that comprised four full days on-site and four full days off-site with a period of isolation from the community at home for the last portion of the time off-site. A 2.3-day self-isolation period was defined as the employee entering isolation with her/his living group within her/his home on the evening of the second day off-work. The employee entered sequestration only if she/he and all members of her/his living group were asymptomatic and afebrile at the time scheduled for entry. Subsequently, the employee reported to the facility at the end of the isolation period (the morning of the fifth day) only if all members of the household remained asymptomatic and afebrile. As for plan category 1–2, we separately considered the case in which the NPIs for category 3–4 were applicable (ρ_i = π_i) and not applicable (ρ_i = 1) to asymptomatic persons. Because the combination of NPIs assembled for this plan was otherwise similar to the NPIs for plan category 1–2, we again assumed a reduction in the residents' risk of infection of 50%.

Plan: Category 5.

For ultimately severe pandemics, we evaluated a plan that included all interventions used in the plan category 3–4 pandemics, increased isolation periods to 3.3 days (while maintaining a 4-day-on/4-day-off staff shift scheduling), and assumed increased social distancing measures to the level at which a resident's risk of infection was reduced by 95%. This might be achieved by completely banishing visitation and imposing strict viral mitigation monitoring on all material and high-priority services entering the facility.

Numerical Simulations.

We solved the model (illustrated in Fig. 2) numerically via stochastic simulations (Matlab, Mathworks) with 100 realizations for each of the intervention plans for an array of pandemic severity levels, separately considering the interventions to be applicable/inapplicable to asymptomatic persons. The simulation approach assumed that the number of individuals transitioning between the various epidemiological states (e.g., susceptible, infected, recovered) were Poisson distributed.