Large kinetic isotope effects in enzymatic proton transfer and the role of substrate oscillations

Abstract

We propose an interpretation of the experimental findings of Klinman and coworkers [Cha, Y., Murray, C. J. & Klinman, J. P. (1989) Science 243, 1325–1330; Grant, K. L. & Klinman, J. P. (1989) Biochemistry 28, 6597–6605; and Bahnson, B. J. & Klinman, J. P. (1995) Methods Enzymol. 249, 373–397], who showed that proton transfer reactions that are catalyzed by bovine serum amine oxidase proceed through tunneling. We show that two different tunneling models are consistent with the experiments. In the first model, the proton tunnels from the ground state. The temperature dependence of the kinetic isotope effect is caused by a thermally excited substrate mode that modulates the barrier, as has been suggested by Borgis and Hynes [Borgis, D. & Hynes, J. T. (1991) J. Chem. Phys. 94, 3619–3628]. In the second model, there is both over-the-barrier transfer and tunneling from excited states. Finally, we propose two experiments that can distinguish between the possible mechanisms.

The subject of this paper is the study of the anomalous kinetic isotope effect (KIE) indicative of tunneling that recently has been observed in certain enzymatic proton transfer reactions (1–3). To better understand what is unusual in the experiments of Klinman and coworkers (1–3), we start by giving a brief overview of the semiclassical theory of KIEs. We then will proceed to discuss models of ground state proton tunneling in the presence of an enzyme and a model we have developed that allows both tunneling from excited states and over-the-barrier processes. The models imply different structures for the enzyme-substrate system, and the paper closes by contrasting these models and proposing experiments that can distinguish between them.

Let us assume that the potential energy barrier has height V and the frequency at the bottom of the reactant well is ω_L, where L can be H, D, or T. In the standard approach an assumption is made that several energy levels are below the top of the barrier and that the over-the-barrier transfer is described by classical dynamics. The transition state theory (4) result for the transfer rate is

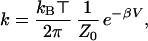1

where β = 1/k_B⊤ is the inverse temperature and Z₀ is the partition function for an oscillator of frequency ω_L. If we describe the motion at the well bottom quantum mechanically, then 1/Z₀ = 2sinh(βω_L/2). If βω_L/2 ≪ 1, one arrives at the familiar textbook result (5) for the transfer rate, k ∼ (ω_L/2π) exp(−βV). However, a typical oscillating frequency for a proton-carbon bond in a transfer reaction is 3,000 cm⁻¹, so in the present problem the opposite limit βω_L/2 ≫ 1 is relevant. In this limit 1/Z₀ ≃ exp(βω_L/2) and the transition state theory result for the rate becomes

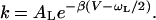2

Eq. 2 has a simple physical interpretation: the energy required for over-the-barrier transfer is the barrier height minus the zero-point energy at the bottom of the reactant well. Note that in the limit βω_L/2 ≫ 1 the TST result for the Arrhenius prefactor A_L = k_B⊤/2π is isotope independent.

Eq. 2 makes the following prediction for the KIE:

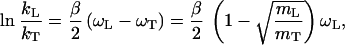3

where L is H or D. Eq. 3 reflects the fact that in the semiclassical theory the KIE measures the isotope-dependent part of the activation energy. If the transferred particles are bound to C atoms the frequency of oscillation for an H atom is of the order of 3,000 cm⁻¹, and Eq. 3 predicts the following values for the isotope effects at room temperature: k_H/k_T ≤ 27, k_D/k_T ≤ 2.7. If we take the ratio of the logarithms of the isotope effects (called the Schaad–Swain exponent) as described by Eq. 2 we find that

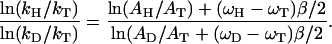4

When the Arrhenius prefactor A_L is the same for all isotopes, the logarithms are equal to zero and the Schaad–Swain exponent is equal to 3.26, independent of temperature.

The assumption implicit in TST that the particle is transferred to the product well by classical over-the-barrier motion is not completely correct because there always will be some degree of tunneling, which will be larger for lighter isotopes. If we plot lnk vs. β = 1/k_B⊤, when there is only over-the-barrier transfer then lnk decreases linearly with increasing β. When tunneling is turned on, the additional transfer mechanism increases the rate and lnk starts to curve upward. The Arrhenius prefactor is the projection at β = 0 of a tangent to the lnk curve. When tunneling is present the Arrhenius prefactor A_L is smaller than the classical prediction. Because H tunnels more easily than D, we expect that A_H < A_D. An empirical rule (3) is that there is H tunneling if A_H/A_T < 0.6 and D tunneling if A_D/A_T < 0.9. We also note that in an alternative model where the activation energy is equal to the barrier height plus a term δG that refers to some reorganization of the protein, the latter term is isotope independent and only the energies required to reach the top of the barrier survive in k_H/k_T, therefore such a theory makes similar predictions as the simple semiclassical model.

Experimental Evidence for Tunneling in Bovine Serum Amine Oxidase (BSAO)

The first series of experiments that showed hydrogen tunneling in enzymatic catalytic reactions was presented in ref. 1. The enzyme that was studied was yeast alcohol dehydrogenase. Later, evidence for tunneling was presented (2) for another system, namely the BSAO reaction. An overview of these experiments has been presented in ref. 3.

In this paper we shall be concerned with the BSAO system where the secondary isotope effect is very small and the theoretical analysis simpler. The evidence for tunneling can be summarized in the following facts: (i) The KIEs are much larger than the ones predicted by the semiclassical theory. In particular, for the BSAO system k_H/k_T was as large as 50 and k_D/k_T as large as 3.2 at room temperature. (ii) The Arrhenius prefactors were found to be inconsistent with purely activated transfer, in particular A_H/A_T ∼ 0.12 and A_D/A_T ∼ 0.51.

We should clarify a possible source of confusion regarding the Schaad–Swain exponent. It often is mentioned that the “semiclassical prediction” for the Schaad–Swain exponent is equal to 3.26. However, this value is obtained from Eq. 4 only when A_H = A_D = A_T = 1. If, on the other hand, we use the values for A_H/A_T and A_D/A_T that were mentioned above, we find that the semiclassical theory predicts a Schaad–Swain exponent equal to 3.5. Therefore, the value 3.2 that was determined experimentally does not agree with the semiclassical prediction.

Modern Theory of Dissipative Tunneling

Tunneling from the Ground State.

Suppose that the potential barrier has the shape of a symmetric double well and a particle that is initially in the reactant well tunnels through to the product well. Because of time-reversal symmetry the particle will execute coherent oscillations between the two wells, and there will be no progress of the reaction. To have localization in the product well, the time-reversal symmetry must be broken by an inelastic collision. It is the interaction with the environment that makes possible a reaction that proceeds through tunneling. Because the dynamics of the bath depends on temperature, the rate of the reaction is always temperature dependent, even when the reaction proceeds through tunneling. Below we give a very brief description of various limits. An excellent review of the modern theory of tunneling in chemical systems can be found in ref. 6. The theory of dissipative tunneling (7, 8) has been extensively used in the study of enzymatic electron transfer (some examples chosen randomly are refs. 9–11).

High temperature.

When the environment is crystalline we can perform a canonical transformation that maps the bath to a set of independent normal oscillations. In condensed matter physics the “small polaron” problem describes hopping of a charge that is coupled to crystal vibrations. If we assume Markovian hopping, then in the nonadiabatic limit (12) one can use Fermi’s golden rule to obtain a transfer rate that has the following form (13):

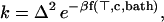5

where Δ is the tunneling matrix element between the initial and final states and f is a function of the temperature ⊤, the coupling strength c of the particle to the environment and of parameters of the bath. Eq. 5 shows that the transfer rate has Arrhenius form even when the transfer proceeds exclusively through tunneling. The origin of the coupling between the proton (or electron) and the environment is electrostatic, and because H, D and T have the same charge we expect that the coupling strength c is isotope independent. This means that the function f in Eq. 5 is isotope independent, and the golden rule result Eq. 5 predicts an isotope effect equal to

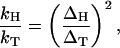6

which is independent of temperature. For the BSAO system, this prediction is refuted by the experiments of Grant and Klinman (2).

Tunneling in solutions is different than in crystalline environments because the solvent dynamics are very slow and anharmonicities are important. The standard theory that describes nonadiabatic tunneling in solution is the Marcus–Levich–Dogonadze model (14), which is closely related to the small-polaron model. This model assumes that the potential energy surface can be modeled by a double well and that tunneling proceeds from the ground state. The coupling to the solvent environment modulates the asymmetry of the double well potential. The probability for tunneling is largest when the potential is almost symmetric, i.e., when the tunneling splitting is maximum. In the Marcus model a single coordinate p is used to describe the configuration of the solvent coordinates. Let’s call p^‡ the configuration that symmetrizes the double well. When p reaches the value p^‡, the proton tunnels instantaneously. For this idea to make sense, the dynamics of the charged environment must be slow compared with the tunneling time. After the proton has tunneled, subsequent motion of the polar groups asymmetrizes the potential and traps the proton in the product well. The solvent atoms are described by classical dynamics, and the reaction barrier is related to the reorganization energy E_r of the medium. The reaction rate is given by

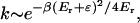7

where ɛ is the exothermicity of the reaction. Similarly to the crystalline case Eq. 5, the rate has an Arrhenius form, and the activation energy is independent of the height of the potential barrier along the reaction coordinate (the barrier height enters the pre-Arrhenius factor). When E_r is almost equal to −ɛ (“inverted region”) the rate behaves as if the reaction were barrierless.

Low temperature.

This is the limit when very few environment modes are excited, so that the analysis of the previous section is not valid. In this case the rate is proportional to a power of temperature, k ∼ ⊤ⁿ (where n = 2 for Markovian hopping) and a plot of k vs. 1/⊤ shows an almost flat plateau. This situation can arise at very low temperatures and has been observed, for example, in enzymatic electron transfer (10). However, this case is never relevant to the experiments of Klinman and coworkers (1–3), which were done at room temperature. We shall return to this point in the Discussion, in connection with recent experiments for the lipoxygenase reaction.

Tunneling from Excited States.

Now we turn our attention to the “above crossover” case where part of the transfer is over the barrier and part takes place via tunneling from the excited states. Wigner (15) was the first to calculate a quantum correction to the TST result. A more sophisticated calculation was performed by Wolynes who made a parabolic approximation for the barrier and found the following result for the rate (4, 16, 17):

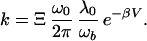8

The factor λ₀/ω_b is the classical (Grote–Hynes) correction (4, 18) to the TST result caused by interaction with the environment. It was first calculated by Kramers (4) and is always smaller than 1. The quantum enhancement factor Ξ is equal to

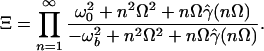9

Here Ω = 2πℏk_B⊤, ω₀ is the frequency at the bottom of the reactant well, ω_b is the frequency at the top of the barrier, and γ̂ is the Laplace transform of the friction function. We emphasize that the quantum enhancement factor Ξ need not be small.

Rate Promoting Vibrations.

For tunneling in condensed phases we have to distinguish among several regimes where the rate has different qualitative behavior. First, we have to distinguish between a low-temperature regime where tunneling takes place mostly from the ground state and a high-⊤ regime where tunneling takes place from excited states. As we already have emphasized, in the low-⊤ regime the rate has an Arrhenius form with the activation energy related to an environment reorganization energy. For this picture to be valid, most of the environment modes have to be excited, which defines an upper-⊤ regime within the low-⊤ region. In a lower-⊤ regime within the low-⊤ region (at temperatures much smaller than the Debye temperature), most of the bath modes are frozen and the rate becomes proportional to ⊤².

However, proton transfer presents an additional complication because of the large proton mass. In particular, the tunneling splitting Δ is very sensitive to the donor-acceptor distance Q:

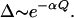10

For a quartic double well, Eq. 10 is exact (6) with Δ ∼exp[−(4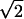/3) V^1/2m^1/2Q]. For electron transfer a typical value for α is 0.5 − 1 Å⁻¹. However, for proton transfer α ∼ 25 − 35 Å⁻¹ (19). This means that small variations of the donor-acceptor distance can affect the rate. Therefore, an intramolecular vibration that affects the potential barrier shape may strongly influence the reaction rate.

This effect always must be taken into account in hydrogen atom or proton transfer. Ref. 6 emphasizes this mode-specificity of proton tunneling. For a different point of view of mode-specificity in biological reactions see ref. 20. In enzymatic reactions, a substrate oscillation that modulates the barrier can be such a rate promoting vibration. Let’s assume that we are in the upper region of the low-⊤ regime (i.e., where the Marcus theory is valid). We have to distinguish between two cases: first, if the temperature is such that there is only a small probability that the rate promoting vibration is excited, then tunneling from the ground state proceeds unassisted; second, if this probability of excitation is large, then the “rate promoting” vibration enhances tunneling. Next, we shall consider how the dissipative tunneling theories discussed in this section have to be modified to incorporate the effect of a “rate promoting” vibration, so that they are appropriate for the study of proton tunneling.

Proton Tunneling from the Ground State

Proton Tunneling in Solution.

In this section we shall give a brief overview of a model for proton transfer that has been developed by Borgis and Hynes (ref. 19 and references therein) in the last few years. Their main focus is proton transfer in polar solvents, but they also have sketched (21) how it can be applied to enzymatic proton transfer. It is a Marcus-like model that includes a reaction-promoting vibration in the sense we discussed above. The main ideas of this model are:

(i) The proton is strongly coupled to charged groups at the active site through electrostatic coupling [this feature also has been stressed in many numerical simulations by Warshel (22)].

(ii) Intramolecular substrate oscillations change the donor-acceptor distance and the potential energy surface.

Voth (23) recently has performed numerical calculations where special care was taken for the proper description of the solvent polarizability, and they also found that intramolecular vibrations enhance the rate.

It should be noted that the effect of the “reaction promoting” substrate mode has the same physical content as the familiar “corner-cutting.” However, the movement of the reaction coordinate along the corner-cutting trajectory has to be fast compared with the motion of all the other degrees of freedom, because otherwise the potential energy landscape would change while the reaction coordinate is midway in the corner-cutting trajectory. On the other hand, the Borgis–Hynes theory (19) uses a microscopic description of the additional degree of freedom (substrate oscillation mode) and can treat the cases where the substrate mode is either faster or slower than the tunneling coordinate.

We shall now make the above ideas more quantitative. Let’s assume that the equilibrium donor-acceptor distance is Q₀ with the corresponding tunneling splitting being Δ₀. When the transfer distance decreases by δQ, the tunneling splitting increases to the value

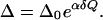11

There is an energy scale associated with the substrate mode (we have set ℏ = 1 throughout the paper):

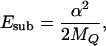12

where M_Q is the reduced mass of the normal mode. Borgis and Hynes (19) found the following result for the reaction rate when the substrate mode is thermally excited (Ω is the frequency of the substrate mode that modulates the barrier height and δG_p^‡ is the activation energy of Marcus’ theory):

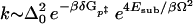13

There are several important consequences:

(i) The activation energy is not related to the barrier height but to δG_p^‡ plus an energy associated with the substrate mode. The barrier height is hidden in Δ₀. When α = 0 we recover the familiar Marcus–Levich–Dogonadze results.

(ii) When the substrate mode is activated the rate does not have an Arrhenius form, but instead is of the form exp(−A₁β + A₂/β).

(iii) The parameter α (and hence E_sub) depends on the mass of the tunneling particle. The reason is that the substrate vibration affects the potential energy surface. If the substrate mode is thermally activated this will lead to a temperature-dependent isotope effect. This corrects the shortcoming of the golden rule calculation that was discussed after Eq. 6.

Another work that has attempted to model the proton transfer by taking into account thermal fluctuations is ref. 24. It is a step in the correct direction, but we think that this work contains some drawbacks. First, Bruno and Bialek assumed without proof that the asymmetry fluctuations of the barrier can be adiabatically decoupled from the tunneling motion. Second, they described the tunneling motion of the proton by using a fluctuating potential barrier, assuming that the fluctuations are so slow that use of classical dynamics is justified. However, a typical intramolecular substrate mode (20) has a frequency 100–500 cm⁻¹ while at room temperature k_B⊤ ∼ 220 cm⁻¹, and the fluctuations of the barrier have to be treated quantum mechanically. As a result, the temperature dependence that they obtained for the rate does not agree either with Eq. 13 or with the prediction of the model we shall now describe.

Proton Tunneling in Crystals.

Suarez and Silbey (25) studied hydrogen tunneling in solids by using a model similar to the Borgis–Hynes model, with the important difference that the environment had not only slow dynamics (as in the solvent environment of the Borgis–Hynes papers), but also fast modes.

The environment is characterized by its spectral density J(ω). If C_i is the coupling of the particle to the normal mode with frequency ω₄ and mass m_i, then

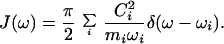14

If the frequency spectrum of the bath has a high-frequency cutoff ω_c, the spectral density can be rewritten as

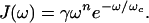15

If the coupling constants C_i are independent of the frequency ω_i (Markovian case), then for small ω it is J(ω) ∼ ω. This spectral density is called ohmic and corresponds to the case where there are no memory effects. The function γ̂ that enters the Wolynes’ quantum correction factor Eq. 9 is the Laplace transform of a friction function associated with the spectral density Eq. 15. If ω_c is finite, the friction has memory. As ω_c→ ∞, the friction becomes ohmic and γ̂ = γ/m₀.

Suarez and Silbey (24) assumed that the barrier is high so that only the lowest doublet can be occupied, and they examined various limits by making a perturbation expansion in Δ (this is the nonadiabatic limit in the sense of ref. 12). We show their results when ω_c < k_B⊤, where ω_c is some cutoff frequency for the bath modes, i.e., the temperature is high enough that most bath modes are excited, which is the situation in the experiments we are discussing that were performed at room temperature. The “local” vibration that modulates the barrier height has frequency Ω, coordinate Q and mass M_Q. When the local vibration is excited, they found that the rate is equal to

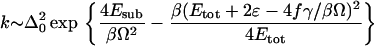16

where E_tot = E_sub + E_Q + E_r and E_Q = 2Q₀²f²/M_QΩ² (f is the coupling of the Q mode to the reaction coordinate), E_r is the reorganization energy, and ɛ is the bias of the potential. Some variables in the last equation were defined in the discussion of the Borgis–Hynes model. In particular, α was defined in Eq. 11, E_sub is the same as in Eq. 12, and Q₀ is the equilibrium transfer distance. For a symmetric potential the result of Eq. 16 reduces to Δ₀²exp{−βE_r/4 + 4E_sub/βΩ²}, which is identical to the Borgis–Hynes result in Eq. 13.

In the next section we shall examine what these results can tell us about enzymatic proton transfer.

Proton Tunneling in BSAO.

In enzymatic reactions the proton is strongly coupled to polar groups at the active site, which participate in the motion of many collective motions of the protein. We can get some insight on the spectra of the normal modes of proteins (which are not the only protein motions) from numerical studies that have been performed for some enzymes (26). At room temperature most of the normal modes are excited, therefore we can use the result in Eq. 16.

The physical picture we propose assumes that the proton is tunneling while coupled to the protein normal mode oscillations caused by the electrostatic coupling to the polar groups at the active site. A comparison of the model ohmic spectral density in Eq. 15 with a realistic calculation of the spectral density for a protein system can be seen in figure 4 of ref. 11.

This physical picture has some similarities to the “conformon” model that was proposed 25 years ago by Volkenshtein (27) for electron transfer, where the electron was coupled to slow protein movements. In the late 1970s Dogonadze et al. (28) criticized this view, claiming that conformation fluctuations could not be modeled as slow collective oscillations, and examined in a more precise manner how thermally driven protein conformation fluctuations influence the reaction rate. That idea was applied to enzymatic proton transfer in ref. 29. However, that work predicts for the H/D isotope effect an Arrhenius form with activation energy proportional to the reduction δω_H of the vibrational frequency of the hydrogen. This quantity (if it is nonzero) is obviously small. However, the experiments of Grant and Klinman (2) show for the H/D isotope effect a difference of activation energies equal to 9.7 kcal/mol (40 kJ/mol, 3,390 cm⁻¹). The coupling to protein conformation fluctuations may have an effect on the reaction rate, even though it cancels out when we measure the ratio k_H/k_T. Because we are interested in the isotope-dependent part of the rate we ignore this effect.

In the next section we shall examine the case where there is both over-the-barrier transfer and tunneling from excited states. In this section we assume that the tunneling proceeds from the ground state.

By using Eq. 16 and neglecting the small terms we find that the isotope effect is

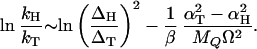17

It is very important that the term exp(−2γ) in Eq. 16, which strongly affects the reaction rate, canceled out because it is isotope independent. The simple result in Eq. 17 is the prediction of this model for the isotope effect. Δ is the tunneling splitting, M_Q and Ω are the mass and frequency associated with the substrate mode that modulates the barrier, and α quantifies the modulation of the barrier according to Eq. 11. We can make the following predictions based on this model and check against the experimental results:

(i) The isotope effect can be fitted by an expression (hyperbola) of the form

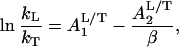18

where L stands for H or D.

(ii) The coefficients A₁, A₂ in Eq. 18 are equal to:

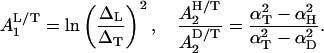19

(iii) It is possible to estimate the effective mass of the substrate normal mode that modulates the barrier:

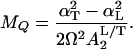20

We face a problem because most of the required quantities are unknown. However, we can use as an approximation for the potential surface the quartic double well and the corresponding tunneling splittings. Then our model predicts an isotope effect that can be fitted by a function of the form of Eq. 18 with the following values: A₁^H/T = 9.2, A₁^D/T = 4.0, A₂^H/T/A₂^D/T = 2.

We need more information to calculate the effective mass M_Q. We have mentioned that for proton transfer α_H ∼ 30 °A⁻¹ and that for the quartic double well the coefficient α depends on the mass of the tunneling particle as α_L ∼ m_L^1/2. For the substrate mode to affect the rate it must be thermally excited at room temperature (where k_B⊤ = 220 cm⁻¹), so to make an order of magnitude estimate we chose Ω = 150 cm⁻¹ and obtained the following value for the effective mass: M_Q ∼ 5.3 × 10⁸ (a.u.)²/A₂^H/T.

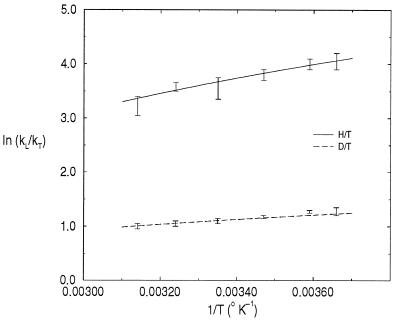
In Fig. 1 we have fitted the results of Grant and Klinman (2) by using two hyperbolas of the form in Eq. 18 and making the following choice for the parameters: A₁^H/T = 8.3, A₂^H/T = 5,050 a.u., A₁^D/T = 2.6, A₂^D/T = 1,580 a.u. These parameters lead to: A₂^H/T/A₂^D/T ∼ 3, M_Q ∼ 105,000 a.u. ∼ 60 m_H. These values are certainly consistent with the predictions of our model that were based on the simple quartic double well potential. The value for the effective mass of the substrate mode M_Q ∼ 60 m_H is realistic, because the mode involves motion of several heavy atoms.

Figure 1.

Isotope effects for the BSAO reaction. The upper curve refers to the H/T effect and the bottom curve to the D/T effect. The bars indicate the experimental results of Grant and Klinman (2). The solid lines are not straight lines. They are the fittings we performed with the hyperbolas of Eq. 18.

In this section we have shown that the model of proton transfer via tunneling from its ground state while coupled to protein collective modes is consistent with the experimental findings. We now will study the case of tunneling from excited states.

Proton Tunneling from Excited States in the BSAO System

We return to Wolynes’ theory in Eqs. 8 and 9, which includes both over-the-barrier transfer and tunneling from excited states. The quantum correction factor Ξ enhances the rate. The question is whether it can fit the experimental results for BSAO. To do such a comparison we need to know the frequency at the top of the barrier ω_b and the friction coefficient γ. However, these parameters are unknown for BSAO.

In Table 1 we show the predictions of Wolynes’ theory for the KIE in BSAO with the following choice of parameters: barrier height V = .010 a.u. (6.3 kcal/mol), ω_HC = 3,000 cm⁻¹, ω_b = 1,000 cm⁻¹, ω_c = 1,000 cm⁻¹, γ/m_Hω_b = 1.0. For these parameters, the crossover temperature is equal to −100°C. Comparison with Fig. 1 shows that the predicted KIEs agree very well with the experimental results. Also shown in Table 1 are the quantum enhancement coefficients Ξ, which are very large, an indication that even a modest increase in the logarithm of the KIE compared with the semiclassical value is caused by massive tunneling.

Table 1.

Values for the KIE for BSAO as calculated by Wolynes’ theory (16) and the corresponding quantum enhancement factors

⊤(°C)	ln(kH/kT)	ΞH	ln(kD/kT)	ΞD
0	4.0	501	1.26	45
10	3.8	363	1.20	36
20	3.6	270	1.15	30
30	3.4	206	1.10	25
40	3.3	160	1.05	21
50	3.2	127	1.01	19

As we saw in the previous section, an excited substrate mode can substantially enhance the reaction rate for ground state tunneling. This raises the question of how such a mode affects the results of Wolynes’ theory.

Our starting point is a proton in a double well coupled to a bath with spectral density as given by Eqs. 14 and 15. This problem has attracted a lot of attention recently (30, 31). When the barrier of the double well is high, the parabolic approximation for the barrier is valid, and Wolynes’ theory (in the absence of a rate-promoting vibration) gives accurate results (30). We assume that the reaction coordinate s is coupled to a harmonic mode Q. If the coupling is antisymmetric (e.g., bilinear csQ) the effect of the Q mode is always to suppress the rate through a Frank–Condon factor (6). If the coupling is symmetric (e.g., cs²Q), the Q oscillation is not reorganized after the transition to the product state and does not contribute to the Frank–Condon factor. In that case, the rate promoting Q vibration enhances the rate. This situation was studied for ground state tunneling by using a short-time expansion for the propagation kernel (32).

We have approached the problem in a different way, without making the short-time approximation. First, we note that the equilibrium point of the Q mode depends on the reaction coordinate s. We have shown by using an evolution operator resummation technique developed in our group (31) that the problem of a particle in a double well coupled symmetrically through cs²Q to an oscillator Q with quantum number n, mass M, and frequency Ω, can be reduced to an equivalent one-dimensional problem with the following effective propagator:

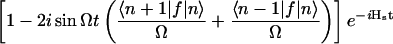21

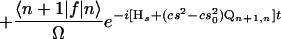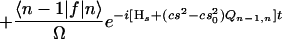where ∓s₀ are the positions of the reactant/product well, α = 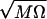and Q_l,m is the matrix element of Q between the eigenstates l, m of the harmonic oscillator and f = cs²Q. The rate then can be calculated by averaging the results over the states n of the Q mode. The proof of Eq. 21 is lengthy and will be presented elsewhere along with numerical calculations by using a method developed by one of us (31) for the study of problems with either high or moderately high barriers. In the latter case the parabolic approximation is not appropriate, and Wolynes’ theory is not accurate.

The coupling constant c in Eq. 21 is unknown, but a simple numerical calculation for a quartic double well (assuming M_Q ∼ 10⁵ a.u. and Ω ∼ 0.001 a.u. as in the previous section) shows that when the barrier height is reduced by 20%, the frequency ω_b at the top of the barrier is reduced by 5%. A few numerical tests with Eq. 8 and by using the barrier parameters that were used for the results of Table 1 can convince one that the rate is strongly enhanced because of the reduction of the barrier height (isotope-independent mechanism), but the KIE is hardly affected by a 5% reduction of ω_b (isotope-dependent mechanism). Therefore, when tunneling takes place from excited states, the Q mode enhances the rate by an isotope independent factor (at least for the kind of barrier that was needed to fit Klinman’s experiments) and the KIEs shown in Table 1 that were calculated by using the simple Wolynes theory, are valid even when a rate-promoting substrate oscillation is excited. Therefore, the experimental results for the KIE in BSAO are consistent with tunneling from excited states, whether the substrate mode is excited or not.

Discussion

The experiments of Klinman and coworkers (1–3) on BSAO cannot be explained by a purely over-the-barrier mechanism for two reasons: the KIE is much larger than predicted by the semiclassical theory Eq. 2 and the ratios of the pre-Arrhenius factors A_L/A_T are smaller than the values expected from an over-the-barrier transfer. In this paper we have shown that two different tunneling mechanisms are consistent with the experiments.

First, if the potential is such that the system is below the crossover temperature and can be considered as a two-level system, the transfer takes place through tunneling from the ground state as described by the Borgis–Hynes/Suarez–Silbey models. The temperature dependence of the KIE is caused (in this model) by the excited substrate oscillation. In fact, if tunneling from the ground state is the transfer mechanism, whether the KIE is ⊤-dependent or not indicates whether the reaction promoting substrate vibration is excited or not.

Second, if the system is above the crossover temperature, the reaction proceeds through transfer from excited states combined with over-the-barrier transfer, as described by Wolynes’ above-crossover theory. By using some reasonable values for ω_b,ω₀ we fitted the enhanced KIE that was observed in experiments. Then, we showed that when a reaction promoting substrate vibration is excited, the values of the KIE calculated by the simple Wolynes above-crossover theory do not change. Of course, only a realistic calculation of the potential energy surface that determines the relevant frequencies can give full credibility to this mechanism.

Nevertheless, if the experiment for BSAO is repeated at lower temperatures, these two mechanisms and a simple linear Arrhenius fitting to Fig. 1 give different predictions for the rates as can be seen in Table 2. In Table 2, the first column (Hynes/Silbey) corresponds to the case when the crossover temperature is higher than −80° C, whereas the second column (Wolynes) corresponds to the case when it is lower. Therefore, an experiment at low temperatures can distinguish among the different possible mechanisms. In addition, the KIE in the tunneling from ground state model is independent of the friction, whereas in the tunneling from excited states it is not. Changing the rigidity of the enzyme and repeating the measurements for the KIEs also can distinguish between the two mechanisms.

Table 2.

Prediction of different models for the KIE in BSAO at ⊤ = −80°C

Model	Hynes/Silbey	Wolynes	Arrhenius
ln(kH/kT)	5.2	7.1	6.6
ln(kD/kT)	1.6	2.1	2.2

Finally, we shall use the conclusions reached in this paper to make some comments on recent results by the Klinman group, which found massive H tunneling in the lipoxygenase reaction (33). Compared with the BSAO results that were discussed in this paper, the intriguing result for the lipoxygenase reaction is that the ratio of the pre-Arrhenius factors A_H/A_D has an enormous value ∼50, which is a consequence of the fact that the rates are almost temperature independent. As we saw in the section on dissipative tunneling, this may happen in two cases. First, in the “deep” tunneling regime, when the bath modes are frozen and the rate becomes proportional to ⊤². However, the experiment was performed at room temperature, so this mechanism is ruled out. Second, in the “inverted region” of Marcus’ theory, when the activation energy (E_r + ɛ)²/4E_r is very small because it happens to be E_r ≃ −ɛ. At room temperature, this is the only possibility to have a “barrierless” transition. Because this is a case of tunneling from the ground state we also can infer that in this experiment the substrate mode is not excited, because the observed KIE was almost temperature independent.

ABBREVIATIONS

BSAO

bovine serum amine oxidase

KIE

kinetic isotope effect

TST

transition state theory