Class-Specific Correlations of Gene Expressions: Identification and Their Effects on Clustering Analyses

Abstract

Current microarray studies primarily focus on identifying individual genes with differential expression levels across different conditions or classes. A potential problem is that they may disregard multidimensional information hidden in gene interactions. In this study, we propose an approach to detect gene interactions related to study phenotypes through identifying gene pairs with correlations that appear to be class or condition specific. In addition, we explore the effects of ignoring class-specific correlations (CSC) on correlation-based gene-clustering analyses. Our simulation studies show that ignoring CSC can significantly decrease the accuracy of gene clustering and increase the dissimilarity within clusters. Our results from a DLBCL (distinct types of diffuse large B cell lymphoma) data set illustrate that CSC are clearly present and have great adverse effects on gene-clustering results if ignored. Meanwhile, interesting biological interpretations may be derived from studying gene pairs with CSC. This study demonstrates that our algorithm is simple and computationally efficient and has the ability to detect gene pairs with CSC that are informative for uncovering interesting regulation patterns.

Introduction

Genes often interact with each other to form transcriptional modules for specific cellular activities or functions.^1,2 DNA microarray technology provides a unique tool to monitor gene-expression levels of thousands of genes simultaneously. To detect gene-transcriptional modules in microarray data, a main step is often the application of clustering analyses,^3–6 which can group genes with similar expression profiles.^4,7,8 In recent years, various clustering-based methods have been proposed, such as hierarchical clustering,⁴ K-means,⁹ and self-organizing map (SOM).^10,11 It is believed that genes with similar expression patterns have similar biological functions, and one can predict functions of unknown genes from their expression similarity with known genes.^4,12

However, biologically, genes involved in the same biological process or pathway may have different expression patterns under different conditions.^13–16 Such genes could be informative and reflect novel biological interactions. For example, in an “on/off case,”¹³ one phenotype is prevalent when the expressions of both genes are either “turned on” or “turned off,” whereas the other phenotype is predominant when only one of these two genes is expressed. As a result, in an on/off case, we can observe that the gene pairs can show strong evidence of a reversal in the signs of the conditional correlations across two phenotypes, which will be referred to as “class-specific correlations” (CSC) in this study. CSC can be highly biologically significant to study disease phenotypes, and therefore it is important to identify them. The idea behind detecting CSC is to find genes that only in pairs, and not individually, discriminate given different phenotypes. Identification of CSC makes it possible to explore the dependence and interactions among genes, as well as to reveal molecular processes that are linked to the study phenotypes.

In most DNA microarray studies, the primary attention was paid to those single genes showing differential expression levels across different experiment conditions.¹⁷ Most tests were constructed solely in terms of marginal distributions of gene-expression profiles that have led to the discovery of novel genes related to study phenotypes in microarray experiments.^18,19 Most of these methods used a one-gene-at-a-time strategy, considering only the association between single genes and the phenotypes. But they may disregard the multidimensional information hidden in gene interactions, which is a potential problem of these methods.^14,20,21 Thus, both genes from a case of CSC are highly unlikely to appear in a gene list produced by a one-gene-at-a-time testing approach.

Although some studies in this direction have been launched,¹³ to our knowledge, there is no practical method for identifying genes with CSC and no related study for exploring the effects of ignoring the existence of CSC on gene-clustering analyses. To address these issues, we started with proposing a method to identify genes with CSC by using DNA microarray data, and then investigated the effects of ignoring the existence of CSC on gene-clustering analyses, by using both simulated data and a well-known DNA microarray data set. Our results demonstrated that our method is simple and computationally efficient to identify genes with CSC, and that ignoring the existence of CSC could dramatically affect the outcomes of gene-clustering analyses.

Material and Methods

For simplicity, we focus only on two-class microarray data. The theory and method presented here can be easily extended to multiple classes. Denote X to be a microarray data matrix with n genes on the rows and m samples on the columns. In the following discussion, we assume that the data matrix X is preprocessed and normalized.^10,22 Samples x(1),…, x(m) are independent observations of an n-dimensional gene expression vector, x(l) = (x_l1,…, x_ln) (l = 1,…, m), with a class-conditional density f(x|y), where y∈{1, 2} is a class variable denoting the biological condition.

Class-Specific Correlations Test

To detect gene pairs with CSC, we first adopt a metric developed by Fisher²³ to identify gene pairs whose correlations significantly change across two classes after multiple testing corrections; then, from the identified gene pair list, we select those gene pairs that show a reversal in the signs of the conditional correlations across two classes. The Fisher's method is given as follows.

Given a pair of genes g_a and g_b, we first define a measure of correlation ρ(g_a, g_b) (in this study we adopt “Pearson's correlation”) between their expression levels. We then obtain both class-conditional correlation coefficients ρ₁ and ρ₂ between g_a and g_b. To test whether the correlation between g_a and g_b changes significantly across two classes, we perform Fisher's z-transformations on ρ₁ and ρ₂. Because z-transformed ρ₁ (or ρ₂) is normally distributed, it allows for detecting difference between ρ₁ and ρ₂ with the following equations:^23,24

$$z_y=0.5{\log }_e\left|\frac{1+{\rho }_y}{1-{\rho }_y}\right|$$ (1)

$$D=\frac{z_1-z_2}{\sqrt{\frac{1}{n_1-3}+\frac{1}{n_2-3}}}.$$ (2)

In Equation (1), z_y is the z-transformed correlation coefficient in class y (y = 1 or 2) and is approximately normally distributed with mean z_y(ρ_y) and variance 1/(n_y − 3).²³ In Equation (2), the resultant D-value then can be examined with a critical value of the standard normal distribution.²⁵ To adjust for multiple testing, we adopt the method of false positive control proposed by Storey.²⁶

Clustering Algorithms

One purpose of this study is to explore the effects of ignoring the existence of CSC on performance of gene-clustering analyses for microarray data. We will perform all clustering analyses based on the Pearson correlation distance.^5,27–29 The Pearson correlation distance between expression profiles of two genes g_a and g_b is defined as d(g_a, g_b) = 1 − |cor(g_a, g_b)|, where cor(g_a, g_b) is the Pearson's correlation coefficient between the expression profiles of genes a and b. Brief descriptions are given below for three clustering algorithms: hierarchical, K-means, and partitioning around medoids (PAM), which are used for clustering analyses in this study.

Hierarchical clustering is a heuristic approach and relies on pairwise similarities between gene-expression profiles. This algorithm minimizes the within-cluster variability and generally displays the degree of similarity between genes as a dendrogram.⁴ In the present study, we use the implementation of “average linkage” hierarchical clustering method.³⁰

K-means clustering is an algorithm that needs to determine the initial cluster centers k in advance. The algorithm starts with setting k centroids randomly. Assigning genes to centroids and selecting new centroids based on current clustering results are then iterated until no significant changes in cluster centroids are observed between iterations.³¹

PAM is similar to K-means clustering, but uses medoids instead of centroids. PAM selects k representative genes (medoids) among a set of genes, assigns the remaining genes to the groups identified by the nearest medoid, and then determines a new medoid for each cluster by finding genes with minimum total dissimilarity to all other cluster elements. Next, all genes are reassigned to their clusters according to the new set of medoids. The procedure is repeated until no more changes of the clustering appear.³²

Evaluation of Effects of Class-Specific Correlations on Gene-Clustering Results

In this study, we compare clustering results measured under three conditions: (1) data with class label y = 1 and 2; (2) data with class label y = 1; and (3) data with class label y = 2. The comparison among three conditions can show the effects on gene-clustering analyses when ignoring the existence of CSC and by using all samples across two classes. We use several evaluation criteria to assess the qualities of clustering results,^33,34 which are described below.

In the case of simulation data, the correct number of clusters is known. Let k be the number of clusters, and denote C⁰_j (j = 1,…,k) be the set of genes that truly belong to the cluster j. Three indices are adopted to compare gene-clustering results.

Index 1:

$$V_1\left(k\right)=\frac{1}{k}\sum _{j=1}^k\left(\frac{n(C_j\cap C_j^0)}{n\left(C_j^0\right)}\right),$$ (3)

where C_j denotes the set of genes being assigned to cluster j by a clustering algorithm; n(C_j∩C⁰_j) denotes the number of overlapping genes between C_j and C⁰_j; and n(C⁰_j) denotes the number of genes truly belonging to cluster j. This index reflects the accuracy rate of gene clustering by a clustering algorithm.

Index 2:

$$V_2\left(k\right)=\frac{1}{k}\sum _{j=1}^{k}d\left(C_j\right),$$ (4)

where d(C_j) is the average Pearson's correlation distance within cluster j. This index represents the average dissimilarity of genes within clusters.

Index 3:

$$V_3\left(k\right)=\frac{1}{k}\sum _{j=1}^k\max d\left(C_j\right),$$ (5)

where maxd(C_j) is the maximal Pearson's correlation distance within cluster j. This index represents the average maximal dissimilarity of genes within clusters.

For a real data set, the optimal number of clusters is unknown, so we cannot investigate the accuracy rates of gene clustering under different conditions via Index 1. However, when genes with similar expression patterns are clustered together, it is expected that they share regulations by some of the same transcription factors and that each cluster contains the genes with minimum dissimilarity. Therefore, we can compare clustering results from the three conditions according to the abilities of minimizing gene dissimilarity within clusters via Indices 2 and 3. Additionally, the biological merit is a main criterion to evaluate genes with CSC. We use the analyses of GO ontology and KEGG pathway³⁵ to extract or infer the biological processes and molecular functions of genes with the highest occurrence among identified gene pairs, which show significant CSC across two classes.

To evaluate the effect of CSC on gene clustering for microarray data, we focus on investigating whether there is a significant difference between values of each index measured from data labeled with y = 1 (or y = 2) and data labeled with y = 1 and 2. For example, we verify whether there is a significant difference between two values of Index 2, which are calculated from data with label y = 1 (or y = 2) and data with label y = 1 and 2, respectively. For simulation data, statistical analyses are carried out by the paired Student's t test, because the data under the two different conditions are matched in pairs. For the real data, statistical inference is based on bootstrapping,^36,37 as described as follows.³⁸

Step 1: Compute the raw difference (I_raw) between the two values of Index 2 calculated from the two conditions for a clustering algorithm under consideration.

Step 2: Generate new independent random samples of size m by sampling with replacement from original samples (y = 1 and 2) and randomly assign them into two groups labeled with y = 1 and y = 2, respectively, where m denotes the size of original samples. Then calculate the resulting difference (I^∗) of two values of Index 2 computed in the two different conditions.

Step 3: Repeat step 2 a large number of times, B (B = 1000), yielding I₁^∗,…,I_B^∗.

Step 4: Based on the empirical null distribution, calculate the bootstrap empirical p value as

$$p=B^{-1}\sum _{I_s^{\ast }\ge I_{\mathit{raw}}}1\mathrm{or}p=B^{-1}\sum _{I_s^{\ast }\le I_{\mathit{raw}}}1(\mathrm{s}=1,2,\dots B).$$

This proportion estimates the probability of obtaining a value as high as I_raw just by chance.

Results

Simulation Data

For this study, we focus on two-class microarray expression data. Simulation studies are carried out to investigate the effects of ignoring the existence of CSC on the performance of gene-clustering analyses for microarray data. For convenience, two classes are labeled as “control” and “treatment,” respectively. The sample size of each class group is equal to 25. For each scenario, each simulated data set consists of a total of 15 genes separated into 3 nonoverlapping clusters containing 5 genes each. To simulate these genes, a multivariate normal distribution is applied to generate the expression profiles of the 15 genes with three blocks (one block represents one cluster) for control and treatment samples. For control samples (or treatment samples), the 15 genes are generated from a multivariate normal distribution with mean 0 and standard deviation 1.0. The following is the covariance matrix for control samples:

$$\sum =\left[\begin{array}{ccc}{\sum }_0& \dots & \dots \\ 0& {\sum }_0& ⋮\\ 0& 0& {\sum }_0\end{array}\right],$$

where ∑₀ is a 5 × 5 symmetric matrix with “1” on the diagonal and “ρ” off-diagonal (ρ is the correlation coefficient between two genes because the variance of each gene is set as 1.0). In simulations, we set only one gene's correlation coefficients in each cluster that appear class specific across two classes. For example, in the control group, the correlation coefficients of gene g with other genes of cluster k (k = 1, 2, or 3) are set to 0.9, whereas in the treatment group, the corresponding correlation coefficients are equal to 0.9. The remaining genes of cluster k have the same covariance matrix across control and treatment samples. We vary the correlation coefficients ρ as five levels (ρ ∈{0.9, 0.8, . . ., 0.5}). For each scenario, we adopt three clustering algorithms as described in Material and Methods section. One thousand replicates are carried out for each scenario, and the effects of ignoring CSC on clustering analyses will be assessed in terms of the three evaluation indices (Indices 1, 2, and 3).

As in Figure 1, our analysis results show strong evidence that the clustering accuracy rate (Index 1) measured from control samples (or treatment samples) is significantly higher (p < 0.001) than that measured from both control and treatment samples for each different correlation coefficient level. This indicates that using all samples across two classes and ignoring CSC can greatly decrease the clustering accuracy rates. For the three clustering algorithms, the hierarchical algorithm and PAM yield higher clustering accuracy rates than does the K-means algorithm when using only control or treatment samples. When using all control and treatment samples, the performance of the hierarchical algorithm on the clustering accuracy rates is the worst among the three algorithms, and its standard deviations of clustering accuracy rates are greater than that of K-means and PAM algorithms. Out of 15 genes, we set 3 genes with CSC, so ideally the clustering accuracy rates are 80% measured from all samples if only these 3 genes are assigned to incorrect clusters. According to Figure 1, the clustering accuracy rates from the hierarchical algorithm are around 70%; the clustering accuracy rates from the K-means algorithm are around 80%; and the clustering accuracy rates from the PAM algorithm are close to 90%. These results indicate that the performance of the PAM algorithm is the best among the three algorithms.

Figure 1.

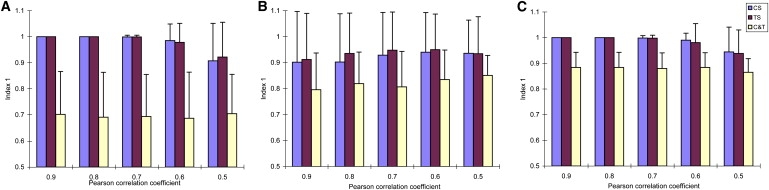
Estimation of Index 1

(A) Hierarchical clustering.

(B) K-means clustering.

(C) PAM.

Abbreviations: CS, control samples; TS, treatment samples; C&T, control and treatment samples. Vertical lines on bars indicate the corresponding standard deviations.

For Indices 2 and 3 as shown in Figures 2 and 3, the values of these two indices measured from all samples are significantly greater (p < 0.001) than those from only control (or treatment) samples. Indices 2 and 3 reveal the dissimilarity level within clusters, and especially for Index 3, the greater values of this index are related to higher possibility of grouping some genes into incorrect clusters. From Figures 2 and 3, the results show that ignoring the existence of CSC in gene clustering can increase the within-cluster dissimilarity, which may mainly result from assigning genes into incorrect clusters. Additionally, we find that the differences among values of Index 2 (or Index 3) measured from three conditions decrease with the decrease of average correlation coefficients of each cluster. Meanwhile, it is observed that the performances of three clustering algorithms on Indices 2 and 3 are similar.

Figure 2.

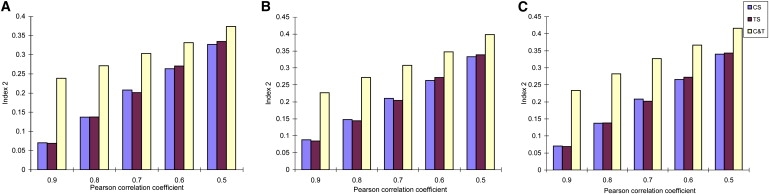
Estimation of Index 2

(A) Hierarchical clustering.

(B) K-means clustering.

(C) PAM.

See Figure 1 for definitions of CS, TS, and C&T.

Figure 3.

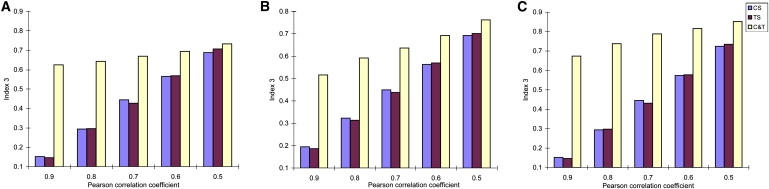
Estimation of Index 3

(A) Hierarchical clustering.

(B) K-means clustering.

(C) PAM.

See Figure 1 for definitions of CS, TS, and C&T.

Further simulation studies, such as using different numbers of arrays in each group and different number of genes per cluster (provided as Supplemental Data), clearly show that the gene-clustering analyses results from total samples always decrease the clustering accuracy rates and increase the within-cluster dissimilarity, compared to those from only control (or treatment) samples (see Tables S1–S12).

Real Microarray Data

In this section, we apply our method to detect the CSC in a publicly available microarray data set, the DLBCL (distinct types of diffuse large B cell lymphoma) data set, and we demonstrate the effects of ignoring the existence of CSC on gene clustering. DLBCL expression data set was taken from the study of Alizadeh et al.¹⁷ DLBCL is the most common subtype of non-Hodgkin's lymphoma. There are 47 samples in the DLBCL data set, among which 24 samples are from “germinal centre B-like” group and 23 samples are from “activated B-like” group. After the expression intensity quality filter as in the original publication, each sample contains 4026 genes.¹⁷ In this study, we label “germinal centre B-like” as “G1” and “activated B-like” as “G2” for convenience.

First we apply our method to detect the gene pairs with CSC in the DLBCL data set. Because the identification of CSC may involve thousands of tests, we apply the “q-value” method²⁶ to control false positives among significant results. The histogram in Figure 4 displays the empirical distribution of the difference between z1 and z2 (transformed correlation coefficients) for every gene pair in the DLBCL data set. The two vertical lines in the histogram mark the significant cut-off values when the significant q-value is set as 0.05 for false positives control. In this study, the cut-off points of (z1 − z2) are set at ±1.45 and we identify 331 gene pairs with CSC in DCBCL. Among the identified gene pairs, the most significant gene pair is GENE941X and GENE435X (for the exact gene names and more information, please refer to Lymphoma/Leukemia Molecular Profiling Project, LLMPP). For G1 samples, there is a high negative correlation between GENE941X and GENE435X; for G2 samples, the situation is reversed and the two genes show a strong positive correlation. The correlation coefficients of this pair of genes are −0.620 and 0.848 in G1 and G2 samples, respectively, and the difference between the corresponding z-transformed correlation coefficients is 1.972. Based on this result, there may be some interaction between these two genes that is associated with the study phenotypes in the experiment.

Figure 4.

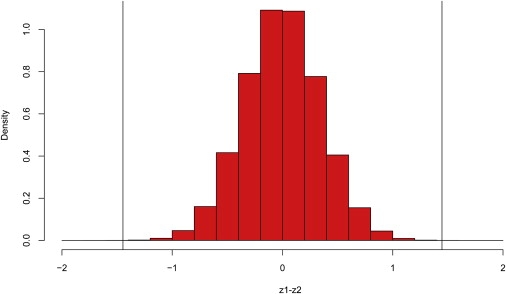
Empirical Distribution of z1 − z2 for gene pairs in the DLBCL Data Set

The two vertical lines mark the significant cut-off values when the significant q-value is set as 0.05.

In Table 1, we list 10 genes with the highest occurrence in identified gene pairs. We use public gene databases of gene ontology and KEGG pathway to annotate those genes. In the present case, 3 out of the 10 genes have no available information in two databases. We briefly investigate the qualitative biological significance of the remaining 7 genes. Based on pathway analyses, these 7 genes are involved in processes such as cyclins and cell-cycle regulation, signal transport pathway, cell adhesion, cell migration, and immune response. GO annotations of these genes indicate that they may play some fundamental roles in cell-function regulations, such as transcription coactivator activity, transcription factor activity, protein binding, DNA (RNA) binding, and receptor activity. Among these 7 genes, some genes have been proved to be associated with DLBCL, for example GENE1212X (IRF-4).^17,39

Table 1.

Ten Genes with the Highest Occurrence from Gene Pairs with Significant CSC in the DLBCL Data Set

	Frequency	Gene ID	Description of the Genes in DLBCL Database
1	22	GENE3943X	unknown; clone = 2013
2	20	GENE3294X	CD38; clone = 123264
3	12	GENE1212X	IRF-4; clone = 270770
4	11	GENE3942X	unknown; clone = 2015
5	10	GENE507X	unknown; clone = 1355820
6	10	GENE19X	MYO1G; clone = 1350823
7	10	GENE1251X	CCND2; clone = 366412
8	10	GENE3384X	ITGAL; clone = 154015
9	9	GENE1472X	ATF-6; clone = 158183
10	9	GENE3872X	TLR6; clone = 1339051

To evaluate the effects of ignoring the existence of CSC on gene clustering, we compare gene clustering results from three different conditions: (1) data from both G1 and G2 samples; (2) data from only G1 samples; and (3) data from only G2 samples. Because of space limitations, we focus on only a handful of prominent genes. Table 2 shows 10 gene pairs with the most significant CSC and the precise values are listed with raw p values and q values for those genes pairs. We apply three selected clustering algorithms to cluster these genes and show the effects of ignoring CSC on gene clustering. For each of the three clustering algorithms, we compute the two index values (Index 2 and Index 3) by Equation (4) and (5) over a range of k values (k denotes the number of cluster) from 2 to 10, because the optimum value for number of clusters is unknown in the experiment. The results are displayed in Tables 3 and 4, respectively.

Table 2.

The Raw p Values and q Values for the Top 10 Gene Pairs with the Most Significant CSC in DLBCL Data Set

	Gene IDs		Raw p Value	q Value
1	GENE941X	GENE435X	2.73e-10	1.99e-3
2	GENE2536X	GENE2364X	1.40e-09	5.13e-3
3	GENE3943X	GENE801X	3.66e-09	8.91e-3
4	GENE258X	GENE455X	6.52e-09	1.01e-2
5	GENE878X	GENE1739X	6.94e-09	1.01e-2
6	GENE2733X	GENE1473X	9.50e-09	1.01e-2
7	GENE2733X	GENE1472X	9.72e-09	1.01e-2
8	GENE713X	GENE507X	1.49e-08	1.08e-2
9	GENE18X	GENE1144X	1.55e-08	1.08e-2
10	GENE1996X	GENE3853X	1.60e-08	1.08e-2

Table 3.

The Average Within-Cluster Dissimilarity Measured from the Three Conditions over Different Numbers of Clusters and Three Different Clustering Algorithms in DLBCL Data Set

		k = 2	k = 4	k = 6	k = 8	k = 10
Hierarchical	G1 and G2	0.52	0.30	0.23	0.16	0.11
	G1	0.53	0.35	0.20	0.12	0.09
	G2	0.21∗∗	0.13∗∗	0.09∗∗	0.07∗∗	0.04∗∗
K-means	G1 and G2	0.52	0.37	0.21	0.17	0.12
	G1	0.51	0.31	0.21	0.15	0.09
	G2	0.34∗∗	0.21∗∗	0.13∗∗	0.07∗∗	0.05∗∗
PAM	G1 and G2	0.56	0.39	0.25	0.18	0.11
	G1	0.54	0.37	0.20	0.13	0.08
	G2	0.34∗∗	0.23∗∗	0.12∗∗	0.08∗∗	0.05∗∗

^∗∗p < 0.01.

Table 4.

The Average Maximal Within-Cluster Dissimilarity Measured from the Three Conditions over Different Numbers of Clusters and Three Different Clustering Algorithms in DLBCL Data Set

		k = 2	k = 4	k = 6	k = 8	k = 10
Hierarchical	G1 and G2	0.90	0.57	0.52	0.40	0.28
	G1	0.98	0.82∗	0.49	0.31	0.27
	G2	0.45∗	0.30∗	0.23∗∗	0.19∗	0.12∗∗
K-means	G1 and G2	0.93	0.76	0.42	0.42	0.31
	G1	0.93	0.68	0.51	0.42	0.27
	G2	0.68∗∗	0.51∗∗	0.34∗∗	0.19∗∗	0.14∗∗
PAM	G1 and G2	0.96	0.83	0.61	0.48	0.29
	G1	0.96	0.89	0.51	0.38	0.24
	G2	0.67∗∗	0.66	0.34∗	0.22∗∗	0.13∗∗

^∗p < 0.05; ^∗∗p < 0.01.

As shown in Tables 3 and 4, for different numbers of clusters k and different clustering algorithms, most values of Indices 2 and 3 calculated from both G1 and G2 samples are significantly greater (p < 0.01) than those from G1 samples. Ignoring CSC leads to incorrectly estimating correlation coefficients between genes, assigning some genes into incorrect clusters, and increasing the within-cluster dissimilarity. Additionally, the values of Indices 2 and 3 measured from both G1 and G2 samples are not significantly greater (p > 0.05) than indices measured from G2 groups. Based on the simulation studies, Indices 2 and 3 can increase with the decreasing mean of correlation levels within clusters. In this case, for G1 samples the mean of correlation coefficients is 0.25, close to that calculated from the total samples.

Based on our simulation results, those three clustering algorithms are performing similarly with respect to Indices 2 and 3. This indicates that there is no algorithm among the three investigated best minimizing the dissimilarity within clusters when clustering genes with CSC are present. From Tables 3 and 4 the results of the three clustering algorithms are similar except the results of the hierarchical clustering algorithm from G2 samples. This is because in some clusters, the hierarchical algorithm assigned fewer genes (even one gene) than other algorithms. These small size clusters have lower within-cluster dissimilarity levels in this case, so that the overall mean and maximal within-cluster dissimilarity may decrease in clustering results by the hierarchical algorithm.

From our simulation study, it is observed that ignoring the existence of CSC can greatly affect the accuracy of gene-clustering analyses for microarray data. In general clustering analyses, clustering algorithms are always applied across all classes without considering the existence of CSC. This can lead to incorrect correlation estimation of gene pairs, and these genes may be incorrectly assigned by those correlation-based clustering algorithms. In the DLBCL data set, taking the hierarchical clustering algorithm, for example, we elucidate the effects of ignoring CSC on gene-clustering results by using genes listed in Table 2. As shown in Figure 5, the plot A is the dendrogram of these genes that is built with both G1 and G2 samples, and plots B and C show the clustering results with only G1 and G2 samples, respectively. It can be observed that the plot A is quite different from plots B and C. Taking GENE941X and GENE435, for example, in the plot A, the two genes are respectively grouped into two distant clusters, which indicates that there seems to be no apparent relationship between these two genes. Whereas, as we point with arrows in plots B and C, where both genes are grouped together first, this indicates that there seems to be similar expression patterns between two genes. As mentioned above, one important function of clustering analyses in microarray data is to search similar functional genes by clustering genes with similar expression patterns. However, the results of Figure 5 indicate that in clustering analyses ignoring the existence of CSC will interfere with the findings of genes with similar expression patterns that may be related to study phenotypes.

Figure 5.

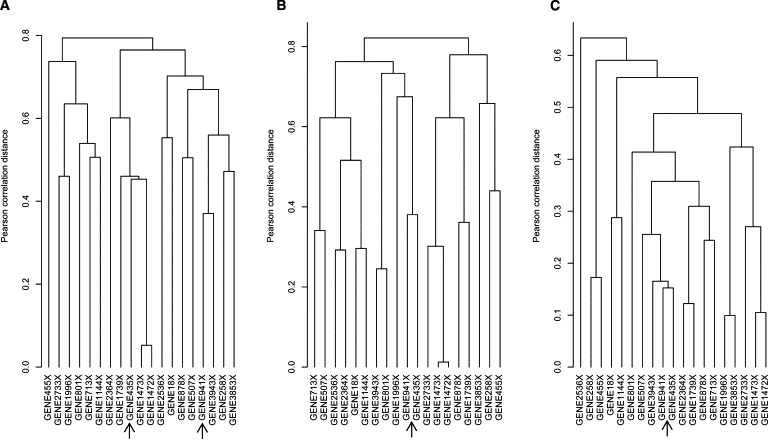
Hierarchical Dendrograms of 10 Gene Pairs with the Most Significant CSC

(A) Data from both G1 and G2 samples.

(B) Data from G1 samples only.

(C) Data from G2 samples only.

Discussion

In this study, rather than focusing on individual genes that have the strongest evidence of differential expressions, we present a novel approach to identify gene pairs with CSC and explore the effects of ignoring CSC on gene-clustering analyses. Identification of gene pairs with CSC makes it possible to explore dependence and interactions among genes and may yield novel biological insights that are undetectable by focusing only on individual genes with strong evidence of differential expressions. Thus, our method can provide complementary evidence to uncover or confirm molecular mechanisms underlying, for example, complex human diseases.

Our results from the DLBCL data set signify that gene pairs with CSC clearly exist and some interesting biological interpretations may be derived from those gene pairs with significant CSC. As shown in Table 1, those identified genes are involved in some crucial biological processes, such as cyclins and cell-cycle regulation, signal transport pathway, and immune response, and these genes may suggest some specific pathway information. These results indicate that our method has the ability to detect gene pairs with CSC and the potential to help identify new gene-regulation patterns.

Because one purpose of gene-clustering analyses is to group genes with similar biological functions and predict functions of genes not studied previously, it is desired that the unannotated genes are placed into clusters composed primarily of genes with known functional annotations.⁴⁰ However, as shown in our results, ignoring existence of CSC between genes can have a great effect on general clustering results, and accordingly may greatly affect the accuracy of gene functional prediction for those unknown genes. Our simulation results show that ignoring CSC greatly decreases the accuracy of clustering analyses and increases the dissimilarity within clusters. One advantage of our method is that we can identify the genes with CSC and correct the relationships of genes to supplement our current knowledge on pathway identification.

The main finding of analyzing the DLBCL data set in our study is that the analyses demonstrate the differences of clustering results measured from different conditions (both G1 and G2 samples; only G1 samples; only G2 samples). The clustering results of the top 10 pairs of genes with significant CSC show that ignoring CSC would increase within-cluster dissimilarity (Tables 3 and 4). These results demonstrate one important pitfall of general clustering analyses without considering CSC, i.e., it would be likely to group some genes into incorrect clusters and thus make wrong determination in gene-function prediction and pathway analyses. Thus it can be more reliable for considering genes with CSC to make gene-clustering analyses.

In addition, because the statistical inference of Fisher's z transformation of correlation coefficients is based on asymptotical normal theory, permutation tests are more reasonable for applying Fisher's z transformation to identify the gene pairs with CSC when the sample size is small. However, it is practically relatively more difficult to implement permutation tests for microarray data analysis, especially for identifying the gene pairs with CSC, because of the thousands of tests involved in a microarray experiment. Thus, applying permutation tests to identify CSC would be very time consuming. A possible path, when the sample size is small (e.g., 15), is to first use our method to select the top gene pairs with the highest D values according to Equations (1) and (2), and then apply permutation tests to these selected gene pairs for empirical p values.

In summary, our algorithm has the ability to uncover gene pairs with CSC that show promising regulation patterns, and it is simple and computationally efficient. One advantage of our algorithm lies in its potential ability to find genes related to study phenotypes that may not be detected by traditional methods. More importantly, it can help to correctly uncover some unknown genes that may be involved in some regulation patterns related to study phenotypes. In addition, although we have illustrated our method by two-class microarray experiments, our method can also be extended to other cases, such as multiple-class studies.

Supplemental Data

Supplemental Data include 12 tables and are available at http://www.ajhg.org/.

Web Resources

The URLs for data presented herein are as follows:

• CSC test, http://z.web.umkc.edu/zhangjig/ (program for our proposed method)

• DLBCL data set, http://llmpp.nih.gov/lymphoma/data.shtml

• LLMPP, http://llmpp.nih.gov/lymphoma/data/figure1/figure1.cdt