Hierarchical organization of eglin c native state dynamics is shaped by competing direct and water-mediated interactions

Abstract

The native state dynamics of the small globular serine protease inhibitor eglin c has been studied in a long 336 ns computer simulation in explicit solvent. We have elucidated the energy landscape explored during the course of the simulation by using Principal Component Analysis. We observe several basins in the energy landscape in which the system lingers for extended periods. Through an iterative process we have generated a tree-like hierarchy of states describing the observed dynamics. We observe a range of divergent contact types including salt bridges, hydrogen bonds, hydrophilic interactions, and hydrophobic interactions, pointing to the frustration between competing interactions. Additionally, we find evidence of competing water-mediated interactions. Divergence in water-mediated interactions may be found to supplement existing direct contacts, but they are also found to be independent of such changes. Water-mediated contacts facilitate interactions between residues of like charge as observed in the simulation. Our results provide insight into the complexity of the dynamic native state of a globular protein and directly probe the residual frustration in the native state.

Globular proteins are characterized by a funnel-like energy landscape with a deep minimum associated with the native state (1–6). The native state is somewhat degenerate and possesses a rugged energy landscape as a result of residual frustration between subtle competing structural conformations (1, 4–7). This frustration may arise in part from the competition of possible interresidue contacts that are explored during the protein's dynamics and can be paralleled with residual entropy in spin glasses (4–6). Under physiological conditions, much of the native landscape is thermally accessible, resulting in incessant fluctuations between available states (1, 3–6). Hence, understanding the organization of the local minima in the native state energy landscape is vital to our understanding of protein function, such as in allosteric proteins and enzymes (8–10). The dynamic nature of the native state is created by a complex interplay of protein and solvent degrees of freedom (11). The complexity is simplified in part because a folded protein possesses a core set of stable contacts that are responsible for maintaining the native structure thereby reducing the number of possible degrees of freedom. The dynamical fluctuations within the remainder of the protein leads to the formation of competing transient contacts, which, in turn, leads to frustration (7).

The importance of the solvent on native state stability and dynamics is widely appreciated. It is well known that water is essential for the stability of many globular proteins, because hydrophobic collapse is considered to be one of the primary driving forces in both the process of creating and maintenance of the folded structure (11–14). Additionally, water is known to play important site-specific structural roles, and some tightly bound waters have been detected through crystallography (11, 15–18). It has been shown that water plays a vital role in mediating hydrophilic contacts and inclusion of these effects in force fields has led to improved protein-folding structural predictions (19). Direct interaction of hydrophilic residues may result in a large desolvation penalty, consequently, an interaction through a water bridge may become preferable (19, 20). Although it has long been appreciated that direct and water-mediated interactions sculpt the protein's native state hierarchy, how this occurs in practice is often unclear. The central goal of this work is to address this question.

In this work we study the long time-scale dynamics of the protein eglin c by using molecular dynamics simulation. Eglin c is a small 70-residue serine protease inhibitor found naturally in the leech Hirudo medicinalis whose dynamics have been studied extensively by NMR relaxation experiments (8, 21–25). Revealing the organization of the energy landscape of eglin c is the first goal to be accomplished in this work. The native state energy landscape is best thought of in terms of a hierarchy of similar conformational states, arranged in a tiered fashion (2–6, 26). Significant work has been done to characterize the energy landscape for peptides, by using, for example, disconnectivity graphs (DGs) (27–29). DGs provide important insight into finer scale splittings of like structural clusters and provide valuable information about the energetic barriers of the system. Constructing these graphs for a protein solvated in explicit water is less straightforward, although a low-resolution DG has been created by Tarus et al. through use of a coarse grained contact clustering algorithm (30). In the spirit of DG, although without the detailed energetics, we have characterized the energy landscape of the native state by using principal component analysis (PCA). We have used PCA to examine the effective dimensionality of the energy landscape and obtain a reduced space in which to study our system. In prior works, low-dimensional reaction coordinates have been shown to be effective in describing protein-folding processes (31–33). The obtained PC space was used to isolate highly preferred protein conformations generated from our simulation. The preference for the system to adopt certain configurations is an indication of local basins in the energy landscape around these configurations. In this way, we have used PCA to unmask a hierarchy of states adopted by the protein within the scope of our simulation. Once a topology of the energy landscape has been obtained, it is possible to search for the sources of the attractors within individual basins. We will show that the observed hierarchical splittings can be characterized by divergent sets of direct interresidue and water-mediated contacts formed. Preferred contacts are naturally passed down through the hierarchy, and branching results in finer segregation of structures and contacts, similar to ultrametric patterns (34). We find evidence of salt bridges, hydrophobic, and hydrophilic transient contacts all contributing to basin definition. In addition, we observe water-mediated interactions forming unique indirect interresidue contacts in addition to helping to facilitate direct contacts.

Results

Comparison with Experimental Results.

Lipari–Szabo model free S² analysis (35) was performed on the simulated trajectory to verify agreement of dynamics from the MD simulation with experiment. Quantitative agreement was found between simulated and experimentally derived backbone order parameters for most residues in the protein (Fig. 1). Excellent agreement is shown for the residues of the N terminus and the entire core of the protein. Some deviations from experiment are found in several residues of the flexible binding loop and a significant reduction in S² is shown in the last three residues of the C terminus, suggesting increased mobility in our simulation. Finding quantitative agreement of S_axis² side-chain order parameters obtained from simulation and those obtained from experiment is typically more difficult (25, 36, 37). Our simulation results show a semiquantitative agreement with those from experiment (data not shown).

Fig. 1.

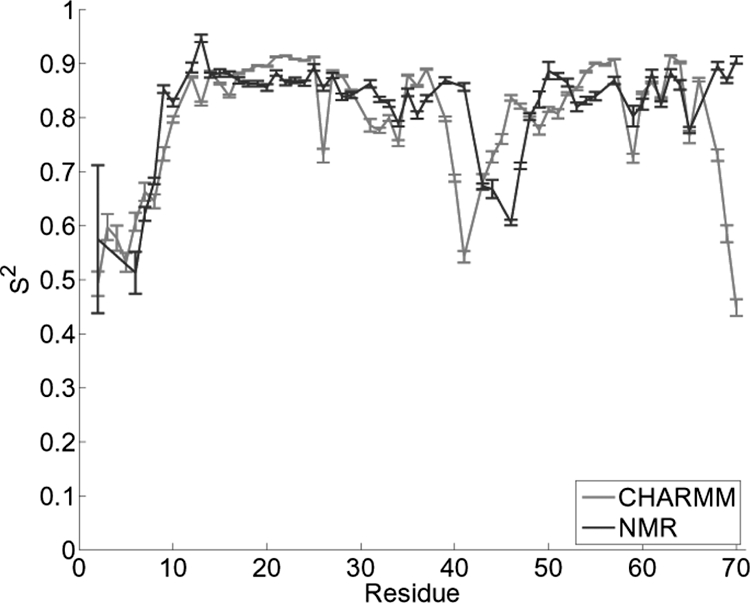
S² obtained from backbone N–H vectors. Shown is a comparison of wild-type eglin c from simulation and NMR experiments.

Principal Component Analysis.

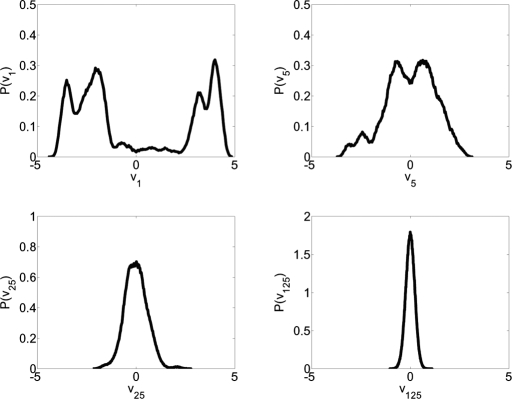
PCA is a powerful linear technique used to aid in the comprehension of complex multidimensional systems by reducing the phase space while retaining essential degrees of freedom. However, the use of PCA on a MD trajectory has the potential to obscure some of the complexity of the system's dynamics. For example, blindly reducing the phase space to the first two PCs would average out important information about conformational substates contained in the higher-order degrees of freedom. To circumvent this issue, we have classified each degree of freedom as belonging to either the essential or nonessential phase space. Characterization of the essential phase space begins by projecting the trajectory into PC space, then histogramming the data along each PC. To classify a PC as a member of the essential phase space, it is assumed that if the trajectory is projected onto a PC in the nonessential space, a histogram of these data will be Gaussian in nature, representing rapid fluctuation within a single state (38). Additionally, it is assumed that a PC belonging to the essential subspace will possess multiple peaks representing the different states available in that degree of freedom (38). A Gaussian was fitted to the histogrammed data by least squares analysis and by using the R² coefficient of determination as a guide, we have created three levels of classification to describe the degree to which the histogrammed data may be considered Gaussian. Anything with a R² coefficient <0.9 is considered to be non-Gaussian; R² from 0.9 to 0.98 the distribution retains some significant non-Gaussian features and may represent a superposition of states that are poorly resolved in that specific dimension; and distributions with R² from 0.98 to 1 are considered to be purely Gaussian in nature and are not considered part of the essential phase space. Representative histograms are shown in Fig. 2. This analysis reveals that the first 4 PCs possess multipeaked distributions with R² <0.9, and the next 7 PCs have distributions with R² values between 0.9 and 0.98. All consecutive PCs possess purely Gaussian distributions. These data suggest that the dynamics of eglin c over the course of this simulation should be described in, at most, an 11-dimensional manifold or ≈3% of the total possible degrees of freedom.

Fig. 2.

Probability distributions P(v_i) for PCs 1, 5, 25, and 125, respectively. These histograms are representative examples of a non-Gaussian distribution (PC 1), a primarily Gaussian distribution which maintains some nongaussian features (PC 5), and purely Gaussian distributions (PCs 25 and 125).

Contact Analysis.

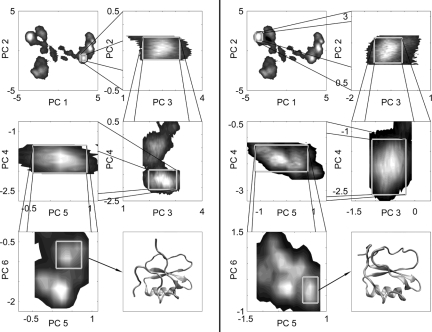
The low dimensionality of the essential phase space permits the subsequent structural analysis. Two-dimensional histograms of the trajectory projected in the first two principal components may be examined to identify high-density regions (≥20% of maximum) within this space. These regions can be considered basins in the energy landscape and henceforth shall be referred to as such. It should be noted that the protein's dynamics are not tightly restricted to basin residence and much of the trajectory exists in more diffuse regions surrounding our tightly defined basins. There are a few additional highly diffuse regions that do not satisfy our definition of a basin and thus are not considered in this work. Data from the basins that meet our ≥20% of maximum criteria can be extracted from the full trajectory and then plotted in the space described by the second and third PCs in an effort to seek additional separation. This process may be repeated until the incorporation of additional degrees of freedom no longer causes any basin splitting (Fig. 3). Basin splitting should cease after the last essential dimension is reached, however, for purposes of maintaining sufficient sample size, our dimension expansion was cut off after 6 PCs. This cutoff ensured that all of the significantly multipeaked dimensions were incorporated in addition to two possibly essential dimensions. The trajectory tends to enter a basin and linger for an extended period before moving on as opposed to rapid fluctuation between states. Originally, the full trajectory possessed an average rmsd of 3.01 Å; however, the average rmsd of each basin decreases as the levels of the hierarchy are transcended, implying that like structures are clustered and filtered into different branches as expected. The structural nature of these basins can be determined by extracting the associated frames from the rest of the trajectory. In principle, with sufficient sampling to ensure multiple basin visitations, it would be possible to construct a form of coarse-grained DG similar to that found in Tarus et al. (30), and, subsequently, from the obtained DG postulate a master equation to describe transition dynamics. However, such unconstrained simulations would be computationally expensive at this time. Alternatively, a master equation may be formulated from computed free-energy profiles between pairs of basins (P. I. Zhuravlev, S. Wu, M. Rubinstein, G.A.P., unpublished work).

Fig. 3.

Progression of the PC-derived basin isolation through the sixth PC. The average structures are shown in the final boxes possessing rmsds of 1.3 Å and 1.2 Å for Left and Right, respectively.

Average structures of each basin were computed based from the extracted frames and evaluated for defining structural features. The system as defined by basins from the first 2 PCs, adopts four globally distinct structures shown in Fig. 4. Most of the divergent structural features that clearly characterize the differences in the four major basins unsurprisingly occur within the flexible binding loop and the solvent-accessible N-terminal tail. A complete contact list was compiled for each basin in the hierarchy. Any non-nearest neighbor and non-next-nearest neighbor residues coming within 2.5 Å of one another were considered to be participating in contact. There are many divergent contacts between the four first-level primary basins, so to simplify our consideration we focus on only the contacts formed by residues within the N-terminal tail and the flexible binding loop. (For more detailed information on these contacts, see supporting information (SI) Table S1.)

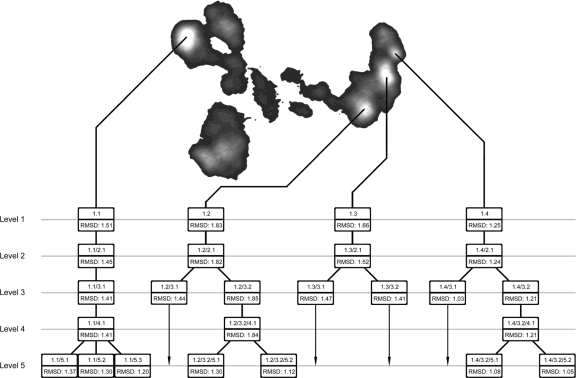
Fig. 4.

Tree of basin hierarchy. Branches terminated before the fifth level could be continued, but no further separation of those branches was found within the range of PCs investigated. Location in the basin hierarchy is referenced by number in the format A/B/C/…, where each letter represents a number X.Y, where X indicates the level at which a basin splitting occurs and Y indicates the chosen branch.

The majority of these transient competing contacts are hydrophobic in nature, but there are many significant hydrogen bonds and several salt bridges observed. These data also show that the majority of the transient contacts are formed between the side-chain atoms and, to a lesser extent, between backbone atoms or between the atoms of the side chains and backbone. Basin 1.1 is characterized by a collapse of the N-terminal tail on to the flexible binding loop and a coordinated migration of the C-terminal tail away from the core of the protein to form a hydrogen bond between L7 and H68 residues. None of the remaining basins possess significant interaction between the N terminus and the binding loop, and the C terminus remains closer to the protein core. Subsequent differentiation between the uppermost basins can be seen in the nature of the contacts possessed by the N terminus. In basins 1.3 and 1.4, the N terminus possesses a structure similar to a single turn of a coil linked by important contacts between the L7 residue and residues E2, F3, and G4 in addition to a contact between residues E2 and E6. This coil structure in the N-terminal tail is completely absent from basins 1.1 and 1.2. In this basin, the tail is extended and possesses no significant self-contacts. One significant contact, the side-chain–backbone hydrogen bond between the backbone carbonyl group on L7 and the side-chain amine hydrogen on W10, was found simultaneously in several basins. This is interesting because previous works (8) have stated that the W10 mutation from the wild-type F has negligible effects on structure. Even if this mutation does not produce any noticeable structural differences in the protein, there may be a significant unanticipated change in the dynamics.

Additional subtle differences between individual contacts formed may be found further along the hierarchy where it is possible to differentiate between structures that differ by as little as a single contact. With this type of analysis, individual local attractors become easily visible and are defined in a physically meaningful way. We hypothesize that the different direct contacts formed in each basin are representative of the inherent frustration in the energy landscape of the protein, and serve to define the basin in which they reside. Interestingly, unexpected contacts were identified between residues of like charge. These contacts suggest that the solvent water may have played a role in mediating some interactions; thus, we evaluated this contribution to basin definition. To investigate these interactions, it was first necessary to establish the existence of persistent water-mediated contacts. By using a procedure developed by Raiteri et al. (39) for determining hydrogen bonds between liquid water molecules, a list of each residue and its respective hydrogen-bonded waters was created at each time step. This list was then scanned for waters that simultaneously participated in hydrogen bonds with multiple residues, and these residues were counted as participating in a water-mediated contact. Results of this test indicated the presence of an abundance of significant water-mediated contacts in all basins. Some of these contacts are seen in >90% of the frames associated with its particular basin. Specific waters typically had relatively low residence times of <500 ps, but some persisted for >10 ns. Across the four primary basins, there is a wide variation in the significant contacts detected, several of which are unique to one basin. Within each basin, many of the contacts remain conserved, but there is a set of contacts that diverge on further basin splitting. The increased structural refinement provided by mapping the basin in higher PC space reveals that the less resolved parent basin is, in fact, a collection of multiple states in which the individual water-mediated contacts exist in vastly different populations (Fig. 5).

Fig. 5.

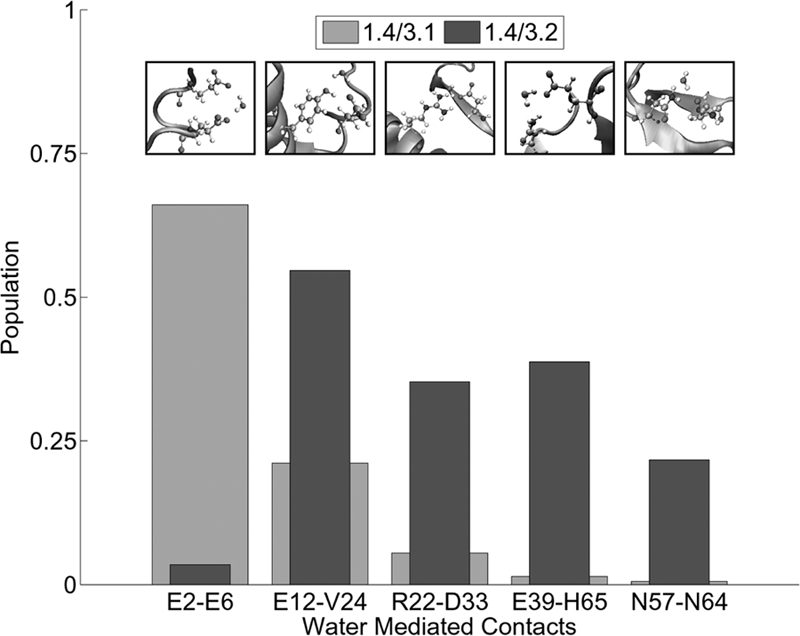
Representative example of how basin splitting segregates water-mediated contacts.

All of the contact populations were determined from samples containing >100 snapshots; however, because of the ambiguity of determining appropriate error limits on the populations of water-mediated contacts, we used a somewhat arbitrary but reasonable definition of a significant population change of a contact. A population change was considered significant if there was a minimum of a 20% relative difference in its population between different substates. Water bridging was found to occur between side-chain and backbone chemical groups alike. Water bridges are found to interact with residues independent of a direct contact in addition to mediating existing direct contacts. This mediation of direct contacts includes, but is not limited to, residues of like charge. Hydrogen bonding to water diminishes repulsion between the like charged residues, allowing them to maintain a direct contact. A representative example of the change in water-mediated contacts created by basin splitting are basins 1.4/3.1 and 1.4/3.2, which are shown in Fig. 6. Details of each water bridge are shown above its population in Fig. 6. This figure features the most prominent types of water bridges, between carbonyls (which reduce the repulsion of the like charges), over a direct hydrogen bond between an alcohol and a carbonyl, and at a salt bridge. Other existing water bridges are found between two alcohols or between an alcohol and a carbonyl in the absence of a direct contact. In some cases, a basin splitting may possess a significant reduction of the presence of a direct contact in one branch but maintenance of a water-mediated form in an opposing branch. Like direct contacts, some water-mediated contacts are binary in nature and can range from very strong to virtually nonexistent in different branches of the free-energy hierarchy, whereas others experience an attenuation associated with less favorable geometries.

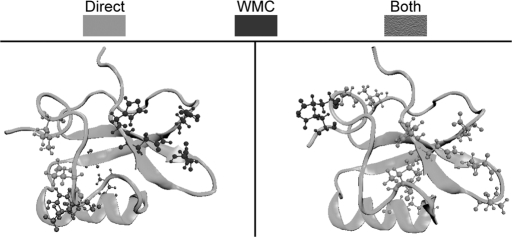
Fig. 6.

Highly significant contact differences emerging from basin splitting between basins 1.4/3.1 (Left) and 1.4/3.2 (Right).

We postulate that the basin splitting detected in this study is a manifestation of the inherent frustration possessed by the protein in the native state and that this frustration is exemplified by a number of distinct contacts that can be used to differentiate one basin from another. Fig. 6 depicts a visual representation of the contact differences emerging from the splitting of basins 1.4/3.1 and 1.4/3.2. Several contacts that are shown to exist in specific regions of the protein in one basin are entirely absent in the other. Additionally, some of the significant identified contacts maintain their locality but swap the exact residues involved. In 1.4/3.1 and 1.4/3.2, R22, a residue in the α-helix, forms a contact with the first β-sheet at either D33 or F36, respectively. Both direct and water-mediated contacts serve to increase structural stability of the protein and, barring an overpowering entropy loss, could explain the preference of the protein for structures within the basins identified in PC space.

Conclusion

The dynamics of wild-type eglin c has been simulated to obtain deeper insight into the energy landscape of the protein in its native state. The veracity of using molecular dynamics to model this system was bolstered both qualitatively and quantitatively by the results obtained by comparing simulated S² model free order parameters with those obtained from NMR experiment. We have demonstrated the startlingly low dimensionality of the energy landscape occupied (≈3% of the total possible degrees of freedom) by the simulation over the course of a 336-ns simulation. Two-dimensional histogramming of the trajectory in the first two PCs reveals a set of basins in the energy landscape around which the system resides for an extended period. We have extended this observation by sequential two-dimensional examination of the trajectory in PC space with increasing PC index. By extracting only the data from a chosen basin and then viewing these data in the next indexed dimension, it is possible to separate large basins into finer-scale basins that only become visible in higher-dimensional space. This technique is only feasible because of the inherent low dimensionality of the active degrees of freedom when viewed in an efficient coordinate system. We have also observed, in agreement with NMR experiments, that the dynamical wealth of the protein resides primarily in the binding loop and the N-terminal tail. A contact list of the highly dynamic portions of this protein was created in an effort to understand the reason the system shows preference for these states. Snapshots of the frames residing within the basin of interest revealed a series of important contacts ranging in nature from salt bridges and hydrogen bonds to hydrophobic interactions. These contacts likely dictate the basin stability and hierarchy. There are a number of highly significant divergent contacts that are found to be important in the first of the basins. These contacts are also significant in the smaller subordinate basins, which themselves may be further differentiated by additional contact differences. In addition to direct contacts, we have also examined the role of water-mediated interactions in the energy landscape of a protein. We have found that there are a number of significant water-mediated contacts formed by the protein throughout the simulation and that a subset of these contacts is unique to certain basins. Within a basin we have found that additional splitting observed on expanding the data into higher-dimensional PC vectors can be characterized by further segregation of both direct and water-mediated contacts. All subsequent basins found as we transcend the hierarchy retain the features of their ancestors. The results of this study exemplify the inherent residual frustration in the energy landscape of globular proteins and provides evidence of the importance of water-mediated interactions.

Methods

Simulation.

An all-atom molecular dynamics simulation of wild-type F10W eglin c was performed by using the CHARMM27 protein-lipid force field (40) and the NAMD program suite (41). The simulation was performed in 7,758 explicit TIP3P water molecules under periodic boundary conditions. The charge of the protein was neutralized by counter ions, followed by the introduction of additional counter and co-ions to reproduce cell concentrations. The first of 25 NMR structures found in the eglin c PDB ID code 1EGL was taken as the initial structure (42). The tenth residue of the protein was mutated from phenylalanine to tryptophan to more closely mimic the conditions used in previous NMR studies (F10W) (8).

Before the commencement of the simulation, the system underwent a series of minimization steps. At constant volume, the entire protein was frozen in place and the water and ions were minimized for 10,000 steps. The protein side chains were then unfrozen and the system was minimized for an additional 10,000 steps. Finally, all constraints were removed from the system and it was minimized for an additional 20,000 steps.

The simulation proceeded with 2-fs time steps by using the SHAKE algorithm and Ewald summation for long-range electrostatics. Short-range nonbonded interactions were calculated at each step and long-range interactions were calculated on even steps only. The pair list was updated every 10 steps. System coordinates were saved every 500 steps (1 ps) for later analysis. At constant volume, the system was gradually heated via langevin dynamics to 300 K in incremental steps of 5 K every 5 ps. On completion of the heating steps, the constant volume constraint was released, and the pressure was moderated by langevin piston (set to 1 atm). The system was allowed to evolve under these conditions for 16 ns to allow some relaxation time. Data collection followed for an additional 336 ns for a total of 352 ns of simulation time.

Comparison with Experimental Results.

Lipari–Szabo model free order parameters S² (backbone) and S_axis² (side chain) values were calculated to show agreement of the simulation with experimentally derived dynamics (37). Lipari–Szabo analysis is a common technique used to evaluate dynamics by examining the flexibility of bond vectors. The simulation was divided into 8-ns windows and the appropriate normalized bond vectors (backbone N–H and side-chain terminal C–CH₃, respectively) were input into Eq. 1.

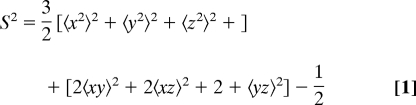In this equation, x, y, and z are the Cartesian components of the unit vectors that describe the direction of the selected bond. Experimental values for both backbone and side-chain order parameters were kindly provided by Dr. Andrew Lee from the Department of Pharmacy, University of North Carolina.

Principal Component Analysis.

Principal component analysis (PCA) was used to simplify the analysis of the trajectory obtained from the MD simulation by redefining the phase space through an optimal linear transform such that the first few PCs contain most of the variance in the data. It has also been shown that >90% of dynamics can be captured by ≈5% of the degrees of freedom (38, 43, 44–47). This promising prospect suggests that much of the high-dimensional phase space theoretically available to proteins may contain little to no interesting information because of constraints on those degrees of freedom. In this study, PCA of the internal coordinates defined by the backbone dihedral angles φ and ψ and the side-chain dihedral angle χ₁ was performed. Dihedral angles are more appealing than raw Cartesian coordinates because they naturally lend themselves to physical interpretation and are independent of global translation or rotation of the molecule (48). The susceptiblity of Cartesian coordinate to produce artifacts has been shown by Mu et al. (49). To eliminate discontinuity problems associated with angular coordinates 0/2π, each angle was instead defined by its sine and cosine components (48). PCA is carried out by diagonalizing a covariance matrix M defined in Eq. 2

where x is the trajectory defined in terms of the appropriate trigonometric components of the φ, ψ, and χ₁ dihedrals. Diagonalization of M produces a set of eigenvectors u, which is a redefinition of the k degrees of freedom available to the system. Eigenvectors are sorted by descending eigenvalues representative of the variance of the data in that dimension so that the greatest variance lies along the vector u₁ and the least along u_k. It is desirable to project the original trajectory data x(t) into PC space to make use of this more efficient coordinate system in which all linear data correlations have been removed. Once the data are projected in to PC space, it is possible to determine which PCs should be considered essential degrees of freedom and which contain essentially Gaussian noise. PCs required for characterization of the essential dynamics possess multipeaked probability distributions within that degree of freedom in which the peaks represent the multiple states in which the protein can explore and single peaked, Gaussian distributions conversely represent degrees of freedom that describe fluctuations within a single state (38).

Identification of Water-Mediated Contacts.

In this study, water-mediated contacts are defined as water molecules, which simultaneously form hydrogen bonds with two or more residues. The water must meet distance and orientation requirements defined by Raiteri et al. (39). Because the Raiteri et al. study considered only water–water hydrogen bonding, some additional requirements were necessary to correctly apply their method to proteins. In our work, any water whose oxygen atom came within 3.5 Å of an oxygen or nitrogen within the protein was added to a list of potential contacts. Selected waters were then tested for additional orientation and distance compliance. The equation used to evaluate this compliance was defined in Raiteri et al. (39) and can be shown in Eq. 3.

This formula was used for both the distance and orientation requirements with a different set of parameters for each case which were also defined in Raiteri et al. (39). In the distance case, d₀ = 2.75, Δ = 0.45, n = 10, m = 16, and d₀ is the X₁X₂ (X = N or O) distance between the protein oxygen or nitrogen and the water oxygen with a cutoff of 3.5 Å or more. In the orientation case, I₀ = 0, Δ = 0.4, n = 4, m = 8, and d₀ is the X₁H + X₂H − X₁X₂ distance between the protein oxygen or nitrogen and the water oxygen with a cutoff of d = 0.5 Å or more. Additional care was taken to ensure that the formula was applied to the appropriate atoms that would be needed to confirm additional orientation requirements needed in the protein system. Waters simultaneously hydrogen bonded to two or more residues are counted as water-mediated contacts.