Gene network dynamics controlling keratinocyte migration

Abstract

Translation of large-scale data into a coherent model that allows one to simulate, predict and control cellular behavior is far from being resolved. Assuming that long-term cellular behavior is reflected in the gene expression kinetics, we infer a dynamic gene regulatory network from time-series measurements of DNA microarray data of hepatocyte growth factor-induced migration of primary human keratinocytes. Transferring the obtained interactions to the level of signaling pathways, we predict in silico and verify in vitro the necessary and sufficient time-ordered events that control migration. We show that pulse-like activation of the proto-oncogene receptor Met triggers a responsive state, whereas time sequential activation of EGF-R is required to initiate and maintain migration. Context information for enhancing, delaying or stopping migration is provided by the activity of the protein kinase A signaling pathway. Our study reveals the complex orchestration of multiple pathways controlling cell migration.

Introduction

Wound healing of skin requires a delicate interplay between cellular proliferation, differentiation and migration as well as fine-tuning of initiation, maintenance and deactivation of these processes (Martin, 1997; Stramer and Martin, 2005; Eming et al, 2007). Imbalances and perturbations of these processes are hallmarks of cancer and lead to suggestions that tumors are ‘wounds that never heal' (Dvorak, 1986). As this decision making is altered in metastasis, an insight into the mechanistic control of cell migration may lead to broad new avenues for therapeutic treatment of cancer (Baselga, 2006).

The dermal-derived hepatocyte growth factor (HGF or scatter factor) is involved in the regulation of migration through the activation of its receptor Met, a proto-oncogene commonly mutated in metastasizing epithelial cells (Birchmeier et al, 2003). However, from a system control point of view, it is not known how the cell produces a sustained and context-dependent migratory response upon stimulation of Met. In general, the functional components that lead to a sustained cellular decision have been discussed controversially.

Cellular responses can be the result of either a single stimulus or a time-sequential activation of different signaling pathways upon an initial trigger signal (Janes et al, 2006). In the latter case, the response is most likely distributed over hours and requires the involvement of both protein signaling and gene regulation in a feedback-entangled process. Elucidating such a complex decision making is inherently difficult. It is hard to define and experimentally observe all required functional cellular components at a sufficiently high sampling rate. Furthermore, only a few detailed in silico models integrating both signaling and gene regulation have been developed so far (Yeang et al, 2005; Ernst et al, 2007). As an alternative, complexity reduction approaches have been proposed to analyze and understand cell functions as hierarchically stacked modules characterized by their input/output functions (Asthagiri and Lauffenburger, 2000; Hornberg et al, 2006; Miller-Jensen et al, 2007).

Here, we propose a different complexity reduction approach based on the timescale separation of cellular events. Such events are encoded in the temporal modulation of molecule concentrations, that is, in changes of mRNA concentrations, protein complex formation, translocation in space, conformational changes or their molecular modifications. They occur on different timescales ranging from milliseconds to seconds (e.g. induced conformational changes) via seconds and minutes (e.g. post-translational protein modification) up to hours and days for gene expression kinetics and/or even years by epigenetic regulation.

Defining cellular elements according to their function allows the application of a timescale separation based on their respective dynamic behavior. It has been shown in systems theory that such a timescale separation of events can be exploited by adiabatically approximating the dynamics of the fast elements, that is, the long-term behavior of these systems can be expressed in terms of the slowly evolving variables (for an overview, see Haken, 2004). Hence, the macroscopic output of a system, or biologically speaking the long-term phenotypic response of a cell, can be expressed in terms of the slowest evolving functional elements of a cell. This concept is referred to as the slaving principle (Haken, 2004).

In this study, we consider a cellular decision that is reached on a timescale of hours. Thus, it is the protein turnover rate in the range of hours that is the slowest evolving variable. Furthermore, we assume the proportionality between protein and mRNA concentrations such that both evolve on the same timescale. Enhancement of the basal biochemical protein activities by post translational events occurs on a much shorter timescale in the order of minutes, for example, shifting the balances between a phosphorylated and non-phosphorylated form, formation and temporal presence of a multimeric protein complex or temporal translocation to its location of activity. Hence, adiabatically approximating these fast protein modulations and describing proteins in terms of their mRNA concentrations leads to the formulation of a gene regulatory network model, whose dynamics should provide information similar to a comprehensive protein interaction network (cf. Supplementary information for a detailed mathematical treatment). As a practical consequence, information on the former network can be easily accessed experimentally by time-resolved DNA microarray measurements.

To gain an insight into the process of the decision to migrate after HGF treatment, we stimulated keratinocytes from heterologous co-cultures (Szabowski et al, 2000) with several dermal-derived soluble factors, including HGF, and acquired time-resolved microarray gene expression data. We further developed a novel gene ranking, filtering and kinetic classification procedure identifying the set of genes responsible for migratory decision making. By inverse modeling based on this set of genes we identified a regulatory network reflecting the experimentally observed gene expression time series. Experimentally verified model predictions under various perturbations outlined the mechanism that controls migratory decision making.

Results

A small set of genes regulate cell migration

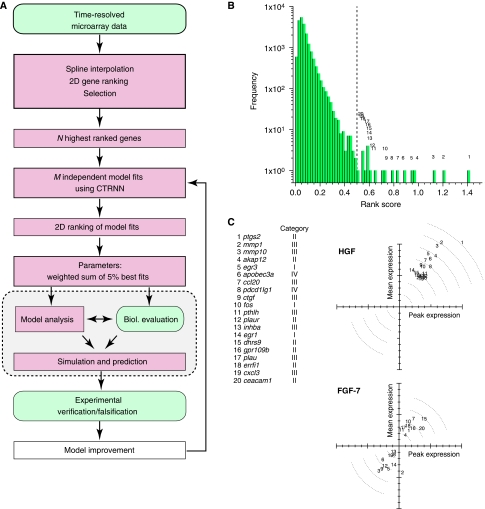
To derive an integrated model of cell migration, we established a workflow for data analysis, inverse modeling and experimental validation (Figure 1A). In the first step, we aimed at identifying genes governing migration. DNA microarray experiments were performed at several time points upon HGF stimulation to obtain the gene expression kinetics from heterologous co-cultures containing primary human keratinocytes and murine cjun-deficient fibroblasts. The latter were chosen to discriminate between human and murine mRNA, based on species-specific sequences and to provide an HGF-free background. Keratinocytes were stimulated with HGF, which induces both proliferation and migration (Birchmeier et al, 2003). Three control experiments using keratinocyte growth factor (FGF-7), granulocyte–macrophage colony-stimulating factor (GM-CSF) and stromal derived factor-1 (SDF-1) as stimuli were conducted, all of which induce cell proliferation, but not migration (Braunstein et al, 1994; Werner et al, 1994; Florin et al, 2004).

Figure 1.

Identification of genes mediating HGF-induced cellular transition to migration. (A) Workflow of data analysis, inverse modeling and experimental validation. (B) Histogram of rank scores for all 20 188 measured genes after HGF stimulation (cf. Materials and methods). The ranks numbered 1–20 correspond to the 20 highest ranked genes (cf. gene list in (C)). (C) Top: mean and peak fold expression of the 20 top-ranked genes upon HGF stimulation. Bottom: expression of the same genes upon FGF-7 stimulation. Data points were normalized to the maximal mean and peak fold expression of the respective experiments (cf. Materials and methods).

The gene expression kinetics from each experiment were ranked according to the absolute value of their mean and peak fold expression (see Materials and methods). The rank distributions show a long tail at high rank scores, likely indicating that only a very few genes mediate the decision of the onset of cell migration or proliferation (cf. Figure 1B). However, genes that are strongly regulated upon the migratory HGF stimulus show a weak or even a downregulated response upon FGF-7 stimulation, which mediates proliferation (cf. Figure 1C). Using other proliferation-inducing stimuli led to the same qualitative results (data not shown). This specific upregulation of genes in response to HGF supports the idea that the ranking identified a set of important genes mediating HGF-induced migration. Indeed, a gene ontology (GO) analysis of the top-ranked genes upon HGF stimulation revealed—among other categories—an enrichment with respect to response to stress, wounding and external stimulus, extracellular region and development (Dennis et al, 2003). Contrary to this, the GO enrichment for upregulated genes upon FGF-7 stimulation found protein targeting, import, transport and localization categories enriched (cf. Supplementary Table IIA and B). As an additional control, the gene expression kinetics were ranked using MaSigPro (Conesa et al, 2006), a statistical procedure to identify genes that have distinct temporal expression profiles across analytical groups. The results of this regression-based ranking method show a good agreement with respect to differentially expressed genes and the respective ranking (cf. Supplementary Figure 2).

To further decipher the cellular information flow in the context of cell migration, we grouped the 50 top-ranked genes into four categories representing (I) transcriptional regulators, (II) genes regulating intracellular information flow (receptors, kinases, phosphatases and other genes involved in signal transduction, e.g. scaffold proteins), (III) genes whose products are secreted by the cell and are involved in matrix remodeling and cell–cell communication or are components of the extracellular matrix and (IV) genes coding for structural proteins in the broadest sense and genes with unknown or unclear functions (cf. Supplementary Table I). Genes from groups (I) and (II) were considered for modeling. Genes from group III producing secreted proteins, acting in a paracrine manner or remodeling the extracellular matrix were excluded, as the time delay between initial regulation and feedback via double paracrine activity is beyond the experimental time window. Genes from group (IV) were excluded because their unknown or unspecified function might lead to misleading model results.

Network topology and dynamics of genes mediating migration

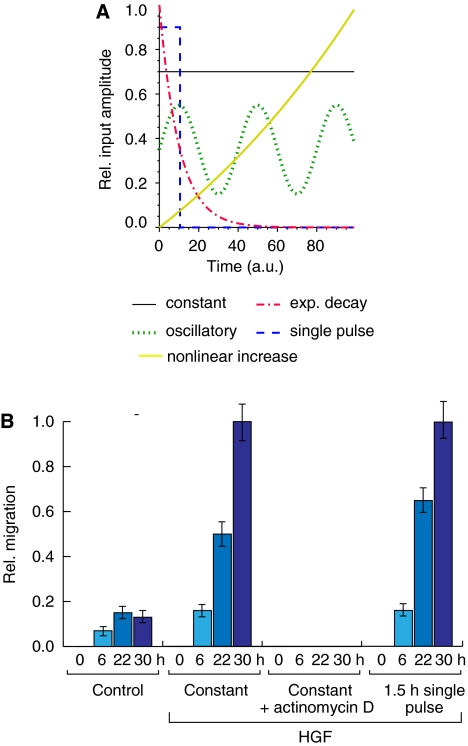
 The causal relationships of the gene expression data (cf. Figure 3A) were inferred using a continuous time recurrent neural network (CTRNN) as an abstract dynamic model for the gene regulatory network mediating the cellular decision to migrate upon an external stimulus. The model describes the mutual influence of genes and their stimulus response as dynamic elements, regardless of how such an interaction or stimulation is realized in concrete biological terms (cf. Supplementary information for a detailed model derivation). The experimental data were repeatedly fitted using a genetic algorithm and the independently obtained network solutions were further ranked according to their robustness to yield biologically plausible parameter estimates (see Materials and methods). In general, the exact functional relationship between the external cellular stimuli and their regulatory impact on the respective genes is unknown. Several possible effective input functions can be assumed for modeling (cf. Figure 2A). A single pulse-like input provided the best fitting results of the model dynamics with the gene expression kinetics. Experimentally, the presence of HGF for 1.5 h is sufficient to initiate a sustained migratory response up to 30 h (Figure 2B), indicating that HGF-induced Met signaling solely acts as an initial trigger. HGF activity, thus, either induces a series of events leading to a lasting, self-sustained migratory response or ‘preconditions' the cell to a responsive state, upon which different system inputs and/or signaling pathways sustain migration.

Figure 2.

An HGF pulse is able to stimulate a sustained migratory response. (A) Hypothetical input functions to the gene regulatory network. Blue: pulse; black: constant; green: oscillatory; yellow: nonlinear increase; red: exponential decay. (B) A short HGF input pulse is able to induce a sustained migratory response. HGF-induced migration distance of HaCaT cells for untreated (control), prolonged incubation (30 h), prolonged incubation (30 h) with actinomycin D inhibition (5 μg/ml) and short time (1.5 h) incubation with 10 ng/ml recombinant human HGF is shown (from left to right). For short time treatment, cultures were washed extensively after stimulation and media were replaced. Error bars denote ±s.d. of the mean migration distance from three independent experiments. Note that migratory responses for a constant and pulsed stimulus are almost indistinguishable.

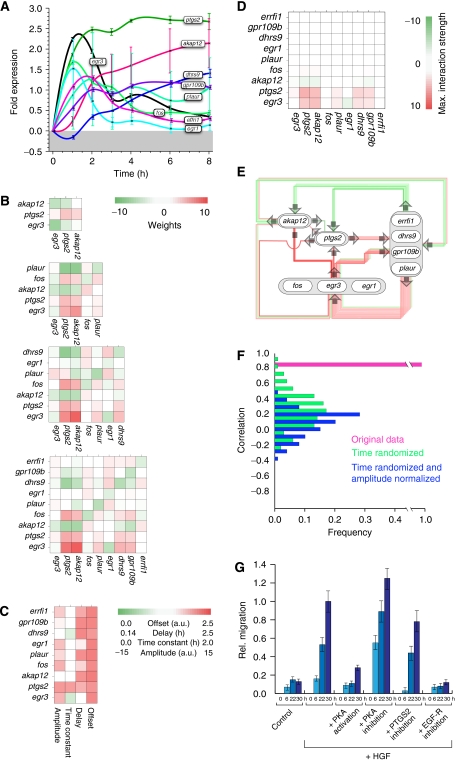
Figure 3.

Gene regulatory network topology of genes mediating HGF-induced migration predicts multiple points of interference. (A) Spline-interpolated gene fold expression time series of all genes considered for the in silico analysis of the nine-node network. Error bars denote the standard deviation of the probe sets' fold expression values for each gene. The minimum error is ±0.08-fold expression, calculated from the mean fold expression of all genes. (B) Interaction weights W_ij for the CTRNNs obtained by inverse modeling for networks of size 3, 5, 7 and 9 genes (from top to bottom). (C) Offsets θ, delays Δτ, time constant τ and input amplitudes I for the nine-gene network. The interaction weights (B) and the parameter values (C) are color-coded. Note that parameter values are mostly robust with increasing network size. (D) Maximal interaction strengths W_ij^max (equation (6)) for the nine-gene network shown in (E). (E) Network diagram for a nine-gene network with interaction weights taken from (B). Note that only the strongest interactions are drawn for better illustration. (F) Histogram of the linear Pearson correlation coefficients of parameter estimates from a nine-gene network using the original (pink), time-randomized (green) and additionally normalized experimental data (blue), having the correlation mean and s.d. values of 0.97/0.01, 0.25/0.24 and 0.13/0.20, respectively (cf. Materials and methods section). (G) Modulation of HGF-induced migration by PKA or EGF-R activity, simultaneous to HGF pulse. To induce a migratory response, HaCaT cells were incubated (30 h) with or without 10 ng/ml recombinant human HGF. PKA activity was modulated by the addition of 1 μM H-89 (Calbiochem) or 200 μM 8-(4-chlorophenylthio)adenosine 3′,5′-cyclic monophosphate sodium salt (Sigma). Inhibition of PKA by the addition of 10 μM myristoylated PKI (14–22) amide, cell-permeable PKA inhibitor (Biomol), gave rise to similar results (data not shown). EGF-R activity was blocked by the addition of 1 μM GW2974 (Sigma). Error bars denote ±s.d. of the mean migration distance from three independent experiments.

The ranking restricted to genes in the functional groups I and II (see above) provides a list of genes with respect to their putative role in mediating cell migration. Modeling of the top-ranked gene interactions started with a small three-gene core network, consisting of the transcription factor egr3, akap12, encoding for A-kinase anchor protein-12, and ptgs2, encoding for prostaglandin-endoperoxide synthase 2 (PTGS-2), also known as Cox-2 (Supplementary Table I). Growing the network in size from three to five, seven and nine genes and each time repeating the inverse modeling workflow qualitatively conserved the topology of this gene core network (cf. Figure 3B, top to bottom) with the signal-to-noise ratio of the parameters increasing with network size (Supplementary Figure 4A).

As a further model verification we performed a bootstrapping test by fitting the data (i) to time-randomized gene expression kinetics and additionally (ii) to amplitude normalized data (cf. Materials and methods). The interaction weights thus obtained showed a low correlation with the original model (cf. Figure 3F), indicating that the solution to the CTRNN obtained from inverse modeling is indeed a result of the temporal order of the experimental gene expression kinetics.

Usually, it is difficult to decide on the optimal model network size that is large enough to comprise all necessary variables, yet admissible for numerical investigation. However, the maximal gene interaction strengths W_ij^max from the learned networks (cf. Materials and methods) showed that all genes in a rank order below fos have a weak regulatory effect in the network (cf. Figure 3D), that is, their dynamics are controlled by the external input and the higher ranked genes. Hence a network with about 10 genes suffices to include most of the genes having a regulatory effect on the cellular decision toward migration. In the following, we thus continue to work with a nine-gene network (see Figure 3A and E for the experimental gene expression kinetics and the inferred topology, respectively, and Supplementary Figure 6 for network model simulations).

All further model verification was conducted experimentally on the protein level. This is justifiable under the presuppositions that (i) protein levels follow mRNA changes over time, assuming the lack of actively regulated protein decay, and (ii) the adiabatic approximation of fast protein signaling events is valid, as described in Introduction (also cf. Supplementary information). As a consequence, information on long-term cellular decisions should be determined—or at least reflected—in the dynamics of the cellular gene regulatory network justifying the translation of the genetic dynamics in our model simulation into protein concentration changes and pathway activity.

ptgs2 fold expression was used as an indicator for model-based analysis of cell migration (ptgs2 fold expression >2), because it represents the highest ranked gene and has been shown to be important for initiation and sustaining of cell migration both in silico and in vitro (compare Figures 3G and 4D and see Supplementary Figure 7).

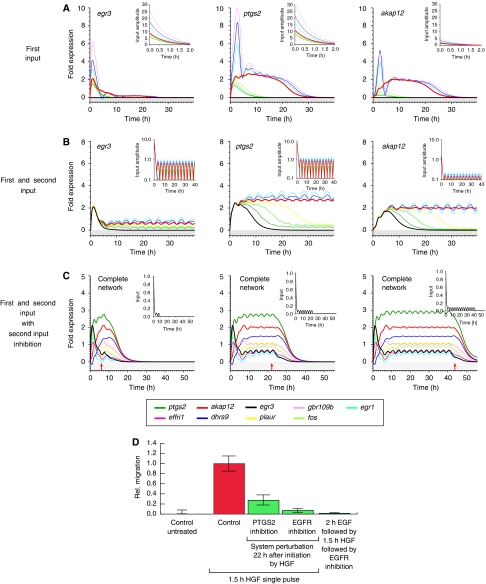
Figure 4.

Sustained migration depends on a second input mediated by the EGF receptor. System response to varied input strengths and shapes is shown. (A) System response to increasing HGF input strength. Input functions are depicted in the small insets. The learned maximal input amplitudes are scaled with the factors {0.0, 0.7, 0.8, 0.9, 1.0, 1.5, 2.0, 3.0} from dark green to pink. (B) System response to a combined initial HGF input and subsequent second periodic input. Simulations were performed with a nine-gene network. The ratio of maximal input amplitudes between the first and the second input increases from 0.0 (black) via 0.04, 0.06, 0.07, 0.08 and 0.1 to 0.12 (purple). Results in (A, B) are shown for egr3 (left), ptgs2 (middle) and akap12 (right). (C) Blocking the second, periodic input at (I) T=7.5 h, (II) T=22 h and (III) T=42.5 h. The red arrows denote the time point of blocking. A sample input function normalized to one is shown in the small insets. (D) Relative migration upon EGF-R blocking or PTGS-2 inhibition 22 h after HGF stimulation. HaCaT cells were stimulated for 1.5 h with 10 ng/ml recombinant human HGF. Cells were washed extensively and further incubated (30 h). Functional perturbation of PTGS-2 (or EGF-R) activity was introduced by the addition of 50 μM meloxicam (4-hydroxy-2-methyl-N-(5-methyl-2-thiazolyl)-2H-1,2-benzothiazine -2-carbox-amide-1,1-dioxide), 5 μM GW 2974 (Sigma) or 150 nM tyrphostin AG1473 (Biomol) 20.5 h after HGF pulse stimulation to culture media. Migratory response was determined in the time window of 22–30 h beginning with the time point of perturbation. Pretreatment of cells with recombinant EGF for 2 h (1 ng/ml) before HGF stimulation is not able to replace EGF-R activity directly blocked after HGF stimulation. Error bars denote ±s.d. of the mean migration distance from three independent experiments.

Using a human keratinocyte cell line (HaCaT) in a Scratch-Assay as a model for wound healing, we tested different model-predicted points of interference. First, it was confirmed that HGF-induced migration predominantly depends on a transcriptional response. Blocking transcription by actinomycin D treatment abolished any migratory response to HGF (Figure 2B), while the cells were still viable as controlled by an MTT viability assay (data not shown).

Blocking the PTGS-2 activity reduced HGF-induced migration. In fact, the potential to inhibit migration appears largest at the onset of cell migration (compare Figure 3G, early and late time points). The network model finds the gene akap12 to be important to cell migration, having mainly an inhibitory effect. This gene's protein product, AKAP-12, regulates the activity of protein kinase A (PKA) by tethering the enzyme near its physiologic substrates. PKA signaling could suppress or negatively regulate HGF-induced migration. Here, in agreement with model predictions, simultaneous stimulation by HGF and enhancement of PKA activity prevent the onset of migration. Decreasing the activity of PKA enhances the early migratory response (6 h time points; Figure 3G). Furthermore, a decreased PKA activity alone is not sufficient to induce a migratory response in the absence of HGF stimulation and also other inhibitors used reveal only an effect on migration in combination with HGF stimulation (see Supplementary Figure 8).

Further down in the gene ranking list, the genes plau/plaur as well as errfi1 and hbegf are found (cf. Supplementary Table I). plaur and plau encode for the plasminogen urokinase activator receptor (PLAU-R) and its ligand plasminogen urokinase activator (PLAU), respectively. It has been shown that the inhibition of the PLAU receptor decreases but not completely abolishes the migratory response (Schnickmann et al, in preparation). HB-EGF is a ligand to the EGF receptor, whereas ErbB feedback inhibitor 1 (ERRFI-1) is a cytoplasmic protein (Wick et al, 1995) that can interact with Erbb-1 and Erbb-2 (two EGF-R isoforms) and modulate their activity. Gene ranking and the network topology (Figure 3E) thus suggest that EGF-R signaling is necessary for HGF-induced migration. As predicted, blocking EGF-R signaling through the application of a double specific inhibitor (GW2974) targeting the activities of both isoforms of EGF-R (Erbb-1 and Erbb-2) abolishes HGF-induced migration (Figure 3G).

The inferred network topologies provide limited information concerning the dynamics of the network. To address the question whether the functional interference is mediated through a crosstalk between the signaling pathways and, additionally, whether the cell integrates this information on the genetic network level, in silico simulations and perturbations followed by experimental validations were performed.

Time sequential signaling triggers and sustains cellular migration

As shown above, the HGF input is required only during the first ≈1.5 h to induce cell migration. The questions whether this initial trigger is sufficient to induce a sustained migratory response or whether an additional input at a later time point is required still remain. Model simulations predict that even a massively enhanced HGF stimulus is not able to induce a permanent system response (cf. Figure 4A). All genes are upregulated with increasing stimulus intensity in a switch-like manner. Yet, the upper, active state is apparently weakly unstable, as the gene expression returns to the lower off state after roughly 24 h, indicating that cell migration likewise would be stopped. This result is contradictory to experimental findings on cell migration, because cells can migrate for days during the process of wound healing.

The discrepancy between model prediction and experimental results can be resolved by assuming that migrating cells receive a repeated HGF input with a minimum period of approximately 1 day or that a different system input is missing in the model. The experimental finding that a transient HGF stimulus already causes a sustained cell migration excludes the former hypothesis (Figure 2B). Different lines of evidence further support the latter interpretation. The time series of a number of genes encoding for receptors and their respective ligands show a 3 h regulation period (Supplementary Table I; also cf. plaur in Figure 3A), suggesting a second, time-lagged periodic input into the system. Furthermore, the identified genes in the network and the network topology itself hint at the influence of autocrine feedback loops (Figure 3E).

Therefore, a second CTRNN model variant was fitted to the gene kinetic data, this time with each gene receiving an additional weak, pulsed input setting in 2.5 h after the first input (see Materials and methods, equation (5)). Under this assumption, model analysis predicts that the cell remains in a responsive state for up to 7–8 h during which the onset of a minimal, permanent, second input suffices to develop a full and sustained migratory response (see Figure 4B). After that time, the cell returns into its previous homeostatic state, requiring again the preconditioning HGF trigger to initiate a new migratory response.

Repeating the inverse modeling workflow with the complex input (insets in Figure 4B and Materials and methods section), essentially the same network topologies and parameters were found as compared with the HGF input-only model (see Supplementary Figure 5A and B). Simulation of network dynamics under the chosen conditions led to a stabilized active system state (Figure 4B) as long as the system received the second input. Blocking the periodic input at any time switched the system off (see Figure 4C). Note that the second input was modeled as periodic because of the fact that it most probably constitutes an autocrine or juxtacrine signaling loop with the corresponding ligand/receptor genes periodically expressed. However, model simulations show that the same results hold true for a constant input as well (data not shown).

Model analysis suggests that the migration-sustaining information is modulated via Errfi1, thereby changing the MAPK pathway activity (Ferby et al, 2006). Also the kinetics of the EGF-R ligand HB-EGF (Supplementary Table I) show a basal cellular expression that is increased in response to HGF stimulation (data not shown). Taken together with the above in silico prediction, the model suggests that continued EGF-R activity starting at around 2 h after the initial HGF stimulation is essential to develop and sustain a migratory system status (Figure 4B). This prediction was tested experimentally by stimulating cells with HGF for 1.5 h and subsequently blocking EGF-R thereafter. In full agreement with the model predictions (Figure 4C), blocking the EGF-R activity stopped cell migration even 22 h after HGF stimulation (Figure 4D). Moreover, EGF-R activation 2 h before HGF stimulation is not sufficient to replace EGF-R activity after HGF stimulation (Figure 4D), further supporting the hypothesis that HGF and EGF-R, respectively, trigger and support migration. In addition, the time-delayed perturbation experiments suggest that the processing and the functional interference of HGF and EGF-R signaling converge on the genetic network level.

A group of modulator genes regulate the second input for sustained migration

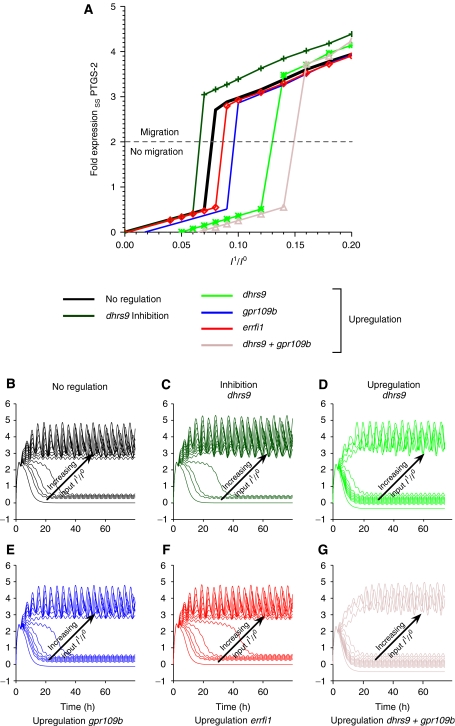
To study the precise regulatory role of dhrs9, gpr109b or errfi1 in the nine-gene network, we changed their expression levels in silico to investigate their modulation effect on cell migration. As above, ptgs2 was used as an indicator for migration. Figure 5B–G depicts the corresponding temporal behavior of ptgs2 with increasing amplitude of the second input upon upregulation or downregulation of the above genes. Downregulation of dhrs9 reduces the switching threshold for migration (Figure 5A, shift of corresponding dark blue curve to the left compared to the black control curve), as the model predicts this gene to be an inhibitor of ptgs2. Upregulation of gpr109b, errfi1 or dhrs9 shifts the migration threshold to larger input amplitudes (Figure 5A, shift of corresponding curves to the right compared to the black control curve). Lastly, upregulating both dhrs9 and gpr109b shows an additive effect of their actions: the second input amplitude has to be significantly increased to induce a migratory system response (Figure 5A, shift of corresponding brown curve to the right compared to all other curves). Model analysis thus reveals a complex modulation of the second input.

Figure 5.

A group of modulator genes regulate the minimum threshold intensity of the second input for sustained migration. (A) Steady-state behavior of ptgs2 as a function of the increasing input amplitude of the second pulsed input. ptgs2 as the highest ranked gene has been shown to be important over the whole period of cell migration. Hence its expression level can be considered as a marker for migration. (B–G) Simulation of ptgs2 expression under increasing second input amplitude with regulated modulator genes. Input amplitudes of the second input I¹ are measured in relation to the initial input strength of the learned amplitude I⁰ of the first input. Ratios are increased from 0 to 0.2 in steps of 0.02. Each line corresponds to the simulated expression level of ptgs2 for a given ratio I¹/I⁰.

PKA signaling provides context information and is able to stop migration at any time

The above model analysis has demonstrated that both the amplitude and the timing of external and/or internal stimuli are important regulatory factors. With this in mind, we investigated the impact of the PKA pathway on the early onset and the later steady-state behavior of cell migration. In silico simulations predict that a pulse-like upregulation of PKA stops cell migration at any time (Figure 6A). To prove this in vitro, cells were stimulated with an HGF pulse to trigger the responsive state and to initiate the migratory response. PKA activity was enhanced at different time points thereafter (Figure 6C, red bars). In full agreement with model predictions, enhancing the PKA activity not only prevents the onset of migration, but also shuts down the system both during the transition phase to migration (enhanced PKA activity after 1.5 h HGF stimulation) and at later time points, when the system has already stably established the migratory system state (perturbation at 22 h after triggering migration by HGF).

Figure 6.

Enhanced PKA pathway activity is able to prevent the onset of migration or stop a developed migratory response at any time. (A, B) Effect of akap12 on simulated gene expression for the nine-gene network. The insets depict the normalized input into the network. (A) A short upshot of akap12 expression at T=5/20/40 h (I/II/III) switches off gene expression and thus cell migration despite continued input signaling. (B) Inhibition of akap12 rescues the system from switching off (I), and (II, III) slightly upregulates ptgs2 (top green line) and downregulates egr3, egr1 and fos expression (bottom, pink, blue and green lines). The strength of downregulation correlates with the transient length for ptgs2 (depicted by gray area) to reach the new steady state. (C) Activation of the PKA pathway at different time points with respect to HGF pulse stimulation (10 ng/ml for 1.5 h) by supplementing culture media with 200 μM 8-(4-chlorophenylthio)adenosine 3′,5′-cyclic monophosphate (Sigma) strongly decreases HGF-induced HaCaT migration. Inhibition of PKA activity by the addition of 0.5 μM H-89 at the time of HGF stimulation slightly increases migration. Inhibition of PKA-activity by H-89 (0.5 μM) directly after HGF pulse stimulation (1.5 h) does not alter development of a migratory response. Inhibition of PKA activity after 22 h, when cells already developed a full migratory response, delays further migration. Error bars denote ±s.d. of the mean migration distance from three independent experiments.

Most interestingly, the complementary approach of decreasing PKA activity and thereby enhancing migration gives rise to a more complex scenario. Model simulations show that a downregulation of akap12 modulates, but does not stop, cell migration. The gene expression levels after akap12 regulation are similar, regardless of the decrease in akap12 expression (cf. Figure 6B). The transient time to reach the new steady state, however, decreases with the increasing strength of this regulation. Moreover, the regulation has antagonistic effects, because akap12 negatively regulates ptgs2 and positively regulates transcription factors, such as egr3, fos or egr1. Upregulation of all these genes promotes cell migration in silico. Which of these regulatory effects dominate are a matter of timing and the presence of the initial trigger HGF, as inhibition of PKA activity without HGF stimulation is not able to induce keratinocyte migration. Indeed, downregulation of PKA activity in vitro during the immediate trigger stage of migration results in a slightly enhanced migration, because the then important factor ptgs2 becomes more active (immediate response in Figure 6C). Late PKA pathway inhibition slows down migration, which can be an effect of transcription factor downregulation (late response in Figure 6C).

These findings indicate a crosstalk between PKA and HGF signaling during the trigger state of migration, whereas at a later stage, signaling via the EGF-R and the transcription factors seems to be dominating. This is again in line with our experimental findings: immediate blocking of the PKA pathway roughens the migration front (Supplementary Figure 7). PKA pathway regulation apparently allows the system to integrate context information that is derived from its environment, namely from cell–cell interaction and from communication with the surrounding tissue. Interestingly, the migration state of cells is not constant as average migration speed increases over time (cf. migration speed at immediate and late time points in Figure 6C).

Discussion

The integrated theoretical and experimental analysis of gene expression kinetics deciphers the dynamics of a surprisingly small, but extremely complex gene regulatory model of migration by inverse modeling.

Many methods for the topological and dynamic reconstruction of gene regulatory networks have been developed in recent years (for reviews, see Bansal et al, 2007; Stolovitzky et al, 2007). In particular, neural networks have been previously applied for modeling signaling pathways and gene networks (Reinitz and Sharp, 1995; D'haeseleer, 2000; Vohradsky, 2001). However, the predictive power of these models, and hence their impact on biology, has been rather limited up to now, which is attributed to the disproportionately large number of unknown parameters with respect to the experimental data and to the indefiniteness of the systems under investigation (Krishnan et al, 2007). Here, we show for the first time that inverse modeling of a gene network can establish an abstract model of a complex biological system that captures well its dynamic properties and has predictive power. This success is most likely due to several reasons: the choice of experimental time window focusing on the decision to migrate and measuring at a sufficiently high sampling rate to capture the gene network dynamics, the choice of gene candidates from ranking, biological function and the cross-validation against proliferative stimuli, the limited number of genes dominating the network dynamics and lastly the combination of fitness and robustness criteria in the search for a biologically plausible gene interaction model.

Model simulations proved efficient to elucidate the dynamic functionality of genes. A schematic overview of the revealed dynamic picture of interactions as well as the time series of events and different possible points and times of interference is provided in Figure 7 and is discussed in detail below. Our model for migration further suggests that the initiation of migration acts in a two-step mechanism. The first input into the system is triggered via the cellular reception of HGF through its Met receptor and subsequent signaling via the MAPK pathway, bringing the cell to a responsive state. Complete development of a migratory phenotype and sustained migration, however, depends on a second input, most prominently via the time-sequential activation of EGF-R, which again feeds into the MAPK pathway. Redundantly to EGF-R, PLAU-R and its ligand PLAU can contribute to the complete development of a migratory response (Schnickmann et al, in preparation). Different EGF-R ligands (such as EGF and HB-EGF) are expressed by keratinocytes both at a basal level and as a result of HGF stimulation (data not shown). The EGF-R mediates cjun-dependent formation of the keratinocyte leading edge (Li et al, 2003; Zenz et al, 2003) and is also an important player during tumor development and progression (Burtness, 2007; Nakamura, 2007; Sharma et al, 2007). Likewise, PLAU-R has been shown in a mouse model to be positively correlated to tumor initiation and growth (Ploplis et al, 2007). A functional connection between HGF and EGF-R signaling for migration and invasion was reported recently (Xu and Yu, 2007; Zhou et al, 2007), but these studies did not consider the temporal order of events and only discussed potential crosstalk at the signaling level.

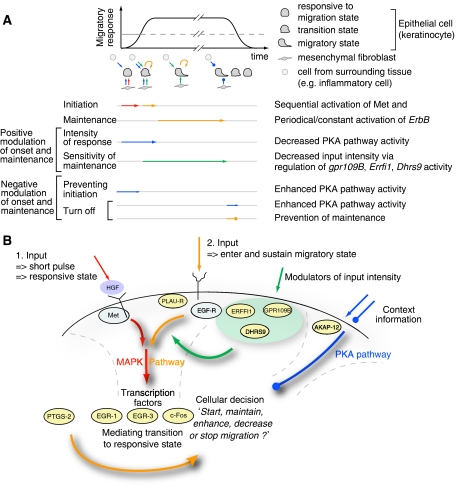
Figure 7.

Time ordered sequential events control cellular decision of migration. Schematic representation of events regulating the initiation, maintenance, modulation and stopping of cell migration. (A) The migratory response depends on a certain threshold of gene activity, as indicated by the dashed line, and proceeds as long as no context information is provided via a stop signal or the sustained activation is depleted. (B) Summary scheme of the model for migration. A first pulse-like HGF stimulus is required to transform the cell into a sensitive state for migration. To initiate and sustain migration, a second input preferably through the EGF-R signaling pathway is required. This second input can be modulated by a number of genes. Context information is integrated through the PKA pathway, which can stop migration at any point in time.

Model simulations based on an initial activation by HGF and subsequent EGF-R input show that the cells remain responsive for approximately 7–8 h, thus sensitizing the system to initiate migration even under adverse environmental conditions. Interestingly, model analysis demonstrates an active modulation of the second input through at least three different gene products, namely the G-protein-coupled receptor 109B (GPR109B), DHRS9 and ERRFI-1. GPR109B is able to regulate cAMP levels and, through that PKA activity (Tunaru et al, 2003), co-regulation DHRS9 and the adenomatous polyposis of the colon gene in colon carcinomas (Jette et al, 2004). An in silico knockdown of dhrs9 increases ptgs2 expression (Figure 5C) and therefore lowers the threshold for initiation of migration. This is in line with the biological observation that prostaglandin, which is synthesized by ptgs2, synergistically enhances tyrosine kinase-dependent signaling in colon cancer cells (Shao et al, 2004), and thus regulates cell motility by modulating EGF-R activity (Banu et al, 2007). The dominant roles of the PKA pathway and PTGS-2 activity with respect to migration are generally accepted in a variety of cell types and tissues (Howe, 2004; Rüegg et al, 2004; Liao et al, 2007). Our results suggest that strongly and persistently upregulated genes, such as akap12 or ptgs2, regulate and determine the global dynamics of the system and the simulated expression levels are indeed suitable indicators of a cellular migration state.

Because the initial Met and the following EGF-R signals converge on the MAPK pathway, there must be features specific for each trigger, which might stem from dynamic regulation dependent on the history of a cell. In fact, it was shown that temporal information encoding can be realized for MAPK signaling via negative feedback regulation (Amit et al, 2007), and that ligand specificity can be achieved through mutual inhibition of distinct compounds in the same pathway (McClean et al, 2007). Comparing the gene expression profiles from this study with those obtained from EGF-only-induced migration of a breast cancer cell line (Amit et al, 2007), one finds similar kinetics for the genes critically involved in the decision toward migration. However, the kinetics of some responding genes differ in the first 3–4 h after stimulation. These alterations are especially prominent for genes modulating MAPK activity (DUSPs) as well as for DHRS9 and GPR109B, which were postulated to modulate EGF-R signaling intensity. Interestingly, although the initial conditions of each epithelial cell type (MCF10A and primary human keratinocytes) are different, they eventually converge to the same gene expression dynamics over time.

A variety of cell types and tissues are known to express secreted soluble factors or cytokines and their respective receptors. Still, a single factor is generally not sufficient to induce a complex cellular response such as migration. Cells typically integrate a variety of internal signals together with environmental stimuli to compute a cellular decision. This mechanism prevents unwanted migration at the wrong time and place. Indeed, neither the transient HGF nor the constant EGF-R input alone can induce or sustain a lasting system response in the model simulation (Figures 4A and 6A). During wound healing, the cellular migration is restricted to the wound edge closely followed by a zone of enhanced proliferation. However, the balance between the proliferative and migratory zones is modulated dynamically depending on the wound type, bacterial infiltration or the inflammatory response (Martin, 1997; Stramer and Martin, 2005; Eming et al, 2007). Therefore, it is critical for a cell to integrate such diverse situations into the decision to migrate, even under circumstances when both HGF and EGF are present. Our data suggest that this kind of context is mediated through the PKA pathway activity (Figure 6), onto which many receptors for paracrine signaling converge. Interestingly, the irregularly shaped migration front induced by decreased PKA activity (see Supplementary Figure 7) is reminiscent of the surface structure of a growing carcinoma. Importantly, it is not the activity of a single factor alone, but a sequence of time-ordered events with respect to HGF stimulation that determines the functional role of PKA signaling to prevent, enhance, decrease or stop migration. It should be noted that the involvement of the main signaling pathways (namely MAPK and PKA pathways) is in agreement with diverse published literature for different epithelial cell types, even if they were not always explicitly shown for keratinocytes. Our contribution to an enhanced understanding of migration is that we unraveled the dynamic interplay of genes mediating the time-dependent order of their activities.

Although biological systems are usually complex, we were surprised to see so few genes establishing a simple, yet robust decision-making switch toward cell migration. Whether this finding of a few genes mediating cell fate decisions holds true in general for cellular processes such as proliferation, differentiation or cell death, or whether this is particularly true for cell migration, cannot be decided at present. It should be noted, however, that our system reduction approach was possible only because the onset and thus the core function for the decision toward cell migration was considered. The complexity of all control or safety elements that guarantee a robust and simple behavior (Lauffenburger, 2000) as well as the actual migration processes was neglected in our study.

The dependency on only a few genes for determining the cell transition toward migration shows a striking resemblance to principles in self-organizing systems (Haken, 2004). At the transition to the emergence of a new global system organization, often a drastic lowering in the degrees of freedom occurs. These degrees of freedom are then determined by a few ordering parameters that rule the emerging macroscopic pattern. If these parameters for system ordering guide one or more subsystems, they are said to enslave the subsystems, representing the key to understand how complex systems can self-organize under far-from-equilibrium conditions (cf. Supplementary information). Such phenomena of self-organization have been observed in many physical, chemical or biological systems undergoing phase transitions, for example, in lasers (Haken, 2004), morphogenesis (Meinhardt and Gierer, 2000), spatiotemporal genome organization (Misteli, 2007) or hematopoietic stem cell organization (Roeder et al, 2005). Although the realization of order parameters is specific to each system, for example, the amplitude modes of a laser cavity or the spatial distribution of morphogens in development, their abstract description on the systems level is the same. In our case, it is the gene expression amplitudes that constitute the order parameters of the cell. Interestingly, if only a few genes act as the ordering parameters to control a cell state transition, then it suffices to determine these genes to gain an understanding of the emergence of new cellular phenotypes.

As a consequence, the slaving principle is simultaneously a curse and a chance for understanding biological processes. On the one hand, it claims that only a cell-wide rebalancing of functional components is able to lead to a state transition, which is very hard to be understood and controlled in all details, for example, for reverting a tumor to a normal cell. On the other hand, system complexity is greatly reduced during the process of transition. If system control is the goal, then it will suffice to focus on the identification and perturbations of the dynamics of the few functional elements mediating the transition. From this point of view, our data analysis and modeling approach might be generally applicable to understand other cellular processes that involve decision making and may well prove instrumental in the attempt to decode and translate the language of cells.

Materials and methods

Cell culture

Normal human skin keratinocytes and dermal fibroblasts (HDF) were derived from adult skin (Stark et al, 1999). HDF obtained from the outgrowth of explant cultures were grown in Dulbecco's modified Eagle's medium (DMEM; Bio Whittaker) supplemented with 10% fetal calf serum (FCS), and cells from passages 4 to 8 were used. Mouse wild-type and cjun−/− fibroblasts were isolated from mouse embryos and immortalized according to the 3T3 protocol (Schreiber et al, 1999) and used together with HDF as feeder cells. Normal human skin keratinocytes were plated on X-irradiated feeder cells (HDFi, 70 Gy; MEFi, 20 Gy) in FAD medium (DMEM/Hams F12 3:1) with 100 U/ml penicillin, 50 μg/ml streptomycin and supplemented with 5% FCS, 5 μg/ml insulin, 0.1 ng/ml recombinant human EGF, 0.1 nM cholera toxin, 0.1 nM adenine and 0.4 μg/ml hydrocortisone (Sigma). For expression profiling, total RNA of human keratinocytes was isolated 1, 2, 3, 4, 6 and 8 h after stimulation with recombinant human cytokines (10 ng/ml HGF, 10 ng/ml GM-CSF, 10 ng/ml FGF-7 or 10 ng/ml SDF-1; all obtained from R&D Systems). Selective trypsinization and collection of human keratinocytes have been described elsewhere (Maas-Szabowski et al, 2001).

Migration assay

Immortalized human keratinocytes (HaCaT cells) were cultured in monoculture with DMEM (10% FCS, 100 U/ml penicillin, 100 μg/ml streptomycin). Subsequently, the cell monolayer was damaged with a ‘scratch' using a pipette tip and cells were treated with 5 μg/ml mitomycin c (Sigma-Aldrich) for 3 h before stimulation. Cells were stimulated at the indicated time points and periods with cytokines and/or inhibitors: 10 ng/ml HGF (R&D Systems), 1 ng/ml EGF (R&D Systems), 150 nM tyrphostin AG1473 (Biomol) (EGF-R inhibitor) or 1 μM GW2974 (Sigma) (EGF-R inhibitor), 50 mM meloxicam (Biomol) (PTGS-2 inhibitor), 0.5 μM H-89 (Calbiochem) (PKA inhibitor) or 10 μM myristoylated PKI (14–22) amide, cell-permeable PKA inhibitor (Biomol), 200 μM 8-(4-chlorophenylthio)adenosine 3′,5′-cyclic monophosphate sodium salt (Sigma) (PKA activator) and incubated for further 30 h. Relative migratory activity was determined by measuring migration distance during culture using standard protocols.

Microarray data acquisition and analysis

Microarray measurements were recorded for four different stimuli from cocultures, namely HGF, FGF-7, SDF and GM-CSF. For each stimulus, within one experiment six probes were taken (time points of 1, 2, 3, 4, 6 and 8 h after initial system stimulation) and further analyzed. Total RNA was isolated, labeled and hybridized to HG-U133-2plus (Affymetrix) according to the manufacturer's protocol. Raw microarray data were processed using the R environment (R Development Core Team, 2007) and the Bioconductor toolbox (Gentleman et al, 2004). Probe annotation was handled with the Bioconductor package hgu133plus2cdf (Bioconductor Project). Normalization was performed using variance stabilization available in the Bioconductor package vsn (Huber et al, 2002). Quality of results was assessed using simpleaffy (Wilson and Miller, 2005). The gene fold expression was calculated with respect to the mean gene expression from two control measurements of an uninduced system at 0 and 8 h. Measurement errors were calculated from the standard deviation in fold expression of the various probe sets for each gene. A lower error bound of ±0.08 fold expression was deduced from averaging the fold expression over all genes and all time points. Microarray data are available from ArrayExpress under the accession number E-TABM-440.

Gene ranking

Gene ranking is based on the peak and mean fold expression of the genes within the experimental time window of 8 h. This uniquely defines the rank position of each gene in a two-dimensional space. The combined rank score s of a gene is then defined as

where FE_t=〈g_i(t)〉_T and FE_p denote the time-averaged mean and peak gene fold expression, respectively, normalized to the maximal peak and maximal mean fold expression of all measured genes.

Data interpolation

Experimental gene expression time series are interpolated for model fitting using a cubic spline function with a sampling interval of Δt=0.1 h.

Neural network model

The time-resolved gene expression data were inferred using a CTRNN as a dynamic model for a gene regulatory network. The CTRNN (Beer, 1995) is defined as the following set of N coupled differential equations describing the fold expression kinetics of N genes g_i. In brief,

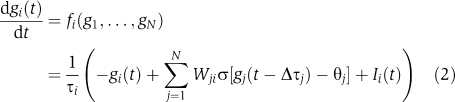τ_i and I_i(t) denote the time constant and external input, respectively, whereas θ_j is an offset term accounting for basal gene expression. Interactions between genes are incorporated by the weighted input of gene j into gene i via the sigmoid activation function

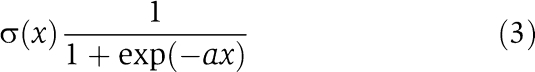The square matrix W_ji describes the directed connection weights between genes (Supplementary Figure 1A and B). The factor a in equation (3) controls the steepness of σ(x) to adjust the transition width between the off and the on state of a gene. The individual summands in the interaction term of equation (2) can be positive or negative, depending on the sign of the interaction weights W_ji, mimicking gene activation or inhibition, respectively. The delay term Δτ_j is a generalization of the original CTRNN definition (Hu et al, 2005; Kim et al, 2007) and accounts for the time delay between gene induction, transcription, translation and final effect of a gene j on any other gene.

Model fitting to the experimental data has been performed twice using two different variants of the input function I_i(t). The first model variant uses an exponentially decaying input function to each gene i

with a fixed decay λ and the initial signaling amplitude I_i⁰ to be learned from the experimental data. We choose λ=((ln(2)).2)h⁻¹, so that the decay of the input amplitude is approximately of the same timescale as the regulation of cellular kinases or phosphatases.

The second model variant has an additional, time-delayed periodic input to each gene i and is modeled as

where δt, p and r denote, respectively, the time lag, the input period and the amplitude ratio with respect to the corresponding learned input amplitude I_i⁰. λ is the same parameter as in equation (4). In this study, we set δt=2.5 h in all cases and use p=4 h and r=0.1 for the inverse modeling. Model simulations use a period of 3 h and an amplitude ratio of r=0.08, if not indicated otherwise. Changing the stimulus period within the above limits does not change system dynamics qualitatively.

Integration of the recurrent neural network is made using a first-order Euler method with a step size of Δt=0.1 h, constituting a good tradeoff between numerical stability of the integration and computational cost. The independent CTRNN parameters together with their respective ranges considered for model fitting are (I) the interaction weights −10⩽W⩽10, (II) the offset, 0⩽θ⩽2.5, (III) the gene time constants 0.14 h⩽τ⩽0.5 h, (IV) the delay 0 h⩽Δτ⩽2 h and (V) the input amplitude −15⩽I⁰⩽15. All parameters, except the time delay, were varied continuously. The latter is varied in multiples of the integration step size Δt=0.1 h. The scaling factor a of the sigmoid activation function is set to 4 for all genes throughout all simulations. All parameter ranges were chosen to yield results within biological reasonable bounds.

The maximal possible interaction between genes was calculated from combining the interaction weights W_ij and the gene offset θ_i into a single quantity, the maximal interaction strength

where σ, g_i^max and θ_i denote the sigmoid activation function, the maximal gene fold expression from the experimental data and the learned interaction weights and offset of gene i, respectively.

Parameter estimation

Model parameters were fitted to the experimentally observed gene fold expression time series with a genetic algorithm (GA) as a global optimization method, using mutation, crossing-over and selection as well as employing an elitist strategy (cf. Supplementary information). The experimental data were interpolated to the integration step size using a cubic spline function (Figures 1E and 3A). This procedure is based on the assumption that gene expression evolves smoothly in between the measured data points due to the lack of rapid gene expression dynamics.

The GA parameter estimation method used a population of 1000 CTRNN networks evolving over 3000 generations. The parameters in each network were randomly initialized and further on varied within the bounds given above. Networks composing the next generation were selected in pairs of two with a probability according to their fitness (equations (7) and (8)). A crossing-over equally mixed the parental parameter sets into one offspring network. The additional mutation rate of 0.02 randomly changed parameters in the offspring. The elitist strategy ensured the unchanged transfer of the fittest network to the next generation.

The fitness of a CTRNN with a given parameter set is given by

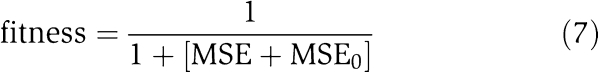where MSE denotes the mean squared error between the spline-interpolated experimental gene expression data g_i^exp and the simulated gene expression values g_i^model,

where T and N denote the total integration time and number of genes, respectively. δ_T is a tolerance parameter that accounts for measurement errors in the experimental data. Throughout this paper, we set δ_T=0.1. The MSE₀ term in equation (7) puts a fitness penalty onto system solutions having an unstable homeostasis state, hence calculating the mean difference from zero, when setting all external inputs to zero (I_i⁰=0):

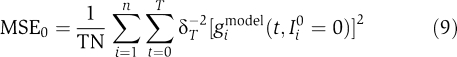For the selection of the correct gene network parameter sets, we performed M=5000 independent GA parameter fits for each network described below, each time starting with a random initial parameter set, setting a predefined number of generations as the stopping criterion (see above). Each of these independent runs is ranked according to fitness (equation (7)) and robustness (see below). The parameter rank score S_p(i) of a fitting run is calculated as

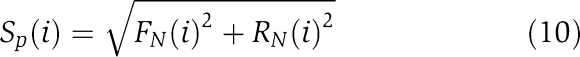where 0⩽F_N⩽1 and 0⩽R_N⩽1 denote the normalized model fitness and robustness of a parameter set of run i, respectively. The model parameters are finally computed from the expectation value of the weighted sum of 5% best ranked parameter fits (Supplementary Figure 3E), using the normalized rank scores S_p(i) as weight function (Supplementary Figure 3 and Supplementary Table IIIA and B). The signal-to-noise ratio of each parameter is calculated from the ratio of the expectation value to standard deviation of the above weighted sum (Supplementary Figure 4).

Calculation of system robustness

Network robustness was determined from a numerical algorithm to calculate the largest Lyapunov exponent (LLE) (Rosenstein et al, 1993). Lyapunov exponents quantify the separation of nearby trajectories on an attracting manifold. A negative LLE is the characteristic of dissipative systems, exhibiting asymptotic stability. The more negative the LLE, the more stable the system. A similar Lyapunov exponent-based method has been previously employed to investigate the sensitivity of a signaling pathway to initial conditions (Aldridge et al, 2006). Here, the algorithm is used to investigate the local stability of the fixed point of the neural network upon stimulation with the learned input function (cf. equation (2)). The algorithm calculates the LLE from the simulated time series of a single gene using the method of delays. The LLE λ_L is approximated via

where Δt is the sampling period of the time series and d_j(i) denotes the distance between the jth pair of simulated expression data at time iΔt with a time lag J and an initial separation C_j. For evaluation of the system robustness, we use the time-averaged divergence of nearby trajectories

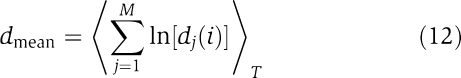where the sum runs over all vectors M=T−(m−1)J from the delay reconstruction of the attractor and the angular brackets 〈 〉_T denote averaging over the total simulation time. The more negative the mean divergence, the faster the network settles back into a stable steady state upon stimulation. Hence, systems preferentially return to zero fold expression or take up a stable, activated state within the shortest time.

For the sake of computational simplicity, the divergence rather than the Lyapunov exponent is used, which still selects networks according to the desired robustness criteria. Further parameters included embedding dimension m=2(N+1), where N is the number of network nodes, and time lag J=1.5 h. The minimal time window for skipping temporally nearest neighbors is W=30 h, which is greater than the longest timescale in the system, as required from the algorithm. Robustness analysis was always performed for the strongest expressed gene ptgs2. Changing the time lag, the embedding dimension or the respective gene for analysis did not alter the estimated level of robustness qualitatively.

Bootstrapping tests

We performed time randomization tests to evaluate the correlation of the inverse modeling solution to the gene expression kinetics. One hundred independent time randomizations of the gene expression data were performed. Parameters were estimated from the 50 fittest out of 100 independent GA model fits. The correlation between the parameters obtained is computed using the linear Pearson correlation coefficient with respect to the parameter estimates obtained from the full model fitting analysis.

Supplementary Material

Supplementary Information

Supplementary Tables I

Supplementary Tables II

Supplementary Tables III