Signal Transduction at Point-Blank Range: Analysis of a Spatial Coupling Mechanism for Pathway Crosstalk

Abstract

The plasma membrane provides a physical platform for the orchestration of molecular interactions and biochemical conversions involved in the early stages of receptor-mediated signal transduction in living cells. In that context, we introduce here the concept of spatial coupling, wherein simultaneous recruitment of different enzymes to the same receptor scaffold facilitates crosstalk between different signaling pathways through the local release and capture of activated signaling molecules. To study the spatiotemporal dynamics of this mechanism, we have developed a Brownian dynamics modeling approach and applied it to the receptor-mediated activation of Ras and the cooperative recruitment of phosphoinositide 3-kinase (PI3K) by activated receptors and Ras. Various analyses of the model simulations show that cooperative assembly of multimolecular complexes nucleated by activated receptors is facilitated by the local release and capture of membrane-anchored signaling molecules (such as active Ras) from/by receptor-bound signaling proteins. In the case of Ras/PI3K crosstalk, the model predicts that PI3K is more likely to be recruited by activated receptors bound or recently visited by the enzyme that activates Ras. By this mechanism, receptor-bound PI3K is stabilized through short-range, diffusion-controlled capture of active Ras and Ras/PI3K complexes released from the receptor complex. We contend that this mechanism is a means by which signaling pathways are propagated and spatially coordinated for efficient crosstalk between them.

INTRODUCTION

Intracellular signal transduction networks are responsible for controlling cell behavior in response to external stimuli, which are most often sensed by specific receptors at the cell surface. In the case of growth factor receptors, binding of an extracellular ligand results in receptor dimerization, tyrosine kinase activation, and phosphorylation of the intracellular portion of the receptor on multiple tyrosine residues, which are rapid processes that prime the receptor for intracellular signaling. The tyrosine-phosphorylated receptor actuates signal transduction by providing a scaffold for the recruitment of various enzymes, either directly or through adaptor proteins, achieved through modular, structurally related protein-protein interaction domains of these enzymes that are distinct from their catalytic domains (1–5). These complexes initiate well-defined intracellular signaling pathways/cascades, which in reality are not independent; rather, these dominant routes of signal relay are linked through parallel interactions in the network, a mode of pathway coregulation termed crosstalk (6,7).

A common theme in intracellular signaling is that enzymes recruited by receptors often act upon laterally mobile substrates associated with the inner leaflet of the plasma membrane. Notable examples include the regulation of small, membrane-anchored GTPases, such as those of the Ras and Rho families, by guanine-nucleotide exchange factors (GEFs) and GTPase-activating proteins (GAPs), and the modification of certain lipid substrates by phospholipases C and D and various phosphoinositide kinases. Although receptor-mediated phosphorylation and conformational changes are important for activation of these enzymes, the membrane localization offered by binding to receptors or other membrane-associated molecules is equally if not more important for their signaling functions (8–11). A simplistic explanation is that membrane localization brings the enzymes into close proximity to their substrates; although this is the essential basis for the rate enhancement, it does not adequately represent the inherent complexity of the problem. The relatively slow lateral diffusion of membrane-associated molecules often dictates the rate of bimolecular association, and in the case of an enzyme-catalyzed reaction, localized zones in which the substrate is depleted and the product of the reaction is enriched tend to arise. Various models relevant to diffusion-controlled binding/reaction on biological membranes and other surfaces (12–18), and to signal transduction reactions in particular (19–24), have been offered.

In this article, we expand on the role of diffusion-controlled kinetics in receptor-mediated signal transduction reactions in cell membranes. Specifically, we introduce the spatial coupling hypothesis, which states that simultaneous recruitment of different enzymes to the same receptor scaffold facilitates crosstalk between different signaling pathways through the local release and capture of activated signaling molecules. We examine the specific case of phosphoinositide 3-kinase (PI3K) localization mediated by cooperative interactions with receptors and active Ras, which was previously considered in the absence of spatial effects (25). These interactions involve the spatial interplay among individual receptor, Ras, GEF, GAP, and PI3K molecules at the plasma membrane, with PI3K acting as both a receptor-binding protein and, as a prominent example of pathway crosstalk, an effector of Ras (26). Ras and PI3K are centrally involved in arguably the most important signaling pathways governing cell proliferation and survival, and accordingly their dysregulation figures prominently in cancer progression (27–30). We contend that the cooperative assembly of receptor/PI3K/Ras complexes is facilitated not by the whole-cell increase in active Ras elicited by cell stimulation, which is often modest, but rather by the local action of a GEF bound to the same receptor complex. In principle, the spatial coupling between GEF and PI3K is achieved by two distinct mechanisms. It might occur via a relatively long-range mechanism whereby receptors recruit PI3K/Ras complexes, which are more likely to form in the vicinity of receptors with GEF bound; this mechanism is shown to be insignificant. Instead, the dominant pathway is a short-range mechanism whereby active Ras is first released by a receptor-bound GEF and then captured by a PI3K molecule already associated with the same receptor complex. Our analysis suggests that activation of Ras and PI3K ought to be tightly colocalized for efficient crosstalk between them.

Although the hypothesis formulated above is reasonably intuitive, a rigorous, quantitative analysis is required to identify the conditions that promote spatial coupling, in terms of species concentrations, rate constants, and other relevant parameters, and to assess the magnitude of its effect on Ras/PI3K crosstalk. To this end, we have developed a two-dimensional Brownian dynamics kinetic model, using methods that build upon our previous algorithm for the efficient and accurate handling of bimolecular association/reaction transitions (23). The algorithm was validated against continuum theory (21) for the simple case of collision coupling, a model mechanism analyzed in detail elsewhere (19,31,32). By comparison, the interactions studied here are considerably more complex and elude an analytical or compartmental modeling description. Further, the Brownian dynamics approach allowed us to directly evaluate the probabilities of short- and long-range interactions to further characterize the spatial coupling mechanism.

METHODS

Molecular interaction network

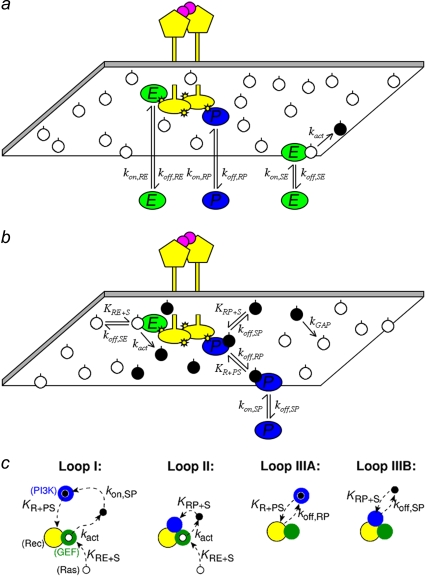
The binding interactions and reactions included in our model, and their specified rate-constant definitions, are illustrated in Fig. 1, a and b. We consider a hypothetical receptor, loosely modeled after platelet-derived growth factor (PDGF) receptors (33), with independent binding sites for two cytoplasmic signaling proteins: Ras-GEF and PI3K. These are modeled after the Grb2-Sos complex and p85-p110 (type IA) PI3Ks, respectively, which bind with high affinity to distinct phosphotyrosine sites on PDGF receptors (2). In this model, we do not explicitly model the adaptor Grb2 or other adaptors, such as Shc. Consistent with the dimerization of PDGF receptors and other receptor tyrosine kinases, the activated receptor complex contains two identical binding sites for each signaling protein. The other molecular player in our model is Ras, which is anchored in the membrane via lipid modifications and exists as a complex with either GDP or GTP. In the GDP-bound (inactive) state, Ras may form a complex with cytosolic or receptor-bound GEF. This complex dissociates either without producing a reaction or with the conversion of Ras to the GTP-bound (active) state. Although guanine-nucleotide exchange is a two-step process, with GDP release followed by uptake of GTP from the cytosol, GDP release is known to be rate-limiting (34,35). PI3K, from the cytosol or while bound to receptors, forms a reversible complex with Ras-GTP; because PI3K interacts with receptors and Ras via distinct subunits (26), we treat these interactions as noncompetitive, as considered previously (25). Other Ras effectors, such as Raf and RalGDS, are not considered here. Finally, active Ras is converted back to the GDP-bound state by GAPs, which accelerate the GTPase activity of Ras (36). As shown in Fig. 1 b, this enzymatic reaction is treated implicitly, characterized by a pseudo-first-order rate constant, k_GAP. This aspect of the model follows the collision-coupling mechanism analyzed in our previous work (23). Assuming that the GAP(s) are far from saturation, k_GAP is equivalent to the V_max/K_M of the enzyme, or the sum of such quantities in the case of multiple GAPs. In results not shown, we also considered the binding of Ras-GAP to receptor sites and its enzymatic action explicitly, which is readily incorporated using the modeling framework described here.

FIGURE 1.

Binding/reaction network and mechanisms of receptor/PI3K/Ras complex formation. (a) GEF (E) and PI3K (P) proteins bind from the cytosol to independent sites on the activated receptor, and each receptor dimer contains two of each site. GEF also binds from the cytosol to Ras-GDP (white circles), which can result in the exchange reaction that produces Ras-GTP (black circle). (b) Receptor-bound GEF engages Ras-GDP by lateral association and also mediates release of Ras-GTP. Free Ras-GTP engages cytosolic and receptor-bound PI3K, and it is converted to Ras-GDP by a pseudo-first-order process that approximates the action of GAPs. (c) We consider four mechanisms by which ternary receptor/PI3K/Ras complexes are formed, depicted as if one were looking down on the inner leaflet of the plasma membrane. Loop I is a long-range mechanism in which Ras-GTP produced by receptor-bound GEF is bound by PI3K from the cytosol as it diffuses away from the receptor complex; the Ras/PI3K complex is subsequently captured by the receptor. Loop II is a shorter-range mechanism whereby PI3K first binds to the receptor and then captures Ras-GTP produced by the GEF before it can diffuse a significant distance from the complex. Once formed, the ternary complex can dissociate and rebind multiple times via the receptor/PI3K (Loop IIIA) or Ras/PI3K (Loop IIIB) linkage.

Binding from the cytosol, whether to receptors or to Ras, is governed by a pseudo-first-order association rate constant that accounts for the cytosolic concentration of GEF or PI3K, assumed constant as in the model by Woolf and Linderman (22); fluctuations in local cytosolic concentrations would be smoothed out considerably by the relatively rapid diffusion of proteins in cytosol (10–100 μm²/s). Formation of a ternary receptor/enzyme/Ras complex, on the other hand, occurs through the mutual diffusion of Ras and receptors in the plasma membrane, considered explicitly (see below). The lateral mobility of Ras in cells (D ≈ 0.2 μm²/s) has been characterized extensively (37–42). In accord with the modular nature of signaling protein domains, we assume that the rates of dissociation and catalysis by enzyme/Ras complexes are unaffected by their receptor-binding status, and likewise the rates of enzyme dissociation from receptors are not altered by the enzyme's association with Ras (Fig. 1 b). Values of the association rate constants governing receptor/enzyme/Ras complex assembly satisfy detailed balance (43). Finally, in this model, we do not explicitly consider the tyrosine phosphorylation status of the receptor, nor do we consider the possible influence of PI3K phosphorylation by the receptor. The probability that an unoccupied receptor site is phosphorylated is assumed constant and effectively lumped into the corresponding association rate constants.

Brownian dynamics algorithm

The basis of the method has been described in detail and validated previously (23). Far from a reactive boundary (receptor-bound enzyme), the particles (membrane-anchored Ras) are advanced according to the first-passage-time method (44,45). The absorbing receptor boundary is defined by a disk of radius S, the encounter distance, assumed to be the same for all receptor- and Ras-containing binding partners. As a particle approaches, that boundary is taken to be approximately planar, and the probability of binding is determined according to well-known one-dimensional propagators (46). To describe all possible chemical interactions, we explicitly specify the reaction rules, or logical statements, such that the decision is made based on the current states of receptors and Ras particles. In this work, we have improved the efficiency and accuracy of the algorithm by using Monte Carlo sampling to choose the time step based on the mean reaction and first-passage times for all possible reactions or particle random walks at the membrane. The model distinguishes between the two interaction modules that describe 1), spatially independent first-order and pseudo-first-order transitions (47,48), and 2), diffusion of and interactions between membrane-associated species (23,49). The two modules are matched after every time step (or multiple time steps), and then all changes associated with this time interval are made simultaneously. Supplemental Material, Data S1 provides a detailed description of the algorithm, which was programmed in C. The simulations run efficiently on regular desktop computers.

We consider the dynamics associated with a single activated receptor complex; that is, we examine the limit where activated receptors (or, more precisely, receptor/GEF complexes) are sufficiently dilute. It bears mentioning that the density of activated receptors depends on the external ligand concentration, such that the fraction of activated receptors relative to the total is low in many biologically relevant circumstances. In this limit, the receptor is fixed at the center of a 5×5-μm simulation box (∼1% of the total plasma membrane area of a mammalian cell), and Ras particles not associated with the receptor complex are moved according to the mutual diffusion coefficient, D, assumed constant. The total number of Ras particles in the simulation box was either 100 or 1000 (4/μm² or 40/μm², respectively); these total Ras densities are consistent with the range of measured Ras expression levels in different cell lines (25,50–52). Periodic boundary conditions are applied at the edges of the box; we confirmed that changing the box size does not significantly affect the results. Moreover, it is assumed that the activated receptor complex is sufficiently long-lived (timescale of minutes), allowing us to focus on average properties of the system at steady state. This assumption is reasonable in the case of PDGF-receptor-mediated activation of PI3K (53), and it is consistent with the assumption of constant cytosolic concentrations. We note that these simplifications do not reflect limitations of the simulation approach, which can readily accommodate more detailed models of particular systems.

Model parameters

All of the binding rate constants were scaled to produce dimensionless parameters that allow us to compare the timescales of the various processes (Table 1). Order-of-magnitude estimates of the parameters were based on the following guidelines. Ras diffuses freely with D = 0.2 μm²/s (37); we take this as the mutual diffusion coefficient, because receptors are typically far less mobile. With an assumed encounter distance of S = 5 nm, the characteristic diffusion rate is D/S² = 8000 s⁻¹. This rate is used to scale the various lifetimes of interactions considered in the model to yield dimensionless lifetimes, τ. Typical values of association rate constants for signaling protein-protein interactions are 1–100 μM⁻¹ s⁻¹ (54–56). Association rate constants in two dimensions are often estimated by geometric considerations, assuming a confinement layer of 3–10 nm (8,57,58). This gives rate-constant values of 0.2–60 μm²/s, but orientational constraints can yield considerably higher (or lower) values (59); we assume a value near the high end of the range. Based on typical values of the equilibrium dissociation constant K_D for signaling protein-protein interactions, in the range of 1–100 nM (56,60,61), interaction lifetimes are taken in the range of 0.01–100 s (τ ≈ 10²–10⁶). For PI3K/receptor binding, the K_D is near the low end (high affinity) of the range (61–63), whereas the K_D for PI3K/Ras binding is near the high end (low affinity) of the range (64). Typical values of catalytic rate constants, k_cat (e.g., k_act in our model), are 1–100 s⁻¹, and typical values of Michaelis constants, K_M, for enzymes are in the range of 1–100 μM, consistent with kinetic analyses of Ras GEFs and GAPs (35,55,65,66). Based on the range of association rate constants cited above, this gives lifetimes of enzyme-substrate complexes in the broad range of 10⁻⁴–1 s (τ ≈ 1–10⁴). The lifetime of the GEF/Ras interaction is likely to be near the low end of the range, because GEFs have a very low affinity for nucleotide-bound Ras and are rapidly displaced by GTP after GDP release (34,35).

TABLE 1.

Model parameters expressed in dimensionless form

Parameter	Definition	Comments	Base value
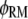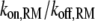		Affinity of receptor interaction	0.1*
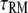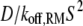		Lifetime of receptor interaction	105*†
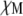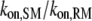		Ratio of Ras/receptor on-rates	1*
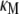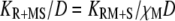		2-D receptor association rate constant	100*
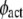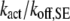		GEF catalytic efficiency	0.1
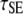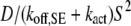		Ras/GEF lifetime	10†
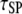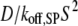		Ras/PI3K lifetime	103†
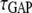		Ras-GTP lifetime	104†

^*In the base case, these parameters are assigned the same value for the two enzymes, GEF (M = E) and PI3K (M = P).

^†Based on D = 0.2 μm²/s and S = 5 nm, a 1 second lifetime corresponds to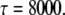

Analysis of the model

We introduce four steady-state metrics used to characterize our simulation results. The first is T_M, the fractional occupancy of the receptor site for molecule M (E (GEF) or P (PI3K)):

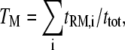(1)

where t_RM,i is the lifetime of the receptor/M complex that has been formed as a result of the ith binding event, and t_tot is the total simulation time. The second metric, M_M, is defined as the fraction of receptor/M binding events that occur via lateral association of a Ras/M complex in the membrane:

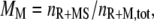(2)

where n_R+MS is the number of Ras-mediated associations of molecule M with its receptor site, and and n_R+M,tot is the total number of receptor/M association events. The quantity 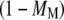is the fraction of receptor/M binding events that occur via recruitment of molecule M from the cytosol. We note that T_M and M_M are equivalent for each of the two independent GEF or PI3K binding sites in the receptor dimer; further, M_M and T_M are related directly to one another, as shown below. These quantities can be manipulated in various ways. For example, the average frequency of PI3K binding from the cytosol to each receptor site is calculated as 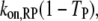that of all PI3K binding events to a receptor site is 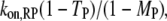and that of Ras-mediated binding of PI3K to each receptor site is given by 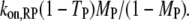All receptor/PI3K encounters dissociate with frequency k_off,RP, and thus the overall frequency of such dissociation events is given by k_off,RPT_P. At steady state, the overall rates of receptor/M binding and dissociation are in balance, yielding the following relationship between T_M and M_M:

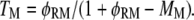(3)

In this article, T_M and M_M were both determined from the simulation results, and the validity of Eq. 3 was later confirmed.

The third metric is C_EP, defined as the GEF/PI3K coincidence ratio, which compares the probability of finding GEF and PI3K molecules bound to the same receptor dimer to the probability of such a complex forming by independent binding events:

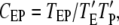(4)

where T_EP is the fraction of the total simulation time in which the receptor dimer has at least one GEF and one PI3K molecule bound, and 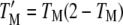is the fraction of the time during which the receptor dimer has at least one M molecule bound. When C_EP = 1, the binding of GEF and PI3K are uncorrelated, whereas when C_EP > 1, the binding of GEF and PI3K are positively correlated.

Last, we define α_GEF as the dimensionless rate of Ras activation by GEF, given by

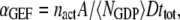(5)

where 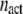denotes the number of such activation events (parsed according to whether the GEF is receptor-bound or not when the reaction occurs), A is the area of the simulation box, and 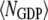is the number of inactive Ras molecules averaged over the simulation time. We note that, by comparison with the effective rate constant invoked in earlier studies (19,23), this definition is not normalized by the fraction of the time that the receptor is “on”; in our model, dividing 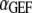for the receptor-bound GEF by 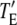yields an approximate analog.

To facilitate the analysis further, we distinguish between three mechanisms by which a ternary receptor/PI3K/Ras complex can form (Fig. 1 c). Loop I is a relatively long-range mechanism whereby Ras is bound by PI3K from the cytosol, and the laterally mobile Ras/PI3K complex is captured by the receptor. Loop II is a shorter-range mechanism whereby unoccupied Ras is captured by PI3K that is already bound to the receptor. Finally, Loop III, the shortest-range mechanism, accounts for fast rebinding; either PI3K dissociates from the receptor in complex with Ras, and the Ras/PI3K complex rebinds (Loop IIIA), or Ras dissociates from and then rebinds receptor-bound PI3K (Loop IIIB). Loops I and IIIA contribute to the Ras-mediated binding of PI3K to receptors as quantified by M_P (Eq. 2).

RESULTS

Interactions between enzymes and membrane-associated substrates tend to stabilize receptor/enzyme complexes: analysis of GEF-mediated Ras activation

Before analyzing the spatial coupling mechanism, which is the main focus of this work, we begin with a brief characterization of the GEF reaction. For the base-case parameter values considered here, the activity of receptor-bound GEF is in the diffusion-controlled regime. Thus, during the association of a GEF enzyme in complex with the receptor, a high fraction (>80% according to continuum theory) of the Ras particles close to the receptor complex are found in the GTP-bound form, whereas a much smaller Ras-GTP fraction (<1%) is found far from the receptor. This localized enrichment of Ras-GTP (or, more precisely, of Ras-GTP generation events) is an important concept to be developed in the analysis of spatial coupling to follow.

In previous work, we applied the Brownian dynamics approach to a well studied, idealized model of signaling protein activation, the collision-coupling mechanism (23). Applied to the Ras system, that model posits that GEF association with a receptor is turned “on” and “off” according to first-order rate constants, Ras-GTP is formed by second-order reaction between the receptor-GEF complex and Ras-GDP particles (GEF/Ras binding assumed to be far from saturation), and the average lifetime of the Ras-GTP state is determined by a first-order rate constant that encapsulates the activity of GAPs. By comparison, the model described here accounts for receptor/GEF and Ras/GEF interactions explicitly, whereas GAP activity remains implicit. If the major purpose of receptor-mediated recruitment of GEF activity to the membrane is to enhance its access to Ras-GDP (67), then at least in terms of binding equilibria it follows from detailed balance that the interaction between GEF and Ras-GDP ought to facilitate receptor/GEF binding. This effect, not accounted for in previous models, is a direct outcome of the modular protein domains used by signaling enzymes for catalytic and noncatalytic interactions.

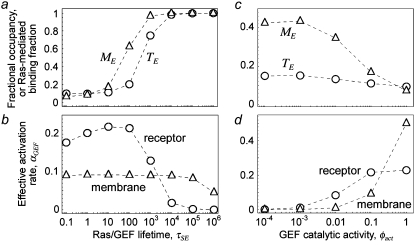
The cooperative binding effect in GEF recruitment was evaluated as a function of the dimensionless lifetime of the Ras/GEF complex, τ_SE, and the catalytic efficiency parameter, φ_act (Fig. 2). Varying τ_SE effectively changes the Michaelis constant, K_M, of the enzyme-substrate pair while holding the catalytic efficiency, k_cat/K_M, constant, whereas varying φ_act has the opposite effect. In the limit of low τ_SE, as in the base case (τ_SE = 10), essentially all receptor/GEF associations occur from the cytosol; the fractional occupancy of each GEF-binding site on the receptor, T_E (Eq. 1), is approximated by 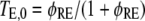in this limit. Under these conditions, the GEF-mediated production of Ras-GTP is modeled effectively using continuum theory (21,23). As τ_SE is increased, T_E increases alongside the fraction of receptor/GEF associations mediated by Ras, M_E (Eq. 2); in fact, the increase in T_E is directly related to the value of M_E via Eq. 3 (Fig. 2 a). At lower values of τ_SE (<10³), the overall dimensionless Ras activation rate, α_GEF (Eq. 5), is around three times higher than that seen in the absence of receptor/GEF binding, which is typical of the fold-increase in overall Ras-GTP levels seen in response to growth factor stimulation; there is a modestly positive relationship between α_GEF and τ_SE in this regime, attributed to the increase in T_E (Fig. 2 b). At higher values of τ_SE (lower K_M and k_cat), we see enzyme saturation effects, and the overall rate vanishes. Reducing the value of φ_act, which increases the fraction of nonproductive interactions between GEF and Ras-GDP, also has this effect, and there is a corresponding increase in T_E and M_E (Fig. 2, c and d). We conclude that although the binding of Ras-GDP tends to stabilize receptor/GEF interactions, GEF enzymatic activity in the diffusion-controlled regime mitigates this effect by depleting Ras-GDP locally.

FIGURE 2.

Interactions between enzymes and membrane-associated substrates tend to promote and stabilize receptor/enzyme complexes: analysis of GEF recruitment. The binding of GEF to the activated receptor was assessed in the absence of PI3K. Various statistical metrics were calculated as a function of the Ras/GEF complex lifetime, τ_SE (a and b), or the GEF catalytic efficiency parameter, φ_act (c and d). Other relevant parameters were set to their base-case values (Table 1), and N_Ras = 1000. (a and c) Fractional occupancy of the receptor binding sites for GEF, T_E (Eq. 1), and fraction of receptor/GEF associations mediated by Ras, M_E (Eq. 2). (b and d) Dimensionless rate of Ras activation, α_GEF (Eq. 5), resulting from formation of receptor/GEF/Ras complexes and Ras/GEF complexes in the membrane.

Spatial coupling between GEF and PI3K recruitment by the same receptor scaffold enhances Ras/PI3K crosstalk

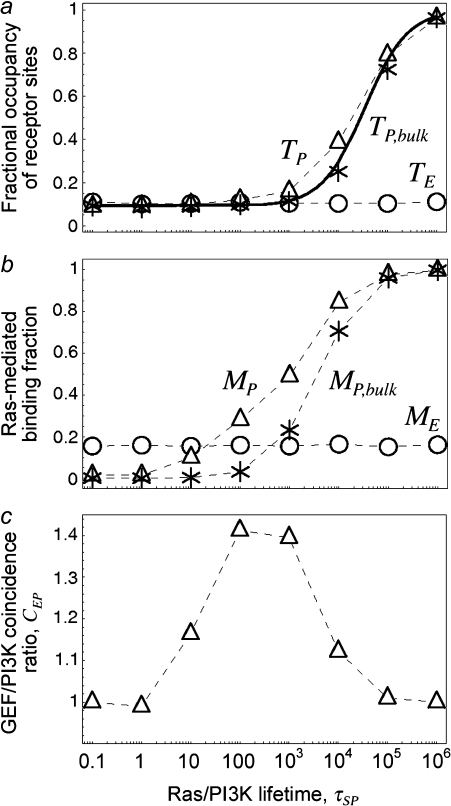
The next progression in our model analysis is to add PI3K and its interactions with the activated receptor and Ras-GTP to test the spatial coupling mechanism, whereby efficient formation of receptor/PI3K/Ras complexes depends on the local release of Ras-GTP from the receptor complex. To simplify the analysis, PI3K was given the same receptor binding properties as the GEF (φ_RP = φ_RE = 0.1, τ_RP = τ_RE = 10⁵, κ_P = κ_E = 100), and the lifetime of the Ras/PI3K interaction, τ_SP, was varied (Fig. 3). As seen in the case of GEF recruitment, the fractional occupancy of receptor binding sites for PI3K, T_P, is enhanced as τ_SP is increased (Fig. 3 a), in tandem with the fraction of receptor/PI3K associations mediated by Ras, M_P (Fig. 3 b). The difference here is that PI3K is engaged by the GTP-bound form of Ras, an interaction that relies on the action of the receptor-bound GEF.

FIGURE 3.

Spatial coupling of GEF and PI3K binding to the same receptor scaffold enhances PI3K recruitment. Various statistical metrics were calculated as a function of the Ras/PI3K complex lifetime, τ_SP; other relevant parameters were set to their base-case values (Table 1), and N_Ras = 1000. (a) Fractional occupancy of the receptor binding sites for PI3K, T_P. For comparison, a second set of simulations was acquired using a bulk activation model, where receptor-bound GEF is catalytically silent, and its average rate of Ras activation is replaced by spontaneous conversion of Ras-GDP to Ras-GTP in the bulk membrane. The solid line is the analytical solution for the bulk activation model (Data S2). (b) Fraction of receptor/PI3K associations mediated by Ras, M_P. (c) Coincidence ratio for simultaneous GEF and PI3K binding to the receptor, C_EP (Eq. 4).

To demonstrate the spatial coupling effect, we compared the simulation results with a bulk activation model, in which Ras-GDP particles are randomly converted to Ras-GTP with a constant probability chosen to match the overall rate in the regular simulation. This simpler model permits an analytical solution (Data S2), which was found to be in good agreement with the corresponding simulations. As expected, the move from localized to global Ras activation means that a higher Ras/PI3K affinity, by as much as an order of magnitude under these conditions, is needed to achieve the same values of T_P and M_P (Fig. 3 b). With the base-case value of τ_SP (τ_SP = 10³), the spatial coupling effect yields a threefold higher ratio of Ras/PI3K versus cytosolic PI3K binding to receptor sites, 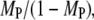as compared with the bulk activation model. We will subsequently show that the magnitude of the spatial coupling effect can be improved upon substantially depending on the model parameters.

The influence of locally produced Ras-GTP suggests that PI3K binding should be positively correlated with the presence of GEF in the receptor complex. This was assessed using the coincidence ratio, C_EP (Eq. 4). When C_EP = 1, the probability of forming a receptor complex containing both GEF and PI3K is random, determined from the product of the probability of finding at least one GEF and the probability of finding at least one PI3K molecule bound to the receptor. When C_EP > 1, the presence of both GEF and PI3K occurs with higher-than-random probability, and the interactions are positively correlated. Under the conditions tested, it was found that GEF and PI3K interactions with receptors are indeed correlated, but only at intermediate values of τ_SP (Fig. 3 c). With low τ_SP, there are very few receptor/PI3K associations mediated by Ras, whereas with high τ_SP, the probability of finding at least one PI3K bound to the receptor is high: 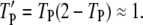At either extreme, PI3K and GEF interactions with the receptor are uncorrelated. In the bulk activation model described above, where receptor-bound GEF is catalytically silent, it was confirmed that C_EP ≈ 1 at all values of τ_SP (data not shown). These results suggest that what is important for Ras/PI3K crosstalk is not the whole-cell level of Ras-GTP, which often increases only modestly upon receptor stimulation, but rather the correlated binding of GEF and PI3K to the same receptor scaffold.

The spatial coupling effect is dominated by short-range, release-and-capture interactions and is characterized by a high efficiency of capture and recapture

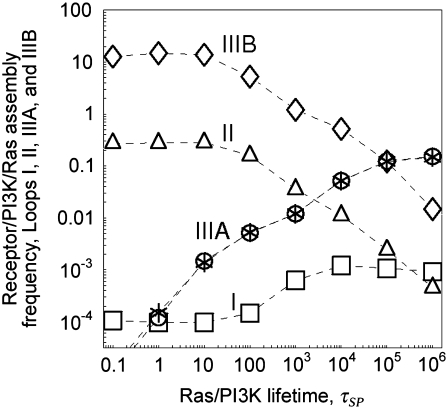
Analysis of the simulations described in the previous section shed further light on the mechanisms by which ternary receptor/PI3K/Ras complexes form. These complexes form initially in one of two ways: either PI3K binds Ras-GTP from the cytosol, and the Ras/PI3K complex is then captured by the receptor, or PI3K binds the receptor and then captures a free Ras-GTP (Fig. 1 c, Loops I and II, respectively). Once formed, the ternary complex is stabilized through recapture of Ras/PI3K and Ras-GTP that dissociate from the complex (Fig. 1 c, Loops IIIA and IIIB, respectively).

The frequencies of the ternary complex formation mechanisms were quantified from simulation results (Fig. 4). As expected, the longer-range Loop I generally occurs very rarely; receptor/PI3K/Ras complexes are nearly always initially formed with PI3K binding to the receptor first and then capturing Ras-GTP (Loop II). As receptor binding sites for PI3K become increasingly saturated (T_E ≈ 1), the frequency of Loop II decreases in favor of the rapid rebinding events, Loops IIIA and IIIB. The prevalance of Loop IIIA versus IIIB is determined by the frequencies of the respective dissociation events (compare 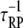and 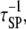respectively) and their probabilities of recapture (which are both close to 1 under these conditions). Across much of the range of τ_SP values, we find that the ratio of rebinding events (Loops IIIA and IIIB) to ternary complex formation events (Loops I and II) is ∼30–50. That is, a receptor/PI3K/Ras complex dissociates and rebinds ∼30–50 times on average before dissociating completely, corresponding to a capture efficiency of 97–98%. Clearly, serial recapture is necessary for a high fractional occupancy T_P in these simulations, because Ras-GTP is only actively produced 19% of the time (the fraction of the time that at least one GEF molecule is associated with the receptor). For sufficiently high τ_SP (τ_SP ≈ 3 × 10³ or greater), the effective lifetime of the ternary complex exceeds the average duration of receptor/GEF association, which further explains why the PI3K and GEF interactions with the receptor are uncorrelated (C_EP ≈ 1) when τ_SP is high.

FIGURE 4.

Quantification of receptor/PI3K/Ras complex formation mechanisms: the spatial coupling effect is dominated by short-range, release-and-capture interactions. For the simulations shown in Fig. 3, the average frequency of receptor/PI3K/Ras complex formation (total events/total time) was computed and categorized according to the mechanisms depicted in Fig. 1 c. The asterisks indicate the frequency of Loop IIIB multiplied by the ratio τ_SP/τ_RP, for comparison to the frequency of Loop IIIA.

We conclude that when the capture of both Ras/PI3K by the receptor and Ras-GTP by receptor-bound PI3K are diffusion-controlled, short-range interactions are favored; a laterally mobile species that has just been released from the receptor complex (as in all of the mechanisms except Loop I) is in the most advantageous position for capture. Thus, spatial coupling is characterized not only by enhanced assembly of ternary receptor/PI3K/Ras complexes but also by serial recapture events that extend the duration of PI3K localization at the membrane.

Conditions promoting spatial coupling: diffusion-controlled capture of Ras-GTP by receptor-bound PI3K is essential, but receptor-bound GEF activity does not need to be diffusion-controlled

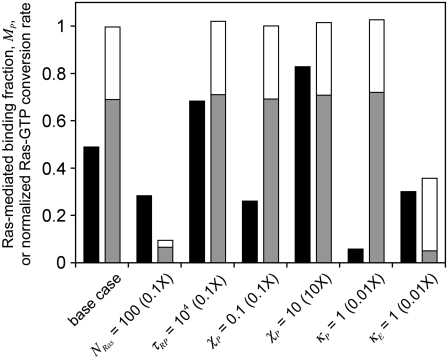
Having established that significant spatial coupling between Ras-GTP release and PI3K recruitment by receptors is plausible, we sought to define parameter conditions that foster the effect (Fig. 5). First, there is the effect of modulating the overall density of Ras. Reducing N_Ras by 10-fold yields a corresponding scale-down in the number of Ras-GTP generation events and average density of Ras-GTP, but the fraction of receptor/PI3K associations mediated by Ras (M_P) is reduced somewhat modestly; the frequency of receptor/PI3K/Ras assembly is reduced by only about threefold (results not shown). This insensitivity is readily understood based on the previous analysis. When there is at least one GEF bound to the receptor, there is a saturation effect in that the Ras-GTP released can only be captured by as many as two receptor-bound PI3K molecules. Relative to the bulk activation model, in which the ratio 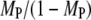tracks the overall rate of Ras-GTP generation (Data S2), the spatial coupling effect is magnified at lower N_Ras.

FIGURE 5.

Conditions promoting spatial coupling: diffusion-controlled capture of Ras-GTP by receptor-bound PI3K is essential, but receptor-bound GEF activity does not need to be diffusion-controlled. All parameter changes are relative to the base case, with parameter values from Table 1 and N_Ras = 1000. The black columns report the fraction of receptor/PI3K associations mediated by Ras, M_P. The two-tone columns report the overall rate of Ras-GTP production, normalized by the base-case value and broken down in terms of the contributions from receptor-bound GEF (gray) and cytosolic GEF (white).

In addition to the rate of Ras-GTP release, we also systematically varied those properties of PI3K that were not explored in Fig. 3: φ_RP, τ_RP, χ_P, and κ_P (Table 1). Varying φ_RP, for example by changing the concentration of PI3K in the cytosol, is relatively uninteresting (results not shown). It modulates the basal value of T_P but has a negligible effect on M_P, as PI3K binding to the receptor from the cytosol and Ras-mediated PI3K/receptor associations (dominated by rebinding events) are modulated in tandem. With φ_RP constant, a decrease in the value of τ_RP increases the rates of PI3K/receptor association and dissociation by the same factor. By increasing the “sampling” rate, M_P is significantly enhanced (Fig. 5). The basis for this enhancement is related to the probability that PI3K binds to a receptor from the cytosol while a GEF molecule is associated with the complex and actively producing Ras-GTP. Indeed, the coincidence ratio, C_EP, is much higher (∼2) than for the base case (∼1.4). The other parameters, χ_P and κ_P, directly affect the efficiency of capture/recapture and thus impact M_P in expected ways (Fig. 5). With κ_P = 1, the interactions are still partially diffusion-controlled, with an apparent capture efficiency of ∼40%, but this translates to an effective lifetime of the receptor/PI3K/Ras complex that is shorter by ∼20-fold ((1–0.4)/(1–0.97)); thus, PI3K recruitment is significantly reduced.

In contrast with the interactions involving PI3K, it is less critical that the action of receptor-bound GEF on Ras-GDP is diffusion-controlled, as modulated by the parameter κ_E (Fig. 5). When κ_E is reduced by 100-fold, with 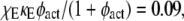the rate of Ras-GTP production by receptor-bound GEF is reduced by a factor of 13 compared with the diffusion-controlled value, and overall the rate of Ras-GTP production is reduced by a factor of almost 3. The value of M_P obtained in this case still clearly outperforms that of the bulk activation model, which, based on the change in Ras-GTP production rate, is ∼0.1. In this case, the Ras-GTP generated in the bulk membrane comprises ∼86% of the Ras-GTP, but the receptor-mediated contribution remains more important, because those Ras-GTP molecules are released locally. Comparison with the N_Ras = 100 case, which yields a similar value of M_P, but with a much lower rate of Ras-GTP produced in the “bulk” membrane, confirms this interpretation.

These results demonstrate that the degree to which PI3K interactions at the membrane are diffusion-controlled matters, because it affects the capture of Ras-GTP produced by receptor-bound GEF and, more importantly, the average number of recapture events. The degree of diffusion control in the interaction of receptor-bound GEF with Ras-GDP, on the other hand, influences PI3K recruitment only to the extent that it affects the rate of Ras-GTP release from the receptor complex.

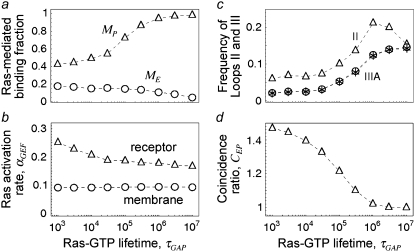
How effective is GAP activity in regulating Ras/PI3K crosstalk?

In the context of our model, GAP activity determines the lifetime of Ras-GTP, embodied in the parameter τ_GAP, which affects PI3K by modulating the spatial range of Ras-GTP released by receptor-bound GEF. This parameter was varied to assess its impact on Ras/PI3K crosstalk (Fig. 6). As one might expect, increasing this lifetime has a positive effect on T_P and M_P (Fig. 6 a). A simple explanation is that the total number of Ras-GTP particles in the system is increased; however, in quantitative terms, it is apparent that the sensitivities of the various metrics to changes in τ_GAP are relatively modest. For example, as the value of τ_GAP is increased over four logs, there is an ∼30% reduction in the Ras activation rate (α_GEF) mediated specifically by receptor-bound GEF (Fig. 6 b), in addition to a constant background value from binding of cytosolic GEF. This dependence is well understood from, and is in quantitative agreement with, the continuum theory (21,23). In the low τ_GAP limit, with the vast majority of Ras particles GDP-bound, increasing τ_GAP from 10³ to 10⁴ yields an overall change in the average number of receptor-generated Ras-GTP particles of approximately eightfold. By comparison, the ratio of Ras/PI3K versus cytosolic PI3K binding to receptor sites, 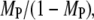increases by only ∼30%, in conjunction with the frequency of Loop IIIA recapture events (Fig. 6 c). In the large τ_GAP limit, we note that most of the Ras particles are in the GTP-bound form, even when GEF is not bound. Accordingly, capture of Ras-GTP from the bulk becomes more prominent (with T_P approaching the value calculated from the bulk activation model (results not shown)), and the interactions of GEF and PI3K with the receptor are uncorrelated in this limit (C_EP ≈ 1, Fig. 6 d). This situation mimics the action of oncogenic, GTPase-deficient Ras mutants such as G12V and Q61L.

FIGURE 6.

Reducing GAP-accelerated conversion of Ras-GTP to Ras-GDP enhances PI3K recruitment but not in proportion to the overall increase in Ras-GTP. The influence of the Ras-GTP lifetime, τ_GAP, on receptor-mediated PI3K recruitment was assessed. Other relevant parameters were set to their base-case values (Table 1), and N_Ras = 1000. (a) Fraction of receptor/PI3K associations mediated by Ras, M_P. (b) Dimensionless rate of Ras activation, α_GEF. (c) Frequencies of Loops II and IIIA as depicted in Fig. 1 c. Asterisk symbols indicate the frequency of Loop IIIB multiplied by the ratio τ_SP/τ_RP = 0.01. (d) Coincidence ratio for simultaneous GEF and PI3K binding to the receptor, C_EP.

We conclude that GAP regulation of Ras, which dictates the size of the Ras-GDP depletion/Ras-GTP enrichment zone, predominantly affects long-range interactions. Provided that most of the total Ras remains in the GDP-bound state, it matters little whether or not the Ras-GTP profiles surrounding neighboring receptor complexes partially overlap, because spatial coupling is dictated by processes that occur at a much smaller spatial range. This finding might attach additional importance to the direct binding of p120 RasGAP to PDGF receptors (2) and certain other tyrosine-phosphorylated receptors. We have performed simulations incorporating this effect, and the conclusions are fairly intuitive; by capturing and consuming Ras-GTP released by receptor-bound GEF, the rate of Ras-GTP release is effectively reduced (results not shown). The consequences of this finding for spatial coupling are well understood based on the analysis presented in the preceding sections.

DISCUSSION

Analysis of a Brownian dynamics model allowed us to characterize a potential mechanism for enhancing crosstalk between Ras and PI3K and other pairs of signaling proteins. The hallmark of this mechanism, termed spatial coupling, is that the receptor/scaffold engages an enzyme (GEF) that modifies a membrane-anchored molecule (Ras), which, in cooperation with the receptor or another member of the receptor complex, mediates the recruitment of a signaling protein with modular domains for interacting with both binding partners (PI3K). For the resulting effect on PI3K recruitment to be significant, it is important that the interactions at the membrane involving PI3K are diffusion-controlled. Thus, the assembly of receptor/PI3K/Ras complexes occurs through short-range capture of Ras-GTP, and, more importantly, the complexes are stabilized by serial recapture events. The results further suggest that what is important for Ras/PI3K crosstalk is not the whole-cell level of Ras-GTP, which often increases only modestly upon receptor stimulation, but rather the presence of GEF and PI3K in the same receptor complex and the rate of local Ras-GTP release. Put another way, spatial coupling effectively converts collisions between the receptor complex and Ras-GDP into opportunities for capture of Ras-GTP by PI3K, rather than relying on rare collisions with Ras-GTP diffusing from the bulk membrane.

Under certain conditions, the model predicts that the coincident interactions of GEF and PI3K with the same receptor scaffold are positively correlated, which might be important for spatially coordinating the functions and coregulation of the Ras and PI3K pathways. It could also form a basis for testing the spatial coupling hypothesis by experiment. In principle, one could estimate the quantitites that determine the coincidence metric, C_EP (Eq. 4), through quantitative cross-linking and immunoprecipitation or by comparing intensities of fluorescence resonance energy transfer between labeled binding partners in cells (68). These measurements are extraordinarily difficult, however, and it seems unlikely that three independently measured ratios could be reliably combined to estimate the value of C_EP at the requisite level of precision. A more sensible strategy might be to coexpress equal numbers of mutant receptors that lack the ability to bind Grb2-Sos or PI3K in cells, which would be expected to yield lower levels of PI3K signaling than in cells expressing the same number of wild-type receptors. The challenging aspect of this approach would be the need to establish equal numbers of Grb2-Sos and PI3K binding sites and confirm equal Ras-GTP loading across the two conditions.

Whereas enrichment of Ras-GTP in the vicinity of the receptor promotes Ras/PI3K crosstalk, we showed that it also negates the opportunity for stabilization of the receptor/GEF complex via association with Ras-GDP. It is interesting that in the case of the Ras-specific GEF Sos, structural and biochemical analyses have indicated that Sos also interacts with Ras-GTP via a distinct structural motif (69), an interaction not considered in the model presented here. In addition to enhancing the GEF activity allosterically, this interaction would tend to stabilize receptor/Grb2-Sos binding. Thus, localized release and capture of Ras-GTP might influence GEF recruitment in the same manner as postulated for PI3K, with one key difference: unlike receptor/PI3K binding, receptor/GEF binding is perfectly correlated with local production of Ras-GTP.

Although we have focused this study on mechanisms of Ras/PI3K crosstalk, many other signaling processes could be facilitated by short-range interactions that result in the cooperative assembly of multimolecular complexes at the plasma membrane. Just as the modification of membrane-anchored molecules by receptor-binding enzymes is a common theme in signal transduction, we find it plausible that the spatial coupling of different enzyme recruitment events, mediated by otherwise independent binding sites on the same receptor, adaptor, or scaffold protein, is a prominent mechanism for the propagation of specific signaling pathways and interpathway crosstalk. In addition to the receptor/PI3K/Ras system analyzed here, other complexes that might form in a similar fashion include receptor/Gab1/PI(3,4,5)P₃, focal adhesion complex/PI3K/Rac, and Git1/Pak/Rac.

This model invokes a number of simplifying assumptions, which can be relaxed as needed in the Brownian dynamics framework. Arguably, the most significant limitation of the model is that it does not consider the compartmentalization of the plasma membrane. The lateral mobilities of Ras and other membrane-anchored molecules are much faster on the microscopic scale than on the macroscopic scale, in a manner consistent with hop diffusion of Ras between adjacent corrals (39,40). We have previously suggested that this is a mechanism by which Ras-GTP might be concentrated for enhanced formation of receptor/PI3K/Ras complexes (25). Roughly speaking, this scenario leads to a situation in which the “complex” releasing and capturing Ras-GTP and Ras/PI3K is not the activated receptor, but rather the entire corral containing the receptor. We are currently analyzing the quantitative implications of this. A complete model might also consider the clustering of Ras-GTP at the plasma membrane, which seems to be mediated by interactions with galectin proteins (70). Clearly, the organization of the plasma membrane and membrane-anchored proteins is a complex and important layer of spatial control in receptor-mediated signal transduction that warrants further characterization through biophysical experiments and modeling.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.