A fast near-field method for calculations of time-harmonic and transient pressures produced by triangular pistons

Abstract

Analytical expressions are demonstrated for fast calculations of time-harmonic and transient near-field pressures generated by triangular pistons. These fast expressions remove singularities from the impulse response, thereby reducing the computation time and the peak numerical error with a general formula that describes the near-field pressure produced by any triangular piston geometry. The time-domain expressions are further accelerated by a time-space decomposition approach that analytically separates the spatial and temporal components of the numerically computed transient pressure. Applied to a Hanning-weighted input pulse, time-space decomposition converts each spatio-temporal integral into six spatial integral evaluations at each field point. Time-harmonic and transient calculations are evaluated for an equilateral triangle with sides equal to four wavelengths, and the resulting errors are compared to pressures obtained with exact and approximate implementations of the impulse response method. The results show that the fast near-field method achieves smaller maximum errors and is consistently faster than the impulse response and methods that approximate the impulse response.

I. INTRODUCTION

As increasingly complex transducer geometries are adopted for emerging applications of ultrasound imaging and therapy, new methods are needed for rapid calculations of pressure fields produced by these transducers. Fast numerical calculations are especially important for simulations of phased array structures containing hundreds or thousands of transducers that generate pressures in large computational domains. Simulation methods that either directly evaluate the impulse response^1-4 or subdivide each transducer into smaller subelements and then superpose the pressure^5,6 provide a convenient model for these calculations, but in the near-field region, the convergence of these methods is relatively slow.⁷ Furthermore, numerical implementations of the impulse response for flat unfocused transducers encounter some difficulties throughout the paraxial region.^8-10

The numerical problems with the impulse response are eliminated with the fast near-field method (FNM) defined previously for circular⁹ and rectangular¹⁰ sources. The FNM also reduces the numerical error and the computation time relative to calculations that employ the impulse response. Further reductions in the computation time with FNM expressions are achieved through a time-space decomposition approach that separates the temporal and spatial components for transient pressure calculations.⁷ The resulting expressions contain a small number of spatial integrals that are evaluated numerically and then multiplied by analytical temporal terms. The time-space decomposition approach applied to a circular piston accelerates transient pressure calculations by exploiting the structure of the FNM integral, achieving the same numerical error as the impulse response in much less time.

The substantial reduction in computation time demonstrated by the FNM for calculations of near-field pressures generated by circular and rectangular pistons motivates the derivation of similar integral expressions for triangular sources. After the impulse response is obtained for right, acute, and obtuse triangular sources, general FNM expressions for time-harmonic and transient inputs are then demonstrated for a triangular source, and the time-space decomposition of the FNM integral is presented for a transient excitation. Based on these expressions for the near-field pressure generated by a triangular source, computation times are evaluated for the same peak numerical errors. For time-harmonic inputs applied to a triangular source, results show that FNM calculations are several times faster than both exact and approximate impulse response calculations, and for pulsed excitations, results demonstrate that FNM calculations performed with time-space decomposition are also much faster than exact and approximate impulse response calculations for triangular piston geometries.

II. TIME-HARMONIC AND TRANSIENT NEAR-FIELD PRESSURE CALCULATIONS FOR TRIANGULAR SOURCES

A. Impulse response calculations for a triangular source

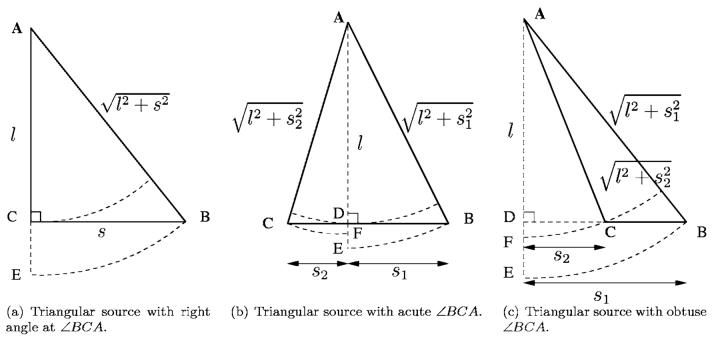
The geometry for a right triangular source with a right angle ∠BCA at vertex C is depicted in Fig. 1(a). For this right triangle and the triangles in Figs. 1(b) and 1(c), the impulse response is evaluated at a point directly over the vertex A (indicated in bold in Fig. 1), where the orthogonal projection of the observation point onto the source plane is exactly coincident with the vertex A, and the distance from the observation point to the source plane along this orthogonal projection is represented by the variable z. In Fig. 1(a), the acute angle ∠CAB=tan⁻¹ (s/l) defines the angular extent of sector EAB with radius $\sqrt{l^2+s^2}$, which has an impulse response of c/(2π) tan⁻¹(s/l) for $(z∕c)\le t\le \sqrt{z^2+l^2+s^2}∕c$. The impulse response for the right triangle ΔABC contained within the sector EAB is obtained by subtracting the impulse response of the region ECB between the curved outer edge of the sector and the near edge of the right triangle so that only the contribution from the right triangle ΔABC remains. The impulse response of the region ECB is $c∕\left(2\pi \right){\cos }^{-1}(l∕\sqrt{c^2{t}^2-z^2})$ for $\sqrt{z^2+l^2}∕c\le t\le \sqrt{z^2+l^2+s^2}∕c$, and therefore the impulse response at an orthogonal distance z above the vertex A is

FIG. 1.

Triangular source geometries defined for near-field pressure calculations. The near-field pressure is evaluated above the vertex A (indicated in bold), and the shape of the triangle (right, acute, or obtuse) is defined by the angle ∠BCA. The height of each triangle is indicated by l, and the bases of the individual right triangles are indicated by s, s₁, and s₂. The acute triangle in (b) is represented by the sum of two right triangles, and the obtuse triangle in (c) is defined as the difference between two right triangles.

$$h_{\text{right}}(z;t)=\{\begin{array}{cc}c∕\left(2\pi \right){\tan }^{-1}(s∕l)\hfill & \text{for}\frac{z}{c}\le t\le \frac{\sqrt{z^2+l^2}}{c}\hfill \\ c∕\left(2\pi \right)\left\{{\tan }^{-1}(s∕l)-{\cos }^{-1}\frac{l}{\sqrt{c^2{t}^2-z^2}}\right\}\hfill & \text{for}\frac{\sqrt{z^2+l^2}}{c}\le t\le \frac{\sqrt{z^2+l^2+s^2}}{c}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (1)

For other triangular sources, the impulse response is readily constructed from the sum or difference between two right triangles. Figure 1(b) contains an example of a triangular source with an acute angle ∠BCA at vertex C. The expression for the impulse response evaluated at a point directly over the vertex A is obtained by evaluating the sum of the contributions from the right triangles ∠CDA and ∠BDA, each with a right angle at vertex D. The resulting impulse response above the vertex A in Fig. 1(b) is represented by

$$h_{\text{sum}}(z;t)=\{\begin{array}{cc}c∕\left(2\pi \right)\left\{{\tan }^{-1}(s_1∕l)+{\tan }^{-1}(s_2∕l)\right\}\hfill & \text{for}\frac{z}{c}\le t\le \frac{\sqrt{z^2+l^2}}{c}\hfill \\ \frac{c}{2\pi }\left\{{\tan }^{-1}(s_1∕l)+{\tan }^{-1}(s_2∕l)-2{\cos }^{-1}(l∕\sqrt{c^2{t}^2-z^2})\right\}\hfill & \text{for}\frac{\sqrt{z^2+l^2}}{c}\le t\le \frac{\sqrt{z^2+l^2+s_2^2}}{c}\hfill \\ c∕\left(2\pi \right)\left\{{\tan }^{-1}(s_1∕l)-{\cos }^{-1}(l∕\sqrt{c^2{t}^2-z^2})\right\}\hfill & \text{for}\frac{\sqrt{z^2+l^2+s_2^2}}{c}\le t\le \frac{\sqrt{z^2+l^2+s_1^2}}{c},\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (2)

where the values of s₁ and s₂ are selected such that s₁ ≥ s₂.

Similarly, Fig. 1(c) contains an example of a triangular source with an obtuse angle ∠BCA at vertex C, where the impulse response is again evaluated at a point directly over the vertex A, but the impulse response is instead evaluated for the difference between two right triangles. The impulse response for the triangle in Fig. 1(c) is

$$h_{\text{diff}}(z;t)=\{\begin{array}{cc}c∕\left(2\pi \right)\left\{{\tan }^{-1}(s_1∕l)-{\tan }^{-1}(s_2∕l)\right\}\hfill & \text{for}\frac{z}{c}\le t\le \frac{\sqrt{z^2+l^2+s_2^2}}{c}\hfill \\ c∕\left(2\pi \right)\left\{{\tan }^{-1}(s_1∕l)-{\cos }^{-1}(l∕\sqrt{c^2{t}^2-z^2})\right\}\hfill & \text{for}\frac{\sqrt{z^2+l^2+s_2^2}}{c}\le t\le \frac{\sqrt{z^2+l^2+s_1^2}}{c}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}},$$ (3)

where the values of s₁ and s₂ are selected such that s₁ > s₂.

1. Time-harmonic impulse response calculations

The time-harmonic pressure generated by these triangular source geometries is proportional to the Fourier transform of the impulse response. Therefore, the formula for the time-harmonic pressure generated by the right triangle in Fig. 1(a) is

$$P_{\text{right}}(z;k)=\frac{\omega {\rho }_{0}v{e}^{j\omega t}}{2\pi }\left\{\frac{j}{k}{\tan }^{-1}\frac{s}{l}{e}^{-\mathit{jkz}}-\frac{j}{k}{\tan }^{-1}\frac{s}{l}{e}^{-\mathit{jk}\sqrt{z^2+l^2+s^2}}+{\int }_{\sqrt{z^2+l^2}}^{\sqrt{z^2+l^2+s^2}}{e}^{-\mathit{jk}\beta }{\cos }^{-1}\frac{l}{\sqrt{{\beta }^2-z^2}}d\beta \right\}.$$ (4)

The time-harmonic pressures that are produced by the remaining triangles depicted in Figs. 1(b) and 1(c) are obtained by adding and subtracting the contributions of two right triangles, as for calculations of the impulse response in Eqs. (2) and (3), respectively.

2. Transient impulse response calculations

Transient near-field pressures are computed with the impulse response through the convolution

$$p(z;t)={\rho }_0\stackrel{.}{v}\left(t\right)\otimes h(z;t),$$ (5)

where the time derivative of the particle velocity $\stackrel{.}{v}\left(t\right)$ is evaluated analytically from the excitation pulse v(t), and the convolution ⊗ is evaluated with the fast Fourier transform (FFT). In particular, the discrete Fourier transforms of $\stackrel{.}{v}\left(t\right)$ and h(z,t) are computed with the FFT, the results are multiplied, and the inverse FFT is applied to the product. The forward and inverse FFT routines are computed with the Fastest Fourier Transform in the West (FFTW) library.¹¹

3. FIELD II

FIELD II is a software package¹² that computes the impulse response either by superposing far-field contributions from small rectangles or by evaluating expressions similar to Eqs. (1)-(3). With both approaches, FIELD II modifies the impulse response according to the area under the impulse response curve.¹³ This modification allows FIELD II to reduce the temporal sampling for impulse response calculations, which are directly applicable to transient and steady-state near-field pressure computations.

4. Smoothed impulse response

The Fourier transform of Eq. (5) is

$$P(z;\omega )=j\omega {\rho }_{0}V\left(\omega \right)H(z,\omega ).$$ (6)

Normally, the excitation v(t) is bandlimited, so the high-frequency components in the Fourier transform V(ω) are negligible. To exploit the bandlimited characteristics of the excitation v(t), the formula for a smoothed impulse response is given by¹⁴

$$h_{\text{smooth}}(z;t)=\frac{O\left(c(t+\Delta t∕2)\right)-O\left(c(t-\Delta t∕2)\right)}{2\pi \mathit{tc}\Delta t},$$ (7)

where O(ct) is the area that is formed by the intersection of the transducer and the sphere with radius ct centered at the observation point, and Δt is the length of the rectangular pulse that smooths the analytical impulse response. The constraint

$$f_{E\max }<\frac{1}{\Delta t}$$ (8)

insures proper smoothing, where f_Emax is the highest-frequency component of the excitation pulse, and Δt=0.02 μs in the simulations that follow. The result obtained from Eq. (7) is then directly applied to calculations of the near-field pressure for time-harmonic and transient inputs.

B. The fast near-field method for a triangular source

Integral expressions that describe the fast near-field method (FNM) for a triangular source excited by a time-harmonic input are obtained by replacing the inverse cosine term with the integral form of the inverse tangent and then exchanging the order of integration in the impulse response expressions for right, acute, and obtuse triangles. After defining a new variable of integration and subtracting the singularity at z=0 from each integrand, the resulting FNM expression for a right triangle [Fig. 1(a)], the sum of two right triangles [Fig. 1(b)] that share a common side of length l, and the difference between two right triangles [Fig. 1(c)] that share a common side of length l is

$$P(z;k)=-\frac{\rho {\mathit{cve}}^{j\omega t}}{2\pi }{\int }_{x_C}^{x_B}\frac{l}{{\sigma }^2+l^2}\times (e^{-\mathit{jk}\sqrt{{\sigma }^2+z^2+l^2}}-e^{-\mathit{jkz}})d\sigma ,$$ (9)

where l represents the height of the triangle, and x_B and x_C represent the x coordinates of B and C, respectively. In Figs. 1(a)-1(c), the values of (x_B,x_C) are (s,0), (s₁,−s₂), and (s₁,s₂), respectively. Thus, a single FNM expression represents all three triangle geometries in Fig. 1, whereas the impulse response requires a separate expression for each triangle in Fig. 1.

1. Transient FNM calculations

The inverse Fourier transform of Eq. (9) generates the FNM expression for the transient response. The transient pressure generated by a triangular source above the vertex A is represented by

$$p(z;t)=-\frac{\rho c}{2\pi }{\int }_{x_C}^{x_B}\frac{l}{l^2+{\sigma }^2}\times \left[v\left(t-\frac{1}{c}\sqrt{z^2+{\sigma }^2+l^2}\right)-v(t-z∕c)\right]d\sigma ,$$ (10)

where the transient excitation is represented by v(t). By retaining the v(t−z/c) term within the integral and subtracting the singularity, Eq. (10) maintains the rapid rate of convergence achieved for time-harmonic calculations with Eq. (9).

2. Time-space decomposition

Transient FNM computations are accelerated by decoupling the temporal and spatial dependence of Eq. (10). The time-space decomposition approach, demonstrated previously for a circular source,⁷ expands the delayed input pulse v(t−τ) in terms of temporal weighting functions g_n(t) and spatially dependent terms f_n(τ) that depend only on the coordinates of the observation point and the variable of integration σ through $\tau =(1∕c)\sqrt{z^2+{\sigma }^2+l^2}$. The decoupled input pulse is thus represented by

$$v(t-\tau )=\mathrm{rect}\left(\frac{t-\tau }{W}\right)\underset{n=1}{\overset{N}{\Sigma }}{f}_n\left(\tau \right)g_n\left(t\right),$$ (11)

where the time duration of the pulse is indicated by the parameter W. The decomposed pulse in Eq. (11) is then inserted into Eq. (10), and then time-dependent terms are factored out of the integral. The result consists of N edge wave terms specified by

$$E_n=-\frac{\rho c}{2\pi }l{\int }_{x_C}^{x_B}\frac{f_n\left(\tau \right)}{{\sigma }^2+l^2}\mathrm{rect}\left(\frac{t-\tau }{W}\right)d\sigma$$ (12)

and a direct wave term given by

$$D=-\frac{\rho c}{2\pi }v(t-z∕c)l{\int }_{x_C}^{x_B}\frac{1}{{\sigma }^2+l^2}d\sigma .$$ (13)

The temporal dependence of the edge wave integrand in Eq. (12) is eliminated when the effect of the rect function is instead shifted to the limits of integration. This operation, which restricts the edge wave contributions by only considering those that have reached the observation point without completely passing the observation point, completely removes all temporal variables from the integrand. As a result, calculations of transient pressure fields are converted into the numerical evaluation and subsequent superposition of N spatial integrals that are weighted by analytical time-dependent terms. Further reduction in the computation time is achieved by storing redundant edge wave calculations from Eq. (12) in the matrix

$$K_n(i,j)=\underset{m=i}{\overset{j}{\Sigma }}{w}_m\frac{f_n\left(\tau \left[{\sigma }_m\right]\right)}{{\sigma }_m^2+l^2}.$$ (14)

In Eq. (14), w_m represents the weights and σ_m represents the abscissas computed for Gauss quadrature, the value of τ[σ_m] is obtained from the relation $\tau \left[{\sigma }_m\right]=(1∕c)\sqrt{z^2+{\sigma }_m^2+l^2}$, and the indices i and j indicate the shortest and longest times that correspond to the limits of integration. The values K_n(i,j) are initialized within the computation procedure only for the points that are needed, and then the time-space decomposition calculations superpose the numerically computed results of the spatial integrals with analytical time-dependent weighting factors to achieve a significant reduction in computation time for transient pressure calculations in the near-field region.

C. Superposition calculations with impulse response and FNM expressions

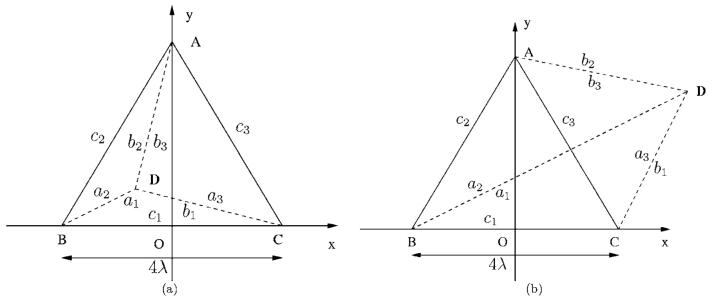
At observation points away from the normal that passes through a vertex of the triangular source, impulse response and FNM calculations project the observation point onto the source plane and then superpose the contributions from two or three triangles as in Fig. 2. The contributions from three triangles are either added, as shown in Fig. 2(a) for an observation point within the lateral extent of the source triangle ΔABC, or added and subtracted as demonstrated in Fig. 2(b) for an observation point outside of the lateral extent of the source triangle. Whether a contribution is added or subtracted depends on the location of the projected observation point in the source plane relative to each side of the triangular source.

FIG. 2.

Superposition operations that calculate near-field pressures generated by the equilateral triangular source ABC, where each side is 4 wavelengths long. The vertex D (indicated in bold) is the projection of the observation point onto the source plane, which partitions the radiating source into three triangles with sides (a_i,b_i,c_i). (a) The field point is located inside of the equilateral triangular source, and the total field is obtained by adding the contributions from the three triangles that share a vertex at D. (b) The field point is located outside of the equilateral triangular source, and the total pressure is obtained by adding and subtracting the contributions from the three triangles that share a vertex at D.

The FNM admits some additional simplifications for near-field calculations of pressures generated by the triangle ΔABC in Fig. 2. If the three lines that are coincident with the three sides of the source triangle ΔABC are defined in the general form E_ix+F_iy+G_i=0, then the distances from the projected observation point to each of the three sides are represented by $l_i=|E_{i}x+F_{i}y+G_i|∕\sqrt{E_i^2+F_i^2}$. Likewise, the sign of each contribution is defined as $S_i=(E_{i}x+F_{i}y+G_i)∕|E_{i}x+F_{i}y+G_i|$ for coefficients E_i, F_i, and G_i chosen such that S_i is positive within the lateral extent of the source ΔABC. Furthermore, the lower and upper limits of integration are defined as $(a_i^2-b_i^2-c_i^2)∕\left(2c_i\right)$ and $(a_i^2+c_i^2-b_i^2)∕\left(2c_i\right)$, respectively. The resulting near-field pressure generated by ΔABC in Fig. 2 is therefore represented by

$$P(x,y,z;k)=-\frac{\rho {\mathit{cve}}^{j\omega t}}{2\pi }\underset{i=1}{\overset{3}{\Sigma }}\left(\frac{E_{i}x+F_{i}y+G_i}{\sqrt{E_i^2+F_i^2}}\times {\int }_{\frac{a_i^2-b_i^2-c_i^2}{2c_i}}^{\frac{a_i^2+c_i^2-b_i^2}{2c_i}}\frac{e^{-\mathit{jk}\sqrt{{\sigma }^2+z^2+l_i^2}}-e^{-\mathit{jkz}}}{{\sigma }^2+l_i^2}d\sigma \right).$$ (15)

Calculations with Eq. (15) compute the values of c_i, E_i, F_i, and G_i only once for each edge of ΔABC, whereas the values of a_i and b_i are calculated once for each (x,y) pair. Unlike the expressions for the impulse response that change depending on the spatial coordinate, Eq. (15) is a general formula that computes the near-field pressure with a single expression that is valid at all points in space.

D. Transient input waveform

Evaluations of the impulse response and the FNM with time-space decomposition are performed for the Hanning-weighted pulse specified by

$$v\left(t\right)=\frac{1}{2}[1-\cos (2\pi t∕W)]\sin \left(2\pi f_{0}t\right)\mathrm{rect}(t∕W),$$ (16)

where rect(t)=1 if t ∈[0,1] and rect(t)=0 otherwise. In the simulations that follow, the input is a Hanning-weighted pulse with center frequency f₀=2 MHz and pulse duration W=1.5 μs. Time-space decomposition performed on this pulse with N=6 yields the entries in Table I, where the spatial edge wave integral in Eq. (12) is evaluated once for each row entry applied to each edge of the source triangle ΔABC in Fig. 2, and then the results are weighted by the temporal basis functions in Table I.

TABLE I.

Basis functions for time-space decomposition with a Hanning-weighted pulse.

Temporal basis functions gn(t)	Spatial basis functions fn(τ)
g1(t)= 1/2 sin(2πf0t)	f1(τ)=cos(2πf0τ)
g2(t)=−1/2 cos(2πf0t)	f2(τ)=sin(2πf0τ)
g3(t)=−1/2 cos(2πt/W)sin(2πf0t)	f3(τ)=cos(2πτ/W)cos(2πf0τ)
g4(t)= 1/2 cos(2πt/W)cos(2πf0t)	f4(τ)=cos(2πτ/W)sin(2πf0τ)
g5(t)= - 1/2 sin(2πt/W)sin(2πf0t)	f5(τ)=sin(2πτ/W)cos(2πf0τ)
g6(t)= 1/2 sin(2πt/W)cos(2πf0t)	f6(τ)=sin(2πτ/W)sin(2πf0τ)

E. Error calculations

For time-harmonic near-field pressure calculations, the numerical error η(x,y,z) is defined as the normalized difference between the reference field and the computed field according to

$$\eta (x,y,z)=\frac{|P(x,y,z)-P_{\mathrm{ref}}(x,y,z)|}{\max \left|P_{\mathrm{ref}}(x,y,z)\right|},$$ (17)

where P_ref(x,y,z) is the reference time-harmonic near-field pressure. For transient near-field pressure calculations, the numerical error η(x,y,z) between the computed transient field and the reference transient field is defined by

$$\eta (x,y,z)=\frac{\parallel p(x,y,z;t)-p_{\mathrm{ref}}(x,y,z;t)\parallel }{{\max }_{x,y,z}\parallel p_{\mathrm{ref}}(x,y,z;t)\parallel },$$ (18)

where ‖·‖ denotes the energy norm with respect to time, and p_ref(x,y,z;t) is the reference transient pressure field as a function of time. The maximum error is defined as η_max=max_x,y,zη(x,y,z), and this value is computed for both time-harmonic and transient excitations.

III. RESULTS

All simulation programs are written in C, then compiled and executed within a matlab-c language MEX interface. The simulations are performed on an eMachines T3958 personal computer with a 2.93-MHz Celeron D processor. The operating system on this computer is Fedora Core 3 Linux. All simulations are run sequentially under similar operating conditions.

A. Time-harmonic near-field pressure calculations

1. Reference pressure distribution

The reference pressure field is computed in Fig. 3 for an equilateral triangular source with sides equal to 4 wavelengths. In Fig. 3, the acoustic field is evaluated in the x=0 plane defined in Fig. 2. The reference near-field pressure distribution in Fig. 3 is obtained when the impulse response is calculated for all triangles with 100 000-point Gauss quadrature. This pressure distribution is selected as the reference because near-field pressures computed with 100 000 abscissas produce normalized errors that converge to 15 significant digits throughout the near-field region, which represents the smallest error achievable with double-precision arithmetic.

FIG. 3.

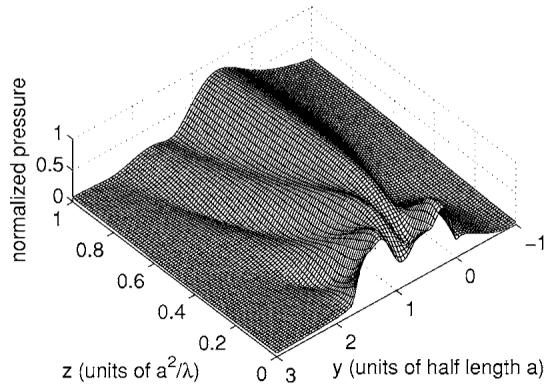
Simulated time-harmonic pressure field in the x=0 plane for an equilateral triangular source with sides equal to 4 wavelengths. The reference field is generated by the impulse response method computed with 100 000-point Gauss quadrature.

2. FNM and impulse response calculations

The numerical errors and computation times for the fast near-field method and the impulse response method are shown in Fig. 4. For the FNM, the exact impulse response, and FIELD II with “use_triangles,” near-field pressures are evaluated in an 81×101-point grid in the x=0 plane as shown in Fig. 3. FIELD II with “use_rectangles” and the smoothed impulse response require an offset due to a singularity on the piston face and are therefore evaluated on a smaller 81×86-point grid. The FNM and the exact impulse response are evaluated with Gauss quadrature, and all three integrals corresponding to the three sides of the source triangles are evaluated with the same number of abscissas. The remaining methods that approximate the uniformly sampled impulse response (i.e., FIELD II and the smoothed impulse response) are evaluated with the midpoint rule as described in the user's guide on the FIELD II website (http://www.es.oersted.dtu.dk/staff/jaj/field/). Figure 4 shows that the error for a given computation time is consistently smaller with the FNM, where smaller errors are located nearer to the horizontal axis on the bottom of this log-log plot. Likewise, the time required to achieve a given error is consistently smaller with the FNM, since the FNM plot is consistently located to the left of the impulse response plot.

FIG. 4.

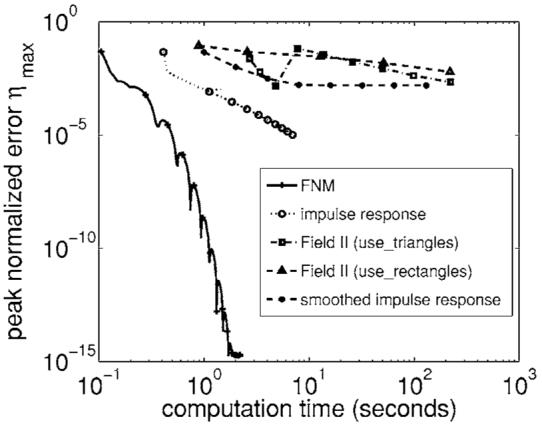
Peak normalized error for calculations of near-field pressures generated by the triangular source in Fig. 2 plotted as a function of the computation time. The results show that the FNM consistently achieves smaller errors in less time than exact and approximate impulse response calculations for time-harmonic excitations.

Comparisons between the impulse response and the FNM evaluated for the same peak error are summarized in Table II. For a 10% peak error, the FNM is 4.39 times faster than the impulse response, and for a 1% peak error, the FNM is 3.44 times faster than the impulse response for this grid and piston geometry. Even greater improvements are observed for smaller peak error values due to the rapid convergence of the FNM. Although these values change somewhat for different source and grid geometries, the FNM is consistently faster than the exact and the approximate impulse response for near-field calculations of time-harmonic pressures.

TABLE II.

Number of Gauss abscissas, computation times, and time ratios that describe the reduction in the computation time achieved with the fast near-field method relative to the impulse response and methods that approximate the impulse response for peak errors of 10% and 1%. The FNM and exact impulse response results are evaluated for time-harmonic calculations on a 81×101-point grid located in the x=0 plane, and the FIELD II and smoothed impulse response results are evaluated on an 81×86-point grid in the x=0 plane that is slightly offset from the transducer face.

	Time-harmonic Near-field computations
	10% peak error				1% peak error
	FNM	Impulse response	FIELD II use_triangles	Smoothed  impulse  response	FNM	Impulse response	FIELD II use_triangles	Smoothed  impulse  response
Parameters	N=8	N=11	fs=16 MHz	fs=32 MHz	N=11	N=12	fs=32 MHz	fs=128 MHz
Time	0.0938 s	0.4112 s	2.7212 s	1.0051 s	0.1286 s	0.4419 s	3.3993 s	4.0130 s
Time ratio	1	4.39	29.02	10.72	1	3.44	26.43	31.21

3. FIELD II calculations

The FIELD II simulation program¹² includes the “use_triangles'” option for calculations that model rectangular and triangular pistons as the superposition of triangular sources. For calculations of time-harmonic pressures with the “use_triangles” option applied to the source geometry in Fig. 2, FIELD II requires a temporal sampling frequency of f_s=16 MHz to achieve a peak error of 10%. The computation time for FIELD II with “use_triangles” is 29.02 times slower than the FNM evaluated on the same grid. For time-harmonic calculations, FIELD II with the “use_triangles” option requires a temporal sampling frequency of f_s=32 MHz to achieve a peak error of 1%. This results in a computation time that is 26.43 times longer than that required for the FNM evaluated on the same grid.

FIELD II also provides a “use_rectangles” option that introduces a numerical singularity on the piston surface, so the pressure is evaluated on a smaller 81×86-point spatial grid that is offset from the piston face. FIELD II with “use_rectangles” evaluated on this reduced grid produces a 10% peak error in 0.8908 s, which is 9.5 times slower than the FNM on the full 81×101-point grid. For a 1% peak error, FIELD II with “use_rectangles” computes the result on the restricted grid in 218.2492 s, which is 1697 times slower than the FNM evaluated on the full grid. Only the four fastest methods (on average) are tabulated, so the FIELD II “use_rectangles” calculation results are plotted in Fig. 4 but not included in Table II.

4. Smoothed impulse response calculations

Time-harmonic calculations with the smoothed impulse response¹⁴ evaluate the pressure on a smaller 81×86-point spatial grid that is offset from the piston face. The offset is required for smoothed impulse response calculations so that the singularity in Eq. (7) on the piston face is avoided. For calculations of the time-harmonic pressure generated by the triangular source depicted in Fig. 2 and evaluated within an 81×86-point subset of the grid shown in Fig. 3, the smoothed impulse calculation converges to a peak error of 10% with a temporal sampling rate of f_s=32 MHz. This computation is completed in 1.0105 s, which is 10.74 times longer than the time required for the corresponding FNM calculation evaluated on a larger 81×101-point spatial grid. Time-harmonic calculations with the smoothed impulse response achieve a peak error of 1% for a temporal sampling rate of f_s=128 MHz. This computation is completed in 3.9983 s, which is 31.26 times longer than the time required to obtain the FNM result with 1% peak error in Table II.

B. Transient near-field pressure calculations

1. Reference pressure distribution

The reference near-field pressure distribution for transient excitations is calculated with impulse response waveforms that are sampled at f_s=524.288 GHz, zero padded, and convolved with FFTs. The resulting temporal variations in the near-field pressure, which are evaluated for an equilateral triangular piston with 4 wavelengths on each side, are then downsampled and stored at f_s=16 MHz. The reference field is calculated for a sound speed of c=1.5 mm/μs on an 81×101-point spatial grid evaluated at 85 time points, and the result at time t=1.8125 μs is shown in Fig. 5. This error reference is accurate to five significant digits for calculations in the x=0 plane.

FIG. 5.

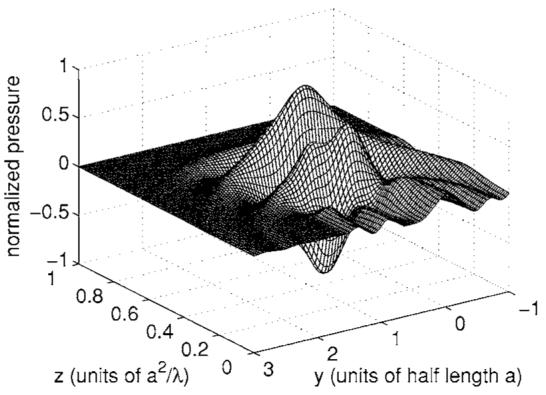
Simulated transient pressure field in the x=0 plane for an equilateral triangular source with sides equal to 4 wavelengths. For this calculation, the excitation is the Hanning-weighted pulse in Eq. (16), and the transient pressure is evaluated at 85 time points in an 81×101-point grid. The result is plotted at 1.8125 μs after the initiation of the input pulse.

2. FNM and impulse response calculations

Figure 6 plots the numerical error as a function of the computation time for the FNM with time-space decomposition and calculations based on the impulse response method. All methods, except for FIELD II with “use_rectangles” and the smoothed impulse response, are evaluated relative to an 81×101-spatial point reference transient pressure distribution computed at 85 time points. FIELD II with “use _rectangles” and the smoothed impulse response are singular at the piston face, so a smaller 81×86-point spatial grid that incorporates an offset from the piston face is again required for transient field computations. The input for the reference is generated by a Hanning-weighted pulse with a center frequency of f₀=2 MHz. The transient near-field pressures are compared for f_s=16 MHz, which is the original sampling rate for the FNM calculations and the resulting rate after downsampling for impulse response calculations. Figure 6 shows that the FNM with time-space decomposition is consistently faster than the impulse response and the methods that approximate the impulse response. Similarly, Fig. 6 indicates that the FNM with time-space decomposition achieves much smaller numerical errors than the impulse response and approximations to the impulse response.

FIG. 6.

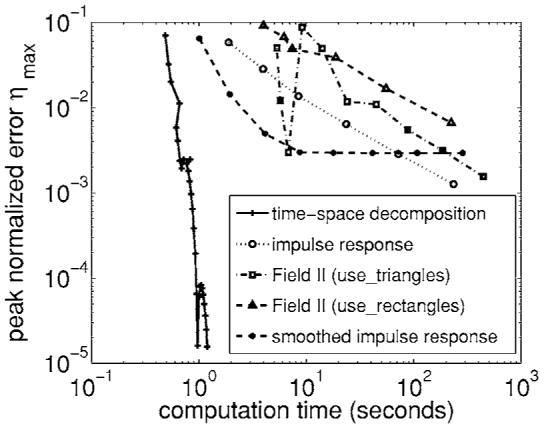
The peak normalized error plotted as a function of the computation time for the FNM/time-space decomposition method, the impulse response method, and methods that approximate the impulse response. These errors and times are evaluated for transient near-field calculations of an equilateral triangular source with sides equal to 4 wavelengths. The excitation for these calculations is a Hanning-weighted pulse with a center frequency of 2 MHz.

Table III shows that the FNM with time-space decomposition achieves a 10% peak error with five Gauss abscissas in 0.4867 s. To achieve a 1% peak error, the FNM with time-space decomposition needs nine Gauss abscissas and the computation time is 0.6160 s. In contrast, the impulse response method achieves a peak error of 10% with a sampling frequency of f_s=128 MHz in 1.8911 s. To achieve a peak error of 1%, the impulse response method requires a sampling frequency of f_s=1 GHz and a computation time of 23.5241 s. Thus, the reduction in the computation time with time-space decomposition applied to the FNM relative to the impulse response is a factor of 3.89 for a peak error of 10% and a factor of 38.19 for a peak error of 1%.

TABLE III.

Comparisons of computation times, input parameters, and time ratios that describe the reduction in the computation time achieved with the FNM and time-space decomposition relative to the exact and approximate impulse response for specified maximum errors of 10% and 1%. For FNM, impulse response, and FIELD II calculations with “use_triangles,” the transient results are evaluated in an 81×101-spatial point computed at 85 time points, and for the smoothed impulse response, the results are evaluated at the same temporal points in a restricted 81×86-point spatial grid.

	Transient Near-field computations
	10% peak error				1% peak error
	FNM	Impulse  response	FIELD II use_triangles	Smoothed impulse response	FNM	Impulse response	FIELD II use_triangles	Smoothed impulse response
Parameters	N=5	fs=128 MHz	fs=16 MHz	fs=32 MHz	N=9	fs=1 GHz	fs=64 MHz	fs=128 MHz
Time	0.4867 s	1.8911 s	5.3317 s	1.0122 s	0.6160 s	23.5241 s	6.8078 s	4.1261 s
Time ratio	1	3.89	10.95	2.08	1	38.19	11.05	6.70

3. FIELD II calculations

The FIELD II result obtained with the “use_triangles” option for the transient excitation in Eq. (16) requires a sampling frequency of f_s=16 MHz to achieve a peak error of 10%, and the computation time for this combination of parameters is 5.3317 s. For a peak error of 1%, FIELD II with the “use_triangles” option requires a sampling frequency of f_s=64 MHz, and the computation time is 6.8078 s. Therefore, the FNM with time-space decomposition is 10.95 times faster than FIELD II with “use_triangles” for a peak error of 10% and 11.05 times faster for a peak error of 1%.

Transient FIELD II calculations that subdivide the aperture into small rectangular sources with “use_rectangles” reach a peak error of 10% with a temporal sampling frequency of f_s=32 MHz in 3.9926 s. FIELD II with “use_rectangles” achieves a peak error of 1% with a temporal sampling frequency of f_s=48 MHz in 221.6569 s. Therefore, the FNM with time-space decomposition is 8.2 times faster than FIELD II evaluated with subdivided rectangular sources for a 10% peak error and 359.81 times faster than FIELD II evaluated with subdivided rectangular sources for a 1% peak error. As for the time-harmonic results shown in Table II, only the four fastest methods (on average) are tabulated, so FIELD II results obtained with “use_rectangles” are not included in Table III.

4. Smoothed impulse response calculations

Transient calculations with the smoothed impulse response in Eq. (7) evaluate the pressure at 85 time points on a smaller 81×86-point spatial grid that is offset from the piston face. The offset is required in order to avoid the singularity in Eq. (7) on the piston face. For calculations of the time-harmonic pressure generated by the triangular source depicted in Fig. 2 and evaluated within an 81×86-point subset of the grid shown in Fig. 3, the smooth impulse calculation converges to a peak error of 10% with a temporal sampling rate of f_s=32 MHz. This computation is completed in 1.0122 s, which is 2.08 times longer than the time required for the corresponding FNM calculation evaluated on a larger 81×101-point spatial grid. Time-harmonic calculations with the smoothed impulse response achieve a peak error of 1% for a temporal sampling rate of f_s=128 MHz. This computation is completed in 4.1261 s, which is 6.7 times longer than the time required to obtain the FNM result with 1% peak error in Table II.

IV. DISCUSSION

A. Time and error calculations

While computer processor speed and memory has increased substantially in recent decades, the size and complexity of ultrasound therapy and imaging simulations has grown accordingly. Simulations of large ultrasound therapy arrays are now applied to thousands of transducer elements and computational volumes spanning hundreds of wavelengths in three dimensions, and simulations of diagnostic imaging arrays have demonstrated a corresponding increase in the number of active elements and the number of scatterers. As a result, large simulations of ultrasound phased arrays can require 24 h or longer on modern computers.

For these large simulations, the evaluation of computational time and numerical error is essential. The computation time remains the primary bottleneck in these time-consuming calculations, but fair comparisons of computation time also require calculations of the numerical error. In recent years, evaluations of the numerical error have been neglected due to the slow convergence of the impulse response and methods that approximate the impulse response. Figures 4 and 6 demonstrate this slow convergence, which is further emphasized by the time-harmonic reference field that requires 100 000 Gauss abscissas for convergence to 15 significant digits and by the transient reference field that requires a sampling frequency of f_s=524.288 GHz for convergence to five significant digits.

The rapid convergence of the FNM demonstrated in Figs. 4 and 6 suggests that the FNM is ideal for calculating near-field pressure reference fields. In Fig. 4, time-harmonic FNM calculations converge within 15 significant digits in less than one-third of the time that the impulse response requires for convergence within five significant digits. Likewise, in Fig. 6, transient FNM calculations with time-space decomposition converges within five significant digits in less than one-fifth of the time that the impulse response requires for convergence within two significant digits. In these simulations of a triangular piston source excited by a pulse with a center frequency of 2 MHz, impulse response calculations require a sampling rate of 1 GHz to achieve only two significant digits of accuracy, whereas the FNM with time-space decomposition requires only nine Gauss abscissas applied to each integral and a sampling rate of 16 MHz to achieve two significant digits of accuracy throughout the near-field region.

B. Advantages of the FNM for time-harmonic and transient calculations

The computational advantages of the FNM are obtained from several sources. First, the FNM replaces time-consuming calculations of inverse trigonometric functions with a ratio of polynomials in the integrand. This reduces the computation time without increasing the numerical error. Second, the FNM reduces the numerical error by subtracting a singularity in the integrand. This step, which reduces the numerical error without significantly increasing the computation time, is particularly effective in eliminating numerical problems that occur along the edge of the source and throughout the paraxial region. Third, the FNM defines a single analytical expression that describes the pressure throughout the near-field region, whereas the impulse response requires multiple expressions to define the field generated by a single source. Thus, relative to calculations that employ exact or approximate calculations of the impulse response, convergence is faster with the FNM, and the FNM expressions are easier to evaluate.

The advantage of the FNM with time-space decomposition is that an integral expression with temporal and spatial dependencies is replaced with an equivalent expression that instead evaluates N spatial integrals for each edge of the triangular source and weights the result of each integral with an analytical temporal term. This results in greatly reduced overhead for transient near-field calculations, considering that the impulse response requires sampling rates of f_s=128 MHz for a peak error of 10% and f_s=1 GHz for a peak error of 1% for the source geometry in Fig. 2. The FNM eliminates these high sampling rates, which therefore facilitates much more efficient utilization of computer memory.

C. FIELD II

The FIELD II calculations with “use_triangles” are evaluated within the same 81×101 spatial grid defined previously for these near-field calculations, whereas the same calculations with subdivided rectangular subapertures (i.e., “use_rectangles”) are evaluated in an 81×86 spatial grid that includes an offset from the piston face. The offset is required for these near-field calculations; otherwise, the error grows excessively large on the piston face, which translates into much longer computation times for 10% and 1% peak errors. This occurs because subdividing the aperture introduces a numerical singularity on the piston face. Although FIELD II reduces the sampling frequency relative to other impulse response calculations, the exact impulse response consistently outperforms FIELD II for these time-harmonic near-field calculations, and the FNM evaluated with Gauss quadrature outperforms both of these by a wide margin. Furthermore, the FNM with time-space decomposition is also considerably faster than FIELD II for transient near-field calculations, and the FNM with time-space decomposition, unlike FIELD II with “use_rectangles,” allows the computational grid to extend up to the piston face.

D. Smoothed impulse response

Unlike the FNM and the exact impulse response, the smoothed impulse response requires an offset from the piston face for near-field calculations. This offset is required because the denominator in Eq. (7) produces a numerical singularity on the piston face. Despite evaluating the near-field pressure on a smaller 81×86-point spatial grid, the smoothed impulse response is slower than the FNM and the exact impulse response for time-harmonic calculations, as demonstrated in Fig. 4 and Table II. The exact impulse response is faster than the smoothed impulse response for these time-harmonic calculations because the exact impulse response is evaluated with Gauss quadrature, and Gauss quadrature generally converges much faster than other numerical integration methods that uniformly sample the integrand. For transient calculations with both exact and approximate impulse response expressions, uniform sampling is required for convolutions with the FFT. In these transient calculations, the smoothed impulse response gains some advantage over the exact impulse response by evaluating the pressure at a smaller number of spatial grid points and by reducing the problems with aliasing at higher frequencies. Nevertheless, as demonstrated in Figs. 4 and 6, the smoothed impulse response converges more slowly than the FNM for time-harmonic and transient near-field calculations.

V. CONCLUSION

A fast near-field method is presented for numerical calculations of the pressure generated by a triangular source. For time-harmonic near-field computations, the FNM expression in Eq. (9) achieves smaller peak errors in less time than the exact impulse response, the smoothed impulse response, and the FIELD II program. The results show that the FNM is 4.39 times faster than the exact impulse response for a 10% peak error, and the FNM is 3.44 times faster than the exact impulse response for a 1% peak error. The FNM is at least an order of magnitude faster than FIELD II and the smoothed impulse response for time-harmonic calculations compared at 10% and 1% peak error values. In transient near-field computations, the FNM in Eq. (10) combined with time-space decomposition achieves a substantial reduction in the computation time relative to exact and approximate impulse response calculations for a given peak error value. Transient near-field pressures are evaluated with a Hanning-weighted broadband pulse, and the resulting transient calculation is transformed into the superposition of six spatial integrals. The results demonstrate that the FNM with time-space decomposition is 3.89 and 38.19 times faster than the impulse response for peak errors of 10% and 1%, respectively, evaluated on an 81×101 spatial grid at 85 time points. Comparisons between smoothed impulse response results evaluated on the smaller 81×86-point offset spatial grid and the FNM with time-space decomposition evaluated on the larger 81×101-point spatial grid indicate that the FNM with time-space decomposition is 2.08 times faster than the smoothed impulse response for a 10% peak error, and the FNM with time-space decomposition is 6.7 times faster for a 1% peak error. Compared to the FIELD II program, the FNM is at least an order of magnitude faster for 10% and 1% peak error values. The results also suggest that the FNM, which eliminates the numerical problems that are encountered in exact and approximate impulse response calculations, provides a superior reference for near-field pressure calculations evaluated with time-harmonic and transient inputs.