Abstract
The unusually strong reversible binding of biotin by avidin and streptavidin has been investigated by density functional and MP2 ab initio quantum mechanical methods. The solvation of biotin by water has also been studied through QM/MM/MC calculations. The ureido moiety of biotin in the bound state hydrogen bonds to five residues, three to the carbonyl oxygen and one for each –NH group. These five hydrogen bonds act cooperatively, leading to stabilization that is larger than the sum of individual hydrogen-bonding energies. The charged aspartate is the key residue that provides the driving force for cooperativity in the hydrogen-bonding network for both avidin and streptavidin by greatly polarizing the urea of biotin. If the residue is removed, the network is disrupted, and the attenuation of the energetic contributions from the neighboring residues results in significant reduction of cooperative interactions. Aspartate is directly hydrogen-bonded with biotin in streptavidin and is one residue removed in avidin. The hydrogen-bonding groups in streptavidin are computed to give larger cooperative hydrogen-bonding effects than avidin. However, the net gain in electrostatic binding energy is predicted to favor the avidin-bicyclic urea complex due to the relatively large penalty for desolvation of the streptavidin binding site (specifically expulsion of bound water molecules). QM/MM/MC calculations involving biotin and the ureido moiety in aqueous solution, featuring PDDG/PM3, show that water interactions with the bicyclic urea are much weaker than (strept)avidin interactions due to relatively low polarization of the urea group in water.
Keywords: hydrogen bond cooperativity, streptavidin, avidin, biotin, desolvation
Introduction
The non-covalent binding association of biotin to avidin (Ka ≅ 1015 M−1)1 and streptavidin (Ka ≅ 1013 M−1)2 is the paragon of high-affinity host-guest/supramolecular interactions and has led to many practical applications.3–8 In contrast to these strong associations, corresponding to femtomolar and tenth picomolar dissociation constants, respectively, noncovalent host-guest binding affinities in water are typically in the range of 101–106 M−1, and protein-ligand binding rarely exceeds 1011 M−1.9 The biotin– (strept)avidin complexes generally exceed estimates of affinities from empirically determined free energy scoring functions and binding surveys.10–13 The mechanism by which biotin– (strept)avidin exceeds normal highest protein-ligand affinities by 102–104 M−1,9 has been subject of much interest. Despite the extraordinary utility of this complex, which has resulted in a plethora of experimental studies,14–21 and the uniqueness of the binding, which has led to many structural and computational studies,22–25 the origin of binding energetics and dynamics of association has not yet been clearly understood.
Protein binding motifs have been identified through crystal structures of protein-ligand complexes,2,26–31 thermodynamic experiments,14,17–21,23,32,33 and molecular dynamics/free energy perturbation simulations.22–25 These studies yielded three hypotheses for the strong binding affinity: (1) Weber and Salemme and co-workers reported the original crystal structure of biotin-streptavidin and suggested that the hydrogen-bonding interactions to the ureido ring system of biotin dominate the stabilization of the complex. (2) Miyamoto and Kollman contended that the energy provided by van der Waals contacts, primarily of the four tryptophan residues that line the binding pocket, is greater than the electrostatic/hydrogen-bonding free energy benefit. (3) Williams and co-workers proposed that the binding of biotin to streptavidin results in a large free energy benefit due to the strengthening of existing nonconvalent interactions within streptavidin.34
The quantitative importance of both hydrogen-bonding residues (Weber-Salemme) and tryptophan contacts (Miyamoto-Kollman) to the 18–20 kcal/mol binding free energy have been verified by Stayton, Stenkamp and co-workers through an elegant series of site-directed mutagenesis experiments.14,18–20,35 Additionally, biotin-streptavidin binding is accompanied by significant flap motions of the 3–4 loop. This facilitates binding by exclusion of solvent molecules from the binding site and increases the contribution of a number of direct hydrogen bonds and hydrophobic interactions with the valerate moiety. Removal of the 3–4 loop in streptavidin results in a reduction of the Ka by 6 orders of magnitude from wild type, nearly half of the binding energy.16,36
Molecular dynamics, and separate electrostatic and van der Waals free-energy calculations of the biotin-streptavidin complex suggested that the largest contribution to the extremely negative free energy of binding is the non-polar van der Waals contribution of the tryptophan residues Trp 79, Trp 92, Trp 108, and Trp 120 rather than electrostatic forces.24,25 The simulations also predict a large electrostatic contribution inside the protein, supported by site-directed mutagenesis experiments studies on streptavidin, which show that mutation of a residue directly hydrogen-bonded to the ureido moiety of biotin results in a substantial decrease in binding energy.14,18–20 However, Kollman et al. proposed that this electrostatic stabilization is similar to that in the water solvent, so the net electrostatic contribution to binding of the ureido group is small.24,25 Therefore, it was contended that the hydrogen-bonding residues merely form a weak recognition pocket and give only small net free energy gain from water to protein.
The hydrogen bonding interactions involved in biotin–(strept)avidin binding and biotin in aqueous solution have been re-evaluated using density functional and ab initio QM and combined QM/MM statistical mechanical calculations.
Computational Methodology
QM
Model structures were optimized using density functional theory with B3LYP/6-31+G(d,p)37–39 and MPWB1K/6-31+G(d,p) functionals/basis set. MPWB1K, developed by Truhlar and co-workers,40 based on the modified Perdew and Wang 1991 functional41 (MPW) and Becke’s 1995 meta correlation functional42 gave excellent overall results in recent benchmarks for nonbonded interactions.40,43 B3LYP has been shown to produce accurate orientations and non-bonding distances compared to protein structures,44 and B3LYP and MP2 have been shown to produce realistic hydrogen bond energies for a series of model complexes involving ligands and protein backbone and side-chain residues.45 Default convergence criteria in Gaussian 03 were met except for the RMS displacements for a few structures (see Supporting Information). The failure of RMS displacements to convergence is a result of the extremely flat potential surface of the hydrogen-bonding complexes for these large models. In such occurrences, changes in electronic energy across several steps were only 10−7 hartrees (6 × 10−5 kcal/mol). For all structures, the optimization step-sizes were decreased in order to facilitate location of the stationary points. All model protein systems were characterized by frequency calculations at the level of theory corresponding to the optimized structures. To determine atomic charges, the CHelpG algorithm, developed by Breneman and Wiberg,46 and natural population analysis (NPA)47–50 have been used.
MP2/6-31+G(d,p) single-point evaluations51 were performed on the density functional optimized geometries to better estimate the magnitudes of weak intermolecular interactions. Correction for basis set superposition error (BSSE) was performed using the counterpoise (CP) method of Boys and Bernardi.52–56
CPCM-SCRF57–60 single-point calculations on DFT geometries utilizing the UAKS cavity size at the HF/6-31+G(d,p) level were carried out on the biotin-residue or biotin-water stationary points for calculation of solvation energies. This method has been shown to be the most accurate standard cavity model for aqueous solvation.61 Free energies of solvation were then added to MP2/6-31+G(d,p) energies. A dielectric constant of 4.33 was used to simulate the environment of multiple tryptophan residues and deeply buried hydrogen-bonding residues encompassing the binding site.62 A dielectric constant of 78.39 was used for water. All reported B3LYP and MPWB1K structures, MP2 energies, CPCM solvation energies, and CP corrections were obtained using Gaussian 03.63
QM/MM
Combined quantum mechanical and molecular mechanics (QM/MM) calculations,64,65 as implemented in BOSS 4.6,66,67 were performed to analyze the properties and energetics of biotin in aqueous solution. The solute was treated with the PDDG/PM3 method,68,69 which has been extensively tested for gas-phase structures and energetics68,69 and has successfully been applied to solution-phase QM/MM studies of SN2,70 SNAr,71 Kemp72 and biotin73 decarboxylations, and Cope eliminations.74 The solvent molecules were represented by the TIP4P water model.75 The Metropolis Monte Carlo (MC) simulations were performed in a periodic box of 750 (minus the number of non-hydrogen atoms of the solute) TIP4P water molecules at 25 ºC and 1 atm in the NPT ensemble.76 Each simulation consisted of 3.2 million configurations of equilibration and 20 million configurations of averaging. The solute energy and energy changes are treated quantum mechanically using PDDG/PM3 and computation of the QM energy and atomic charges were performed for every solute move. The partial charges were obtained from the CM3 charge model77 and the PDDG/PM3 wavefunction unscaled for negatively charged solutes or scaled by 1.14 for neutral charged solutes.78 Solute-solvent and solvent-solvent intermolecular cutoff distances of 12 Å were employed.
MD
Molecular dynamics were performed on a monomer of unliganded avidin (PDB 1AVE),27 and the unliganded streptavidin tetramer (PDB 1SWC)16 using AMBER 8.79 The crystal structure for unliganded streptavidin contains two subunits adopting an open conformation for the 3–4 loop. The related loop in unliganded avidin, however, remains in the closed conformation for each subunit. From the protein crystal structures, hydrogen atoms and a cubic box of TIP3P75 water molecules extending 10 Å from the solute were added using the xLEaP module of AMBER. Crystal waters were removed. The Duan et al. (ff03) force field80 was employed to describe the proteins, and long-range electrostatic forces were treated using the particle mesh Ewald (PME) method.81,82 Trajectories were integrated with a 1 fs time step. All simulations were carried out under constant temperature (300 K) and pressure (1 atm). The avidin system was equilibrated for 110 ps and the streptavidin for 250 ps. The SHAKE algorithm83 was used for all hydrogens with a nonbonding pair cutoff of 10 Å. Average structures were generated using the PTRAJ utility for the unliganded avidin over 60–110 ps and for unliganded streptavidin over 200–250 ps.
Results and Discussion
The binding energy of each hydrogen-bonding residue in the (strept)avidin binding site that interacts with the ureido of biotin was evaluated through the application of two model systems. The first model treats the hydrogen-bonding residues as separate entities, and the latter mimics the protein environment where all residues are interacting with the ligand in concert. Binding energies obtained for the isolated residue-biotin complexes are referred to as isolated residue binding energies (IRBEs) and those derived from the protein binding site models are labeled binding site residue binding energies (BSRBEs). The aim of this differentiation is to explore the energetic effect of the hydrogen-bonding array in the protein binding site upon each particular residue–biotin interaction. This is determined quantitatively by the difference in IRBE and BSRBE for a designated residue. The resultant quantity is defined as the hydrogen bond cooperativity involving specific hydrogen-bonding interactions of one biotin to one subunit. Following the analysis of biotin– (strept)avidin hydrogen-bonding interactions, the binding energetics of biotin– and unliganded (strept)avidin–water complexes are presented.
Isolated Hydrogen-Bonding Residues
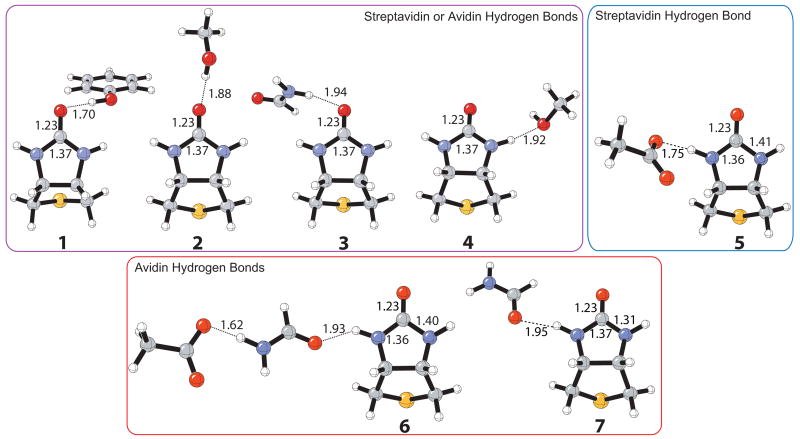
Biotin bound to (strept)avidin accepts three hydrogen bonds to the ureido carbonyl and one to each –NH group. The optimized isolated residue–biotin complexes at the B3LYP/6-31+G(d,p) level are shown in Figure 1. Hydrogen bond complexes, 1–7, represent the five hydrogen bonds that are made with the ureido of biotin in either the streptavidin or avidin binding site. Methanol is used as the mimic for a serine residue, phenol for tyrosine, acetate for aspartate, and formamide for an asparagine residue. These residue models have been used successfully for the investigation of mechanism and stereoselectivity of enzyme catalyzed reactions.84,85
Figure 1.
Optimized structures of the isolated hydrogen-bonding residues for streptavidin and avidin model binding sites at the B3LYP/6-31+G(d,p) level.
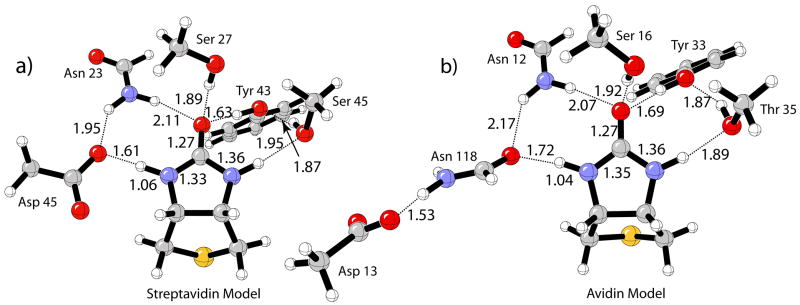
The fully optimized protein binding site models for streptavidin and avidin shown in Figure 2 served as a starting point for the calculation of the isolated complexes. Each individual hydrogen-bonding residue to the ureido moiety was constrained to match the optimized angle and dihedral angle in the streptavidin model, and the remaining variables were allowed to relax. For example, the initial geometry of the Tyr-OH---ureido hydrogen bond complex was obtained by removing all other hydrogen-bonding residues from the optimized streptavidin–biotin model (Figure 2a); the dihedral angle C=O(ureido)---O-C(Tyr) was constrained and the remaining variables were optimized, including the hydrogen bonding length. All other IR complexes were obtained in an analogous manner. These restraints caused structures 2, 3, and 7 not to be true minima in the gas phase as indicated by frequency analysis. The very small imaginary frequency (ca. −20 cm−1) in these structures corresponds to an in-plane bending motion of the residue to form an additional hydrogen bond to the carbonyl oxygen or –NH group of biotin. However, for comparison with the hydrogen bond energies obtained for the (strept)avidin complex (Figure 2), these dihedral constraints were necessary in order to maintain only a single hydrogen bond to biotin.
Figure 2.
B3LYP/6-31+G(d,p) optimized binding site models: a) streptavidin; b) avidin.
Table 1 gives IRBES for complexes, 1–7, involving isolated hydrogen-bonding residues and the bicyclic heterocycle of biotin. The IRBEs for the isolated complexes, computed at MP2/6-31+G(d,p)//B3LYP/6-31+G(d,p) and MP2/6-31+G(d,p)//MPWB1K/6-31+G(d,p) levels of theory, show excellent agreement in gas phase (Table 1, column 2) and CPCM model (column 3). The gas phase binding energies are quite high, especially for complexes involving a charged residue. The reported values in column 3, involving CPCM solvation corrections to mimic the interior of a protein, are more in line with the expected values for such hydrogen bonding complexes. Hydrogen bonds by the tyrosine or serine models to the urea carbonyl oxygen, as well as the urea NH bond to the aspartate are the strongest (~5 kcal/mol), while the NH---O hydrogen bonds (4, 6, 7) are all about 3 kcal/mol, in agreement with expected magnitues.86 Our discussion concentrates on quantities given by the CPCM model in column 3.
Table 1.
Isolated Residue Binding Energies (IRBEs) in kcal/mol for Streptavidin and Avidin
| Isolated Complex a | IRBEvacb | IRBECPCMc |
|---|---|---|
| Streptavidin or Avidin | ||
| Tyr 43/33 1 | −12.9 (−11.8) | −5.3 (−5.2) |
| Ser 27/16 2 | −8.0 (−7.8) | −4.7 (−3.0) |
| Asn 23/12 3 | −9.6 (−9.7) | −2.7 (−2.4) |
| Ser 45/Thr 35 4 | −8.9 (−9.5) | −3.5 (−2.6) |
| Streptavidin | ||
| Asp 128 5 | −28.5 (−28.9) | −5.3 (−5.2) |
| Avidin | ||
| Asn 118-Asp 13 Pair 6 | −16.7 | −3.6 |
| Asn 118 7 | −9.6 | −2.6 |
See Figure 2 for residue identification.
MP2/6-31+G(d,p)//B3LYP/6-31+G(d,p). MP2/6-31+G(d,p)//MPWB1K/6-31+G(d,p) in parentheses.
CPCM/HF/6-31+G(d,p) level corrections to MP2 energies using the dielectric of ether (ε = 4.33).
Streptavidin Model
The model systems for the streptavidin and avidin binding sites consist of the ureido of biotin in presence of the key first- and second-shell hydrogen-bonding residues. The optimized streptavidin–biotin structure at the B3LYP/6-31+G(d,p) level of theory is shown in Figure 2a. The corresponding MPWB1K/6-31+G(d,p) optimized structure is given in Supporting Information.
Calculated hydrogen-bonding energies for each of the five residues to the ureido moiety in the streptavidin model at the MP2/6-31+G(d,p)//B3LYP/6-31+G(d,p) and MP2/6-31+G(d,p)//MPWB1K/6-31+G(d,p) levels are reported in Table 2. The calculated individual hydrogen-bonding energy of each residue in the binding site was obtained in the following manner: starting from the optimized model shown in Figure 2a, the residue of interest was removed, and a single-point calculation of the energy of the structure with the missing residue was computed. The energy change resulting from removal of a hydrogen-bonding residue is defined as the residue deletion energy (RDE) (see Supporting Information). This energy involves interaction energies of the residue with biotin and other neighboring groups. In the streptavidin model, Asp 128 makes a hydrogen bond to Asn 23 and Tyr 43 hydrogen bonds with the adjacent Ser 45 (Figure 2). The energy of interaction of each residue of the binding site with biotin only is defined as the binding site residue binding energy (BSRBE). The BSRBEs are estimated by subtracting the energy calculated for hydrogen-bonding of the residue with neighboring non-biotin residues from the RDE (eq 1).
Table 2.
Binding Site Residue Binding Energies (BSRBEs) in kcal/mol for Hydrogen-Bonding Residues of the Streptavidin Model and Binding Enthalpy Changes from Site-Directed Mutagenesis Studies
| Streptavidin Residues | BSRBEvaca | BSRBECPCMb | ΔΔHWT – mutant (25°C) c |
|---|---|---|---|
| Tyr 43 | −19.9 (−20.6) | −10.2 (−11.1) | Y43A = 8.9 ± 1.4 19,20 |
| Ser 27 | −12.9 (−12.6) | −4.1 (−3.4) | S27A = 1.6 ± 0.7 19,20 |
| Asn 23 | −2.7 (−2.7) | −2.9 (−3.5) | N23A = 6.9 ± 0.7 19,20 |
| Asp 128 | −38.2 (−55.7) | −12.3 (−11.6) | D128A = 5.9 87 |
| Ser 45 | −11.4 (−16.8) | −5.7 (−5.6) | S45A = 6.1 87 |
MP2/6-31+G(d,p)//B3LYP/6-31+G(d,p). MP2/6-31+G(d,p)//MPWB1K/6-31+G(d,p) in parentheses.
CPCM/HF/6-31+G(d,p) level corrections to MP2 energies using the dielectric of ether (ε = 4.33).
| (1) |
For example, the BSRBE for the Tyr 43 in streptavidin is computed by subtracting the energy of the Tyr 43–Ser 45 complex from the RDETyr. The BSRBEs for all five hydrogen-bonding residues for the streptavidin model, defined as the energy of interaction between each residue model and the bicyclic heterocycle of biotin, are given in Table 2.
The calculated BSRBEs of column 3 can be compared to experimental site-directed mutagenesis studies reported in column 4. The ΔΔHWT-mutant quantity reported corresponds to the change in enthalpy of binding between wild type streptavidin and the corresponding mutant. The computed BSRBEs are analogous to residue X-to-null mutations, so perfect agreement of columns 3 and 4 is not expected. A direct comparison between these two energies is most appropriate when the mutant structure shows minimal disruption of the hydrogen bonding residues and water does not replace the missing side-chain atoms. This situation is applicable for the S45A,18 Y43A,20 and N23A.20
In S45A, biotin shifts toward Asp 128, but only an average variation of 0.1 Å is observed in the hydrogen bond lengths to the ligand. The calculated BSRBECPCM for Ser 45, −5.7 kcal/mol, is very close to the experimental value, 6.1 kcal/mol (Table 2, column 3).18
Y43A results in a 180° rotation of the neighboring Phe 29 to fill the void created by deletion of the large tyrosine side-chain.20 Yet, as in the case of S45A, hydrogen-bonding lengths to biotin are moderately perturbed, ± 0.2 Å.20 The experimental value, 8.9 kcal/mol, corresponding to a loss of hydrogen-bonding functionality, is comparable to the BSRBECPCM, 10 kcal/mol (Table 2, columns 3).19
The BSRBECPCM for N23A is lower than the observed value by 4 kcal/mol.20 However, deletion of this residue results in the loss of hydrogen-bonding interactions to Asp 128 side-chain and the backbone NH functionalities of Leu 25, Gly 26, and Ser 27.2 These interactions are expected to be quite favorable as a single NH---O hydrogen bond in formamide dimers has been reported to be approximately 5 kcal/mol in the gas phase at the MP2/aug-cc-pVDZ level,88 rivaling the hydrogen bond with the urea carbonyl of biotin, −2.7 kcal/mol (Table 2, column 2). As a consequence, the mutated unbound protein structurally alters to compensate for the removal of this residue.20 In contrast, the biotin-bound mutant structure displays little deviation compared to the native. It is likely that the destabilization of the mutant unliganded-protein is a significant factor contributing to the relatively higher binding enthalpy obtained from the mutation experiment.
The overestimations of BSRBE for Asp 128 and Ser 27 (Table 2, column 3) compared to experiment are reasonable due to structural changes and substitution of water for the mutated residue.20,35 In D128A, biotin shifts away from the side-chain of alanine, and presumably, strengthens interactions with residues of the opposing side of the binding pocket.35 In addition, a water molecule is observed within 0.5 Å of the Asp 128 carboxylate in the wild type.35 Similarly, the water observed in the S27A mutant crystal structure resides in the position occupied by the side-chain in the wild type.20 Therefore, the computational binding enthalpies of Asp 128/Ser 27–biotin interactions are likely to be higher than those obtained from mutation experiments, particularly due to the water–biotin hydrogen bonds gained in the mutants.
Overall, the calculated BSRBEs in streptavidin are quite large, in agreement with experimental mutagenesis studies, in particular for the Tyr 43, Asp 128, and Ser 45 models, which give among the largest energy changes reported for removing single hydrogen bonding residues.18,19,35
Avidin Model
The optimized avidin model is shown in Figure 2b. There are two important differences between the streptavidin and avidin models: in avidin, (1) Asn 118 replaces Asp 128; (2) the charged aspartic acid residue (Asp 13) is not in direct contact with the ligand, but is in the second shell, as opposed to Asp 128 in streptavidin.
The calculated BSRBEs for the avidin model are shown in Table 3. These can be compared to IRBEs, given in Table l. The trends are similar to the streptavidin results (Table 2), and we concentrate on column 3, the CPCM corrected values, in the following discussion. The hydrogen-bonding energies for Tyr 33 and Asn 12, which form hydrogen bonds to the carbonyl of the ureido moiety, and the Thr 35 hydrogen bond to the –NH group remain almost identical between the streptavidin (Table 2, column 3) and avidin models (Table 3, column 3). Only a slight difference is observed for the streptavidin Ser 27 hydrogen bond to the carbonyl of the bicyclic urea, which is calculated to be approximately 1 kcal/mol higher than that for Ser 16 in the avidin model. The greatest difference, however, is observed in the interaction energy for the Asp 13–Asn 116---NH(ureido) hydrogen bond, −9.0 kcal/mol, compared to −12.3 kcal/mol for the Asp 128---NH(ureido) hydrogen bond in the streptavidin model. It is apparent that the magnitude of the hydrogen-bonding interaction is quite sensitive to the position of the aspartic acid.
Table 3.
Binding Site Residue Binding Energies (BSRBEs) in kcal/mol for the Hydrogen-Bonding Residues of the Avidin and Avidin with Asp 13 Removed Models
| Protein Residues | BSRBEvaca | BSRBECPCMb |
|---|---|---|
| Avidin | ||
| Tyr 33 | −18.1 | −9.4 |
| Ser 16 | −11.3 | −3.2 |
| Asn 12 | −4.9 | −3.1 |
| Asn 118–Asp 13 Pair | −20.5 | −9.0 |
| Thr 35 | −13.1 | −6.0 |
| Avidin with Asp 13 removed | ||
| Tyr 33 | −15.3 | −8.1 |
| Ser 16 | −9.8 | −2.7 |
| Asn 12 | −8.3 | −1.4 |
| Asn 118 | −5.0 | −3.5 |
| Thr 35 | −13.5 | −6.7 |
MP2/6-31+G(d,p)//B3LYP/6-31+G(d,p).
CPCM/HF/6-31+G(d,p) level corrections to MP2 energies using the dielectric of ether (ε = 4.33).
Avidin Model (Asp 13 Removed)
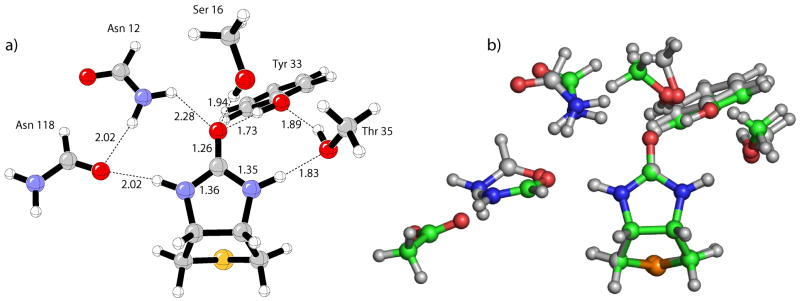
To further assess the influence of the aspartate residue on the binding energy, the avidin model with the Asp 13 removed was optimized with B3LYP (Figure 3a). The geometrical changes resulting from the deletion of Asp 13 in avidin are displayed by the superposition of the bicyclic urea bound to either of the avidin models (Figure 3b). The most significant deviations occurs with Asn 118 and Asn 12 residues, while Tyr 33, Ser 16, and Thr 35 remain relatively unperturbed. To understand the binding energetics of this model structure, the calculated BSRBEs are reported in Table 3. As expected, the largest reductions in binding energy results from Asn 118 of 5.5 kcal/mol, which is now devoid of the second-shell aspartate hydrogen bond, and Asn 12 of 1.7 kcal/mol (Table 3, column 3). Small decreases in BSRBE are predicted for Tyr 33 and Ser 16 of 1.3 and 0.4 kcal/mol, respectively.
Figure 3.
a) B3LYP/6-31+G(d,p) optimized avidin model with Asp 13 removed. b) Superposition of the urea heavy atoms in avidin (green carbon atoms) and avidin with Asp 13 removed (gray carbon atoms) models.
Another important consequence of the removal of the aspartate in avidin is an increase in hydrogen bond lengths for the three residues surrounding the ureido carbonyl ranging from 0.05 Å to 0.17 Å and the significant lengthening of the Asn 118 hydrogen bond to the –NH group by 0.3 Å. Thr 35 hydrogen bond to the opposing –NH group is shortened by 0.06 Å, resulting in the only, albeit modest, increase in BSRBE compared to avidin of 0.7 kcal/mol (Table 3, column 3).
(Strept)Avidin Hydrogen Bond Cooperativity
The difference in energy between the IRBE (Table 1) and BSRBE (Tables 2 and 3) values is defined as the cooperative hydrogen-bonding energy (ΔΔEcoop-x) (eq 1).
| (1) |
Cooperativity is the sum in total binding energy versus the sum of individual hydrogen bonds. The cooperative hydrogen-bonding energies with the CPCM model for all the residues in the streptavidin and avidin binding sites to the bicyclic urea are shown in Figure 4. Gas phase and MPWB1K cooperative hydrogen bonding energies parallel the results shown in Figure 4 and are given in the Supporting Information.
Figure 4.
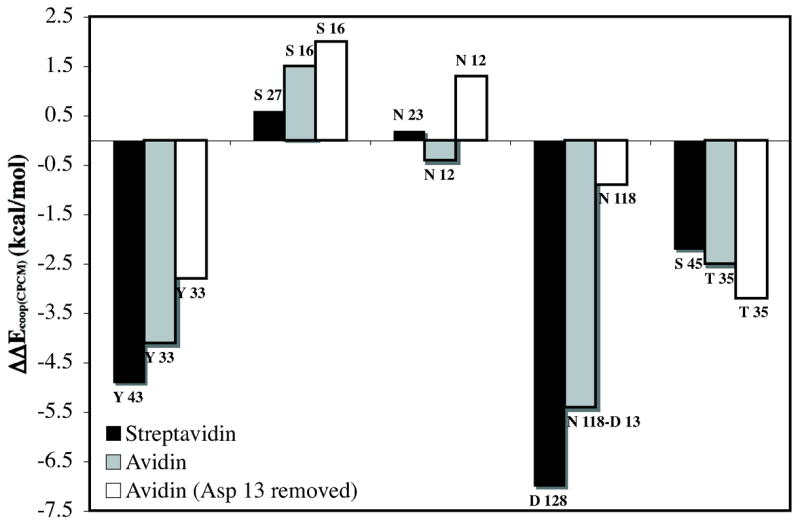
Computed hydrogen bond cooperativity (IRBE – BSRBE) for streptavidin, avidin, and avidin with Asp 13 removed models. Negative values correspond to increased (cooperative) hydrogen bonding, while positive values correspond to negative (anti-cooperative) hydrogen-bonding. Values correspond to CPCM model (ε = 4.33).
The cooperative hydrogen-bonding energy, ΔΔEcoop, is large for the hydrogen bond acceptors Asp 128, and Ser 45, interacting with the urea NHs, and for the strongest hydrogen bond donor, Tyr 43, to the carbonyl oxygen. While this work was in progress, Stenkamp and Stayton and co-workers characterized the S45A/D128A double mutant in streptavidin. The free energy change (ΔΔG298) between wild type and the double mutant was 1.4 kcal/mol higher than the sum of the ΔΔG298 values for S45A and D128A single mutations.87 Our results support that non-additivity in this case is due to the large hydrogen bond cooperativity associated with these two residues.
The hydrogen bond cooperativity values (ΔΔEcoop) for avidin and avidin with Asp 13 removed are also reported in Figure 4. Streptavidin has ~4 kcal/mol larger cooperative binding energy than avidin. More than half of the difference in cooperative hydrogen bond energy is due to the more favorable BSRBE of the aspartate directly interacting with the bicyclic urea in streptavidin.
When the Asp 13 is removed from avidin, ΔΔEcoop(CPCM) is significantly reduced by 7 kcal/mol. The remaining neutral residues still provide cooperative hydrogen bonding energy of −3.6 kcal/mol. However, a decrease in cooperativity is observed for all residues except for the Thr 35 hydrogen bond to the –NH group of the bicyclic urea (Figure 4). The larger cooperative hydrogen bond energy for this residue of −0.7 kcal/mol is likely due to strengthened interactions reflected in a shorter hydrogen bond length (Figure 3). The Ser 16 and Asn 12 hydrogen bonds to the carbonyl of the biotin become significantly anti-cooperative at approximately +1.5 kcal/mol. Although some cooperativity is maintained with only neutral residues, the aspartate residue is critical for the large non-additive binding energies (ΔΔEcoop(CPCM)) predicted for avidin and streptavidin of −11 and −14 kcal/mol, respectively.
Origin of Hydrogen Bond Cooperativity
Cooperative interactions are important for the stability of many hydrogen-bonded systems.89–94 Predictions of hydrogen bond cooperativity involving systems containing urea functionality have been reported in previous theoretical work.95–97 Masunov and Dannenberg applied ab initio and density functional theory calculations to a contiguous chain of urea molecules (Figure 5a) and demonstrated that hydrogen-bonding became stronger as the number of molecules increased, due to mutual polarization of the ureas as a function of chain length.95
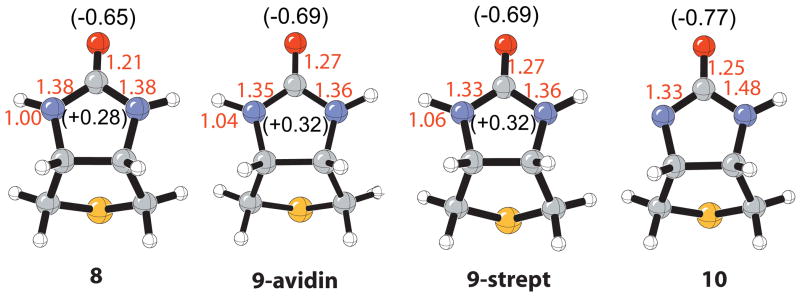
Figure 5.
Comparison of bond lengths (Å) and charges (NPA) of isolated bicylic urea unit of biotin (8), the urea group when bound in the (strept)avidin model binding sites (9), and the conjugate base (10). Structures were optimized by B3LYP/6-31+G(d,p).
The origin of biotin–(strept)avidin hydrogen bond cooperativity is similar, the induced polarization of the urea function of biotin causes strong interactions with the first and second contact-shell hydrogen-bonding residues. The strongly polarized urea allows interactions to work in a cooperative (non-additive) way.98 This mechanism to achieve hydrogen bond cooperativity has been shown to enhance binding in other hydrogen bond complexes, such as peptides and proteins,95,99–113 nucleic acid pairs,114 β-diketone fragments,115 and carboxylic acid dimers.116,117
A polarized urea function resulting from hydrogen bonds was first reported by Blessing through analysis of more than 100 crystal structures.118 This study revealed that with increasing strong hydrogen-bonding to the urea oxygen there is a progressive lengthening of the C-O bond and corresponding shortening of the C-N bond. The computed structure of biotin surrounded by the hydrogen-bonding residues in the (strept)avidin binding site is in agreement with this observation. Figure 5 shows optimized geometries for the bicyclic urea 8, the bicyclic urea bound in (strept)avidin 9 (Figure 2), and deprotonated bicyclic urea, 10. The C-O bond of the urea increases from 1.21Å to 1.27Å upon binding both the (strept)avidin models, 9. Yet, the C-N bond decreases from 1.38Å to 1.33 Å for streptavidin (9-strept) while the avidin bicyclic urea (9-avidin) is not as dramatically perturbed. This difference in geometry is likely manifested in the differing ΔΔEcoop between the streptavidin and avidin models, as shown in Figure 4. It is important to note that the C-O bond length change of 0.06 Å is quite dramatic since the C-O bond length of 1.25 Å in the conjugate base, 10, is actually shorter. The augmented negative charge to the carbonyl oxygen and positive charge to the remaining urea atoms mirror the geometrical perturbations from the isolated to bound (strept)avidin bicyclic urea (Figure 5).
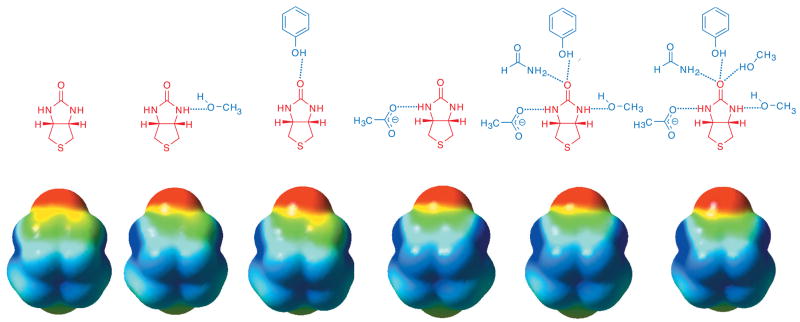
Electrostatic potential surfaces in various hydrogen-bonding complexes are shown in Figure 6. This shows a gradual increase in electron density on the carbonyl and a gradual decrease of electron density on the nitrogen and carbon atoms of the urea functionality with growing number of hydrogen bond donors and acceptors to the biotin model. The electrostatic potential of the bicyclic urea hydrogen-bonded to acetate (aspartic acid model) is nearly identical to the streptavidin model system (far right) supporting the critical role of a charged species in generating significant polarization of the ureido group of biotin.
Figure 6.
Electrostatic potential surfaces of bicyclic urea from B3LYP/6-311++G(d,p)//B3LYP/6-31+G(d,p) calculations. From left (isolated ureido moiety) to right (streptavdin model) there is an increase in red (oxygen becoming more negative) and an increase in blue surface area (nitrogens becoming more positive).
The evidence for significant polarization of the ureido moiety in Figure 6 is reflected in the calculated dipole moment of the ureido moiety in various cases. The computed dipole moment of the bicyclic molecule is exceptionally large (15.72 D) in the geometry it has in the streptavidin model as compared to 5.40 D of the unperturbed ureido structure (MP2/6-31+G(d,p)//B3LYP/6-31+G(d,p)).119 The hydrogen-bonding residues in streptavidin interacting with the ureido moiety lead to a nearly 300% increase in dipole moment. The structural relationship between the three residues and a polarized ureido oxygen is indeed reminiscent of an oxyanion hole, an important component of catalysis in proteases120 and esterases,121 as initially postulated by Weber et al.2
Biotin in Aqueous Solution
The strong oxyanion hole-like binding interaction in streptavidin should be compared to solvation of biotin and the predicted binding site in water. To obtain information about aqueous solvation, QM/MM/MC calculations were applied to various electronic structures of the bicyclic urea of biotin and multiple conformations of D-(+)-biotin using the TIP4P potential for water and the semi-empirical PDDG/PM3 for the solutes.68,69
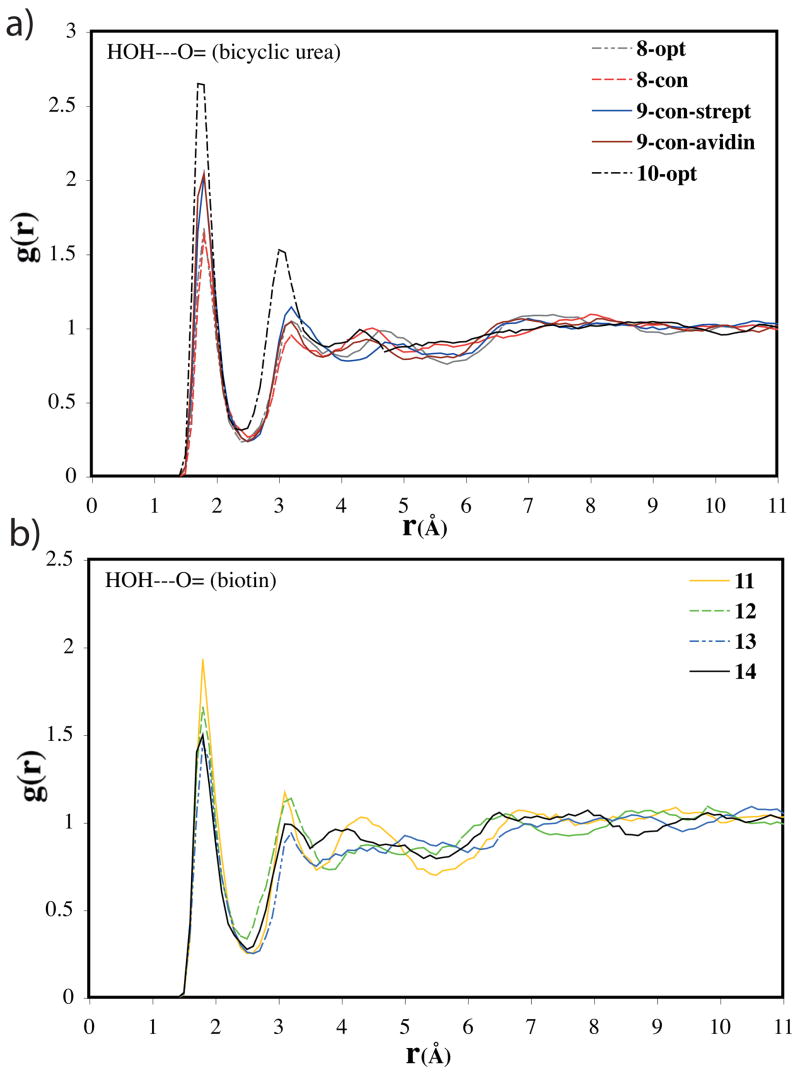
Five separate simulations have been carried for various bicyclic urea ground state solutes: (1) the bicyclic urea from the streptavidin-model (Figure 2a) with internal coordinates fixed at those values (9-con-strept), (2) the bicyclic urea from the avidin-model (Figure 2b) with internal coordinates fixed at those values (9-con-avidin) (3) the bicyclic urea geometry optimized in gas phase by B3LYP/6-31+G(d,p) with internal coordinates of the solute fixed at those values (8-con), (4) the urea optimized by PDDG/PM3 in water (8-opt), (5) the bicyclic urea conjugate base optimized by PDDG/PM3 in the liquid phase (10-opt).
Solute-solvent energy pair distributions for the simulations involving the various geometries of the ureido moiety, 9-con-strept, 9-con-avidin, 8-con, and 8-opt, are shown in Figure 7. The solute-solvent energy pair distributions record the average number of solvent molecules that interact with the solute with an associated energy. The most favorable hydrogen-bonding interactions are reflected in the left-most region, with energies more attractive than -3 kcal/mol. The large bands near 0 kcal/mol result from the many distant water molecules in outer shells.
Figure 7.
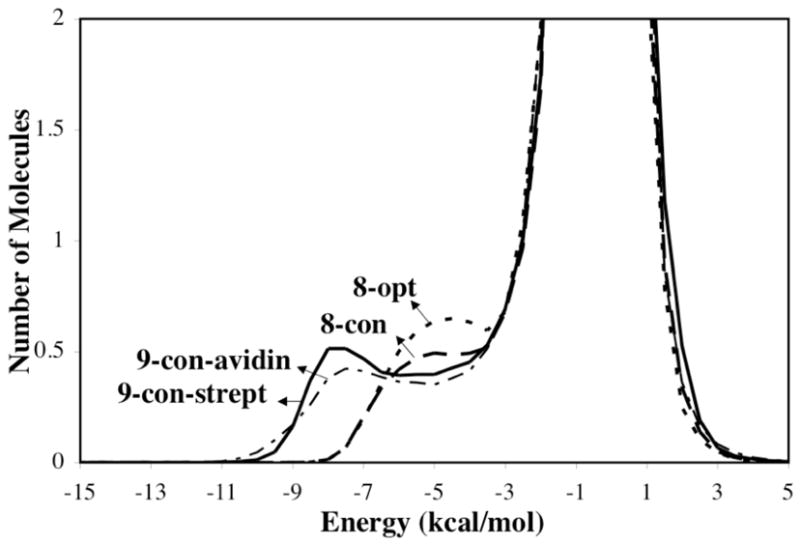
Solute-solvent energy pair distributions for different structures of the ureido moiety. The ordinate records the number of solvent molecules that interact with the solute with interaction energies on the abscissa. Units for the ordinate are number of molecules per kcal/mol.
The outstanding feature of Figure 7 is the presences of waters with especially large energies of interaction for the 9-con polarized structures compared to 8-con and 8-opt, arising from stronger hydrogen bonds with the solute. The differing distribution of 8-con and 8-opt compared to those of the 9-con structures suggests that water does not strongly polarize the solute unlike the (strept)avidin binding sites. The solvation of the water-perturbed bicyclic-urea is thus not particularly unusual.
The coordination of water to the carbonyl oxygen of the bicyclic urea is better quantified by radial distribution functions (rdfs). Shown in Figure 8a are the rdfs for the four structures discussed above. The number of contact waters to the carbonyl oxygen is determined by integrating the first peak of the rdf from 1 to 2.5 Å. The polarized structures of 9-con-avidin and 9-con-strept involve 2.6 and 2.7 hydrogen bonds to the carbonyl, respectively. While 8-con and 8-opt involves only 2.3 or 2.2 hydrogen bonds to water, respectively. On average, the bicyclic urea forms two hydrogen bonds between the carbonyl oxygen and water. But, the artificially polarized bicyclic ureas can form up to three hydrogen bonds to its carbonyl, more like an alkoxide. 9-con-avidin is slightly less polarized than 9-con-strept, which results in a slightly smaller probability to form a three hydrogen-bonded system. The sensitivity of solvent hydrogen bonds to the ureido carbonyl oxygen was also found in a recent study by Acevedo and Jorgensen on the aqueous solvent effects upon of biotin decarboxylation.73 The ureido conjugate base carbonyl oxygen 10-opt occupies 5.0 hydrogen bonds. The similar geometries between the 9-con bicyclic ureas and the conjugate base (Figure 5) do not translate to comparable ranges of hydrogen bond accepting ability of the carbonyl oxygen. Nevertheless, the rdfs support that the bicyclic urea is uniquely polarized when bound to the (strept)avidin binding sites (Figure 8a).
Figure 8.
Computed HOH---O= radial distributions functions for different structures of (a) bicyclic urea and (b) D-(+)-biotin.
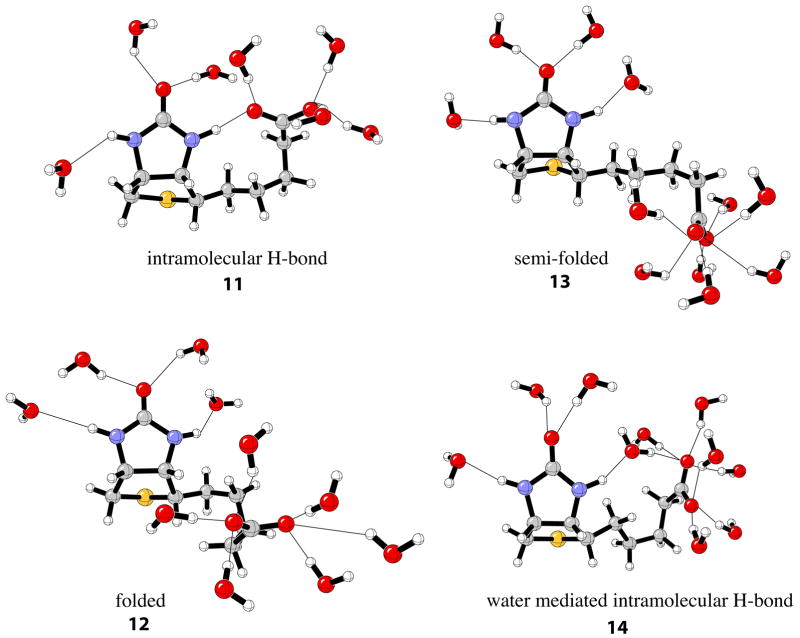
The critical factors for hydrogen bond cooperativity in the (strept)avidin binding sites are the charged aspartate residues present in each biotin binding site. Biotin has been shown to adopt multiple conformations in the gas phase122 and in aqueous solution.123 On possible conformation is an intramolecular hydrogen bond involving the near –NH group and the carboxylate tail 11 shown in Figure 9. However, this conformation must compete with other conformers, such as folded 12, semi-folded 13, and water-mediated intramolecular H-bond 14. These four representative biotin conformers were initially optimized in the gas phase then subject to QM/MM/MC simulations to gain insight into the energetics in water.
Figure 9.
Representative conformations of biotin in aqueous phase from QM/MM/MC simulations.
Shown in Figure 8b are the rdfs for each of the biotin conformers. Similar radial distribution functions around the carbonyl oxygen of the ureido moiety are predicted for the intramolecular hydrogen bond conformer of biotin and the polarized structures, 9-con. This is reasonable, since the ureido moiety in 11 is polarized by the intramolecular hydrogen bond involving the carboxylate tail of biotin. As expected, integration yields 2.6 water molecules hydrogen-bonded to the carbonyl oxygen for conformer 11 compared to 2.2–2.3 waters for conformers 12–14. However, the computed relative free energies of solvation, ΔΔGsolv, for the various conformations of biotin reported in Table 4 show the intramolecular hydrogen bond conformer will not contribute significantly to the overall ensemble of solvated geometries.123 The relative biotin solvation energies strongly disfavor conformation 11 compared to 12–14 (Table 4). The energy gained by the intramolecular hydrogen bond in 11 does not exceed the penalty for disrupting the apparently more favorable solvation of the carboxylate by water. This is in agreement with work by Li and co-workers where the intramolecular hydrogen-bonded conformation was observed only fleetingly during a 15ns simulation trajectory of neutral biotin.123 The predicted most favorable conformations, 12 and 14, are in qualitative agreement with NMR experiments that predict a compact structure of biotin in aqueous solution.124,125
Table 4.
Relative Free Energy of Solvation, ΔΔGsolv (kcal/mol), D-(+)-biotin conformations from QM/MM/MC Simulations
| Solute | EQM solute | EMM solute-solvent van der Waals | EQM/MM solute-solvent electrostatic | ΔΔGsolva |
|---|---|---|---|---|
| 11 | −154.5 | −12.7 | −177.7 | +37.3 ± 2.2 |
| 12 | −141.2 | −9.3 | −202.3 | +2.8 ± 2.0 |
| 13 | −149.4 | −10.9 | −193.9 | +17.6 ± 1.2 |
| 14 | −141.8 | −9.0 | −205.9 | 0.0 |
ΔGsolv = (Esolute-solvent electrostatic + Esolute-solvent van der Waals) − EQM. ΔΔGsolv = ΔGsolv (11,12,13 or 14) − ΔGsolv (14).
To assess the net binding energy in water, the ureido group with four coordinating waters (two to the carbonyl oxygen and one to each –NH group), in accordance with QM/MM/MC predictions, was optimized at the B3LYP/6-31+G(d,p) level (see Supporting Information). The energies for each water molecule interacting with the ureido of biotin were calculated in an analogous fashion to BSRBEs using MP2/6-31+G(d,p)//B3LYP/6-31+G(d,p) level with CPCM corrections using a dielectric of water (ε = 78.39). A total binding energy of −14.2 kcal/mol was calculated for the four water molecules hydrogen-bonded to the ureido of biotin. This is considerably lower than the total BSRBE of streptavidin (−35.2 kcal/mol) and avidin (−30.7) reported in Tables 2 and 3, column 3. Furthermore, the calculated dipole moment on the ureido moiety with four coordinating water molecules is only 9.27 D, while the induced dipole moment of the ureido in the streptavidin model is 15.72 D. Biotin in aqueous solution is polarized much less than biotin in the (strept)avidin binding sites, and the hydrogen bonds to the ureido group are much stronger when bound to the protein.
Solvation of Unliganded (Strept)Avidin: Why Avidin is a Better Binder than Streptavidin
The total BSRBEs for streptavidin or avidin minus −14.5 kcal/mol for biotin-water interactions provide estimates of the binding energies for the protein-ligand complex. Free energy contributions from residues providing favorable hydrophobic/packing interactions have been shown by Lazaridis et al. to be nearly identical in streptavidin and avidin.126 Thus, the BSRBE quantities predict that streptavidin is the better binder, while experiment has shown the free energy of binding is 2–3 kcal/mol better with avidin.1,21 However, the interaction of bound water molecules with the hydrogen-bonding residues in the unliganded protein needs to be taken into account.
In the absence of a ligand bound to (strept)avidin, the binding site is occupied by water.2,26 The solvation energy of the streptavidin and avidin binding sites were obtained by determining the number and geometric placement of occupying waters that are interacting with the bicyclic urea hydrogen bonding residues using classical molecular dynamic simulations (see Computational Methodology). Average structures for unliganded (strept)avidin are shown in Supporting Information.
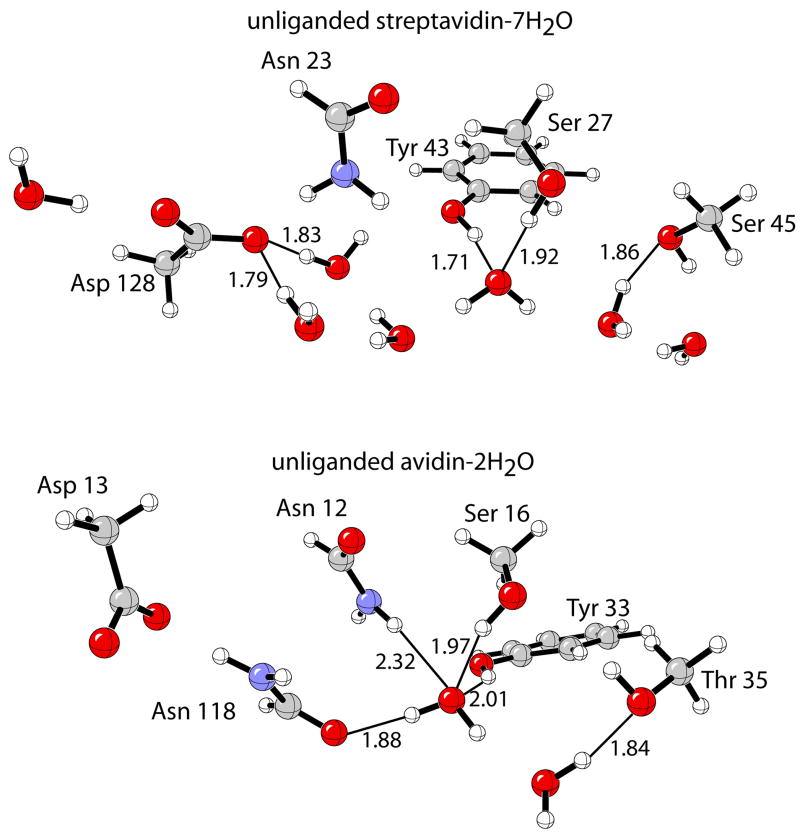
The generally proposed open conformation of the 3–4 loop in unliganded streptavidin16 is predicted to facilitate an influx of water molecules to line the binding cavity. Molecular dynamics show that for the subunits with an open conformation, B and D, there are five waters: two interacting with the oxyanion hole residues (Ser 27, Asn 23, Tyr 45), three waters hydrogen-bonded to Asp 128 with two hydrogen-bonding to the inner binding-site-oxygen and one to the outer, exposed to bulk solvent. Additionally, there are two waters interacting with the side-chain of Ser 45, a member of the 3–4 loop. In subunit D, however, a disordered rotamer conformation of Ser 45 is observed, such that it is not arranged to bind biotin, unlike in subunit B. Therefore, we choose to focus on subunit B where the hydrogen-bonding residues are best pre-arranged to bind biotin. The placement and number of waters is consistent with crystallographic studies2 and previous calculations on unliganded streptavidin,24 which predict five to six waters in the binding site.
Contrary to streptavidin, the 3–4 in avidin remains in a closed conformation in absence of biotin.27 Dynamics studies show that unliganded avidin contains two water molecules hydrogen-bonded to each other. One of the waters is found in the deepest part of the binding cavity bound to Asn 118 and the oxyanion hole side-chain residue atoms of Ser 16 and Tyr 33 and loosely to Asn 12. The other water is hydrogen-bonded to the side-chain of Thr 35. This structural depiction for the solvated binding site is in excellent accord with deductions from the crystal structure.27
B3LYP/6-31+G(d,p) optimizations were performed starting from the computed average atomic coordinates of the (strept)avidin binding sites and bound waters, as shown in Figure 10. Due to dramatic distortions resulting from unconstrained optimizations, constraints were designed to impose the geometric integrity of the protein scaffold to locate realistic minima corresponding to nature. Fixing interatomic distances between the residue side-chain and intra-residue side-chain angles and dihedral angles, and then optimizing the remaining degrees of freedom determined the streptavidin–7H2O and avidin-2H2O complexes.
Figure 10.
Model protein binding sites for streptavidin and avidin in complex with water at the B3LYP/6-31+G(d,p) level.
The binding energies of two and seven water molecules in the avidin and streptavidin binding sites, were determined from the energy to transfer the H2O molecules from the unliganded (strept)avidin–H2O complexes into bulk aqueous solution. The resulting binding energies include energetic contributions from the hydrogen-bonding interactions between the individual water molecules and the protein side-chains. To account for the energy corresponding to the H2O–H2O hydrogen bonds in the protein, the binding energy of the water complex was subtracted from this energy difference. The binding energy of the unliganded (strept)avidin–nH2O complexes, ΔEprotein–water binding, was calculated by eq 2.
| (2) |
Only six waters were transferred out of the streptavidin binding sites, in accord with the crystal structure (PDB 1STP), which shows that the water molecule hydrogen-bonded to the outside oxygen of Asp 128 remains bound with biotin. The energy corresponding to the transfer of a water molecule into bulk water is taken as the experimental value of the free energy of solvation for water, −6.3 kcal/mol.127 Different dielectric constants (ε = 4.33, 78.39) were applied to the CPCM-SCRF treatment of the unliganded (strept)avidin–nH2O complexes due to the uncertainty of the dielectric of the unliganded protein binding pocket. Nevertheless, the binding energy (ΔEprotein–water binding) for streptavidin remains approximately 8 kcal/mol larger than avidin. Hydrogen-bonding distances shown in Figure 10 indicates that the larger desolvation energies for the streptavidin binding site is derived from the stronger H2O–Asp 128/Tyr 43 hydrogen bonds compared to the analogous sites in avidin.
Further sampling may yield alterative configurations for the water–binding site interactions, in addition to the consideration of other crystal structures of unliganded streptavidin.128 However, it is clear that the key factors giving rise to the large number of occupying waters in streptavidin are the first-shell aspartate residue, which renders the binding pocket more polar, and the open conformation of the 3–4 loop. Avidin will bind biotin more strongly than streptavidin because the placement of Asp 13 reduces the large desolvation penalty resulting from a first-shell charged residue and provides good hydrogen-bond cooperativity via juxtaposition to Asn 118. The evolutionary driving force for avidin to bind biotin with greater affinity is not achieved by strengthening interactions with the ligand, but by weakening binding interactions with water.
Conclusion
Quantitative investigation of the binding interactions within the streptavidin and avidin binding sites demonstrate that the hydrogen-bonding residues induce a polarized electronic structure of the ureido moiety of biotin, which causes the non-covalent hydrogen-bonding interactions with the ligand to be unusually strong. This relationship between the residues and ligand create a cooperative effect: the binding energy inside the protein is larger than expected based on the sum of individual hydrogen-bonds. The biotin–(strept)avidin complexes that form strong stabilizing oxyanion holes provide superior hydrogen-bonding interactions compared to the electrostatic interactions in aqueous solution. Streptavidin is predicted to have larger cooperative hydrogen-bonding energy compared to avidin, but the large inherent binding energy is counteracted by the higher desolvation energy of streptavidin.
Supplementary Material
Energies and Cartesian coordinates of all structures calculated at B3LYP/6-31+G(d,p) and MPWB1K/6-31+G(d,p) including counterpoise corrections, solute-solvent energy pair distributions for biotin, MD average structures of unliganded (strept)avidin, and complete refs. 63 and 79. This material is available free of charge via the Internet at http://pubs.acs.org.
Acknowledgments
We are grateful to the National Science Foundation (CHE-0548209) and DARPA for financial support of this research. This research was also facilitated through the Partnerships for Advanced Computational Infrastructure (PACI) through the support of the National Science Foundation. The computations were performed on the National Science Foundation Terascale Computing System at the Pittsburgh Supercomputing Center (PSC) and on the UCLA Academic Technology Services (ATS) Hoffman Beowulf cluster. J.D. would like to acknowledge the National Institutes of Health, UCLA Chemistry-Biology Interface training program for financial support through a traineeship.
References
- 1.Green NM. Advan Protein Chem. 1975;29:85–133. doi: 10.1016/s0065-3233(08)60411-8. [DOI] [PubMed] [Google Scholar]
- 2.Weber PC, Wendoloski JJ, Pantoliano MW, Salemme FR. J Am Chem Soc. 1992;114:3197–3200. [Google Scholar]
- 3.Wilchek M, Bayer EA. Methods Enyzmol. 1990;184:5–45. doi: 10.1016/0076-6879(90)84256-g. [DOI] [PubMed] [Google Scholar]
- 4.Wilbur D, Pathare P, Hamlin D, Stayton P, To R, Klumb L, Buhler K, Vessella R. Biomol Eng. 1999;16:113–118. doi: 10.1016/s1050-3862(99)00044-3. [DOI] [PubMed] [Google Scholar]
- 5.Hamblett KJ, Kegley BB, Hamlin DK, Chyan MK, Hyre D, Press OW, Wilbur DS, Stayton PS. Bioconjug Chem. 2002;13:588–598. doi: 10.1021/bc010087t. [DOI] [PubMed] [Google Scholar]
- 6.Demidov VV, Bukanov NO, Frank-Kamenetskii D. Curr Issues Mol Biol. 2000;2:31–35. [PubMed] [Google Scholar]
- 7.Bontempo D, Maynard HD. J Am Chem Soc. 2005;127:6508–6509. doi: 10.1021/ja042230+. [DOI] [PubMed] [Google Scholar]
- 8.Howarth M, Chinnapen DJF, Gerrow K, Dorrestein PC, Grandy MR, Kelleher NL, El-Husseini A, Ting AY. Nature Methods. 2006;3:267–273. doi: 10.1038/NMETHXXX. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhang X, Houk KN. Acc Chem Res. 2005;38:379–385. doi: 10.1021/ar040257s. [DOI] [PubMed] [Google Scholar]
- 10.Houk KN, Leach AG, Kim SP, Zhang X. Angew Chem Int Ed. 2003;42:4872–4897. doi: 10.1002/anie.200200565. [DOI] [PubMed] [Google Scholar]
- 11.Böhm HJ. J Comput -Aided Mol Des. 1992;6:593–605. doi: 10.1007/BF00126217. [DOI] [PubMed] [Google Scholar]
- 12.Böhm HJ. J Comput -Aided Mol Des. 1994;8:243–256. doi: 10.1007/BF00126743. [DOI] [PubMed] [Google Scholar]
- 13.Kuntz ID, Chen K, Sharp KA, Kollman PA. Proc Natl Acad Sci USA. 1999;96:9997–10002. doi: 10.1073/pnas.96.18.9997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chilkoti A, Tan PH, Stayton PS. Proc Natl Acad Sci USA. 1995;92:1754–1758. doi: 10.1073/pnas.92.5.1754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Freitag S, Le Trong I, Chilkoti A, Klumb LA, Stayton PS, Stenkamp RE. J Mol Biol. 1998;279:211–221. doi: 10.1006/jmbi.1998.1735. [DOI] [PubMed] [Google Scholar]
- 16.Freitag S, Le Trong I, Klumb L, Stayton PS, Stenkamp RE. Protein Sci. 1997;6:1157–1166. doi: 10.1002/pro.5560060604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.González M, Bagatolli LA, Echabe I, Arrondo JLR, Argaraña CE, Cantor CR, Fidelio GD. J Biol Chem. 1997;272:11288–11294. doi: 10.1074/jbc.272.17.11288. [DOI] [PubMed] [Google Scholar]
- 18.Hyre D, Le Trong I, Freitag S, Stenkamp RE, Stayton PS. Protein Sci. 2000;9:878–885. doi: 10.1110/ps.9.5.878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Klumb LA, Chu V, Stayton PS. Biochemistry. 1998;37:7657–7663. doi: 10.1021/bi9803123. [DOI] [PubMed] [Google Scholar]
- 20.Le Trong I, Freitag S, Chu V, Stayton PS, Stenkamp RE. Acta Cryst. 2003;D59:1567–1673. [Google Scholar]
- 21.Swamy M. J Biochem Mol Biol Int. 1995;36:219–225. [PubMed] [Google Scholar]
- 22.Dixit SB, Chipot C. J Phys Chem A. 2001;105:9795–9799. [Google Scholar]
- 23.Dixon RW, Kollman PA. Proteins: Struc Funct and Genet. 1999;36:471–473. [PubMed] [Google Scholar]
- 24.Miyamoto S, Kollman PA. Proteins: Struc Funct and Genet. 1993;16:226–245. doi: 10.1002/prot.340160303. [DOI] [PubMed] [Google Scholar]
- 25.Miyamoto S, Kollman PA. Proc Natl Acad Sci USA. 1993;90:8402–8406. doi: 10.1073/pnas.90.18.8402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rosano C, Arosio P, Bolognesi M. Biomolecular Engineering. 1999;16:5–12. doi: 10.1016/s1050-3862(99)00047-9. [DOI] [PubMed] [Google Scholar]
- 27.Pugliese L, Coda A, Malcovati M, Bolognesi M. J Mol Biol. 1993;231:698–710. doi: 10.1006/jmbi.1993.1321. [DOI] [PubMed] [Google Scholar]
- 28.Hendrickson WA, Pahler A, Smith JL, Satow Y, Meritt YS, Phizackerley RP. Proc Natl Acad Sci USA. 1989;86:2190–2194. doi: 10.1073/pnas.86.7.2190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Livnah O, Bayer EA, Wilchek M, Sussman JL. Proc Natl Acad Sci USA. 1993;90:5076–5080. doi: 10.1073/pnas.90.11.5076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Freitag S, Le Trong I, Klumb L, Stayton PS, Stenkamp RE. Protein Sci. 1997;6:1157–1166. doi: 10.1002/pro.5560060604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pahler A, Hendrickson WA, Gawinowicz Kolks MA, Argarana CE, Cantor CR. J Biol Chem. 1987;262:13933–13937. [PubMed] [Google Scholar]
- 32.Marttila AT, Hytönen VP, Laitinen OH, Bayer EA, Wilchek M, Kulomaa MS. Biochem J. 2003;369:249–254. doi: 10.1042/BJ20020886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Stayton PS, Freitag S, Klumb LA, Chilkoti A, Chu V, Penzotti JE, To R, Hyre D, Le Trong I, Lybrand TP, Stenkamp RE. Biomolecular Engineering. 1999;16:39–44. doi: 10.1016/s1050-3862(99)00042-x. [DOI] [PubMed] [Google Scholar]
- 34.Williams DH, Stephens E, O’Brien DP, Zhou M. Angew Chem Int Ed. 2004;43:6596–6616. doi: 10.1002/anie.200300644. [DOI] [PubMed] [Google Scholar]
- 35.Freitag S, Chu V, Penzotti JE, Klumb LA, To R, Hyre D, Le Trong I, Lybrand TP, Stenkamp RE, Stayton P. Proc Natl Acad Sci USA. 1999;96:8384–8389. doi: 10.1073/pnas.96.15.8384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chu V, Freitag S, Le Trong I, Stenkamp RE, Stayton PS. Protein Sci. 1998;7:848–859. doi: 10.1002/pro.5560070403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Becke AD. Phys Rev A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 38.Lee C, Yang W, Parr RG. Phys Rev B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 39.Becke AD. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 40.Zhao Y, Truhlar DG. J Phys Chem A. 2004;108:6908–6918. [Google Scholar]
- 41.Perdew JP. In: Electronic Structure of Solids. Ziesche P, Eschig H, editors. Akademie Verlag; Berlin: 1991. p. 11. [Google Scholar]
- 42.Becke AD. J Chem Phys. 1996;104:1040–1046. [Google Scholar]
- 43.Zhao Y, Truhlar DG. J Chem Theory Comput. 2005;1:415–432. doi: 10.1021/ct049851d. [DOI] [PubMed] [Google Scholar]
- 44.Morozov SV, Kortemme T, Tsemekhman K, Baker D. Proc Natl Acad Sci USA. 2004;101:6946–6951. doi: 10.1073/pnas.0307578101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hao MH. J Chem Theory Comput. 2006;2:863–872. doi: 10.1021/ct0600262. [DOI] [PubMed] [Google Scholar]
- 46.Breneman CM, Wiberg KB. J Comput Chem. 1990;11:361–373. [Google Scholar]
- 47.Reed AE, Weinstock RB, Weinhold F. J Chem Phys. 1988;83:735–746. [Google Scholar]
- 48.Wiberg KB, Rablen PR. J Comput Chem. 1993;14:1504–1518. [Google Scholar]
- 49.McAllister MA, Tidwell TT. J Org Chem. 1994;59:4506–4515. [Google Scholar]
- 50.Reed AE, Curtiss LA, Weinhold F. Chem Rev. 1988;88:899–926. [Google Scholar]
- 51.Møller C, Plesset MS. Phys Rev. 1934;46:618–622. [Google Scholar]
- 52.Duijneveldt FBv, Duijneveldt-van de Rijdt JGCMv, Lenthe JHv. Chem Rev. 1994;94:1873–1885. [Google Scholar]
- 53.Gutowski M, Duijneveldt-van de Rijdt JGCMv. J Chem Phys. 1993;98:4728–4737. [Google Scholar]
- 54.Frisch MJ, Del Bene JE, Binkley JS, Schaefer HF. J Chem Phys. 1986;84:2279–2289. [Google Scholar]
- 55.Schwenke DW, Truhlar DG. J Chem Phys. 1985;82:2418–2426. [Google Scholar]
- 56.Szalewicz K, Cole SJ, Kolos W, Bartlett RJ. J Chem Phys. 1988;89:3662–3673. [Google Scholar]
- 57.Klamt A, Schüürmann G. J Chem Soc, Perkin Trans 2. 1993:799–805. [Google Scholar]
- 58.Andzelm J, Kölmel C, Klamt A. J Chem Phys. 1995;103:9312–9320. [Google Scholar]
- 59.Barone V, Cossi M. J Phys Chem A. 1998;102:1995–2001. [Google Scholar]
- 60.Cossi M, Rega N, Scalmani G, Barone V. J Comput Chem. 2003;24:669–681. doi: 10.1002/jcc.10189. [DOI] [PubMed] [Google Scholar]
- 61.Takano Y, Houk KN. J Chem Theory Comput. 2005;1:70–77. doi: 10.1021/ct049977a. [DOI] [PubMed] [Google Scholar]
- 62.Simonson T, Brooks CL., III J Am Chem Soc. 1996;118:8452–8458. [Google Scholar]
- 63.Frisch MJ, et al. Gaussian 03, revision C02. Gaussian, Inc.; Wallingford, CT: 2004. [Google Scholar]
- 64.Warshel A, Levitt M. J Mol Biol. 1976;103:227–249. doi: 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
- 65.Kaminshi GA, Jorgensen WL. J Phys Chem B. 1998;102:1787–1796. [Google Scholar]
- 66.Jorgensen WL. BOSS; Version 46. Yale University; New Haven, CT: 2004. [Google Scholar]
- 67.Jorgensen WL, Tirado-Rives J. J Comput Chem. 2005;26:1689–1700. doi: 10.1002/jcc.20297. [DOI] [PubMed] [Google Scholar]
- 68.Repasky MP, Chandrasekhar J, Jorgensen WL. J Comput Chem. 2002;23:1601–1622. doi: 10.1002/jcc.10162. [DOI] [PubMed] [Google Scholar]
- 69.Tubert-Brohman I, Guimarães CRW, Repasky MP, Jorgensen WL, Brauman JI. J Am Chem Soc. 2003;25:138–150. [Google Scholar]
- 70.Vayner G, Houk KN, Jorgensen WL, Brauman JI. J Am Chem Soc. 2004;126:9054–9058. doi: 10.1021/ja049070m. [DOI] [PubMed] [Google Scholar]
- 71.Acevedo O, Jorgensen WL. Org Lett. 2004;6:2881–2884. doi: 10.1021/ol049121k. [DOI] [PubMed] [Google Scholar]
- 72.Acevedo O, Jorgensen WL. J Am Chem Soc. 2005;127:8829–8834. doi: 10.1021/ja051793y. [DOI] [PubMed] [Google Scholar]
- 73.Acevedo O, Jorgensen WL. J Org Chem. 2006;71:4896–4902. doi: 10.1021/jo060533b. [DOI] [PubMed] [Google Scholar]
- 74.Acevedo O, Jorgensen WL. J Am Chem Soc. 2006;128:6141–6146. doi: 10.1021/ja057523x. [DOI] [PubMed] [Google Scholar]
- 75.Jorgensen WL, Chandrasekhar J, Madura JD, Impey W, Klein ML. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 76.Jorgensen WL. In: Encyclopedia of Computational Chemistry. Schleyer PvR., editor. Vol. 3. Wiley; New York: 1998. pp. 1754–1763. [Google Scholar]
- 77.Thompson JD, Cramer CJ, Truhlar DG. J Comput Chem. 2003;24:1291–1304. doi: 10.1002/jcc.10244. [DOI] [PubMed] [Google Scholar]
- 78.Udier-Blagovi M, Morales De Tirado P, Pearlman SA, Jorgensen WL. J Comput Chem. 2004;25:1322–1332. doi: 10.1002/jcc.20059. [DOI] [PubMed] [Google Scholar]
- 79.Case DA, et al. Amber 8. University of California; San Francisco: 2004. [Google Scholar]
- 80.Duan Y, Wu C, Chowdhury S, Lee MC, Xiong G, Zhang R, Cieplak P, Luo R, Lee T. J Comput Chem. 2003;24:1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 81.Darden T, York D, Pedersen L. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 82.Essmann U, Perera L, Berkowitz ML, Darden T, York D, Pedersen L. J Chem Phys. 1995;103:8577–8593. [Google Scholar]
- 83.van Gusteren WF, Berendesen HJC. Mol Phys. 1977;34:1311. [Google Scholar]
- 84.Tantillo DJ, Jiangang C, NHK Curr Opin Chem Biol. 1998;2:743–750. doi: 10.1016/s1367-5931(98)80112-9. [DOI] [PubMed] [Google Scholar]
- 85.Cannizzaro CE, Ashley JA, Janda KD, Houk KN. J Am Chem Soc. 2003;125:2489–2506. doi: 10.1021/ja020879d. [DOI] [PubMed] [Google Scholar]
- 86.Fersht AR, Shi JP, Knill-Jones J, Lowe DM, Wilkinson AJ, Blow DM, Brick P, Carter P, Waye MMY, Winter G. Nature. 1985;314:235–238. doi: 10.1038/314235a0. [DOI] [PubMed] [Google Scholar]
- 87.Hyre DE, Le Trong I, Merritt EA, Eccleston JF, Green NM, Stenkamp RE, Stayton PS. Protein Science. 2006;15:459–467. doi: 10.1110/ps.051970306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Vargas R, Garza J, Friesner RA, Stern H, Hay BP, Dixon DA. J Phys Chem A. 2001;105:4963–4968. [Google Scholar]
- 89.Jeffrey GA, Saenger W. Hydrogen Bonding in Biological Structures. Springer-Verlag; Berlin: 1991. [Google Scholar]
- 90.Scheiner S. Hydrogen Bonding. Oxford University Press; New York: 1997. [Google Scholar]
- 91.Guo H, Sirois S, Proynov EI, Salahub DR, Hadzi D, editors. Chapter 3. John Wiley & Sons Ltd; New York: 1997. [Google Scholar]
- 92.Çarçabal P, Jockusch RA, Hünig I, Snoek LC, TKR, Davis BG, Gamblin DP, Compagnon I, Oomens J, Simons JP. J Am Chem Soc. 2005;127:11414–11425. doi: 10.1021/ja0518575. [DOI] [PubMed] [Google Scholar]
- 93.Williams DH, Maguire AJ, Tsuzuki W, Westwell MS. Science. 1998;280:711–714. doi: 10.1126/science.280.5364.711. [DOI] [PubMed] [Google Scholar]
- 94.Suhai S. J Qunatum Chem. 1994;52:395–412. [Google Scholar]
- 95.Masunov A, Dannenberg JJ. J Phys Chem B. 2000;104:806–810. [Google Scholar]
- 96.Dovesi R, Causa’ M, Orlando R, Roetti C. J Chem Phys. 1990;92:7402–7411. [Google Scholar]
- 97.Belosldov RV, Li ZQ, Kawazoe Y. Mol Eng. 1999;8:105–120. [Google Scholar]
- 98.Steiner T. Chem Commun. 1997:727–734. [Google Scholar]
- 99.Ludwig R. J Mol Liq. 2000;84:65–75. [Google Scholar]
- 100.Ludwig R, Reis O, Winter R, Weinhold F, Farrar TC. J Phys Chem B. 1998;102:9312–9318. [Google Scholar]
- 101.Ludwig R, Weinhold F, Farrar TC. J Phys Chem A. 1997;101:8861–8870. [Google Scholar]
- 102.Kobko N, Paraskevas L, del Rio E, Dannenberg JJ. J Am Chem Soc. 2001;123:4348–4349. doi: 10.1021/ja004271l. [DOI] [PubMed] [Google Scholar]
- 103.Guo H, Gresh N, Roques BP, Salahub DR. J Phys Chem B. 2000;104:9746–9754. [Google Scholar]
- 104.Guo H, Salahub DR. Angew Chem Int Ed. 1998;37:2985–2990. doi: 10.1002/(SICI)1521-3773(19981116)37:21<2985::AID-ANIE2985>3.0.CO;2-8. [DOI] [PubMed] [Google Scholar]
- 105.Guo H, Karplus M. J Phys Chem. 1994;98:7104–7105. [Google Scholar]
- 106.Zhao YL, Wu YD. J Am Chem Soc. 2002;124:1570–1571. doi: 10.1021/ja016230a. [DOI] [PubMed] [Google Scholar]
- 107.Wieczorek R, Dannenberg JJ. J Am Chem Soc. 2003;125:8124–8129. doi: 10.1021/ja035302q. [DOI] [PubMed] [Google Scholar]
- 108.Moisan S, Dannenberg JJ. J Phys Chem B. 2003;107:12842–12846. [Google Scholar]
- 109.Salvador P, Kobko N, Wieczorek R, Dannenberg JJ. J Am Chem Soc. 2004;126:14190–14197. doi: 10.1021/ja0492788. [DOI] [PubMed] [Google Scholar]
- 110.Viswanathan R, Asensio A, Dannenberg JJ. J Phys Chem A. 2004;108:9205–9212. [Google Scholar]
- 111.Sheridan RP, Lee RH, Peters N, Allen LC. Biopolymers. 1979;18:2451–2458. [Google Scholar]
- 112.Van Duijnen PT, Thole BT. Biopolymers. 1982;21:1749–1761. [Google Scholar]
- 113.Morozov AV, Tsemekhman K, Baker D. J Phys Chem B. 2006;101:4503–4505. doi: 10.1021/jp057161f. [DOI] [PubMed] [Google Scholar]
- 114.Asensio A, Kobko N, Dannenberg JJ. J PHys Chem A. 2003;107:6441–6443. [Google Scholar]
- 115.Gilli G, Bellucci F, Ferretti V, Bertolasi V. J Am Chem Soc. 1989;111:1023–1028. doi: 10.1021/ja00269a047. [DOI] [PubMed] [Google Scholar]
- 116.Subramanian K, Lakshmi S, Rajagopalan K, Koellner G, Steiner T. J Mol Struct. 1996;384:121–126. [Google Scholar]
- 117.Turi L, Dannenberg JJ. J Am Chem Soc. 1994;116:8714–8721. [Google Scholar]
- 118.Blessing RH. J Am Chem Soc. 1983;105:2776–2783. [Google Scholar]
- 119.The dipole for the bicyclic urea in the streptavidin model binding site is derived by subtracting the dipole vector contributions of the surrounding hydrogen-bonding residues from the total dipole moment.
- 120.Menard R, Storer AC. Biol Chem Hoppe-Seyler. 1992;373:393–400. doi: 10.1515/bchm3.1992.373.2.393. [DOI] [PubMed] [Google Scholar]
- 121.Nachon F, Asojo OA, Borgstahl GE, Masson P, Lockridge O. Biochemistry. 2005;44:1154–1162. doi: 10.1021/bi048238d. [DOI] [PubMed] [Google Scholar]
- 122.Strzelczyk AA, Dobrowolski JC, Mazurek AP. J Mol Struct (THEOCHEM) 2001;541:283–290. [Google Scholar]
- 123.Lei Y, Li H, Zhang R, Han S. J Phys Chem B. 2004;108:10131–10137. doi: 10.1021/jp049207v. [DOI] [PubMed] [Google Scholar]
- 124.Fry DC, Fox TL, Lane MD, Mildvan AS. J Am Chem Soc. 1985;107:7659–7665. [Google Scholar]
- 125.Tonan K, Adachi K, Ikawa S. Spectrochim Acta, Part A. 1998;54:989–997. [Google Scholar]
- 126.Lazaridis T, Masunov A, Gandolfo F. Proteins: Struct Funct and Gen. 2002;47:194–208. doi: 10.1002/prot.10086. [DOI] [PubMed] [Google Scholar]
- 127.Gonçalves PFB, Stassen H. Pure Appl Chem. 2004;76:231–240. [Google Scholar]
- 128.Korndörfer IP, Skerra A. Protein Science. 2002;11:883–893. doi: 10.1110/ps.4150102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Energies and Cartesian coordinates of all structures calculated at B3LYP/6-31+G(d,p) and MPWB1K/6-31+G(d,p) including counterpoise corrections, solute-solvent energy pair distributions for biotin, MD average structures of unliganded (strept)avidin, and complete refs. 63 and 79. This material is available free of charge via the Internet at http://pubs.acs.org.