Evolution exacerbates the paradox of the plankton

Abstract

Can biodiversity evolve and persist in a uniform environment? This question is at the heart of the plankton paradox: in the natural world we observe many species sharing few resources, whereas the principle of competitive exclusion would lead us to expect that only a few species could coexist in such circumstances. To bridge the gap between theory and observation, previous studies have shown that the maximum number of species that can stably coexist is equal to the number of essential resources and that even more species can coexist out of equilibrium. These studies were viewed as a significant step toward a resolution of the paradox. Evolutionary dynamics, however, have been studied in this context only in limited cases, and it is largely unknown how mutations impact ecologically stable multispecies states, and whether large species consortia can spontaneously evolve. In the present study we introduce evolution to the standard ecological model of competition for essential resources. Combining numeric and analytic approaches, we find that ecologically stable species communities are severely destabilized by long-term evolutionary dynamics. Moreover, the number of species in spontaneously evolved consortia is much lower than the number of available resources. Contrary to expectations based on studies of two resources, these limits on biodiversity are not results of the occasional emergence of superspecies, superior to all competitors; nor are they alleviated by the inclusion of tradeoffs in resource utilization. Rather, we show that it is an accelerated depletion of limiting resources, combined with the essentiality of resources to all species, that leads invariably to catastrophic extinctions.

The original formulation of “The paradox of the plankton” by Hutchinson (1) in 1961 was particularly draconian:

How it is possible for a number of species to coexist in a relatively isotropic or unstructured environment all competing for the same sorts of materials… According to the principle of competitive exclusion… we should expect that one species alone would outcompete all of the others (1).

One way of achieving multispecies coexistence was indicated by Petersen in 1975 (2) using a consumer-resource model of ecological interactions (3–6). Within this model, as many species can coexist in equilibrium as there are resources (2, 7), and even larger numbers of species can persist out of equilibrium (8, 9). The impact of evolutionary dynamics on species coexistence has been considered for species competing for two essential resources, where it has been argued that one species that can drive all its competitors to extinction—a “superspecies” (10)—will eventually arise (10–13). For a general number of resources, it is unknown whether rounds of mutation and selection would push systems toward or away from points of high biodiversity.

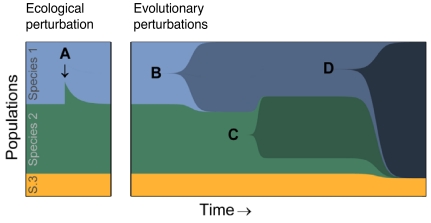
Although competition for resources determines ecological dynamics, any actual population is also subject to mutations that determine long-term evolutionary dynamics (Fig. 1). In the absence of mutations, species properties are fixed, and the system will reach an equilibrium in which species abundances and resource concentrations are not changing with time, or a dynamic coexistence in which the species abundances fluctuate but never decrease below a certain extinction threshold (8, 9). Such states are stable under ecological perturbations, such as small changes in species abundances (Fig. 1A). Beneficial mutations appearing in a given species could lead to microevolutionary adaptation of this species (Fig. 1B), speciation (Fig. 1C), or multiple extinctions (Fig. 1D).

Fig. 1.

Schematic illustration of ecological and mutational perturbations of species consortia. Abundances of each species (height of the different color bands) are shown as a function of time, starting with an ecologically stable system. After an ecological perturbation—a small deviation from equilibrium values of the concentrations of resources or abundances of species—an ecologically stable system will return to its equilibrium (A). After an adaptive mutation in one of the species, the new mutant lineage might (B) replace only its ancestor, thus keeping the number of species constant (i.e., microadaptation); (C) invade a new niche and coexist with its ancestor and the other initial species, thus incrementing the number of species by one (i.e., speciation); or (D) drive more than one other species to extinction, thus decreasing the number of coexisting species (i.e., extinction).

We construct a model that incorporates evolutionary dynamics and ecological interactions to investigate two fundamental questions: (i) whether highly diverse consortia are likely to emerge during evolution, and (ii) whether ecologically stable consortia, in which the number of species approximates the number of resources (2, 9), persist over evolutionary times. Our model tracks the evolution of n(t) species whose interactions are described by the standard model of competition for k essential resources (8, 9, 14–23), as described in Methods. A similar modeling approach was taken in studies of the evolution of food webs (24) or when resources are substitutable (25). Species are described by their requirements (inverse affinities) for and consumption of each resource. Mutants are introduced as new species whose requirement and consumption parameters are small variations on the parameters of one of the existing species (introducing random species unrelated to any existing ones was considered in ref. 26). At each adaptive step, a new mutant lineage is introduced at a low initial abundance, and the dynamics of resource competition are played out according to the ecological equations until a steady-state solution (or a persistent state with bounded fluctuations) is reached. After each mutation, the total number of species can increase by one, decrease, or remain the same, and the evolution of biodiversity is examined by monitoring the number of species as a function of time.

The system is presumed to be isolated from other communities (i.e., no migration). In addition, we assume a low mutation rate such that the time between the appearance of beneficial mutations is much longer than the equilibration time of the ecological dynamics. We make this assumption, which may not apply in certain cases (27), to account for persistent rather than transient coexistence; a high mutation rate would produce a rolling, mutation-driven state with high turnover of many similar species (28), few of which would persist if mutations stopped and the system were allowed to equilibrate. Although transient species may underlie biodiversity in some real biological systems, it is the ability of persistent coexistence to resolve the paradox of the plankton that is the focus of this work.

Results

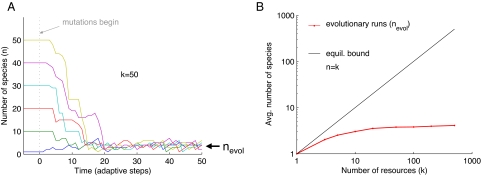
Trajectories of the number of species from six representative numerical realizations of evolution in an environment with 50 resources are shown in Fig. 2A. The different trajectories start with different numbers of species in equilibrium, but quickly converge, and after approximately 20 rounds of mutation and selection, they are indistinguishable. After the initial transient phase, the number of species remains consistently low—large species complexes never seem to naturally arise. Not only is evolution in this model apparently incapable of spontaneously finding biodiverse consortia, it also leads to a quick decline in biodiversity when starting with many species coexisting in ecologically stable configurations.

Fig. 2.

The number of species maintained by evolution is small, even when the environment contains many resources. (A) Typical trajectories of the number of species in an environment with k = 50 resources, starting with six different initial numbers of species (1, 10, 20, 30, 40, and 50) in ecological equilibrium. Once mutations are introduced (t = 0), all these trajectories quickly reach an evolutionarily stable state with a small number of species (n_evol). (B) The average number of species sustained by evolution is increasing very weakly with the number of resources in the environment (n = n_evol, red curve) compared with the largest possible number of species that can coexist in equilibrium in the absence of mutations (n = k, black line). For a given k, the value of n_evol is the average of 500 adaptive steps of 20 evolutionary runs, skipping the first 500 steps of each run. See SI Appendix.

One may expect that such constraints on biodiversity depend on the number of resources available in the environment. Considering ecological stability alone, the maximal number of species that could coexist in equilibrium is equal to the number of resources. Evolution, however, dramatically changes this picture (Fig. 2B): regardless of the number of resources available, the number of species that can coexist is very small. Fig. 2B shows the average number of species sustained over evolutionary time (n_evol) for numbers of resources (k) that span more than two orders of magnitude. Even when resources number in the hundreds (which is well greater than realistic estimates of number of essential resources), the number of species sustained over evolutionary time is fewer than five. These results depend on the assumption that the rate of beneficial mutations is low, but are only weakly dependent on other details of the mutational process [supporting information (SI) Fig. S1].

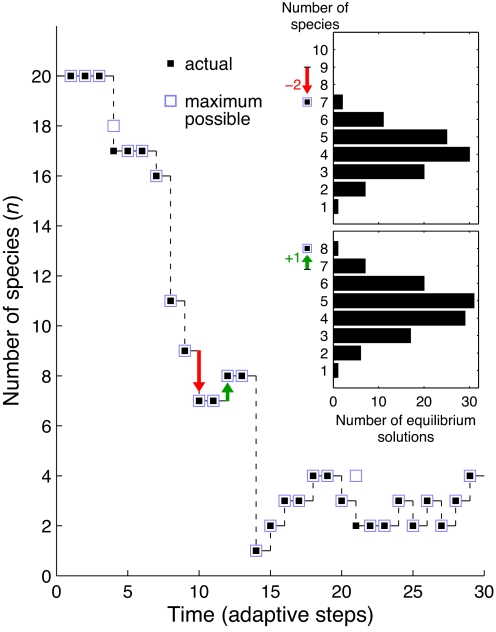
The decline of large, ecologically stable consortia after the spread of an advantageous mutation has two possible explanations: the first is that ecological equilibria that comprise many species and include the new mutant lineage exist, but such equilibria are inaccessible to the ecological dynamics. The actual equilibrium reached thus contains fewer species than the largest equilibrium state, which could have been attained had the abundances of species and resources been manually altered after the appearance of the new mutation. The second is that the number of remaining species is equal to the maximum attainable number. In this case, the specific values of the species and resource abundances at the time of mutation do not prevent the dynamics from finding a maximally biodiverse solution. To distinguish between these two explanations, we analytically determined, at each adaptive step, all of the subsets of species that contain the last added beneficial mutation and that are ecologically stable (SI Appendix). We compared the size of the largest such stable subset of species with the actual number retained after each adaptive step in the simulations (Fig. 3 and Fig. S2). The striking agreement between the maximal and the actual argues in favor of the second explanation: the decline in the number of species is a consequence of the evolved properties of the species and not of historical constraints imposed on the ecological dynamics.

Fig. 3.

Decline in community size is determined by properties of the evolved species rather than by constraints on the ecological dynamics. Shown is the number of species as a function of time in a typical evolutionary run with k = 20 resources. The actual number of species obtained in the simulation following each adaptive step (black squares) almost always equals the size of the largest possible subset of species at that step that includes the new beneficial mutant, and that can coexist in equilibrium (blue squares). Only two cases are seen in this example in which the actual number of species reached is smaller than the maximal possible (empty blue squares at t = 4 and t = 21). (Inset) Distributions of number of species within all of the species subsets that include the new mutant lineage and allow ecological equilibrium at two representative adaptive steps of extinction and speciation (down-pointing red arrows and up-pointing green arrows). The maximum of each distribution, corresponding to the largest possible stable species consortium, is indicated by the blue squares. The arrows indicate the actual change in the number of species at these two steps.

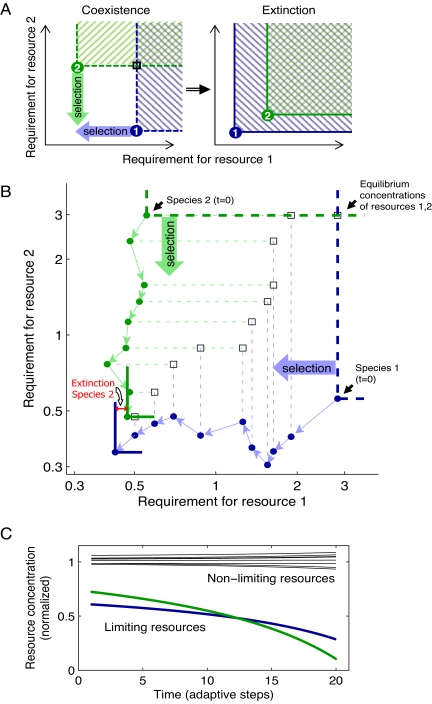
Both the collapse of large consortia of species and the inability of evolution to build up such consortia are determined by the balance between speciation and extinction. This balance is shaped by changes in the equilibrium concentrations of resources. In equilibrium, resources that are most limiting for one of the species tend to be at lower concentrations compared with nonlimiting ones. Further, because adaptation by natural selection improves the affinity of an evolving species to its most limiting resource, the equilibrium concentrations of such limiting resources are steadily driven down (Fig. 4A). Although nonlimiting resources may also undergo depletion, selection drives limiting resources to lower concentrations than nonlimiting ones (see analytic proof in SI Appendix). Ultimately, as a limiting resource is being repeatedly depleted by the spread of mutant lineages, its concentration may decrease below the threshold needed to support one or more of the other species, thereby driving them to extinction. Figs. 4 B and C demonstrate this point for two species competing for 10 resources. Key to such extinctions is the essentiality of all resources to all species, which is inherent to the model. The depletion of the limiting resources relative to the nonlimiting ones also helps explain why adaptation rarely explores new niches associated with a currently nonlimiting resource. The most limiting resource for a new mutant lineage is likely to be one that is already limiting one of the existing species, as such resources are present at the lowest concentrations. The inability of new and old to coexist when limited by the same resource implies that a mutant lineage often replaces at least one of the other species. We conclude that the spread of a beneficial mutation rarely leads to an increase in the number of species and is, in fact, likely to trigger several extinctions (29) (see detailed discussion in SI Appendix and Figs. S3–S6).

Fig. 4.

Depletion of limiting resources by evolutionary adaptation leads to extinctions and reduces the chance for speciation. Schematic diagram (A) and simulation results (B) show two evolving species (“1,” blue; “2,” green) characterized by their minimal requirement for each of two resources (green and blue points). (B) Species are competing for a total of 10 resources, but only the two limiting ones are shown. Resource concentrations on the L-shaped lines going through these points result in growth rates that exactly balance the mortality rate (i.e., zero isoclines). Net growth for each species is positive above its zero isocline (hashed in A). Intersection of the zero isoclines is required for species coexistence and defines the equilibrium concentration of resources (black squares). At such equilibrium, each species is limited by a different resource (species 1 by resource 1 and 2 by 2). Selection acts to reduce requirement for the most limiting resource of each species (blue and green heavy arrows) and pushes the corresponding limiting resource down (individual adaptive steps are shown in B by thin blue and green arrows). Ultimately, this results in extinction of one of the species (species 2), as the resource limiting the other species falls below its requirement (A and B, solid blue isocline contains solid green isocline). (C) Smoothed curves of data from the simulation in B show the concentration of the two limiting resources decreasing compared with the eight other nonlimiting resources (black). Values are normalized by the median concentration of all resources.

Discussion

Based on intuition from two resources (10), it might be expected that events of mass extinction are consequences of invasion by superspecies—species superior to all species they drive extinct. Although superspecies are indeed the agents of extinction when only two resources are present, the importance of superspecies decreases quickly with the number of resources, and the invading mutant is typically superior in one-on-one competition to only approximately half of the species that it drives to extinction (Fig. S7). In addition, it has been suggested that tradeoffs in the utilization of resources—whereby species can improve their efficiency at using some resources only at the expense of getting worse at using others—are necessary for coexistence (10, 30), restoring biodiversity by preventing or retarding the evolution of superspecies. Because superspecies do not play a critical role in the dynamics that we see, we would not expect our results to change significantly when tradeoffs are added to the model. Indeed, in the presence of explicit tradeoffs, the fundamental result does not change: the number of species sustained over evolutionary time is small even when resources are many (Table S1). Neither the presence of superspecies nor the absence of tradeoffs contributes substantially to low biodiversity. Rather, it is the rapid depletion of limiting resources, which we demonstrate analytically and numerically, that is the prime cause of extinction and the greatest impediment to the development of biodiversity.

Resolutions of the paradox of the plankton based on ecological models must also make sense in light of evolution. Previous work on models of competition for essential resources in uniform environments has identified ecologically stable solutions in which the number of species equals the number of resources, leading to a reformulation of the paradox: how can there be more species than resources? More recently, chaotically fluctuating states have been discovered with even more species than resources. Evolution, however, does not seem to favor any of these solutions. Neither does evolution in such models allow for the spontaneous generation of communities with more than a few species. The underlying reason for this is the strong dependence among coexisting species induced by the essentiality of all resources that hampers speciation and often leads to ecological collapse of several species simultaneously. Alternative forms of species interactions, such as competition for substitutable resources and exchange of toxic or essential materials, may be more robust to the diversity-limiting effects of mutation. However, in the classical model of competition for essential resources, the paradox of the plankton is really Hutchinson's (1): how can the number of species in a uniform environment ever greatly exceed one?

Methods

Mutation-Ecology Model.

The mutation–ecology model describes dynamics of species that are subject to repeated rounds of mutation and selection. Mutation involves the generation of a mutant species by perturbing the properties of one of the existing species. The new mutant lineage is introduced to the community at an initial low abundance. This is followed by a selection phase in which species compete for resources according to the ecological set of differential equations described in the following paragraphs.

Selection.

Let n be the number of species present at the beginning of the selection phase, with abundances N_i (i = 1, …, n), competing for k essential resources whose concentrations are denoted by R_j (j = 1, …, k). The coupled dynamics of species and resources are described by the system of differential equations (2, 14, 16):

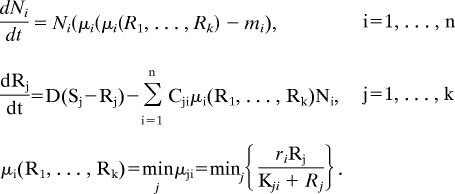Here, D is the system's turnover rate; S_j is the supply concentration of resource j; m_i and r_i are the mortality rate and maximal growth rate of species i; and K_ji and C_ji are the requirement and the consumption rate of resource j by species i. The equation for μ_i is based on Liebig's law of the minimum (31), which states that the growth rate is determined by the most limiting resource. The growth rate vanishes when any one of the resource concentrations goes to zero, and it is in this sense that all resources are essential. The results we present are for D = m_i = 0.25, r_i =1, and S_j = 10 (for all i and j). Simulations of the differential equations are run until either a steady state or a persistent state of bounded fluctuations is obtained: a steady state is detected by the vanishing of time derivatives. If the time derivatives do not approach zero after a long time, indicating regular or chaotic fluctuations, we examine the mean of the abundances over two successive time windows containing several fluctuations (this happens in our simulations <10% of the time). If the change in the mean between the two windows is below a preset threshold, this state is assumed to be persistent. After reaching either of these persistent states (equilibrium or bounded fluctuations), n is recalculated as the number of species that did not become extinct during the competition phase (i.e., with N_i > 1). It is one of these remaining species that provides the background for the mutation that follows.

Mutation.

Mutation results in a new species with index i′ = n + 1, whose parameters K_ji′, C_ji′ are defined by small perturbations on one of the existing species with index i^m. Assuming a fixed mutation rate per individual, i^m is chosen from the existing i = 1,…, n species with probabilities

We assume that changes in each of the K_ji′, C_ji′ parameters are independent (See SI Appendix for more information on the mutational process). The selection coefficient, s = μ_i′/m − 1, of a mutation at the time of its appearance is determined only by the values of its resource requirements K_ji′ and the resource concentrations R_j at that time. Mutations are repeatedly drawn until one is found that has a selection coefficient larger than 1/N_TOT and thus has a greater chance of spreading than a neutral mutation would have. With probability P_drift (s) = 2s, the new mutant lineage escapes loss by drift and it is introduced to the environment with an initial abundance N_i′ = 1/P_drift(s). The number of species increases by one to n + 1. The system of differential equations for the next selection phase is now updated by adding a new equation for the abundance of the mutant species and by adding the appropriate consumption terms to the resource equations. The initial conditions are determined by the species and resource abundances that were reached at the end of the previous competition round, together with the initial abundance of the new mutant species.