DNA supercoiling inhibits DNA knotting

Abstract

Despite the fact that in living cells DNA molecules are long and highly crowded, they are rarely knotted. DNA knotting interferes with the normal functioning of the DNA and, therefore, molecular mechanisms evolved that maintain the knotting and catenation level below that which would be achieved if the DNA segments could pass randomly through each other. Biochemical experiments with torsionally relaxed DNA demonstrated earlier that type II DNA topoisomerases that permit inter- and intramolecular passages between segments of DNA molecules use the energy of ATP hydrolysis to select passages that lead to unknotting rather than to the formation of knots. Using numerical simulations, we identify here another mechanism by which topoisomerases can keep the knotting level low. We observe that DNA supercoiling, such as found in bacterial cells, creates a situation where intramolecular passages leading to knotting are opposed by the free-energy change connected to transitions from unknotted to knotted circular DNA molecules.

INTRODUCTION

DNA replication, transcription and recombination are greatly facilitated by type II DNA topoisomerases that catalyze passages of one double-helical region through another (1,2). While the possibility of passing DNA segments through each other is generally beneficial, it may lead to the creation of DNA knots that are deleterious for living cells if not removed efficiently (3,4). In 1997, a seminal paper demonstrated that topoisomerase II-mediated strand passages occur in a selective way that greatly reduces the formation of knots (5). Since then many experimental, theoretical and simulation approaches addressed the question of how topoisomerases select intermolecular passages that preferentially lead to unknotting rather than to knotting of randomly fluctuating DNA molecules (5–10). In those studies, the circular DNA that was used or modeled as a substrate of DNA topoisomerases was torsionally relaxed. However, in living cells the DNA is rarely torsionally relaxed. In bacterial cells, the DNA is negatively supercoiled by the action of DNA gyrase while, in eukaryotic cells, ongoing transcription or replication expose the DNA to torsional stress (11–13). We, therefore, have analyzed the effect of DNA supercoiling on DNA knotting. Our numerical simulations and model building reveal that DNA supercoiling inhibits intramolecular passages leading to DNA knotting. As a consequence we propose that one of the important biological functions of DNA supercoiling is to reduce formation of DNA knots.

If freely fluctuating, long, circular DNA molecules were permitted to undergo random intermolecular strand passages, they would be very frequently knotted (14–18). However, when circular DNA molecules are isolated from bacteria, they are rarely knotted unless the host strain is defective in DNA gyrase (19) or topoisomerase IV (20) or when topoisomerase inhibitors are added (21). That the inhibition of gyrase, which is not the unknotting enzyme per se, results in increased formation of knots suggests that DNA supercoiling may favor unknotting. Indeed, studies of the DNA decatenation activity of topoisomerase IV from Escherichia coli revealed that this enzyme decatenates supercoiled catenanes four times faster than torsionally relaxed catenanes, thus demonstrating that supercoiling facilitates simplification of DNA topology (22). However, in 1999 a simulation study that specifically addressed the effect of supercoiling on DNA knotting led to the conclusion that negative supercoiling promotes DNA knotting (23). According to that study, even very small, naturally supercoiled DNA plasmids (2.4 kb) were predicted to adopt highly knotted configurations in vivo if specialized type II DNA topoisomerases did not bring the knotting level below the so-called topological equilibrium (5). Intrigued by the contradiction between the experimental and numerical results, we performed simulation studies with the hope of resolving the contradiction. We first addressed the question whether knotting is favorable when the torsional tension is maintained in knotted DNA molecules at the same level as in unknotted supercoiled DNA. Addressing this point, we abstracted from the point how quickly the interplay between DNA gyrase, topoisomerase I and topoisomerase IV re-establishes the same level of torsional tension after a knotting event. Subsequently, we have considered direct consequences of the fact that knotting event changes the linking number of the concerned DNA molecules and partially re-establishes the torsional tension in the DNA that becomes knotted. We have found that the earlier modeling study by Podtelezhnikov et al. (23) did not account for the changes of DNA linking number associated with the topoisomerase-mediated strand passage from supercoiled unknots to supercoiled knots and also neglected the homeostatic mechanisms that maintain a quasi constant level of torsional stress in DNA (24,25). When these factors are taken into account, the numerical simulations agree with the biochemical data and point out that DNA supercoiling inhibits DNA knotting.

MATERIALS AND METHODS

Simulation procedure

To generate an equilibrium ensemble of modeled DNA molecules, we have applied a Metropolis Monte Carlo calculation procedure. In our procedure, the worm-like chain evolved by crankshaft rotations of subchains (26) and by slithering moves. Slithering moves are based on the principle that when each segment in a subchain is represented as a vector, then changing the order of the vectors does not change the sum of the vectors. This principle allows us to select a random subchain (set of consecutive vectors) and replace it by a circularly permutated set where just one segment (vector) is moved from the first to the last position of the subchain. During the crankshaft rotations and the slithering moves, the chain behaves like a phantom chain permitting intersegmental passages, but a new configuration is only considered when the smallest distance between any two nonconsecutive segments is >2 nm. For each new considered configuration, the total elastic energy (bending plus torsional) is calculated. If the energy of a trial configuration is lower than that of the starting configuration, it is always accepted and serves then as the starting configuration for the next trial. If the trial configuration has a higher total energy than the starting configuration, then it also can be accepted, but only with an exponentially suppressed probability P = exp(−Δ E/K_BT), where ΔE = E_NEW − E_OLD is the energy difference between the two configurations. It is important to add here that the Monte Carlo calculation procedure only serves to sample the configuration space and is not intended to reflect the actual kinetics of modeled DNA molecules. Typical simulation runs investigating knotting probability at a given level of DNA supercoiling (see Figure 2A for example) involved 2 100 000 Monte Carlo moves. The first 100 000 were given to the system to reach equilibrium and were not taken into the statistics. We averaged our results over 10 such independent runs.

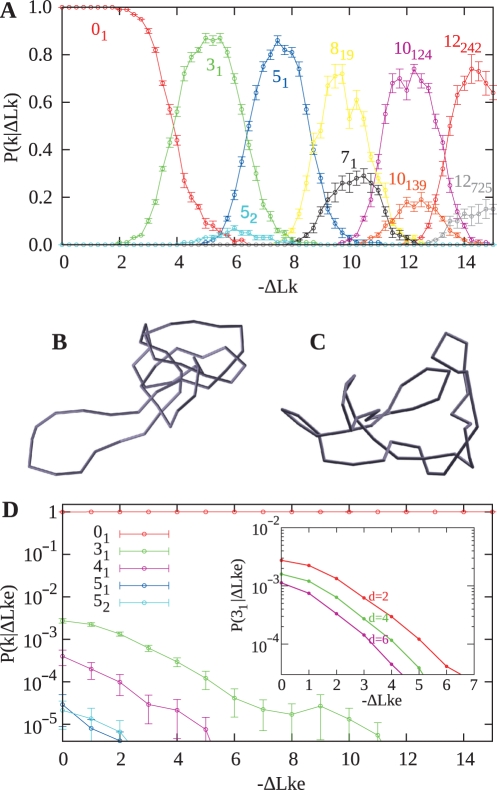
Figure 2.

Comparison of probabilities of knotting in simulations that keep the ΔLk constant and those that maintain the same effective level of DNA supercoiling. (A) Conditional probability profiles of various knots obtained in numerical simulations where ΔLk was kept constant. (B) Snapshot of knot 10₁₂₄ that has a torsionally relaxed appearance despite having ΔLk = −12. (C) Snapshot of the unknot with ΔLk = −12 reveals that supercoiling is present. (D) Conditional probability profiles of various knots obtained in numerical simulations where ΔLke was kept constant. The logarithmic scale shows that knotting is many orders of magnitude lower than knotting in simulations shown in (A). Inset in (D) shows how changes of the effective diameter of modeled DNA affect the probability of trefoil knot formation for a given ΔLke.

The knot type of the analyzed configurations was recognized by calculating the Alexander polynomial (27). The introduced writhe bias practically assured that the formed chiral knots were all of negative type (23,28).

RESULTS

DNA model

The mechanical properties of DNA are very well approximated by abstracting from its helical structure and assuming that it forms an elastic rod with a 2 nm diameter. When such an elastic rod is closed into a circle, without introducing any torsion, the resulting state corresponds to a torsionally relaxed circular DNA. When torsion is introduced by twisting the rod several times before gluing its two ends together, the rod adopts a coiled configuration that corresponds to the supercoiled form of DNA since ‘primary structure’ of the elastic rod represents already a double helix. For practical reasons (e.g. computing time), in simulation studies investigating the overall equilibrium shapes of DNA molecules, one replaces the continuous version of an elastic rod model with a discrete (composed of straight segments) version of a worm-like chain (23). In our simulations, the worm-like chain was built by replacing each Kuhn statistical segment of the freely jointed model with five segments whose connections are given bending and torsional resistance. The bending energy of such a chain (E_b) is given by the formula 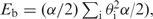where α is the bending modulus of DNA, and 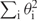is the sum of the squares of the angles between all pairs of adjacent segments. The energy of torsional deformation (E_t) of such a worm-like chain is given by E_T = (2π² C/L)(Δ Lk − Wr), where C is the torsional rigidity constant of DNA, L is the length of the modeled DNA chain (we use L = 1000 nm), ΔLk is the number of turns by which the rod was twisted before gluing its two ends together and Wr is the 3D writhe of the analyzed configuration of the worm-like chain model. The writhe is a measure of chirality of oriented closed curves in space and can be estimated by averaging the sum of oriented self-crossings over many projections (2D Wr) along equally distributed directions in the space. In every projection, each positive crossing is scored as +1 and each negative crossing is scored as −1 (2,29) (Figure 1A and B). The writhe of a given configuration of a DNA molecule is calculated for the axial line of the entire circular molecule.

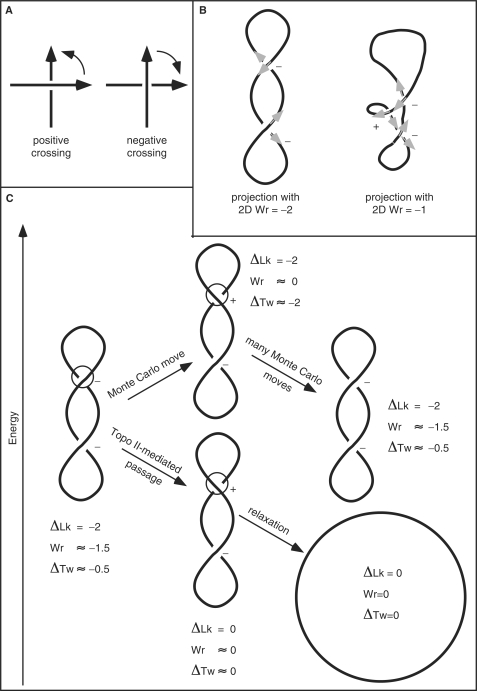
Figure 1.

Topology and numerical simulation of supercoiled DNA. (A) Crossing sign convention. When the axis of circular DNA molecules is considered as an oriented curve (see B), each perceived crossing can be given a sign according to the rotation direction needed to align the imaginary arrow on the overlying segment with the imaginary arrow on the underlying segment while the rotation can not exceed 180°. Positive crossings require a counter-clockwise rotation to align the arrows while the opposite applies to negative crossings (2). In writhe (Wr) calculations, positive crossings score as 1 and negative as −1. (B) Writhe of a given projection (2D writhe) and a global Wr. The same rigid configuration of supercoiled DNA can have different 2D writhe depending on the direction of the projection. In a lateral projection the molecule reveals two negative crossings, but in a ‘tilted’ projection one observes an additional positive crossing. The 3D global writhe is usually denoted as Wr and is the average over all 2D writhe values. (C) Differences between topological and physical consequences of Topo II-mediated passages and those occurring in standard Monte Carlo simulations. In standard Monte Carlo simulations, the linking number of modeled DNA does not change after intersegmental passage. This contrasts with the physical and biological fact that such intersegmental passages change the linking number by 2. Energetic and topological consequences of intersegmental passages in standard Monte Carlo simulations (upper pathway) are compared to consequences of real Topo II-mediated passages (lower pathway). Notice that although the minimal move that results in an intersegmental passage changes the Wr value by nearly 2, the writhe change is different between an equilibrium state before the passage and an arbitrary state after the passage.

To model DNA under conditions of significant charge neutralization, as is the case in vivo, we have set the hard-core repulsion radius to 1 nm (30). However, we have also checked that the conclusions of our study are not changed when the modeled DNA has a higher effective diameter, like 5 nm, for example, as in simulations performed in ref. (18). The DNA modeled in this study corresponds to 3 kb circular DNA molecules (i.e. slightly bigger than a popular cloning vector pUC18); the bending modulus α was set to 0.943 × 10⁻²⁰ J, while the torsional rigidity constant C was set to 3 × 10⁻¹⁹ J nm as in the earlier simulation studies (23).

Topological differences between real and simulated chains

To understand the Metropolis Monte Carlo numerical calculation approach (see Materials and methods section), it is very important to consider why the modeled supercoiled unknotted DNA molecules do not relax to nonsupercoiled circles in spite of being permitted to undergo multiple intersegmental passages during the simulation procedure that always accepts the lower energy configuration. Supercoiled DNA molecules, in solution in the absence of DNA topoisomerases, will tend to minimize their free energy and can achieve this by optimal partition of their ΔLk into writhe (Wr), with the consequent bending stress, and into the change of twist ΔTw = ΔLk − Wr), with the consequent torsional stress (Figure 1C). The actual optimal partition value between Wr and ΔTw is a function of ionic conditions. The writhe can absorb about 60% of ΔLk at low-ionic strength and about 90% at high-ionic strength (30). The partition of ΔLk into Wr and ΔTw decreases the energy of the molecules since both torsional and bending energies grow with the square of the respective deformation angle. The partition is biased toward writhe as the writhe does not translate directly into the bending angle and the values of bending and torsional rigidity constants are different.

Let us consider now a supercoiled DNA molecule whose configuration has a nearly optimal ΔLk partition for given conditions (75% into Wr and 25% into ΔTw, in this example) but is permitted to undergo intramolecular strand passage reactions such as those mediated by type II DNA topoisomerases (Figure 1C). In real DNA molecules, each intermolecular passage mediated by type II DNA topoisomerases changes the ΔLk by 2 or −2 depending on the direction of the passage (2,31,32). Therefore, a DNA molecule that has a ΔLk of −12, for example, requires just six passages to become completely relaxed and the free-energy gradient favors and selects passages that lead to the relaxation (see the lower pathway in Figure 1C). However, in standard Metropolis Monte Carlo simulations of supercoiled DNA, the ΔLk value is entered as a fixed parameter of the model and remains unchanged after intramolecular passages (see upper pathway in Figure 1C). In contrast to ΔLk, the writhe (Wr) of modeled molecules changes after each passage that changes the sign of the concerned crossing (see upper pathway in Figure 1C), since the writhe is determined by the actual momentary trajectory of the simulated chain. Therefore, after a DNA strand passage simulation event, the energy of the modeled molecule that already had close to optimal ΔLk partition would go up since the partition of ΔLk between the writhe and ΔTw would not be as favorable as it was before the strand passage. As a consequence, such passages will only be rarely accepted, as moves leading to new configurations. In cases where such moves will be accepted, the modeled molecules will evolve further and will tend to return to the vicinity of the energy minimizing configurations with the optimal partition of ΔLk into ΔTw and Wr. This return can be achieved either by a reverse passage or by a combination of many crankshaft and slithering moves (Figure 1C).

The nonphysical behavior of the simulated chains that do not change the linking number after intersegmental passages is, therefore, convenient for modeling supercoiled DNA as it allows for efficient sampling of the available configuration space of the molecules with a given ΔLk, while the path by which a new state is reached is not relevant for the sampling. In addition, the molecules do not get relaxed and it is not necessary to supercoil them again. Therefore, the modeling approach that permits strand passages but maintains constant DNA linking number has proved to be a reliable method for simulation studies of DNA supercoiling of unknotted DNA molecules (26,30). Previously, this nonphysical behavior of modeled chains was considered to be advantageous and there was no concern that it could lead to artifacts. We will show below that there are situations where that nonphysical behavior of modeled chains may be misleading.

Knots that keep their linking number, but lose supercoiling

Addressing the influence of DNA supercoiling on DNA knotting, we have checked first whether our numerical calculation procedure can reproduce the results of Podtelezhnikov et al. (23). For this reason, we have performed many independent Metropolis Monte Carlo simulations in which the ΔLk was kept at a given constant value and the modeled chains were permitted to lower their energy. In agreement with Podtelezhnikov et al., we observed that higher the initial supercoiling level of the modeled molecules, the more complex were the knots into which the modeled molecules were converted to (Figure 2A). Also, the overall appearance of the knots was very similar to those observed by Podtelezhnikov et al., revealing that the knots obtained in the simulation were practically torsionally relaxed i.e. they were not supercoiled (Figure 2B and C). A snapshot of a knot 10₁₂₄, which was the most frequent knot observed for DNA molecules with ΔLk = −12, reveals a configuration free of torsional stress (Figure 2B). For comparison, a snapshot of unknotted molecules with ΔLk = −12 shows plectonemic interwinding, demonstrating that the molecules are under torsional stress (Figure 2C).

Reintroduction of DNA supercoiling disfavors knot formation

In studies where the Metropolis Monte Carlo calculation method was shown to closely reproduce the experimentally observed physical behavior of supercoiled DNA circles, the phantom chain was maintained in the unknotted form by not accepting moves that changed unknotted circles into knotted ones (30). However, Podtelezhnikov et al., allowed the phantom chains to change the knot type. As a consequence, the modeled chains with fixed ΔLk were permitted to lower their free energy by formation of torsionally relaxed knots with high writhe (23). However, if formation of torsionally relaxed DNA knots would have happened in living bacterial cell, then DNA gyrase would re-establish their torsional tension by changing their original ΔLk. It is well known now that a complex homeostatic mechanism in bacterial cells maintains a practically constant level of torsional tension at given growth conditions (24,25). Too strong negative supercoiling activates bacterial topoisomerase I (Topo I) that partially relieves the torsional stress in vitro (33) and in vivo (25); torsionally relaxed DNA is, on the other hand, the preferred substrate of DNA gyrase that reintroduces DNA supercoiling (34). In addition, the expression of the gene encoding Topo I is activated by increased supercoiling (35) and the genes encoding gyrase are activated by DNA relaxation (36,37). The fine-tuning of DNA supercoiling to a nearly constant level is very important for normal functioning of DNA and for regulatory response to changing growth conditions (38). Additional gene products participate in the intricate regulatory network that homeostatically regulates the torsional tension of DNA in bacterial chromosomes (38,39). The existence of homeostatic mechanisms regulating the torsional tension of DNA in cells was neglected in the previous consideration of the interplay between supercoiling and knotting (23).

To a first approximation, interplay between DNA gyrase, Topo I and also Topo IV (25) would be expected to result in the same level of torsional tension in knotted and unknotted DNA molecules. This means that the linking number of torsionally relaxed knotted DNA would be decreased by approximately the same number as that of torsionally relaxed unknotted DNA of the same size. Torsionally relaxed chiral knots have an equilibrium linking number (Lk₀) different from torsionally relaxed unknots (14). This results from the fact that the DNA linking number (Lk) is the sum of DNA twist (Tw) and writhe (Wr), Lk = Tw + Wr (11). In torsionally relaxed DNA forming a knot, the twist of the DNA is the same as in torsionally relaxed unknotted DNA molecules. However, the writhe is different. Therefore, the equilibrium linking number of knotted DNA molecules differs from that of unknotted DNA molecules and the difference is equal to the average writhe of relaxed knotted DNA molecules. Importantly, the average writhe of relaxed knotted DNA is independent of length and depends only on knot type (40–42). The writhe of relaxed knots was calculated earlier (40–42) and confirmed by Podtelezhnikov et al. (23). For the knots relevant for this study, i.e. the left-handed 3₁, 5₁, 5₂, 7₁, 8₁₉, 10₁₂₄, 10₁₃₉, 12₂₄₂, 12₇₂₅ and achiral 4₁ knot, the corresponding writhe values were taken as: −3.42, −6.23, −4.57, −9.03, −8.59, −11.17, −11.38, −13.57, −13.68 and 0, respectively. Thus, for example, the equilibrium linking number (Lk₀) of a left-handed trefoil knot is decreased by ∼3.42 compared to the equilibrium linking number of an unknotted DNA circle (40).

Knowing the difference between the equilibrium linking number of unknots and various knots, we can introduce a correction into the ΔLk of modeled knotted DNA so that the effective ΔLk (ΔLke), which is defined as the difference between the actual Lk and the equilibrium linking number for the given knot, does not change after intersegmental passage from a supercoiled unknot to a given knot (this amounts to replacing the torsion energy by E_T = (2π²C / L)(ΔLke − Wr)². This operation is needed for the calculation of the free-energy difference between the unknot and a given knot, that are both supercoiled to the same extent. Thus, for example, if a modeled unknotted molecule with ΔLke = −5 forms after the intersegmental passage a left-handed trefoil knot, its ΔLk is changed to −8.43 to maintain the same effective level of supercoiling as before the passage (ΔLke = −5). Upon introducing the procedure that keeps the ΔLke constant, we can check whether the modeled supercoiled molecules still ‘escape’ from supercoiled unknots into supercoiled knots. To this aim, we proceeded with a new round of Metropolis Monte Carlo simulations in which phantom chains were free to change their knot type, but before calculating the energy of the trial configuration, we determined the new knot type and adjusted the ΔLk accordingly to keep the same ΔLke as before the passage. Figure 2D shows that upon applying this procedure, the frequency of knot formation decreased by several orders of magnitude when compared to the situation presented in Figure 2A. Importantly, only relatively simple knots were observed, similar to those seen earlier with relaxed DNA (14,15). Inset in Figure 2D shows that the knotting attenuation by DNA supercoiling is even stronger for the modeled DNA with a higher effective diameter [d = 5 nm was used by Podtelezhnikov et al. (23)]. It is important to add here that the low probability of knotting, observed by us, simply reflected the thermodynamic equilibrium for DNA kept at constant ΔLke. It is a qualitatively different situation to experiments described by Rybenkov et al. where the type II DNA topoisomerases were lowering the knotting level below that at so called topological equilibrium (22). We propose that DNA gyrase provides the energy gradient that acts against DNA knotting.

Topological and energetic consequences of intramolecular passages from unknots to knots

We have shown above that replenishing of DNA supercoiling by DNA gyrase inhibits DNA knotting. The precise extent of the inhibitory effect depends on the actual level of ΔLke maintained by DNA in knotted DNA molecules. We have assumed, above, that the ΔLke maintained by DNA in vivo is similar for different knot types, including unknots. However, the energetic costs of DNA supercoiling are higher in knotted than in unknotted DNA molecules (Figure 4) and therefore the absolute value of ΔLke maintained by DNA gyrase in knotted DNA molecules may be lower than that in unknotted DNA molecules of the same size. To be independent from any assumptions regarding the ΔLke, we consider now the ‘worst case’ scenario where DNA gyrase does not intervene to re-establish the supercoiling, but where the topoisomerase-mediated passage from negatively supercoiled, unknotted DNA molecules to negative trefoils changes the DNA linking number by −2 (as necessary for this type of reaction).

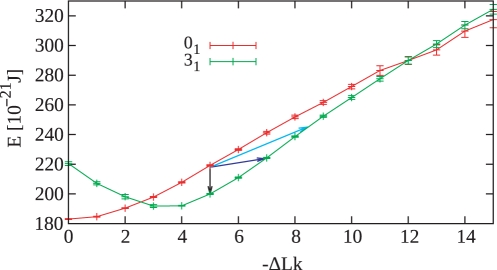
Figure 4.

Comparison of energy difference between supercoiled unknot and left-handed trefoil knots with corresponding ΔLk. The light blue arrow indicates the energy difference between unknot and trefoil knot with the same ΔLke. The dark blue arrow indicates the energy difference between the unknot and a trefoil knot resulting from one round of a Topo II-like action. The black arrow indicates the energy difference between the unknot and a trefoil knot formed under the unrealistic assumption that topoisomerase II could mediate an intramolecular passage reaction without changing the linking number. The energy values were obtained by simulations of 3 kb DNA molecules that formed unknotted circles or left-handed trefoil knots, respectively. Note that left-handed trefoil knots reach their minimal energy state for ΔLk ≈ −3.5 and that this closely corresponds to the average writhe of torsionally relaxed left-handed trefoil knots (40–42) which by definition would have ΔLke = 0.

In Podtelezhnikov et al. (23) and also in our repetition of their calculations (Figure 2A), left-handed trefoil knots were most favored when the modeled small DNA circles had ΔLk = −5. We therefore analyzed the case in which a negatively supercoiled DNA with ΔLk = −5 is converted by an intermolecular passage into a left-handed trefoil knot. Bacterial topoisomerase IV (Topo IV), which is a type II DNA topoisomerase, can mediate such a reaction and its action, in contrast to DNA gyrase, is not associated with active introduction of DNA supercoiling. The main physiological function of Topo IV is decatenation of replication and recombination intermediates and DNA unknotting (2,20,43,44).

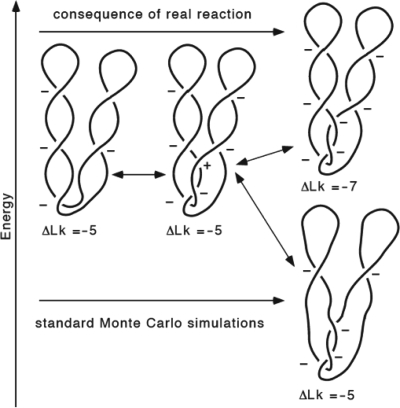
As shown in Figure 3, negatively supercoiled DNA can form a left-handed trefoil knot by an intermolecular passage between neighboring coils of an interwound superhelix. For this to happen, a positive accidental overlap needs to be converted to a negative nonreducible crossing by the action of a type II DNA topoisomerase. In a real reaction (upper right, Figure 3), such an intermolecular passage changes a positive crossing into a negative one and this decreases the linking number by 2, i.e. in this example, the ΔLk changes from −5 to −7. Since negatively supercoiled DNA is already underwound, such an intramolecular passage increases the free energy of the molecule (see dark blue arrow in Figure 4). For this reason, in real reactions, the free-energy gradient acts against such an intramolecular passage. However, in the simulation studies by Podtelezhnikov et al., the same type of intramolecular passage was favored by the free-energy gradient due to the unphysical assumption that DNA linking number stays unchanged after knotting (see the lower right part of Figure 3 and the corresponding energy change indicated with the black arrow in Figure 4). Figure 4 permits us also to see the energy difference between unknots and trefoils with the same ΔLke (compare unknots and trefoils that differ in their linking number by 3.42 such as the case indicated with the light blue arrow). The arrows in Figure 4 show the difference of energy for the corresponding knotting event starting from the 3 kb unknot of ΔLk = −5. However, the ΔLk of this size DNA in bacterial cells is about −15. At that level of supercoiling, a strand passage that changes the ΔLk = −15 unknot into a ΔLk = −17 trefoil would be much more strongly opposed by the high-energy difference than the passage between the ΔLk = −5 unknot to the ΔLk = −7 trefoil (Figure 4).

Figure 3.

Energetic and topological consequences of a Topo II- mediated strand passage leading to conversion of supercoiled unknot into knot (upper pathway) as compared to corresponding knotting event in standard Monte Carlo simulations (lower pathway).

The example discussed above shows that knotting is opposed by the free-energy gradient of sufficiently supercoiled DNA molecules even without replenishment of DNA supercoiling by DNA gyrase. This is due to the fact that knotting events change the linking number of the concerned DNA molecules. However, a complete or partial replenishment of DNA supercoiling after knotting events is expected to additionally limit the lifetime of DNA knots. It is important to note that our studies do not provide any information about the actual kinetics of knotting and unknotting in vivo.

Above, we considered the topological and energetic consequences of forming negative knots with irreducible topological crossings. However, it is also possible to have DNA knots with positive irreducible crossings and such knots can be formed as a result of site-specific recombination acting on negatively supercoiled DNA (45). The question arises, then, whether negative supercoiling would oppose or favor type II topoisomerase-mediated formation of knots with positive crossings. Let us analyze the topological consequences resulting from formation of a right-handed trefoil out of a negatively supercoiled DNA with ΔLk = −10, for example. The Topo II-mediated passage that would create positive trefoils out of negatively supercoiled DNA would change the ΔLk of the DNA to −8. However, at the same time the ΔLke would change to that of the right-handed trefoil in its relaxed form, i.e. to 3.42. Therefore, the absolute value of ΔLke would increase from 10 to 11.42 as a result of the knotting event. This example demonstrates that negative supercoiling should also inhibit formation of knots with positive crossings.

DISCUSSION

We have provided evidence that the results of Podtelezhnikov et al. (23) indicating that supercoiling promotes DNA knotting were a direct consequence of not accounting for two biological mechanisms: (i) If DNA gets torsionally relaxed as a result of knotting, the homeostatic mechanisms within cells re-establish its original level of supercoiling and this eliminates the energetic gain caused by knotting. (ii) Type II topoisomerase-mediated intramolecular passages leading to knots change the linking number of the affected DNA molecules.

It is appropriate to discuss here an earlier biochemical study by Wasserman and Cozzarelli (46) demonstrating that when negatively supercoiled DNA is incubated with an excess of Topo II one observes twist-type knots with negative crossings. That study seems to support a possibility that negative supercoiling promotes knots formation, which would differ from the conclusions here. However, the authors of that earlier study clearly stressed that the formation of knots was only observed when an excess of topoisomerase was used and that this presumably caused formation of topoisomerase-mediated adhesion between branches of supercoiled DNA molecules. Topoisomerase action within such a constrained state leads then to formation of twist knots. A somewhat similar stimulation of knotting was observed when an excess of Topo I was incubated with relaxed nicked DNA molecules (47). Therefore, in both of these cases the observed frequency of knotting does not reflect the topological equilibrium state dictated by the properties of DNA molecules that are freely fluctuating in a solution. In contrast, the study of Podtelezhnikov et al. and also our current study were intended to investigate the topological equilibrium of freely fluctuating negatively supercoiled DNA molecules.

Over the last 10 years, several studies addressed the question of how DNA topoisomerases maintain the DNA knotting level below the topological equilibrium that would be obtained if topoisomerase-mediated intersegmental passages were occurring at random (8–10,48). These studies, in large part, explored nonsupercoiled DNA since the original experiments were performed using nonsupercoiled DNA molecules (5). Although the experiments measuring the steady-state catenation and knotting level in systems where gyrase supercoils DNA molecules and where Topo IV acts on them are more difficult than those performed with relaxed DNA molecules, they would be more likely to provide us with important information on the effect of DNA supercoiling on DNA decatenation and unknotting activity. Simulations reported here constitute a step in this direction.