Photochemistry of hydrogen-bonded aromatic pairs: Quantum dynamical calculations for the pyrrole–pyridine complex

Abstract

The photochemical dynamics of the pyrrole–pyridine hydrogen-bonded complex has been investigated with computational methods. In this system, a highly polar charge-transfer state of ¹ππ* character drives the proton transfer from pyrrole to pyridine, leading to a conical intersection of S₁ and S₀ energy surfaces. A two-sheeted potential-energy surface including 39 in-plane nuclear degrees of freedom has been constructed on the basis of ab initio multiconfiguration electronic-structure data. The non-Born–Oppenheimer nuclear dynamics has been treated with time-dependent quantum wave-packet methods, including the two or three most relevant nuclear degrees of freedom. The effect of the numerous weakly coupled vibrational modes has been taken into account with reduced-density-matrix methods (multilevel Redfield theory). The results provide insight into the mechanisms of excited-state deactivation of hydrogen-bonded aromatic systems via the electron-driven proton-transfer process. This process is believed to be of relevance for the ultrafast excited-state deactivation of DNA base pairs and may contribute to the photostability of the molecular encoding of the genetic information.

As is well known, hydrogen bonds are of universal importance in chemistry and biochemistry. Although the structure and the functionality of hydrogen bonds in the electronic ground state have been investigated with powerful experimental and computational methods for decades and are thus quite well understood (1), much less is known about the role of hydrogen-bond dynamics in excited electronic states of chemical or biochemical systems. Fluorescence quenching of aromatic chromophores by protic solvents and fluorescence quenching in intermolecularly or intramolecularly hydrogen-bonded aromatic systems are well known phenomena, but are still poorly understood at the atomistic level (2–4). One reason for our limited knowledge of excited-state hydrogen-bond dynamics is the extremely short time scale of some of these processes (presumably of the order of 10 fs or less). Another reason is the difficulty of performing accurate ab initio electronic-structure calculations for excited states of complex polyatomic systems.

It has recently been proposed that electron-driven proton-transfer processes along hydrogen bonds could play a decisive role for the ultrafast excited-state deactivation of biological molecules and supermolecular structures, such as DNA base pairs, peptides, or UV-protecting pigments (5–7). The computational studies suggest that proton-transfer processes driven by charge-transfer (CT) states of ¹ππ*, ¹nπ*, or ¹πσ* character provide barrierless access to conical intersections (8) of the excited-state and ground-state potential-energy surfaces, where ultrafast internal conversions take place. This particularly efficient mechanism of energy dissipation could be essential for photostability of the molecular encoding of the genetic information of life (9). Recent experimental results for DNA base pairs or biomimetic models thereof seem to support this conjecture (10–12).

Although ab initio calculations of electronic excitation energies, minimum-energy reaction paths, and energy profiles, as well as minima of conical intersection seams can provide valuable insight, a true mechanistic understanding requires the computational treatment of the nuclear dynamics of the photochemical process. Such calculations are challenging because of the large number of nuclear degrees of freedom, the large excess energy provided by UV photons, and extremely strong non-Born–Oppenheimer effects at conical intersections (8). Very recently, a few ab initio on-the-fly trajectory simulations have been performed on hydrogen-detachment and hydrogen-transfer processes in biomolecular systems (13, 14). Although such simulations can provide useful mechanistic insight, they have limitations because of the rather significant de Broglie wavelength of the proton, the approximate treatment of the nonadiabatic dynamics at the conical intersections, the inevitable compromises with respect to the accuracy of the ab initio methods, and the very limited number of trajectories that can be calculated.

In this work, we describe the first attempt of a fully quantum mechanical treatment of nonadiabatic photochemical dynamics of a hydrogen bond in a biomimetic system. We adopt the hydrogen-bonded pyrrole–pyridine aromatic pair (15) as a model of the Watson–Crick base pairs in DNA. Multiconfiguration ab initio methods have been used for the characterization of the potential energy (PE) surfaces of the relevant electronic states. An approximately 39-dimensional analytic PE surface of the reaction-path-Hamiltonian type (16) has been constructed. We report the results of reduced-dimensional time-dependent quantum wave-packet calculations and calculations in the framework of multilevel Redfield theory (17, 18). In the latter approach, the few most important nuclear degrees of freedom are explicitly taken into account, whereas the many weakly coupled degrees of freedom are treated approximately in perturbation theory and the Markovian approximation.

Results and Discussions

One-Dimensional Potential-Energy Surfaces.

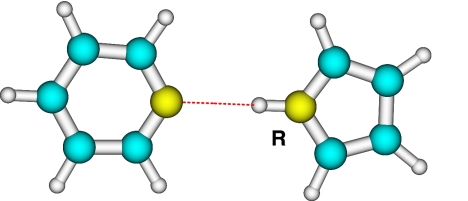
The equilibrium structure of the hydrogen-bonded model system, planar pyrrole–pyridine, is displayed in Fig. 1. The NH distance R of pyrrole is defined as the reaction coordinate for the hydrogen transfer.

Fig. 1.

Structure of the pyrrole–pyridine complex in the electronic ground state.

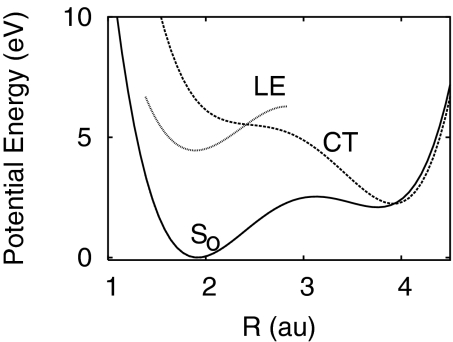
Fig. 2 gives an overview of the potential-energy surfaces of the three lowest electronic states of pyrrole–pyridine as functions of the hydrogen-transfer coordinate R (15). It can be seen that the hydrogen atom is bonded to pyrrole in the electronic ground state. The lowest locally excited (LE) singlet state of the complex is of ¹ππ* character and ¹B₂ symmetry. The lowest singlet CT state is of ¹B₂ symmetry and ¹ππ* character. It is optically dark, i.e., it cannot be excited directly from the S₀ state by a one-photon transition. The potential energy of the CT state intersects the energies of the LE state and the S₀ state at 2.4 a.u. and 3.9 a.u., respectively, see Fig. 2. The structures of pyrrole–pyridine at the ground-state equilibrium geometry and the conical intersection can be found in supporting information (SI) Text and Tables S1 and S2. The CT–S₀ energy crossing visible in Fig. 2 becomes a conical intersection when the vibrational modes of B₂ symmetry, are taken into account.

Fig. 2.

One-dimensional PE functions for hydrogen transfer of the three lowest electronic states of pyrrole–pyridine: diabatic ground S₀ state, CT (¹ππ*) state and LE (¹ππ*) state.

Two-Dimensional Quantum Wave-Packet Dynamics.

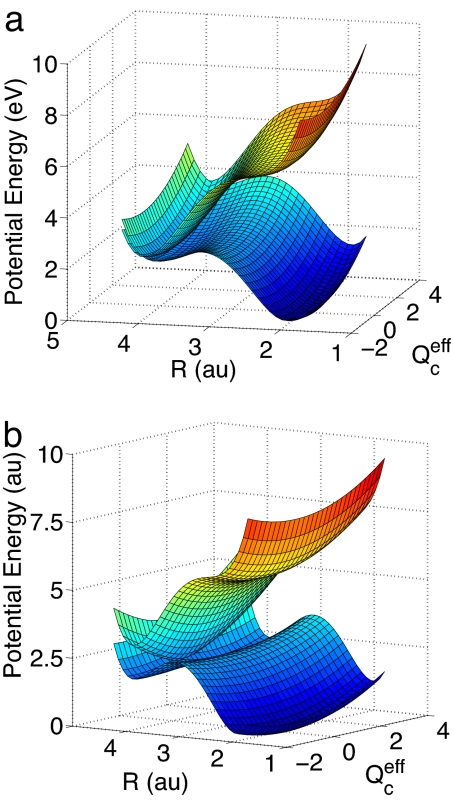
As the simplest nontrivial model, we consider the two-dimensional model including the reaction coordinate R and the effective coupling coordinate Q_c^eff (see Methods). The diabatic and adiabatic potential-energy surfaces of this two-dimensional model are displayed in Fig. 3 a and b, respectively, as functions of R and the effective coupling coordinate Q_c^eff. As expected, the diabatic potential-energy surfaces are smooth functions of nuclear geometry, see Fig. 3a. The double-cone shape of the adiabatic surfaces of the CT–S₀ conical intersection can be clearly seen in Fig. 3b.

Fig. 3.

Diabatic (a) and adiabatic (b) PE surfaces of the S₀ and CT (¹ππ*) states as functions of the hydrogen-transfer coordinate R and the effective coupling coordinate Q_c^eff. For sake of clarity, the diabatic coupling is exaggerated (λ = 20 λ_c^eff).

In the present system, the diabatic coupling constants λ_i of all coupling modes are found to be rather small. Therefore, λ_c^eff is also relatively small. This implies that the probability of electronic population transfer is low. For clarity, we therefore consider in the following only P₁^d, the population probability of the electronic ground state. The population probability of the CT state remains near unity on the time scale of a few picoseconds.

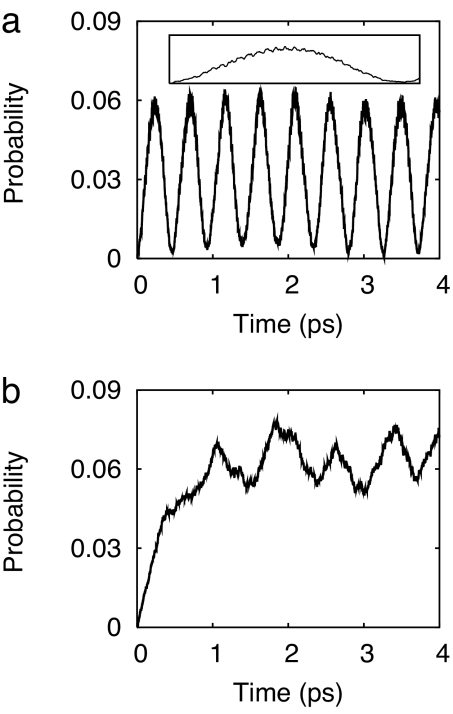
When the lowest vibrational level of the electronic ground state is vertically placed into the CT state, we observe that oscillatory diabatic population transfer takes place with a period of ≈500 fs, see Fig. 4a. The lack of irreversible electronic population transfer is the result of the restriction to just two nuclear degrees of freedom, the weak coupling at the CT–S₀ conical intersection, and the rather small CT–S₀ energy gap in the hydrogen-transferred complex, see Fig. 2. The superimposed weak and rapid oscillations (period of ≈19 fs, see Inset in Fig. 4a), reflect the time scale of vibrational motion along the hydrogen-transfer coordinate. In this two-dimensional model, the conical intersection clearly represents a major bottleneck for the radiationless deactivation of the CT state.

Fig. 4.

Electronic population probability of the diabatic S₀ state, obtained by the two-dimensional wave-packet calculations (a) and the three-dimensional wave-packet calculations (b). The Inset of a is the diabatic population of the S₀ state within the first oscillation period.

Three-Dimensional Quantum Wave-Packet Dynamics.

To get an impression of the effect of the so-called tuning modes on the reaction dynamics, we add the effective tuning mode Q_t^eff, resulting in a three-dimensional conical intersection (see Methods). The addition of a third mode leads to a qualitative change of the electronic population dynamics. The population probability of the diabatic S₀ state now increases monotonically within the first picosecond. The regular oscillations of the two-mode model are replaced by irregular fluctuations of the electronic population probability. The time average of P₁^d(t) over the first 4 ps has increased from ≈0.03 in Fig. 4a to ≈0.06 in Fig. 4b. The weak rapid oscillations arising from the oscillatory hydrogen-transfer dynamics are still visible, but are more irregular than in Fig. 4a.

Multilevel Redfield Dynamics.

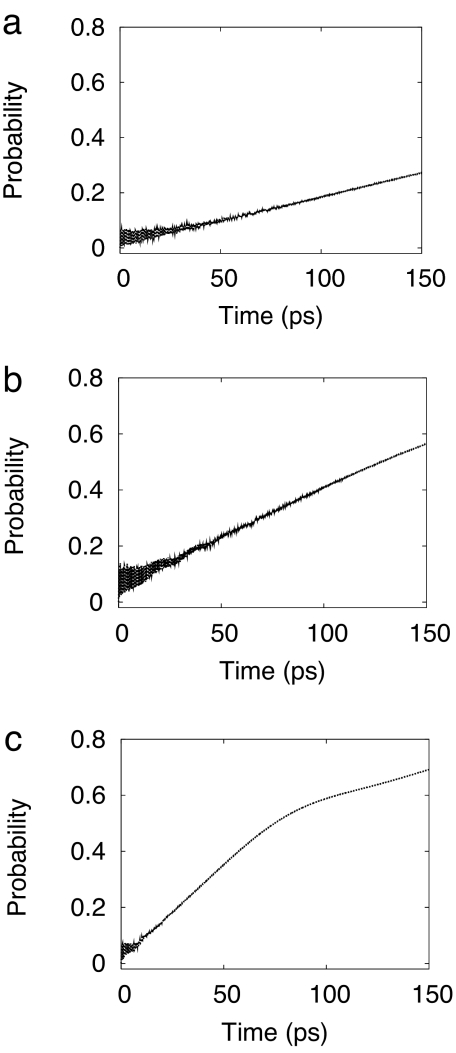
The reduced density matrix of the system Hamiltonian, which includes the reaction coordinate R and the effective coupling mode Q_c^eff, has been propagated in time, employing a Redfield tensor that has been constructed from the remaining 19 vibrational modes of A₁ symmetry (see Methods). The coupling of the reaction coordinate with the bath of the remaining A₁ vibrational modes has a significant impact on the electronic population dynamics, see Fig. 5a. After an initial transient behavior, the population probability of the S₀ state increases linearly with time, as expected for an incoherent rate process. Rapid fluctuations are still visible but die out on a time scale of ≈100 ps. The existence of these transient fluctuations reflects the fact that the data in Fig. 5 have been obtained from a truly microscopic dynamical theory rather than from an approximate rate expression.

Fig. 5.

Electronic population probability of the diabatic S₀ state, obtained from the reduced-density-matrix propagations within the original model (a), for increased interstate coupling strength (b), and for increased system–bath coupling strength (c).

These features can be understood as follows. The system-bath-coupling slowly drains the vibrational energy out of the hydrogen-transfer vibrational motion. The large excess energy of the system is thus transferred to the A₁ modes on a time scale of a few hundred picoseconds. The vibrational damping thus reduces the recurrence of the vibrational wave packet to the conical intersection, resulting in the lack of transfer of electronic population to the CT state.

According to these calculations, the internal-conversion dynamics from the CT state to the S₀ state takes place on a rather long time scale of a few hundred picoseconds. One reason for the slow radiationless decay of the CT state is the relatively weak diabatic coupling at the CT–S₀ conical intersection. Another reason is the unfavorable location of the CT–S₀ conical intersection in a shallow secondary well of the S₀ potential-energy surface (see Fig. 2), where the density of states of the S₀ surface is rather low. As far as we can tell, our computer simulation of the radiationless decay dynamics should be qualitatively correct, which implies that the rather slow radiationless decay dynamics is a property of this particular pyrrole–pyridine complex. Indeed, existing calculations of the reaction-path potential-energy profiles of related singly or doubly hydrogen-bonded aromatic systems, e.g., indole–pyridine, the 2-aminopyridine dimer (11), or the guanine–cytosine Watson–Crick base pair (5) indicate a topography of the CT–S₀ conical intersection that is more favorable for rapid radiationless decay.

To obtain insight into the role of the interstate coupling strength at the conical intersection and the strength of the system-bath coupling, we have performed additional reduced-density-matrix propagations, varying the parameters of the ab initio-based model.

First, we increase the interstate coupling by multiplying λ_c^eff by a factor of 2. In this modified model, the rate of internal conversion increases by approximately a factor of 2, see Fig. 5b. The interstate coupling at the CT–S₀ conical intersection is thus the rate-limiting factor in this model.

In a further calculation, we have increased the system-bath coupling strength by a factor of 2. Because the Redfield tensor is of second order in the system-bath coupling strength, it increases by a factor of 4. As a result, the internal conversion rate increases by a factor of ≈4 (Fig. 5c), compared with the original model (Fig. 5a). The ground-state population probability begins to saturate at ≈70 ps, see Fig. 5c. The damping of the hydrogen-transfer dynamics is thus another rate-limiting process in this system.

In the original and the modified model, the interstate coupling strength and the system-bath-coupling strength are rather low. As a result, the internal conversion process takes place on a rather long time scale (a few hundreds picoseconds). In this limiting case, the internal-conversion rate is approximately linearly and quadratically dependent on the corresponding coupling parameters. This simple relationship is not expected to hold for more general situations with strong interstate coupling at conical intersections. However, the present results are useful for the understanding of the general mechanism of the internal-conversion dynamics in biomolecular systems.

Conclusions

We have investigated the nonadiabatic dissipative dynamics of the pyrrole–pyridine hydrogen-bonded complex, which is triggered by the photoinduced electron-driven proton-transfer process. The potential-energy surfaces of the relevant electronic states have been characterized by ab initio electronic-structure calculations at the CASSCF level. A 39-dimensional model of potential-energy surfaces has been constructed, which is based on ab initio energy gradients along the hydrogen-transfer reaction coordinate and ab initio vibronic-coupling constants at the conical intersection of the CT state with the S₀ state.

The nonadiabatic quantum dynamics of this multidimensional model system has been investigated, employing time-dependent wave-packet and reduced-density-matrix methods. Assuming vertical electronic excitation of the CT state, we have explored the time evolution of the population probabilities of the CT state and the S₀ state. To gain insight into the microscopic mechanisms of the radiationless decay dynamics of this system, we have performed time-dependent quantum wave-packet calculations involving the two or three most relevant nuclear coordinates.

To reveal the effect of the remaining, more weakly coupled, vibrational degrees of freedom, we have adopted a system-bath approach (Redfield theory) with ab initio determined Redfield tensor elements. The results illustrate the evolution from a quasiperiodic electronic population dynamics (for the case of two nuclear degrees of freedom), via a stochastically fluctuating electronic population dynamics (for the case of three vibrational degrees of freedom), to a nonradiative rate process, when all 39 degrees of freedom of the model are taken into account.

The pyrrole–pyridine hydrogen-bonded complex has been chosen as a representative model for the investigation of the ultrafast hydrogen-bond photochemistry of DNA base pairs (10, 12). Pyrrole–pyridine can also serve as a model for fluorescence quenching through intermolecular hydrogen bonding between aromatic chromophores in solution (4). The radiationless decay dynamics of pyrrole–pyridine has been found to be comparatively slow (of the order of a few hundred picoseconds). The rather weak vibronic coupling at the CT–S₀ conical intersection and the relatively slow damping rate of the hydrogen-transfer mode have been identified as the origin of the relatively slow internal-conversion dynamics in pyrrole–pyridine. The extension of the present methodology can be used to treat the radiationless decay dynamics of the guanine-cytosine and adenine-thymine Watson–Crick base pairs, for which extremely fast internal conversion rates are expected (5, 10, 12).

Methods

Ab Initio Calculations.

The ab initio calculations have been performed at the complete-active-space self-consistent-field (CASSCF) level with the 6–31(G)d basis set. The active space includes all π and π* orbitals. The CASSCF gradients, frequencies, and PE surfaces have been calculated with the Gaussian 03 package (19).

Construction of the Potential-Energy Surfaces.

Our goal is the construction of the potential-energy surfaces of the nonadiabatically coupled S₀, LE, and CT states, including all relevant in-plane vibrational coordinates of the system. To avoid the singular derivative coupling at the conical intersections (8), we construct quasidiabatic potential-energy surfaces. We adopt the NH distance R of pyrrole as the reaction coordinate of the system. The remaining in-plane vibrational degrees of freedom are treated approximately in the spirit of the reaction-path-Hamiltonian approach (16). We focus on the conical intersection of the CT state with the S₀ state, because the dynamics at this intersection is decisive for the time scale of the internal conversion process. The LE–CT conical intersection remains to be characterized.

The planar pyrrole–pyridine complex has C_2v symmetry. The symmetry species of the normal modes are

The 20 A₁ modes consist of the reaction coordinate R and 19 so-called tuning modes of the CT–S₀ conical intersection, whereas the 19 B₂ modes are so-called coupling modes. The modes of A₂ and B₁ symmetry are not involved when the potential-energy surfaces are described in the so-called linear-vibronic coupling model (20) and will not be considered in what follows.

Because the proton-transfer reaction implies large-amplitude motion in the reaction coordinate R, the linear vibronic-coupling parameters of the tuning and coupling modes and the vibrational frequencies have to be considered as functions of this coordinate. To take into account the R dependence of the intrastate linear coupling constants κ_i⁽¹⁾, κ_i⁽²⁾ of the tuning modes, we represent them as fourth-order polynomials of R. For the interstate vibronic-coupling constants λ_i, on the other hand, we adopt their ab initio values at R = R_c, where R_c = 3.9 a.u. is the location of the CT–S₀ conical intersection. This simplification of the model is appropriate, because the non-Born–Oppenheimer dynamics at conical intersections depends essentially on the λ_i at this geometry. The dependence of the vibrational frequencies of all nonreactive modes on the electronic state and the reaction coordinate is neglected in the present linear-vibronic coupling model.

The intrastate coupling parameters, κ_i^(k) (k = 1,2), are obtained as the gradients of the adiabatic S₀ and CT energies with respect to Cartesian displacement coordinates (8). They are transformed to dimensionless ground-state normal coordinates, by using the L-matrix (21) of the latter. Analytical functions κ_i^(k)(R) are obtained by a least-squares fit of the ab initio data to fourth-order polynomials of R for each of the 19 tuning modes of A₁ symmetry.

The interstate coupling parameters λ_i are obtained by the projection of the nonadiabatic coupling vector (22) [or h vector (23)] on the ground-state normal coordinates of B₂ symmetry, see the discussions in refs. 8 and 24. The resulting diabatic potential model includes the large-amplitude proton-transfer coordinate R, 19 linearly coupling tuning modes of A₁ symmetry, and 19 linear coupling modes of B₂ symmetry. The dependence of the κ_i^(k)(R) on the reaction coordinate R (see SI Text and Fig. S2 for characteristic examples) results in a significant coupling of the tuning modes with the reaction coordinate. The coupling modes, on the other hand, are strongly coupled with the tuning modes and the reaction coordinate at the CT–S₀ conical intersection. As a result, all 39 in-plane nuclear degrees of freedom in this model are coupled to each other. We refer to SI Text for a more detailed description of the 39-dimensional potential-energy surface.

Treatment of the Time-Dependent Nuclear Dynamics.

In this work, we did not attempt to perform time-dependent quantum wave-packet dynamics calculations with the inclusion of all 39 vibrational modes of the potential-energy surface. Such a calculation would be extremely challenging. There exist several concepts that allow the reduction of the computational problem to a smaller number of effective nuclear coordinates. One concept is the definition of effective modes or cluster modes (25, 26). For a symmetry-allowed conical intersection, as is the case here, these effective modes are just the gradient-difference and nonadiabatic coupling (or g, h) vectors (22, 23). The atomic displacement vectors associated with the g and h vectors are illustrated in Fig. S1. Within the linear-vibronic-coupling model, the effective tuning and coupling modes are given by (see refs. 20 and 25)

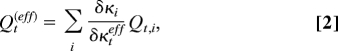with the coupling strengths and frequencies

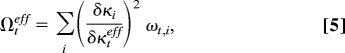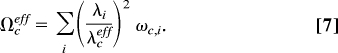Within the effective-mode approximation, the 39-dimensional dynamics problem is reduced to a three-dimensional problem, involving the reaction coordinate R, as well as the effective tuning and coupling modes. In this approximation, the anharmonic couplings arising from the R dependence of the κ_i^(k) are ignored. The B₂ modes with frequencies >1,720 cm⁻¹ do not give any contribution in the branching space of the conical intersection. The effective coupling coordinate Q_c^eff thus can be constructed by considering all B₂ modes with frequencies <1,720 cm⁻¹.

To account for the nonseparability of the reaction coordinate and the tuning modes Q_t,i, we have used multilevel Redfield theory (17, 18). Adopting a system-bath model, the nuclear coordinates of the system Hamiltonian are chosen as the reaction coordinate R and the effective coupling coordinate Q_c^eff, resulting in a two-state two-mode model.

The remaining A₁ modes are considered as a bath composed of harmonic oscillators with dimensionless coordinates Q_t,i, momenta P_t,i, and frequencies ω_t,i:

The system-bath coupling is given by

The κ_i^(k)(R) are fourth-order polynomial functions of R (see SI Text). Interestingly, the κ_i^(k)(R) for different tuning modes have approximately the same R dependence, that is

with

With this approximation, the system-bath coupling becomes

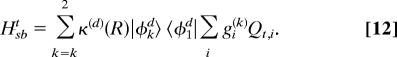The coupling between the system and the bath is completely determined by the spectral function of the bath. In the above approximation, the spectral functions read

We replace the δ functions by Lorentz functions to obtain continuous spectral functions. The full-width half-maximum of these Lorentz functions is 13 meV (see Fig. S3 for a characteristic example).

It is straightforward to construct the Redfield tensor for this system-bath coupling model (27). Note that the elements of the Redfield tensor are not empirical parameters but are determined from the ab initio calculations.

The preparation of the initial state by the absorption of an UV photon is approximately described as vertical excitation from the lowest vibrational level of the electronic ground state to the CT state. As mentioned above, the actual electronic excitation takes place from the S₀ state to the LE state, from which the wave packet switches to the CT state (see Fig. 2). We have simplified the problem by assuming direct electronic excitation to the CT state.

The wave packets are propagated on the two coupled surfaces by using the split-operator method, as discussed (28). We have used 64 grid points from 0.83 a.u. to 4.83 a.u. for R. Ten and 6 harmonic-oscillator basis functions are used for the effective tuning and coupling coordinates, respectively. The wave packets are propagated for 4 ps with a time step of 0.1 fs.

We use the split-operator method for the short-time propagation of the reduced density operator (29):

where the system Liouville superoperator L_s and the dissipative superoperator D describe the reversible system dynamics and the irreversible dissipative dynamics, respectively. The short-time propagator e^−iLsdt/2 is evaluated in the eigenstate representation. The operator D in the eigenstate representation is time-local (17). Therefore, the short-time propagation governed by D leads to a system of linear differential equations for the matrix elements of the reduced density matrix (29). The fourth-order Runge–Kutta method is used to evaluate the short-time propagator e^Ddt for every time step. In this way, we can disentangle the propagation of the fast system dynamics and the slow dissipative dynamics. It permits us to propagate the reduced-density matrix for a very long time duration with high numerical stability.

The numbers of the grid points and harmonic basis functions, which are used to generate the matrix representation of Hamiltonian, lead to a system Hilbert space of dimension 768. This space is truncated to 500 basis functions in the propagation of the reduced density matrix. The reduced density matrix is propagated for 150 ps with a time step of 50 fs.

The observables of primary interest of the present study are the time-dependent populations probabilities of the electronic states (8). Adiabatic and diabatic electronic population probabilities are defined as the expectation values of the corresponding projection operators with the time-dependent wave packet. Although the adiabatic electronic population probabilities, P_i^a, are the observables that most directly reflect the electronic decay dynamics, their computation is very expensive when the system Hilbert space is large. We therefore consider the diabatic population probabilities, P_i^d, for the qualitative discussion of the nonadiabatic dynamics of the multimode non-Born–Oppenheimer system.