Photoelectron Spectroscopy and Electronic Structure Calculations of d¹ Vanadocene Compounds with Chelated Dithiolate Ligands

Abstract

Gas-phase photoelectron spectroscopy and density functional theory have been used to investigate the electronic structures of open-shell bent vanadocene compounds with chelating dithiolate ligands, which are minimum molecular models of the active sites of pyranopterin Mo/W enzymes. The compounds Cp₂V(dithiolate) [where dithiolate is 1,2-ethenedithiolate (S₂C₂H₂) or 1,2-benzenedithiolate (bdt), and Cp is cyclopentadienyl] provide access to a 17-electron, d¹ electron configuration at the metal center. Comparison with previously studied Cp₂M(dithiolate) complexes, where M is Ti and Mo (respectively d⁰ and d² electron configurations), allows evaluation of d⁰, d¹ and d² electronic configurations of the metal-center that are analogues for the metal oxidation states present throughout the catalytic cycle of these enzymes. A “dithiolate-folding effect” that involves an interaction between the vanadium d orbitals and sulfur p orbitals is shown to stabilize the d¹ metal center, allowing the d¹ electron configuration and geometry to act as a low energy electron pathway intermediate between the d⁰ and d² electron configurations of the enzyme.

Introduction

The bent metallocene class of molecules (Cp₂M(L)₂, Cp = η⁵-cyclopentadienyl) provide access to many small molecules that contain metal-dithiolate ligation,¹ and are therefore useful as models of the pyranopterin-dithiolate system of the mononuclear molybdenum-containing enzymes that catalyze a wide range of oxidation/reduction reactions in carbon, sulfur and nitrogen metabolism.^2-6 This class of molecules allows access to d⁰ (M = Ti, Hf, Zr), d¹ (M = V, Nb) and d² (M = Mo, W) metal electron configurations, the same electron configurations as the metal center during the enzyme catalytic cycle. Bent metallocenes are known with a variety of different dithiolate ligands, many of which have been crystallographically characterized.¹ A common structural motif of metallocene dithiolates is a folding along the S···S vector, as illustrated in Figure 1.⁷ Interestingly, the range of fold angles observed for metallocene dithiolates encompasses the range of fold angles that has also been observed in protein crystal structures of pyranopterin-dithiolate sites (7-30°).^8-12 The exact role of the pyranopterindithiolate coordination in the overall catalytic cycle of molybdenum enzymes is not yet established,¹³ but the unusual ability of ene-1,2-dithiolate ligands to stabilize metals in multiple oxidation states has long been recognized.^14,15 Proposed functions for the pyranopterin-dithiolate ligand include acting as an electron transfer conduit from the metal to other prosthetic groups¹⁶ and/or acting as a modulator of the oxidation/reduction potential of the metal site.^16,17 Modeling of the active site of the mononuclear molybdenum enzymes with small molecules has revealed useful information about the activity of these enzymes.¹⁸

Figure 1.

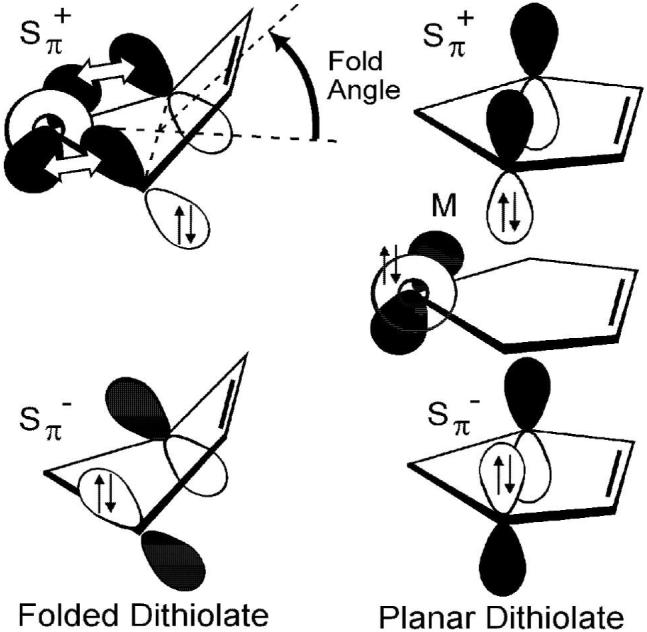
Representations of the valence orbitals of folded versus flat dithiolates. In the d⁰ case the metal orbital (M) is empty, and the S_π⁺ orbital can interact upon folding. In the d² case the metal orbital (M) is filled, and a planar orientation minimizes a filled-filled interaction. The S_π^- orbital does not have the correct symmetry to interact with the metal orbital.

A general bonding description of Cp₂MX₂ compounds is well understood,^19-21 and Lauher and Hoffmann first explained the variation in fold angle for Cp₂M(dithiolate) compounds as due to the occupancy of the metal d-orbital in the equatorial plane (or metal in-plane orbital, M_ip) with respect to the dithiolate ligand. This orbital is empty for the d⁰ molecules, in which the metallocycle is folded along the S···S vector, and filled for the d² molecules, in which the metallocycle is nearly planar. The observed folding for the d⁰ systems facilitates interaction of the filled S_π orbitals with the empty M_ip orbital, as shown in Figure 1. In the case of Cp₂Ti(bdt), which has a formally Ti(IV) d⁰ metal center, the dithiolate ligand can be thought of as a six-electron donor. Each of the thiolate σ-orbitals provides two electrons, and two additional electrons come from the symmetric (S_π⁺) orbital. Thus, folding the dithiolate ligand effectively stabilizes Cp₂Ti(bdt) as an 18-electron complex.^22,23 In contrast, for the d² metal system, folding of the ligand would bring a filled S_π orbital into close proximity with the filled M_ip orbital; the observed nearly planar metallocycle minimizes the filled-filled interaction between the ligand and metal-based orbitals.¹²

Previously, we have investigated the electronic structures of the d⁰ and d² metal centers of the metallocene dithiolates as active site models for molybdopterin enzymes.^12,22 This study examines the d¹ metal electron configuration that is observed for molybdopterin enzymes, and its role as an intermediate in facilitating electron transfer between the d⁰ and d² electron configurations of the enzyme active site. The electronic structures of the compounds Cp₂V(dithiolate) [where dithiolate is 1,2-ethenedithiolate (S₂C₂H₂), 1,2-benzenedithiolate (bdt) and Cp is cyclopentadienyl] are examined by gas-phase photoelectron spectroscopy (PES) and density functional theory (DFT). This study fills in the connection between our previous studies of Cp₂M(dithiolate) (M= Mo, Ti) that investigated the respective electronic structures of d² and d⁰ metal centers. Investigation of Cp₂V(dithiolate) as a model of the intermediate d¹ electron configuration of pyranopterin Mo/W enzymes leads to a basic understanding of how the electronic and geometric structures of the d⁰, d¹ and d² electron configurations facilitate electron transfer to and from the enzyme active site.

Experimental methods

General

Electronic absorption (dichloromethane solutions on a modified Cary 14 with OLIS interface, 280-1280 nm) and mass spectrometry (direct ionization on a JEOL HX110) were used to identify the compounds. The compound Cp₂V(bdt), was synthesized according to published procedures²⁴ and under anaerobic conditions using a glove box. Cp₂V (Strem), Cp₂VCl₂ (Aldrich), anhydrous THF (DriSolv) and anhydrous hexane (DriSolv) were used as supplied. The EPR spectrum of Cp₂V(S₂C₂H₂) was obtained at X-band at 77 K on a Bruker 300E spectrometer in the Electron Paramagnetic Resonance Facility at The University of Arizona. The X-ray crystallographic structure of Cp₂V(S₂C₂H₂) was determined by the Molecular Structure Laboratory at The University of Arizona.

Synthesis of Cp₂V(S₂C₂H₂)

To a suspension of freshly prepared Na₂(S₂C₂H₂)²⁵ (0.068 g, 0.5 mmol) in THF (5 ml) was added a suspension of Cp₂VCl₂ (0.126 g, 0.5 mmol) in THF (8 ml). The mixture was stirred for 2 hrs and allowed to stand overnight at room temperature. The red/purple mixture was then filtered, evaporated to dryness under vacuum and washed with hexane (3 × 4 ml) to remove a blue impurity. The residue was dissolved in the minimum volume of THF (∼8 cm³), layered with hexane (∼10 ml) and allowed to stand overnight at room temperature, then refrigerated at -20 C for 3 days to yield dark purple block crystals suitable for crystallography. Yield: 0.052 g, 40%. UV/Vis/Near-IR: 10800 (ε = 400), 12900 (140) sh, 18400 (520), 21700 (310) sh, 23700 (210), 24900 cm^-1 (400 M^-1 cm^-1) shoulder, and very intense UV transitions starting at 27500 cm^-1. EPR: g₁ = 2.007, g₂ = 1.995, g₃ = 1.995, A₁ = 55.3, A₂ = 25.1, A₃ = 93.3 (10^-4 cm^-1). MS calculated m/z for VS₂C₁₂H₁₂: 270.9820 (100), obs. 270.9822 (100); calc. 271.9850 (15.12), obs. 271.9863 (16.35); calc. 272.9789 (9.92), obs. 272.9784 (10.64 % normalized intensity).

X-ray Crystallographic Analysis

Data were collected for Cp₂V(S₂C₂H₂) on a Bruker SMART 1000 CCD detector X-ray diffractometer. The structure was solved using SIR92.²⁶ Refinements were performed using SHELXL²⁷ and illustrations were made using XP. Solution was achieved utilizing direct methods followed by Fourier synthesis. Hydrogen atoms were added at idealized positions, constrained to ride on the atom to which they are bonded and given thermal parameters equal to 1.2 U_iso of that bonded atom. A parameter describing extinction was included, but refined to zero and was removed prior to final refinement cycles. The final anisotropic full-matrix least squares refinement based on F² of all reflections converged (maximum shift/esd = 0.000) at R₁ = 0.0644, wR₂ = 0.0986 and goodness-of-fit = 1.040. “Conventional” refinement indices using the 1972 reflections with F > 4 sigma(F) are R₁ = 0.0389, wR₂ = 0.0855. The model consisted of 136 variable parameters; no restraints were used. There were no correlation coefficients greater than 0.50. The highest peak on the final difference map was 0.495 e Å^-3 located 0.82 Å from S1. The lowest peak on the final difference map was -0.343 e Å^-3 located 0.72 Å from C2. Scattering factors and anomalous dispersion were taken from International Tables Vol. C Tables 4.2.6.8 and 6.1.1.4.

Photoelectron spectroscopy

Photoelectron spectra were recorded using an instrument, procedures and calibration that have been described in detail previously.²⁸ The electron detection and instrument operation are interfaced to a National Instruments PCIe-6259 multi-function data acquisition card and custom software. During data collection the instrument resolution (measured using fwhm of the argon ²P_3/2 peak) was 0.020-0.030 eV. The sublimation temperatures (at 10^-5 Torr, monitored using a “K” type thermocouple passed through a vacuum feed-through and attached directly to the sample cell) were 190-200°C for Cp₂V(S₂C₂H₂) and 195-210°C for Cp₂V(bdt). The samples sublimed cleanly without evidence of decomposition. In Figure 3, the vertical length of each data mark represents the experimental variance of that point. The valence ionization bands in the He I spectra are represented analytically with the best fit of asymmetric Gaussian peaks as described previously.²⁹ The peak positions are reproducible to about ±0.02 eV (3). The analytical ionization bands that model the He I spectra are also used to model the ionizations in the He II spectra, with only the intensities of the analytical bands allowed to vary to account for the changes in photoelectron cross-sections with the change in excitation source energy from He I to He II.

Figure 3.

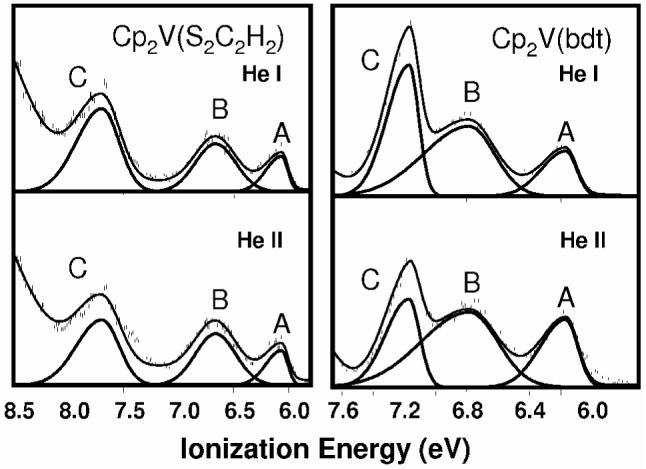
Low energy valence region of the gas-phase photoelectron spectra of Cp₂V(S₂C₂H₂) and Cp₂V(bdt) with He I and He II excitation. Band C is due to the S_π^- orbital, B is the S_π⁺/V bonding orbital, and A is the singly-occupied S_π⁺ /V anti-bonding orbital.

Computational Methods

The Amsterdam Density Functional theory suite (ADF 2006.01b, using default parameters except for the options given in parentheses) was used to study the electronic structures of Cp₂M(S₂C₂H₂) and Cp₂M(bdt), where M is V and Mo.^30-34 The optimized geometries of Cp₂V(S₂C₂H₂), Cp₂V(bdt) and Cp₂Mo(bdt) (Tables S1 - S3, respectively, in Supporting Information) were obtained in C_s symmetry. Cp₂V(S₂C₂H₂), Cp₂V(bdt) and Cp₂Mo(bdt) were constructed such that the Cp rings were staggered with respect to each other, as similarly found in the crystal structure, and such that the C_s plane was coincident with the xy-plane. In Cp₂V(S₂C₂H₂), Cp₂V(bdt) and Cp₂Mo(bdt) the C_s plane bisects the metal atom and all three ligands. A generalized gradient approximation, with the correlation of Perdew, et al.³⁵ and exchange correction of Handy and Cohen³⁶ (GGA OPBE), was used for calculations of the optimized geometries. The calculations employed double- or triple-zeta basis sets with Slater type orbitals and polarization functions for all elements (DZP for C, H and S and TZP for V and Mo). Higher level basis sets did not give significantly different results for comparison of ionization energies. Calculations on the ground-state molecules were performed in the spin-unrestricted mode since each molecule contains one unpaired electron. Relativisitic effects were considered for all atoms by using the Zero Order Regular Approximation (relativistic scalar ZORA).^37,38 The numerical integrals in ADF were evaluated to six significant figures (integration = 6.0) and the convergence criteria of the energy, gradients, and estimated coordinate uncertainty were tightened (converge E = 0.001, grad = 0.001, rad = 0.001). The self-consistent field (SCF) convergence limits were also tightened. (convergence 1e-6 1e-6). Analytical frequency calculations (AnalyticalFreq) were also carried out on the optimized geometry of Cp₂Mo(bdt), and there were no imaginary frequencies.

ΔSCF calculations of the ionized states were performed at the fixed geometry of the neutral molecule, with one electron removed from the relevant orbital. The first positive ion of each molecule is a closed-shell singlet, but the higher positive ion states (corresponding to ionization of electrons from orbitals below the HOMO) contain two unpaired electrons and were calculated as both spin-unrestricted singlets and triplets. The ΔSCF estimate of the ionization energy is the difference between the calculated total energy of the ionized state and that of neutral ground state molecule.

Fold angle potential curves were created by utilizing the Linear Transit option in the Geometry block along with the Geovar keyword. Linear Transit calculations were run such that the fold angle was fixed every five or ten degrees through some range (e.g. 60° to -60°) and all geometric parameters, other than the fold angle, were allowed to fully optimize at each step.

Results and Discussion

Crystallography

There is one crystallographically independent molecule in the structure of Cp₂V(S₂C₂H₂). The structure (Figure 2, Table 1 and S4) is similar to that of Cp₂V(bdt), as published by Stephan.²⁴ Two cyclopentadienyl rings and two sulfur atoms complete a pseudo-tetrahedral coordination sphere of vanadium. The ene-dithiolate chelates to the V center through the two S atoms and shows folding along the S···S vector as illustrated in Figure 1, with a fold angle of 38.5°. The V-C and V-S distances average 2.302 and 2.425 Å, respectively. These compare with the V-C and V-S distances published for Cp₂V(bdt) (2.30 and 2.431 Å).²⁴ The S1-V-S2 angle of 81.14 (3)° is similar to that of 79.8° in Cp₂ V(bdt).²⁴ It is interesting to note that the bond lengths for the analogous titanium compounds are longer for M-C(Cp) (2.387 Å for Cp₂Ti(S₂C₂H₂) and 2.37 Å for Cp₂Ti(bdt)) whereas the M-S bond lengths and S-M-S angles are very similar (2.417 Å and 83.23° for Cp₂Ti(S₂C₂H₂) and 2.416 Å and 82.2° for Cp₂Ti(bdt)). The trend of Cl-M-Cl angles for Cp₂MCl₂ compounds is Ti/Zr > V/Nb > Mo.^39,40 This trend is not echoed for Cp₂M(bdt) (M= Ti, V and Mo) with the S-M-S angles of: 82.0, 79.8 and 82.1°, respectively. The effect of the electron density along the z-axis is overpowered, presumably, by the formation of the chelate ring.

Figure 2.

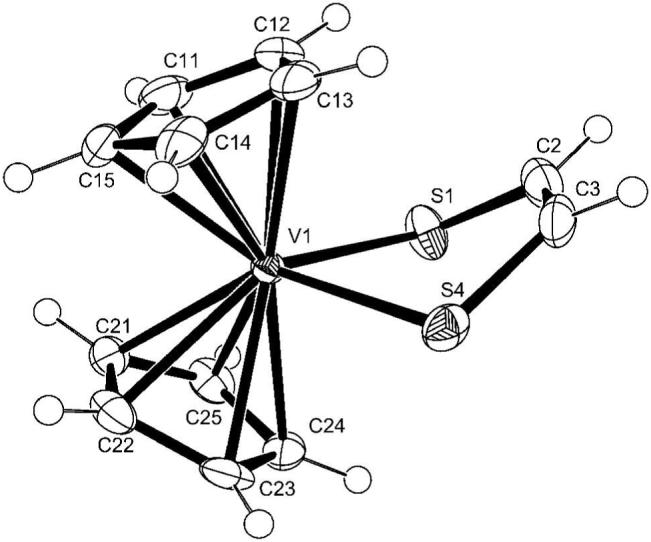
ORTEP representation of Cp₂V(S₂C₂H₂) with 50% thermal ellipsoids.

Table 1.

X-ray crystallographic parameters of Cp₂V(S₂C₂H₂)

Empirical Formula	C12H12S2V
Formula weight	271.28
Temperature	170(2) K
Wavelength	0.71073 Å
Crystal system	Monoclinic
Space group	P2(1)/c
Unit cell dimensions	A =1.3051(10) Å
	B =7.5236(7) Å
	C =13.3767(12) Å
	β=104.849(2)°
Volume	1099.76(17) Å3
Z	4
Density (calculated)	1.638 Mg/m3
Absorption coefficient	1.240 mm-1
Reflections utilized	12814
Independent reflections	2675 [R(int) = 0.0497]a
Final R Indices	R1 = 0.0389, wR2 = 0.0855a
[I>2σ(I)]
R Indices (all data)	R1 = 0.0644, wR2 = 0.0986a

^aR(int) = Σ|F_o²-<F_o²>|/Σ[F_o²], R₁ = Σ||F_o|-|F_c||/Σ|F_o|, wR₂ = {Σ[w(F_o²-F_c²)²] / [Σw(F_o²)²]}^½, w = 1/[σ²(F_o²)+(0.0466P)²] where P=(F_o²+2F_c²)/3

EPR

Previous studies of Cp₂VX₂ (where X is a monoanionic ligand, such as an alkyl or halide) have utilized electron paramagnetic resonance (EPR) to determine the molecular orbital character of the vanadium d¹ electron. The EPR spectrum of Cp₂V(S₂C₂H₂) (Figure S2) is similar to that of Cp₂VCl₂ reported previously.^39-42 The trend of the Cl-M-Cl angle to decrease with M, changing from Ti to V to Mo, and single crystal EPR studies led to the conclusion that the HOMO of the V and Mo compounds is primarily along an axis normal to the plane bisecting the Cl-M-Cl angle. Lowering the symmetry from C_2v to C_s allows this axis to be labeled z, and the orbital was calculated as |Ψ₀> = a|d_z2> + b|d_x2 - _y2>, where a = -0.963 and b = 0.270 (Mulliken charges, a²:b² = 20.5:1) for Cp₂VCl₂.⁴⁰ This is close to the observed a = -0.976 and b = 0.218 (a²:b² 20.0:1) for (C₅H₄Me)₂VCl₂. These EPR parameters have been compared with those of Cp₂VCl₂, calculated as Mulliken charges.⁴⁰ Using more current methods, a similar comparison can be made between the observed EPR and symmetry-adapted fragment orbital (SFO) parameters calculated by DFT. For Cp₂VCl₂, the singly-occupied, spin α orbital SFO component corresponding to d_z2 is 0.801 and that to d_x2 - _y2 is -0.033, giving a ratio of a²:b² = 24.1:1.⁴³ This is in agreement with previous experiments (see above) concluding that the singly-occupied orbital is of primarily d_z2 character.

The higher g values and lower A(⁵¹V) values of Cp₂V(S₂C₂H₂) reflect the softer coordination environment and covalent nature of the dithiolate ligand compared to the two chloride ligands in Cp₂VCl₂. Previous studies of Tp*MoOXY (where Tp* = hydrotris(3,5-dimethyl-1-pyrazolyl)borate; (X,Y) = Cl, or toluenedithiol (tdt)) exhibit a similar trend in the g and A(^95,97Mo) values with change in coordination sphere.⁴⁴ The higher g values and lower A(^95,97Mo) values of Tp*MoO(tdt) compared to Tp*MoOCl₂ are attributed to a low energy charge transfer transition in Tp*MoO(tdt) (9010 cm^-1, ε = 520) that can mix sulfur character into the ground state.⁴⁴ Tp*MoOCl₂ does not exhibit a similar charge transfer transition, but has a d → d transition as the lowest energy band. Comparing the electronic spectra of Cp₂VCl₂ and Cp₂V(S₂C₂H₂) (Figure S3), there is a low energy ligand-to-metal charge transfer transition¹⁵ for Cp₂V(S₂C₂H₂) (10800 cm^-1, ε = 400), but Cp₂VCl₂ lacks a similar low energy transition. The difference in the low energy charge transfer transitions between Cp₂VCl₂ and Cp₂V(S₂C₂H₂) would account for the greater g and lower A(⁵¹V) values exhibited by Cp₂V(S₂C₂H₂) compared to Cp₂VCl₂.^45,46

Photoelectron Spectroscopy

Spectroscopic evidence supporting the Lauher and Hoffmann¹⁹ description of the electronic structure includes our recent PES study of the nearly planar metallocycle, Cp₂Mo(bdt),¹² and the folded metallocycle, Cp₂Ti(bdt), for which ionizations from primarily metal based orbitals and primarily S p_π based orbitals can be experimentally distinguished from one another.^12,22,47 The S p_π based orbitals of the two sulfur atoms form a symmetric and antisymmetric pair. The symmetric (S_π⁺) orbital combination has the right symmetry and energy to match the M_ip orbital upon folding of the dithiolate unit, whereas the antisymmetric sulfur (S_π^-) orbital combination does not (Figure 1). The substantial mixing of the out-of-plane S_π⁺ orbital and the M_ip orbital upon folding is shown experimentally in the PE spectra of Cp₂Ti(bdt) by the increase in intensity of the S_π⁺ ionization band relative to the S_π^- ionization band with change in ionization source energy from He I to He II. In order for this “dithiolate-folding effect” to be present there must be effective coupling between the S p_π orbitals and the C p_π orbitals derived from the ene-dithiolate ligand backbone.²² Such coupling raises the energy of the S_π⁺ orbital above that of the S_π^- orbital, and poises the energy of the S_π⁺ orbital for interaction with the metal-based in-plane orbital (M_ip). This electronic structure facilitates the “dithiolate-folding effect” as only the S_π⁺ orbital has the correct symmetry to overlap with the metal based in-plane orbital. For example, we have previously shown that Cp₂Ti(bdt) and Cp₂Ti(S₂C₂H₂), which both have an unsaturated carbon-carbon bond linking the two S atoms, show a dithiolate-folding effect. However, if a saturated dithiolate ligand is present, such as in Cp₂Ti(S₂C₃H₆),²² the coupling between the pπ orbitals on the two S atoms is greatly reduced and the ordering of the S_π orbitals is reversed in comparison to the unsaturated dithiolate.

The low energy valence regions of the gas-phase photoelectron spectra of Cp₂V(S₂C₂H₂) and Cp₂V(bdt), collected with both He I and He II photon sources, are presented in Figure 3. Comparison of the He I spectra with their titanocene analogs²² in Figure 4 reveals a similar overall ionization profile in each case, except for the presence of the weak band A at low energy (6.06, and 6.17 eV for Cp₂V(S₂C₂H₂) and Cp₂V(bdt), respectively), as expected for the additional electron in the vanadium complexes.

Figure 4.

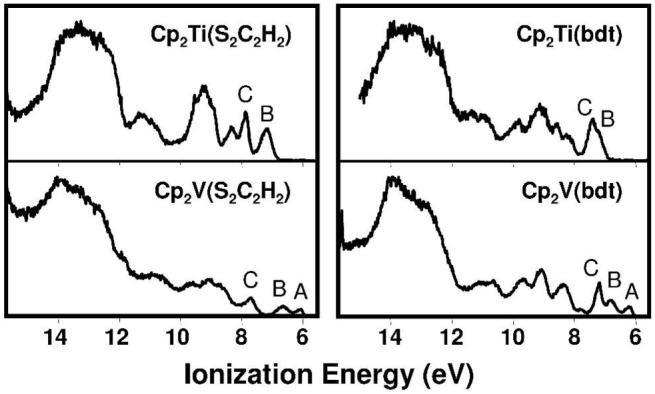
The spectra of Cp₂V(S₂C₂H₂) and Cp₂V(bdt) have one more band (band A) than their respective titanocene analogs.

Table 2 lists the changes in areas of ionization bands B and C relative to the first ionization band A with change in ionization source from He I to He II for Cp₂V(S₂C₂H₂) and Cp₂V(bdt). From previous experimental studies^48-50 and calculations of atomic photoionization cross-sections,⁵¹ it is expected that ionizations from molecular orbitals with significant Ti 3d contributions will increase in intensity compared to ionizations of primarily S 3p character when data collected with a He II photon source are compared to data collected with a He I photon source (Table 2). The changes in relative areas of the bands in Cp₂V(S₂C₂H₂) and Cp₂V(bdt) are similar, indicating that the atomic character of the molecular orbitals for the two molecules is similar. Band C in the titanocene dithiolate spectra is assigned to a S_π^- ionization, which does not mix significantly with the empty metal d acceptor orbital, and hence decreases in intensity significantly relative to the S_π⁺ band (band B).²² The destabilization of band B in the vanadocene dithiolate spectra compared to the related ionization in the titanocene spectra can be attributed to the interaction of the additional vanadium d¹ electron with the S_π⁺ orbital, which decreases the fold angle and lowers the bonding interaction of S_π⁺ with M_ip. Band C in the spectra of Cp₂V(S₂C₂H₂) and Cp₂V(bdt) decreases in intensity relative to both the first and second bands, and can therefore also be assigned to S_π^- (Table 2). Band C shows little change in ionization potential between the vanadocene and titanocene dithiolate spectra consistent with its non-bonding interaction with M_ip. Band A increases slightly with respect to band B in Cp₂V(bdt) and decreases slightly in Cp₂V(S₂C₂H₂), indicating mixing of metal and sulfur character and making absolute assignment difficult at this point. Comparison with the titanium analogs indicates that bands A and B both have mixed vanadium and S_π⁺ character.

Table 2.

Ionization energies, band shapes, and He I and He II band areas for Cp₂V(S₂C₂H₂) and Cp₂V(bdt)

Cp2V(S2C2H2)
Band	I.E.a (eV)	Band Width High (eV)	Band Width Low (eV)	Relative Areab
				He I	He II
A	6.06	0.34	0.14	1	1
B	6.67	0.43	0.43	2.46	2.69
C	7.70	0.54	0.36	4.41	3.58

Cp2V(bdt)
Band	I.E. (eV)	Band Width High (eV)	Band Width Low (eV)	Relative Area
				He I	He II
A	6.17	0.36	0.16	1	1
B	6.78	0.69	0.38	3.15	2.28
C	7.17	0.34	0.14	2.65	1.20

^aVertical ionization energy

^bAreas are relative to Band A.

Computations

DFT calculations provide additional insight into the metal-ligand interactions for Cp₂V(S₂C₂H₂) and Cp₂V(bdt) indicating that upon dithiolate folding the mixing of metal d and sulfur p_π orbitals can be favored by their energy and symmetry match. The calculated molecular structures of Cp₂V(S₂C₂H₂) and Cp₂V(bdt) in general agree with the reported structures determined from X-ray crystallography (Table S4).^24,52 The Cp rings were staggered with respect to each other in the initial input guess geometries similar to the crystal structure of the ene-dithiolate complex and as determined to be a true minimum from the frequency analysis of the related Mo molecule. Rotation of the two Cp ligand rings has been shown to be a low energy process⁵³ and therefore additional Cp orientations were not explored. The calculated fold angles for the coordinated dithiolates are smaller than those determined crystallographically. For Cp₂V(S₂C₂H₂) the calculated angle is 29.9° and the experimental angle is 38.5°, and for Cp₂V(bdt) the calculated angle is 36.6° and the experimental angle is 41.0 and 40.1°.²⁴ Solid state effects likely contribute to the differences between the calculated and crystallographic fold angles.⁵⁴

The energies of the ionizations observed for Cp₂V(S₂C₂H₂) and Cp₂V(bdt) by photoelectron spectroscopy are compared with those calculated by the ΔSCF method in Table 3. The ground states of the neutral molecules have s = ½ (V⁴⁺, d¹, ²A’); ionization from the SOMO will lead to a singlet state, but ionization from the doubly-occupied orbitals leads to either singlet or triplet state configurations with singlet:triplet band relative intensities approximately 1:3. Table 3 shows the calculated values for the singlet and triplet states of Cp₂V(S₂C₂H₂) and Cp₂V(bdt) using the ΔSCF method. For Cp₂V(S₂C₂H₂), the calculated singlet/triplet state separation for band B is 0.53 eV and should be discernable in the experiment, although the band maximum will be dominated by the triplet state. The calculated energy for the formation of a triplet state (6.57 eV) agrees well with the observed ionization energy maximum for band B (6.67 eV), and no distinct ionization is observed for the singlet state. For band C, the calculated singlet/triplet state separation is 0.14 eV, which is less than the width of the vibrational manifolds associated with these ionizations, and a singlet state shoulder on the triplet state ionization is not observable. Again, the calculated vertical ionization for the triplet state (7.77 eV) agrees well with the observed band maximum for band C (7.70 eV).

Table 3.

Experimental and calculated orbital ionization energies (eV) for bands A, B and C of Cp₂V(S₂C₂H₂) and Cp₂V(bdt)

Band	I.E.a	Labelb	Kohn-Sham Orbital Energyc		ΔSCFd
			α-spin	β-spin	Singlet	Triplet
Cp2V(S2C2H2)
A	6.06	V d1/Sπ+	-3.87		6.12
B	6.67	V d1/Sπ+	-4.91	-4.40	7.10	6.57
C	7.70	Sπ-	-5.68	-5.50	7.91	7.77
Cp2V(bdt)
A	6.17	V d1/Sπ+	-4.21		6.22
B	6.78	V d1/Sπ+	-5.21	-4.83	7.18	6.77
C	7.17	Sπ-	-5.36	-5.11	7.27	7.10

^aExperimental vertical ionization energy.

^bPrimary character.

^cThe calculated orbital energy for the ground state.

^dThe difference in total energy between molecular ground state, and the molecule with an electron removed from the specified orbital.

A similar assignment is given for Cp₂V(bdt) based on the ΔSCF calculations. The increase in ionization energies for bands A and B and the decrease in ionization energy for band C from Cp₂V(S₂C₂H₂) to Cp₂V(bdt) observed in the photoelectron spectra also is obtained from the calculations. The observed separation in energy between bands B and C is different for Cp₂V(S₂C₂H₂) and Cp₂V(bdt) (1.03 and 0.39 eV, respectively) correlating with the separation in energy between the S_π⁺ and S_π^- for their titanocene analogues (0.70 and 0.22 eV, for Cp₂Ti(S₂C₂H₂) and Cp₂Ti(bdt), respectively). This trend, which is reproduced computationally, is presumably due to different inductive effects of the ligands and the greater involvement of the benzene ring in the π-system of the ligand for Cp₂V(bdt) and Cp₂Ti(bdt). In general, the calculated singlet/triplet separations for Cp₂V(S₂C₂H₂) and Cp₂V(bdt) are small and within the experimental band widths for the ionizations, which is in agreement with previous studies of vanadium(IV) systems.^55,56

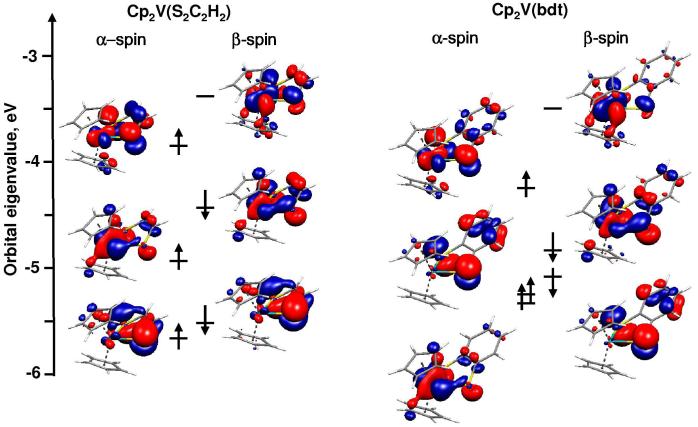
Also included for comparison in Table 3 are the Kohn-Sham orbital energies for the α and β spin electrons. Early calculations of metal complexes with a partially-filled metal d orbital bury the partially-filled orbital below the filled ligand orbitals,^57-61 but in the present calculations the orbital ordering agrees with the calculated and observed sequence of ionizations. Contour plots of the spin α and β orbitals for Cp₂V(S₂C₂H₂) and Cp₂V(bdt) that correspond to the ionizations evaluated by photoelectron spectroscopy are shown in Figure 5. The contour plots show that for Cp₂V(S₂C₂H₂) and Cp₂V(bdt) the SOMOs are substantially delocalized with greater sulfur 3p character than vanadium d_z2 character, in agreement with the greater g and lower A values observed in the EPR experiment. The contour plots for Cp₂V(bdt) also show that the orbital character is extended onto the benzene π-system (the orbital percent contributions shown in Figure 5 are given in Table S5).

Figure 5.

Spin correlation diagrams for Cp₂V(S₂C₂H₂) and Cp₂V(bdt) showing α- and β-spin eigenvalues, molecular orbital character and electron occupations based on ground state configuration.

The description of these orbitals is consistent with the S_π⁺ and V d_z2 orbitals forming a bonding and anti-bonding pair of orbitals, as shown in Figure 5, where the SOMO is the anti-bonding combination and the next orbital is the doubly-occupied bonding combination. This bonding/anti-bonding combination explains the strong vanadium and sulfur character mixing observed for bands A and B in the photoelectron spectra. Overall, the orbital picture corresponds to the bonding interaction proposed by Lauher and Hoffman.¹⁹

DFT calculations also offer insight into how the dithiolate-folding effect and the fold angle influence the oxidation/reduction and electron transfer properties of the active site metal center. Using the linear transit option in the ADF package, potential energy curves for Cp₂V(bdt) as neutral and cation molecules can be constructed to show how the fold angle changes with oxidation of the d¹ M_ip orbital. Figure 6 shows a fold angle potential energy curve plot for Cp₂V(bdt) and [Cp₂V(bdt)]⁺, where the change in relative energy with fold angle is compared. The potential energy curve of the neutral Cp₂V(bdt) molecule shows that the energy minimum lies at approximately 37°. Oxidation of the M_ip orbital leads to an increase in the fold angle from 37° to 40°, resulting in a deeper potential well for the cation. The potential energy curve for the d¹ and d⁰ electronic configurations of Cp₂V(S₂C₂H₂) is similar (Figure S1).

Figure 6.

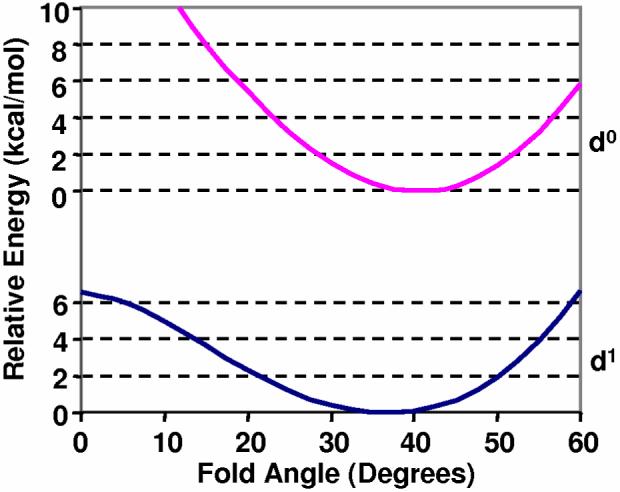
Potential energy diagrams showing the calculated total energy with change in fold angle for the neutral (d¹) and cation (d⁰) of Cp₂V(bdt).

Figure 7 presents the potential energy curves of the neutral (d²), cation (d¹) and dication (d⁰) of Cp₂Mo(bdt) obtained from the gas-phase linear transit calculations with varying fold angle. The figure shows the calculated relative total energies between the optimized geometries of each electron configuration, along with the relative energy perturbation caused by dithiolate-folding for each electronic configuration (d², d¹, and d⁰).⁶² For Cp₂Mo(bdt) the calculated fold angle for the neutral (d²) molecule exhibits a potential minimum at 0°. Upon oxidation from M_ip the fold angle increases to 25° for the cation (d¹), and to 35° for the dication (d⁰). This range of fold angles is consistent with the DFT analysis by Domercq et al.⁶³ The analytical frequency calculations for Cp₂Mo(bdt) show that the folding vibration is the lowest energy vibration in the molecule at 28 cm^-1, and a nearly classical description of the vibronic states is appropriate for these curves and thermal populations will be significant during electron transfer. This trend in the calculated fold angles for the Cp₂Mo(bdt) series in Figure 7 follows that of the neutral d², d¹ and d⁰ metallocene dithiolate crystal structures (vida supra).

Figure 7.

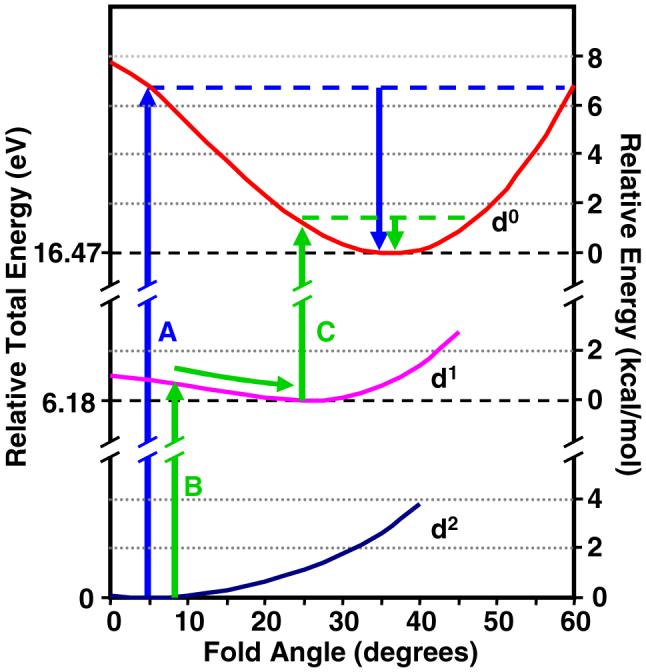
The gas-phase potential energy curve plots of the neutral (d⁰), cation (d¹) and dication (d²) of Cp₂Mo(bdt) are shown with relative total energies (eV, left-hand side) and relative potential energies with change in fold angle (kcal/mol, right-hand side). The oxidation along Path A (blue arrows and line) from the d² to d⁰ electron configurations involves a large energy barrier to oxidation and larger reorganization energies with change in fold angle. Paths B and C (green arrows and lines) show the two-step two-electron oxidation of the d² to d¹ to d⁰ electron configurations. Utilization of the shallow d¹ potential curve poises oxidation to occur with minimal reorganization energies with change in fold angle.

Figure 7 not only shows the increase in fold angle with oxidation, but also gives insight into the role of the d¹ electron configuration in molybdopterin enzymes during substrate turnover. The relative energies between the d², d¹, and d⁰ configurations will be reduced from the gas-phase values in Figure 7 by stabilization of the cations in the molybdopterin enzyme environment. Oxidation starting from the d² configuration and proceeding to the d⁰ electron configuration without geometry reorganization along path A, followed by reorganization of the d⁰ configuration to the minimum of the potential well (blue arrows and line in Figure 7), is a high energy process with a large reorganization energy. The reorganization energy is approximately 0.26 eV (7 kcal mol^-1). Alternatively, oxidation from the d² to d¹ electron configurations allows access to the shallow d¹ potential with little reorganization energy investment upon changing the fold angle from 5° to 25° (arrow B). Likewise, oxidation from the folded geometry of the d¹ configuration allows a low energy investment to the folded structure of the d⁰ electronic configuration (arrow C). The coupling of paths B and C (green arrows and line) through the d¹ electron configuration results in a two-step two-electron oxidation of the d² to d⁰ electron configuration with smaller barrier and reorganization energies. The shallow potential surface calculated for the d¹ electron configuration and the low frequency of the dithiolate folding motion provide an intermediate that can effectively link the d² and d⁰ electron configurations and geometries. Thus, the potential curves of Figure 7 show how sequential one-electron transfers coupled to fold angle variation offer a reaction pathway for reoxidation of molybdenum enzymes with a lower overall energy barrier than two-electron oxidation without the d¹ configuration or the dithiolate-folding effect. These smaller energy barriers allow the reoxidation of the metal center to occur with concomitant electron transfer and change in the fold angle.

Conclusions

The vanadocene dithiolate systems compare well with previous studies of the titanocene and molybdocene dithiolate electronic structures,^22,47 thus completing the d⁰, d¹, and d² configurations found in mononuclear molybdenum protein active sites. The crystallographic and computational data also supports the change in fold-angle upon filling the metal in-plane orbital.

Comparison of the PES of vanadocene systems with their respective titanocene analogs shows that their electronic structures are similar, with the exception of the extra electron in the vanadium complexes. For Cp₂V(S₂C₂H₂) and Cp₂V(bdt) both the SOMO and the next lowest energy orbital show considerable vanadium and sulfur character, forming a bonding and anti-bonding pair. The SOMO is only half-filled, so the resulting contribution to the bond order from this interaction is one half. The ΔSCF calculations compare well with the PES spectra of Cp₂V(S₂C₂H₂) and Cp₂V(bdt) and place the SOMO as the lowest energy orbital.

The use of DFT calculations further supports the importance of the d¹ electronic configuration as a low energy pathway for reoxidation of the metal center during catalysis. Two-electron oxidation of the d² electronic configuration to the d⁰ configuration requires a larger relative energy investment for the removal of both electrons and geometric reorganization of the fold angle. The intermediate d¹ electronic configuration offers a low energy pathway where a minimal amount of energy is required for reoxidation and geometric reorganization of the fold angle bridging the d² and d⁰ electronic configurations.

The variation in dithiolate fold angle with formal d electron count observed for Cp₂M(dithiolates) supports the hypothesis that the change in the dithiolate fold angle effectively stabilizes d⁰ and d¹ metal centers via π-donation from S_π⁺ to the M_ip orbital. This “dithiolate-folding effect” has implications for Mo/W enzymes since folding of the pyranopterindithiolate cofactor poises the metal center for reoxidation and geometric reorganization, modulating the reactivity of the enzyme active site as the metal center passes through the M(IV), M(V), and M(VI) formal oxidation states during electron and oxygen atom transfer.