Multilocus Patterns of Nucleotide Polymorphism and the Demographic History of Populus tremula

Abstract

I have studied nucleotide polymorphism and linkage disequilibrium using multilocus data from 77 fragments, with an average length of fragments of 550 bp, in the deciduous tree Populus tremula (Salicaceae). The frequency spectrum across loci showed a modest excess of mutations segregating at low frequency and a marked excess of high-frequency derived mutations at silent sites, relative to neutral expectations. These excesses were also seen at replacement sites, but were not so pronounced for high-frequency derived mutations. There was a marked excess of low-frequency mutations at replacement sites, likely indicating deleterious amino acid-changing mutations that segregate at low frequencies in P. tremula. I used approximate Bayesian computation (ABC) to evaluate a number of different demographic scenarios and to estimate parameters for the best-fitting model. The data were found to be consistent with a historical reduction in the effective population size of P. tremula through a bottleneck. The timing inferred for this bottleneck is largely consistent with geological data and with data from several other long-lived plant species. The results show that P. tremula harbors substantial levels of nucleotide polymorphism with the posterior mode of the scaled mutation rate, θ = 0.0177 across loci. The ABC analyses also provided an estimate of the scaled recombination rate that indicates that recombination rates in P. tremula are likely to be 2–10 times higher than the mutation rate. This study reinforces the notion that linkage disequilibrium is low and decays to negligible levels within a few hundred base pairs in P. tremula.

DISENTANGLING the forces shaping genetic variation within and between species has long been of interest in population genetics. The combined action of genetic drift and mutation makes up the foundation of the neutral theory of molecular evolution (Kimura 1983) and patterns of genetic variation expected under the neutral theory are well understood (e.g., Hudson 1990; Nordborg 2001). Researchers have increasingly used deviations from neutral expectations as a way of identifying genes or genomic regions that may be under the influence of natural selection (Nielsen 2001; Thornton et al. 2007). However, care must be taken to ensure that the potentially confounding effects of demography, such as population bottlenecks and population subdivision, are taken into account, because demographic processes can also result in systematic departures from neutral expectations (Charlesworth et al. 2003). For instance, both positive selection and bottlenecks are expected to result in reduced levels of nucleotide polymorphism and an excess of singleton mutations (Kaplan et al. 1989; Tajima 1989), while balancing selection and population subdivision are expected to enhance levels of genetic variation and increase the numbers of mutations segregating at intermediate frequencies (Charlesworth et al. 1997; Wakeley 1998).

Multilocus studies of nucleotide polymorphism have been extremely useful for disentangling the effects of natural selection and demography, since natural selection is expected to act on a relatively small number of genes, while demographic changes are expected to affect the entire genome of an organism (Charlesworth et al. 2003; Thornton et al. 2007). Many studies have documented genomewide departures from neutral expectations in both plants and animals, (e.g., Haddrill et al. 2005; Hamblin et al. 2005, 2006; Ometto et al. 2005; Schmid et al. 2005; Heuertz et al. 2006; Pyhäjarvi et al. 2007; Zhu et al. 2007), thereby casting doubt over methods that use the standard neutral model as a baseline to infer the action of positive and/or negative selection (e.g., Nordborg et al. 2005; Schmid et al. 2005).

Many of these studies have dealt with either human commensals (such as Drosophila melanogaster and D. simulans) or cultivated plants, where the population biology of the species has, to a greater or a lesser degree, been influenced by human disturbances. This is particularly true for cultivated plants that have been through severe domestication bottlenecks (Tenaillon et al. 2004; Wright et al. 2005; Hamblin et al. 2006; Caicedo et al. 2007; Kolkman et al. 2007; Zhu et al. 2007). This stands in stark contrast to forest trees that largely persist in an undomesticated state (Savolainen and Pyhäjärvi 2007). Forest trees are also ecologically dominant in many ecosystems and many species have wide geographic distributions, making forest trees excellent organisms for studying the relationships between naturally occurring genetic and phenotypic variation (Neale and Savolainen 2004; Savolainen and Pyhäjärvi 2007; Neale and Ingvarsson 2008). The lack of anthropogenic influence on many forest tree populations suggests that extant populations are the result of natural evolutionary forces and that speciation, adaptation, and demography will therefore not be confounded by human disturbances (Savolainen and Pyhäjärvi 2007; Neale and Ingvarsson 2008).

This does not mean that patterns of polymorphism in forest trees largely conform to neutral expectations, however. Recent studies of Norway spruce (Picea abies) and Scots pine (Pinus sylvestris) found strong evidence for bottlenecks resulting in systematic departures from neutral expectations (Heuertz et al. 2006; Pyhäjarvi et al. 2007). In Norway spruce, the data also suggested both ancient and current population subdivision (Heuertz et al. 2006). Similarly, two multilocus data sets of candidate genes for cold hardiness and wood quality in Douglas fir (Pseudotsuga menziesii), and drought stress in Loblolly pine (P. taeda) showed a systematic excess of low-frequency mutations as indicated by negative average values of Tajima's D (Krutovsky and Neale 2005; Gonzalez-Martinez et al. 2006). Loci in the latter two studies were specifically chosen as likely candidate genes involved in regulating several traits of ecological importance (Krutovsky and Neale 2005; Gonzalez-Martinez et al. 2006). The nonrandom selection of loci makes it difficult to generalize from these data sets and it is not clear to what degree these patterns of polymorphism are representative of the Ps. menziesii and P. taeda genomes.

European aspen (Populus tremula, L. Salicaceae) is a deciduous, obligately outcrossing tree with a geographic distribution ranging throughout Eurasia (Eckenwalder 1996). A recent study of patterns of polymorphism and linkage disequilibrium (LD) in P. tremula showed high levels of synonymous polymorphism and low levels of LD (Ingvarsson 2005b). There was also a quite striking excess of low-frequency polymorphisms in P. tremula (Ingvarsson 2005b) and this excess was enhanced when data from multiple populations were pooled. The reason for this excess of low-frequency polymorphisms was not clear, but one possible explanation was past demographic changes in population size (Ingvarsson 2005b). However, the study by Ingvarsson (2005b) was based on only 5 genes, and at least 2 of these genes were later shown to be likely targets of natural selection (Ingvarsson 2005a; Talyzina and Ingvarsson 2006), so it is not clear how general these results are. Here I present data from a multilocus resequencing study of 77 short gene fragments (average length 550 bp) in P. tremula. The aim is to generalize the results from Ingvarsson (2005b), using a set of loci chosen to provide a representative coverage of the P. tremula genome, to answer questions pertaining to the demographic history of P. tremula and to study whether past demographic processes result in systematic departures from neutrality.

MATERIALS AND METHODS

Plant material, selection of loci, and DNA sequencing:

Samples of P. tremula were collected from the SwAsp collection, which has been described in detail elsewhere (Luquez et al. 2008), and from two central European populations (FRA and AUT described in Ingvarsson 2005b). Depending on the locus, sequences were obtained from either 12 or 19 diploid individuals, representing 24 or 38 haploid genomes of P. tremula.

The coding regions for 558 unique P. tremula genes were extracted from PopulusDB (Sterky et al. 2004, http://poppel.fysbot.umu.se) as previously described (Ingvarsson 2007). These sequences were aligned to the P. trichocarpa genome sequence (Tuskan et al. 2006, http://genome.jgi-psf.org/Poptr1_1/Poptr1_1.home.html), using BLAT (Kent 2002) to obtain exons and to predict the location of introns. A total of 124 genes were selected on the basis of predicted exon and intron lengths. For 44 genes, primers were designed to amplify a fragment between 500 and 850 bp and that contained a predicted intron of at least 300 bp. For the remaining 80 loci, primers were designed to exclusively amplify exon sequences, ranging in size from 500 to 850 bp. All primers were designed using the Primer3 software (Rozen and Skaletsky 2000). Gene fragments were amplified from diploid genomic DNA and directly sequenced on Beckman CEQ8000 capillary sequencers at Umeå Plant Science Centre. All fragments were sequenced in both directions.

Sequences were base called and assembled with PHRED and PHRAP (Ewing et al. 1998). Heterozygous bases were called with the Polyphred program (Nickerson et al. 1997) and confirmed by visual inspection of the corresponding trace files using the CONSED trace file viewer (Gordon et al. 1998). For all gene fragments, homologous regions from P. trichocarpa were extracted from the publicly available genome sequence (Tuskan et al. 2006) and were added to the sequences data sets from P. tremula. Regions with missing or low-quality data were trimmed from all sequences. Multiple sequence alignments were made using Clustal W (Thompson et al. 1994) and adjusted manually using BioEdit (http://www.mbio.ncsu.edu/BioEdit/bioedit.html). Alignments were annotated on the basis of the corresponding gene from the P. trichocarpa genome sequence. All sequences described in this article have been deposited in the GenBank/EMBL databases (accession nos. EU752500–EU754117).

Population genetic analyses:

Population genetic analyses were performed using computer programs based on the publicly available C++ class library libsequence (Thornton 2003). Nucleotide diversity was calculated from either the average pairwise differences between sequences (π, Tajima 1983) or the number of segregating sites (θ_W, Watterson 1975). Diversity statistics were also calculated separately for noncoding, silent, and replacement sites. The frequency spectrum of mutations was summarized using either Tajima's D (Tajima 1989) or the standardized version of Fay and Wu's H (Fay and Wu 2000; Zeng et al. 2006). The latter statistic requires the use of an outgroup sequence so mutations can be polarized into ancestral or derived states (Fay and Wu 2000).

When calculating the frequency spectra of segregating mutations there are problems with pooling data from loci with different sample sizes. To equalize data from fragments with different sample sizes, I randomly sampled 16 sequences from each locus and used these data to calculate the expected and observed frequency spectra for both synonymous and nonsynonymous sites. Intron sites were not considered because of the limited number of genes with intron data.

Since DNA sequences were obtained from genomic DNA it was not possible to directly analyze linkage disequilibra between SNPs, as the phases of different mutations were not known. To obtain estimates of linkage disequilibrium between pairs of SNPs I used the program dipdat (http://home.uchicago.edu/∼rhudson1/source/misc/dipld.html), which estimates the squared correlation coefficients between sites (r²) from unphased, diploid data. Kelly's Z_nS statistic (Kelly 1997) was then calculated by averaging over all pairwise sites for each locus. I also used the program maxdip (http://home.uchicago.edu/∼rhudson1/source/maxdip.html), which estimates the scaled recombination rate, (ρ = 4N_er) from unphased, diploid data using the composite-likelihood method of Hudson (2001). For calculations of the recombination rates, low-frequency mutations (<10%) were excluded from all loci.

It has been shown that misidentification of the ancestral state of mutations can bias statistics that depend on accurate polarization of mutations into ancestral and derived states [e.g., Fay and Wu's H (Baudry and Depaulis 2003)]. Because derived mutations are expected to be rare, ancestral misidentification is more likely to result in an excess of high-frequency derived variants that in reality are low-frequency variants. Baudry and Depaulis (2003) suggested a method for estimating the rate of misidentification of mutations. This method uses data on trinucleotide polymorphisms to estimate the probability of detecting a second mutation in the outgroup (P_D). If all mutations are equally likely, the rate of undetected mutations, and hence of misidentified sites, P_M, = P_D/2. In reality, however, the probabilities of undetected mutations depend on the transition/transversion ratio, which is usually greater than one, suggesting that P_M > P_D/2. The numbers of transitions and transversions were therefore estimated for all polymorphic and fixed mutations in the data set and all sites with more than two segregating alleles were scored to provide a rough estimate of P_D.

Coalescent simulations and demographic modeling:

I used approximate Bayesian computation (ABC) to fit a range of demographic scenarios to the sequence data. Since replacement polymorphisms are much more likely to be under the influence of both positive and negative selection, all simulations were restricted to data from silent sites (synonymous and noncoding sites). However, as noted above, most of the sequenced regions contained relatively few noncoding sites (mean number of noncoding sites is 148 bp), so the data largely consist of synonymous mutations.

The ABC method has been described in detail elsewhere (Beaumont et al. 2002) and is outlined only briefly here. A large number of replicate simulations are performed for each demographic model. Each model is characterized by a number of parameters that are treated as random variables and for each simulation, values for these parameters are drawn from some prior distributions. The ABC framework is then used to repeatedly sample from the posterior distribution of these parameters. Simulated data are summarized using a number of summary statistics (S_sim) that are also calculated from the observed data (S_obs). For the current data set, each sample consists of 77 simulated loci. Simulated samples were accepted if they were deemed to be sufficiently close to the observed data; i.e., simulations were accepted if ‖S_sim − S_obs‖ ≤ δ, where S_obs is the set of summary statistics calculated from the original data and δ is a prechosen tolerance (Beaumont et al. 2002). Conditional on acceptance, these estimates are subsequently weighted and adjusted using local-linear regression. Accepted data points are weighted according to ‖S_sim − S_obs‖ and local-linear regression is used to adjust the parameters (Beaumont et al. 2002). All simulations used an Epanechnikov kernel to weight and adjust parameters as described in Beaumont et al. (2002). The ABC method has been shown to provide parameter estimates that are closer to the true parameters and that have smaller errors than estimates obtained from simple rejection-based sampling (Beaumont et al. 2002). For all simulations I summarized the data using Watterson's θ (Watterson 1975), nucleotide diversity π (Tajima 1983), Tajima's D (Tajima 1989), the standardized version of Fay and Wu's H (Fay and Wu 2000; Zeng et al. 2006), and Kelly's Z_nS (Kelly 1997).

As suggested by Pritchard et al. (1999), the posterior probability of different models can be estimated on the basis of the same summary statistic approach that forms the basis for the ABC method described in the preceding paragraph. The posterior probability of a given model is obtained by simply counting the number of simulated points that fall within the tolerance region, ‖S_sim − S_obs‖ ≤ δ. However, as pointed out by Beaumont (2008), this method can be rather inefficient. Instead, Beaumont (2008) suggested that the posterior probabilities of different models are estimated directly by including a model indicator, a categorical variable M that takes on the values (1, … , n), where n is the number of different models that are being compared. Model selection is then included in the ABC regression framework by using categorical regression to estimate the coefficients β in a multinomial logistic regression model

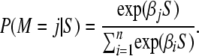(1)

These coefficients were estimated using the regression approach described above, implemented using the VGAM package implemented in the statistical package R (R Development Core Team 2007).

In addition to the standard neutral model, I investigated three different demographic models: a single size change, exponential growth/decline, and a single bottleneck and recovery. For the size change model, looking backward in time, the current population size, N₀, was assumed to have instantaneously changed in size to N_A at time T. The prior distribution for the logarithm of the ancestral population size (in units of the current population size) was take to be uniform in the range 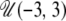, where 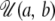denotes the uniform distribution, with minimum equal to a and maximum equal to b. This thus corresponds to sizes of the ancestral population in the range 0.001N₀ ≤ N_A ≤ 1000N₀. Similarly, the prior distribution for the logarithm of the time of the size change was 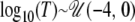, where T is measured in units of 4N₀ generations. The size change model thus covers the entire range from large increases to moderate reductions in N₀. For the exponential growth model, the current population was assumed to have been changing in size at a constant rate, starting T generations ago and continuing until the present. Before population growth was initiated, the ancestral population size was equal to N_A. The prior distributions of the time of growth and ancestral population sizes were uniform on the log₁₀ scale, with 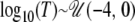and 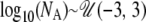, respectively. With both the time of growth and ancestral population size specified, the growth rate, α, is implicitly given by α = log(N₀/N_A)/T. Again, this scenario includes possibilities for both population growth (N₀ > N_A) and population decline (N₀ < N_A). For the bottleneck simulations, I assumed that a single bottleneck occurred from an ancestral population of the same size as the current population size (N₀). The bottleneck was assumed to end at time 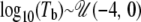. The effect of a bottleneck is largely dependent on the ratio of the population size during the bottleneck to the duration of the bottleneck (Eyre-Walker et al. 1998), i.e., N_b/t_d. I therefore arbitrarily fixed the duration of the bottleneck to t_d = 0.015 and varied the population size during the bottleneck (N_b) to simulate bottlenecks of different strengths, 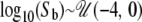. For all simulations, values of the scaled mutation rate per site, θ = 4N₀μ, were drawn from 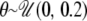and values of the scaled recombination rate ρ = 4Nc per site were drawn from 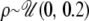. For each rejection sample, consisting of 77 simulated loci, the observed number of silent sites per locus was used, so that even if the per site values of θ and ρ were the same across loci in each simulation step, the per locus values of θ and ρ varied according to the number of sites per locus.

For model selection, 3 × 10⁵ samples were generated for each of the four different demographic models and the 1200 points closest to the set of summary statistics chosen were used (P_δ = 0.001). An additional 7 × 10⁵ were subsequently simulated for the bottleneck model. From the total 10⁶ simulations from the bottleneck model, the 1000 closest data points (corresponding to P_δ = 0.001) were used to estimate the mode and the 0.95 highest posterior density (HPD) limits for the parameters of the model. A range of different values of P_δ were tried (0.01–0.0005) but this had little effect on the posterior modes of the estimated parameters (results not shown), confirming that ABC estimates are only weakly dependent on P_δ (Beaumont et al. 2002). All simulations were performed and analyzed using the program ms (Hudson 2002) and with scripts written in R. The ABC analyses were performed using R-scripts generously provided by M. Beaumont (available at http://www.rubic.rdg.ac.uk/∼mab/stuff/). The posterior densities, including modes and HPD intervals, for the estimated parameters were computed using the local-likelihood method of Loader (1999), as implemented in the R-library locfit.

To assess the fit of the parameters estimated from the posterior distributions, I performed posterior predictive simulations (Gelman et al. 2004). The rationale behind posterior predictive simulations is that if the model fits the data, replicated data from the model should look similar to the observed data. I therefore generated 10⁵ new data sets by repeatedly drawing from the posterior distribution of the parameters. These simulated data sets were summarized using a variety of summary statistics and were then compared to the corresponding summary statistics from the observed data. The posterior predictive simulations thus constitute an important “self-consistency check” (see p. 159 in Gelman et al. 2004) of the model. Furthermore, as pointed out by Thornton and Andolfatto (2006), posterior predictive simulations also provide a means for assessing the fit of individual loci to the estimated demographic model through the calculation of posterior predictive P-values. Posterior predictive P-values were calculated for all loci from the empirical distribution function for each locus derived from the 10⁵ simulated data sets. Two-sided P-values were calculated because the signal from the data is two-sided (Thornton and Andolfatto 2006). Multiple-test corrections were performed using the false discovery rate (FDR) (Storey and Tibshirani 2003) as implemented in the qvalue package in R.

RESULTS AND DISCUSSION

Patterns of nucleotide polymorphism:

I amplified and sequenced fragments from 124 loci and I obtained sequences that could be reliably scored for 77 loci that were retained for the analyses presented in this article.

These 77 loci represent 76 unique genes as one gene was represented by two different fragments (supplemental Table S1). The remaining loci failed for either of two reasons. For a large fraction of the loci, primers amplified two paralogous copies, which were apparent from a number of sites at which all individuals were heterozygous. This is not unexpected since Populus has gone through at least two rounds of whole-genome duplications and most segments in the Populus genome have a parallel “paralogous” segment elsewhere in the genome (Tuskan et al. 2006). The other reason for sequence failure was that the amplified fragment contained polymorphic indels. Since sequencing was based on PCR products amplified from genomic DNA, this resulted in unreadable chromatograms after a polymorphic indel site. Not surprisingly, the occurrence of polymorphic indels was largely restricted to fragments containing intron sequences.

The average length of the 77 sequenced fragments was 554 bp and these fragments were located on 18 of the 19 chromosomes present in Populus, with a median of three fragments per chromosome. There were also 17 loci that were located on scaffolds that at present have not been anchored to any of the 19 chromosomes in the P. trichocarpa genome sequence. A total of 42,659 bp of aligned sequence (excluding gaps) were obtained from each individual across the 77 loci and close to 1.36 Mb of sequence data were generated for the entire sample of individuals.

Average levels of polymorphism at various types of sites are summarized in Table 1 together with Tajima's D (Tajima 1989) and Fay and Wu's H (Fay and Wu 2000) that summarize different aspects of the frequency spectrum. A total of 811 segregating sites were identified, of which 263 were singletons. About 20% of all sites screened were synonymous positions but the majority of the segregating sites identified were still synonymous (Table 1). Mean polymorphism at synonymous sites (θ_S = 0.0129) is roughly two-thirds of the value reported in Ingvarsson (2005b). This is likely due to a nonrandom selection of loci included in Ingvarsson (2005b) that favored the inclusion of loci that had shown high levels of polymorphism in other species. Still, P. tremula harbors substantial levels of polymorphism compared to many other long-lived plant species such as many conifer species (Heuertz et al. 2006; Savolainen and Pyhäjärvi 2007) and P. tremula has levels of polymorphism comparable to specieswide samples from Arabidopsis (Ramos-Onsins et al. 2004; Schmid et al. 2005) or maize (Wright et al. 2005).

TABLE 1.

Levels of nucleotide polymorphism in P. tremula

	All	Noncoding	Synonymous	Replacement
Sites	42,659	4,307	8,266	30,115
Segregating sites	811	86	464	261
Watterson's θ	0.0048	0.0055	0.0129	0.0022
Nucleotide diversity (π)	0.0042	0.0048	0.0120	0.0017
Tajima's Da	−0.425	−0.329	−0.173	−0.648
Fay and Wu's Ha	−0.572	−0.267	−0.459	−0.271

^aAverage across loci.

Interestingly, nucleotide polymorphism at noncoding sites (in this case only introns) was even lower than previously found in P. tremula (π_nc = 0.0048 compared to π_nc = 0.0160 in Ingvarsson 2005b). This could be an artifact caused by the sequencing strategy. Sequences were generated directly from genomic DNA and loci with introns containing polymorphic insertions and/or deletions are thus more likely to fail during contig assembly since chromatograms become unreadable once a polymorphic indel site is reached. It is possible that this resulted in a bias against loci with relatively high levels of polymorphism, if nucleotide and indel polymorphisms are positively correlated. However, there are no significant differences in levels of polymorphism in coding regions between fragments that contain introns and fragments containing only exon sequences (Kruskal–Wallis test, χ² = 1.029, d.f. = 1, P = 0.310), suggesting that such an effect is unlikely. One possible explanation is that the introns included in the present sample are short (average intron size is 148 bp). Halligan et al. (2004) found that sites close to intron splice sites were highly constrained in Drosophila. Since the number of these more constrained sites is roughly constant across introns, shorter introns will consequently have a larger proportion of sites that are under selective constraint. This pattern has also been found in humans, where Gazave et al. (2007) documented a strong positive correlation between intron size and sequence divergence between humans and chimpanzees. More data are needed to determine whether these patterns also hold in Populus.

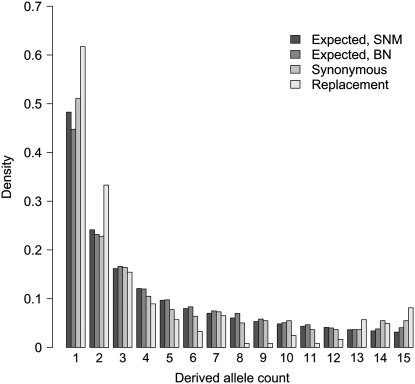
There was a greater excess of singletons at replacement sites, as indicated by significantly lower values of Tajima's D at replacement sites (Wilcoxon's signed rank test, P < 0.0019, see also Figure 1). In fact, judging by Figure 1 there appear to be excesses of both low- and high-frequency derived variants at replacement sites while silent sites primarily show an excess of high-frequency, derived variants. The majority of the genes had ratios of replacement to silent polymorphism (π_a/π_s) that were substantially smaller than unity, suggesting strong purifying selection at amino acid replacement sites (median π_a/π_s = 0.083 for sequences with coding regions exceeding 100 codons).

Figure 1.—

Observed frequency spectrum at silent and replacement sites and the expected frequency spectrum under the standard neutral model (SNM) and the bottleneck model (BN) with parameter values sampled from the posterior distribution obtained by the ABC approach (see Figure 3).

Using a single P. trichocarpa sequence as an outgroup, the average divergence at synonymous sites was K_s = 0.047 and at replacement sites K_a = 0.010. Similar to what was seen in the intraspecific polymorphism data, divergence from P. trichocarpa also suggests the predominant action of purifying selection at most of the genes surveyed since the median K_a/K_s value is 0.160. This value is in line with earlier estimates of K_a/K_s between P. tremula and P. trichocarpa from much larger sequence sets (Unneberg et al. 2005; Ingvarsson 2007). The neutral theory predicts that intraspecific polymorphism should be correlated with divergence, if the mutation rate varies between gene regions (Kimura 1983). Interestingly, there were no such patterns in the P. tremula data, as the correlation between diversity and divergence at synonymous sites was low (Spearman's rank correlation r_S = 0.064, P = 0.580).

I used the method of Baudry and Depaulis (2003) to estimate the probability of ancestral misidentification for the current data. The total number of sites across the 77 loci with three nucleotides segregating is 12, yielding an estimate of P_D = 0.86%. The estimated transition/transversion ratio for the observed data is 1.82 and applying Equation 3 from Baudry and Depaulis (2003) yields an estimate of the proportion of misidentified sites of P_M = 0.49%. Haddrill et al. (2005) suggested another way to estimate P_M. Briefly, the probability of a back mutation in the P. trichocarpa lineage is D_xy/2, where D_xy is the net divergence between P. tremula and P. trichocarpa. As only one-third of all possible mutations result in a misoriented site, the probability of a site being misoriented is approximately D_xy/6. Using this method, the estimated P_M does not exceed 1.9% for any locus, and the average probability of misorientation across loci is 0.6%, which is very close to the estimate derived above using the method of Baudry and Depaulis (2003) (0.5%). Such a low misidentification rate (<1%) will likely have only minor effects on statistics that depend on an accurate identification of ancestral states, such as Fay and Wu's H (Baudry and Depaulis 2003). Therefore, misidentification of ancestral states does not seem to be a major factor influencing the observed excess of high-frequency derived sites seen in P. tremula.

Linkage disequilibrium:

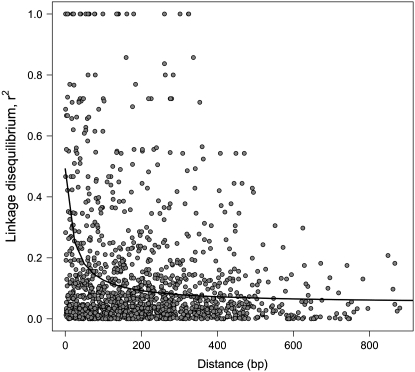
LD, measured as the squared allele-frequency correlation (r²), declined to <0.1 in ∼200 bp (Figure 2). Of the 1308 pairwise comparisons made, 53 were significant by Fisher's exact test after Bonferroni corrections. Estimates of the scaled recombination rate (ρ = 4N₀c) varied substantially across genes. For five genes ρ could not be estimated because of too few polymorphic sites occurring in high enough frequencies (>10%). For an additional 15 loci the ρ-estimate converged to an upper limit set by the maxdip program (ρ_max = 5000), suggesting that recombination was high for these genes, but that it could not be precisely estimated. Averaging across all genes for which estimation of ρ was possible, and excluding genes where the maxdip program converged to the upper limit set by maxdip, yielded a mean recombination fraction per site of ρ = 0.0137. Using the naive estimate of θ at synonymous sites from Table 1 thus suggests that ρ/θ ∼ 1 in P. tremula. This is clearly an underestimate of the true ρ/θ-ratio, as loci known to have high recombination rates, but where more accurate estimations were not possible, were excluded from the calculation (see also below). Furthermore, many recombination events will go undetected when recombination rates are inferred from sequence data, again leading to an underestimate of ρ (Nordborg 2001).

Figure 2.—

Linkage disequilibrium (within genes) as a function of the distance between sites pooled across the 77 genes. The solid line is the theoretical expectation of r² (from Equation 1 in Ingvarsson 2005b). Only mutations with frequencies exceeding 10% are included.

These results are similar to those obtained by Ingvarsson (2005b), where LD was calculated separately for five different genes. Using this greatly expanded set of genes, these results further strengthen the view that low linkage disequilibria and high recombination rates are general features of P. tremula. These observations mirror data from other long-lived plant species. For instance, conifers are predominantly outcrossing and generally have levels of LD that extend only a few hundred base pairs (Brown et al. 2004; Heuertz et al. 2006) although in some species LD can extend across genes or even over greater distances (Kado et al. 2003; Krutovsky and Neale 2005). Similarly, many predominantly outcrossing plants, such as maize (Remington et al. 2001) and sunflower (Liu and Burke 2006), also have high recombination rates and low levels of LD. This stands in stark contrast to predominantly selfing species where LD can extend for several hundred kilobases (Nordborg et al. 2002; Hamblin et al. 2005; Zhu et al. 2007).

Model selection and inferences on model parameters:

I used approximate Bayesian computation to evaluate a number of different demographic scenarios, including the standard neutral model, population size change, population growth, or a single bottleneck. Simulations of the various demographic scenarios used only variation at silent sites. This assumes that synonymous sites are neutral or at least effectively neutral, which is reasonable given that patterns of codon bias are relatively weak in P. tremula (Ingvarsson 2007).

The ABC model selection approach of Beaumont (2008) clearly indicates that P. tremula has gone through a bottleneck, as the posterior probability for the bottleneck model was 0.975 (Table 2). The standard neutral model is clearly inadequate to explain the data, both because of a general excess of low-frequency variants (average Tajima's D = −0.173) and because of an excess of high-frequency derived variants seen across loci (average Fay and Wu's H = −0.459, Table 1). This model is associated with a posterior probability of 0.021. Simultaneously negative values of both Tajima's D and Fay and Wu's H across loci are also difficult to explain under the exponential growth (decline) and size change models, which both have posterior probabilities <0.01.

TABLE 2.

Posterior probabilities for alternative demographic models

Model	Posterior probability
Standard	0.021
Bottleneck	0.975
Exponential growth	0.002
Size change	0.003

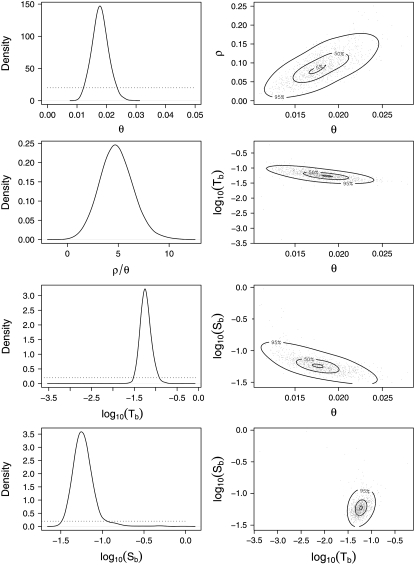
Posterior distributions from the different parameters of the bottleneck model are summarized in Figure 3. All four parameters of the model (θ, ρ, T_b, and S_b) were simulated using uniform priors. Nevertheless, there are distinct modes in the posterior distributions for all four parameters (Figure 3), suggesting that the data contain enough information to estimate these parameters. The posterior mode of θ = 0.0177 with a 95% credible interval of 0.0129–0.0231. It appears that ρ is less well estimated than θ (Figure 3) and this should not come as a surprise since only the Z_nS statistic carries information about recombination, whereas θ_W, π, and Z_nS all provide information about θ. More powerful summary statistics that depend on ρ could be used, but as the original data are unphased, such estimators would be computationally very intensive. Also, using more sophisticated estimates of ρ [such as Hudson's composite-likelihood estimator (Hudson 2001)] does not guarantee better estimates, as shown above where Hudson's estimator failed to converge for a large fraction of the loci. Nevertheless, the mode of the posterior distribution for ρ/θ is 4.47, with a 95% HPD interval of (0.94, 8.71), confirming the high levels of recombination that have been suggested by the rapid decline of LD in Populus (see above and Ingvarsson 2005b).

Figure 3.—

Approximate posterior distributions for the parameters of the bottleneck model and joint bivariate distributions for pairs of parameters.

There are fairly strong correlations between θ and the other parameters in the posterior distributions (Figure 3). This is to be expected since several different combinations of parameters can give rise to the same pattern in the data. Higher values of θ are therefore consistent with both an earlier timing and greater strength of the inferred bottleneck (Figure 3). The posterior mode of S_b = 0.056 with a 95% credible interval of 0.035–0.105. The strength of the bottleneck, S_b, is really a compound parameter determined by the population reduction and the length of the bottleneck. In my simulations I arbitrarily fixed the duration of the bottleneck to 0.015 × 4N₀ generations and this should be kept in mind when interpreting the posterior distribution of S_b. Thus, if the bottleneck had a shorter duration than 0.015 × 4N₀ it implies a more severe reduction in population size, while a longer-lasting bottleneck implies less severe reductions in N₀.

Posterior predictive simulations:

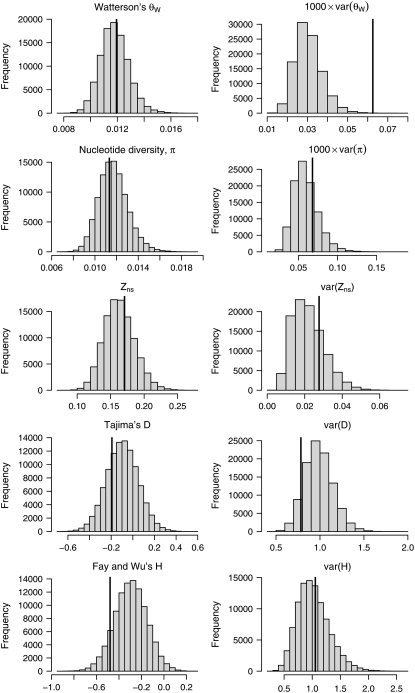
The simulated data sets were summarized using both the mean and the variance across loci of five different summary statistics: Watterson's θ_W, nucleotide diversity π, Kelly's Z_nS, Tajima's D, and the standardized Fay and Wu's H. The results from the posterior predictive simulations are summarized in Figure 4. As can be seen from Figure 4, there is generally a good agreement between observed and simulated data sets. The only real discrepancy is that the variance among loci for Watterson's θ_W is substantially higher in the observed data compared to the simulated data (Figure 4). This could indicate that mutation rates vary among loci, even if no such variation was apparent from the low correlation between intraspecific nucleotide diversity and interspecific divergence at synonymous sites. Interestingly the observed variance for π falls within the distribution of simulated values (Figure 4). The frequency distribution simulated under the bottleneck model is also included in Figure 1 and it appears to fit the observed data better than the frequency spectrum under the standard neutral model. It is possible that more complex demographic models could explain the large variance in θ_W (see below).

Figure 4.—

Means and variances of summary statistics calculated from 10⁵ posterior predictive simulations based on parameters drawn from the posterior distributions shown in Figure 3. Values of the corresponding summary statistics for the observed data are shown by vertical lines.

If a subset of the loci have been under the influence of positive selection, their inclusion could bias the average values of the summary statistics used to evaluate the different demographic models. This would result in patterns that are incompatible with the neutral model and hence in the rejection of the neutral model in favor of an alternative demographic explanation. Such rejection would occur even if the majority of loci conform to neutrality if the lack of fit of the neutral model is generated by the action of positive selection at only a small fraction of the loci.

Under the neutral model, between 5 and 11 loci showed significant values of D, H, or Z_nS, a number that drops to between 1 and 6 after controlling the FDR (Table 3). These numbers correspond to between 5 and 10% of the genes being under positive selection, an amount that seems excessively high. However, under the bottleneck model, between 2 and 6 loci are outliers, and after FDR correction only 2 of these loci remain significant (Table 3). This shows that accounting for a bottleneck in the simulations clearly reduces the number of the outlier loci, serving as yet another consistency check for the bottleneck model. Another thing worth pointing out is that if the summary statistics used to describe the sequence data were unduly influenced by selection at a few loci, the variance in H and D across loci would also be inflated. However, this is not observed; in fact, if anything the variance in D across loci appears to be somewhat lower than expected (Figure 4). Taken together, this suggests that natural selection does not contribute substantially to the observed excess of low-frequency and high-frequency derived sites across the 77 loci in P. tremula.

TABLE 3.

Number of outlier loci for the standard neutral model (SNM) and the bottleneck model (BN)

	SNM		BN
	Unadjusteda	FDRb	Unadjusteda	FDRb
Tajima's D	5	1	3	0
Fay and Wu's H	7	4	2	0
Kelly's ZnS	11	6	6	2

^aSignificance determined using unadjusted P-values.

^bSignificance controlling the false discovery rate.

There is also an excess of high-frequency derived variants at replacement sites (Table 1, Figure 1), although this pattern is less pronounced than for silent sites. Since the excess of high-frequency mutations at silent sites appears to be explained by a past reduction in population size in P. tremula, it is likely that these processes also influence mutations at replacement sites. There is also a marked excess of low-frequency sites at replacement sites, as evidenced by a negative Tajima's D (Table 1). This additional class of low-frequency replacement mutations likely represents an excess of slightly deleterious amino acid-changing mutations that persist in low frequency in the population at mutation–selection balance.

The demographic history of P. tremula:

One parameter of particular interest for understanding the demographic history of P. tremula is the timing of the bottleneck, T_b. The posterior mode of T_b, which is given in units of 4N₀ generations, is 0.055 with a 95% credible interval of 0.035–0.103 (Table 2 and Figure 3). To convert this to absolute time, estimates of both N₀ and the generation time of P. tremula are needed. For the data on the timing of genome duplications in Populus to be compatible with fossil data, Tuskan et al. (2006) concluded that the synonymous substitution rate per year in the genus Populus is roughly sixfold lower than estimates from Arabidopsis (Koch et al. 2000). Using the estimate of the synonymous mutation rate from Koch et al. (2000) of 1.5 × 10⁻⁸ per site per year suggests that the corresponding mutation rate in Populus is 2.5 × 10⁻⁹ per site per year. However, after correcting for the long generation time of Populus, which is likely on the order of ≥15 years, the synonymous mutation rate is more comparable to that from other angiosperms per generation. Using an estimate of μ = 2.5 × 10⁻⁹, a generation time of 15 years and the posterior mode of θ = 0.0177 yield an effective population size of N₀ ≈ 118,000 for P. tremula. Assuming this estimate of the effective population size of P. tremula and 15 years per generation, the timing of the bottleneck in P. tremula is dated to ∼388 thousand years ago (KYA) with a 95% credible interval of 244–730 KY. The upper value of this estimate is close to the period in the early Quaternary (∼700 KYA) that marks the beginning of the period of the strong climatic fluctuations that have continued until the present (Comes and Kadereit 1998). It is notable, however, that the lower bound is substantially older than the initiation of the last full glacial period, which commenced ∼100 KYA and lasted until ∼10 KYA.

It is well established from palynological data that Populus underwent both a range contraction and a reduction in population size in the early Dryas period (∼12–13 KYA, Williams et al. 2002). The timing of this event is clearly far too recent to be compatible with that estimated from the bottleneck model. Nevertheless, a bottleneck occurring ∼250–750 KYA is largely consistent with data from several other plant species. For instance, multilocus sequence data suggest that Norway spruce (P. abies) went through a severe bottleneck about ∼150–300 KYA (Heuertz et al. 2006). Following that bottleneck, the Eurasian Norway spruce population diverged into two genetically differentiated domains, an event that has been dated to ∼40 KYA on the basis of both palynological and genetic data (Heuertz et al. 2006). Pyhäjarvi et al. (2007) showed that Scots pine, P. sylvestris, has likely gone through a bottleneck and estimated the time of the bottleneck to be ∼2 MYA. Their estimate, however, is associated with large uncertainties, as relatively few bottleneck parameters were investigated and both more recent and more ancient bottlenecks are compatible with the data. Similarly, in Arabidopsis thaliana, the demographic history appears to have been complex, likely involving both population subdivision and repeated bottlenecks during the Pleistocene (Schmid et al. 2005).

As was suggested by earlier studies (Schmid et al. 2005; Heuertz et al. 2006; Pyhäjarvi et al. 2007), the models implemented and explored in the ABC analyses are most likely too simplistic. It is more likely that P. tremula has gone through repeated population size contractions and expansions over the last millennia, as many other plant species have (Webb and Bartlein 1992; Hewitt 2004). Such periods of alternating range expansions and contractions will probably have involved periods of population subdivision into glacial refugia and other complicating factors (Webb and Bartlein 1992). Whatever consequences these complex demographic histories may have for multilocus patterns of nucleotide polymorphism, the current data, when viewed through a few summary statistics, appear to be adequately described by fairly simple demographic scenarios and it would be hard to justify investigating substantially more complex models at this point. As more data accumulate, there might be reasons to revisit these questions and to use more sophisticated demographic models.

There are other demographic forces that are known to result in an excess of high-frequency derived sites. One such process is population subdivision and/or admixture that has been shown to result in an excess of negative values of H, especially when there is unequal contribution from different subpopulations (Przeworski 2002). There is, however, little evidence for population subdivision in P. tremula, in chloroplast DNA, at microsatellite markers, or at SNPs (Petit et al. 2003; Hall et al. 2007), although Ingvarsson (2005b) detected low, but significant population subdivision across Europe (median F_ST = 0.065). Another possibility is hybridization with another species. Hybridization rates are known to vary across the genome and might thus result in the introduction of low-frequency variants only at some loci, thereby inflating among-locus heterogeneity. P. tremula is known to hybridize with other species of Populus in parts of its range (Lexer et al. 2005), so this is a possibility that may deserve further attention in the future. I did analyze the current data set using Structure (Pritchard et al. 2000) to determine whether there was any signal of population subdivision in this expanded SNP data set. There were no clear signals of population subdivision, and the results showed typical signs of an unstructured population, such as a roughly equal allocation of individuals to the inferred populations and with all individuals showing similar proportions of admixture (data not shown). This lack of population subdivision in P. tremula likely reflects the high dispersal capabilities that are characteristic of Populus, which has both wind-dispersed seeds and pollen. Taken together, this suggests that population subdivision is an unlikely explanation for the observed excess of derived variants at high frequencies.

Summary:

This study reinforces the notion that P. tremula harbors substantial levels of nucleotide polymorphism and that linkage disequilibrium is low and decays within a few hundred base pairs (Ingvarsson 2005b). These conclusions are based on a data set of 77 loci, significantly increasing the size of a previous data set based on only 5 loci (Ingvarsson 2005b). The loci used in this article were sampled without prior knowledge of their function and are evenly distributed across the P. tremula genome. This point is worth emphasizing since this increases the likelihood that data from these loci provide an accurate and unbiased view of genomewide patterns of polymorphism in P. tremula. The data suggest the predominant action of purifying selection across the P. tremula genome as evidenced by a median K_A/K_S value of 0.160. There was also a significant excess of low-frequency mutations at replacement sites, likely indicating the segregation of deleterious amino acid-changing mutations at low frequencies in P. tremula.

A previous study found a large excess of low-frequency mutations in P. tremula (Ingvarsson 2005b), but that study investigated only the folded frequency spectrum (i.e., Tajima's D). Here I have shown that there is also an excess of high-frequency derived variants, which is observed at both silent and replacement sites. A number of different demographic scenarios were evaluated to explain these observations and the data were found to be largely consistent with one (or more) historical reductions in the effective population size of P. tremula. The timing of the bottleneck in P. tremula, inferred from the demographic modeling, is largely consistent with data from several other long-lived plant species (e.g., Heuertz et al. 2006; Pyhäjarvi et al. 2007) and with the timing of known climate changes during the Quaternary (Comes and Kadereit 1998; Williams et al. 2002). These results suggest that it is important to take into account systematic departures from neutral expectations, when trying to infer the action of positive selection, or it will lead to inflated numbers of false positives. One approach is to incorporate alternative demographic scenarios into the null model that is used as a baseline against which loci are compared. This is relatively easy to implement, using existing software. However, this still requires that the demographic model is correctly specified and that it accurately captures any influences that past demographic events may have had on levels of nucleotide polymorphism. An alternative approach is to derive empirical genomewide distributions for different summary statistics of polymorphism data and then evaluate whether loci fall in the extremes of these distributions. Such empirical approaches have already been advocated and applied to polymorphism data from A. thaliana (Nordborg et al. 2005; Schmid et al. 2005), although it should be borne in mind that this approach critically relies on the assumption that the effects of selection are relatively rare across the genome (see, for instance, Hahn 2008). As large multilocus data sets are increasingly becoming available for different organisms, the possibilities for using such empirical distributions should increase. What will ultimately be the best approach for separating the effects of natural selection at specific loci from genomewide effects of past demographic events remains to be determined.