Critical Importance of Length Scale Dependence in Implicit Modeling of Hydrophobic Interactions

Hydrophobic interactions play an essential role in the stability and folding of proteins¹ and significant progress has been made in understanding their nature and properties.^2,3 In particular, it has been recognized that hydrophobic solvation has a dependence on the solute size.^4–6 Qualitatively speaking, the hydrogen bonding network of water persists near small nonpolar solutes such that the solvation free energy is dominated by an entropic cost and scales roughly with the solute volume. On the other hand, large solutes disrupt the water hydrogen bond network to form an interface and the solvation free energy is dominated by an enthalpic component, which is proportional to the surface area. The crossover from small to large length scale regimes occurs around 10 Å.^6,7 Exposed nonpolar amino acid sidechains are within the small length scale regime, while folded proteins typically fall in the large length scale regime. Consequently, the length scale dependence of hydrophobic solvation has significant implications in the equilibrium of disordered, partially folded and folded conformations and is thus an important consideration in implicit modeling of solvation for simulating protein folding and conformational transitions.

Implicit solvent models aim to capture the mean influence of solvent molecules around the solute via direct estimation of the solvation free energy.^8,9 They can substantially reduce the computational cost, at the expense of a reduction in details. In general, the total solvation free energy is decomposed into electrostatic and nonpolar components. While the former can be quite reliably computed using a continuum electrostatics treatment, such as through efficient generalized Born (GB) approximations,¹⁰ the later proves to be more complex and is typically estimated from the solute surface area (SA), A, as,

$$\mathrm{\Delta }{G}_{\text{np}}=\gamma A+b,$$ (1)

where γ is an effective surface tension coefficient. The constant b does not affect the solute conformational equilibrium and can be dropped. The linear relationship has been justified by theoretical considerations and experimental observations,^12,13 however, various deficiencies exist.¹⁴ In particular, it has been argued that the nonpolar component needs to be decomposed further into a cavity hydration term and a solute-solvent dispersion interaction term.¹⁴ Nonetheless, the length scale dependence of hydrophobic solvation is largely neglected and a fixed, i.e., context independent, γ is used in virtually all the implicit solvent models. Here, we illustrate several deficiencies of fixing γ, mainly by examining the potentials of mean force (PMFs) of pair-wise and three-body interactions of nonpolar peptide side chain analogs. We then propose an empirical nonpolar model to capture the context dependence of γ and demonstrate that it can resolve these deficiencies.

Neglecting the length scale dependence of hydrophobic solvation has two main consequences, over stabilizing the pair-wise interactions and predicting a wrong sign in the multi-body contributions. For small solutes, the effective surface tension of closely packed nonpolar n-mers (n=1,2,3), defined as ${\gamma }^{(\text{n})}=\mathrm{\Delta }{G}_{\text{np}}^{(\text{n})}/A^{(\text{n})}$, scales linearly with the effective size.² Thus, γ⁽ⁿ⁾ ~ γ⁽¹⁾ n^1/3. By definition, the dimer stability and three-body contribution are given as,

$$W^{(2)}={\gamma }^{(2)}{A}^{(2)}-2{\gamma }^{(1)}{A}^{(1)}={\gamma }^{(2)}\mathrm{\Delta }{A}^{(2)}+2\mathrm{\Delta }{\gamma }^{(2)}{A}^{(1)}$$ (2)

$$\delta F^{(3)}=W^{(3)}-3W^{(2)}={\gamma }^{(3)}\mathrm{\Delta }{A}^{(3)}-3\mathrm{\Delta }{\gamma }^{(2)}\mathrm{\Delta }{A}^{(2)}+3(\mathrm{\Delta }{\gamma }^{(3)}-2\mathrm{\Delta }{\gamma }^{(2)})A^{(1)}$$ (3)

where ΔA⁽ⁿ⁾ = A⁽ⁿ⁾ − nA⁽¹⁾ and Δγ⁽ⁿ⁾ = γ⁽ⁿ⁾ − γ⁽¹⁾. The second term in Eqn. 2 is positive as Δγ⁽²⁾ > 0, but vanishes if γ is assumed to be constant. Hence, fixed γ models predict more negative W⁽²⁾, i.e. over estimate the dimer stability. Such over stabilization can be (improperly) compensated by using a small γ. This explains why small γ values have been empirically found to be optimal in simulating peptide folding.¹¹ Given γ⁽ⁿ⁾ ~ γ⁽¹⁾n^1/3, Eqn. 3 yields δF⁽³⁾ ~3(Δ;γ⁽³⁾-2Δγ⁽²⁾)A⁽¹⁾ ~ −0.24γ⁽¹⁾A⁽¹⁾. As the nonpolar solvation free energies of amino acid side chains are about 2–3 kcal/mol, the analysis predicts negative, i.e., cooperative, three-body contributions on the order of 0.5 kcal/mol. On the contrary, with γ fixed, δF⁽³⁾ = γ (ΔA⁽³⁾ − 3ΔA⁽²⁾), which is positive according to the simple geometric consideration that ΔA⁽³⁾ − 3ΔA⁽²⁾ > 0. The implications of these consequences are substantial: on one hand, sufficiently large γ is required to maintain the stability of compact folded structures; one the other hand, small γ is desirable so as not to under estimate the probability of extended conformations with exposed nonpolar sidechains and not to over stabilize loosely packed misfolded conformations. This analysis is also in agreement with certain limitations of a GBSW/SA model¹¹ observed in extensive peptide folding simulations, such as difficulties in stabilizing hydrophobic cores (Chen and Brooks, unpublished results).

To verify the above analysis, we computed the PMFs of pair-wise and three-body interactions of Leu and Phe sidechain analogs in various configurations in TIP3P water¹⁵ as well as in a GBSW/SA implicit solvent.¹¹ The solutes were described by the CHARMM22 all-atom force field.¹⁶ The free energy perturbation method¹⁷ was used with 1.0–2.0 nanoseconds (ns) NVT sampling at every 0.25 Å along the reaction coordinates. Particle Mesh Ewald (PME) method¹⁸ was used for long-range electrostatics. The largest separation distances sampled were about 10 Å beyond the contact minima and thus sufficiently large to accurately estimate the baselines. For trimers, only one monomer was translated along the reaction coordinate with the other two fixed. The solutes were solvated by about 800~950 TIP3P molecules in rectangular boxes with periodic boundary conditions. The box sizes were determined by 100 ps NPT equilibrium simulations at 298 K for at the contact minima. The convergence of the PMFs is mostly within 0.05 kcal/mol, estimated by comparing the results using only the first and second half of sampling. PMFs in the implicit solvent were computed by simply translating the solutes along the reaction coordinates.

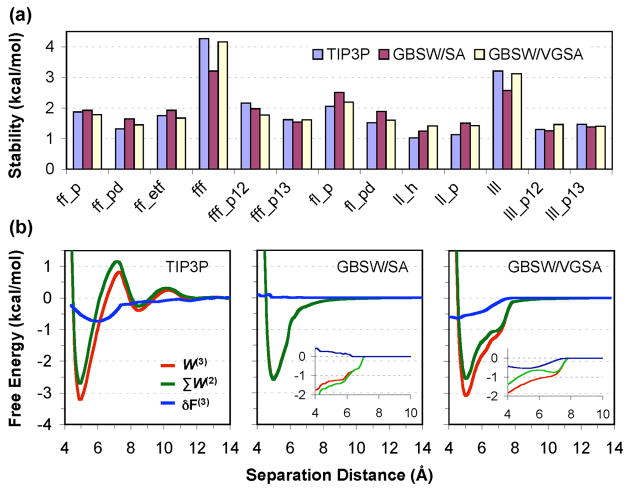
In this study, we focus on the stabilities and multi-body effects at the contact minima. To examine the full capability of fixed y models, we have assigned independent y for aliphatic (Leu) and aromatic (Phe) carbons and optimize the values to minimize the root-mean-square deviation (RMSD) from the TIP3P results. The optimized γ values are 0.015 and −0.005 kcal/mol/Ų for Leu and Phe respectively. The results are summarized in Figure l-(a). The RMSD of stabilities in GBSW/SA from those of TIP3P is 0.42 kcal/mol for all clusters and 0.26 kcal/mol for dimers. Even with γ optimization, GBSW/SA substantially under estimates the trimer stabilities, while over estimating the dimer stabilities by an average value of 0.15 kcal/mol, in agreement with the above analysis. This is essentially due to the inability of fixed γ models to capture the cooperativity of three-body hydrophobic associations. As illustrated in Figure l-(b), the three-body contribution of the hydrophobic association of a Leu trimer in TIP3P is about − 0.5 kcal/mol at the contact minimum, also similar to the value estimated above.

Figure 1.

(a) Stabilities of dimers and trimers in TIP3P, GBSW/SA, GBSW/VGSA solvents. Notations: f: Phe, 1: Leu, p: parallel, pd: parallel displaced, etf: edge-to-face, p12/p13: pairs from trimers. (b) PMFs of Leu trimer in different solvents. The green traces were constructed by summing two pair-wise PMFs (p12 and p13). The inserts plot the nonpolar contributions. Note that SA leads to anti-cooperativity at contact minimum (~5 Å) instead of cooperativity as in TIP3P and GBSW/VGSA.

The main difficulty in including the length scale dependence is efficient and reliable estimation of some effective local curvature, R_c, from which one might derive the local γ using theoretical relations such as in the scaled particle theory⁵,

$$\gamma (R_c)\sim {\gamma }_{\infty }(1-2\delta /R_c),$$ (4)

where γ_∞ is the limiting sufficient tension and the Tolman length δis related to the solvent size. Taking advantage of the limited number of nonpolar functional groups in proteins, one can estimate the effective curvature for each group based on the number of nonpolar group contacts made. For this, the local contact mass is first computed,

$$M_c(i)=m(i)+\sum _{j\ne i}m(j)H(d_{ij}),$$ (5)

where m(i) is the effective mass of nonpolar group i, which is related the actual molecular mass. H(d_ij) is a contact switching function that equals one at short distance and decreases smoothly to zero at large distance. The inter-group average distance is defined as $d_{ij}={(\sum \sum r_{nm}^{-1})}^{-1}$ to allow some resolution of different contact poses, which is important for planar functional groups such as aromatic rings. Then the effective local curvature can be estimated as,

$$R_c={(\kappa M_c(i))}^{1/3}+R_0,$$ (6)

where the constant κ is related the mass density and R_o is related to the solvent size. Eqn. 6 may be considered as the first term in an shape and density expansion which includes a spherical shape and uniform packing density. In this work, we used δ=0.9, κ=0.33, R₀=2.3. The adjustable parameters in this empirical model, referred as SA model with varying gamma (VGSA), include mainly functional group specific parameters such as the limiting gamma and effective mass, as well as input atomic radii and solvent probe size for the surface area calculation.

We have parameterized the GBSW/VGSA model based on PMFs of dimers and trimers of representative peptide nonpolar sidechain analogs. The results for the Leu and Phe related PMFs are summarized in Figure l-(a). A previously optimized set of input radii¹¹ were used with a solvent probe size of 0.7 Å and γ_∞=30 cal/mol/Ų. The RMSD of dimer and trimer stabilities in the GBSW/VGSA from the TIP3P values is 0.26 kcal/mol for all and 0.21 kcal/mol for dimers. More importantly, the new model is able to reproduce the stability of trimers without over-stabilizing pair-wise interactions. The mean difference of dimer stabilities in TIP3P and GBSW/VGSA is 0.04 kcal/mol (compared to 0.15 kcal/mol in GBSW/SA). Figure 1-(b) illustrates that the key to the improved performance of the GBSW/VGSA model is the correct estimation of cooperative three-body contributions from the nonpolar solvation term.

In summary, it is critical to capture the length scale dependence of hydrophobic associations and popular implicit solvent models with context independent surface tension has fundamental limitations. An empirical model is proposed to capture the context dependence of the effective surface tension. Further co-optimization of the new model together with other components of the force field is currently ongoing and might lead to significant improvement in the ability to accurate simulation of protein folding and conformational transitions.