Calsequestrin-Mediated Mechanism for Cellular Calcium Transient Alternans

Abstract

Intracellular calcium transient alternans (CTA) has a recognized role in arrhythmogenesis, but its origin is not yet fully understood. Recent models of CTA are based on a steep relationship between calcium release from the sarcoplasmic reticulum (SR) and its calcium load before release. This mechanism alone, however, does not explain recent observations of CTA without diastolic SR calcium content alternations. In addition, nanoscopic imaging of calcium dynamics has revealed that the elementary calcium release units of the SR can become refractory independently of their local calcium content. Here we show using a new physiologically detailed mathematical model of calcium cycling that luminal gating of the calcium release channels (RyRs) mediated by the luminal buffer calsequestrin (CSQN) can cause CTA independently of the steepness of the release-load relationship. In this complementary mechanism, CTA is caused by a beat-to-beat alternation in the number of refractory RyR channels and can occur with or without diastolic SR calcium content alternans depending on pacing conditions and uptake dynamics. The model has unique features, in that it treats a realistic number of spatially distributed and diffusively coupled dyads, each one with a realistic number of RyR channels, and that luminal CSQN buffering and gating is incorporated based on experimental data that characterizes the effect of the conformational state of CSQN on its buffering properties. In addition to reproducing observed features of CTA, this multiscale model is able to describe recent experiments in which CSQN expression levels were genetically altered as well as to reproduce nanoscopic measurements of spark restitution properties. The ability to link microscopic properties of the calcium release units to whole cell behavior makes this model a powerful tool to investigate the arrhythmogenic role of abnormal calcium handling in many pathological settings.

INTRODUCTION

Calcium transient alternans (CTA) is characterized by beat-to-beat alternations of the peak cytosolic calcium (Ca²⁺) concentration. The origin of CTA in cardiac myocytes is still not fully understood (1). CTA was originally thought to be caused primarily by alternations of the duration of the cardiac action potential (AP). However, experiments by Chudin et al. (2) demonstrated that the Ca²⁺ handling machinery of cardiac myocytes has instabilities of its own that can result in CTA independently of action potential duration (APD) alternans. In these experiments, isolated myocytes were paced with periodic AP waveforms and, at fast pacing rates, CTA was observed to occur. Due to the bidirectional coupling of the membrane voltage and Ca²⁺ machinery of the cell (1), instabilities in the Ca²⁺ system can lead to APD alternans that has been shown both in mathematical models (3) and experiments (4) to promote fibrillation. Cellular alternans has also been linked to electrocardiographic T-wave alternans (4), which are a strong marker for susceptibility to sudden cardiac arrest (5–7). Elucidating the origin of intracellular CTA has thus become an important problem in excitation-contraction (EC) coupling.

There have been recent attempts (8,9) to construct models of intracellular Ca²⁺ dynamics to explain the occurrence of CTA. These models have incorporated the experimentally observed relationship between the amount of Ca²⁺ released from the sarcoplasmic reticulum (SR) and the SR Ca²⁺ load. In particular, the steepness of the release-load relationship at high load (10,11) has been proposed as a possible mechanism of CTA (12). (Other factors might coregulate CTA, e.g., the rate of SR Ca²⁺ reuptake (1).) Shiferaw et al. (8) incorporated the nonlinear SR release-load relationship in a mathematical model where discrete Ca²⁺ release events are spatially averaged over the cell. In the model of Shiferaw et al., the diastolic SR Ca²⁺ content displays alternans whenever there is CTA. Although this model partially accounts for observed features of CTA, more recent experimental observations appear inconsistent with a steep SR release-load relationship being the only cause of CTA. In particular, Picht et al. (13) have reported the observation of CTA without diastolic SR load alternans. These observations suggest the possibility of other mechanisms capable of producing CTA without diastolic SR alternans.

The main aim of this article is to identify a new mechanism to explain these observations using a physiologically more realistic model where both luminal gating of SR Ca²⁺ release and the spatially distributed nature of unitary Ca²⁺ release events are treated explicitly. Although this multiscale myocyte model is used here primarily to study alternans, it could be used more generally to study a wide range of arrhythmogenic mechanisms linked to abnormal Ca²⁺ handling.

Luminal gating of SR Ca²⁺ release

A crucial element in modeling EC coupling is the mechanism by which luminal Ca²⁺ controls SR release. In the Shiferaw model, it was assumed that the amount of SR Ca²⁺ release is a phenomenological nonlinear function of the SR Ca²⁺ load which becomes steep for high loads (8). The origin of this nonlinear relationship, however, is not well understood. Calcium release from the SR is regulated by the ryanodine receptors (RyRs), which open upon a rise in the local cytosolic Ca²⁺ concentration (14). There is a growing body of experimental evidence showing that luminal Ca²⁺ regulates the sensitivity of the RyRs by the interaction of auxiliary proteins (triadin-1/junctin, T/J) with the luminal Ca²⁺ buffer calsequestrin (CSQN) (e.g., (15–17)). In particular, Györke et al. (16) have demonstrated the role of CSQN and the T/J complex in regulating the luminal Ca²⁺ dependence of the activity of purified RyR channels in lipid bilayers. Additionally, Terentyev et al. (15) have shown that unitary Ca²⁺ release events—the so-called Ca²⁺ sparks—in transgenic mice with over(under)-expressed CSQN show longer (shorter) refractory periods, thus demonstrating the crucial role of CSQN in modulating the activity of the RyRs. The picture emerging from these experiments is one where, for high luminal Ca²⁺ concentration, CSQN is mostly bound to luminal Ca²⁺ and unbound from T/J, and the RyR sensitivity to Ca²⁺ in the proximal space is higher, i.e., its transition rate from the closed to the open state is higher. On the other hand, for low luminal concentration, CSQN binds to the T/J complex thereby decreasing RyR sensitivity, with a lower transition rate from the closed to the open state.

These experimental observations lead us to test two hypotheses in this article. The first is that the refractoriness of the RyR channels associated with the delay in CSQN unbinding from T/J can cause CTA independently of whether or not the SR load is alternating. The second is that the Ca²⁺ concentration dependence of the CSQN binding/unbinding kinetics can explain the steepness of the observed SR release-load relationship at high load. The motivation for testing this second hypothesis is that this nonlinear release-load relationship is well characterized experimentally. It thus provides a valuable benchmark for testing our mathematical model even if, as we conclude here, its steepness at high load may not necessarily be the primary cause of CTA.

Spatially distributed discrete nature of Ca²⁺ dynamics

To test these hypotheses theoretically, it is necessary to develop a mathematical model capable of predicting how the gating kinetics of individual Ca²⁺ release channels influences the whole cell Ca²⁺ transient. This task is made especially arduous by the fact that the whole cell Ca²⁺ signal is the summation of discrete release events occurring at a large number of Ca²⁺ release units (CRUs) spatially distributed throughout the cell, as postulated by the local control theory of EC coupling (18); a single CRU typically consists of a few L-type channels in close proximity with a much larger number (∼50–100) of RyRs. The spatially distributed nature of Ca²⁺ release is manifest in a number of phenomena ranging from Ca²⁺ waves (19–23), to intracellular spatially discordant alternans (i.e., distinct regions of the cell with CTA of opposite phase) (24–26), to triggered activity (19,27,28) associated with spontaneous release of Ca²⁺ at high SR load.

Previous discrete models of intracellular Ca²⁺ dynamics can be broadly categorized into two classes. The first class includes models that treat the stochastic dynamics of CRUs to varying degrees of physiological realism (29–34), but assume that the CRUs are not diffusively coupled. While these models have shed light on various aspects of both local and whole-cell Ca²⁺ dynamics, such as the distribution of spark life time (30) and the gradedness of Ca²⁺ release (31–33), respectively, they do not reproduce CTA even when the Ca²⁺ cycling dynamics is coupled to a whole set of membrane ionic currents (33). The second class consists of models that explicitly treat the diffusive coupling between CRUs to study spatiotemporally complex behavior such as intracellular Ca²⁺ waves (35–41). These models, however, do not generally incorporate a physiologically detailed description of the stochastic dynamics of CRUs and do not couple the Ca²⁺ activity to whole cell membrane currents. Hence, they have so far not been used to study phenomena such as CTA that are governed by the bidirectional coupling between the intracellular Ca²⁺ activity and the membrane voltage dynamics. In short, none of the existing models that take into account the discrete and spatially distributed nature of Ca²⁺ release events are able to faithfully reproduce the generation of Ca²⁺ transient alternans with or without SR content alternans (13).

The model developed in this article distinguishes itself from previous models by its attempt to be both physiologically realistic and truly multiscale. Efficient numerical algorithms are developed that allow us to treat for the first time simultaneously (to our knowledge), in a whole cell model, the dynamics of a realistic number of ∼10,000 diffusively coupled CRUs interacting with Ca²⁺ sensitive membrane currents and other whole cell membrane currents, with each CRU having a realistic number of ∼100 RyR channels. Furthermore, the model takes into account CSQN-mediated luminal gating of RyR sensitivity based on recent experimental data (16,42,43). As we show here, both luminal gating of RyR sensitivity and diffusive coupling between CRUs turn out to be crucial ingredients for the genesis of CTA which have not been considered in previous modeling studies of CTA, and the model can reproduce CTA both with and without SR content alternans in qualitative agreement with experimental observations (13).

DESCRIPTION OF THE MODEL

In this section we will describe the most important aspects of our multiscale myocyte model. A more detailed description of the equations and model parameters is given in the Appendix. In Elementary Ca²⁺ Release Unit Structure we describe the intracellular compartments and the various currents in our model. In Cell Architecture we briefly describe the geometry of ventricular myocytes, which we use to realistically implement our spatially extended model. Finally, in the subsections Luminal Gating and Luminal Buffering we present a new mathematical formulation of CSQN-mediated luminal gating and buffering that takes into account the transition from monomeric to dimeric forms of CSQN with increasing luminal free Ca²⁺ concentration.

Elementary Ca²⁺ release unit structure

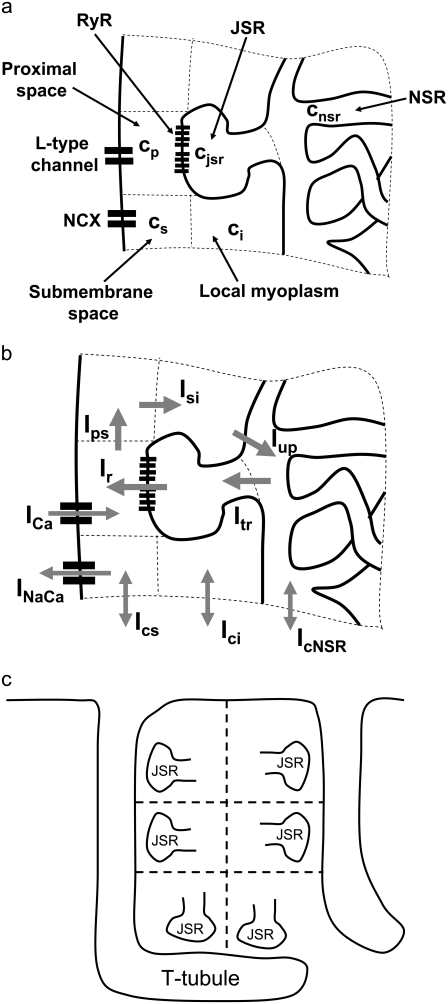
Excitation-contraction coupling, the process by which cardiac myocytes transform the membrane depolarization signal into cell contraction, is a complex process that spans multiple scales (44,45). Calcium ions (Ca²⁺) enter the cell upon membrane depolarization, triggering discrete Ca²⁺ release events at the elementary CRUs of the SR, an intracellular store whose primary function is the sequestration and release of intracellular Ca²⁺. These Ca²⁺ sparks (46,47) are highly localized in space (∼1 μm) and time (∼20 ms). The SR is a sac-like structure which forms a spatially dense network of interconnected tubules and cisternae. The SR tubular network is usually referred to as network SR (NSR), while the cisternae are referred to as junctional SR (JSR). These cisternae are localized in close proximity to the T-tubules, cell membrane invaginations that form also a dense structure in ventricular myocytes (48). The cisternae are usually called dyads, and the space between a dyad and the sarcolemma is referred to as the dyadic junction. We will also refer to the dyadic junction as the proximal space of the corresponding dyad.

Upon cell membrane depolarization, L-type Ca²⁺ channels colocalized with the dyads (49,50) open, allowing Ca²⁺ entry and increasing the Ca²⁺ concentration in the proximal space. The pronounced rise in Ca²⁺ concentration in the proximal space is sensed by a cluster of RyR channels in the dyad, estimated to have from 50 to 250 RyR channels (14,50), which open and release a larger amount of Ca²⁺ from the JSR. The resulting localized rise in Ca²⁺ concentration, a Ca²⁺ spark, constitutes an elementary release event. Calcium sparks are typically independent of each other, although Ca²⁺ released from a spark can trigger neighboring sparks in conditions of elevated SR Ca²⁺ load (19). After Ca²⁺ is released from a dyad, it diffuses to the submembrane space. The submembrane space is the region of the cell which is close to the sarcolemma, and in which concentrations are sensed by the ion channels corresponding to Ca²⁺ sensitive membrane currents, including the Ca²⁺ current I_Ca and the sodium-calcium exchanger current I_NaCa (8,44,51). Subsequently, Ca²⁺ diffuses to the myoplasm, where it activates the cell's contractile machinery. In the myoplasm, the SERCA pump reuptakes a fraction of the Ca²⁺ into the NSR, while most of the rest is extruded from the cell by the sodium-calcium exchanger current in the submembrane space. For a comprehensive description of EC coupling, see Bers (44).

Our goal is to construct a myocyte multiscale model from which whole-cell dynamical behavior, in particular CTA and spatial Ca²⁺ dynamics, can be obtained from the properties of the microscopic Ca²⁺ handling dynamics described above. Due to the relatively slow (compared to voltage) Ca²⁺ diffusion, such microscopic processes are essentially local in nature. Until now, physiologically detailed models of intracellular Ca²⁺ dynamics (e.g., (8,32,51)) have assumed global Ca²⁺ compartments (for example, Greenstein and Winslow (32) assumes a global cytoplasmic compartment). A novel feature of our model is that the entirety of Ca²⁺ dynamics takes place in local units which comprise a dyadic junction and its vicinity, including its proximal and submembrane spaces, the region of myoplasm close to it, its corresponding junctional SR, and the region of the nonjunctional SR in the vicinity of the dyadic junction. Furthermore, as we will discuss in more detail in the next section, these basic units are coupled by Ca²⁺ diffusion, thereby endowing our model with spatial organization.

The elements playing a role in the process described above, and which constitute an elementary release unit in our model, are schematically depicted in Fig. 1 a. As described in the next subsection, our cell model consists of N coupled units, and we will denote the quantities associated to unit n by a superindex (n), where n = 1,2,…,N. In every unit we have a local cytosol, a submembrane space, a proximal space, a JSR space, and an NSR space with volumes 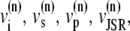and 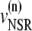and Ca²⁺ concentrations 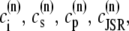and 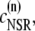respectively. The experimentally measured cytoplasmic Ca²⁺ concentration c_i corresponds in our model to the average

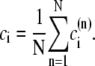(1)

In the following, we describe the Ca²⁺ currents in a CRU, which are depicted in Fig. 1 b. Within each unit, there are diffusive currents between the proximal space and the submembrane space 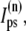between the submembrane space and the local myoplasm 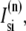and a refilling diffusive current between the local part of the NSR and the SR, 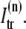Additionally, we have a local uptake current 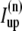and a release current 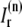from the JSR into the proximal space. There are diffusive currents between the submembrane spaces, local NSRs, and local myoplasmic spaces of spatially adjacent units. There are several L-type channels per dyadic junction, which release Ca²⁺ into the proximal space. For each channel, we have implemented a fully stochastic version of the Markov model of Mahajan et al. (52). The total number of RyR channels per dyadic junction has been estimated to vary between 50 and 250 (14,50), and we will consider 100 RyR channels. The number of L-type Ca²⁺ channels has been estimated to be between 1/4 and 1/10 of the number of RyR channels. However, for simplicity, we will consider only four L-type channels per dyad as in Bondarenko et al. (53). A larger number of LCC channels per dyad would result in a more heterogeneous I_Ca current amplitude per CRU, since different numbers of channels could open within some narrow time interval. Rather than increasing the number of L-type Ca²⁺ channels per CRU, we will include the effect of heterogeneity in the I_Ca signal by considering variations in the proximal space volume (54) (which affects the concentration of Ca²⁺ in the proximal space) as will be discussed in the next section.

FIGURE 1.

(a) Structure of an elementary Ca²⁺ release unit (CRU). Each unit consists of local cytosolic, submembrane, proximal, JSR, and NSR compartments. L-type Ca²⁺ channels release Ca²⁺ into the proximal space and the sodium-calcium exchange current acts on the submembrane space. (b) Currents in a CRU. The arrows illustrate the average direction of Ca²⁺ flow. The form of the currents is detailed in the Appendix. (c) Schematic illustration of the heterogeneous orientation of the T-tubules inside the myocyte. The dyadic junctions are oriented along the T-tubules.

The dynamics of RyR gating is a central feature of our model and will be discussed in a separate section. Finally, in each submembrane space we have electrogenic Na-Ca exchangers. The magnitude of the current in each submembrane space, determined by the number of exchangers per unit, was chosen so that the resulting whole cell sodium-calcium exchange current is physiological. The form of the currents and more details can be found in the Appendix.

Cell architecture

In the past subsection we described Ca²⁺ dynamics in a single CRU. A ventricular myocyte has between 10,000 and 100,000 such units (14,32,44). In this subsection we discuss the spatial architecture of the diffusively coupled units that constitute our myocyte model.

The cell membrane has invaginations (the T-tubules) at the so-called Z-planes, which are spaced approximately every 2 μm in the longitudinal direction of the cell (14). Inside the cell, the T-tubules form a complex network which is concentrated on the Z-planes (48). The invagination of the cell membrane into this tubular network allows a more uniform influx of Ca²⁺ into the cell resulting in a more even recruitment of Ca²⁺ sparks throughout the cell volume. Accordingly, most dyadic junctions are localized in close proximity to the T-tubules. As a result of this arrangement, CRUs are distributed uniformly throughout the cell volume in a regular pattern. For simplicity, we will model the myocyte as a three-dimensional grid, where each element of the grid corresponds to a CRU. We will assume that heterogeneities in the spatial configuration of the elementary units can be spatially averaged and incorporated into effective diffusion coefficients as will be discussed below.

The average separation of the CRUs has been measured using various techniques. Chen-Izu et al. (14) report an average transverse separation of 1.05 μm and an average longitudinal separation of 1.87 μm, while Parker et al. (55) report 0.76 μm in the transverse direction and 1.8 μm in the longitudinal direction; we will use a longitudinal separation of l_L = 1.84 μm and a transverse separation of l_T = 0.9 μm.

The total number of CRUs can be estimated to be 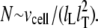By processing several confocal microscopy images, Satoh et al. (56) estimate the average volume of ventricular myocytes to be ∼v_cell ≈ 30 pl, which yields N ∼ 20,000. The three-dimensional grid by which we represent the myocyte has n_x = 65 units in the longitudinal direction, and n_y = 27, n_z = 11 units in the two transverse directions (see Table 1). These dimensions were chosen to approximately reproduce the observed myocyte shape aspect ratio of 140 μm × 30 μm × 12 μm (56). Note that the units themselves are longer in the longitudinal direction.

TABLE 1.

Cell architecture parameters

Parameter	Description	Units
N	Number of CRUs	19,305
nx	Number of CRUs along length	65
ny	Number of CRUs along width	27
nz	Number of CRUs along height	11

A large fraction of the cell volume is occupied by myofilaments and mitochondria (44). Therefore, we will consider an effective cytosolic volume of v_cyto = 10.0 pl < v_cell. This cytosolic volume is composed from the individual cytosolic volumes of the release units. For unit n, we denote the corresponding volumes by a superindex (n). We take 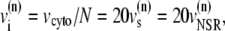and for the JSR we use 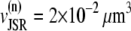(57) (see Table 2).

TABLE 2.

CRU effective volumes

Parameter	Description	Units
vi	Local cytosolic volume	0.5 μm3
vs	Local submembrane space volume	0.025 μm3
vJSR	Local JSR volume	0.02 μm3
vNSR	Local NSR volume	0.025 μm3
〈vp〉	Proximal space volume average*	0.00126 μm3

^*The proximal volume v_p is different for each CRU.

The characteristics of the elements constituting the CRUs have considerable variation, from the number of RyR channels per unit (14,50) to the number of L-type channels colocalized with the unit (53). While, in principle, most of the parameters of a release unit should have random variation, for simplicity we only consider heterogeneity in the volume of the proximal space. The combined effect of the variation in all the parameters will ultimately affect the excitability of the release unit to Ca²⁺ triggering and the amount of Ca²⁺ released during a spark. The proximal space volume affects the sensitivity of the release unit since it directly affects the maximum Ca²⁺ concentration reached in that unit in response to Ca²⁺ entry through LCC channels, and thus whether or not Ca²⁺-sensitive RyR channels are activated. We will consider a different volume for each proximal space, 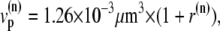where r⁽ⁿ⁾ is a random number drawn from a Gaussian distribution with mean 0 and standard deviation 0.3, truncated so as to restrict r⁽ⁿ⁾ to the interval (−0.8, 0.8). We note that we choose the random numbers r⁽ⁿ⁾ at the beginning of a simulation and do not change them subsequently. The average proximal space volume, 1.26 × 10⁻³ μm³, is obtained by considering the proximal space as a cylinder of radius 200 nm and height 10 nm (30). We find that this proximal space volume heterogeneity modulates the high voltage region of the graded release curve, consistent with the results of Bondarenko et al. (53), and that, in turn, this modulation decreases the propensity for CTA (see Results).

In our model, spatially adjacent units are coupled by diffusive currents. As detailed in the Appendix, the currents have the form (c₁−c₂)/τ, where c₁ and c₂ are the Ca²⁺ concentrations in the compartments of the adjacent spaces which are coupled by the current, and τ is a characteristic diffusion time which depends on the effective Ca²⁺ diffusion coefficient and the geometrical arrangement of the units. Because the contractile elements of the cell are arranged longitudinally, Ca²⁺ has more difficulty diffusing in the transverse direction of the cell, as has been demonstrated by comparing the wave propagation speed in the transverse and longitudinal directions (22). Commonly used values for the transverse and longitudinal diffusion coefficients are D^T = 0.15 μm²/ms and D^L = 0.30 μm²/ms (35). The characteristic time for diffusion between compartments of two neighboring CRUs can be roughly estimated to be on the order of τ ∼ l²/D, where l and D is the separation between CRUs and diffusion coefficient, respectively. For the cytosolic and NSR compartments we use the corresponding longitudinal and transverse CRU separations l_L and l_T, while for the submembrane compartments we use a separation 200-nm shorter to account for the width of the dyadic junction.

Several factors complicate the crude estimation of the times for diffusion τ described above. First, the submembrane spaces should be coupled along the T-tubules: when the T-tubules are oriented in the transverse direction, adjacent units in the transverse direction should be coupled, and similarly when the T-tubules are oriented in the longitudinal direction. Although the T-tubules invaginate in the transverse direction, they branch out and bend inside the cell so that both orientations are possible (see Fig. 1 of Soeller and Cannell (48) and the schematic representation in Fig. 1 c). We assume that the majority of the submembrane coupling occurs between transversally adjacent units, but that some longitudinally adjacent units are also coupled. We incorporate this assumption into the model by increasing the longitudinal submembrane diffusive timescales, representing a weaker effective coupling in the longitudinal direction due to the smaller number of units coupled in that direction. In addition, experiments show that CRUs are intercalated between Z-planes in the periphery of the myocyte (14), and modeling studies suggest that these intercalated CRUs increase the probability of wave initiation (35). We include the effect of these extra CRUs by decreasing the longitudinal time constants by a factor of 2. As the previous discussion suggests, the values that one obtains from the estimates above are very crude; thus, rather than adopting a fixed set of values throughout the article, we explore the effect of varying the diffusive timescales in Diffusive Coupling (see later). We find that stronger diffusive coupling promotes the onset of CTA. The values of the diffusive timescales that we use for the other plots are somewhat smaller than what one obtains by the estimates above and are listed later in Table 9. We have checked that the speed of Ca²⁺ waves in our model (∼85 μm/s) agrees with the experimental values (50 ∼ 150 μm/s) (58,59).

TABLE 9.

Diffusive timescales

Parameter	Description	Units
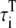	Transverse cytosolic*	2.93 ms
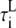	Longitudinal cytosolic*	2.32 ms
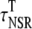	Transverse NSR*	7.2 ms
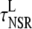	Longitudinal NSR*	24.0 ms
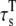	Transverse submembrane*	1.42 ms
	Longitudinal submembrane*	3.4 ms
τtr	JSR refilling time	5.0 ms
τps	Proximal to submembrane	0.022 ms
τsi	Submembrane to cytoplasm	0.1 ms

^*The effect of varying these quantities is shown in Fig. 11.

We emphasize that, besides the voltage, there is no global variable that couples the release units. When the action potential is clamped, the only influence of one unit upon another is through the diffusion of Ca²⁺.

Luminal gating

In this section, we will construct a model for luminal gating of the RyR channels which regulate Ca²⁺ release from the SR. It is well known that SR Ca²⁺ content affects, in a nonlinear way, the amount of Ca²⁺ that is released from the SR upon stimulation. In particular, the experiments in the literature (10,11) show that, for low SR content (<500 μM), Ca²⁺ release is quite small, while it increases markedly as SR Ca²⁺ content is increased. Some models of intracellular CTA (8) are based on this observation.

There is experimental evidence that an important mechanism by which luminal Ca²⁺ controls SR Ca²⁺ release is by modulation of the activity of RyR channels through interactions with the Ca²⁺ luminal buffer CSQN. CSQN is the main buffering protein in the SR, and is localized mainly in the JSR (60). In experiments in vitro, it was shown (42) that CSQN forms dimers as the Ca²⁺ concentration rises above ∼500 μM, and forms higher order polymers at concentrations of a few millimolar. Lipid bilayer experiments (16) have shown that the activity of RyR channels is modulated by the interaction of CSQN with the auxiliary proteins triadin-1 and junctin (T/J): the open probability of purified RyR channels sharply increases upon addition of T/J, and it decreases again when CSQN is present. Furthermore, when Ca²⁺ concentration on the luminal side is increased from 20 μM to 5 mM (binding to and polymerizing CSQN), the open probability of the channels increases again. In addition, in vivo experiments (15) show that transgenic mice with over(under)-expressed CSQN result in Ca²⁺ sparks with longer (shorter) refractory periods.

These experiments suggest that CSQN acts as a luminal Ca²⁺ sensor and regulates RyR channel activity by attaching to the T/J complex of the RyR channels. Although there is so far no comparable data on the physiological range of c_JSR, these observations indicate that polymerization of CSQN might modulate RyR sensitivity by inhibiting the attachment of CSQN to the T/J complex. We will construct a simple model of CSQN luminal gating by assuming that only CSQN monomers can bind to and inhibit RyR channels. Although this might be an oversimplification, we believe that such a model captures the general features of CSQN modulation of RyR activity.

In vitro experiments in Park et al. (42) show that a sharp transition from CSQN monomers to dimers occurs as c_JSR is increased past ∼500 μM. Denoting CSQN monomers by M and CSQN dimers by D, and assuming rates k₁(c_JSR) and k₂(c_JSR) of dimerization and monomerization dependent on luminal Ca²⁺ concentration c_JSR, respectively, we have the dimerization reaction

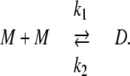(2)

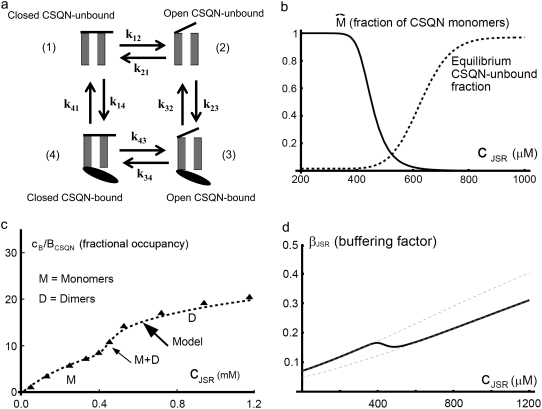
The transition rates are believed to be fast (61), so we assume that the dimers and monomers are in equilibrium, obtaining [M]²ρ = [D], where ρ ≡ k₁/k₂ is assumed to depend on the luminal Ca²⁺ concentration. The monomer and dimer concentrations are related to the total CSQN concentration, B_CSQN (assuming no higher polymeric forms, which is approximately true at physiological concentrations (42)), by B_CSQN = [M] + 2[D]. Note that B_CSQN refers to the concentration of CSQN molecules, not of CSQN binding sites; the binding capacity of CSQN will be included below. Solving these equations for the relative monomer concentration 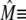[M]/B_CSQN, we obtain

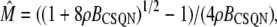(3)

an expression for 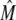in terms of B_CSQN and the parameter ρ. To account for the small range of luminal Ca²⁺ concentration over which the monomer-to-dimer transition occurs as observed in Park et al. (42), we will take ρ to have a sharp dependence on luminal Ca²⁺, c_JSR, with parameters chosen so that 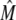decreases from 1 to 0 at c_JSR ∼500 μM. For simplicity, we take a sigmoid function

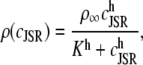(4)

where ρ_∞ = 5 × 10³, K = 850 μM, and h = 23. We remark that we choose a large Hill coefficient so as to reproduce the experimentally observed sharp transition from monomers to dimers as a function of c_JSR. In addition to our hypothesis that only the monomeric form of CSQN can effectively bind to the T/J complex, we assume that the RyR channels have four distinct states, schematically depicted in Fig. 2 a: closed CSQN-unbound (1), open CSQN-unbound (2), open CSQN-bound (3), and closed CSQN-bound (4). The transition rates from the closed to the open states are assumed to depend on the proximal Ca²⁺ concentration for the CSQN-unbound and CSQN-bound states, respectively, as

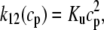(5)

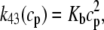(6)

where K_u > K_b implies that CSQN-unbound channels have a higher open probability than the CSQN-bound channels. The transition rates from the closed to open states are assumed to be constant and independent of whether the RyR channel is CSQN-bound or CSQN-unbound:

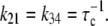(7)

FIGURE 2.

(a) Schematic representation of the four-state Markov model representing the four possible states of a RyR channel: closed CSQN-unbound (1), open CSQN-unbound (2), open CSQN-bound (3), and closed CSQN-bound (4). (b) Fraction of monomers 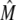(solid line), and equilibrium value of the CSQN-unbound fraction of RyR channels (dashed line), as a function of the JSR free Ca²⁺ concentration c_JSR. (c) Fractional occupancy, c_B/B_CSQN, as a function of free Ca²⁺, c_JSR. Experimental values for cardiac CSQN from Park et al. (42) (triangles, solid line), and corresponding theoretical prediction from Eq. 14 (dashed line). (d) Buffering factor β_JSR(c_JSR) (thick solid line), and the buffering factors that result from assuming that n = n_M or n = n_D (thin dashed lines) as a function of c_JSR.

The transition rates between the closed CSQN-unbound and the closed CSQN-bound states are obtained by assuming simple kinetic rates for CSQN monomer binding and unbinding to the T/J complex, i.e., we assume for simplicity that the binding rate depends linearly on the monomer concentration [M], and that the unbinding rate is constant:

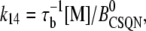(8)

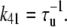(9)

where τ_u and τ_b are the characteristic unbinding (slow) and binding (fast) times, and 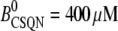is the normal CSQN concentration and guarantees that 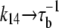for low c_JSR. We will choose these constants based on experimentally measured spark restitution curves. The transition rate from the open CSQN-unbound to the open CSQN-bound state is taken to be the same as the one from the closed CSQN-unbound to the closed CSQN-bound state, k₂₃ = k₁₄. Finally, to satisfy detailed balance, k₁₂k₂₃k₃₄k₄₁ = k₁₄k₄₃k₃₂k₂₁, we set the transition rate from the open CSQN-bound to the open CSQN-unbound to be

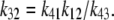(10)

The value of the parameters can be found later in Table 10 and further details can be found in the Appendix.

TABLE 10.

RyR Markov model parameters

Parameter	Description	Value
Ku	CSQN-unbound opening rate	3.8 × 10−4μM−2 ms−1
Kb	CSQN-bound opening rate	5 × 10−5μM−2 ms−1
τu	CSQN unbinding timescale	125.00 ms
τb	CSQN binding timescale	5.0 ms
τc	RyR closing timescale	1.0 ms
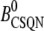	Normal CSQN concentration	400 μM

We will model each dyad as having 100 RyR channels. Each channel evolves stochastically, independent of the other channels in the dyad. However, to avoid keeping track of the ∼20,000 × 100 RyR channels in the myocyte, we only keep track in each dyad of the number of channels that are in each of the four states. As described in the Appendix, these numbers can be updated in each time-step in a way that is equivalent to individually evolving each channel. Therefore we are able to speed up the simulations by a factor of ∼20 (from 100 RyRs and four L-type channels to the number of RyR channels per state and four L-type channels).

A crucial feature of the model described above is that the transition rate from the CSQN-unbound to the CSQN-bound states depends dynamically on the luminal Ca²⁺ concentration through the dependence of the monomer concentration [M] on c_JSR. In Fig. 2 b we plot the fraction of monomers 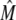(solid line) and the equilibrium value of the CSQN-unbound fraction of channels (dashed line) that results from the rates in Eqs. 8 and 9 as a function of c_JSR. Our luminal gating model result in the following qualitative behavior: just before a dyad fires, its luminal Ca²⁺ content is high, and therefore the fraction of CSQN-unbound RyR channels is also high (see Fig. 2 b). When a spark occurs, the luminal Ca²⁺ decreases, and hence the fraction of monomers increases. The monomers bind to the T/J complex of the RyR channels and the fraction of CSQN-bound channels increases. These channels have a lower open probability, and therefore the spark terminates shortly thereafter. Subsequently, the JSR refills, and eventually the luminal Ca²⁺ concentration becomes high enough that the concentration of monomers decreases. CSQN unbinds from the T/J complex of the RyR channels, and the dyad returns to its original, excitable state. Although previous models have incorporated CSQN modulated luminal gating of RyR channel activity (51,62), a novel feature of our model is that this modulation is incorporated naturally, resulting from the dynamics of CSQN binding and unbinding from the T/J complex. The various rate parameters are chosen so as to reproduce experimental results and can be found in the Appendix. In particular, the characteristic binding and unbinding times, τ_b and τ_u, determine the spark restitution properties. It has been observed experimentally that after a spark occurs, sparks elicited shortly thereafter in the same dyad have a smaller amplitude (43,63,64), and that the amplitude of these second sparks recovers gradually so that sparks elicited after ∼400 ms have the same amplitude as the first spark. The possibility that the smaller amplitude of sparks is due to local refilling of the local JSR stores after depletion is not consistent with the nanoscopic measurement of Ca²⁺ blinks (local JSR depletions (43)), which show a much faster recovery timescale than local recovery of spark amplitude. The characteristics of the spark amplitude recovery curve discussed above indicate that the binding time constant τ_b should be short, while the unbinding time constant τ_u should be of the order of 100 ∼ 200 ms (see Eqs. 8 and 9). We choose these constants so as to reproduce the spark restitution curve in Brochet et al. (43) (Fig. 4), as discussed in Results and detailed later in Table 10.

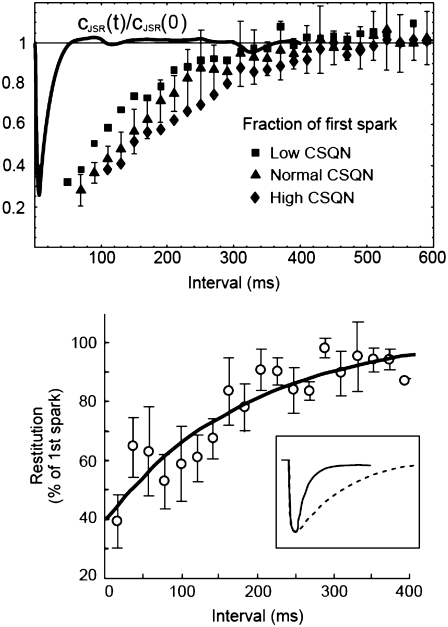
FIGURE 4.

(Top) Average amplitude of a spark as a function of the time elapsed after a previous spark occurred in the same CRU for low (squares), normal (triangles, solid line), and high (diamonds) CSQN concentration. The points were grouped in 20-ms intervals; the error bars are the standard deviation in each group for normal CSQN. The horizontal dashed line indicates full spark amplitude recovery. In qualitative agreement with experiments, higher CSQN prolongs the spark refractory period. The solid line is a typical normalized JSR depletion curve, c_JSR(t)/c_JSR(0), showing that the recovery from refractoriness is not associated with local JSR refilling. (Bottom) Experimental results from Brochet et al. (43).

Luminal buffering

Most of the Ca²⁺ in the JSR is buffered by CSQN, which can bind tens of Ca²⁺ ions per CSQN monomer. Since in our model luminal gating of the RyR channels is inextricably linked to the conformational state of CSQN, i.e., whether it is in monomer or dimer form, an accurate description of CSQN buffering is necessary to quantitatively model experiments in which CSQN properties are modified (15,65). In what follows, we incorporate experimental data on the binding capacities of monomeric and dimeric CSQN in a model of CSQN buffering which is consistent with our scheme for luminal gating.

In vitro experiments (42) have shown that different polymeric forms of CSQN have different buffering capacities. CSQN in dimeric form can absorb up to n_D ∼ 30 Ca²⁺ per CSQN molecule (i.e., 60 per dimer), while CSQN in monomeric form can absorb up to n_M ∼ 15 Ca²⁺ (see Fig. 6 of Park et al. (42)). For simplicity, we will assume that the monomeric and dimeric forms have the same affinity for Ca²⁺, and that the only difference in their buffering capacity is the number of buffering sites (the subsequent analysis could be generalized to account for different affinities). With these assumptions, the rate of change in bound luminal concentration c_B is given by

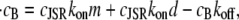(11)

where m and d are the concentration of free buffering sites on the monomer and dimer forms, respectively; c_JSR is the concentration of free Ca²⁺; and k_on and k_off are the rates of binding and unbinding, respectively. The concentration of monomeric buffering sites is 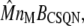and the concentration of occupied monomeric buffering sites is 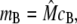so the concentration of free monomeric sites is

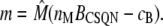(12)

FIGURE 6.

(a) Averaged cytosolic Ca²⁺ concentration c_i; (b) calcium current I_Ca; and (c) sodium-calcium exchanger current I_NaCa as a function of time for a pacing period T = 400 ms showing no CTA.

Similarly, the concentration of free dimeric sites is

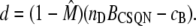(13)

Inserting these expressions into Eq. 11 and assuming that CSQN buffering is fast (51), we can solve for the steady-state solution to obtain the bound Ca²⁺ concentration as a function of the free Ca²⁺ concentration c_JSR

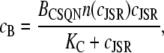(14)

where

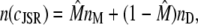(15)

and K_C = k_off/k_on. Fig. 2 c (from Park et al. (42)) shows the experimentally measured amount of Ca²⁺ bound, c_B, over the total concentration of CSQN as a function of c_JSR (triangles) and the theoretical value obtained from Eq. 14 (thick dashed line).

Differentiating the total Ca²⁺ concentration in the JSR,

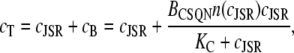(16)

with respect to time, we obtain

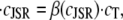(17)

where

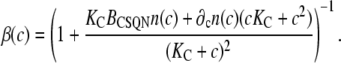(18)

Note that if the buffering capacities of dimers and monomers are assumed equal, ∂_cn = 0, we recover the rapid buffering approximation expression (66), with a monotonous increase of β(c) with c. In Fig. 2 d we plot the buffering factor β(c) (thick solid line) and the buffering factors that result from assuming that n = n_M (upper dashed line) or n = n_D (lower dashed line) as a function of c. The buffering factor β(c) has a marked dip at the monomer-dimer transition, suggesting that, as c increases past the monomer-dimer transition, the number of new CSQN buffering sites on dimers can bind a substantial amount of Ca²⁺.

Before proceeding to Results, we summarize the main novel aspects of our model:

• Our model is the first physiologically detailed model of a Ca²⁺ cycling in ventricular myocytes simulating a realistic number of diffusively coupled dyads. Such model will not only allow us to determine the effect of microscopic release characteristics on macroscopic variables, but also opens the way to study spatial intracellular Ca²⁺ dynamics in the context of a physiologically detailed model.

• Our model treats dynamically the modulation of RyR channels by luminal Ca²⁺ through CSQN, and integrates the luminal gating with a model of luminal buffering that takes into account experimental evidence of the variation of CSQN buffering capacity due to Ca²⁺-induced conformational changes. The dynamical delay in the gating mechanism provides a novel mechanism for alternans.

RESULTS

The excitation-contraction machinery of ventricular myocytes is based on the interplay between the I_Ca current and release of Ca²⁺ from the SR. This interaction has been characterized by important experiments, which we have used to benchmark our model. In particular, our model reproduces graded release of Ca²⁺, the graded dependence of the SR release current on I_Ca, discussed in Graded Release. In Dyadic Junction Refractoriness we analyze the recovery of the release properties of dyadic junctions after release. Another important benchmark is the SR release-load relationship, which is discussed in its own subsection. In the subsections Action Potential Clamp Pacing and Calcium Transient Alternans we pace our model with an action potential clamp and study the resulting Ca²⁺ transients, relating the origin of the CTA that we observe to alternations in the fraction of CSQN-unbound RyR channels. In Analysis of Alternans Dynamics we study theoretically the conditions necessary for the genesis of CTA. Finally, in the section Effects of Microscopic Parameters on Alternans, we describe the effect that various microscopic parameters have on the onset of whole cell CTA.

Graded release

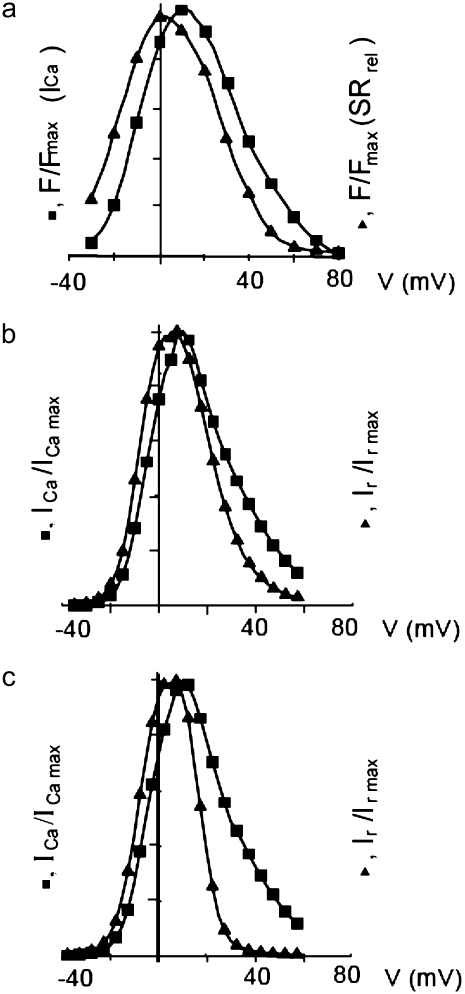
One of the most important characteristics of the excitation-contraction coupling machinery of the cell is the graded release of Ca²⁺ from the SR in response to varying stimuli strength. The interaction of the I_Ca current with Ca²⁺ release from the SR was clearly demonstrated in the experiments of Wier et al. (67), who showed that, when depolarizing rat ventricular myocytes to various clamp pulse voltages, both the peak I_Ca current and the peak SR Ca²⁺ release exhibit a bell-shaped curve when plotted as a function of the clamp voltage, with the SR release curve displaced ∼10 mV toward lower voltages. To reproduce such a curve, we depolarize the simulated myocyte from −80 mV to various step potentials, and measure the average I_Ca (solid line) and SR release (dashed line) currents during the first 20 ms after depolarization. The initial concentration of free luminal Ca²⁺ is 650 μM. Our model reproduces the experimental observations, as can be observed in Fig. 3. Fig. 3 a shows the experimental result from Wier et al. (67) averaged over many cells, while Fig. 3 b shows our simulation results.

FIGURE 3.

(a) Peak L-type Ca²⁺ current (squares, rightmost curves) and peak SR release current (triangles, leftmost curves) measured in Wier et al. (67) upon depolarization to various test voltages (horizontal axis). (b) Same quantities obtained with our model, including heterogeneity in the proximal volumes, i.e., 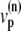= 1.26 × 10⁻² μm³(1 + r⁽ⁿ⁾), where r⁽ⁿ⁾ is a random number, different for each CRU. (c) Same as in panel b, but with no heterogeneity in the proximal volumes, i.e.,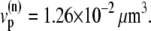

We have found, in agreement with Bondarenko et al. (53), that heterogeneity in the release unit parameters modulates graded release. However, as opposed to heterogeneity in the number of L-type Ca²⁺ channels considered in Bondarenko et al. (53), our model has heterogeneity in the proximal space volume, as was discussed in Elementary Ca²⁺ Release Unit Structure (above). For comparison, we show in Fig. 3 c the graded release curve corresponding to no heterogeneity. The results show that proximal space volume heterogeneity modulates the high voltage region of the graded release curves, as discussed in Rovetti et al. (54). In this region, the decay of the curve is due to a decreasing driving force, which is compensated by a distribution in the sensitivity of the release units due to heterogeneity. On the negative voltage side, on the other hand, the decay of the curve is caused by a decreasing open probability of the L-type channels, which is not affected by the distribution of the proximal space volumes. We note that in Bondarenko et al. (53) heterogeneity was introduced by multiplying a single channel I_Ca in each CRU by a random number, rather than by considering the addition of a random number of independent L-type Ca²⁺ channels in each CRU. These approaches are not necessarily equivalent since the L-type channels might fire at different times, thus not significantly increasing the probability of initiating a spark.

Dyadic junction refractoriness

After Ca²⁺-induced Ca²⁺ release, subsequent release is of smaller magnitude if insufficient time is given for recovery. This recovery from refractoriness, which is a crucial characteristic of the excitation-contraction coupling machinery of the cell, is observed both at the level of whole cell Ca²⁺ transients (20), and at the level of spark magnitude and firing probability at single dyads (43,63,64). In our luminal gating model, there are two factors that can affect local recovery from refractoriness: 1), refilling of the local JSR; and 2), slow unbinding of CSQN from the T/J complex in the JSR. Sobie et al. (63,64) examined repetitive sparks elicited by addition of 50 nM Ryanodine to a quiescent rat ventricular myocyte. It was found that the recovery of spark amplitude is much faster than the recovery of spark triggering probability; in addition, nanoscopic imaging of local JSR depletions (i.e., blinks) (43) show that local JSR refilling is not the limiting factor governing local recovery from release. In our model, the limiting factor is the recovery from CSQN-binding, which is controlled by a slow rate of CSQN unbinding from the T/J complex, τ_u = 125 ms. The binding time τ_b is set by the observation that the spark triggering probability immediately decreases after a spark is elicited, which implies that the rate of CSQN binding to the T/J complex should be fast; we set τ_b = 2 ms.

To measure the recovery properties of sparks, we simulate a myocyte held at a potential of 10 mV and collect pairs of sparks occurring in the same CRU during 1 s. During this time, c_JSR averaged over all units had a nearly constant value of ∼800 μM. In the top panel of Fig. 4 we show the amplitude of the second spark normalized by the amplitude of the first spark as a function of the time elapsed between the two sparks for low (3 mM, squares), normal (10 mM, triangles), and high (30 mM, diamonds) concentration of CSQN buffering sites. The figure shows that our model reproduces the observed properties of local recovery from Ca²⁺ induced Ca²⁺ release and the experimental results of Terentyev et al. (15), which show that the refractory period in individual CRUs increases when CSQN is overexpressed in transgenic mice.

To verify that the spark refractoriness is caused by recovery in the availability of RyR channels and not by refilling of the local JSR stores, we plot in the top panel of Fig. 4 also a typical JSR depletion curve, i.e., c_JSR(t)/c_JSR(0) as a function of time for a single CRU (solid line). As the figure shows, the JSR stores refill much faster than the CRUs recover their original excitability. This result agrees with the experimental observations of Brochet et al. (43), where JSR refilling and spark restitution properties were measured simultaneously, in particular with Fig. 4 B of Brochet et al. (43), reproduced here in the bottom panel of Fig. 4.

SR release-load relationship

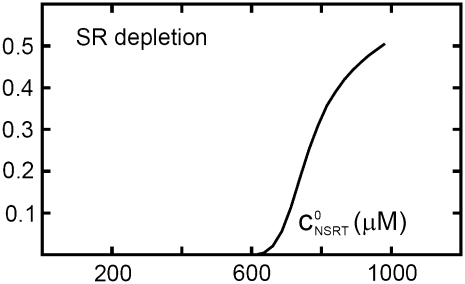
The effect of luminal Ca²⁺ on the Ca²⁺ release properties of the SR is often referred to as the SR release-load relationship. In Shannon and Bers (11), the amount of Ca²⁺ released after a voltage clamp step was measured in isolated rabbit ventricular myocytes as a function of the total SR Ca²⁺ load (see also (10)). For values of the total SR load c_SRT <∼90 μmol/l cytosol, there was almost no Ca²⁺ release, while the release increased sharply between 90 and 120 μmol/l cytosol. In terms of the free Ca²⁺ concentration (after accounting for buffering), the nonlinearity was found in these experiments to occur for concentrations larger than c_SR ∼500 μM, approximately the same concentration at which our model exhibits the sharp transition from mostly CSQN-bound RyR channels to mostly CSQN-unbound RyR channels as a function of c_SR observed in Fig. 2 b. Since the CSQN-unbound channels have a higher open probability, this sharp increase in the fraction of CSQN-unbound channels results in a steep SR release-load relationship. We remark that the model leading to Fig. 2 b was based on the experimentally observed nonlinearity of the CSQN buffering capacity, an independent observation which gives support to the hypothesis that CSQN-mediated gating mechanisms underlie the nonlinearity of the SR release-load relationship. The SR depletion is defined as (11)

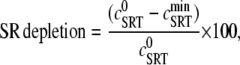(19)

where 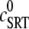is the SR load just before release and 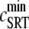is the minimum SR load shortly after release. In Fig. 5 we show the SR depletion as a function of c_SR before release. To vary c_SR just before release, we start the simulation with a load of 400 μM and the corresponding equilibrium fraction of CSQN-unbound channels (dashed line in Fig. 2 b) and keep the voltage at −80 mV until the SR refills to the desired value of c_SR. For loads at ∼400 μM, CSQN monomers bind quickly to T/J, so it is reasonable to assume the equilibrium value for the initial fraction of CSQN-unbound channels. We remark, however, that the unbinding time is slow and the resulting SR release curve may depend on the number of channels that become CSQN-unbound before the voltage step. When the desired SR load is reached, Ca²⁺ release is triggered by a step depolarization from −80 mV to 10 mV. The results in Fig. 5 are in qualitative agreement with experiments.

FIGURE 5.

SR depletion, 100 × ((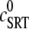 – 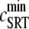)/ 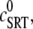as a function of the initial free Ca²⁺ SR load, 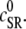A strong nonlinear increase in release for loads larger than 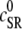∼ 600 μM is observed.

Action potential clamp pacing

The Ca²⁺ cycling machinery of cardiac myocytes and its membrane potential are often thought of as separate dynamical systems coupled by the Ca²⁺-dependent currents (1). The fact that the Ca²⁺ system can have instabilities of its own was clearly demonstrated by the experiments of Chudin et al. (2), who paced isolated myocytes with periodic voltage-clamp waveforms and studied the dynamics of the resulting CTA. Since our principal aim is to construct a model of the Ca²⁺ cycling machinery of the cell that explains the origin of calcium-induced alternans, we will follow their approach and study the behavior of our model under a periodic voltage-clamp.

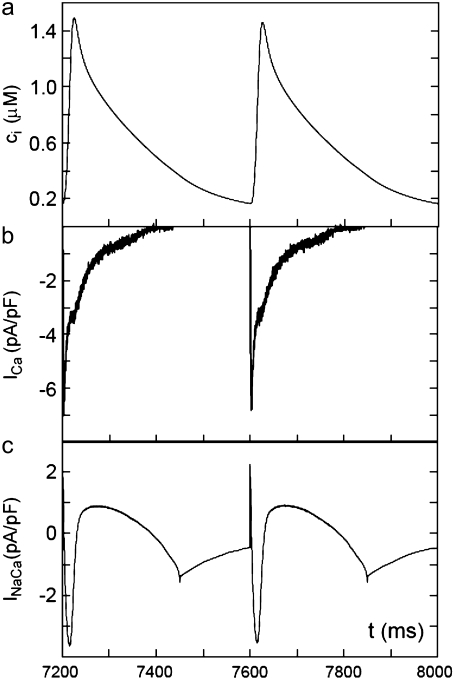
Following Shiferaw et al. (8), we will model the action-potential clamp used in Chudin's experiments as

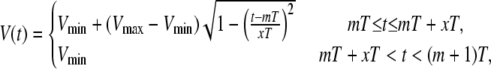(20)

where V_max = 15 mV, V_min = −80 mV, T is the pacing period, and x = APD/T, where APD is the action potential duration. As in Shiferaw et al. (8), we take the phenomenological expression x(T) = a/(a + T) with a = 2/3, which represents the observed shortening of the APD with decreasing pacing cycle length. In Fig. 6 a we plot the averaged cytosolic Ca²⁺ concentration c_i as a function of time that results from pacing our model with a period T = 400 ms. In Fig. 6 b we plot the calcium current I_Ca, and in Fig. 6 c we plot the sodium-calcium exchanger current I_NaCa as a function of time. We remark that the I_Ca results from the summation of single channel currents determined by independent Markov models at each L-type channel.

Calcium transient alternans

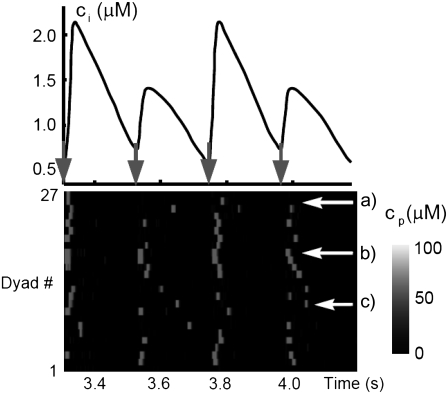
The fact that single dyadic junctions have a refractory period determined by the slow unbinding of CSQN from the T/J complex allows the possibility of release alternans at the level of a single dyadic junction. Given the stochasticity of the release at the microscopic level, the question arises of whether or not these microscopic alternans can coherently result in macroscopic, whole cell CTA. This is a fundamental problem when one considers the question of CTA in the context of local release; in single pool models, by definition, an instability immediately results in whole cell CTA. In the top panel of Fig. 7 we plot the averaged cytosolic Ca²⁺ concentration c_i (Eq. 1) as a function of time for a pacing period of T = 220 ms. In the bottom panel we show the proximal space Ca²⁺ concentration c_p as a function of time for a transversal line of dyads across the myocyte, indexed in the vertical axis. This panel shows that, even though there is well-defined whole cell CTA, individual dyads do not necessarily reflect this, since, in the time interval shown, there are some dyads firing only in the beats with large c_i, some firing every beat, and some firing irregularly, examples of which are indicated with the horizontal arrows and marked as a, b, and c, respectively. The vertical arrows in the top panel indicate the time of pacing. In Fig. 8 a we show the maximum values of the averaged Ca²⁺ cytosolic concentration during steady state pacing for different pacing periods. A bifurcation to CTA appears when the pacing period is decreased at <300 ms. As we will see in the next subsection, the onset to CTA can be affected by various microscopic parameters. Further insight into the mechanism of alternans can be gained by plotting both the total free SR content, defined as

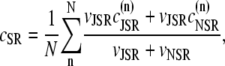(21)

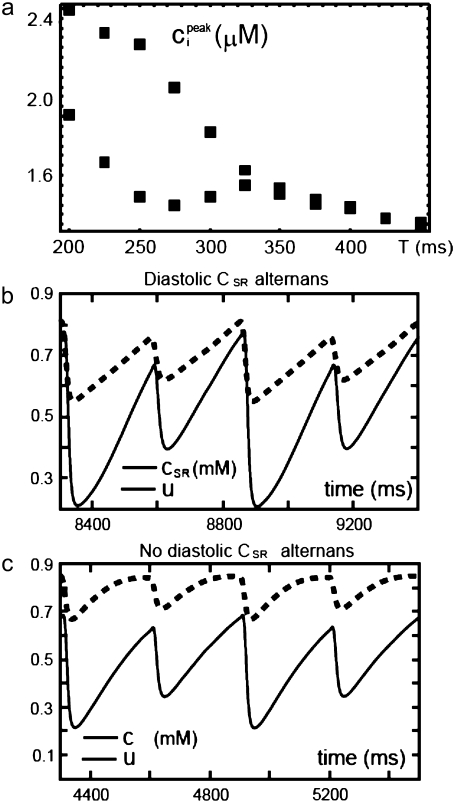
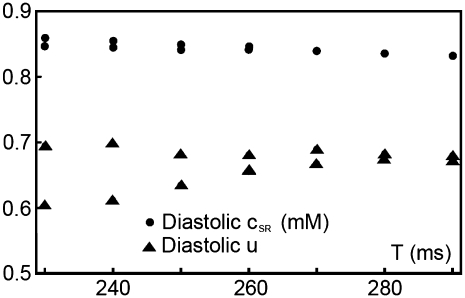
and the total number of CSQN-unbound RyR channels as a function of time. In Fig. 8 b we show the SR Ca²⁺ content c_SR (dashed line, mM) and the fraction of CSQN-unbound RyR channels in the myocyte, f (solid line), as a function of time. Since the CSQN-unbound RyR channels have a higher open probability, they are important in determining the sensitivity of the release units, and, consequently, the size of the Ca²⁺ transient. In the figure we see that, for the parameters used, both the diastolic values of f and c_SR alternate. This is not unexpected since, after a large release, uptake by the NSR can be insufficient to bring the SR content back to its original level by the next beat. On the other hand, f is dependent on the SR content. Therefore, alternations in f are likely to promote alternations in c_SR, and vice versa. However, experiments show that it is possible to have CTA without diastolic alternations in c_SR. Picht et al. (13) measured c_SR during CTA in rabbit ventricular myocytes and observed that, in some of the cells, CTA was not accompanied by alternations in the diastolic value of c_SR. In our model, the recovery of RyR channels from CSQN binding provides a mechanism for the genesis of CTA independent of alternations in c_SR. In particular, if the timescale of CSQN-unbinding is slow enough compared with the NSR uptake timescale, alternations in f can occur without alternations in c_NSR. In Fig. 8 c we show the free SR content c_SR in mM (dashed line) and the fraction of CSQN-unbound RyR channels in the myocyte, f (solid line), as a function of time for a simulation in which the uptake parameters were modified (the modified parameters are v_up = 0.9 μM ms⁻¹, K_NSR = 1200 μM, K_i = 0.123 μM, ξ = 0.1, and τ_u = 270 ms). We remark that in the experiments of Picht et al. (13), this type of alternans was observed only in a fraction of the myocytes. While f shows clear diastolic alternans, c_SR does not show significant diastolic alternations. As the period is decreased, small alternans develop in the diastolic SR content, as shown in Fig. 9, but they remain small when compared with the alternations in the fraction of unbound channels. This shows that alternations in the number of available (i.e., CSQN-unbound) RyR channels can generate CTA without significant diastolic alternations in SR content.

FIGURE 7.

(Top) Averaged cytosolic Ca²⁺ concentration c_i as a function of time for a pacing period T = 220 ms showing CTA. (Bottom) Proximal Ca²⁺ concentration along a transversal line (27 CRUs) showing how the CTA results from noisy individual signals. In the interval shown, there are dyads firing only in the beats with large c_i, every beat, and irregularly, examples of which are indicated with the horizontal arrows and marked as a, b, and c, respectively.

FIGURE 8.

(a) Peak averaged cytosolic Ca²⁺ concentration c_i on alternate beats during steady-state pacing as a function of pacing period T. A transition to CTA occurs as the pacing period is decreased. (b) Free SR content in mM (dashed line) and the fraction of CSQN-unbound RyR channels in the myocyte, f (solid line) as a function of time for the original parameters. SR release alternans are accompanied by diastolic SR alternans. (c) Free SR content c_SR in mM (dashed line) and the fraction of CSQN-unbound RyR channels in the myocyte with modified parameters, f (solid line) as a function of time. Although there are SR release alternans, no significant diastolic SR alternans are present (see discussion in text).

FIGURE 9.

Diastolic SR content (circles) and fraction of CSQN-unbound channels f (triangles) at steady state pacing as a function of the pacing period T for the modified parameters used in Fig 8 (c).

Analysis of alternans dynamics

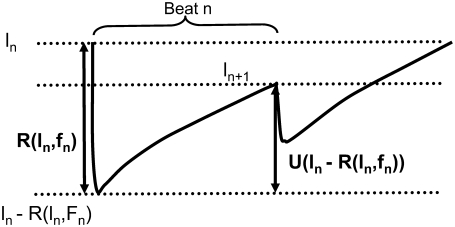
In this subsection we investigate theoretically the relative contributions of the steep SR release-load relationship and the recovery of RyR channels from CSQN binding to the genesis of CTA. In particular, we discuss the conditions required for CTA without diastolic SR content alternans. Our analysis is a direct extension of an iterative map analysis previously developed in the literature (1,8), which studies the onset instabilities in the beat-to-beat dynamics of SR load. Here, we will generalize this method by including the beat to beat dynamics of the CSQN-unbound RyR channels. For simplicity, we consider deterministic dynamics in a single CRU. Let l_n be the SR load and f_n be the fraction of CSQN-unbound channels just before the n^th beat. Let R(l_n, f_n) be the amount by which the SR content decreases just after the n^th beat as a function of these variables. Let U(l_n – R) be the amount of Ca²⁺ that is uptaken after SR release decreases the load to l_n – R (see Fig. 10). Furthermore, let g(l_n – R) be the fraction of RyR channels that remain in the CSQN-unbound state just after the load is decreased to l_n – R by SR release (since binding is fast, we assume it does not depend on its value before release). We then have the following map relating these quantities at beat n + 1 to their values at beat n:

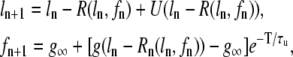(22)

where we have assumed that the recovery of the unbound channels fraction relaxes exponentially to the equilibrium CSQN-unbound fraction g_∞ of RyR channels for large SR load (see Fig. 2 b) with a time constant τ_u.

FIGURE 10.

Functions used in the map analysis: R(l, f) is the amount by which the SR content decreases as a function of the load l and fraction of CSQN-unbound fraction f, and U(l) is the amount of uptaken Ca²⁺ after the load decreases to l after release.

In the absence of alternans, the SR load and fraction of CSQN-unbound channels have the same values every beat, l_n = l, f_n = f. The conditions for the onset of alternans can be studied by introducing small perturbations from these values, l_n = l + δl_n, f_n = f + δf_n, and studying their beat-to-beat evolution. Growth of these perturbations corresponds to the development of alternans. Inserting these expressions in Eq. 22 and linearizing, we obtain

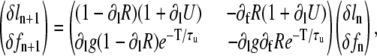(23)

where the derivatives are evaluated at the values l, f. The condition for alternating growth of the perturbations is that the eigenvalue of the matrix in Eq. 23 with the largest magnitude is <−1 (for alternans, this eigenvalue is negative). This condition results in that alternans develop when

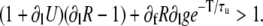(24)

This equation is the key to understanding the relative contributions of steep SR release-load relationship, uptake, and recovery of CSQN-bound channels. If we can neglect CSQN-mediated effects, ∂_fR = 0, ∂_lg = 0, or τ_u ≪ T, then we recover the criterion presented in the literature (1,8), that alternans occur only when

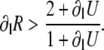(25)

In this case, alternans develop as a result of a combination of a steep SR release-load relationship (large ∂_lR) and poor uptake (small ∂_lU; we note that here ∂_lU is negative since a smaller Ca²⁺ load results in more uptake). In the more general case described by Eq. 24, in addition to steep SR release-load relationship and poor uptake, alternans can result from a combination of steep dependence of release on the fraction of CSQN-unbound channels (large ∂_fR), large nonlinearity in CSQN binding due to the steep CSQN polymerization as a function of c_JSR (large ∂_lg), or insufficient time to recover from CSQN binding (large τ_u/T). In particular, it might be possible that the first term vanishes, (1 + ∂_lU)(∂_lR – 1) = 0, but that the second term is enough to cause alternans by itself, 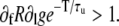This shows that, in principle, alternans can occur independently of a steep SR release-load relationship.

We can use Eq. 25 to justify our claim that in the simulations shown in Fig. 8 c the alternations in the fraction of CSQN-unbound channels drive the alternans, rather than the very small, but still present, alternations in the SR content. The drop in the SR content in beats with large release is ∼180 μM, and in beats with small release it is ∼130 μM, so the difference in SR depletion is ∼50 μM. The difference in SR content before release is ∼10 μM. Thus, since in this argument we are neglecting the effects of f on release, we can estimate that ∂_lR ≈ 5. We can also estimate ∂_lU by noting that a release R ≈ 180 μM is reuptaken so that by the next beat the load is approximately within 10 μM of its previous value l₀. Therefore, the amount of reuptaken Ca²⁺ after the load is reduced to l is in this case at least U ≈ 170 μM/180 μM × (l₀ – l) = 0.94(l₀ – l), and thus we estimate ∂_lU ≈ −0.94. The condition in Eq. 25 is not fulfilled and this shows that the steepness of the SR release-load relationship and uptake alone cannot cause the observed release alternans.

Another important question is what are the conditions to observe release alternans without diastolic SR alternans. We can obtain the relative amplitudes of alternations in diastolic SR content and in the fraction of CSQN-unbound RyR channels by finding the eigenvector of the matrix in Eq. 23 corresponding to alternans, which is

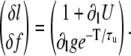(26)

This gives the relative amplitudes of the diastolic SR content and CSQN-unbound fraction of RyR channel alternans. We see that, to have no significant SR content alternans with release alternans, we must have 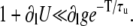The left-hand side is small if ∂_lU ≈ −1, which corresponds from Eq. 22 to constant l_n (no SR alternans). In our simulations, the SR content attains a steady-state value in diastole (∂_lU ≈ −0.94), while in the experiments of Picht et al. (13) it has a more triangular shape and does not attain steady state while still reaching the same SR diastolic value. Although in both cases this results in ∂_lU ∼ −1, this qualitative difference indicates that the mechanism by which this is accomplished in both cases is different. Details of the uptake dynamics allowing the uptake for a large release to exactly balance the uptake for a small release without reaching steady state are a separate subject of investigation and are not considered here. Our analysis shows that, independently of how the SR load is kept constant at diastole, CSQN-mediated recovery of the RyR channels from the unbound state can produce release alternans.

As an additional proof of the principle that CTA can be driven by alternations in the fraction of unbound CSQN channels independently of alternations in diastolic SR content, we have modified the parameters so that the NSR content does not fluctuate appreciably (e.g., as if it were highly buffered) and have observed cases in which the diastolic alternations of the SR content are negligible, while the alternations in SR release and in the CSQN-unbound fraction are still large (not shown).

The steep release load relationship (Fig. 5) has been proposed by various studies (8,12) as a mechanism for the genesis of CTA. Our results support the hypothesis that there is another complementary variable, the number of available RyR channels, which, together with the SR content, determines the amount of Ca²⁺ released from the SR.

EFFECT OF MICROSCOPIC PARAMETERS ON ALTERNANS

In this section we will discuss the effect of some microscopic properties of the CRUs on the onset of CTA that our spatially distributed model is uniquely capable of investigating.

Diffusive coupling

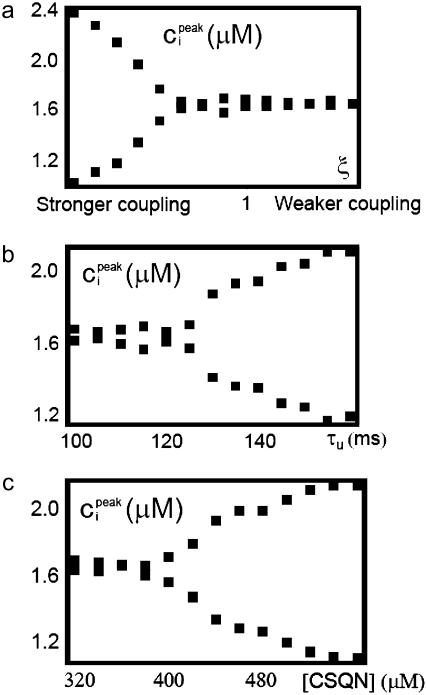
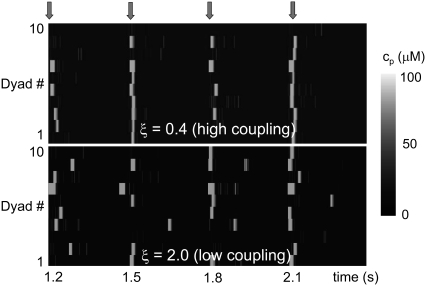
Whole cell CTA results from the summation of the stochastic activity of a large number of CRUs. Even though we have argued that one can expect beat-to-beat alternations in the release at individual dyads based on their gating dynamics, CRUs are highly stochastic and, as shown in the bottom panel of Fig. 7, they do not necessarily fire in phase with the whole cell CTA. If the CRUs fired independently from each other, one would expect them to fire incoherently, resulting in no CTA. The reason that the release at the level of single dyadic junctions do not dephase stochastically is that neighboring dyadic junctions are coupled diffusively: if, averaged over the myocyte, CRUs are firing in an off-on-off-on pattern resulting in whole cell CTA, Ca²⁺ diffusion will increase the probability that an individual CRU will fire in a beat in which the majority of CRUs (and, in particular, a majority of its neighboring CRUs) are firing, thus reinforcing and maintaining the CTA. Without diffusive coupling, the release at individual CRUs would desynchronize, resulting in no whole cell CTA. To test this hypothesis, we varied the diffusive coupling timescales close to the onset of alternans. In Fig. 11 a we show the peak values of c_i during steady-state alternans as a function of a parameter ξ, which controls the coupling strength. The parameter ξ scales all the nearest-neighbor diffusive timescales (i.e., τ → ξτ for the τ-values specified later in Table 9), so that higher ξ corresponds to weaker coupling. The figure shows that, as argued above, diffusive coupling promotes the onset of alternans. In Fig. 12 we show the firing pattern along a transversal line including 10 CRUs for two values of the diffusive timescales' scaling factor ξ. Large coupling (Fig. 12, top, ξ = 0.4) promotes CRU firing synchronization, while for low coupling (Fig. 12, bottom, ξ = 2.0) CRUs fire more independently.

FIGURE 11.

(a) Maximum averaged cytosolic Ca²⁺ concentration c_i on alternate beats during steady-state pacing as a function of the coupling strength scaling factor ξ. The parameter ξ scales all the nearest-neighbor diffusive timescales (i.e., τ → ξτ). Stronger coupling promotes CTA. (b) Maximum averaged cytosolic Ca²⁺ concentration c_i on alternate beats during steady-state pacing as a function of the unbinding time τ_u. Larger unbinding time promotes CTA. (c) Maximum averaged cytosolic Ca²⁺ concentration c_i on alternate beats during steady-state pacing as a function of the concentration of CSQN sites. A larger concentration of CSQN sites promotes CTA. When not varied, the parameter values are τ_u = 125 ms, [CSQN] = 400 μM, and ξ = 0.4.

FIGURE 12.

Proximal Ca²⁺ concentration along a transversal line of 10 CRUs for large (top, ξ = 0.4) and low diffusive coupling (bottom, ξ = 2.0). Large coupling promotes CRU firing synchronization, while for low coupling CRUs fire more independently. The arrows on top indicate pacing, with period T = 300 ms.

Calsequestrin unbinding time

By directly affecting the duration of the CRU recovery from release, the CSQN unbinding timescale τ_u has an important effect on the onset of CTA. The timescale of recovery has been estimated to be ∼180 ms (43). In Fig. 11 b we show the peak values of c_i during steady-state pacing as a function of τ_u. The plot shows that CTA is promoted by larger τ_u.

Calsequestrin concentration

In vivo experiments with transgenic mice overexpressing CSQN resulted in CTA at rapid pacing rates for all the transgenic mice in the experiment and no CTA for the control mice (65). The mechanism by which CSQN overexpression might promote alternans was investigated in Terentyev et al. (15), which showed that overexpression of CSQN results in longer CRU refractory periods. This phenomenon is qualitatively reproduced by our model in the top panel of Fig. 4, where we show the CRU restitution curves at various levels of CSQN. One of the novel features of our model is the realistic modeling of the dual role of CSQN as a buffer and as a regulator of RyR activity, which allows us to investigate the role of CSQN in promoting CTA. In Fig. 11 c we show the maximum averaged cytosolic Ca²⁺ concentration c_i on alternate beats during steady-state alternans as a function of the concentration of CSQN buffering sites (i.e., sites that bind Ca²⁺). As observed in experiments, a larger concentration of CSQN promotes CTA.

Heterogeneity of CRU properties

We have also observed that heterogeneity in the release properties (in our case, the proximal volumes 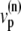) inhibits CTA (data not shown). As we have discussed, heterogeneity smoothes the high-voltage part of the release curve (compare Fig. 3, b and c). As the membrane voltage V decreases after the upstroke, it will recruit sparks with a probability roughly determined by the release curve. If this curve decays sharply on the high voltage side, there will be a sharp increase in spark recruitment when the voltage decreases at ∼V = 0 mv. This results in many sparks occurring in a relatively short time interval, thereby facilitating the recruitment of other sparks through diffusion. As discussed above, sustaining whole cell CTA against the tendency of CRUs to fire independently of each other relies on sparks influencing each other through diffusion. On the other hand, if the release curve is smooth, spark recruitment is more gradual, and diffusive coupling is less effective, as there are less sparks being recruited in a given time interval. Thus, it seems that some degree of stochasticity in CRU release properties is beneficial (in the sense that it suppresses whole cell CTA).

MODEL LIMITATIONS

While our model goes beyond previous efforts in constructing a myocyte Ca²⁺ cycling model that captures the spatial dynamics of Ca²⁺ release and luminal CSQN-mediated luminal gating, it has some limitations that we now discuss.

Various experimental measurements that we have used to calibrate different parts of our model come from different species: data on CSQN polymerization (Fig. 2 c) corresponds to canine CSQN (42), graded release curves (Fig. 3) correspond to rat, and spark restitution curves (Fig. 3) and the L-type Ca²⁺ current correspond to rabbit (43,52). Thus, our model at this point can be used to draw conclusions about alternans only in a general and qualitative way. However, it could be adapted to a particular species if enough experimental measurements are available.

As presented here, the model incorporates only elements necessary to describe Ca²⁺ cycling and, for simplicity, we have paced the model with a phenomenological action potential waveform (Eq. 20) and used a fixed intracellular sodium concentration at each rate (Eq. 47). We note, however, that the model can be easily coupled to existing electrophysiological models. In preliminary explorations we have successfully coupled it to the Fox model of ionic membrane currents (68) as modified in Sato et al. (69).

In the experiments of Picht et al. (13), the SR content reaches the same diastolic value without attaining steady state, even though the systolic value alternates. In our model, the SR content reaches the same diastolic value by attaining steady state. While these mechanisms are different, they are related to uptake dynamics and are not central to our argument. Understanding the uptake dynamics that allows systolic SR alternans without diastolic SR alternans is open for future studies.

Our model neglects mechanoelectric feedback effects, which are increasingly being recognized to affect cellular electrophysiology. In particular, stretch-activated channels (70) are not considered, and while the rate of Ca²⁺-Troponin-C binding is tension-dependent (71), we have taken it to be constant. The effect of mechanoelectric feedback on alternans will be explored elsewhere.

The estimates for the effective diffusive timescales later in Table 9 are crude and may oversimplify the complex geometry of the dyadic junctions, including spatial anisotropy of Ca²⁺ diffusion and the heterogenous orientation of neighboring units. Although the effect of simultaneously scaling all these timescales was explored in Fig. 11 a, they were not independently varied.

RyR channels can be inactivated by cytosolic Ca²⁺ (see (72) and references therein). Our model does not include cytosolic inactivation of the RyR channels. Although, as discussed below, our results suggest CSQN-mediated luminal gating of RyR is the primary mechanism for the genesis of CTA, the possible role of cytosolic inactivation sites was not investigated here.

DISCUSSION

We have developed a multiscale myocyte model that allows the study of the origin of CTA at the subcellular level. In our model, whole cell CTA results from the coherent summation of irregular alternations of release at the level of single dyadic junctions. The alternans are caused by an alternation in the number of RyR channels that are available to open (CSQN-unbound), which in turn alternate because of the slow recovery associated to the CSQN-unbinding timescale. Importantly, our model admits CTA without significant alternations in diastolic SR Ca²⁺ content, as observed in the experiments of Picht et al. (13). However, in most cases, alternations in diastolic SR content accompanied CTA. The reason is that the SR content and the number of available RyR channels are strongly coupled to each other: the rate of CSQN-binding depends strongly on c_JSR through its effect on the number of CSQN monomers, Eq. 8, while the diastolic SR content depends on the number of available RyR channels in the previous beat (many available RyR channels → large release → low diastolic SR content). Thus, alternations in the diastolic SR content will typically promote alternations in the number of available RyR channels, and vice versa. However, when the uptake is enough to reduce or eliminate the dependence of the diastolic SR content on the number of available RyR channels in the previous beat, one can observe CTA without significant alternations in diastolic SR Ca²⁺ content as in Fig. 8 c.

Another important feature of our model is that, for the first time, it simulates a realistic number (∼20,000) of diffusively coupled, physiologically detailed elementary release units, where each unit has a realistic (∼100) number of RyR channels. Our numerical method for efficiently simulating the behavior of the RyR channels at a single unit, which tracks only the number of RyR channels in a given state, is equivalent to the independent evolution of the Markov model for each unit. This method, detailed in the Appendix, works because the release current only depends on the number of channels in the open state. The model was numerically simulated using C++ in a desktop Mac with a 2 GHz Intel Core Duo processor. Running a 1-s simulation takes 55 min of computation time.

In heart failure (HF), a characteristic of abnormal Ca²⁺ handling is increased RyR leakiness, which results in diminished SR release. In our model, low levels of CSQN result in increased RyR leak since CSQN monomers inhibit the activity of the RyR channels. However, we have found that lower CSQN levels alone inhibit CTA, which are generally associated with HF. Our findings suggest that CTA in HF are caused by other changes, such as increased intracellular sodium concentration (which increases the activity of the exchanger) or downregulation of the SERCA pump. A thorough exploration of the broader changes associated with HF using our model is beyond the scope of this article and will be pursued elsewhere. Besides HF and alternans, our model might also provide a useful framework to study the cellular mechanisms of triggered arrhythmias such as catecholaminergic polymorphic ventricular tachycardia, which has been linked to mutations resulting in reduced CSQN levels (73). In particular, our model shows that such a reduction shortens RyR refractoriness (Fig. 4) and enhances RyR activity, which could promote spontaneous calcium release.

RyR channels can be inactivated by cytosolic Ca²⁺, and it has been suggested that luminal Ca²⁺ might regulate the activity of the RyR channels by permeation to cytosolic inactivation sites (see (72) and references therein). Therefore, whether or not cytosolic Ca²⁺ inactivation of the RyR channels can also produce CTA, independently of luminal Ca²⁺ regulation, is an important question. Our results suggest that inactivation of RyR channels alone is insufficient to produce CTA. This conclusion is supported by the fact that the timescale for recovery from inactivation is a strongly nonlinear function of Ca²⁺ concentration in our model due to the cooperative nature of the CSQN monomer-dimer transition, and that this nonlinearity is essential for CTA to occur. Since there is no obvious analog of this strong nonlinearity in the case where RyR channel activity is only gated by cytosolic Ca²⁺, it is unclear whether CTA can occur in this case. In addition, there is compelling experimental evidence for CSQN-mediated luminal Ca²⁺ regulation of the RyR channels, and experiments with CSQN-altered transgenic mice show an altered propensity to alternans (65), in agreement with our model results (Fig. 11 c). Thus, while we do not rule out a possible contribution of cytosolic Ca²⁺ inactivation, we believe that the principal mechanism for the genesis of CTA lies in the luminal Ca²⁺ regulation of SR release. The incorporation of cytosolic RyR inactivation to our model is a subject for further research.

Diffusive coupling between adjacent release units was found to promote whole cell CTA by synchronizing the patterns of CRU Ca²⁺ release alternans. In addition to being a crucial element in any model studying the nanoscopic origin of CTA, diffusive coupling and spatial structure allow for the future study of other intracellular Ca²⁺ dynamics phenomena observed in experiments, like intracellular Ca²⁺ waves (19–23), intracellular spatially discordant alternans (24–26), and spontaneously triggered activity (19,27,28). The understanding of such arrhythmogenic phenomena requires a model of intracellular Ca²⁺ dynamics that realistically couples the various membrane currents with the Ca²⁺ handling machinery of the cell and that takes into account the local, spatially extended nature of the excitation-contraction process. As the resolution of imaging techniques continues to improve, models will be needed which can, with a multiscale approach, address the relation of the measured nanoscopic structures to whole cell signals. Our model allows us to explore the effect of various microscopic variables on whole cell signals, in particular on the origin of CTA. In our model, larger CSQN unbinding time, larger CSQN concentration, and stronger diffusive coupling between neighboring CRUs promote alternans, while heterogeneity in the CRU properties inhibits alternans.

APPENDIX

Model variables

Here we describe the basic characteristics of our model. It has 14N variables, where N is the number of CRUs, N = 19,305. For a given CRU, these 14 variables are the concentrations in the five CRU compartments; two concentrations of Ca²⁺ bound to Troponin-C in the local cytosolic and submembrane compartments; three variables that describe the number of RyR channels in the different states of the four-state RyR Markov model; and four variables that describe the state of each of the four L-type channels in the L-type channel Markov model (see Table 3).

TABLE 3.

Model variables

Variable	Description	Units
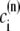	nth Unit cytosolic Ca2+ concentration	μM
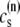	nth Unit submembrane Ca2+ concentration	μM
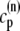	nth Unit proximal space Ca2+ concentration	μM
	nth Unit NSR Ca2+ concentration	μM
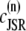	nth Unit JSR Ca2+ concentration	μM
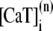	nth Unit Ca2+-Troponin-C cytosolic concentration	μM
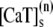	nth Unit Ca2+-Troponin-C submembrane concentration	μM
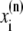	Number of RyR channels in nth unit in state i
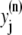	State of jth L-type channel in nth unit

These variables evolve, as will be described below in more detail, by means of 7N diffusively coupled differential equations for the concentrations 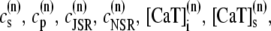4N L-type channel Markov models describing the state 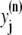of four L-type channels per CRU, j = 1, 2, 3, 4, and N Markov models that give the number of RyR channels in the states of the RyR four-state model for each CRU, 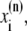i = 1, 2, 3, where n = 1,…,N.

Dynamics of Ca²⁺ cycling in an elementary unit

In what follows we describe the Ca²⁺ dynamics in the n^th CRU. To simplify the notation, we will omit here the superscript (n) when there is not the possibility of confusion, with the understanding that the currents and concentrations (and the heterogeneous proximal space volume v_p) refer to those at the n^th unit. The dynamics of Ca²⁺ cycling in the n^th CRU is described by the equations

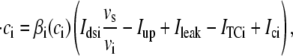(27)

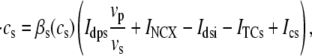(28)

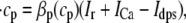(29)

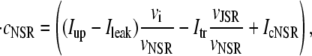(30)

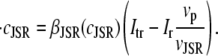(31)

In what follows we comment on the various currents and terms in Eqs. 27–31. We note that, in general, the results of calibration of mathematical expressions in whole-cell models are not necessarily valid when the same expressions are used in a CRU. The concentrations used in whole cell current expressions are averaged concentrations, while the concentration in CRUs might differ significantly from the average. Since the average of a function is not generally equal to the function of the average, the result of averaging a current over many CRUs is not necessarily the same as using averaged concentrations in a single pool model current. Therefore, in some cases we adjust the whole-cell current parameters that have been calibrated in previous whole cell models while keeping the same functional form.

Instantaneous buffering functions β(c)

The term β_X(c_X) accounts for instantaneous buffering in compartment X using the rapid buffering approximation (66). For example, instantaneous buffering in the cytosolic compartments is given by β_i(c_i) as

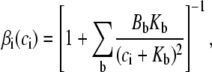(32)

where the sum is over the instantaneous cytosolic buffers Calmodulin, SR sites, Myosin (Ca), and Myosin (Mg), with buffer dissociation constants K_CAM, K_SR, K_MCa, and K_MMg and total concentration of buffering sites B_CAM, B_SR, B_MCa, and B_MMg, respectively. In addition to Calmodulin, we consider instantaneous buffering in the submembrane space by the subsarcolemmal sites of high affinity (51) with total concentration of sites and dissociation constant B_SLH and K_SLH, respectively. As we will discuss below, we assume that the concentration of the proximal space rapidly equilibrates, (see, for example, (30)), so we do not require knowledge of the instantaneous buffers in the proximal space. The values for the buffer parameters are in Table 4, and were obtained from the literature (44,51).

TABLE 4.

Buffering parameters

Parameter	Value	Units
KCAM	7.0	μM
BCAM	24.0	μM
KSR	0.6	μM
BSR	47.0	μM
KMCa	0.033	μM
BMCa	140.0	μM
KMMg	3.64	μM
BMMg	140.0	μM
KSLH	0.3	μM
BSLH	13.4	μM
BT	70.0	μM
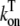	0.0327	(μM ms)−1
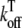	0.0196	ms−1

Luminal buffering was described in detail in Luminal Buffering, where it was argued that the expression for β_JSR(c_JSR) is

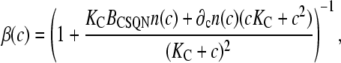(33)

where

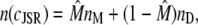(34)

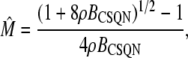(35)

and

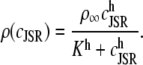(36)

The parameters for luminal buffering are in Table 5. We note that B_CSQN represents concentration of CSQN molecules. Taking an average buffering capacity of 25 sites per CSQN molecule, we would have a concentration of CSQN buffering sites of 10,000 μM. Measurements of CSQN buffering sites concentration range from 3 mM (74) to 14 mM (75). The effect of varying the concentration of CSQN (as has been done with transgenic mice (15,65)) is explored in Fig. 11 c. Shannon and Bers (75) reports a dissociation constant of 630 μM and Mitchell et al. (76) reports a dissociation constant in the range 400–600 μM; we take K_C = 600 μM.

TABLE 5.

Luminal buffering parameters

Parameter	Description	Value
BCSQN	Concentration of CSQN molecules	400 μM
KC	Dissociation constant of CSQN	600 μM
nM	Buffering capacity of CSQN monomers	15
nD	Buffering capacity of CSQN dimers	35
ρ∞	Asymptotic ratio of dimers to monomers	5000
K	Dimerization constant	850 μM
h	Dimerization exponent (steep)	23

Troponin C dynamic buffering currents, I_TCi and I_TCs

These currents describe the rate of change in the concentration of Ca²⁺ bound to Troponin C in the cytosolic and submembrane compartments, [CaT]_i and [CaT]_s. These quantities satisfy

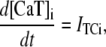(37)

with

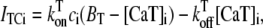(38)

and analogous expressions apply for the submembrane compartments, replacing the subscript i by s. Here, k_on and k_off are the on- and off-rate constants for Ca²⁺-Troponin C binding, and B_T is the total concentration of Troponin C buffering sites.

Uptake current I_up

We use the uptake current from Shannon et al. (51)

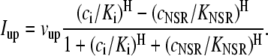(39)

See Table 6 for parameters used.

TABLE 6.

Uptake and leak current parameters

Parameter	Value	Units
vup	0.3	μM ms−1
Ki	0.123	μM
KNSR	1700	μM
H	1.787
gleak	1.035 × 10−5	ms−1
KJSR	500	μM

Leak current I_leak

The leak current has the form Shiferaw et al. (8)

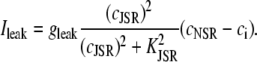(40)

See Table 6 for parameters used.

Sodium-calcium exchange current I_NaCa

We used the exchange current as in Shannon et al. (51)

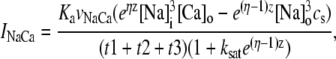(41)

where

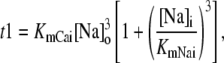(42)

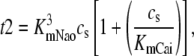(43)

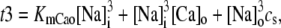(44)

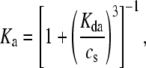(45)

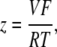(46)

and the values of the parameters can be found in Table 7.

TABLE 7.

Sodium-calcium exchanger current parameters

Parameter	Value	Units
vNaCa	1.05	μM ms−1
KmCai	3.59	μM
KmCao	1.3	mM
KmNai	12.3	mM
KmNao	87.5	mM
Kda	0.11	μM
ksat	0.27
η	0.35
[Ca2+]o	1.8	mM
[Na+]o	136	mM

The internal sodium concentration [Na⁺]_i adjusts slowly upon a change in pacing rate, reflecting the new equilibrium between sodium influx due to the sodium current, and sodium extrusion by the sodium-calcium exchanger and the sodium-potassium pump. This process occurs over many beats and is not essential for modeling Ca²⁺ dynamics. Therefore, following Shiferaw et al. (8), we will adopt a phenomenological expression for [Na⁺]_i as a function of the pacing period T,

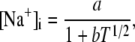(47)

where a = 78 mM, b = 10 s^−1/2, and T is in seconds. These values yield [Na⁺]_i ≈ 14.2 mM for T = 0.2 s and [Na⁺]_i ≈ 7.1 mM for T = 1 s.

Calcium current, I_Ca

Each CRU is assumed to have four L-type channels, l = 1, 2, 3, 4. The Ca²⁺ flux into the proximal space of the n^th CRU is given by

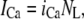(48)

where the single channel current is (77)

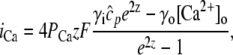(49)

z = VF/(RT), and 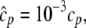i.e., the concentration of the proximal space in mM units. The gating of each L-type channel is simulated by stochastically evolving the seven-state Markov model developed in Mahajan et al. (52), with their constants 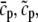and r₂ modified to 1.5, 0.5, and 6.0, respectively. The value N_L is the number of channels in the open state, 1 ≤ N_L ≤ 4. The parameter values are in Table 8.

TABLE 8.

Calcium current parameters

Parameter	Value	Units
PCa	L-type channel permeability	11.9 μmol C−1 ms−1
γi, γo	Activity coefficient of Ca2+	0.341
F	Faraday's constant	96.5 C mmol−1
R	Universal gas constant	8.314 J mol−1 K−1
T	Temperature	308 K
[Ca2+]o	External calcium concentration	1.8 mM

Release current, I_r

The JSR in each CRU releases Ca²⁺ into the proximal space through multiple RyR channels. In our model, each CRU has 100 RyR channels. The release current for the n^th CRU is given by (30)

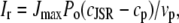(50)

where P_o is the fraction of RyR channels that are in the open states (states 2 and 3 in Fig. 2 a), and J_max = 1.47 × 10⁻² μm³ ms⁻¹. The gating of the RyR channels used to obtain P_o will be described in the next subsection.

Diffusion from proximal space to submembrane space, I_dps

We use a diffusive current of the form I_dps = (c_p – c_s)/τ_p with τ_p = 0.022 ms. This time corresponds to diffusion over a distance of ∼80 nm, the average distance to travel slightly out of the proximal space, which has a cylindrical shape with radius 200 nm. Since τ_p is significantly smaller than other timescales in the problem, we assume, following Hinch (30), that c_p rapidly equilibrates so that 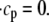We remark that, in this approximation, the proximal space instantaneous buffering factor β_JSR is not needed. Using Eq. 27 and the expressions for I_r and I_dps to solve for c_p, we obtain

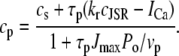(51)

Diffusion from NSR to JSR, I_tr

The JSR refilling current is given by I_tr = (c_NSR – c_JSR)/τ_tr. From nanoscopic imaging of JSR depletions (43), the translocation time from NSR to JSR has been estimated to be ∼30 ms. We choose τ_tr = 5 ms, so that when taking into account the buffering factor β_JSR ∼ 0.15 (see Fig. 2 d), the effective refilling time is 5 ms/β_JSR ∼ 30 ms.

Nearest-neighbor diffusive currents, I_ci, I_cs, and I_cNSR

The diffusive currents couple neighboring dyadic junctions. Here, to avoid confusion, it is necessary to distinguish quantities corresponding to the n^th CRU with the superindex (n). The cytosolic diffusive current is given by

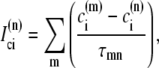(52)

where the sum is over the (at most six) nearest neighbors, 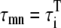if units m and n lie along one of the transverse directions, and 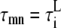if they lie along the longitudinal direction (the values for these timescales are in Table 9). More precisely, the CRUs can be labeled with indices 1 ≤ n_x ≤ 65, 1 ≤ n_y ≤ 27, and 1 ≤ n_z ≤ 11 denoting their position in the three-dimensional grid so that (n) → (n_x, n_y, n_x), with x representing the longitudinal direction. Then, for 1 < n_x < 65, 1 < n_y < 27, and 1 < n_z < 11, we have

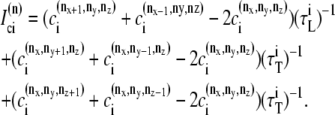(53)

When the unit is in the border (i.e., n_x = 1, 65, n_y = 1, 27, or n_z = 1, 11), we modify the previous expression appropriately to impose no-flux boundary conditions.

Similar expressions are used for the submembrane and NSR diffusive currents I_cs and I_cNSR.

Diffusion from submembrane to myoplasm, I_dsi

We use a diffusive current of the form I_dsi = (c_s – c_i)/τ_si with τ_si = 0.1 ms, estimated as the time it takes for a Ca²⁺ ion to diffuse ∼200 nm into the cytosolic compartment. Since this timescale is fast, we assume instantaneous equilibration, 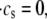obtaining from Eq. 28

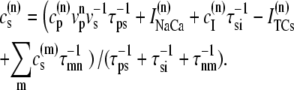(54)

RyR gating Markov model

As described in Luminal Gating, we consider a four-state Markov model with the following states: closed CSQN-unbound (1), open CSQN-unbound (2), open CSQN-bound (3), and closed CSQN-bound (4). The rates of transition from state i to state j, k_ij, are

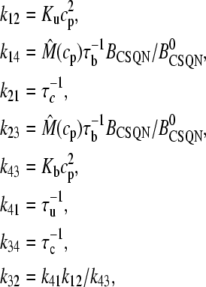(55)

where 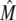is given by Eq. 35 and the parameters are in Table 10. We note that 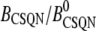is only different from 1 when we modify CSQN concentration.

A direct simulation of the stochastic evolution of each one of the 100 × 20,000 = 2 × 10⁶ RyR channels in the myocyte would be computationally prohibitive, since diffusive coupling between adjacent CRUs requires the simultaneous processing of RyR gating dynamics. To reduce the computation time to reasonable levels, we do not simulate each individual channel in a given CRU, but rather keep track of the number of channels in a given CRU that are in each state. 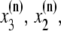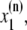The number of states in the n^th dyad in the open CSQN-bound (3), open CSQN-unbound (2), and closed CSQN-unbound (1) are denoted by and respectively (the number of RyRs in the closed CSQN-bound state is 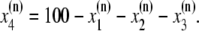) Henceforth we will omit the superscript (n). The release current I_r depends only on the fraction of states in the open states P_o = (x₂ + x₃)/100, rather than on which particular channels are in each state. Therefore, at each time step we only need to compute the number of channels that make transitions from one state to another. Since we have the probabilities for the transition of an individual channel, the distribution of the number of channels making a transition from state j can be obtained from a multinomial distribution with the number of trials being the number of RyRs in state j and the probabilities of success being the probabilities of transition to another state given by the expressions in Eq. 55. We remark that, so far, this is an equivalent mathematical formulation of the process that requires, for the large number of RyR channels we consider, less computational effort. Further approximations allow us to increase the efficiency of the simulation. In practice, the probabilities of transition per unit time are small and we can treat transitions to different states as independent. For example, if at time t there are x₁ channels in the closed unbound state, the probability that x₁₂ of these channels makes a transition to the open unbound state and x₁₄ channels make a transition to the closed bound state in the time interval [t, t + Δt) is

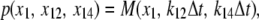(56)

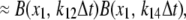(57)

where M(n, p, p′) is the multinomial distribution with success probabilities p and p′ in n trials and B(n, p) is the binomial distribution with success probability p in n trials. We note that this method is equivalent to the binomial τ-leaping method (78).

Computationally, we use Poisson or Gaussian approximations to the binomial distribution. Which approximation works better for B(n, p) depends both on n and p, and in our simulations both of these may change on each time step (in particular during sparks), so we determined before the simulations the region in the (n, p) space where each approximation was to be used. Denoting 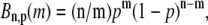P_n,p(m) = (np)^me^−np/m!, and 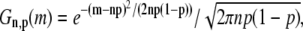the probabilities of choosing m using the binomial, Poisson, and Gaussian distributions, we define for each n and p the errors

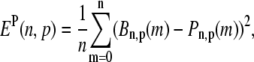(58)

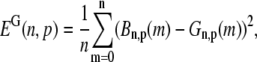(59)

with the intent to use a Gaussian approximation when E^G(n, p) < E^P(n, p) and a Poisson approximation when E^G(n, p) ≥ E^P(n, p). To simplify the computations, we approximate the numerically found region in which E^P(n, p) < E^G(n, p) by the set of points (n, p) satisfying 100 p < 6.6 + 52n^−1/2, and use a Poisson approximation in this case and a Gaussian approximation otherwise. The Poisson distributed numbers are generated using the Knuth algorithm and the Gaussian distributed numbers with the Box-Mueller algorithm (79).

In summary, at each time step we have x_i, the number of RyR channels in state i. The number of channels x_ij making a transition from state i to state j is approximated by

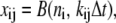(60)

where B is a random number generated to approximate a binomial distribution as described in the previous paragraph. After all the x_ij values have been determined in this way, the number of RyRs in each state in the next step is updated as

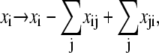(61)

where the sum is over the two states that are accessible to state i.

Initial conditions and model integration

Initial conditions have to be supplied for the 14N variables of our model. We find that, due to the intrinsic randomization caused by the stochastic nature of the model at the CRU level, the steady-state whole-cell behavior of the model during pacing does not depend on the initial conditions, although the first beats show transient behavior. In addition, even for identical initial conditions the simulation produces different results at single CRUs. 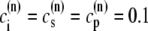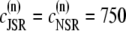Thus, the precise values of the initial conditions are not crucial when we are interested in steady-state behavior and we use the initial values μM, μM, (i.e., 70% of the RyR channels in the closed CSQN-bound state and 30% of the RyR channels in the closed CSQN-unbound state), 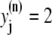(i.e., the L-type channels start in the closed two-state of Mahajan et al. (52)), and 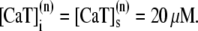In any case, we always discard the first beats.

For the graded release curves (Fig. 3) and the spark restitution curves (Fig. 4) we start with the same initial conditions, except that 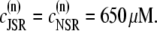In addition, we wait 1 s before collecting pairs of sparks in the restitution curve, and depolarizing to higher voltages in the graded release curve, to reach steady state and allow randomization to occur.

The SR depletion curve (Fig. 5) depends on how many RyR channels are in the CSQN-unbound state. We set the initial conditions to be the same as before, except that we set the initial SR and JSR content at 400 μM. Then, we keep the myocyte at −80 mV during various intervals and depolarize the cell, obtaining points with various values of SR content before release.

The fastest timescales in the model are diffusion from the proximal space to the submembrane space, and from the submembrane space to the cytosol. In the numerical integration of the model, it was assumed that equilibration of these processes is instantaneous (Eqs. 51 and 54). The fastest of the remaining timescales is the mean open time of the L-type channels, ∼1 ms, and we found that an adequate time step was Δt = 0.1 ms. The results do not change if we use Δt = 0.02 ms. The ODEs were integrated using the explicit Euler method and the Markov models were updated every timestep as described in the previous section.