How Topological Constraints Facilitate Growth and Stability of Bubbles in DNA

Abstract

The bubbles in double-stranded DNA, essential for gene transcription and replication, occur in mechanically constrained situations. Through an elastic model incorporating topological constraint, we show that, when a stretched double helix is underwound above a critical value of twist, a bubble can spontaneously form, yielding extension and torque behaviors quantitatively in agreement with magnetic tweezers experiments. We find that, unlike thermal bubble in an unconstrained DNA, the bubbles in these constrained states can grow and stabilize, provided that tension and length of DNA are above critical values.

INTRODUCTION

Two single strands of a DNA molecule are self-assembled into a double-helix (duplex) structure via hydrogen-bonding (H-B) and stacking interactions among neighboring bases to store genetic information (1). Yet, as has been widely studied (2–6), thermal excitation can induce not only global denaturation above a melting temperature ∼350 K but also local opening of the duplex structure, called a bubble, ubiquitously at a physiological temperature. They are the phenomena arising from a competition between entropically favorable single-strand (ss) state and energetically favorable double-strand state. The energy only in orders of k_BTs is required to break a basepair (bp), but, due to a high energy barrier (≈11 k_BT) to initiate a bubble, the bubble occurrence is rare at a physiological temperature (5). Bubble formation is highly sequence-dependent (7,8). AT basepairs formed by two H-Bs are weaker than GC basepairs by three H-Bs. Due to the stacking interactions, the dissociation free energies of a bp depend on identity of neighboring nucleotides and on their directions, thus having 10 different values. As a result, bubbles, if they can, occur preferably at AT-rich regions.

When a DNA is in an unconstrained situation like in a free solution, such thermal bubbles are unstable and decay (4,6). In addition to the initiation energy, the free energy of forming a bubble of n broken bp has two contributions (4). The first is nε where ε is the energy for unbinding a bp. The other is the entropic contribution, α log(n + 1), where α ≥ 1.5 is a statistical factor. Then, the net free energy cost of forming a bubble is always positive and monotonically increases with its size n (4). The thermal bubbles, thus, should shrink with characteristic times known to be in μs order from a fluorescence correlation spectroscopy experiment (6).

In contrast, in vivo, the DNA is condensed into a chromosome in a fascinating hierarchy of folded and coiled structures (1). Stable bubbles are essential for exposing DNA sequences to be read during transcription and replication processes (1) and for promoting protein binding, e.g., in DNA looping (9). In these situations, enzymes such as RNA polymerase and helicase (10) exert torques and forces on the DNA to actively open bubbles. Sometimes, e.g., during the replication process, single-stranded DNA binding proteins bind to unpaired bases within a bubble to assist its stability (11,12).

The bubble formation in the presence of a torsional strain is subject to a topological constraint, namely, the White theorem (13,14). It says the sum of twist (Tw), the number of helical winding of double strands (ds) around each other, and writhe (Wr), the number of coiling of the ds axis about itself, should be fixed to a topological invariant called the linking number (Lk) (13). For example, if a DNA is twisted so as to have Lk less than Lk₀ = ω₀L/2π of B-DNA, the most typical DNA in vivo which has the right-handed natural helicity ω₀ = 2π/3.57 nm (L is the DNA contour length), to conserve the linking number it can permit bubbles to form and/or writhe to exhibit in the form of supercoils (Fig. 1, a and b).

FIGURE 1.

Schematic views on conformations of an extended dsDNA (a) underwound, and (b) overwound by magnetic tweezers. (c) Relative extensions versus σ of a λ-DNA in Neukirch (19) (experimental data, squared) and theoretical predictions (dotted, Eq. 6 and solid, Eq. 10) under applied forces F. Below the critical values of σ denoted by crosses (×), a bubble emerges leading to little variation in extension.

It has been a long-standing issue how the bubbles and supercoils in such mechanically and topologically constrained states interplay in response to the negative torsional strain characteristic of native DNAs for biological functions (15,16). For the case of circular DNAs, Fye and Benham (17) and Benham and Mielke (18) showed, using their phenomenological model and numerical computations, the importance of topological constraint on the bubble phenomena. Here we study the bubbles of linear DNA subject to the mechanical as well as topological constraints imposed by enzymes (such as RNA polymerase) unwinding and histone binding in the gene transcription process. We pose a fundamental question: how can the constraints facilitate a large bubble to form and stabilize?

The bubbles in similar situations have recently been emulated by single-molecule experiments using magnetic tweezers (10,19–21). In these experiments, a dsDNA tether is anchored on surface at an end and stretched at the other with a force F by a magnetic bead which can be twisted (shown schematically in Fig. 1). The overtwist is represented by σ = (Lk – Lk₀)/Lk₀ ≡ ΔLk/Lk₀. The elastic behaviors of a λ-phage DNA (48,000 bp long) are manifested in extension curves (19) (Fig. 1 c); at a weak force F = 0.44 pN, the relative extension z/L along the direction of the force is symmetric with respect to σ → −σ. For F ≲ 1 pN; however, it becomes highly asymmetric. In an overwound state (σ > 0), the dsDNA is coiled around itself (supercoiled), forming plectoneme loops (see Fig. 1 b) for a small force. A number of theoretical works were done to show how the plectonemic transition gives rise to precipitous contraction (19,22–24). In contrast, a native DNA is often in an underwound state (σ < 0), and in the presence of a considerable force, a bubble instead of plectoneme loops is reported to occur at a weakly bonding site and relieve the torsion and the contraction (Fig. 1 a) (21).

In this article, we present an elastic model of the constrained DNA explaining its distinctive elastic response for σ < 0 and F ≳ 137; 1 pN in the magnetic tweezers experiments mentioned above. More importantly, we use it to predict the novel nature of the bubble formation that underlies, i.e., its constraint-induced stability and growth.

A constrained dsDNA without a bubble

Our main task is to evaluate the DNA's free energy function ℱ(n), for given σ and F, as a function of bubble size n (open bp number). To this end, we first study an elastic model for a bubble-free but constrained DNA and calculate its free energy ℱ₀. In a coarse-grained description in terms of local center-of-mass position r(s) and torsional twist Ω(s) per unit length at an arc length s, we describe a bubble-free dsDNA subject to a force F using an (effective) energy functional, ℋ (25),

(1)

where the first two terms are bending and torsional energies involving characteristic persistence lengths l_p and C, respectively, in unit of k_BT = β⁻¹, and f = βF. Implicit within the integral are two constraints arising from chain inextensibility |∂r(s)/∂s| = 1 and the White theorem. The latter couples the bending and torsional degrees of freedom in an intricate way, which poses a challenge to evaluate.

Utilizing three Euler angles, θ(s), φ(s), and ψ(s) at an arc length s (θ(s) is the polar angle between the unit tangent vector ∂r(s)/∂s at s and z axis), we rewrite the above energy functional as and the excess linking number as (22). ℱ₀ then can be obtained from the partition function

(2)

a path integral over all possible angles satisfying the White theorem as indicated by the delta function.

Following the procedures used in Bouchiat and Mezard (25), considering small undulation approximation (26), θ⁴ ≪ 1, appropriate to the range of forces considered here, we obtain (a brief outline of the derivation is given in the Appendix)

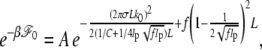(3)

where Due to thermal undulation of the strand, the force-dependent effective torsional persistence length is smaller than the bare value C by 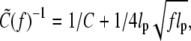as first noted in Moroz and Nelson (26). In terms of the free energy can be rewritten as

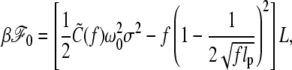(4)

apart from the negligible term due to A.

The first term in the above accounts for the torsional energy for a constrained DNA. When f increases to infinity, also increases to C and ΔLk = σω₀L/2π is entirely stored as ΔTw to give the torsional energy 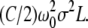This means, for a finite f,

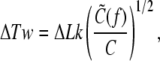(5)

which predicts how the number ΔTw of induced twist increases as the force increases. In the range of forces >1 pN, ΔTw/ΔLk is >0.92 while ΔWr/ΔLk is <0.08, so our small undulation approximation appears to be consistent.

The average relative extension 〈z/L〉 in the absence of bubbles is given as

(6)

a remarkably compact form compared with those of the literature (25,26). The first two terms in parentheses represent the well-known result given by the wormlike chain model without torsion (27). The third term indicates the contraction by the excess twist (Eq. 5) coupled with the tension. We compare Eq. 6 with experimental data (19) (see Fig. 1). Two parameters, l_p and C, are chosen so as to give the best fit to the data points in the interval −0.02 ≲ σ ≲ 0.02. For F = 1.1 pN, l_p = 45.1 nm, and C = 110.0 nm. For small range of σ, the theoretical prediction (dotted curves) reasonably well describes the elastic behaviors of constrained DNAs, which are symmetric with σ → −σ.

For a larger negative value of σ, larger discrepancy is apparent. For the tension F ≳ 137; 1 pN we consider here, the Wr contribution via plectoneme loops is shown to be small as shown earlier, giving way to the bubble formation for negative σ. Furthermore, for the σ-range considered in Fig. 1 c, the experiment done by Strick et al. (21) showed that a single bubble instead of multiple bubbles emerges and grows at the most AT-rich region of λ-phage DNA. It is because considerably more energies are required to break a GC pair than an AT pair and also to initiate an additional bubble once a bubble is formed. For this reason, we consider below the model of an undertwisted DNA allowing a single bubble to remedy the discrepancy.

A constrained dsDNA with a bubble

Assume that a bubble of size n occurs at an arc length, say s = L₁. Then, we regard the DNA as a compound of two duplexes of length L₁ and L – L_b – L₁ and a single-stranded (ss) flexible loop of the length 2L_b = 2nd where d is the ss intrabase distance. ℱ(n) is obtained as the sum of the free energy ℱ_d(n) of the duplex part and ℱ_s(n) of the bubble, ℱ(n) = ℱ_d(n) + ℱ_s(n). Let us consider how the constraint affects ΔLk and the free energy of the duplex part. Each basepair in the absence of the bubble has a linking number (σ + 1)θ₀/2π (θ₀ = aω₀ with a ds intrabase distance a = 0.34 nm). In the presence of the bubble, the duplex part will have a decrease in the linking number,

(7)

where N = L/a, the total number of basepairs. Adapting Eq. 4 to this case, we have

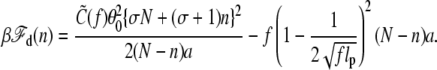(8)

The first term means that the unwound DNA has less torsional energy due to the bubble. At a critical bubble size n_c = |σ|N/(σ + 1), the first term vanishes, i.e., the torsional strain applied on the ds is removed. On the other hand, Eqs. 7 and 8 show that, in an overtwisted DNA (σ > 0), the ds part has an increased linking number and torsional energy due to the bubble. Thus, the bubble formation is energetically always unfavorable for the overtwisted DNA, which is relevant to living organisms that survive in a high-temperature environment under sea.

The free energy cost (in k_BT) to form a bubble of size n bp is given by ε_I + nε + α log (n + 1) (5). The first term, the energy barrier to initiate a bubble, is ∼11 k_BT (5). ε(T), the average unbinding energy per bp, is ∼1.4 k_BT, which refers to the AT-rich region of λ-phage DNA (28). The third term accounts for an entropy reduction associated with forming a loop closure, with the exponent α ≈ 1.76 for a self-avoiding chain (29). The free energy change (in k_BT) per bp of a single strand induced by the force is well described by a freely-jointed chainlike model in the force range 1 ∼ 10 pN as 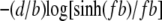(28,30), where b is the Kuhn length in ssDNA. From these contributions, we obtain

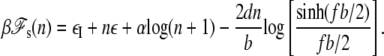(9)

The constrained DNA allows a bubble if ℱ = ℱ_d + ℱ_s is <ℱ₀. This is satisfied when reduction of the torsional energy due to its formation exceeds the free energy cost for creating it. This condition complicatedly depends on the parameters such as F, N, and σ, as we discuss below.

The relative extension of DNA in the presence of a bubble can be obtained as :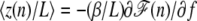

(10)

The equation indicates how an asymmetric elongation behavior for σ < 0 as compared with Eq. 6 emerges with a bubble of the relative size x = n/N. To compare this with the experimental data in Fig. 1, we first replace n by its thermal average

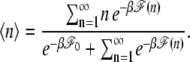(11)

We numerically calculate 〈n〉 as a function of σ and f for each curve in Fig. 1 c with the values of l_p and C already used. The solid lines in Fig. 1 are the predictions of Eq. 10 for σ < 0, where we use d = 0.56 nm and b = 2.7 nm suggested in Bockelmann et al. (31). The theoretical lines are in a good agreement with the experimental curves. Now let us focus on the case for F = 1.1 pN. The solid line, Eq. 10, abruptly deviates from the dotted line, Eq. 6, at a critical value σ_c (denoted by ×), below which the extension does not vary sensitively with σ. Fig. 2 a is the plot of 〈n〉 as a function of σ, where it indeed shows that the bubble abruptly emerges at <σ_c ≈ −0.018. Remarkably, 〈n〉 is always much smaller than n_c, which means an applied torsional strain does not relax entirely via the bubble, mainly due to the large energy cost to break basepairs aforementioned. The fact that the torsional strain is partially relieved via the bubble is strongly inferred by the experiment done by Strick et al. (21). Furthermore, our data suggests that at typical experimental conditions for λ-phage DNA they studied, several hundred basepairs are open to form a bubble, which remains to be experimentally verified.

FIGURE 2.

(a) The average bubble size 〈n〉/N versus σ and (b) the torque required to retain σ for N = 48,000 bp and F = 1.1 pN. Below the torsional twist lower than a critical value σ_c ≈ −0.018, a bubble emerges discontinuously and grows.

Associated with the bubble formation is the transition behavior of the torque Γ required for the DNA to retain the σ. Fig. 2 b shows the torque obtained from 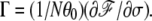In the absence of the bubble, 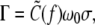in accord with Moroz and Nelson (26); as the stretching force is increased, so is the torque. When a bubble emerges and partially alleviates the torsional strain, a smaller torque is expected. Our result shows that the double helix can sustain a negative torque up to −3 k_BT, beyond which it gives way to the bubble. Interestingly, in the regime σ < σ_c, Γ remains almost as a constant at ∼−2.5 k_BT, which also agrees considerably with the corresponding value of Γ estimated in an experiment (21).

Fig. 3 shows 〈n〉 as a function of F for several σ-values. When the DNA is not much twisted (σ = −0.010), the bubble does not occur in the force range of our concern. However, when σ has considerable values, the force enhances the bubble formation as it increases above a critical value.

FIGURE 3.

The average bubble size 〈n〉/N versus F at various values of σ for N = 48,000 bp.

We also investigate how the bubble formation depends on N. Fig. 4 a shows 〈n〉/N as a function of σ for several values of N at a fixed force F = 1.1 pN; Fig. 4 b shows 〈n〉 versus N for fixed values of σ and F. The latter reveals that a bubble can form in a dsDNA longer than the critical length N_c, which decreases sensitively with undertwist |σ| but varies little with F. This leads to a striking conclusion that, in a shorter DNA under constraint, the bubble formation is harder and thus its double-helical structure is maintained more stably against the imposed negative twist unless it is very high. This may be relevant to the bubble occurrence in chromosome, where topologically constrained length of DNA can effectively increase via histone octamers release. The chromosome DNA, initially stable when wrapped around the histones, may become unstable with respect to bubble formation by releasing them in the presence of unwinding machineries such as RNA polymerase.

FIGURE 4.

(a) The average bubble size 〈n〉/N versus σ for several values of N at F = 1.1 pN. (b) The average bubble size 〈n〉 versus N for σ = – 0.02 and – 0.03 at F = 1.1 pN.

Free energy landscapes of the constrained bubbles

To gain further understanding of the nature of the bubble formation, we now analyze the behavior of Δℱ = ℱ(n) − ℱ₀. Fig. 5 shows the profile of βΔℱ(x) with x = n/N for various negative values of σ at F = 1.1 pN and N = 48,000 bp. For small enough values of |σ|, Δℱ is always positive, which means forming a bubble is unfavorable. Even if a bubble happens to occur due to thermal excitation, it is always unstable or metastable and so it decays. When σ decreases to the critical value σ_c, which we discussed, the free energy minimum, attained at x = x_c, goes to zero. If the σ decreases further below, the 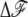can have a negative minimum value at x = x_m > x_c, meaning that, once the bubble crosses over the initial energy barrier by thermal excitation, a bubble of size Nx_m is formed. In contrast to the transient thermal bubbles (in a free DNA), our study shows this bubble (in stretched underwound DNA) can stably exist for a long time once it occurs. The σ_c and the associated x_c are those at which the minimum value is zero. Interesting enough, x_c is nonzero, meaning that the bubble formation in a long DNA occurs discontinuously like the first-order transition, in consistency with the literature (32,33).

FIGURE 5.

The profiles of the free energy ΔF/k_BT for various values of σ for F = 1.1 pN and N = 48,000 bp.

SUMMARY AND CONCLUSION

In conclusion, based upon an elastic model incorporating bending and twisting of strands and their coupling via a topological constraint, we have studied the elastic behavior of an underwound stretched DNA and the bubble formation that is induced. When a negative torsional twist imposed on the DNA exceeds a critical magnitude, a stable bubble emerges and partially eliminates the strain, yielding elongational and torsional responses behaviors in good agreements with single-molecule experiments.

Our theoretical analysis also shows that the bubble formation can be enhanced as the extensional force and the DNA length increase. Notably, there is a critical length of DNA for given applied torque and force, beyond which a bubble can be induced. We conjecture that this length-dependent instability of DNA double helix against an external torque may assist the bubble initiation and formation by RNA polymerase during gene transcription by releasing histone octamers from DNA. We expect that a single-molecule, in vitro experiment using magnetic tweezers may support the length dependence of the critical torque for allowing a bubble.

Intriguingly, the torque-induced bubble can be stabilized under a topological constraint even without the aid of single-stranded DNA binding proteins. This is the unique feature of the constrained bubbles that thermally induced unconstrained bubbles cannot exhibit. Our free energy landscapes of bubble formation further show that stability of the constrained bubbles is controlled by the force and torque, beyond the critical values of which the bubble of a certain size becomes stable. It leads to a conclusion that the constraints in vivo, facilitated by enzymes such as RNA polymerase, enlarge and stabilize the thermally induced bubbles, which otherwise are unstable.

APPENDIX A: A BRIEF OUTLINE OF DERIVING EQ. 3

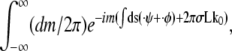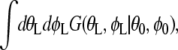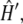Representing the δ-function in Eq. 2 as the integral over ψ of Eq. 2 can be done to yield where From the analogy of a quantum particle in magnetic and electric fields (25,26), the integral over θ and φ part can be given by where G is a propagator G(θ_L,φ_L|θ₀,φ₀) = and ε_n and Ψ_n(θ) are the eigenvalue and eigenvalue for the operator respectively. In the second term solely explains the topological effect, without which it reduces to the case of the usual wormlike chain under a tension f. In the long chain limit, G is dominated by the ground state eigenvalue of We will treat the f strong enough to allow small undulation approximation, i.e., θ ≪ 1. We obtain the lowest eigenvalue as 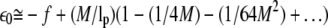with 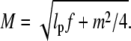Keeping terms up to third terms in ε₀, we obtain

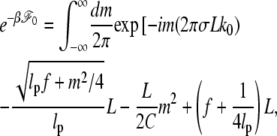(12)

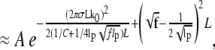(13)

where 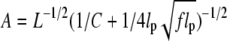is a negligible term depending upon the system size irrelevantly.