Scaling Theory of Polymer Translocation into Confined Regions

Abstract

We examine the voltage-driven polymer translocation from a spacious region into a confined region imposed by two parallel planes, so that the entry is impeded by the entropic confinement but aided by the electric field inside the confined region. Two modes of entry are examined: linear translocation where a chain enters the confined region with chain ends, and hairpin translocation where a chain enters the confined region by forming a hairpin. Our calculation shows that translocation time increases with polymer length for linear entries but decreases with polymer length for hairpin entries. Applying to electrophoresis of DNA molecules through periodic spacious and confined regions, our theory shows that the dominance of hairpin translocations leads to the experimentally observed faster migration of longer DNA molecules. Our theory predicts experimental conditions for the validity of this law in terms of polymer length, size of the confined region, and solution conditions.

INTRODUCTION

Polymer translocation from a spacious region into a confined region is ubiquitous in biology and nanotechnology. For example, protein molecules translocate to other cellular compartments through narrow membrane channels (1), polymer molecules are driven from solutions into gel matrices in electrophoresis (2), and DNA/RNA molecules are forced into micro- or nanofluidic channels and protein channels (3–14).

The phenomenon of polymer translocation is controlled by many factors (15). Chief among the contributing factors is the entropic barrier arising from the reduction of polymer conformations in the confined regions. Therefore, a driving force is required for successful translocation. While the entropic barrier imposed by the restricted space is common, the driving force can take different forms, or a combination of them. For instance, DNA molecules can be driven into a confined region by an electric field, a pressure-driven flow (6), or an electro-osmotic flow due to the surface charge of the confined region (16,17). In biological cells, the specific binding of specific signal sequences initiates the entry of a protein molecule to a narrow transmembrane channel (1).

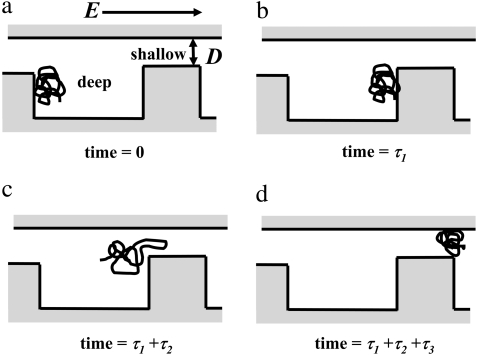
Microfluidic channels with periodic spacious and confined regions (3,4) demonstrate such interplay between entropic barrier and driving force. In these devices, the migration time of DNA molecules showed dramatic molecular weight dependence, with longer DNA molecules traveling faster under applied electric fields (3,4,18,19). A typical system consists of periodic strips of deep and shallow regions with heights 1.5–3.0 μm and 75–100 nm, respectively. The DNA molecules, in kilobase-pairs length scale, are driven through the periodic constrictions by an applied electric field, as depicted in Fig. 1. The molecules are unrestricted laterally so that they are confined between two horizontal parallel surfaces placed at distances much larger than the sizes of DNA molecules. For each period, which consists of a deep region followed by a shallow region, a DNA molecule first travels through the deep region with time τ₁. It then stops momentarily at the interface between the deep and shallow regions, and takes τ₂ to enter the shallow region. Finally, it takes τ₃ to finish passing through the shallow region. A DNA molecule thus takes time τ₁ + τ₂ + τ₃ to travel through one period (20). Because of the height difference, the electric field in deep regions is much lower than that in shallow regions (19,21), making τ₃ negligible compared to τ₁ + τ₂. In general, confinement effect is unimportant in deep regions so that the electrophoretic behavior of the DNA molecules is the same as that in a free solution. Consequently, τ₁ is independent of molecular weight of the DNA molecule, as is well known in the capillary electrophoresis (22). Therefore, the molecular weight dependence comes essentially from τ₂, the time for the DNA molecule to enter the shallow region from the deep region. The above description is consistent with fluorescence microscopy observations (4).

FIGURE 1.

The DNA molecule starts at the beginning of the deep region as shown in panel a. Driven by the electric field E (the arrow indicates the direction of the movement of the chain), it takes time τ₁ to migrate to the end of the deep region as shown in panel b. The polymer molecule then takes τ₂ to enter the shallow region, as sketched in panel c. Once the polymer molecule enters the shallow region successfully, it takes τ₃ to finish passing through the shallow region, as shown in panel d.

To understand the molecular basis of the above described experimental results, several theoretical attempts (3,19,23,24) and computer simulations (20,21,23,25,26) have been reported in the literature. Han et al. (3,4) considered DNA translocation into the confined region as an activation process and assumed that translocation time was in the Arrhenius form τ₂ ∼ τ₀ exp(F*), where F* ∼ 1/E is the free energy barrier of translocation into the shallow region and E is the electric field in the shallow region. They argued that the activation probability was proportional to the contact area between the slit and DNA molecule RD, where R ∼ N^ν is the size of the DNA with N segments, and D is the height of the shallow region. Using size exponent 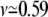for a flexible self-avoiding chain, the prefactor τ₀ is approximately 1/RD ∼ 1/N^νD. Thus, τ₂ always decreases with chain length N in this model. Sebastian et al. (24) drew analogy between the present problem and the Kramer's problem of a phantom polymer inside an asymmetric double potential well. In this model, 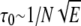if the polymer crosses the free energy barrier between the two wells in hairpin conformations, and τ₀ is independent of N if the polymer crosses the barrier in linear conformations (21). Note that these theories are derived without accounting for the statistics of the DNA molecules inside the particular geometry of the system. By performing Monte Carlo simulations, Chen and Escobedo (23) found that the free energy barrier for a Gaussian chain to enter the shallow region increased with chain length and approached a constant value in low electric fields, while it decreased with chain length in high electric fields. Streek et al. (25) found that, by increasing the height of the shallow regions in their simulations, a fast and a slow state of DNA migration through the periodic regions resulted from nonequilibrium dynamics. Tessier et al. (21) performed detailed Monte Carlo simulations with system dimensions similar to that of the experiments (3,4). In agreement with experimental observations, the mobility of the DNA increased with molecular weight in their simulations. They attributed this effect mainly to the deformation of the DNA molecules taking place during τ₂. Panwar and Kumar (20) simulated the system with a Gaussian chain and found that the mobility of the chain could change nonmonotonically with molecular weight, depending on the relative magnitudes of τ₁, τ_2, and τ₃. Recently, Lee and Joo (26) studied the system with both linear and star-branched polymers using Brownian dynamics simulations of bead-spring chain models, and found that the size of the polymer appeared to be the determining factor of the total migration time.

In this article, we present an analytically tractable scaling theory and calculate τ₂ using the statistics of self-avoiding chains under confinement. Two modes of polymer entry to the confined region are considered: linear translocation, which is led by a chain end; and hairpin translocation, which is led by a hairpin of chain segments. By constructing their free energies and the corresponding translocation times, we find that the N dependence of τ₂ is dictated by the statistics of chain tail(s) in the spacious region. For self-avoiding polymers, τ₂ ∼ N^0.31 for linear translocations and τ₂ ∼ N^−0.38 for hairpin translocations. Our calculation suggests that the decrease of translocation time with increasing chain length observed in experiments can be ascribed to the dominance of hairpin translocations. Furthermore, we predict that translocation time increases with chain length if linear translocations dominate, which is favored by short chains.

THEORY

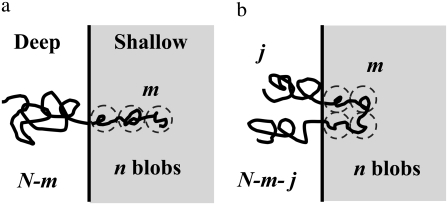
We consider a polymer chain entering a confined region composed of two parallel planes (shallow region) from a spacious region (deep region). When the polymer molecule is trying to enter the shallow region, part of the chain partitions into the shallow region and the rest of the chain still resides in the deep region, as shown in Fig. 2. The free energy of the whole chain is the sum of free energies of polymer segments inside the shallow region and those inside the deep region.

FIGURE 2.

Two modes of translocation (from the top view of geometry in Fig. 1). (a) For a linear translocation, the chain enters the shallow region with a chain end, forming n blobs in a linear series, with m segments in the shallow region and a tail of N – m segments in the deep region. (b) For a hairpin translocation, the chain enters the shallow region with a hairpin, with m segments in the shallow region and two tails of j and N – m – j segments in the deep region. In the deep region, there are two linear chains of blobs, each with n/2 blobs.

The free energy of segments in the shallow region has two competing contributions: 1), energy gain due to the electric field; and 2), conformational entropy lost due to the geometric confinement. We assume that the electric field is negligible and does not perturb the chain conformation in the deep region. The deep region is assumed to be wide and deep enough that the confinement effect on the chain is unimportant in the spacious region.

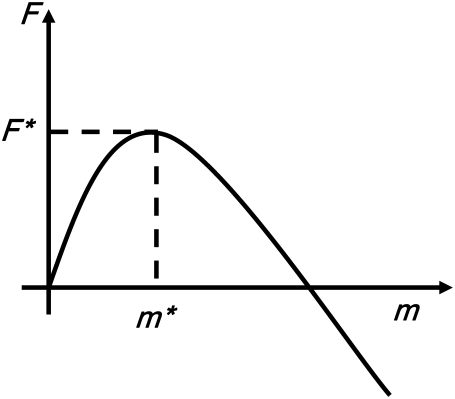
A typical free energy profile (15,27) for a chain entering the shallow region is illustrated in Fig. 3. The translocation process is described by the number of polymer segments in the shallow region m with free energy F(m). The process is at first unfavorable because of the entropic confinement imposed by the shallow region. As the chain proceeds further, after a critical number of inserted segments m*, the critical insertion size, the electrostatic free energy gain dominates and the translocation becomes favorable. Therefore, the free energy barrier of translocation is F* = F(m*) – F(0). In this section, we construct the free energy expression F(m) for linear and hairpin conformations. In the rest of the article, the units of length, energy, and force are the Kuhn length l, thermal energy k_BT, and k_BT/l, respectively. Since we use only scaling arguments in various key steps, the equality sign in the following equations omits all numerical prefactors arising from the nonuniversal aspects of the problem.

FIGURE 3.

Typical free energy profile of translocation as a function of the number of segments in the shallow region m. The value m* is the critical number of segments in the shallow region beyond which the translocation process is favorable.

Confinement free energy in shallow region

Consider m polymer segments in the shallow region with height D and constant electric field E. In view of the simplicity and success of the blob model of polymer chains in confined regions (28), we adopt the blob model. We assume that the segments inside the shallow region form a series of blobs with diameter D each, and the electric field aligns the blobs in linear but does not influence the segment statistics inside them. There are g = D^1/ν segments in each blob, and within the blobs, the chain statistics is unaltered by confinement (28). Therefore, the number of blobs is n = m/g = m/D^1/ν. It is to be noted that the size exponent ν is 0.59 for the experimental conditions of the literature (3,4,18,19), corresponding to the statistics of the self-avoiding flexible chains. The free energy of confinement is (28)

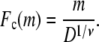(1)

The blob picture is satisfactory only if the persistence length l_p is much smaller than D and if it contains enough segments m to obey the self-avoiding walk statistics (29).

Electrostatic free energy in shallow region

The conformations of a chain during linear and hairpin translocations are shown in Fig. 2. Each segment in the shallow region experiences an electrostatic force f = qE, where q is the net charge of each segment, and E is the magnitude of the uniform electric field in the shallow region. The product qE is positive. Each blob has g = D^1/ν segments.

Let us first calculate the electrostatic energy when there is only one blob (with g segments) inside the shallow region. The electrostatic energy gain is the sum from each segment and can be written as 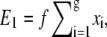where x_i is the distance of the i^th segment away from the interface between the deep and shallow regions. A blob of length D ensures that 0 ≤ x_i ≤ D. Alternatively, the sum can be expressed as 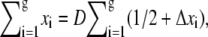where −1/2 ≤ Δx_i ≤ 1/2 is the normalized position of the i^th segment relative to the center of the blob. If the distribution of segments is symmetric about the center of the blob, then 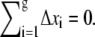By making this assumption, the electrostatic energy of the blob becomes E₁ = gfD/2. Now suppose that there are two blobs in series aligning in the direction of the electric field. Starting with one blob, the situation is equivalent to translating all segments in that blob by a distance D in the direction of the electric field and creating another blob in the place of that blob. Thus, starting with one blob, translating it into the new site of the blob and then creating another blob in the place of the original one, the electrostatic energy gain is E₁ + gfD. It follows that the electrostatic energy for two blobs is E₂ = E₁ + E₁ + gfD. Similarly, when there are n blobs inside the shallow region, the electrostatic energy change with respect to n – 1 blobs is equivalent to translating the first blob by a distance (n – 1)D, so that it moves to the end, and creating another blob in place of the first blob. The electrostatic energy of the n blobs is therefore E_n = E_n−1 + E₁ + gf(n – 1)D = nE₁ + gfD[(n – 1) + (n – 2) + … + 1] = n²gfD/2. Since n = m/g and g = D^1/ν, the electrostatic free energy of m segments assuming a linear conformation of blobs in the shallow region is

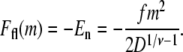(2)

The same result can be derived by an equivalent argument. By assuming that E is uniform, the energy of a blob (with g segments) at a distance Dn′ from the entrance to the shallow region is −fgDn′. Therefore, for n blobs, the net gain due to the electric field is 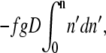which results in the same expression as Eq. 2. The negative sign indicates that the electric field drives the chain into the shallow region and favors translocation by competing against the positive confinement free energy given by Eq. 1. The rodlike limit (ν = 1) eliminates the D dependence in Eq. 2, recovering the result for an infinitely narrow channel (30). Note that Eq. 2 does not apply for Gaussian chains (ν = 0.5) (also see (28)) as statistical independence among perpendicular directions demands that the electrostatic energy does not depend on D. Therefore, we will confine our discussion to non-Gaussian chains.

For hairpin translocations, the entry is led by segments somewhere in the middle of the chain as illustrated in Fig. 2 b. We assume that a hairpin of n blobs forms a loop of two linear strings of n/2 blobs side by side due to the pulling by the electric field. The electrostatic energy for a hairpin conformation is then

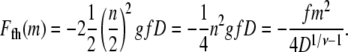(3)

Note that it is exactly half of its linear counterpart (Eq. 2). It is to be noted that in this flexible chain model, relevant for chain lengths much larger than l_p, bending energy associated with chain stiffness is neglected.

Free energies of chain tails in deep region

We model a chain tail in the deep region as a chain anchored to a hard wall in a semi-infinite half-space (31). The partition sum (with respective to the free state) of such a chain with j segments is (32,33)

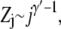(4)

where γ′ = 0.69 for a self-avoiding chain. The free energy of a j-segment chain tail in the deep region is then

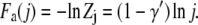(5)

Free energies of linear and hairpin conformations

With the above elements, we are in a position to construct the free energy profiles of linear and hairpin translocations. A chain in a linear conformation partitions between the deep and the shallow regions in the conformation shown in Fig. 2 a. Using Eqs. 1, 2, and 4, the probability of realizing a linear conformation with m segments in the shallow region and N – m segments in the deep region is

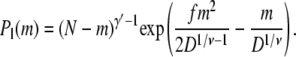(6)

The free energy of a state F gives the relative probability P of realizing that state, according to P = exp(–F). The translocation process is assumed to be in quasiequilibrium (that is, the typical relaxation times for conformational change of the polymer are shorter than the typical translocation time) so that it is solely dictated by the relative free energies among various states.

For hairpin conformations, the chain enters the shallow region with segments somewhere between the two ends, forming a hairpin in the shallow region as shown in Fig. 2 b. If there are m segments in the hairpin and j and N – m – j segments in the two tails in the deep region, respectively, using Eqs. 1, 3, and 4, the probability of the hairpin conformation is

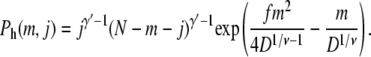(7)

It follows that the corresponding free energies of linear and hairpin conformations are

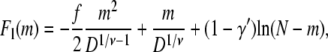(8)

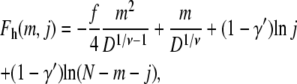(9)

respectively. In general, the above free energies have a maximum as a function of m, as illustrated in Fig. 3. Note that in writing Eqs. 7 and 9, we implicitly assume that the two chain tails in the deep region do not interact. If a monomer at the interface between the shallow and the deep regions is allowed to move up and down in the range of height D, the probabilities in Eqs. 6 and 7 would have an additional front factor D. It follows from free energy F = −k_BT ln P that there would be terms of ∼ln D, which are ignored in Eqs. 8 and 9 for simplicity. Their effects are secondary compared to the D dependence appearing in the electrostatic and confinement terms.

RESULTS

Critical insertion size

Translocation into the shallow region is initially unfavorable because of the geometric confinement with free energy ∼m/D^1/ν. After a critical number of inserted segments m*, the translocation process becomes favorable and the translocation free energy profile is dominated by the electrostatic energy ∼–fm²/D^1/ν−1. The translocation time is largely determined by the height of the free energy barrier F(m*) relative to the free state in the deep region. Note that this height is different for linear and hairpin translocations. For hairpin translocations, it has an additional dependence on j, which is F_h(m*, j). The value m* computed in physical distance corresponds to the critical hernia nucleation length in the simulations of Tessier et al. (21). We will refer to m* as the critical insertion size for both linear and hairpin translocations.

We consider first the linear translocation. Using Eq. 8, the linear critical insertion size m*_l is given by solving ∂F_l/∂m = 0. The solution is

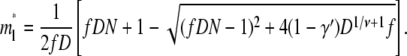(10)

For large N, such that N ≫ D^(1−ν)/2ν f^−1/2, the second term in the square root of Eq. 10 becomes negligible. The value m*_l now takes the simple form

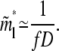(11)

Note that, in the rest of the article, a variable with tilde on top denotes an approximation that is valid for large N.

For hairpin translocations, the critical insertion size m*_h depends on j, the length of a tail in the deep region. Solving ∂F_h/∂m = 0 for a fixed j, we get

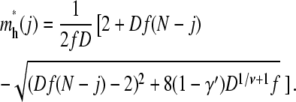(12)

Similarly, Eq. 12 reduces to

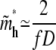(13)

for large N and is independent of the tail length j. Note that, from Eqs. 11 and 13, 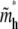is exactly twice 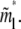Since a hairpin forms a loop of two linear blobs side by side in our model, the critical length of a hairpin, in physical distance, is the same as its linear counterpart for N ≫ D^(1−ν)/2ν f^−1/2. The exact solution Eq. 10 converges to the asymptotic limit Eq. 11 for large N. The exact result still neglects coefficients of O(1), due to the nature of the blob theory. Physically, the approximations, Eqs. 11 and 13, ignore the change of entropy of chain tail(s) in the deep region when the chain translocates into the shallow region, which is negligible for large N.

Relative probabilities of translocation modes

The translocation is linear if the chain attains the conformation of Fig. 2 a, with the critical number of segments m_l* in the shallow region and N – m_l* segments in the deep region. Using Eqs. 6 and 11, the probability of linear translocation is

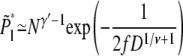(14)

for large N.

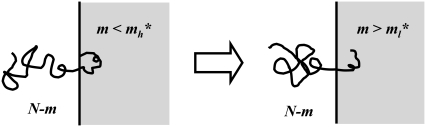
Nevertheless, we argue from a physical point of view that one more situation leads to linear translocations. Fig. 4 depicts a chain conformation with a hairpin of m segments in the shallow region and only one tail with N – m segments in the deep region, which results from an insertion led by a hairpin that is too close to one of the chain ends. If m_l* < m < m_h*, the hairpin is too short for hairpin translocations but more than enough to undergo a linear one. Therefore, the conformation shown on the left of Fig. 4 leads to a linear translocation. Effectively, this consideration accounts for the fact that hairpins that are too close to chain ends lead to linear translocations.

FIGURE 4.

A hairpin entry with m_l* < m < m*_h and only one tail in the deep region leads to a linear translocation. The chain enters the shallow region as a hairpin but m does not exceed the hairpin critical insertion size m*_h. The chain end forming the hairpin has no entropic penalty to prevent itself from proceeding into the shallow region and gaining electrostatic energy. If m is larger than the linear critical insertion length m_l*, linear translocation occurs.

The probability of the hairpin conformation shown on the left of Fig. 4 is given by P_h(m, 0) from Eq. 7, that is

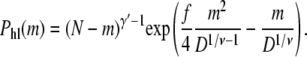(15)

This conformation will lead to a linear translocation if m_l* < m < m_h*. The total probability of hairpin-to-linear translocation is

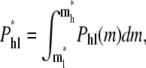(16)

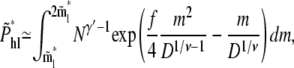(17)

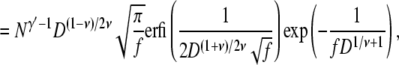(18)

where 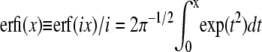is the imaginary error function. The total probability of the conformations that lead to linear translocations is then P_l* + P*_hl.

For hairpin translocations, the probability that a chain conformation leads to a hairpin translocation is

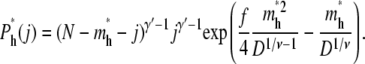(19)

For large N, it becomes

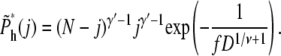(20)

Equations 7 and 13 were used in getting the above result. The value j is between 0 and N – m_h*, because there are already m_h* segments in the shallow region. The total probability of hairpin translocation is

(21)

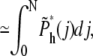(22)

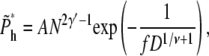(23)

where A = Γ(γ′)²/Γ(2γ′) = 1.94, and Γ(x) is the γ-function. The approximation is valid for large N.

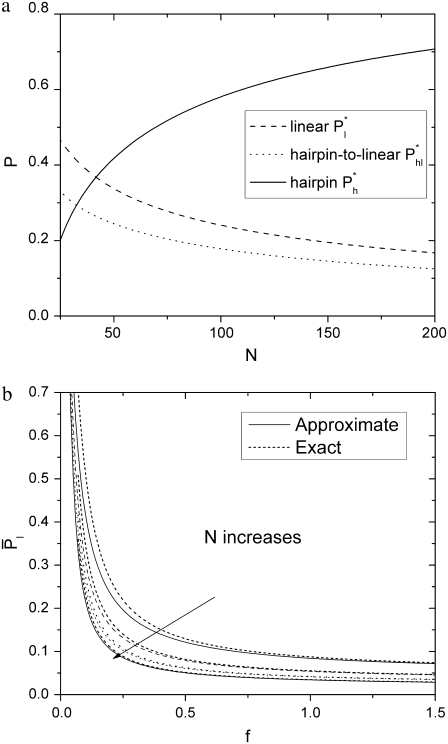
The relative probabilities of the three different entry mechanisms are shown in Fig. 5 a. Linear translocations, with probabilities P*_l and P*_hl, are favored by short chains. Hairpin translocations, with probability P*_h, dominate for long chains. In general, P*_h changes more rapidly with N compared to P*_l and P*_hl.

FIGURE 5.

(a) Relative probabilities of different translocation modes. The probability of hairpin translocation increases with N. The values D = 1.5 and f = 0.08 are used. (b) Probability of linear translocations (Eq. 24) decreases with increasing N and f. The values D = 1.5, N = 30, 60, 90, and 120 respectively. Solid lines are calculated using approximations Eqs. 14, 18, and 23. Dotted lines are calculated using exact formulas. The approximation works well for large N.

Probability of linear translocations

P*_l, P*_hl, and P*_h are relative probabilities of conformations that lead to their corresponding modes of translocation. Hence the probability of linear translocations among all translocation events is

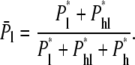(24)

Using the approximated formulas Eqs. 14, 18, and 23, 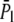is plotted in Fig. 5 b. The exact numerical results are plotted on the same graph for comparison. The exact result still neglects coefficients of O(1), due to the nature of the blob theory. From the integration that leads to Eq. 23, it is clear that long chains favor hairpin translocations simply because they have more chance of forming hairpins.

Linear and hairpin translocation times

When a polymer molecule is trapped at the end of the deep region and tries to enter the shallow region, electrostatic force, with the help of thermal fluctuations, attempts to pull segments into the shallow region against the entropic confinement until the number of segments in the shallow region exceeds the critical insertion size m*. Polymer segments may be inserted into and retracted back from the shallow region many times before a thermal fluctuation makes the translocation successful. The process can be mapped to a one-dimensional random walk under a free energy profile similar to the one shown in Fig. 3, with the initial condition m(t = 0) = 0, reflecting boundary condition at m = 0 and absorbing boundary condition at m = N (for linear translocations). The reflecting boundary condition at m = 0 accounts for the fact that whenever the last segment is retracted from the shallow region to the deep region, the whole chain would still stick to the entrance of the shallow region and try the insertion again due to the weak electric field in the deep region. The absorbing boundary condition at m = N represents the complete insertion into the shallow region. The dynamics is governed by the Fokker-Planck equation

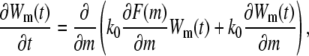(25)

where W_m(t) is the probability that there are m segments in the shallow region at time t and k₀ is a phenomenological rate constant depending on the friction between one monomer and the confined region. Applying the initial condition and boundary conditions to Eq. 25, the average translocation time into the shallow region can be written as (31,34)

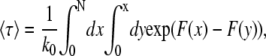(26)

which can be evaluated numerically.

If the chain spends a significant amount of time entering the shallow region, as in most experiments (3,4,18,19), the free energy barrier imposed by the shallow region is considerably larger than the thermal energy k_BT. This condition allows us to take the saddle point approximation to Eq. 26. The result is

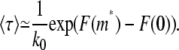(27)

This is the same as the average time needed to cross a free energy barrier in Kramer's reaction rate theory (35) and of the same form of τ₂ assumed in the previous studies (3,4,19,21). The approximation is good for the case that F(m*) – F(0) is considerably larger than k_BT, realized by low electric forces f and narrow gap heights D. Equation 27 will be used for both linear and hairpin translocation times. We take F(0) to be zero by assuming that no segments are fixed at the entrance of the shallow region. Therefore, F(m*) is the free energy barrier height for a particular free energy profile.

It is instructive to write down the free energy barriers for the two translocation modes explicitly, denoted by F* in Fig. 3. Since linear translocations can be achieved by two mechanisms, linear and hairpin-to-linear translocations as depicted in Figs. 2 a and 4, the effective free energy barrier of linear translocation is

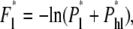(28)

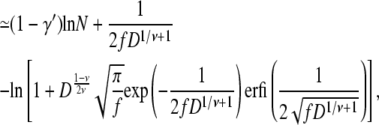(29)

where Eqs. 14 and 18 are used in the last equation, valid for large N. Similarly, the effective free energy barrier for hairpin translocation is obtained, by using Eq. 23, as

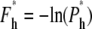(30)

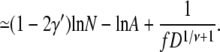(31)

From Eqs. 29 and 31, we observe that the free energy barriers are composed of two parts, one depending on N and the other depending on f and D. For hairpin translocations, the part that depends on f and D is at least twice as large as that for linear translocations. However, given that 1 – γ′ = 0.31 and 1 – 2γ′ = −0.38, the free energy barrier increases with N for linear translocations and decreases with N for hairpin translocations. As N increases, the free energy barrier for hairpin translocations can be lower than its linear counterpart and eventually can dominate the mode of translocation.

Using Eqs. 27 and 29, the average linear translocation time is

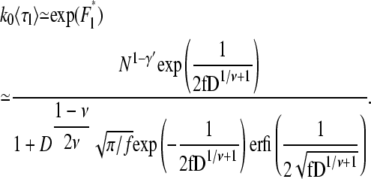(32)

Note that the linear translocation time, 〈τ_l〉 ∼ N^1–γ′ ∼ N^0.31, increases with N for self-avoiding flexible chains. Similarly, the average hairpin translocation time is

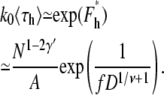(33)

Equations 27 and 31 were used. 〈τ_h〉 ∼ N^1–2γ′ ∼ N^−0.38 decreases with N for self-avoiding flexible chains.

If both linear and hairpin translocations are allowed, as in actuality, the free energy barrier is F* = −ln(P*_l + P*_hl + P*_h) and the translocation time is given by

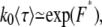(34)

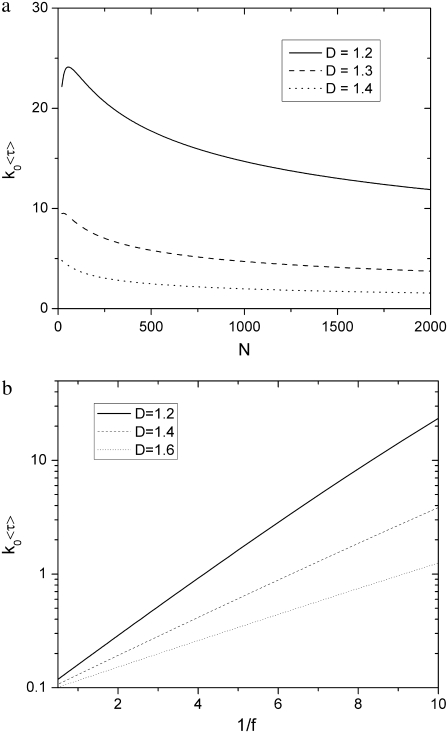
which is plotted in Fig. 6 a using exact formulas. The exact result still neglects coefficients of O(1), due to the nature of the blob theory. Indeed, Eqs. 32 and 33 can be viewed as the limiting cases of Eq. 34 for P*_l + P*_hl ≫ P*_h and P*_h ≫ P*_l + P*_hl, respectively. Equation 34 suggests that the translocation time increases with N when linear translocations dominate and decreases with N when hairpin translocations dominate. The electric field response of the translocation time is shown in Fig. 6 b.

FIGURE 6.

(a) Average translocation time 〈τ〉 exhibits a crossover from linear to hairpin translocations as N increases for D = 1.2, while this feature is missing for wider gaps. Exact formulas with f = 0.1 are used. (b) The value 〈τ〉 is a function inverse electric force 1/f with N = 100. The exact formulas are used.

DISCUSSION

We have investigated polymer translocation from a spacious region into a confined region by using equilibrium self-avoiding chain statistics. When the free energy barrier of translocation is sufficiently higher than k_BT, the linear translocation time 〈τ_l〉 ∼ N^1–γ′ exp(1/2fD^1/ν+1) ∼ N^0.31 and the hairpin translocation time 〈τ_h〉 ∼ N^1–2γ′ exp(1/fD^1/ν+1) ∼ N^−0.38. The results are valid for low electric forces f, narrow gap heights D and long chain lengths N, and are different from those predicted by previous simpler models (19,24). In our theory, the N dependence on translocation time is due to the fact that linear translocations are led by chain ends which can only happen near the two chain ends, while hairpin translocations are led by hairpins which can be formed anywhere between the two chain ends so that the number of possible hairpins increases with N. In addition, hairpin translocations are favored by wide gaps and high applied voltages.

Our result can be applied to explain the N dependence of the voltage-driven DNA translocation time in periodic microfluidic channels (3,4). Since the electrophoretic mobility is independent of N in the deep regions and the time through the shallow regions is negligibly small, the N dependence of the translocation time arises predominantly from the insertion from the deep region into the shallow region. Our major prediction is that the translocation time either decreases with N (τ ∼ N^−0.38) if hairpin-translocation dominates or increases with N (τ ∼ N^0.31) if linear-translocation dominates. These predictions are to be contrasted with Sebastian and Paul (24) where τ ∼ N⁰ and N⁻¹, respectively, for linear and hairpin translocations, and with the literature (3,4), where τ ∼ N^−0.59. Our prediction τ ∼ N^−0.38 for long chains where hairpin translocations dominate, agrees with τ ∼ N^−0.42 obtained by fitting the experimental data (4). Nevertheless, direct quantitative comparison with experimental results is difficult due to many reasons described below.

We have assumed that the deep region is much larger than the radius of gyration of the translocating polymer so that confinement effect is unimportant. In some experiments, the deep regions, although decades deeper than the shallow regions, are comparable to the size of the DNA, imposing a weak confinement to the chain (3). Furthermore, we assume that the chain behaves flexibly inside the shallow region. In reality, the height of the shallow regions may be comparable to the persistence length of DNA (3,5). In this case, confinement free energy of semiflexible chains (5,36) and bending energy of hairpins have to be taken into account. In our calculations, all surfaces are assumed to be neutral. If otherwise, the applied electric field would induce an electro-osmotic flow. Nevertheless, electro-osmotic flow was suppressed by high buffer concentrations in experiments (19). In our model, the weak electric field in the deep region and the electric field gradient at the interface between the regions are ignored, which might influence the chain statistics. We have assumed that the translocation time is much longer than the longest relaxation time of the polymer, so that the chain is in quasiequilibrium during translocation. Given that the relaxation times of the DNA used in the experiments are ∼10 ms while translocation into a shallow region happens in seconds, this assumption is justified. However, nonequilibrium dynamics is possible under high electric fields, resulting in fast translocations observed in simulations (21). Higher order translocation modes, such as double hairpins, are ignored in this theory. They serve as higher order corrections since they require a higher degree of chain deformation and are entropically unfavorable. Most importantly, the translocation time expressions are valid only when the free energy barrier is higher than k_BT. If otherwise, the translocation time cannot be approximated by Eq. 27 and the full expression Eq. 26 has to be evaluated numerically. Then the translocation coordinates of a hairpin chain, which depends on both m and j, are two-dimensional, which complicates the problem significantly. Finally, we note that there is another definition of hairpin translocation coordinates. Instead of the definition shown in Fig. 2 b, a symmetric definition of variables can be adopted such that there are m segments in the shallow region, leaving two tails of N – j – m/2 and j – m/2 segments, respectively, in the deep region. The expressions of translocation times and probabilities are more involved under this definition. Nevertheless, the results remains the same for large N, which makes the change of entropy of the tails unimportant during translocation.

The hairpin conformation shown in Fig. 2 b assumes that the two series of blobs align side by side. This idealized situation may be discouraged by the excluded volume interaction between the two series of blobs. One possible model to account for this effect is to assume that, at the expense of introducing one more parameter, the hairpin makes an angle α at the turning point so that the two series of blobs keep a distance away from each other. Then we need to substitute f → f cos(α/2) in expressions involving hairpins, such as Eqs. 7 and 9. The critical insertion length Eq. 13 measured in physical distance, however, will stay the same for large N due to the cancellation of the factor cos(α/2). Finally, additional parameters can be introduced in devising different boundary conditions in solving Eq. 25, the Fokker-Planck equation.

The main concept that arises from our present theory is that the molecular-weight dependence of the translocation time of DNA is dictated by the relative propensity of hairpin conformations versus linear conformations. If hairpin conformations dominate at the entrance to the shallow regions, the translocation time decreases with molecular weight. If linear conformations dominate, the translocation time is predicted to increase with molecular weight.