Abstract
In this review, we give an overview of recent literature on the structure and stability of unimolecular G-rich quadruplex structures that are relevant to drug design and for in vivo function. The unifying theme in this review is energetics. The thermodynamic stability of quadruplexes has not been studied in the same detail as DNA and RNA duplexes, and there are important differences in the balance of forces between these classes of folded oligonucleotides. We provide an overview of the principles of stability and where available the experimental data that report on these principles. Significant gaps in the literature have been identified, that should be filled by a systematic study of well-defined quadruplexes not only to provide the basic understanding of stability both for design purposes, but also as it relates to in vivo occurrence of quadruplexes. Techniques that are commonly applied to the determination of the structure, stability and folding are discussed in terms of information content and limitations. Quadruplex structures fold and unfold comparatively slowly, and DNA unwinding events associated with transcription and replication may be operating far from equilibrium. The kinetics of formation and resolution of quadruplexes, and methodologies are discussed in the context of stability and their possible biological occurrence.
INTRODUCTION
G-quadruplexes of repeat sequences of the kind AGnTm spontaneously fold into stable compact structures in solution, especially in the presence of K+. The resulting structures are compact, resistant to DNAses, generally have high melting temperatures, and appear to be dominated by the presence of the so-called G-quartet stacks (Figure 1). Such sequences are found in telomeres, and at a surprisingly high frequency in other parts of the genome, especially in promoters (1,2). There is now an immense literature on both the biology and physical properties of such sequences (3–6). The literature through the mid-1990s has been reviewed in a book (7). It is now believed by some that G-quadruplex oligonucleotide structures are important biological regulators, both in DNA and RNA (3–6,8–17).
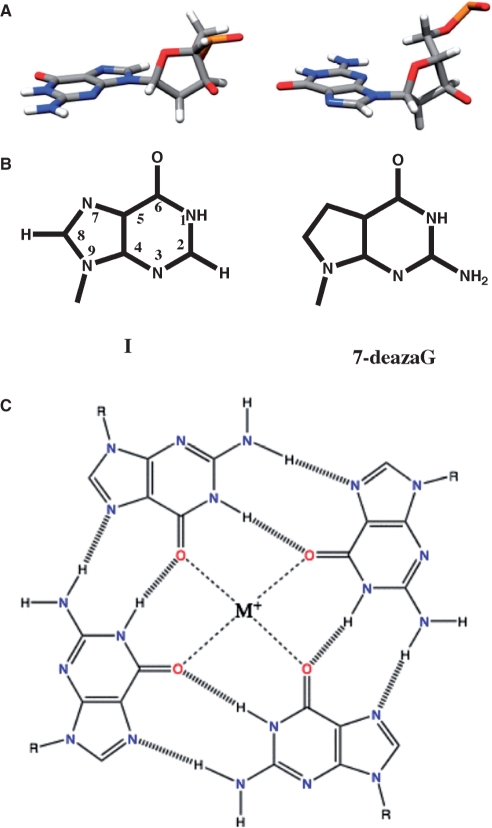
Figure 1.
Chemical structures of G-quartets and quadruplexes. (A) Anticonformation (top left) and syn conformation (top right) of guanosine. (B) Inosine (left) and 7-deazaG (right) variations. (C) G-quartet with metal ion coordination to GO6.
There have been recent reviews of G-quadruplexes, focusing mainly on the structural aspects of observed quartets (18–24) or on telomerase biology (25).
The wider interest in such structures has been highlighted by numerous sessions in international conferences (cf. ACS Pacifichem 2005 Chemical Congress, Honolulu, Hawaii, USA, and recently a 2.5 day conference ‘First International Meeting on DNA Quadruplex DNA’ held in Louisville April 2007, devoted entirely to G-quadruplex DNA). This meeting covered a wide area of topics, and was widely reported [(13); http://pubs.acs.org/cen/coverstory/85/8522cover.html]. However, that meeting did not focus on or address the problems of stability and kinetic control of the possible structures, even though this may be of great biological relevance. It has been reported that there are 26 possible topologies of G-quadruplexes, yet only a few (6) have been observed in vitro (19), raising the question of what determines the stability, whether kinetic or thermodynamic, of allowable structures? Although there is a significant literature on the stability and kinetics of quadruplex structures (26,27), the relationships between the observed stability, kinetics and structures have not been addressed recently.
The physical chemistry of G-quadruplexes is complex and fascinating. Despite a large body of published work on structure and other properties, our understanding of their basic physical properties is rather limited. Of the more than 1300 papers mentioning G-quadruplexes since the late 1980s, a modest fraction has been devoted to their physical properties. This includes more than 90 structures that have been deposited in the protein data bank (June 2008).
Even for short sequences comprising 3–4 G-quartets, it is not known what determines their structures in terms of sequence space, experimental conditions, thermodynamics and kinetics. In part, this may be attributed to the ad hoc and piecemeal individual approaches to the problem, which is sufficiently complex that it requires the concerted efforts of teams of researchers having complementary skills to analyze systematically a wide range of properties on the same set of systems, using agreed upon parameter variation. This point will be taken up further in the Discussion section.
In this review, we focus on the stability and kinetics of intramolecular quadruplexes by mining the literature for information on the stability and dynamics of such structures, the multiple conformations that are routinely observed (28–30) highlighting the empirical difficulties and any problems with design and analysis. In particular, we attempt to address the following questions regarding quadruplex formation that are directly amenable to experimental and computational methods:
What are the possible structures of G-quadruplexes?
What are the relative stabilities of such structures?
What are the likely forces (energies) that are responsible for their stability?
What determines whether these structures form in vitro?
What are the possible consequences of G-quadruplex formation?
How might in vitro understanding inform about the cellular context?
To begin to answer these questions, we will provide a brief overview of the current state of knowledge including structural data, thermodynamics and kinetics of quadruplex formation in vitro, the influence of sequences and solution conditions as well as considerations related to sample history and preparation, and relation to possible conditions in vivo such as macromolecular crowding, water activity and protein binding.
Here, we will focus mainly on the unimolecular (foldback) structures for practical reasons, namely these are the ones studied in greatest detail, are the most likely forms to exist in vivo and because the physical chemistry is much easier to analyze (structures are independent of concentration, faster and concentration independent kinetics, reversible concentration-independent thermodynamics and easier to determine detailed conformations).
The implications of these features for biological activity and design will be addressed. Finally, we propose that a consortium be established to analyze this problem systematically, using accepted standards of experimental design, and suggest the guidelines for establishing such a consortium.
QUADRUPLEX TOPOLOGIES AND STRUCTURES
There have been several excellent reviews of G-quadruplex structures published recently (18–24). J. L. Huppert maintains a website http://www.quadruplex.org/?view=quadbase including information and access to an algorithm for locating putative quadruplex sequences (PQS) in genomic data.
We provide a brief overview here for the purpose of the subsequent discussion of their properties in solution.
G-quartets are based on the formation of a (nearly) square planar array of four guanine bases, as shown in Figure 1A and B. Although the structure appears to be stabilized by a hydrogen-bonding network involving N7:N2H and O6:N1H, this is unlikely to be the source of the thermodynamic stability of such structures in the solution state (see Thermodynamics and kinetics section). Indeed, the central core of the G-quartet produces a specific geometric arrangement of lone pairs of electrons from the four GO6, which can coordinate a monovalent ion of the correct size, such as Na+ or K+. Generally, these structures do not form in the absence of such ions. The smaller Na+ ion can sit in the plane formed by these atoms, whereas the larger K+ requires a nonplanar component, which may in fact lie between two such G-quartets, as shown in Figure 2. In fact, this allows additional coordination of the metal ions, i.e. to satisfy the usual hexacoordinate stereochemistry of the alkali metal ions. In order to accommodate this stereochemistry, the individual nucleobases may dome out of the plane somewhat (31), to an extent balanced by the stacking energies (see Thermodynamics and kinetics section for more detail).
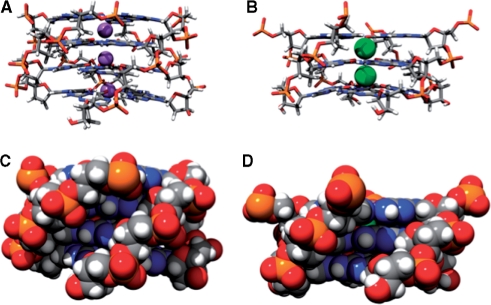
Figure 2.
Stacked quartets with coordinated monovalent ion. (A) Parallel stacked quartets with Na+ stabilization (purple spheres) from (d(TGGGGT)4), (B) parallel stacked quartets with K+ stabilization (green spheres) from (dA(GGGTTA)3GGG), (C) d(TGGGGT)4 stacking in space filling representation, (D) dA(GGGTTA)3GGG stacking in space filling representation. Loops have been removed from C and D for clarity.
Indeed, a feature of G-quadruplex structures is that they comprise a stack of two or more G-quartets, [or tetrads for those who prefer Greek roots (OED), (7)], linked by the phosphodiester backbone and stabilized by specific monovalent ion binding. In the context of a unimolecular structure, the organization of the chain direction (reading 5′ to 3′) gives rise to a large number of possible topologies.
Figure 3 displays some basic topologies. These topologies impose certain constraints in local structures including the syn/anticonformation about the glycosyl bond of the quartet quanines (Figure 1).
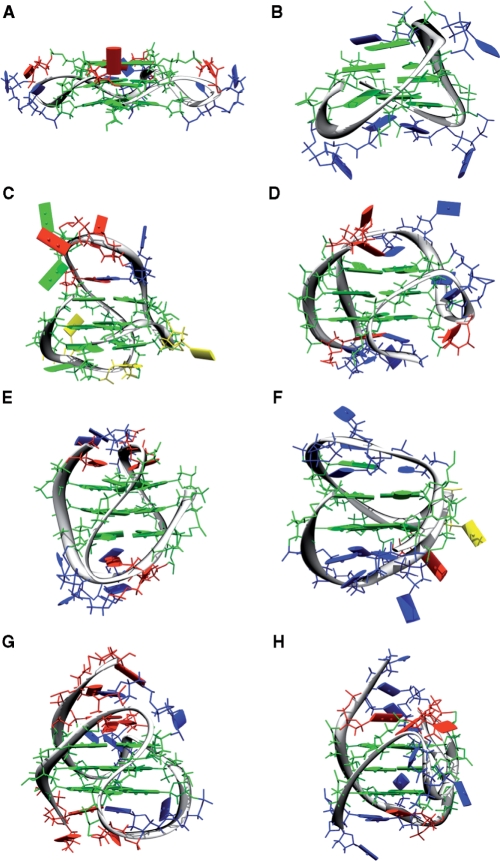
Figure 3.
Observed quadruplex topologies. (A) All ‘parallel’ double chain reversal loops (dA(GGGTTA)3GGG: K+ form) (35), (B) all lateral loops d(GGTTGGTGTGGTTGG) (36), (C) lateral, lateral, double chain reversal loops d(GGGCGCGGGAGGAATTGGGCGGG) (37), (D) double chain reversal, lateral, lateral loops d(TTA(GGGTTA)3GGGA) (38), (E) lateral, diagonal, lateral loops dA(GGGTTA)3GGG (39), (F) diagonal, double chain reversal, diagonal loops (dGGTTTTGGCAGGGTTTTGGT) (40), (G) NMR-derived hybrid 1 (dAAA(GGGTTA)3GGGAA) (41) and (H) the NMR-derived hybrid 2 (dTTA(GGGTTA)3GGGTT) (42). Guanines are shown as green, thymine as blue and adenine as red oblongs.
Overview of possible and actual structures
Even within the context of a small sequence space, the possible structural diversity of folding topologies of quadruplex structures is high (32,33). It has been reported that the total number of possible topologies is 26 different folds for molecules that comprise three loops with contiguous G-quartet strands (33). However, this does not take into account the recently reported unexpected fold of the c-kit promoter quadruplex structure (34) in which the strands contributing to the G-quartets are not contiguous. Of the original 26 folds, only six have been experimentally determined, namely the all ‘parallel’ double chain reversal loops [dA(GGGTTA)3GGG: K+ form] (35), all lateral loops d(GGTTGGTGTGGTTGG) (36), lateral, lateral, double chain reversal loops d(GGGCGCGGGAGGAATTGGGCGGG) (37), double chain reversal, lateral, lateral loops d(TTA(GGGTTA)3GGGA) (38), lateral, diagonal, lateral loops dA(GGGTTA)3GGG (39), diagonal, double chain reversal, diagonal loops d(GGTTTTGGCAGGGTTTTGGT) (40) (Figure 3) (33).
Of the 96 structures (as of May 2008), deposited in the protein databank many of them are actually similar, with the same sequences in different environments. In the case of the human telomere repeat, d(GGGTTA)n, there are 208 possible structures when the eight possible quartet orientation combinations are considered with the 26 possible folds. Experimentally, only four actual structures have been determined for the human telomere repeat; the other two topologies that have been determined were for different sequences. These are the original NMR derived basket fold from Patel [dA(GGGTTA)3GGG:Na+ form (39)], the all-parallel (double chain reversal) loop crystal structure derived fold from Parkinson and Neidle [dA(GGGTTA)3GGG: K+ form (35), the NMR-derived hybrid 1 (dAAA(GGGTTA)3GGGAA: K+ form (41)] and the NMR-derived hybrid 2 (dTTA(GGGTTA)3GGGTT: K+ form (42) folds reported by Yang and Patel (38,43) as shown in Figure 3. These represent the remarkable diversity in single-chain topology. The dA(GGGTTA)3GGG:Na+ form has loops of lateral, diagonal and lateral. The hybrid 1 has loops from the 5′ end of the double chain reversal, lateral and lateral, whereas hybrid 2 has lateral, lateral and double chain reversal loops. These represent the remarkable diversity in single-chain topology, and raise three important questions. First, how is the topology affected by the coordinating cation; second, how do the loop regions determine the topological fold; third, why have so few been observed in the laboratory—is it a lack of sequence space coverage, thermodynamics or kinetics; and fourth, to what extent is the environment, crystalline or otherwise, a suitable biological mimic? As Figure 3 shows, the different topologies vary greatly not only in the planarity and stacking of the bases in the quartets, but also in the disposition of bases in the connecting loops.
We will attempt to shed light on some of these questions in the following sections. The human telomere studies have attempted to focus on structures that may be biologically relevant. However, in all of these studies, including others on promoter regions, the sequences that have been used are short single quadruplex-forming sequences out of context with respect to the long-flanking (duplex) sequences. In most cases, single or multiple flanking bases have been added, that may or may not be part of the natural flanking base sequences, so as to obtain a single species that can be examined by NMR or X-ray crystallography. The question as to whether these modifications force the topology into something different from the original context is unknown. In reality, there may be several topologies present, or other interactions such as quadruplex-binding proteins that stabilize a particular fold and are absent present in the structural studies. However, much of this information is not available so cannot be expected to be included in the current structural studies. These considerations are discussed in greater detail below.
Why is it so difficult to force a distinct topology?
The major problem with designing sequences for specific topologies is that the loops of 1–3 bases can easily span the distance needed for a lateral or double-chain reversal loop for up to a four G-quartet stack. Typically, loops of 3–4 bases are needed for a diagonal. In the case of the human telomere repeat d(TTAGGG)n, this makes all 26 topologies theoretically accessible.
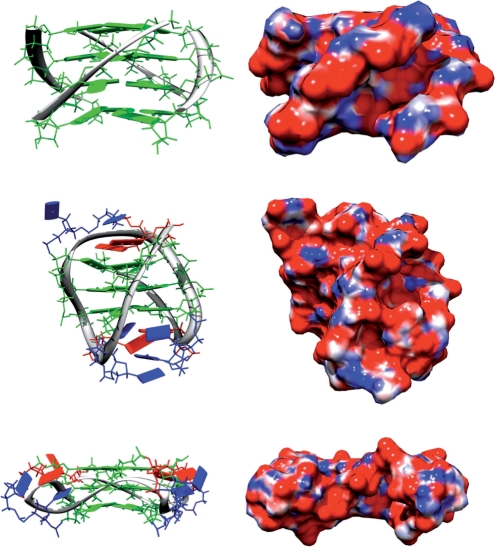
It should be noted for the all parallel high resolution (0.95 Å) crystal structure (44) d(TGGGGT)4 has the following distances: O3′ top stack to O5′ bottom stack for three G-quartet stacks is 7.3–7.9 Å: O3′ top stack to O5′ bottom stack for four G-quartet stacks is 11.1–12.2 Å, O5′ to O5′ of the adjacent same stack 14–15 Å, O3′ to O3′ of adjacent same stack 15–16 Å, O5′ to O5′ of the opposite same stack 19–21 Å, O3′ to O3′ of opposite same stack 20–22 Å (Table 1). Furthermore, the topology-dependent groove widths (Figure 1) give rise to different electronic distributions from the negatively charged phosphates. This is shown in Figure 4, which shows the space filling models colored by electrostatic potential calculated for 150 mM K+ using the Poisson–Boltzmann program APBS (45,46). These three representative structures demonstrate that shape, electrostatics and topology are intimately linked. The double chain reversal ‘propeller’ structure (Figure 3, bottom) is a flat, plate like object compared to the other topologies, which appear more globular in shape. Indeed, the propeller structure stands out among all the topologies so far solved experimentally in terms of its overall shape, groove structures and electrostatic potential, suggesting that it should have physical properties that are readily distinguishable from all of the other folds as a group (not shown). Using the APBS program, we have calculated the electrostatic energy of different conformations of the human telomere sequence d(GGGTTAGGGTTAGGGTTAGGG). The parallel form was calculated to be 2769 kcal mol−1, hybrid 1 2904 kcal mol−1, hybrid 2 2925 kcal mol−1 and basket form 2867 kcal mol−1. In order to compare the same number of nucleotides and thus atoms, the flanking bases were truncated. This shows that the electrostatic energy (essentially due too the unfavorable interactions between the closely spaced phosphodiesters) is high, and differs by up to 156 kcal mol−1 for these three conformations. For comparison the energy of an unfolded strand that was subjected to molecular dynamics and then energy minimized was 1842 kcal mol−1. Although this represents only one possible instance of an ensemble of conformations, it is expanded with respect to the folded conformations, and shows a much lower unfavorable electrostatic energy, as expected. These values imply that the folding has to overcome a rather large electrostatic energy that must be compensated by other forces. In part, this is likely to arise from ion condensation and specific ion binding, as discussed in more detail below.
Table 1.
Loop distances as defined by O3′-O5′ distancesa
| PDB Code | Sequence | Loop 1 | Loop 2 | Loop 3 |
|---|---|---|---|---|
| 143D | dA(GGGTTA)3GGG (39) type: antiparallel basket | 12.1 l | 19.7 d | 14.3 l |
| 148D | d(GGTTGGTGTGGTTGG) (36) type: antiparallel chair | 12.3 l | 13.8 l | 12.0 l |
| 1I34 | dGGTTTTGGCAG GGTTTTGGT) (40) type: hybrid | 19.0 d | 11.3 r | 20.4 d |
| 1KF1 | dA(GGGTTA)3GGG) (35) type: parallel | 10.8 r | 11.3 r | 9.7 r |
| 2HY9 | dAAA(GGGTTA)3GGGAA (41) type: hybrid | 11.1 r | 16.2 l | 11.5 l |
| 2JPZ | dTTA(GGGTTA)3GGGTT (42) type: hybrid | 15.8 l | 12.6 l | 11.9 r |
| 2F8U | d(GGGCGCGGGA GGAATTGGGCGGG) (37) | 15.8 l | 12.8 l | 6.0 r |
| 2GKU | d(TTA(GGGTTA)3GGGA) (38) type: hybrid | 11.9 r | 17.2 l | 8.8 l |
aThese are taken from the first structure in the PDB files for NMR structures, therefore are part of the ensemble of structures that satisfy the spatial constraints. l, lateral; r, double chain reversal; d, diagonal. Distances are in Å.
Figure 4.
Topologies give rise to radically different structural appearance. Structures and electrostatic potential colored surfaces of the parallel (top), ‘basket’ lateral, diagonal, lateral loop (middle) and the all double chain reversal (bottom) topologies. The electrostatic surfaces are colored red (−10 kT/e) to blue (10 kT/e) and the bases are guanine in green, thymine in blue, and adenine in red.
The conclusion is that although these are pioneering studies, there are insufficient numbers of different structures even to begin to elucidate what the rules are for obtaining the different folds. This has important consequences as techniques such as circular dichroism (CD), that are being used to examine quadruplex ‘folds’, are not definitive due to the paucity of different structures from which conclusions have been drawn (47). Some of these conclusions may well be true, but we do not currently have the data to support them fully. This point will be explored in more detail below.
Methods of determining structures
There are many approaches, both direct and indirect, to determining conformations of macromolecules at various levels of resolution. Although high-resolution structures (i.e. at or near atomic resolution) are desirable for discussing and designing experiments at the molecular level, in some instances low-resolution information can be sufficient for a particular problem, such as for fold or topology determination, or simply for quality control, i.e. verification that a particular structure is present and the purity of the structure. Here, we give a brief overview of the techniques commonly used for nucleic acids (NAs) conformational analysis, with an emphasis on the advantages and pitfalls in the quadruplex arena.
Atomic resolution
There are three main methodologies in use to assess the 3D structures of quadruplexes at atomic resolution: single crystal diffraction, which has to date provided more than 50 structures including those with bound ligands, high-resolution solution state NMR (30 structures) (24), and molecular modeling with relaxation. The highest resolution structures are obtained by X-ray diffraction, and in one case there is a sub-Å resolution structure that is a valuable resource for detailed analysis of bonding (44). NMR produces significantly poorer definition structures than crystallography. Some of this is real (dynamics, exchanging conformations) and some of it reflects the limitations of the methodology (18,19,48,49). Crystallography produces the structure of the form that actually crystallizes under the given conditions, whereas other methods in principle measure the broader ensemble properties. Nevertheless, for both NMR and X-ray studies, it is the norm to manipulate the sequences to improve the yield of crystals or to reduce the number of competing conformations that are present (and that thus interfere with, e.g. spectral and structural analysis). Generally speaking, published NMR structures have been obtained only after considerable sequence manipulations, and/or in the presence of a fairly substantial background of aggregated material (cf. higher order structures) as well as alternative conformations, which often are present at the 10% or greater level (17,28,49,50). The significance of this observation will be taken up later.
Although de novo modeling is at the mercy of the quality of force fields and how to deal with electrostatics (specific and nonspecific) (51–53), modeling does not have to worry about alternative conformations per se, and has the advantage that it deals with individual energy terms, i.e. allows parsing of terms that are not accessible to experiment (51–57). Advances in the quality of the force fields used have improved the overall quality of the calculations, though the loops remain particularly problematic (52,53,56–58). However, when combined with, for example biophysical data, reliable and valuable models of complex structures can be generated (59).
Spectroscopy
The electronic spectroscopies have long been used to characterize the structures of quadruplexes (60), as well as provide a convenient sensitive signal for monitoring transitions or ligand binding. The latter is uncontroversial. CD spectra are routinely used, along with electrophoresis, to assign folds (29,59–65). However, the interpretation of optical properties such as hypochromicity or the shape and sign of CD bands (cf. Figure 5) is controversial (47). Although the CD spectra of A-, B- and Z-DNA are quite different and have been backed by theoretical calculations (66–69), the situation with G-quadruplexes is much less clear. An empirical study that has been much cited showed CD spectra of different structures. However, the authors pointed out that there was no simple relationship between fold and shape of the CD spectrum (47). Although there have been ab initio calculations of the CD of proteins and NAs duplexes (69,70), there has been little work on the theoretical analysis of quadruplex CD. Calculations for an antiparallel DNA d(G4T4)4 (71) showed an essentially conservative CD spectrum in the range 220–320 nm with a maximum at 260 nm and a minimum at 245 nm (zero crossing at 250 nm) that only slightly resembled the experimental spectrum (whose structures were not independently verified). More recently, Gray et al. (72) have carried out calculations for two stacked quartets in which the quartets have the same or opposite polarities for hydrogen bonding (i.e. clockwise or anticlockwise cf. Figure 1). These quartets can stack such that they both have the same polarity or opposite polarity, and specifically the rotation angle between the stacks which gives rise to quite different stacking interactions, which is a major determinant of the intensity and shape of the CD spectrum, and specifically the rotation angle between the stacks. The calculated CD spectra of these two simple states are quite different. The same polarity stacks show a minimum at 235 nm, a maximum at 260 nm (zero crossing at 250 nm) and a second, broad positive band at ∼295 nm (similar to the spectrum often attributed to the parallel conformation). The opposite polarity stacks however gave an inverted spectrum with a quasi conservative spectrum having a minimum at 265 nm, a maximum at 295 nm and a zero crossing at ∼280 nm (often attributed to the antiparallel conformation (cf. Figure 5B). As the authors pointed out, the intensities of the calculated spectra seem to be substantially in error. It is our contention that until either accurate calculations can be done, in which the influence of quartet rotation, additional induced CD from looped bases are systematically accounted for or a rigorous empirical database can be generated, in which the CD spectra of quadruplex samples whose structure has been unequivocally determined on that sample under the same conditions, the interpretation of CD in structural terms is unwise as it amounts to a circular argument.
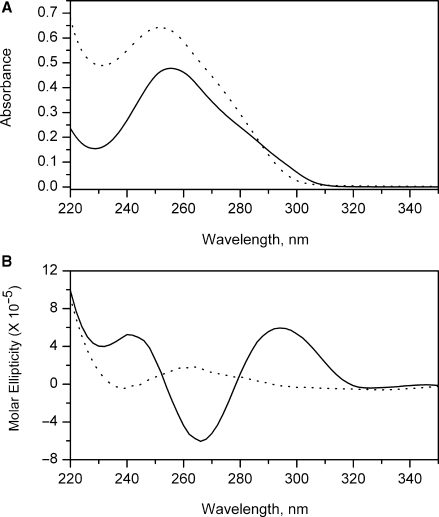
Figure 5.
Absorbance and CD spectra. UV absorbance (A) and circular dichroic (B) spectra of the human telomere quadruplex sequence 5′AGGG(TTAGGG)3 in phosphate buffer (pH 7.0) containing 200 mM NaCl. Spectra obtained at 20°C are indicated by the solid line and correspond to the fully folded quadruplex form. Spectra obtained at 95°C are indicated by the dotted line, and correspond to the denatured, unfolded form.
Use of fluorophores
The 2-aminopurine is a fluorescent base that is a common replacement for A or G and is relatively unperturbing (except in a G-quartet in this instance). This base can be incorporated during the synthesis of an oligonucleotide, and be used to report on events in or near loops for example, or as a measure of solvent exposure (61) by emission properties and the influence of externally titrated quenchers (Stern–Volmer analysis). Other fluorophores can be incorporated in loops or at the free 5′ and 3′ ends. The latter may permit more flexibility in what can be used, although aromatic groups at the ends of quadruplexes can ‘end paste’ and stabilize the structure (18,28,73).
The fluorescent properties can be used to monitor unfolding transitions, either as the quantum yield changes, shift in emission maximum or often most reliably by changes in anisotropy, with due care from the influence of temperature on the fluorescent properties. If a donor and acceptor pair can be introduced at different positions, the fluorescence resonance energy transfer (FRET) efficiency can be monitored as a function of temperature to probe thermodynamic and kinetic stability (unfolding should decrease the FRET) (74–76), though stabilization by end-pasting for example needs to be considered (18,28,73). FRET may also be used as a poor man's structural probe, i.e. by measuring several pairwise distances. In general, one would label the folded oligonucleotide to avoid influencing the final structure during refolding. This could be achieved using labels containing the maleimido group, which reacts with phosphorothioate groups that can be incorporated at any desired DNA backbone position.
This requires careful choice of donor/acceptor pairs, and due care needs to be taken to account of the orientation factor κ2. The use of 2/3 (complete orientational randomization of the emission dipole over the fluorescence lifetime) without independent evidence is not recommended. However, the fluorescence anisotropy can provide limits on the values of κ2, as described in detail many years ago (77,78). Distances between ends of various structures were provided in Figure 1 for small (three-stack) quadruplexes. FRET would have to be able to discriminate reliably between distances close to 10 Å and distances close to 20 Å. This would necessitate choosing FRET pairs with R0-values close to these distances. As the recovered distance R is R0(1 − E/E)1/6 the error in R is determined mainly by errors in R0, i.e. in (κ2)1/6. Although 0 < κ2 < 4 using a value of 2/3 means the maximum error in the upper limit is 34% (for κ2 = 4). If anisotropy measurements were able to limit κ2 to say 0.1–3 for example, the error in the distance would be <30%, which might be adequate to discriminate between some folds. Single molecule FRET has been used recently to estimate the distribution of conformational states in the human telomere sequence (30).
However, the lower end is short for FRET. A similar approach that is active over this distance range is electron spin resonance (ESR), in which the dipole–dipole interaction between two spin labels can be measured, as has been done extensively on rhodopsin for example (79,80) and more recently NAs (81).
NMR can also be used spectroscopically to assess quadruplex formation simply by measuring the exchangeable protons in the 10–12 p.p.m. range. For well-behaved, small complexes, there GN1H protons and the GNH2 protons can be counted, aided by the difference in the spectra between H2O and D2O. In G-quadruplexes, the exchange of imino protons with solvent is exceedingly slow (49) and takes days to exchange for deuterium in D2O solvent (49). This is quite unlike DNA duplexes or triple helices, where the imino protons typically exchange in seconds or minutes (49,82). The extreme kinetic stability of the imino protons is associated with low amplitude fluctuation of the quartets, which do not permit access of water or base, and further correlated with the very high thermodynamic and kinetic stability of the quadruplex structure as a whole (see below).
Patel's group and others have pioneered the use of low-level 15N enrichment in the G (83) and which has been successfully used by other groups (17). Each G is systematically substituted with a 15N-labeled nucleotide at a few percentage enrichment (the natural abundance of 15N is 0.37%). As 15N has a spin 1/2, it causes a predictable splitting of the attached N1H hydrogen due to the one bond scalar coupling. This coupling can be exploited to edit a 1H spectrum, so that only the imino proton attached to 15N (rather than 14N) is detected. This of course can provide an unequivocal assignment, as well as a count of the GN1H that are involved in hydrogen-bonding structure, and whether they are in fact in a unique environment.
H-bond donors and acceptors can also be determined with such a labeled system. This is because in NAs where H-bonding involves N–H:::N interactions, the covalent character of the H-bonds contains a scalar coupling interaction between the donor and acceptor N, which is of the order of a few hertz in Watson–Crick and Hoogsteen bases pairs, and can this be readily detected as a splitting in the NMR spectrum. This has been used to great advantage in DNA duplexes, triplexes and quadruplexes (84–91).
Hydrodynamics
Hydrodynamic techniques such as sedimentation velocity and translational diffusion measurements, as well as those techniques that supply information about the rotational diffusion (e.g. NMR) give information about molecular size/shape and hydration. For simple bodies where the departure from spherical symmetry is modest, the frictional properties can be described by (66):
| 1 |
where, Dt, Drot are the diffusion coefficients for translation and rotation, respectively, η is the solvent viscosity ah is the hydrated radius of the particle, V is the hydrated volume and Ft and Fr are asymmetry parameters that are unity for a sphere. Analytical and semi-analytical expressions exist for the dependence of F on the axial ratio for ellipsoids of revolution and cylinders (66,92–96). Thus, translational diffusion coefficients scale as the inverse of the linear dimension (cube root of mass or volume), whereas rotational diffusion scales as the inverse cube of the linear dimension. As the asymmetry increases, e.g. in the formation of ellipsoid of rotation or cylindrical symmetry, Frot deviates more quickly from unity than Ft as the axial ratio increases (66).
Although the number of parameters that can be determined is small, and they relate to global properties, it is now possible to measure hydrodynamic parameters with very high precision, even in presence of a distribution of species. Both dynamic light scattering (DLS) and sedimentation velocity experiments provide an estimate of the most probable frictional coefficient, the effective width of the particle distribution, as well as the fraction of species of significantly different size/shape. NMR, and under appropriate circumstances, fluorescence anisotropy can provide complementary rotational friction data, which when combined offer a rather critical test of the correctness of a proposed structure. This is because hydrodynamic parameters can be calculated with reasonable accuracy using bead models (97,98). If the coordinates of proposed structure are available (or of a family of structures), then the hydrodynamic properties can be calculated, and compared with the experimental values. Those models that lie well outside of the experimental values, within the limitations of the model approach itself, can be rejected. This general approach, in conjunction with other spectroscopic data, was used to demonstrate that the widely used X-ray crystal structure of the human telomere (99) is not the dominant form in free dilute solution (61).
The same approach can be used also to calculate other hydrodynamic and mechanical properties of macromolecules, including rotational diffusion constants and mass distributions such as the radius of gyration. Rotational diffusion [cf. Equation (1)] is in general more sensitive to size and shape than translation diffusion, but is often more difficult to measure. In order to compare observed and calculated hydrodynamic properties, it is necessary to know the partial specific volume (psv) of the particle under the conditions of interest, as well as the effect of a hydration layer on the frictional properties. Whereas for proteins, the simple weighted sum of tabulated psv for the constituent amino acids generally is sufficient for calculation of psv (100), there is no such approach that is accurate for NAs structures, so the value is either assumed based on a small number of published measurements for different NAs (66,101), or can be measured. For duplex DNA, the psv is typically in the range 0.55–0.58 ml/g in 100 mM KCl (101). However, the psv for quadruplex structure is not accurately known, but could be measured either from density increments (102) or by sedimentation in two or more solvents of different density [e.g. H2O versus D2O (101)]. The latter method is of lower accuracy. For a psv of ∼0.6 ml/g, an error of 1% produces an error of around 1.5% in the buoyancy terms (1 = psv.ρ). A second source of uncertainty is how to treat the hydration layer. This is discussed in detail in the publications on the programs for calculating frictional properties (97,98,103). In effect, it seems to amount to adding a monolayer of solvent to the anhydrous particle, or an increase in the radius of the diameter of an electrostricted water molecule (∼2.5–2.8 Å) (103–105). In practice, this is achieved by varying the bead size in the calculations. Clearly, such calculations need to be carefully calibrated for distinguishing small variations within a series of related structures. Additional size and shape information can be obtained by static light scattering or SAXS, such as the radius of gyration, maximum dimension and full-shape analysis using the entire scattering curve (106,107), which can reduce many of the uncertainties at a global level of analysis. Despite these limitations, hydrodynamic methods could become a very valuable means for rapidly assessing particular models and for quality control of quadruplexes to be used in any study for which the conformation(s) needs to be known.
Electrophoresis
Electrophoretic mobility is commonly used to assess the number of states present and the kinds of folded structures that may be present (62). Unlike duplex DNA, where the mobility essentially tracks according to the number of base pairs, at least for moderate length oligonucleotides, such that the size can be estimated by comparison with a ladder of known lengths, this is not true of small quadruplexes, which have a more compact structure. Electrophoretic mobility is partly a hydrodynamic phenomenon, and it also depends on the net effective charge of the molecule and the nature of the gel which determines the frictional resistance to motion (108,109). However, for DNA and RNA duplexes, as the net charge scales with the number of base pairs, calibration is straightforward, unless there are deviations from the rigid cylinder such as in for A-tract structures. As the interest here is the degree of curvature, this requires a very different calibration (110,111). Small quadruplexes do have a high formal negative charge, but many are also relatively squat (globular) compared with DNA duplexes or a DNA triplexes, making the shape and net charge distribution more difficult to estimate (but see Figure 4 for comparison of shapes and charge distributions). Furthermore, the degree of ion condensation (112,113) for such structures may be small (112–116), so that the effective charge-independent of Debye–Hückel screening may be relatively high compared with a duplex form, where the condensed fraction leaves a net charge of around 0.24 e− per phosphate (109,112,113,117). The clear exception is the propeller structure (Figure 4) which is more asymmetric, and thus the degree of ion condensation for this structure may well differ significantly from the other structures. This is considered in greater detail in Thermodynamics and kinetics section. It is notable that the structures shown in Figures 3 and 4 are mostly rather compact and appear roughly spherical, whereas the parallel propeller structure appears as a plate, and thus would impart considerably greater hydrodynamic drag than the antiparallel and mixed hybrid structures (61). Further, the electrostatic potential energy profile of these structures varies markedly, suggesting that the effective charge could be substantially different for these structures. The electrophoretic mobility under a single set of conditions is therefore not necessarily a reliable indicator of size per se, one of the things for which it is actually routinely used (59,60,62,64). Again, as for CD, due caution should be used without a reliable set of mobility markers whose structures have been verified for those particular samples.
Chemical modification
Inosine or 7-deaza-dG (Figure 1) substitution for G is expected to disrupt hydrogen bonding and therefore the stability of quadruplexes (118,119). Inosine will also decrease the H-bonding in Watson–Crick GC base pairs, whereas 7-deazadG will not. However, the rather different electronic structure of 7-deazadG indicates that H-bonding disruption can be only part of the story (57), which is in part why several substitutions have to be made to disrupt the structure (56,57,118,120–123). Although one intramolecular H-bond is lost by substitution there are also changes in the numbers of water molecules that are involved, indicating that there may be a significant entropic component (124). The effect of single or double inosine substitutions at various positions in a 22 nt the human telomeric sequence was studied in both K+ and Na+ buffers (119). For the single substitutions, the loss of stabilization free energy at 310 K ranged from 2.2 to 3.1 kcal mol−1 in K+ buffer, and from 1.4 to 2.6 kcal mol−1 in Na+ buffer with a difference on average of 0.5–2.5 kcal mol−1 for the two forms (albeit at different total concentration of cation). As the apparent enthalpy change also decreased by the substitutions, clearly interactions other than H-bonding are affected.
DMS footprinting is a commonly used technique for detecting bases involved in G-quartets [(118,125,126) others]. The N7 can be methylated if it is accessible to solvent and not involved in intramolecular hydrogen bonds, as in the classical G-quartet (Figure 1). The interpretation of the rate constant for modification however relies on assumptions about the mechanism of the reaction and what determines the chemical reactivity. This requires very careful calibration against authentic structures. As such, its main use is corroboration, in conjunction with other low-resolution techniques.
THERMODYNAMICS AND KINETICS
It is often stated that G-quadruplex structures are unusually stable, but rarely is it said with respect to what. In fact, the intramolecular quadruplexes are not thermodynamically more stable than some other intramolecular NA folds. For example, the stability of DNA duplexes of the same number of nucleotides, at 1 M strand concentrations, is of comparable stability as intramolecular quadruplexes containing three quartets (127) (and see below). Similarly, ΔG(310) of stabilization of short RNA hairpins (17 nt, loop size >5) in 100 mM salt is typically >5 kcal mol−1, (128) and much higher where the loop is of the type GNRA or UUCG (129,130). As will be shown below, for intramolecular G-quadruplex folds of ∼22 nt, the ΔG(310) of stabilization under similar salt conditions is comparable to or lower than of intramolecular DNA duplexes. However, the unfolding kinetics are very slow compared with DNA or RNA hairpin kinetics (see below).
The basic thermodynamic relationships that are relevant to quadruplex stability can be summarized as:
| 2 |
| 3 |
| 4 |
where, ΔG is the Gibbs free-energy change, T is the absolute temperature ΔH and ΔS are the enthalpy and entropy changes, respectively. For practical purposes, ΔG is equivalent to ΔA, the Helmholtz free-energy change, in condensed media. ΔCp is the change in heat capacity, which can be seen to be a more fundamental quantity than ΔH or ΔS. Equations (2–4) show how the experimentally accessible thermodynamic parameters depend on temperature. ΔH and ΔS are not independent, as measurement of ΔG, usually from an equilibrium constant [Equation (2)] and enthalpy (e.g. by calorimetry) automatically assigns ΔS. Furthermore, from Equations (3 and 4) the temperature dependence of ΔG is ΔG0 + ΔCp (T − T0) −TΔCpln(T/T0), where the superscript 0 refers to a reference temperature. A nonzero Cp implies that ΔH and ΔS respond differently to temperature. In the context of G-quadruplex unfolding, it is observed that ΔH is positive at T = Tm, which means that ΔS is also positive at this temperature. If ΔCp for unfolding is also positive, as is expected for denaturation in general, then ΔH decreases with decreasing temperature, leading to conclusion that at some sufficiently low temperature, the enthalpy change becomes zero, and also the concept of a temperature of maximum thermal stability, i.e. both cold and hot denaturation. This will be considered further in the section on measuring thermodynamic parameters, below.
The parameters may also depend on other extrinsic variables such as pressure, dielectric constant, ionic strength, etc. Variation of these latter parameters can provide information about additional molecular properties of the system, and indirectly about the forces involved in stability. For intramolecular quadruplexes (single strand), the parameters are independent of oligonucleotide concentration, whereas for multiple strands, the entropy (and thus ΔG) does depend on the deviation of the strand concentration from that in the chosen standard state, which must therefore be specified carefully.
Thermodynamic methods
Temperature variation
By far, the commonest thermodynamic variable used for characterizing NAs is temperature. If there is a difference in some signal S between the folded and unfolded states, varying the temperature will allow measurement of the transition between these states. For a simple two-state transition, F⇔U, the population of the states pf and pu will be related to the equilibrium constant as
| 5 |
In the limit that the enthalpy difference ΔH between the states is independent of temperature, the equilibrium constant is simply K(T) = K(ref)exp[ΔH/R(1/Tref − 1/T)]. Tref is an (arbitrary) reference temperature and K(ref) is the equilibrium constant at that temperature. For a pure two-state transition, the value of ΔH is the thermodynamic enthalpy difference, and is also known as the van't Hoff enthalpy. This can be derived by calculating K(T) from the melting curves (provided that proper upper and lower boundaries can be obtained), and from a plot of ln(K) versus 1/T, the slope is ΔH/R. Frequently, the observed melting curves are not so simple, in part because the optical parameters [e.g. absorbance, CD or fluorescence (74)] that are used to monitor the transition are themselves temperature dependent, or the transition is not two-state, which can give rise to baselines that are not flat (see below). This is difficult to distinguish from temperature effects on the molecular system itself, such as low enthalpy transitions at lower temperature, or because ΔH is not actually independent of temperature [cf. Equation (3)]. In fact, there is no good reason a priori to believe that the heat capacity of such systems is the same in the folded and unfolded states, nor that the heat capacity in these states is independent of temperature (117,131). This is a complication to which we will return. It is common therefore to use the temperature at which the transition is 50% complete, i.e. Tm (the melting temperature). The Tm value has the advantage that it is the most precisely determined melting parameter (see below). It is usually determined from the derivative of the transition curve with respect to temperature, which can under some circumstances lead to an error such as when the cooperativity is low (132,133). However, it is often inappropriately used as a surrogate for thermodynamic stability. Where comparisons are to be made between systems, the relevant thermodynamic parameter is ΔG at a chosen reference temperature, such as 298 K or 310 K. For an intramolecular system, the relationship between the thermodynamic parameters is simple [Equations (2–4)]. At T = Tm K = 1 and thus ΔG = 0. ΔH can also be determined by curve fitting. It is easy to calculate ΔG at any other temperature, i.e. as
| 6 |
for ΔCp ≠ 0, the correction becomes: ΔG(T) = ΔH· T(1/Tm − 1/T) [ΔH0 + ΔCp(T − Tm)]
Equation (6) shows that in fact the free-energy change at the desired temperature is proportional to ΔH and to the increase of Tm. Tm thus is related to ΔH and ΔG(310) as Tm = 310. ΔH/[ΔH − ΔG(310)]. It also shows that Tm is not a linear function of ΔH, although over a sufficiently narrow range it may appear so (62). This in fact demonstrates the simpler thermodynamics of a unimolecular system, where Tm = ΔH/ΔS. However, measurements of Tm are useful for additional thermodynamic analysis, as the variation with respect to salt concentration, water activity, etc. can be analyzed (see below).
It should be noted that ΔH obtained from a van't Hoff analysis is not always equal to the true (calorimetric) ΔH in these systems (134), and can be in error by more than a factor of 2. Clearly, any attempt to establish a common reference temperature under these conditions is suspect. This is related to a combination of the presence of multiple conformations, and the slow folding kinetics which can lead to technical difficulties in measuring equilibrium thermodynamic quantities, as described below.
Thermal denaturation monitored by spectroscopic methods
Spectroscopic methods for monitoring melting rely on there being a distinct difference in spectroscopic properties between the folded and unfolded states, and that there is (preferably) a linear dependence of the signal on concentration, i.e. the Beer–Lambert law holds, i.e. S = σ.c, where c is the concentration and σ is the specific spectroscopic response, such as an absorption coefficient. This is not obeyed when there are aggregation events for example, or for instrumental reasons (e.g. stray light). The latter does not affect NMR however.
Thermal denaturation (‘melting’) of G-quadruplex structures is accompanied by distinctive changes in UV absorbance or circular dichroic spectra, as shown in Figure 5. These changes provide a convenient window for monitoring denaturation, and entry into the thermodynamics of the denaturation process. Several reviews that describe these methods and the subsequent analysis of the data have appeared (135–139). Labeling of G-quadruplex forming oligonucleotides with either fluorescent base analogs or with suitable acceptor–donor FRET pairs allows monitoring the denaturation process by fluorescence spectroscopy, with greatly improved sensitivity (139) (and see Quadruplex topologies and structures section above). Because of the availability of these excellent reviews, we will not review these methods in detail again here, but rather will limit our discussion to some problems and pitfalls that are perhaps not commonly recognized and which were not emphasized before.
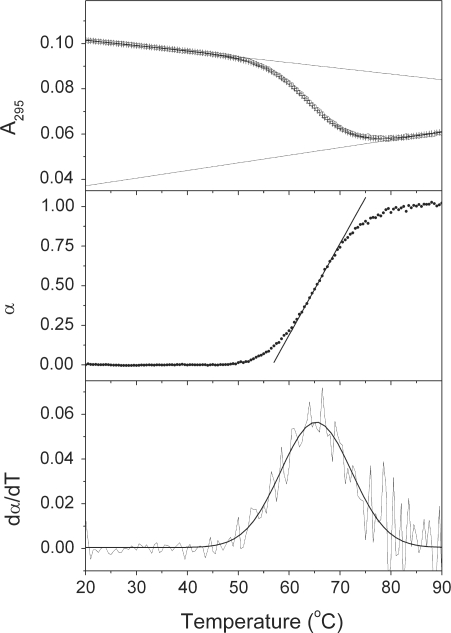
Monitoring any of these spectroscopic signals as a function of temperature provides a denaturation transition curve (‘melting curve’), which contains thermodynamic information. Figure 6 shows examples of such transition curves transformed in a variety of ways. Figure 6A shows raw absorbance data collected at 295 nm, a wavelength particularly sensitive to disruption of G-quadruplexes (138). Figure 6B shows the same data after transformation and normalization to show the fraction denatured (α) as a function of temperature. The first derivative of the transition curve in panel B is shown in Figure 6C. This is a common approach to directly estimating the Tm of a transition, and also for enhancing the detection of multiple intermediates that differ in their Tm-values. Specific analytical equations are available for extracting thermodynamic parameters from each of these curves are available, as is described in detail in (135,136). Application of these equations yield a thermodynamic profile for the denaturation process that includes the free-energy change (ΔG), the enthalpy change (ΔH) and the entropy change (ΔS). In principle, but rarely in practice, the change in heat capacity [ΔCp, cf. Equation (3)] might also be obtained from thermal denaturation curves. There are, however, numerous potential pitfalls in reliably obtaining these thermodynamic parameters.
Figure 6.
Thermal unfolding curves for the human intramolecular quadruplex. Transition curves for the denaturation of the Na+ form of the human telomere quadruplex sequence 5′AGGG(TTAGGG)3 in phosphate buffer (pH 7.0) containing 200 mM NaCl. (A) Absorbance at 295 nm versus temperature. The lines were calculated to fit the pre- and post-transition baselines. (B) Fraction of unfolded molecules (α) versus temperature after correction of the data in panel (A) for the sloping baselines and normalization. The straight line indicates the slope at the transition midpoint. (C) First derivative of the data in panel (B).
The first pitfall is the difficulty in establishing reliable pre- and post-transition baselines. Any transformation of the primary data or any attempt to directly analyze the primary data by curve fitting must include choices concerning these baselines. As is seen in Figure 5A, these baselines often slope to a significant degree. Such slopes may arise from intrinsic physical phenomenon, such as the intrinsic temperature dependence of fluorescence or from absorbance changes resulting from solvent expansion. More insidiously, though, such slopes could arise from additional reactions that complicate the study of the denaturation transition. As one example, pretransition melting reactions are common (140). These may involve thermally driven processes like helix–helix transition or single-strand base unstacking that precede the actual helix melting transition. Such transitions may have small enthalpy values, leading to broad, featureless melting transitions. Attempts to ‘correct’ sloping baselines that arise from such complications would lead to an oversimplification of the true reaction mechanism, and to a loss of information. Even in the absence of such complications, baselines present practical problems. There are disturbing reports that document that the lengths of the pre- and post-transition baselines selected and used in data analysis directly affect the values of the thermodynamic parameters extracted from the data (141–144). Investigators of G-quadruplex denaturation should be fully aware of these difficulties, and should describe in detail their procedures for establishing baselines for analysis.
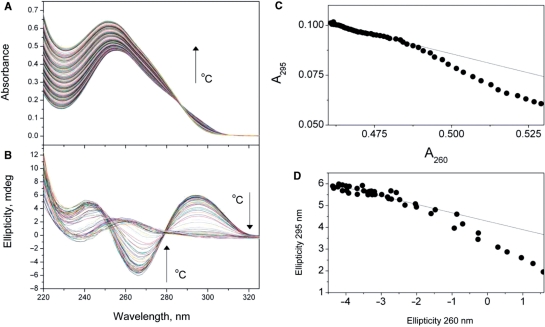
A second pitfall is the common assumption that denaturation reactions are simple two-state processes, and simply pass from a folded ‘native’ state to an unfolded denatured state without any intermediates. The two-state assumption must be justified by some experimental test. A classical test, first utilized for protein denaturation studies, is to obtain denaturation curves by two (or more) different physical methods (144). If transition curves obtained by the multiple methods are exactly superimposable, that is consistent with a two-state mechanism. More recent tests utilizing multiple wavelength data have appeared. A dual- wavelength parametric test for a two-state denaturation transition monitored by spectroscopy was described (145). In this test, data obtained at two different wavelengths are plotted against one another. For a two-state transition, such a plot should be strictly linear. Deviations from strict linear behavior signal that the denaturation process is not two-state, and likely has intermediate states that are significantly populated. Singular value decomposition (SVD) provides an additional test of the two-state assumption (146,147). With modern diode array spectrophotometers, it is easy to collect entire spectra as a function of temperature, instead of single wavelength data. A set of spectra as a function of temperature defines a 3D surface that is easily converted to a matrix. SVD of the matrix rigorously enumerates the number significant spectral species required to account for the spectral changes. For a two-state transition, there should be only two significant spectral species, corresponding to the folded and unfolded forms. Any number of species greater than two indicates a violation of the two-state assumption, and signals the presence of intermediates. SVD (or a similar multivariate analysis method) has been used to characterize the denaturation of G-quadruplex or other four-stranded structures (148,149). Figure 7 shows examples of whole-spectra UV and CD melting data, and the two-wavelength test of the two-state assumption for the thermal denaturation of the human telomere quadruplex in Na+ solution. For both UV and CD datasets, there are clear deviations from strict linearity, a sure indication that the denaturation reaction is not a simple two-state process, and that intermediate states are populated to a significant degree and must be included in any reaction mechanism. SVD analysis cannot be illustrated in a simple way, but the details of such an analysis are illustrated in refs (59,146,149).
Figure 7.
Whole-spectra melting data and the test of the two-state assumption. Thermal denaturation of the human telomere quadruplex sequence 5′AGGG(TTAGGG)3 in a solution containing 0.185 M NaCl is shown as monitored by UV absorbance (A) or CD (B). The corresponding two-wavelength parametric plots to test the two-state assumption (144) are shown in (C and D). The nonlearity of the the data in panels C and D indicate that the denaturation of the quadruplex is not a simple two-state process, and the intermediate states must be included in the reaction mechanism.
As alluded to above, another pitfall is the neglect of heat capacity changes (ΔCp) that may accompany quadruplex denaturation. Heat capacity changes are correlated with exposure of hydrophobic surface areas (150,151) as well as increasing fluctuations among microstates associated with the less compact forms (117), so it would be surprising indeed if the unfolding of quadruplex structures, with the concomitant exposures of the bases, was not accompanied by a nonzero ΔCp value. Unfortunately, it is enormously difficult to fit reliably transition curves to obtain derivative values of the primary thermodynamic parameters (143). Small heat capacity changes could manifest themselves as contributors to sloping baselines, and might easily be ‘corrected out’ at the expense of systematic errors in enthalpy values. Even if data such as shown in Figure 6 are further transformed to construct a van't Hoff plot of ln K versus T−1, problems remain. Nonzero ΔCp values should lead to curvature in the van't Hoff plot. However, Monte Carlo simulations of van't plots showed that for ‘small’ (<|200| cal mol−1 deg−1) ΔCp values, which is of order observed for NA unfolding (see below), no curvature could in fact be observed within the typical error of experimental data, but that slopes were systematically biased away from true enthalpy values (152). Much larger ΔCp values, however, would be expected to become manifest especially by calorimetric methods.
There is little that can be done to overcome these pitfalls in the analysis of spectroscopic transitions curves, but these difficulties must be acknowledged. Calorimetry offers another tool that may overcome at least some of the problems.
Calorimetric melting (differential scanning calorimetry)
Differential scanning calorimetry (DSC) (19,20), in which differential heat capacity is measured as a function of temperature, offers a method for measuring the thermodynamics of G-quadruplex denaturation as directly as possible. The advantage of calorimetry is that total denaturation enthalpy values can be measured without recourse to any curve fitting or assumed models. Model-free calorimetric enthalpy values can thus be obtained directly from the primary data. In addition, calorimetric thermograms can also be fit to particular thermodynamic model. Comparison of the model-free calorimetric enthalpies with such calculated model dependent enthalpies provides additional insight into the denaturation process, and in particular provides quantitative information about the cooperativity of the melting or the presence of intermediate states. Haq et al. (153) have provided a practical guide for the use of DSC for the study of the stability of multistranded DNA structures.
DSC studies are also plagued by baseline uncertainties. Processing of DSC data involves two types of baseline corrections. The first is subtraction of independently measured buffer baselines to correct for instrumental variances over the temperature range study. This correction is straightforward and poses no difficulties. The second baseline correction involves choices similar to those discussed above, although in this case it is heat effects that contribute to baseline slopes and nonlinearities. Even though calorimetry represents the gold standard for denaturation studies, it is not entirely without it own uncertainties, and investigators should describe and justify fully the choices that were made in baseline corrections.
Some representative results
Table 2 shows some representative results for denaturation studies of the human telomere quadruplex structure obtained by van't Hoff analysis of spectroscopic data. Data were selected for similar cation concentrations. The results are not comforting. Enthalpy estimates for the denaturation of the Na+ form of the quadruplex range from 38.0 to 72.7 kcal mol−1, nearly a 2-fold difference. For the K+ form, enthalpy values range from 49.0 to 77.5 kcal mol−1. Even worse, the free-energy change at 310 K varies from the marginally stable (0.9 kcal mol−1) to the very stable (7.3 kcal mol−1), which is attributable most likely in the errors in the enthalpy, as Tm values are expected to be rather accurate. These differences are unacceptably large, and the origins of the differences are by no means clear. The sequences used in these studies differed slightly, but it is difficult to believe that nucleotide end effects could exert such an enormous influence. These data point to the need for additional studies to reduce the uncertainty in thermodynamic parameters.
Table 2.
Energetics of human telomere quadruplex unfolding
| Sequence | Cation | Tm°C | ΔH kcal mol−1 | ΔS cal mol-K−1 | ΔG(310K) kcal mol−1 | Reference |
|---|---|---|---|---|---|---|
| 1. 5′-(TTAGGG)4 | 70 mM Na+ | 49 | 38.0 | 119 | 1.4 | (154) |
| 70 mM K+ | 63 | 49.0 | 147 | 3.8 | ||
| 2. 5′-AGGG(TTAGGG)3 | 100 mM Na+ | 56 | 54.0 | 163 | 3.1 | (138) |
| 100 mM K+ | 63 | 57.0 | 169 | 4.4 | ||
| 5′-TTAAGGG(TTAGGG)3 | 100 mM Na+ | 44 | 38.5 | 121 | 0.9 | |
| 100 mM K+ | 55 | 63 | 193 | 3.5 | ||
| 3. 5′-GGG(TTAGGG)3 | 100 mM Na+ | 63.7 | 72.7 | 192 | 5.8 | (155) |
| 100 mM K+ | 69.3 | 77.5 | 202 | 7.3 | ||
| 4. 5′-AGGG(TTAGGG)3a | 100 mM Na+ | 42.8 | 51.4 | 153 | 0.9 | (156) |
| 100 mM K+ | 61.8 | 66.2 | 186.5 | 4.9 |
ΔH, ΔS and ΔG are for the unfolding direction.
aFluorescently labeled on 5′ and 3′ ends.
A detailed spectroscopic and calorimetric study of the stability of the K+ form of the human telomere quadruplex sequence (TTAGGG)4 was recently reported (157). SVD was used to analyze temperature dependent circular dichroic spectra and to show that quadruplex denaturation was not a simple two-state process. At least three species, corresponding to the folded, unfolded and one intermediate, were required in the reaction mechanism. DSC thermograms clearly showed two transitions. The total calorimetric enthalpy for the overall denaturation process was dependent on KCl concentration, and varied from 32.1 kcal mol−1 at 100 mM to 36.3 kcal mol−1 at 400 mM. Heat capacity changes, Δ Cp, were not evident in the DSC data, but may have been difficult to detect because of the complexity of the reaction and the difficulties in selecting reliable baselines. This study clearly indicates, at the least, that quadruplex denaturation is more complicated than was assumed in the studies shown in Table 2, and that intermediate states are significantly populated along the denaturation pathway.
Isothermal titration calorimetry (ITC) is most commonly used for binding studies, but a recent novel application used the method to study the enthalpy of G-quadruplex folding (158). In this application, unstructured oligonucleotides were mixed with excess monovalent cation solutions in the calorimeter to monitor the total enthalpy of folding (which includes any contribution from specific ion binding, see below). By repeating the experiment at several temperatures, heat capacity changes could be estimated. The remarkable result was that apparent Δ Cp values, approaching 1 kcal mol−1 (159) and larger were observed. Such a large heat capacity difference, comparable to that observed in small proteins (151,160), would give rise to a large step in the DSC profile, which is not observed, and also imply cold denaturation at modest temperatures. For example, for a quadruplex that melts with a Tm value of 333 K and an enthalpy change at the temperature of 50 kcal mol−1 (cf. Table 2), then over the normal accessible temperature range from 273 K to 373 K, the enthalpy would change 10 kcal mol−1 for Δ Cp = 0.1 kcal mol−1 K−1 and 100 kcal mol−1 for ΔCp = 1 kcal mol−1 K−1, with a change in sign at 283 K. For the latter case, the temperature of maximum stability would be 286.5 K when ΔG would be 3.4 kcal mol−1 less stable than if ΔCp were zero.
In contrast, for short oligonucleotides, ΔCp is of the order 80 cal.mol−1 K (131,161–163) and higher for multistrand structures (117). A large ΔCp may be associated with residual structure in the unfolded ensemble (and see below).
Multiple conformations
Numerous structures can form in vitro (63) depending on the conditions, and may coexist. If multiple conformations are possible, then they will form. The question is one of populations. Many of the NMR analyses of quadruplexes have shown the existence of significant populations of alternative species (18,28,29,50), and they have been detected or assumed to be present by other spectroscopic or thermodynamic approaches (30,62,134,164–166).
As described above, multiple states can be detected at equilibrium even where there is substantial cooperativity, where the states become substantially populated, or a wide range of probes is used. If multiple conformations exist on a folding/unfolding pathway, they can be detected if they have significant populations and their properties become distinguishable. For example, the UV-melting at a fixed wavelength may appear multiphasic (167) in which case a fitting procedure according to an unfolding model is straightforward (see below). If two alternative folds exist via a common precursor, or there is a mixture of independently folded states only kinetics are needed to resolve the ambiguity (see below) [N1⇔D + N2⇔D ≠ N2⇔I⇔D, etc.]. Within the context of a spectroscopic melting study, these two models differ as follows:
N1⇔D + N2⇔D (two folded conformations in equilibrium with the unfolded state)
| 7 |
Allowing interconversion between N1 and N2 has no effect because there are only two degrees of freedom in this scheme. The populations of the species are given by:
where, D = K1K2 + K1 + K2 and thus n1/n2 = K2/K1,
ΔS is the change in signal during an unfolding transition, Δσ is the specific signal difference (e.g. absorption coefficient difference between state I and the end state) and K1, K2 are the unfolding equilibrium constants This model specifically indicates that with coexistent states N1 and N2 that melt with different Tm-values, will show that the population of the more stable structure will first increase (as the less stable structure melts) before eventually declining to zero.
| 8 |
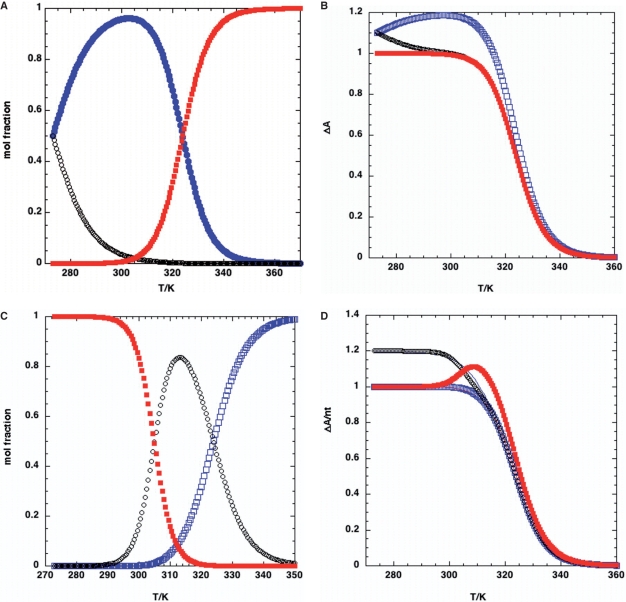
These models differ in that the initial (native) points have in principle distinguishable properties. Model 1 starts with a mixture of states that independently evolve toward the common end state, whereas model 2 implies that the two states present at low T (i.e. N and I, populations determined by K2 at sufficiently low temperature for example) evolves through the intermediate state I. This is why although the same number of states is involved in the two mechanisms, the unfolding behavior may be different depending on the specific values of the equilibrium constants, their enthalpy differences and the values of Δσ. Figure 8 shows a simple simulated comparison of an optical unfolding experiment in which there is an unfolded ensemble at high temperature, and a folded ensemble at low temperature. The two models differ in the folded ensemble. The first model posits two alternative conformations that do not interconvert directly on any realistic experimental timescale (they interconvert exclusively through the unfolded state). The second model posits a sequential pathway with a fully native fold proceeding to the unfolded ensemble via an obligatory intermediate. The relative populations of N1 and N2 are determined by the ratio K2/K1. In this simulation, these have been made equal at low temperature. At low T, the distributions of I and N are determined by the equilibrium constant between them. Depending on the assumptions, the denaturation curve may appear either monophasic or biphasic. The simulated curves were fitted to the equation for a single transition, i.e. three parameters, assuming that the heat capacity difference between states is zero. All curves in this instance are well represented by a single transition, but the recovered enthalpies did not match the input values. For biphasic curves, of course one would fit a two-state transition of some kind for which the parameters would be better defined, assuming the correct model were chosen (sic).
Figure 8.
Thermal profiles for two folding pathways. The populations of states in two possible pathways as described in the text was calculated. Model (i) Two species connected by unfolded state: N1⇔D + N2 ⇔ D. The reference temperature, Tref = 273 K. The equilibrium constant K0 for unfolding at 273 K = 1E − 5. The unfolding enthalpies were Δ H1 (N1) = 40 kcal mol−1, Δ H2(N2) = 60 kcal mol−1. For these parameters, Tm1 = 324 K Tm2 = 305 K. (A) Populations as a function of temperature. Red square: state D; open black circles: state N2; filled blue circles: state N1. (B) Changes in absorbance as a function of temperature for εN1 = εN2 (filled red squares), εN1 = 1.2, εN2 = 1 (open blue squares) and εN1 = 1, εN2 = 1.2 (open black circles). Best fit to a single transition with εN1 = εN2: ΔH = 40 kcal mol−1; K0 = 9.7 E−6 at 273 K; Tm = 324 K. Model (ii) sequential unfolding N ⇔ K1 I ⇔ K2 K1 = K2 = 1E−5 at 273 K, Δ H1 = 30 kcal mol−1, Δ H2 = 20 kcal mol−1. For these parameters, Tm1 = 305 K, Tm2 = 324 K. (C) Populations of N (red squares), I (black circles) and U (blue squares). The populations of N and I are equal at 305 K, and N is dominant at low temperature. (D) Thermal melting profile using the populations in C, and difference absorption coefficients of (a) ΔεN = ΔεI = 1 (blue squares) (b) ΔεN = 1.2 ΔεI = 1 (black circles); (c) ΔεN = 1 ΔεI = 1.2 (blue squares). The fits for conditions a and b to a single folding transition are shown as thin continuous lines, and the recovered parameter values were: (A) K(273) = 8.7 E−6, ΔH = 40.5 ± 0.07 kcal mol−1, Δε = 1.0, R2 = 0.99997. (B) K(273) = 1.68 E−4; ΔH = 31.6 ± 0.3 kcal mol−1, Δε = 1.19, R2 = 0.99895. Parameter estimates are thus unreliable if the wrong model is used, even where the data appear as a simple transition.
Model 1 corresponds to the situation described by Olsen et al. (134). In fact, these considerations suggest approaches to producing states enriched in one or other structure. Not only is the rate of cooling important (62), but also the final temperatures may determine the distribution of structures present. This is determined largely by the enthalpy difference between the native folds.
Treating the observations as a single transition (a common assumption) yields unreliable thermodynamic parameters, as well as giving a false view of the unfolding process. In principle, multiple wavelength observations (i.e. if the spectra of all states differ) can define the minimal number of states (a single wavelength is an inadequate test), especially when combined with a formal analytical technique that deals with the large datasets ensuing from a spectral decomposition of an unfolding experiment. Programs using SVD for example are well suited to this kind of analysis (64) and see above.
Given these considerations, it is germane to question the meaning of some of the reported thermodynamic analyses.
Kinetics of formation and dissociation of quadruplexes
There are two major reasons for determining the kinetics of formation and dissociation of quadruplexes. The first is that it is the only unambiguous means to obtain information about the mechanism of a complex reaction pathway. As described above, under equilibrium conditions, it is not possible to discriminate among different pathways that connect initial and final states, and only detect intermediates if they become sufficiently populated with respect to the analytical techniques available. The second major reason for measuring kinetics is to discover the general timescale of events, how they are modulated by conditions and additional factors such as small molecule ligands or possible binding proteins, to discover whether they are in fact commensurate with relevant biological time scales.
Kinetics methods
The kinetics of G-quadruplex folding can be broadly divided into three types depending on the number of individual polynucleotide molecules contributing the quadruplex: unimolecular, bimolecular or tetramolecular. The kinetics of these processes has been comprehensively reviewed recently (168). Generally, formation of bimolecular and tetramolecular quadruplexes is sufficiently slow at micromolar oligonucleotide concentration and physiological temperature that the progress of the reaction can readily be followed by conventional techniques.
Slow mixing
Han et al. (169) found by electrophoretic assays that formation of a bimolecular quadruplex for an oligonucleotide with tandem repeats of the human telomere sequence follows a second-order kinetics with k = 0.003 M−1 s−1 at room temperature (i.e. 3 × 10−9 s−1 at 1 μM or a half life of over 7 years), while Wyatt et al. (170) demonstrated by gel filtration that the sequence d[TTGGGGTT] forms a parallel stranded tetrameric structure in a fourth-order process (k = 1.6 × 104 M−3 s−1). To emphasize the slow progress and high molecularity of this reaction, these authors pointed out that at 100 µM strand concentration and room temperature, the amount of tetraplex formed over a 2-day period was undetectable, while at 200 µM oligonucleotide, the half-time for tetramer formation was about 700 min at 22°C in 100 mM K+ solutions. Their studies indicated that the rate-limiting step in tetrameric quadruplex formation is a slow association of a pair of dimers that exist in relatively rapid equilibrium with single-stranded monomers. Additional studies indicated that the dissociation rate constant for the tetramer is ∼8 × 10−6 s−1 (t1/2 = 59 days) at 37°C.
Analysis of thermal hysteresis
If the rate of heating or cooling is faster than the rates of interconversion between the folded and unfolded states, then the folding or unfolding lags behind, leading to noncoincident heating and cooling curves. This has been observed even in intramolecular quadruplex melting, especially at low salt concentrations, and makes thermodynamic analysis very difficult (62,75,171). The kinetics of association and dissociation of multimeric quadruplexes have been extensively studied by Mergny's laboratory using this approach. This group utilized detailed analysis of the thermal hysteresis in nonequilibrium melting profiles (results are summarized in reference (168)). This approach is capable in principle of giving both the association and dissociation rate constants as well as the apparent activation energies of both steps. As summarized in Mergny's review article (168), tetramolecular quadruplex association reactions generally exhibit negative apparent activation energies. Negative apparent activation energies or nonlinear Arrhenius plots are commonly observed in protein and NA folding and can result from any of several effects including (i) a temperature-induced change in the rate-limiting step(s); (ii) a change the heat capacity of the activated complex; or (iii) a temperature-induced change the ground state of the reaction (172,173). The kinetics of association were found to be generally faster in K+ compared to Na+ by 20- to 50-fold. Since the dissociation kinetics were largely unaffected by ion concentration, the authors surmised that the well-known stabilizing effect of K+ compared to Na+ (and see subsequent section) was due to an increase in the association rate constant.
The kinetics of intramolecular folding and unfolding of G-quadruplexes is of interest because these studies can suggest possible folding pathways that involve rearrangements in secondary and tertiary structure that are necessarily obscured by the slow kinetics of multimolecular association processes. The kinetics and mechanism of intramolecular folding processes including formation of simple structures such as hairpins as well as folding of more complex topologies such as ribozymes, Holliday junctions and riboswitches (174).
Intramolecular oligonucleotide folding has been investigated by a number of spectroscopic techniques that track different aspects of the dynamics of the folding–unfolding transitions. Among these are multi-wavelength UV spectroscopy, changes in fluorescence emission of appropriately labeled oligonucleotides, FRET (see above) studies, and solid phase methods such as surface plasmon resonance (SPR).
The method of single-molecule FRET has recently been utilized by two groups to assess the kinetics of G-quadruplex folding and unfolding (and see Quadruplex topologies and structures section). As applied to G-quadruplexes, this method relies on the use of a ‘tiny telomere’ construct (59) in which a single-stranded telomeric sequence of interest is linked to a DNA duplex at the 3′ end. Typically, the 5′ end of the telomeric sequence is tagged with a fluorescence donor (such as Cy5) and an acceptor (such as tetramethylrhodamine) is attached to the duplex at a location such that the efficiency of Förster energy transfer from donor acceptor changes by a measurable amount when the quadruplex structure forms. In the systems studied so far, transfer efficiencies ranging from 5% to 70% have been observed during folding/unfolding processes. FRET can either be monitored in solution (yielding the average properties of the ensemble under a set of defined conditions) or with a confocal microscope and suitable optics. With the latter system, quite low (e.g. picomolar) oligonucleotide concentrations are used which allows observation of single molecules. One counts the number of molecules within a particular small range of transfer efficiencies and constructs a histogram of the distribution of molecules with different transfer efficiencies. This serves as a convenient indicator of the distribution of conformational states (30).
Ying et al. (175) studied the human telomere sequence with an additional 5′-G, by single molecule spectroscopy. In summary, they found two stable folded conformations in both Na+ and K+ solutions. At low Na+ (10 mM), they observed a species characterized by higher FRET efficiency (0.85) and another with a lower efficiency (0.35). Addition of K+ (10 mM) increased the fraction of the species with the higher transfer efficiency. Analysis of the temperature dependence of interconversion of the two populations allowed estimation of the thermodynamic parameters for each species in the presence of the two cations. In 100 mM NaCl, ΔH = −7.3 kcal mol−1 and ΔS = −25 e.u., whereas in 100 mM KCl, the thermodynamic parameters were found to be 3.6 kcal mol−1 and 10 e.u. The kinetics of unfolding was assessed by trapping the unfolded species with the complementary oligonucleotide. At pH 7.4 in 10 mM Tris–HCl, 100 mM NaCl, the two species disappeared at approximately the same rate (τ = ∼740 s at 20°C and ∼180 s at 37°C). Based on the analysis of the distance dependence of the FRET efficiencies in conjunction with model building, the authors suggested that one conformation is the parallel structure and the other is the antiparallel structure. This again points to the prevalence of multiple conformations originating from the same sequence, which are condition and history dependent (and see above).
In a more recent study, single-molecule FRET (176) was used to explore the dynamics of K+-driven folding of individual oligonucleotide molecules modeling the human telomeric sequence. A 5′-acceptor labeled oligonucleotide mimicking the human telomeric sequence (5′-Cy5-(GGGTTA)3GGG) was linked to a 29-nt stem containing a 3′-biotin for immobilization the oligonucleotide to a streptavidin-conjugated surface. A complementary 29-nt oligonucleotide that contained a tetramethylrhodamine-modified dT donor fluorophore was annealed to the G-rich oligonucleotide. Analysis of the population frequency versus FRET histograms in 2 mM K+ revealed the presence of high efficiency (∼0.8), medium efficiency (∼0.6) and low efficiency (∼0.3) FRET states. Evidence was presented that the twofolded states consisted of two ‘sub-species’ characterized by relatively short and long lifetimes. The two limiting folded states were suggested to be the parallel and antiparallel conformations. The time dependency of changes in FRET efficiency in single molecule experiments revealed that a fraction of the molecules rapidly switched between states, while others remained in the same FRET state for longer periods. The decay times of the long- and short-lived states was found to be ∼190 s and 20 s, respectively, at room temperature. Conventional bulk spectrofluorometric experiments showed that when 80 nM DNA was mixed with 2 mM K+, FRET development was biphasic with time constants τ of 9 and 250 s at room temperature. The long-lived, folded states in K+ were assigned to the parallel and antiparallel conformations. The structures of the short-lived states are not known, but the authors suggested that they are more compact that the unfolded states may consist of structures with less than the full complement of bound cations. These states were suggested to consist of obligatory folding intermediates.
FRET detection was also used to determine the unfolding kinetics of the human telomere, by trapping with a labeled peptide nucleic acid (PNA) (i.e. rendering the reaction irreversible). The excess PNA was shown to be zero order, so the observed transient could be attributed to the first-order unfolding of the quadruplex, followed by very much faster hybridization to the PNA. Although the kinetics were biphasic, the data were analyzed in terms of a weighed mean lifetimes approach, giving an apparent opening rate constant of 0.006 s−1 (t1/2 = 115 s) at 37°C in 100 mM Na+, and about 100-fold slower in 100 mM K+ (177).
Surface plasmon resonance
Unimolecular folding of telomeric sequences has also been studied by SPR. In this technique, the unfolded oligonucleotide is typically immobilized on a solid surface (the sensor chip). A solution of a complementary oligonucleotide in the presence of a fold-inducing cation is pumped across the chip at a known flow rate. The complementary oligonucleotide traps any unfolded immobilized G-rich oligonucleotide as a duplex. The rate of folding can be deduced in theory from the time dependence of signal changes occurring during the hybridization stage. Once the complex is formed, the chip is washed with buffer alone to give the rate of unfolding as the cation dissociates. Zhao et al. (178) utilized SPR to study folding of a (TTAGGG)4 model of the human telomere. Rate constants determined at 25°C for folding in K+, Na+ and Li+ derived by this method were 1.2 × 10−2 s−1, 7.0 × 10−3 s−, and 8.6 × 10−6 s−1, respectively. The corresponding rate constants for unfolding were 1.3 × 10−3 s−1, 4.6 × 10−3 s−1 and 1.9 × 10−2 s−1. Values ΔG°folding for each system were estimated from the apparent equilibrium constants calculated from the ratios of the folding and unfolding rate constants. This is predicated on the assumption that the reaction is two-state, and that therefore Kd = koff/kon. In general, as observed at equilibrium and by more refined studies in which folding is seen to be multiexponential (see below), this ratio of apparent rate constant may agree with the true equilibrium constant only fortuitously. In fact, the kinetically estimated equilibrium constant did not agree with values independently determined by equilibrium methods, by one to two orders of magnitude. Additional complications with the SPR approach (179,180) result from nonhomogeneous reaction conditions (e.g. flow effect), matrix binding effects, as well as the complex multiparameter fitting procedures required to extract values of the rate constants of interest. The problems and solutions to these technical difficulties have been recently reviewed (181). Thus, it may not be too surprising that the results obtained do not agree with the results obtained by more direct methods.
Temperature jump
Relaxation methods developed by M. Eigen and coworkers (124) are based on the return to equilibrium of a system after a small perturbation by a rapid change in a parameter such as pressure or temperature. If the perturbation is sufficiently small, the response is linear in concentration. Specifically, for a single-step unimolecular reaction the relaxation rate constant is simply the sum of the forward and reverse reaction rate constants. The approach is applicable in the neighborhood of the Tm and provides a direct measure of the folding and unfolding rate at a given temperature. This approach was used in conjunction with hysteresis analysis to measure association and dissociation kinetics of the Oxytricha intramolecular quadruplex (74). It was shown that the unfolding rate constant was extremely small, and that the association was characterized by negative apparent activation energy. This latter requires a complex multistep process, such as the well-known zippering mechanism common in DNA duplex folding (182).
Stopped flow kinetics
Stopped flow has a long history in enzyme kinetics (124), but has not been used for NA folding kinetics. Recently, Gray and Chaires (164) used the characteristic changes in UV absorption that accompany G-quartet stacking to monitor folding equilibria induced by mixing oligonucleotide models of the human telomere d[AGGG(TTAGGG)3] (ODN1), d[TTGGG(TTAGGG)3A] (ODN2) and d[TTGGG(TTAGGG)3] with KCl or NaCl. The titrations showed that folding is cooperative with respect to [cation] with Hill coefficients of 1.5–2.2 for K+ and 2.4–2.9 for Na+, in keeping with a binding stoichiometry of 2 K+ and 3 Na+ for these oligonucleotides. Cation half saturation concentrations for folding were 0.5–1 mM for K+ and 4–13 mM for Na+ depending on the oligonucleotide. SVD of the wavelength dependence of the binding isotherms indicated that folding generally proceeds for ODN1 and ODN2 through at least one intermediate according to the Scheme 1:
where U, F and In represent unfolded, folded and one or more cation-stabilized intermediates, respectively.
The kinetics of folding was investigated using multi-wavelength stopped flow spectrophotometry (164). K+-driven folding of the three above oligonucleotides as measured over the wavelength range 275–320 nm could be fit to a single exponential process with a relaxation time τ of ∼10 ms for ODN2 in 50 mM KCl at 25°C. Similar folding kinetics was observed for the other two oligonucleotides in K+ solutions. In contrast, Na+-induced folding of the three sequences required three consecutive exponentials to describe the complete time course of folding (for ODN1 in 100 mM NaCl at 25°C, τ1 = 60 ms, τ2 = 800 ms and τ3 = 12 s). The rate constant for K+ folding was sigmoidal with respect to [K+], while the rate constant associated with the rapid phase of Na+-induced folding was hyperbolic with respect to this cation. The folding rates also tended to decrease with increasing temperature. The saturation kinetic behavior and the apparent negative activation energies are consistent with multistep folding pathway outlined above in which a rapidly formed intermediate I in rapid equilibrium with U undergoes a rate-limiting conformational change leading to formation of either F (for K+) or additional intermediates In (for Na+). The sigmoidal dependence of the folding rate constant on [K+] suggests that at least two cations are required to stabilize I, while the hyperbolic dependence in Na+ suggests that a single cation is necessary for formation of the first intermediate. The subsequent intermediates may also be stabilized by additional bound Na+ ions.
The following describes a possible mechanism that incorporates elementary steps from previous studies of oligonucleotide folding with the known structures of the final state and that is consistent with the kinetic data. For a polynucleotide initially in the absence of cations, the first step may consist of rapid neutralization of backbone charge by added cation, resulting in collapse of extended polynucleotide to give an ensemble of compact hairpin structures. These hairpins may collapse further to form double hairpins with Na+ or K+-stabilized stacked quartets and an all-parallel strand topology (the chair structure). In K+, the chair may undergo a single-strand reversal to form the thermodynamically stable state consisting of one antiparallel strand and one lateral loop in the rate-limiting step. In forming the topologically more complex Na+-stabilized fold, two relatively slower cation-dependent steps involving chain reversals and diagonal loop formation would be required to form the final stable topology.
In summary, the studies outlined earlier show that formation tetramolecular quadruplex structures proceeds via dimerization of a ‘rapidly’ formed duplex structure. Since the rate of complex formation depends on the fourth power of the monomer concentration, the actual time required for tetramerization is strongly dependent on the initial concentration of monomers and the nature of the cation (183) and can vary from a few minutes to days. On the other hand, formation of bimolecular quadruplexes is a second-order process and is relatively slower than unimolecular quadruplex formation.
The formation of ‘simple’ monomolecular quadruplexes as driven by either K+ or Na+ is kinetically complex. Different spectroscopic methods that probe different structural features may give different folding kinetics. Some of these differences may result from the specific sequences or conditions [e.g. heterogeneous (liquid–solid phase) reaction conditions]. However, with the exception of the SPR data summarized above, the kinetic studies suggest that cation-driven quadruplex folding is a multistep process with detectable amounts of obligatory intermediates. These intermediates may reflect the presence of partially folded structures and/or structures with less than a full complement of bound cations. The intermediates are rate-limiting because relatively high-activation energies are required to produce conformational changes necessary for formation of complex topologies that may require one or more strand reversals and positioning of loops. However, in conclusion, it is worth repeating the classical caveat of kinetics: kinetics alone cannot prove a mechanism, but unlike equilibrium studies, it can disprove a mechanism.
WHAT ARE THE LIKELY FORCES THAT STABILIZE Q-QUADRUPLEX STRUCTURES?
The general principles of macromolecule stability are well known (160,184), and for NA duplexes and to a lesser extent triplexes have been described in some detail (112,113,117,167,185–191). Although the same principles must apply to quadruplexes, the issue of the balance of forces for quadruplexes has not received much attention. Short quadruplexes at least are significantly different from duplex and triplexes because of the nature of the H-bonding interactions, the stacking of G-quartets, and the involvement of specific ionic interactions (direct inner spheres coordination) as well as any nonspecific electrostatic effects of ionic interactions.
The description of the stability of any structure is best couched in terms of the free-energy contributions, as described earlier for duplex and triplex NAs.
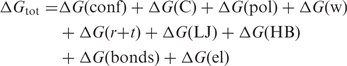 |
9 |
Here each component is defined as follows: conf reflects the conformational differences for the strands and folded state, C is the Coulombic force (mainly enthalpic), pol is the polyelectrolyte effect (chiefly entropic), w is the hydration (entropic) term, rt is the rotational–translational freedom (entropic), LJ is the Lennard-Jones or van der Waals term, HB the hydrogen bonding (enthalpic) term. The bonds term arises from bond length and angle (enthalpic) factors, and el refers to electronic interactions (including polarization and the exchange terms involved in, for example, the hypochromic effect in the bases). Each contribution to ΔGtot can in principle be decomposed into separate enthalpic and entropic parts. In terms of computation, the standard parsing of the free energy of stabilization of a structure is couched in simple terms that can be loosely separated into the potential energy and the entropic contributions. For a highly cooperative two-state folding transition (and see below for recent studies concerning the cooperativity and number of intermediates), the potential energy terms can be described as a molecular mechanics potential such as Equation (10). Generally, it is assumed that all individual components are independent and harmonic (51–53). Until recently, the polarizability of various groups was ignored (amber.scripps.edu).
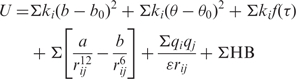 |
10 |
Here, the terms are due to bond stretching, bending, torsion (τ), a van der Waals function that is commonly described by the 6–12 function, the Coulombic terms and possibly explicit hydrogen bond terms.
The Coulombic term includes both formal charges and partial atomic charges, as well as some function to describe the effective dielectric constant ε. The latter depends on the details of the model being used (full atom discrete model with explicit solvent versus continuum model etc. (192). Furthermore, the summation as r−1 converges rather slowly, though modern programs have largely overcome the computational problem using the Ewald method (193–195). The issue of the partial charges is also complicated and they have to be carefully calculated from a relatively high-level theory, and thus for isolated nucleotides. However, the nucleotides are aromatic systems, and as such are quite polarizeable. As the rings stack to form the folded structure, the interactions between the π electrons changes the electronic distribution and thus the charges. If one assumes local (i.e. atomic) polarizabilities, this is fairly straightforward to treat, if computationally expensive. A fully anisotropic polarizability (a tensor quantity) would be considerably more involved to implement. Current versions of mechanics programs treat polarizability in a fairly simple manner (196–198).
The treatment of hydrogen bonds can be explicit or implicit, depending on the implementation. As the H-bond in biological system is largely electrostatic and van der Waal's, these terms (properly calibrated) can be sufficient to account for the H-bond energy. However, H bonds in principle have a covalent character to them, and this can be detected by for example NMR methods (84–86,199). Density functional theory (DFT) calculations have shown how the scalar contribution depends on distance and orientation of the donor and acceptor atoms (85).
These force fields do not account for optical effects that arise from the pi stacking, including the hypochromicity and CD. The same mechanics force field can be used both for calculated a potential energy (or in principle the difference between two states, see below).
As the important determinant of stability is actually the free-energy difference between the state of interest and all other possible (realizable) states, the entropic components also need to be understood. The configurational entropies of the folded and unfolded states for example can be calculated from (long) dynamics calculations or Monte-Carlo sampling. However, the largest differences in entropy are likely to arise from the solvation and electrostatic terms, as the numbers of associated water and counterions may be very different between the compact and extended states. As the nature of a nonfolded G-rich DNA strand is unknown, and experimentally very difficult to evaluate (ensemble of conformations, variable degrees of base–base stacking that depend on temperature and salt), such calculations are presently daunting. For this reason, modeling stability generally looks at the neighborhood of the local energy minimum of the folded state to evaluate its resistance to substantial perturbation. This is not thermodynamic stability, but may be relevant to kinetic stability. However, calculations of free energies associated with the folding landscape have been attempted (51,56).
H-bonds
Each quadruplex is associated with the formation of two H bonds per G, or eight per quartet. The acceptors and donors in the strand state are probably hydrogen bonding to water, so the net change in the number of H-bonds is zero, and thus the enthalpy change from intramolecular H-bond formation is relatively small (101). However, there may be a favorable entropy change due to the release of water into the bulk solvent. As pointed out many years ago (200), not satisfying an H-bond in a folded structure such as by deletion of a donor or acceptor as is done with inosine or deazadG substitution (118,119) or a ‘misfold’ imposes a significant loss of potential energy, perhaps 3 kcal mol−1 (124) see above]. As pointed out above, there may be a small net energy gain in the folded state from the covalent character of the NH::N H-bonds formed (85), as well as from change in the dipole interaction energy in a region of lower dielectric permittivity compared with full exposure to water. Generally, however, the contribution of H-bonding to the free energy of stabilization is thought to be small (117,201,202).
Generalized van der Waals
The potential energy from van der Waals interaction in a well-optimized structure is large and negative, because of the very large number the small favorable interaction energies between pairs of atoms. As each atom is essentially close packed, then any expanded structure in vacuo will result in a large net unfavorable energy. However, in a solvent the unfolding of a NA or protein is compensated by an essentially equal number of similar van der Waals interactions with the solvent molecules, such that the net stabilization energy is rather small (124).
‘Stacking’ π–π interactions
As the π–π stacking interactions between quartets are likely to be large, increasing the number of quartets increases the net favorable energy. This is likely to be roughly linear per stack added, though the actual net favorable energy can be offset by unfavorable strain from loop lengths, which is itself structure dependent (62,75,171,203).
The stacking interactions are similar to those found in other NA structures, and likely account for a substantial part of the net stabilization free energy. The most destabilizing component in NAs at neutral pH is the very unfavorable electrostatic interactions between the oxygen atoms in the phosphodiester bonds, which bear a formal charge of –1. This is exacerbated when a NA strand folds, and this unfavorable energy needs to be offset by all other favorable interactions, or by neutralization by counterions. In quadruplexes, the specific site binding of approximately one monovalent ion per quartet is one part of a favorable stabilization.
Ion binding and solvation
Nonspecific ion binding and hydration
In quadruplexes, there are two kinds of ion binding. The first is the nonspecific interaction with the electrostatic field of the negatively charged phosphodiesters, including both ion condensation and Debye–Hückel counterion atmosphere. Such ions interact as outer sphere complexes (i.e. the species retain their hydration coordination). The second is specific binding of ions such as K+ and Na+ that coordinate to the GO6 atoms of the G-quartets (Figure 1), forming inner sphere complexes with release of water of hydration (see below).
The standard way of estimating number of ions released or absorbed on folding is to use thermochemistry. The melting temperature will depend on the concentration of salt if the charge density differences between the states:
| 11 |
N is the number of formal charges, and ζ = e2/εkTb is the so-called Bjerrum length and r is the axial spacing of the formal charges. For NA unfolding, the formal charge arises for the phosphodiesters, i.e. 1 negative charge per nucleotide (except the terminal one). The formal charge leads to a high intrinsic electrostatic free energy, which is unfavorable. Increasing the ionic strength leads to Debye–Hückel shielding and thus lowering of the potential. If the charge density exceeds a critical value, which depends on geometry as well as the number of charges, then ions will condense and neutralize the charge. The critical parameter for nonspherical objects is the so-called Bjerrum length. Thus, a random coil oligonucleotide has about 44% of the charge neutralized by condensed ions, whereas a B-DNA duplex has around 76% of the charge neutralized, as the charge density is higher (113). For a B-DNA coil transition, [(1/ζs − 1/ζd] ≈ 0.27 at 310 K. Thus for a B-DNA polymer, about 0.27 ions are released per phosphate on melting. In other words, a 21-mer duplex will release 10.8 ions/mol on unfolding. The ion condensation is somewhat higher for the squatter A-structure (∼82%), so the ion dependence of unfolding is clearly conformation dependent. The condensation model has been verified by experiment and extensive Poisson–Boltzmann calculations. The latter have shown that short oligonucleotides deviate somewhat owing to so-called end effects (the ends of a duplex have a lower charge density than those in the interior) suggesting that these theoretical values would overestimate the experimental values for short oligonucleotides (204,205). More recently, Manning (114,115) has shown that even a spherical charge distribution will condense ions, depending on the actual charge density, and also on the ionic strength, albeit less than a cylinder. The condensation idea is important, because it influences the Debye–Huckel screening, which depends on the net charge, Thus, if 76% of the charges are neutralized in the duplex, whereas only 44% are in the strand state, then the net charge on the strands is higher than in the duplex, and therefore increasing ionic strength will favor the strand. This is the origin of the N/2 term in Equation (11). Conversely, if a folded, intramolecular fold such as a quadruplex were to condense less ions than the unfolded state, then the salt-dependent stability would be the reverse of the duplex-strand transition, i.e. ion condensation would favor the strand state, and increasing ionic strength would favor the folded state.
Unfortunately, there seem to be no Poisson–Boltzmann calculations carried out on small, well-defined quadruplexes, for which one might imagine that the specific of topology and thus charge density would be important. Experimental measurements of stability as a function of [K+] have been published. Olsen et al. (134) showed the dependence of Tm on [K+] [cf. Equation (12)] to estimate the number of potassium ion taken up on folding of different intramolecular quadruplexes, and obtained values of ΔnK in the range 0.4–1.9 mol−1 quadruplex formed. The meaning of this is unclear, other than there is a net uptake of K+ on folding. The uptake per mole of formal negative charge varied from 0.03 to 0.07. However, not all of the phosphates are involved in the G-quartet stacks (i.e. the loops are perhaps more like single strands), and whose ion-condensing properties are unclear. If the uptake of ions is normalized, rather arbitrarily, to the number of nonloop phosphates, the uptake is much larger, i.e. 0.05–0.16 mol−1 phosphate. These are still low numbers when one takes into account also that these structures are binding 2–3 ions specifically, i.e. close to 0.1 ion/phosphate.
In contrast, the data for FRET-tagged TG4TTAG3TTAG3TTAG3 of (75) showed a much stronger dependence on the potassium in concentration, which using the estimated van't Hoff enthalpy implies 3.3 ± 0.3 K+ taken up per mole quadruplex formed, or about 0.17 ions per phosphate. Again, the binding of two to three specific ions in the G-quartets would itself account for 0.1–0.15 K+ per phosphate. Similarly, the same sequence titrated with Na+ showed lower stability than with K+, but the slope of 1/Tm versus ln[Na] with the tabulated van't Hoff enthalpies again implied ∼3 ions/mol quadruplex. Although the discrepancies among the various sequences and methodologies are substantial, the number of ions taken up per quadruplex formed is comparable to the expected number of specific ions bound, suggesting that the ionic strength effects may be quite small compared with the more familiar duplex folding. Given the uncertainties regarding ion condensation, it is unclear whether these numbers are merely fortuitous.
Nucleotides exposed to solvent (unfolded states) are hydrated. However, approximately four water molecules per nucleotide is released on unfolding of DNA duplexes (206,207). The number of water molecules released or taken, Δnw up can be estimated from melting studies using a formalism essentially equivalent to that of nonspecific ion binding thus:
| 12 |
where, w is the activity of water. It is possible to determine the amount of water released or taken up during a transition by using osmolytes to affect the water activity, provided they can be shown to be true osmolytes and do not interact directly with either state of the solute of interest (206,208).
Such studies have been carried out for duplex and triplex DNA (206). It is also possible to combine electrostatics and hydration simultaneously by varying the concentration of salt, which alters water activity. In DNA duplex unfolding, the stabilizing effect of increasing ionic strength is opposed by the decrease in water activity (as the duplex is more hydrated than the strands), e.g. (207):
| 13 |
The first term on the right-hand side of Equation (13) is the nonideality effect of salt on the DNA, the second term represents the decrease in water interaction due to replacement by salt, the third is the nonideality term from salt–water interactions and the final term is the electrostatic salt–salt nonideality effect. The nonideality and cross terms in Equation (14) become especially important at higher salt concentrations, such as approaching the 1 M standard state (207) often used in NAs thermodynamics (where the polyelectrolyte contribution is zero) (127,185).
Hydration and electrostatics have been studied by Marky's group (134), who showed that small foldback structures (2 and 3 quartets) are associated with ∼13 waters per mole quartet released on folding. This is opposite to DNA duplex folding, which is associated with an uptake of water (206,207). Small molecule osmolytes thus stabilize the quadruplexes. Further, other cosolvents such as primary alcohols that not only decrease the water activity, but also the bulk dielectric constant, were shown to increase quadruplex stability (209), which is opposite to the well-known effect of alcohols on DNA duplex solubility and thermodynamic stability. This behavior was interpreted in terms of favorable electrostatics for folding
Specific ion binding
In a formal sense, the ion binding is described by a simple thermodynamic square as shown in Scheme 2:
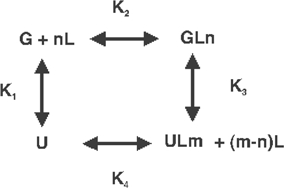
where, G is the folded quadruplex, U is the unfolded DNA, L is a ligand and n, m are the ligand binding stoichiometries. For such a scheme, K1K2 = K3K4.
The apparent dissociation constant for unfolding would be
| 14 |
L is a ligand such as K+ and n, m are the toichiometries of the ligand bindings  is the concentration of L. Here if m, n are greater than 1, it is assumed that the cooperativity of binding is very high (cf. Hill model).
is the concentration of L. Here if m, n are greater than 1, it is assumed that the cooperativity of binding is very high (cf. Hill model).
The temperature dependence of folding, as in UV melting for example, would be (117):
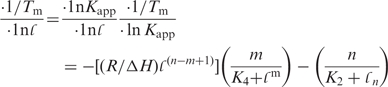 |
15 |
This becomes a linear function of  when K4 is large compared with
when K4 is large compared with  , and K2 is small compared with
, and K2 is small compared with  . The slope approaches n, the number of ions bound in the folded state. At low values of
. The slope approaches n, the number of ions bound in the folded state. At low values of  compared with K2, the slope of 1/Tm versus ln(
compared with K2, the slope of 1/Tm versus ln( ) will decrease, and this gives an indication the apparent affinity for the ion.
) will decrease, and this gives an indication the apparent affinity for the ion.
In an optical titration, the observed signal depends on the specific absorption coefficient. In the limit that m = 0 (no bound ions in the unfolded state), and for simplicity the absorption coefficient of G = GL and U = UL, then the absorbance profile as a function of  will be:
will be:
| 16 |
where, nt is the total DNA concentration, ΔA is the difference in absorbance between the folded and unfolded states and Δε the corresponding difference absorbance coefficients. The assumption that metal binding does not in itself affect the absorption coefficients of the nucleotides is for illustrative purposes only and represents the simplest case. Equation (16) is a Hill equation and will show positive binding cooperativity of L at a fixed temperature. Note that as K3K4 = K1K2, the effective Hill constant K can be written also as K2(1 +K1). In most cases, the values of K1 would be large, so the apparent dissociation constant for e.g. K+ would be K1K2, as expected for an exclusive binding mechanism. Under such conditions, the Hill coefficient n is an indicator of the number of ions bound during folding (164).
The apparent binding of K+ or Na+ to some (human telomere) sequences is highly cooperative and occurs with an apparent affinity in the range 0.5–2 mM for K+ and 5–15 mM Na+ (75,119,164). These affinities are apparent as they are accompanied by folding, as in Scheme 2. If all of the stabilization were from K+ coordination, then the overall binding energy would be of the order 4 kcal mol−1, which is comparable to the observed free energy for short quadruplexes (cf. Tables 2 and 4). Indeed, in the absence of K+ or Na+, and only macrocation counterions present, the fraction of the folded state is (presumed) small. As the specific ion binding to the unfolded state is also likely to be small, the stabilization due to specific ion binding should be substantial (i.e. the ratio of K2 to K4 in scheme 1), which overcomes the unfavorable electrostatic interactions due to folding. For a three-quartet stack structure 2–3 specific ions are bound (164), which has only a small influence on the net charge of the oligonucleotide (∼10% reduction for a 22-mer). The binding of K+ to the thrombin aptamer has been estimated at 5 μM by mass spectrometry (210). This corresponds to 7.3 kcal mol−1 of binding energy at 298 K, which would suggest that the unfolded ensemble and a metal-free folded states are nearly balanced.
Table 4.
Observed thermodynamics of unfolding G-quadruplexes at 110 mM K+
| Species | Tm/K | ΔH/ kcal mol−1 | ΔG(293)/ kcal mol−1 | ΔG(310)/ kcal mol−1 |
|---|---|---|---|---|
| NHEIIIa | 357 | 41 | 7.6 | 5.4 |
| 22GGa | 339 | 34–45b | 4.7 | 2.9–3.8 |
| G3TTAc | 355 | 66 | 11.5 | 8.4 |
| G3ATc | 321 | 27.5 | 2.4 | 0.94 (3.2) |
| G3T2c | 345 | 40 | 6 | 4.1 (6.9) |
| Myc-1c | 357.5 | 45 | 8.1 | 6.0 (9) |
aData from Olsen et al. (134) for 0.075 M. NHEIII: d(TG4AG3TG4AG3TG4A2G2); 22GG, d(AG3T2AG3T2AG3T2AG3); G3TTA, Q-d(TG3T2AG3T2AG3T2AG3)-F (Q, F quencher and fluorophore, respectively); G3AT; F-d(G3A3G3T3G3T3G3)-Q; G3T2, F-d(G3T2G3T2G3T2G3)-Q; Myc-1, F-d(G4AG4TG4AG4)-Q.
bvan't Hoff and calorimetric enthalpies—transition not pure two state.
The hexa hydrated K+ ion present in solution coordinates to the O6 of at least four bases, and generally is nearly octahedral in quadruplexes (cf. Figures 2 and 3). As oxygen ligands are replaced by oxygen ligands, one can envision that the enthalpy change of pure ion binding is relatively small. For comparison, the enthalpy of binding of potassium to crown ethers has been measured at around 3–4 kcal mol−1 (211,212). The value of ΔG(310) for potassium binding to 18-6 crown ethers in aqueous solution was measured at around 2.5 kcal mol−1 ion (211,213), and as expected a somewhat more favorable 3.1 kcal mol−1 in organic solvents (212,214). This includes the energy of desolvation and conformational rearrangement of the crown ether on complexation, but is a rough model for the binding of a single K+ to a preformed quadruplex. Given the observed net ΔG(310) of formation of three-stack quadruplexes is in the range 5–10 kcal mol−1, it is plausible that the energy of potassium binding and reorganization (K2 in scheme 1) accounts for a substantial fraction the net favorable free energy. This further implies that under appropriate circumstances, the population of the unfolded state in the absence of cation could be significant. This in general accord with the kinetics of formation of the human telomere quadruplex initiated by sodium or potassium (164) in which cation binding is highly cooperative, both under equilibrium conditions and in the early phase of the approach to equilibrium. This showed rapid ion binding followed by a slower, quasi irreversible first-order (reorganization) process, implying a net binding energy in this stage of ∼5 kcal mol−1. Nevertheless, this analysis is highly simplified, and really reflects our current lack of understanding of the energetics of quadruplex formation and stability.
Free energy of ion exchange
Hud and coworkers (31) have recently summarized the literature on ion binding to G-quadruplexes. The difference in stability between sodium and potassium forms is well documented, though there is a tendency for these ions stabilized different structures, in which the coordination stereochemistry of the ions also differ (cf. Figure 2) (119). Experimentally, the difference in free energy between potassium and sodium binding is of the order 1.5–2.5 kcal mol−1 (75,164,215–217). It has been argued that the major determinant of this difference is the difference in dehydration energy of Na+ versus K+ (217). In the bound state, the covalent contribution to the quartet H-bond strengths correlated with cation and N2–H2 … N7 H-bond lengths in K+, Na+ and NH4+ structures (86). Furthermore, direct observation of Na+ by NMR showed quite different mobility depending on position in the structure, and short residence times at any position (218). The residence time of the central ion was determined to be 250 ms using 15NH4+ and NMR spectroscopy (216) and mixed cation studies showed that different sites are unequal (219–221). This is in agreement with calculations that indicate essentially free mobility of small ions (e.g. Na+), but much slower exchange for large ions such as K+ (222).
Starting with a quadruplex structure in K+, then formally the exchange can be written as a series of steps thus:
Q′K⇔Q + K+
K+ + 6H2O⇔K+ (aq)
Na+ (a)⇔Na+ + 6H2O
Q + Na+⇔Q*Na+
where Q is quadruplex, Q*Na is the quadruplex–Na complex in a different state to that in the K+ complex. Step 1 corresponds to the significant barrier to removal of a coordinated ion, including any contingent conformational rearrangement of Q′ to Q. This is followed by the favorable free energy of solvation of the K+ in step 2. Steps 1 + 2 are analogous to the dissociation of an ion from a crown ether discussed above, which costs ∼2.5 kcal mol−1 ion, and can be designated ΔG(K) = ΔG1 + ΔG2. Steps 3 and 4 are the reverse of the potassium release, and result in a final structure in which Q* may be different from Q′. In the context of the crown ether, model, this will be associated with a free energy change ΔG(Na+) = ΔG3 + ΔG4. Therefore, the net cation exchange free energy is ΔΔG=ΔG(K+)−ΔG(Na+), i.e. ∼2 kcal mol−1 for a three stack quadruplex. Clearly, this includes not only the difference in hydration energy (ΔG2 − ΔG3), but also the corresponding energy differences associated with coordination energy and conformational reorganization corresponding to Q′ and Q′(ΔG1 − ΔG4). An actual parsing of the component energies has yet to be achieved.
Number of quartets and length of loops
In Quadruplex topologies and structures section, we alluded to the restrictions imposed by loop length on possible topologies and by implication the contribution to the overall stability of different quadruplex structures. Although we have argued so far that bases stacking and specific ion binding may be the dominant stabilizing interactions, the length and sequence of these loops is important. For example, for intramolecular structures that contain single nucleotide loops, substitution of an A for a T decreased the Tm by 8°C (203) (up to around 1 kcal mol−1 of subsistent). Similarly, replacing nucleotide with nonnucleotide linkers had substantial effects on both stability and folding kinetics (171). Loop length clearly influences the energetics of quadruplexes, because changing the length from 1 nt to 2 or 3 is associated with a change on overall fold (165). In general, one would expect the stability to increase with the number of stacks. Rachwal et al. (62) showed that for increasing n in the context (GnT)4 ΔG(310) increased linearly for n = 4–7 (∂ΔG(310)/∂n = 2 kcal mol−1 in 5 mM potassium), whereas the molecule with n = 3 was more stable then either n = 4 or n = 5. Similarly, in the series (GnT2)4, the free-energy change was also linear in n, apart from one anomaly, with a slope of 1.65 kcal mol−1. Interestingly, the apparent number of potassium ions taken up on folding barely increased with n (from 2.5 to 3.5 for n = 3 to 7), but showed a larger variation in response to Na+, but again nonlinearly with respect to n. This was interpreted that only a fraction of the possible quartets were formed, which is consistent with the weak dependence of ΔG and ΔH on n. The presence of the T2 loops was suggested to allow for different topologies (antiparallel rather than parallel) (62). Nonspecific ion dependencies might also account for some of the anomalous estimates of the number of ions bound, as may the annealing history of the nucleotides (e.g. the rate of cooling and final temperature, cf. Figure 8). In any event, this all points to the complexity of dealing with quadruplex structures, and the need for simple but rigorous methods to establish what structures are present and the mole fractions under the experimental conditions when multiple conformations are present.
Nature of the unfolded state
Because thermodynamics refers to changes in state functions, all thermodynamic considerations must include nature of the unfolded state. Even very high quality energy calculations on a particular structure imply little about net thermodynamic stability.
The rather dense purine sequences of G-tracts suggest that the single stranded state at normal temperature and salt conditions is unlikely to be remotely like an extended strand or a random coil; significant base stacking of nearest neighbors is to be expected. Telomeric DNA can be prevented from forming quadruplex structures by ensuring that there are no high Z cations present. Thus, Li+ generally does not stabilize quadruplex structures readily, in part because its small size does not allow for simultaneous optimal bonding to the quartet oxygens (63), though this depends on the sequence and linkers (171). A macrocation such as the tetramethylammonium (TMA) ion will also prevent quadruplex formation better than Li, because the ion is simply too large to fit into the cavity of the quartet. Human telomere DNA dissolved in a solution containing only TMA as the counterion does not form a quadruplex. However, its CD spectrum has a classical conservative exciton coupling shape, indicative of significant base stacking, but not consistent with G-quadruplex folded structures (R.D. Gray and J.B. Chaires, unpublished data). Thus, the strand state is by no means a random coil. This has obvious implications for folding/unfolding thermodynamics. In principle, FRET could be used to assess the distribution of end-to-end distances in the unfolded state (78). The large decrease in quenching observed on unfolding short quadruplexes (119) indicates that with a suitable choice of donor–acceptor pairs and by manipulating the salt concentration to shift the unfolding transition, the variation of the distance distribution over a range of unfolding conditions (salt + T) could be obtained. Such FRET experiments in TMA might provide useful information about the distribution of size and shape in the unfolded form, and thus the degree of stacking in the strand state.
DISCUSSION
Given the preceding brief overview, we now discuss the factors that determine formation of known structures, and what can actually form, in terms of kinetic versus thermodynamic control, and how these might be modulated by cellular environments.
The cellular environment is of the order 70% water, i.e. the water activity is at most 0.7, neglecting effects on the activity coefficient [cf. Equation (13)]. NA folding is associated with altered hydration. The effect of water activity can be estimated using osmolytes to influence the water activity, and the data can be analyzed in terms of preferential hydration as described by Timasheff (223–226) and by Parsegian (227,228). The variation in the free energy of folding is approximately given by ΔΔG = −RTΔlna/a0, where a is the water activity and a0 is the water activity in the standard state (55.5 M) and Δ is the change in the number of associated water molecules. For quadruplex folding from a single strand, Δ can be a large number, though for some quadruplexes it is relatively small. Given the range reported for Δ of 3–20 water molecules released per mole quadruplex formed (depending on structure), this implies a stabilization ΔΔG due to dehydration from 55.5 M water to the cellular milieu of a low value of 0.7 kcal mol−1 to a high value of 4.9 kcal. (134). The dehydration would stabilize quadruplexes compared with duplexes, which are more hydrated than the single strand and thus the quadruplex state.
The other aspect of the low water activity in cells is that much of this results from the presence of proteins and other macromolecules, which collectively account for >75% of the intracellular biomass. This macromolecular matrix in itself (disregarding for the moment any specific or nonspecific direct interactions) can influence folding energy and kinetics as described by Minton (229), based on considerations of the coefficients of the virial expansion of state. Both theoretically and experimentally, it is shown that the presence of noninteracting matter will favor the more compact state, i.e. if there is a change in volume in a reaction, then the equilibrium constant and rate constant will be affected by the concentration of added polymer. For protein concentrations as high as 20%, this can lead to large changes in equilibrium constant, with ΔΔG values of the order several kcal/mol for protein folding and aggregation (230–232). Note that this would synergize the effects of water activity on hydration. Sugimoto (233,234) have used crowding conditions in vitro to determine the influence on conformation and stability. They found that the crowding conditions caused a change in the structure of the quadruplex, owing to different excluded volumes (cf. Figures 3 and 4), and also that duplexes formed between G-rich and complementary C-rich strands were destabilized, at least as far as enthalpy changes were concerned. Interestingly, as the crowding also decreases the water activity, it was argued that crowding conditions stabilized the parallel G-quadruplex structure because it releases water on formation (233). Separating the contributions from crowding, solvation and electrostatics is complex, as they are not linearly independent parameters [cf. Equation (13)]. A degree of separation may be achieved by using a range of small molecule osmolytes to probe water activity effects, and large, truly physically excluded noninteracting polymers for crowding effects in comparison with the small molecules (206,208).
In vivo this is much more complex, because the proteins present in the nucleus are clearly not neutral particles, but rather a collection of architectural, structure and sequence selective molecules.
Intragene quadruplex formation
The folding of a single-strand G-rich overhang such as the one that exists in telomeres is a very different proposition from the formation of a G-quadruplex in an internal position, such as identified in numerous promoters (60,235). This area of research has been recently reviewed (236). In the former case, the folding is free to occur from an unconstrained end, and does so on a potentially stabilizing nucleus of double-stranded B-like DNA (59). In contrast, from the point of view of energetics, the internal G-quadruplexes require the separation of the DNA strands to form a loop (very unfavorable) followed by the G-rich strand forming a quartet while being tethered at both ends, leaving the complementary strand as a loop, or as an i-motif as shown in Figure 9. Based on estimates of the energies of formation of these structures (134,237,238), it is possible to calculate the cost of formation of such a structure, as follows.
Figure 9.
Formal model for formation of an internal G-quadruplex or other intramolecular structure. Duplex DNA with a G-quadruplex potential sequence (top) unwinds and histones redistribute, leading to base-pair dissociation and formation of an open loop (middle). The G-rich strand forms a unimolecular G-quadruplex structure in the presence of a single-stranded complementary C-rich strand. This potentially could form an intramolecular i-motif as shown (third from top). The quadruplex and/or the C-rich strand may be stabilized by proteins (as shown at bottom) or other ligands. The binding energy required to overcome the unwinding is discussed in the text.
For the illustrative purposes, we consider the formation of the NHEIII Myc structure, and the 22GG described by Olsen et al. (134). The energy of unwinding the DNA (loop creation) can be calculated for the actual G-rich sequences using the nearest neighbor model for closed DNA (238), and for AT rich sequences and a random 50% GC sequence.
The Tm depends on the fraction GC and the ionic strength as (238):
| 17 |
The values of Tm for three different GC contents and three ionic strength values are given in Table 3. The GC contents were chosen to represent the average GC content in human genomic DNA, an AT-rich region and a GC-rich region such as containing a region of high G-quadruplex forming potential (12). The ionic strength covers the range used experimentally and the average intracellular monovalent ion content. The ΔH values are taken from ref. (238) using the equation for random sequence
Table 3.
Calculated thermodynamics of unfolding of a B-DNA duplex in closed DNA
| fGC | [Na]/M | Tm/K | ΔH/ kcal mol−1 bp | ΔG(293) kcal mol−1 | ΔG(310) kcal mol−1 |
|---|---|---|---|---|---|
| 0.2 | 0.075 | 345.9 | 8.0 | 29.3 | 19.9 |
| 0.5 | 0.075 | 358.4 | 8.5 | 37.3 | 27.6 |
| 0.8 | 0.075 | 371 | 9.1 | 45.7 | 35.7 |
| 0.2 | 0.11 | 349 | 8 | 30.8 | 21.4 |
| 0.5 | 0.11 | 361.2 | 8.5 | 38.6 | 29 |
| 0.8 | 0.11 | 373.4 | 9.1 | 46.9 | 36.9 |
| 0.2 | 0.2 | 353.9 | 8 | 33 | 23.8 |
| 0.5 | 0.2 | 365.6 | 8.5 | 40.6 | 31.1 |
| 0.8 | 0.2 | 377.3 | 9.1 | 48.6 | 38.8 |
Loop size = 24 nt, i.e. for a 22-mer + 1 base at either end.
For an intramolecular fold, the Tm is the temperature at which ΔG = 0 and ΔH = TmΔS. Thus, the value of ΔG can be calculated at any other temperature, T, according to:
| 18 |
Note that the duplexes are stabilized by salt less than the quadruplexes. ∂Tm/∂log(M) = (3.09 − f)6.52 for the duplexes [Equation (17)] = 17 at f = 0.5, and 13–23 for the two quadruplexes (134). In contrast, the salt dependence of Ristano and Fox (75) was ∂Tm/∂log(K) = 28.4. This no doubt reflects the stabilization of the quadruplex by specific ion binding as well as any ion condensation/Debye screening effects. Thus, in the absence of any stabilization of the quadruplex, its formation does not overcome the very unfavorable strand separation energy, by an amount >30 kcal mol−1 for 200 mM salt and a GC fraction of 0.8. Even for an AT-rich sequence, the quadruplex formation is around 20 kcal mol−1 short in free energy. The van't Hoff enthalpy estimates from ref. (75) are significantly higher than from ref. (134) and were surprisingly temperature sensitive even at K+ concentrations well above the mid-point affinities for the ion (low mM). Table 4 also illustrates the point that ΔG(310) values do not necessarily rank the same way as the Tm values. Although Tm is generally determined with high precision (often to better than ±0.5 K, but see Thermodynamic methods section) the ΔH values are frequently imprecise or inaccurate (cf. Table 2). Extrapolation to a common reference temperature can also lead to error. For example, ΔG(310) for 22GG varied 0.9 kcal mol−1 for a range of ΔH of 9 kcal mol−1, whereas NHEIII and G3TTA have similar Tm values but very different calculated stabilities at 310 K, owing to the substantial difference in ΔH.
i-Motif formation
To some extent, this energy cost might be offset if the complementary strand were to form a stable structure, such as the i-motif (239–242). However, this structure is at best marginally stable at physiological pH and temperature though the actual state of protonation of the cytosines in the nucleus is far from clear. The reason for this is that the i-motif involves H-bonding between cytosines, on which one of the pair must be protonated on N3. To be stable at physiological pH this requires raising the pK of one of the paired cytosines from ∼4.5 to >7, which costs at least 3.5 kcal mol−1 C:CH+ formed at 310 K. Thus, these structures are stable only at low pH (243). Based on the data presented for the isolated cRET C-rich sequence (65), the intramolecular i-motif structure has an insignificant population above pH 7 and at 310 K (<1%). This does not include the unwinding stress and junction with neighboring duplex, although it is possible to build models, as yet unrefined, that simultaneously incorporate a G-quadruplex and an intramolecular i-motif on the complementary strand (65,244) (Figure 9). Experimentally, the duplex wins over the quadruplex (243,245,246), as expected on thermodynamic grounds (see above).
An alternative is that a quadruplex becomes stabilized by a protein or other ligand, or that the single-stranded complement is similarly stabilized by a binding partner, such as a DNA.RNA hybrid as in Escherichia coli (8), which is typically a rather short hybrid duplex that is important in transcription initiation, or a ss binding protein. The binding energy would have to be of the order 20–30 kcal mol−1 for this to be effective. A binding free energy of even 20 kcal mol−1 is equivalent to a dissociation constant of 10−14 M. Another alternative is that supercoiling stress generated by transcription might supply this energy (even transiently), though one might expect the less AT-rich regions to form a bubble in preference to a GC-rich sequence, unless again there are additional proteins that could stabilize on the other strand.
It is clear that such a structure will not spontaneously form without some help. It has been suggested that supercoiling such as during transcription can propagate the necessary stress back toward the promoter to cause unwinding of sequences (247), and thus permit the formation of the G-quadruplexes (236). It is unclear why AT-rich sequences would not melt in preference to the GC-rich sequences, given the very large difference in stability. Furthermore the applied torsional stress would surely change as the transcription proceeds, so that at some point the G-quadruplex would revert to the duplex state. However, as the kinetics of reversion are typically very slow, this might not be possible unless other proteins were to accelerate the kinetics. Nevertheless, the implication was also that the system operates far from equilibrium, implying that an understanding of the kinetics is extremely important. Indeed, it has been proposed that specific DNA-binding proteins bind to the single strand region in the torsionally stressed Myc promoter (235).
Risitano showed that in fact the ds moiety of the human telomeres is preferentially double stranded at physiological pH, but an increase the number of G-stacks favored the quadruplex over the duplex such as for the c-myc G-rich sequence, even in the presence of a large excess of the complementary C-rich strand (75). An issue here is that there is a competition between a free duplex and strand + quadruplex, i.e.
The distribution of species is simply give by the ratios of the dissociation constants, viz K1 = a.b/ab and K2 q/a, where Q is the quadruplex structure folded from the G-rich strand A and B is the complementary C-rich strand.
The Δ G(310) values for the quadruplex formation of all species based on the Tm and the published ΔH was in the range 6–7 kcal mol−1 (Tables 2 and 4). For oligomers of 19–20 bp long, the nearest neighbor parameters of SantaLucia (127,248,249) can be used to estimate the ΔG of the duplex at equimolar strand concentrations of 0.25 μM. For the G-rich sequence, the ΔG310 are in excess of 20 kcal mol−1, which far exceed the measured stability of the quadruplexes. The excess C-rich strand (5- to 50-fold) is thus in very large excess of the values of K1K2, and this should easily outcompete the quadruplex for all sequences studied, in agreement with (243,245,246). For an internal loop, the penalty will be higher than for a free duplex (238).
Do quadruplex structures actually exist in vivo?
Major arguments in favor of G-quadruplex formation in vivo include the ready ability of the G-rich sequences widely found in genomic DNA, as single strands spontaneously form a stable quadruplex structures in solution. Furthermore, the prevalence of such G-potential sequences that far exceeds chance is argued to be preserved for a functional purpose. The latter argument has considerable weight but not specifically for the formation of any particular structure. As discussed earlier, thermodynamic arguments favor the telomere as the most likely place to find G-quadruplexes in vivo. The 3′ single-stranded overhang could simply form a dead-end quadruplex that cannot be used by telomerase. Such a structure would however protect the end of the chromosome from unwanted dimerization (which would interfere with replication and with subsequent accurate chromosome segregation during mitosis, i.e. leading to aneuploidy) as well as avoiding endo and exo nuclease activity.
It is experimentally very difficult to demonstrate the presence on any specific DNA structure in vivo (and even harder to prove its absence!). Maizels (12) and Bryan (14) have recently summarized the evidence for the existence of quadruplex telomeric G4 DNA in vivo [see Kipling, pp. 65–68 (7) for a summary of older data]. An overview of the differences in complexity of telomere replication among various organisms is given by Gilson and Geli (250). The best evidence exists for ciliates such as Oxytricha and Stylonychia (which have a very different kind of chromatin than mammals and a very large number of telomeres). The fundamental paper by Schaffitzel et al. (251) described the generation of quadruplex-specific single chain antibodies. Two were selected, one having high affinity (Kd = 0.13 nM) for parallel four-stranded DNA, and a second one having 2–3 nM affinity for both parallel and antiparallel G-quadruplexes. These two antibodies showed no significant affinity for any other kinds of DNA or RNA, or other polyanions (although no proteins were tested). Only the latter showed a positive result in the indirect immunostaining technique on isolated nuclei from Stylonychia lemnae, and then only in the vegetative state (i.e. not during replication). This was interpreted as the existence of the quadruplex in the vegetative state only, presumably as a means of protecting the short 3′ overhang from dimerization or excision by nuclease. Indeed, the multiple chromosomes from the vegetative state tend to aggregate end-to-end in this organism, via the intermolecular G-quadruplex, and this may explain why the in vivo chemical modification experiments failed to detect quadruplex in these organisms (125,126). In a recent subsequent paper, it was argued that the quadruplex dimers are stabilized by the TBPα2β2 complex, even though TBPα itself stabilizes the single stranded state, and anchors the chromosome to a nuclear scaffold (252). TBPβ is recruited by TBPα bound to ss telomere ends, promoting a profound conformational change in the DNA, to form a specific antiparallel G-quadruplex dimer. For subsequent replication, this complex must be resolved. As the authors emphasized, the unfolding kinetics are intrinsically very slow, in vitro the t1/2 may be years (169), so something must promote this dissociation of the proteins and DNA dimer. It is worth noting that the (observed) rate constant for the approach to equilibrium (as opposed to the unidirectional rate constants) and thus the half-life for formation and dissociation of a structure are the same. Consider the simple intramolecular folding mechanism:
| 19 |
The binding of ions that initiates folding is assumed to be fast (see above for ion binding rates), whereas the subsequent isomerizations are slow, but k2≫k−2 [the overall dissociation constant is K1K2/(1 + K2) <10−3 M]. If one were to start the reaction with adding ion to unfolded nucleotide, the formation of Q will proceed exponentially toward equilibrium, according to:
| 20 |
where kobs = k2mn/(mn + K1) + k−2 and thus the half life of formation is ln2/kobs.
In contrast, the spontaneous unfolding from Q will occur with the same rate constant kobs provided that there is nothing to mop up the resulting strand or ions. Only the initial rates differ in the two directions. Anything that binds Q will slow down the rate of approach to equilibrium, and similarly anything that sequester U will do so too, as the rates depend on the concentration of U and Q.
It was further proposed (252) that telomerase itself acts as the resolvase, after being recruited by phosphorylation of TBPβ. A major conclusion, ultimately based on known in vitro properties of G-rich oligonucleotides, is that if quadruplexes are formed, they need to be resolved (by proteins), and cells appear to devote considerable effort to prevention of G-quadruplex formation, because they are too stable for replication or transcription. Homologs of the TBP proteins have been identified in vertebrates, namely POT1 and TPP1(253,254), though their mechanism of action remains unclear (255). Of the 21 proteins listed as being able to bind to quadruplex DNAs in vitro, only one quadruplex was a fold-back structure (14). Many other proteins can be shown in vitro to have affinity for such structures, but their functional significance is unclear. Recently, it has been argued that only the extreme end of vertebrate telomeres form quadruplexes (256), and a protein proposed to be needed for human telomere unfolding has been characterized (257). Much of the evidence for quadruplex formation in mammalian DNA in vivo is generally circumstantial and to date no high selectivity antibodies for human quadruplex structures are available. Quadruplex binding ligands typically have rather modest affinity and selectivity even for the small numbers of structures tested, and do not always bind in the manner expected or designed (258,259) (260,261). For example, the tetraporphyrin TmPyP4 shows a selectivity of only 20-fold (ΔG310 < 2 kcal mol−1) over B-DNA yet was used to demonstrate the presence of a quadruplex structure (236). New developments in quadruplex-binding ligands show substantially higher affinity and selectivity for the human telomere sequence (262), and these might be useful for such experiments, with the caveat that the ratio of nonquadruplex DNA to potential quadruplex DNA is very large, and that selectivity also needs to be assessed against protein binding and a wide variety of alternative DNA structures.
T-loops
The biology of telomeres was summarized in a recent review regarding their need for maintenance, and what happens when the length is not maintained (263). An alternative model for avoiding the problems association with a free 3′ single strand is for it to loop back and become buried in the proximal part of the telomeres, perhaps by strand invasion. This is called the t-loop mechanism (264–271). The original description of the t-loop (272) indicated that long telomeres (many kilobases long) can loop back on themselves and the 3′ single strand overhang of a hundred or so bases invade the duplex strand and compete for the same sequence with the complement. Although the length of the telomeres is much greater than the persistence length of DNA at physiological salt concentrations, opening of an internal loop within the duplex and forming in essence an intermolecular duplex is, as explained above, energetically unfavorable. In fact, it was observed that in the absence of a stabilizing factor, the efficiency of t-loop formation was very low; only substantial formation of a loop structure was observed in the presence of the telomere specific protein TRF2 (272). Indeed, the loop model does not formally require strand invasion, only that there is some interaction stabilized by for example protein. Indeed, it has recently been argued that just the single strand-overhangs form a t-loop stabilized by what amounts to a dimeric G-quadruplex (269). However, this is not in agreement with original models based on large loops that imply circularization of the lengthy double-stranded portion of the telomere. Although the binding energy for a loop of this size would be small if the DNA were naked, the entropic cost could be quite substantial, as the probability of finding a small number of configurations in which the end is close to a specific part of the telomere is small compared with all the other possible configurations (273). However, the telomeres are normally bound up in histones (274,275), even if the linker histone distribution differs somewhat from ‘average’ DNA, and are regulated by acetylation and deacetylation (274,276). We note that the chromatin rearrangement implies connection of the physical problem to metabolism via ATP hydrolysis and acetylation events. This also begs the question as to the remarkable length variation of telomeres, even in mammals. The critical length for humans seems to be 6–8 kb, though actually maintained at 8–12 kb with a long ss 3′ overhang (>100 nt), whereas ciliates have very short 3′-ss overhang (266).
PROSPECTS AND CONCLUSIONS
It is clear from the foregoing that despite the extensive efforts expended to date, we still have a very limited view of what determines the folding and relative stability of different quadruplex structures, and how fast they form. Even worse, for the most part the relationship to in vivo formation is even murkier. The latter is a consequence of at least two factors. First is that in vitro experiments concentrate on simple, relatively well-defined systems under conditions that typically do not approximate those found in vivo, as described in part in Discussion section. Furthermore, it turns out that even the short intramolecular complexes are surprisingly complex, and detailed analysis is hampered by the presence of multiple conformations and slow folding kinetics. Nevertheless, the basic principles of the energetics of G-quadruplex formation do need to be considered in any biological model, as well as the question as to where the energy comes from. Thus, the thermodynamics and kinetics of small oligonucleotides have value in that it is possible to examine them in great detail under a wide variety of well-controlled conditions. This allows one to sample the possible range of behaviors within a realistic range energies and timescales, which ultimately must be relevant to the biological conditions. It appears that naked G-potential DNA alone has physical properties that are not commensurate with some of the proposed biological functions and thus requires protein binding to provide the energy to manipulate these properties. It is further notable that some of the proposed functions of such DNA, such as found in promoters, may need to be coupled to unwinding events, and operate far from equilibrium. Under these conditions an understanding of kinetics is essential.
We have argued that the specific ion binding and general electrostatics are a critical component for the energetics, and folding rates of G-quadruplexes, that distinguish them from most other DNA or RNA folds. However, there are disturbing variations in basic thermodynamic properties that need to be addressed to establish whether these variations arise from experimental artifacts or there are real differences that are sensitive to conditions and small variation in sequence.
To accomplish this goal, we believe that an agreed upon and reliable set of rapid and inexpensive techniques is needed to determine the topology of any quadruplex, and assess its purity. This is likely to come from a combination high-resolution spectroscopic and hydrodynamic techniques, such as NMR and AUC. First, methods are needed for rapid assessment of the topological structure(s) that is (are) present (277) and whether the state is unique and thus can be manipulated by variation of conditions until it is. This is a prerequisite for subsequent structural and functional analysis, purely as an analytical quality control. Second, it would make it possible to prepare a standardized set of oligomers of known structures to determine whether even simpler methods that exist can make useful distinctions among possible structures (database approach).
To this end, we propose that a consortium be established to address major unresolved questions, or at least enlighten the present authors who confess having more questions than answers. Some of these are listed below.
Systematic studies of the thermodynamics (ΔH, ΔS and ΔCp) for defined sequences under different conditions, analogous to the extensive work published for DNA and RNA duplexes, in order to establish useful relationships between sequence and stability under various conditions of temperature and salt concentration.
Develop reliable methods of rapid determination of topology of new sequences. This might ultimately be achieved using simple and cheap methods such as (electro)hydrodynamics + CD + 1D NMR for example, once a database of the properties of authenticated structures has been established under the appropriate conditions. This entails generating a set of authenticated standards that can be reproduced according to specific procedures. The use of nonnucleotide linkers (171) in comparison with nucleotides to establish contributions from loops to CD.
Investigate in greater detail the nature of the unfolded ensemble of states, perhaps using methods outlined in the text. This is essential to understand thermodynamic stability.
Quality control: what methods should be used to establish that a new sample is in a particular state (cf. #2)?
Determine the role of electrostatics in stabilization and kinetics of G-quadruplex structures. This will require additional methods such as capillary electrophoresis and careful salt-dependent analysis of the thermodynamics to establish the difference between nonspecific and specific ion binding, as well as the interplay with hydration. Detailed calculations of the ionic contributions are also required to interpret such data. The electrostatics relate closely to issues of electrophoretic mobility.
A systematic computation of CD for varied twist and wedge angles and induced CD of loop bases (and see #2).
Develop structure-specific antibodies that can be used both for quality control, and also for probing the possible presence of structures in higher eukaryotes under different cellular conditions.
Apply novel methodologies to assess kinetic stabilization such as single molecule force measurements as described for RNA (278,279)
Develop a realistic but experimentally tractable DNA system for telomeres and promoter G-quadruplex forming sequences that include nucleosome assemblies, and are compatible with optical and hydrodynamic approaches for example. This is an area where a dialogue between the physical biochemists and biologists would be especially valuable to ensure that the problem is defined appropriately in a biological context.
Finally, there is a substantial literature on targeting G-quadruplexes for possible anticancer drug development (18,60), which is beyond the scope of this review. However, the physical principles apply equally to this area. Furthermore, the presence of G-quadruplexes in normal or other cells is not a requirement, only that they can form under certain (possibly pathological) conditions, and as such will be stabilized by the specific ligand and thereby interfere with cell replication and/or survival.
FUNDING
This work was funded in part by NIH grant No. P20RR018733 from the National Center for Research Resources, the Kentucky Challenge for Excellence and the Neal Radnew Trust. Funding to pay the open access charge for this article has been waived by NAR.
Conflict of interest statement. None declared.
ACKNOWLEDGEMENTS
We thank Paula J. Bates and a reviewer for a critical reading of the article and valuable comments.
REFERENCES
- 1.Huppert JL, Balasubramanian S. Prevalence of quadruplexes in the human genome. Nucleic Acids Res. 2005;33:2908–2916. doi: 10.1093/nar/gki609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Huppert JL, Balasubramanian S. G-quadruplexes in promoters throughout the human genome. Nucleic Acids Res. 2007;35:406–413. doi: 10.1093/nar/gkl1057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cech TR. Beginning to understand the end of the chromosome. Cell. 2004;116:273–279. doi: 10.1016/s0092-8674(04)00038-8. [DOI] [PubMed] [Google Scholar]
- 4.Chan S, Blackburn EH. Telomeres and telomerase. Philos. Trans. R. Soc. Lond. B-Biol. Sci. 2004;359:109–121. doi: 10.1098/rstb.2003.1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Blackburn EH. Switching and signaling at the telomere. Cell. 2001;106:661–673. doi: 10.1016/s0092-8674(01)00492-5. [DOI] [PubMed] [Google Scholar]
- 6.Lingner J, Cech TR. Telomerase and chromosome end maintenance. Curr. Opin. Genet. Dev. 1998;8:226–232. doi: 10.1016/s0959-437x(98)80145-7. [DOI] [PubMed] [Google Scholar]
- 7.Kipling D. The Telomere. Oxford: Oxford University Press; 1995. [Google Scholar]
- 8.Duquette ML, Handa P, Vincent JA, Taylor AF, Maizels N. Intracellular transcription of G-rich DNAs induces formation of G-loops, novel structures containing G4 DNA. Genes Dev. 2004;18:1618–1629. doi: 10.1101/gad.1200804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Huber MD, Lee DC, Maizels N. G4 DNA unwinding by BLM and Sgs1p: substrate specificity and substrate-specific inhibition. Nucleic Acids Res. 2002;30:3954–3961. doi: 10.1093/nar/gkf530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sun H, Yabuki A, Maizels N. A human nuclease specific for G4 DNA. Proc. Natl Acad. Sci. USA. 2001;98:12444–12449. doi: 10.1073/pnas.231479198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sun H, Bennett RJ, Maizels N. The Saccharomyces cerevisiae Sgs1 helicase efficiently unwinds G-G paired DNAs. Nucleic Acids Res. 1999;27:1978–1984. doi: 10.1093/nar/27.9.1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Maizels N. Dynamic roles for G4 DNA in the biology of eukaryotic cells. Nat. Struct. Biol. 2006;13:1055–1059. doi: 10.1038/nsmb1171. [DOI] [PubMed] [Google Scholar]
- 13.Bates P, Mergny JL, Yang D. Quartets in G-major – the first international meeting on quadruplex DNA. EMBO Rep. 2007;8:1003–1010. doi: 10.1038/sj.embor.7401073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Oganesian L, Bryan TM. Physiological relevance of telomeric G-quadruplex formation: a potential drug target. BioEssays. 2007;29:155–165. doi: 10.1002/bies.20523. [DOI] [PubMed] [Google Scholar]
- 15.Oganesian L, Moon IK, Bryan TM, Jarstfer MB. Extension of G-quadruplex DNA by ciliate telomerase. EMBO J. 2006;25:1148–1159. doi: 10.1038/sj.emboj.7601006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kumari S, Bugaut A, Huppert JL, Balasubramanian S. An RNA G-quadruplex in the 5′ UTR of the NRAS proto-oncogene modulates translation. Nat. Chem. Biol. 2007;3:218–221. doi: 10.1038/nchembio864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yang DZ, Hurley LH. Structure of the biologically relevant G-quadruplex in the c-MYC promoter. Nucleos. Nucleot. Nucl. 2006;25:951–968. doi: 10.1080/15257770600809913. [DOI] [PubMed] [Google Scholar]
- 18.Patel DJ, Phan AT, Kuryavyi V. Human telomere, oncogenic promoter and 5′-UTR G-quadruplexes: diverse higher order DNA and RNA targets for cancer therapeutics. Nucleic Acids Res. 2007;35:7429–7455. doi: 10.1093/nar/gkm711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.da Silva MW. NMR methods for studying quadruplex nucleic acids. Methods. 2007;43:264–277. doi: 10.1016/j.ymeth.2007.05.007. [DOI] [PubMed] [Google Scholar]
- 20.Gilbert DE, Feigon J. Multistranded DNA structures. Curr. Opin. Struct. Biol. 1999;9:305–314. doi: 10.1016/S0959-440X(99)80041-4. [DOI] [PubMed] [Google Scholar]
- 21.Phan AT, Kuryavyi V, Patel DJ. DNA architecture: from G to Z. Curr. Opin. Struct. Biol. 2006;16:288–298. doi: 10.1016/j.sbi.2006.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Burge S, Parkinson GN, Hazel P, Todd AK, Neidle S. Quadruplex DNA: sequence, topology and structure. Nucleic Acids Res. 2006;34:5402–5415. doi: 10.1093/nar/gkl655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huppert JL. Four-stranded DNA: cancer, gene regulation and drug development. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2007;365:2969–2984. doi: 10.1098/rsta.2007.0011. [DOI] [PubMed] [Google Scholar]
- 24.Huppert JL. Four-stranded nucleic acids: structure, function and targeting of G-quadruplexes. Chem. Soc. Rev. 2008;37:1375–1384. doi: 10.1039/b702491f. [DOI] [PubMed] [Google Scholar]
- 25.Mergny JL, Riou JF, Mailliet P, Teulade-Fichou MP, Gilson E. Natural and pharmacological regulation of telomerase. Nucleic Acids Res. 2002;30:839–865. doi: 10.1093/nar/30.4.839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hardin CC, Perry AG, White K. Thermodynamic and kinetic characterization of the dissociation and assembly of quadruplex nucleic acids. Biopolymers. 2000;56:147–194. doi: 10.1002/1097-0282(2000/2001)56:3<147::AID-BIP10011>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
- 27.Mergny JL, De Cian A, Ghelab A, Sacca B, Lacroix L. Kinetics of tetramolecular quadruplexes. Nucleic Acids Res. 2005;33:81–94. doi: 10.1093/nar/gki148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Phan AT, Kuryavyi V, Luu KN, Patel DJ. Structure of two intramolecular G-quadruplexes formed by natural human telomere sequences in K+ solution. Nucleic Acids Res. 2007;35:6517–6525. doi: 10.1093/nar/gkm706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Freyer MW, Buscaglia R, Kaplan K, Cashman D, Hurley LH, Lewis EA. Biophysical studies of the c-MYC NHE III1 promoter: Model quadruplex interactions with a cationic porphyrin. Biophys. J. 2007;92:2007–2015. doi: 10.1529/biophysj.106.097246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Okamoto K, Sannohe Y, Mashimo T, Suguyama H, Terazime M. G-Quadruplex structures of human telomere DNA examined by single molecule FRET and BrG-substitution. Bioorg. Med. Chem. 2008;16:6873–6879. doi: 10.1016/j.bmc.2008.05.053. [DOI] [PubMed] [Google Scholar]
- 31.Engelhart AE, Plavec J, Persil O, Hud NV. Nucleic Acid-Metal Ion Interactions. In: Hud NV, editor. London: Royal Society of Chemistry; 2008. [Google Scholar]
- 32.Esposito V, Galleone A, Mayol L, Oliviero G, Virgilio A, Randazzo L. A topological classification of G-quadruplex structures. Nucleosides Nucleotides Nucleic Acids. 2007;26:1155–1159. doi: 10.1080/15257770701527059. [DOI] [PubMed] [Google Scholar]
- 33.Webba da Silva M. Geometric formalism for DNA quadruplex folding. Chemistry. 2007;13:9738–9745. doi: 10.1002/chem.200701255. [DOI] [PubMed] [Google Scholar]
- 34.Phan AT, Kuryavyi V, Burge S, Neidle S, Patel DJ. Structure of an unprecedented G-quadruplex scaffold in the human c-kit promoter. J. Am. Chem. Soc. 2007;129:4386–4392. doi: 10.1021/ja068739h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Parkinson GN, Lee MP, Neidle S. Crystal structure of parallel quadruplexes from human telomeric DNA. Nature. 2002;417:876–880. doi: 10.1038/nature755. [DOI] [PubMed] [Google Scholar]
- 36.Schultze P, Macaya RF, Feigon J. Three-dimensional solution structure of the thrombin-binding DNA aptamer d(GGTTGGTGTGGTTGG) J. Mol. Biol. 1994;235:1532–1547. doi: 10.1006/jmbi.1994.1105. [DOI] [PubMed] [Google Scholar]
- 37.Dai J, Chen D, Jones RA, Hurley LH, Yang D. NMR solution structure of the major G-quadruplex structure formed in the human BCL2 promoter region. Nucleic Acids Res. 2006;34:5133–5144. doi: 10.1093/nar/gkl610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Luu KN, Phan AT, Kuryavyi V, Lacroix L, Patel DJ. Structure of the human telomere in K+ solution: an intramolecular (3 + 1) G-quadruplex scaffold. J. Am. Chem. Soc. 2006;128:9963–9970. doi: 10.1021/ja062791w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yang Y, Patel DJ. Solution structure of the human telomeric repeat d[AG3(T2AG3)3] G-tetraplex. Structure. 1993;1:263–282. doi: 10.1016/0969-2126(93)90015-9. [DOI] [PubMed] [Google Scholar]
- 40.Kuryavyi V, Majumdar A, Shallop A, Chernichenko N, Skripkin E, Jones R, Patel DJ. A double chain reversal loop and two diagonal loops define the architecture of a unimolecular DNA quadruplex containing a pair of stacked G(syn)-G(syn)-G(anti)-G(anti) tetrads flanked by a G-(T-T) Triad and a T-T-T triple. J. Mol. Biol. 2001;310:181–194. doi: 10.1006/jmbi.2001.4759. [DOI] [PubMed] [Google Scholar]
- 41.Dai J, Punchihewa C, Ambrus A, Chen D, Jones RA, Yang D. Structure of the intramolecular human telomeric G-quadruplex in potassium solution: a novel adenine triple formation. Nucleic Acids Res. 2007;35:2440–2450. doi: 10.1093/nar/gkm009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dai J, Carver M, Punchihewa C, Jones RA, Yang D. Structure of the Hybrid-2 type intramolecular human telomeric G-quadruplex in K+ solution: insights into structure polymorphism of the human telomeric sequence. Nucleic Acids Res. 2007;35:4927–4940. doi: 10.1093/nar/gkm522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Phan AT, Kuryavyi V, Luu KN, Patel DJ. Structure of two intramolecular G-quadruplexes formed by natural human telomere sequences in K+ solution. Nucleic Acids Res. 2007;35:6517–6525. doi: 10.1093/nar/gkm706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Phillips K, Dauter Z, Murchie AI, Lilley DM, Luisi B. The crystal structure of a parallel-stranded guanine tetraplex at 0.95 A resolution. J. Mol. Biol. 1997;273:171–182. doi: 10.1006/jmbi.1997.1292. [DOI] [PubMed] [Google Scholar]
- 45.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dong F, Olsen B, Baker NA. Vol. 84. San Diego: Academic Press; 2008. Biophysical Tools for Biologists: Vol 1 in Vitro Techniques; pp. 843–870. [Google Scholar]
- 47.Dapic V, Abdomerovic V, Marrington R, Peberdy J, Rodger A, Trent JO, Bates PJ. Biophysical and biological properties of quadruplex oligodeoxyribonucleotides. Nucleic Acids Res. 2003;31:2097–2107. doi: 10.1093/nar/gkg316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lane AN. Nuclear magnetic resonance studies of drug-DNA complexes in solution. Meths. Enzymol. 2001;340:252–281. doi: 10.1016/s0076-6879(01)40426-5. [DOI] [PubMed] [Google Scholar]
- 49.Feigon J, Koshlap KM, Smith FW. Nucl. Magn. Reson. Nucleic Acids. 1995;261:225–255. doi: 10.1016/s0076-6879(95)61012-x. [DOI] [PubMed] [Google Scholar]
- 50.Dai JX, Carver M, Punchihewa C, Jones RA, Yang DZ. Structure of the Hybrid-2 type intramolecular human telomeric G-quadruplex in K+ solution: insights into structure polymorphism of the human telomeric sequence. Nucleic Acids Res. 2007;35:4927–4940. doi: 10.1093/nar/gkm522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sponer J, Spackova N. Molecular dynamics simulations and their application to four-stranded DNA. Methods. 2007;43:278–290. doi: 10.1016/j.ymeth.2007.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Perez A, Marchan I, Svozil D, Sponer J, Cheatham TE, Laughton CA, Orozco M. Refinement of the AMBER force field for nucleic acids: improving the description of alpha/gamma conformers. Biophys. J. 2007;92:3817–3829. doi: 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fadrna E, Spackova N, Stefl R, Koca J, Cheatham TE, Sponer J. Molecular dynamics simulations of guanine quadruplex loops: Advances and force field limitations. Biophys. J. 2004;87:227–242. doi: 10.1529/biophysj.103.034751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jayaram B, McConnell K, Dixit SB, Das A, Beveridge DL. Free-energy component analysis of 40 protein-DNA complexes: a consensus view on the thermodynamics of binding at the molecular level. J. Comput. Chem. 2002;23:1–14. doi: 10.1002/jcc.10009. [DOI] [PubMed] [Google Scholar]
- 55.Trent JO. Drug-nucleic acid interactions. Meths. Enzymol. 2001:340, 290–326. [Google Scholar]
- 56.Stefl R, Cheatham TE, Spackova N, Fadrna E, Berger I, Koca J, Sponer J. Formation pathways of a guanine-quadruplex DNA revealed by molecular dynamics and thermodynamic analysis of the substates. Biophys. J. 2003;85:1787–1804. doi: 10.1016/S0006-3495(03)74608-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Stefl R, Spackova N, Berger I, Koca J, Sponer J. Molecular dynamics of DNA quadruplex molecules containing inosine, 6-thioguanine and 6-thiopurine. Biophys. J. 2001;80:455–468. doi: 10.1016/S0006-3495(01)76028-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Perez A, Lankas F, Luque FJ, Orozco M. Towards a molecular dynamics consensus view of B-DNA flexibility. Nucleic Acids Res. 2008;36:2379–2394. doi: 10.1093/nar/gkn082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ren JS, Qu XG, Trent JO, Chaires JB. Tiny telomere DNA. Nucleic Acids Res. 2002;30:2307–2315. doi: 10.1093/nar/30.11.2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Sun D, Liu WJ, Guo KX, Rusche JJ, Ebbinghaus S, Gokhale V, Hurley LH. The proximal promoter region of the human vascular endothelial growth factor gene has a G-quadruplex structure that can be targeted by G-quadruplex-interactive agents. Mol. Cancer Ther. 2008;7:880–889. doi: 10.1158/1535-7163.MCT-07-2119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Li J, Correia JJ, Wang L, Trent JO, Chaires JB. Not so crystal clear: the structure of the human telomere G-quadruplex in solution differs from that present in a crystal. Nucleic Acids Res. 2005;33:4649–4659. doi: 10.1093/nar/gki782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Rachwal PA, Brown T, Fox KR. Effect of G-tract length on the topology and stability of intramolecular DNA quadruplexes. Biochemistry. 2007;46:3036–3044. doi: 10.1021/bi062118j. [DOI] [PubMed] [Google Scholar]
- 63.Lee JY, Yoon JM, Kihm HW, Kim DS. Structural diversity and extreme stability of unimolecular Oxytricha nova telomeric G-quadruplex. Biochemistry. 2008;47:3389–3396. doi: 10.1021/bi702013d. [DOI] [PubMed] [Google Scholar]
- 64.Antonacci C, Chaires JB, Sheardy RD. Biophysical characterization of the human telomeric (TTAGGG)(4) repeat in a potassium solution. Biochemistry. 2007;46:4654–4660. doi: 10.1021/bi602511p. [DOI] [PubMed] [Google Scholar]
- 65.Guo K, Pourpak A, Beetz-Rogers K, Gokhale V, Sun D, Hurley LH. Formation of pseudosymmetrical G-quadruplex and i-motif structures in the proximal promoter region of the RET oncogene. J. Am. Chem. Soc. 2007;129:10220–10228. doi: 10.1021/ja072185g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Cantor CR, Schimmel PR. Biophysical Chemistry. San Francisco: W.H. Freeman; 1980. [Google Scholar]
- 67.Sprecher CA, Baase WA, Johnson WC. Conformation and circular-dichroism of DNA. Biopolymers. 1979;18:1009–1019. doi: 10.1002/bip.1979.360180418. [DOI] [PubMed] [Google Scholar]
- 68.Johnson WC, Itzkowit MS, Tinoco I. Circular-dichroism of polynucleotides – dimers as a function of conformation. Biopolymers. 1972;11:225–&. doi: 10.1002/bip.1972.360110117. [DOI] [PubMed] [Google Scholar]
- 69.Woody RW. Biochemical spectroscopy. Meths. Enzymol. 1995;246:34–71. doi: 10.1016/0076-6879(95)46006-3. [DOI] [PubMed] [Google Scholar]
- 70.Sreerama N, Woody RW. Numerical computer methods, Pt D. Meths. Enzymol. 2004;383:318–351. doi: 10.1016/S0076-6879(04)83013-1. [DOI] [PubMed] [Google Scholar]
- 71.Ito H, Tanaka S, Miyasaka M. Circular dichroism spectra of DNA quadruplexes [d(G(5)T(5))](4) as formed with G(4) and T-4 tetrads and [d(G(5)T(5)) center dot d(A(5)C(5))](2) as formed with Watson-Crick-like (G-C)(2) and (T-A)(2) tetrads. Biopolymers. 2002;65:61–80. doi: 10.1002/bip.10162. [DOI] [PubMed] [Google Scholar]
- 72.Gray DM, Wen JD, Gray CW, Repges R, Repges C, Raabe G, Fleischhauer J. Measured and calculated CD spectra of G-quartets stacked with the same or opposite polarities. Chirality. 2008;20:431–440. doi: 10.1002/chir.20455. [DOI] [PubMed] [Google Scholar]
- 73.Monchaud D, Teulade-Fichou MP. A hitchhiker's guide to G-quadruplex ligands. Org. Biomol. Chem. 2008;6:627–636. doi: 10.1039/b714772b. [DOI] [PubMed] [Google Scholar]
- 74.Brown NM, Rachwal PA, Brown T, Fox KR. Exceptionally slow kinetics of the intramolecular quadruplex formed by the Oxytricha telomeric repeat. Org. Biomol. Chem. 2005;3:4153–4157. doi: 10.1039/b511706b. [DOI] [PubMed] [Google Scholar]
- 75.Risitano A, Fox KR. Stability of intramolecular DNA quadruplexes: comparison with DNA duplexes. Biochemistry. 2003;42:6507–6513. doi: 10.1021/bi026997v. [DOI] [PubMed] [Google Scholar]
- 76.Koeppel F, Riou JF, Laoui A, Mailliet P, Arimondo PB, Labit D, Petitgenet O, Helene C, Mergny JL. Ethidium derivatives bind to G-quartets, inhibit telomerase and act as fluorescent probes for quadruplexes. Nucleic Acids Res. 2001;29:1087–1096. doi: 10.1093/nar/29.5.1087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Dale RE, Eisinger J. Intramolecular distances determined by energy-transfer – dependence on orientational freedom of donor and acceptor. Biopolymers. 1974;13:1573–1605. [Google Scholar]
- 78.Lakowicz JR. New York: Kluwer Academic; 1999. Principles of Fluorescence Spectroscopy. [Google Scholar]
- 79.Altenbach C, Cai KW, Klein-Seetharaman J, Khorana FG, Hubbell WL. Structure and function in rhodopsin: mapping light-dependent changes in distance between residue 65 in helix TM1 and residues in the sequence 306-319 at the cytoplasmic end of helix TM7 and in helix H8. Biochemistry. 2001;40:15483–15492. doi: 10.1021/bi011546g. [DOI] [PubMed] [Google Scholar]
- 80.Yang K, Farrens DL, Altenbach C, Farahbakhsh ZT, Hubbell WL, Khorana HG. Structure and function in rhodopsin. Cysteines 65 and 316 are in proximity in a rhodopsin mutant as indicated by disulfide formation and interactions between attached spin labels. Biochemistry. 1996;35:14040–14046. doi: 10.1021/bi962113u. [DOI] [PubMed] [Google Scholar]
- 81.Cai Q, Kusnetzow AK, Hubbell WL, Haworth IS, Gacho GPC, Van Eps N, Hideg K, Chambers EJ, Qin PZ. Site-directed spin labeling measurements of nanometer distances in nucleic acids using a sequence-independent nitroxide probe. Nucleic Acids Res. 2006;34:4722–4730. doi: 10.1093/nar/gkl546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Guéron M, Leroy JL. Nuclear magnetic resonance and nucleic acids. Meths. Enzymol. 1995;261:383–413. doi: 10.1016/s0076-6879(95)61018-9. [DOI] [PubMed] [Google Scholar]
- 83.Phan AT, Patel DJ. Differentiation between unlabeled and very-low-level fully N-15,C-13-labeled nucleotides for resonance assignments in nucleic acids. J. Biomol. NMR. 2002;23:257–262. doi: 10.1023/a:1020277223482. [DOI] [PubMed] [Google Scholar]
- 84.Dingley AJ, Masse JE, Feigon J, Grzesiek S. Characterization of the hydrogen bond network in guanosine quartets by internucleotide (3h)J(NC') and (2h)J(NN) scalar couplings. J. Biomol. NMR. 2000;16:279–289. doi: 10.1023/a:1008307115641. [DOI] [PubMed] [Google Scholar]
- 85.Dingley AJ, Masse JE, Peterson RD, Barfield M, Feigon J, Grzesiek S. Internucleotide scalar couplings across hydrogen bonds in Watson-Crick and Hoogsteen base pairs of a DNA triplex. J. Am. Chem. Soc. 1999;121:6019–6027. [Google Scholar]
- 86.Dingley AJ, Peterson RD, Grzesiek S, Feigon J. Characterization of the cation and temperature dependence of DNA quadruplex hydrogen bond properties using high-resolution NMR. J. Am. Chem. Soc. 2005;127:14466–14472. doi: 10.1021/ja0540369. [DOI] [PubMed] [Google Scholar]
- 87.Liu AZ, Majumdar A, Hu WD, Kettani A, Skripkin E, Patel DJ. NMR detection of N-H center dot center dot center dot O=C hydrogen bonds in C-13,N-15-labeled nucleic acids. J. Am. Chem. Soc. 2000;122:3206–3210. [Google Scholar]
- 88.Majumdar A, Patel DJ. Identifying hydrogen bond alignments in multistranded DNA architectures by NMR. Acc. Chem. Res. 2002;35:1–11. doi: 10.1021/ar010097+. [DOI] [PubMed] [Google Scholar]
- 89.Grzesiek S, Cordier F, Dingley AJ. Nuclear magnetic resonance of biological macromolecules, Pt A. Meths. Enzymol. 2001;338:111–133. doi: 10.1016/s0076-6879(02)38217-x. [DOI] [PubMed] [Google Scholar]
- 90.Wohnert J, Dingley AJ, Stoldt M, Gorlach M, Grzesiek S, Brown LR. Direct identification of NH center dot center dot center dot N hydrogen bonds in non-canonical base pairs of RNA by NMR spectroscopy. Nucleic Acids Res. 1999;27:3104–3110. doi: 10.1093/nar/27.15.3104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Dingley AJ, Cordier F, Grzesiek S. An introduction to hydrogen bond scalar couplings. Concepts Magn. Reson. 2001;13:103–127. [Google Scholar]
- 92.Eimer W, Pecora R. Rotational and translational diffusion of short rodlike molecules in solution – oligonucleotides. J. Chem. Phys. 1991;94:2324–2329. [Google Scholar]
- 93.Eimer W, Williamson JR, Boxer SG, Pecora R. Characterization of the overall and internal dynamics of short oligonucleotides by depolarized dynamic light-scattering and NMR relaxation measurements. Biochemistry. 1990;29:799–811. doi: 10.1021/bi00455a030. [DOI] [PubMed] [Google Scholar]
- 94.Delatorre JG, Martinez MCL, Tirado MM. Dimensions of short, rodlike macromolecules from translational and rotational diffusion-coefficients – study of the gramicidin dimer. Biopolymers. 1984;23:611–615. [Google Scholar]
- 95.Tirado MM, Garciadelatorre J. Rotational-dynamics of rigid, symmetric top macromolecules – application to circular-cylinders. J. Chem. Phys. 1980;73:1986–1993. [Google Scholar]
- 96.Tirado MM, Garciadelatorre J. Translational friction coefficients of rigid, symmetric top macromolecules – application to circular-cylinders. J. Chem. Phys. 1979;71:2581–2587. [Google Scholar]
- 97.de la Torre JG, Huertas ML, Carrasco B. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys. J. 2000;78:719–730. doi: 10.1016/S0006-3495(00)76630-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Byron O. Biophysical Tools for Biologists: Vol 1 in Vitro Techniques. Vol. 84. San Diego: 2008. Hydrodynamic modeling: The solution conformation of macromolecules and their complexes; pp. 327–375. [DOI] [PubMed] [Google Scholar]
- 99.Parkinson GN, Lee MPH, Neidle S. Crystal structure of parallel quadruplexes from human telomeric DNA. Nature. 2002;417:876–880. doi: 10.1038/nature755. [DOI] [PubMed] [Google Scholar]
- 100.McRorie DK, Voelker PJ. Fullerton, CA: Beckman Instruments, Inc; 1993. Self-associating Systems in the Analytical Ultracentrifuge. [Google Scholar]
- 101.Bonifacio GF, Brown T, Conn GL, Lane AN. Comparison of the electrophoretic and hydrodynamic properties of DNA and RNA oligonucleotide duplexes. Biophys. J. 1997;73:1532–1538. doi: 10.1016/S0006-3495(97)78185-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Kratky O, Leopold H, Stabinger H, editors. New York: Academic Press; 1973. The Determination of the Partial Specific Volume by a Mechanical Oscillator Technique. [DOI] [PubMed] [Google Scholar]
- 103.de la Torre JG. Hydration from hydrodynamics. General considerations and applications of bead modelling to globular proteins. Biophys. Chem. 2001;93:159–170. doi: 10.1016/s0301-4622(01)00218-6. [DOI] [PubMed] [Google Scholar]
- 104.Lane AN, Lefevre JF. Vol. 239. San Diego: Academic Press Inc; 1994. Nuclear Magnetic Resonance, Pt C; pp. 596–619. [Google Scholar]
- 105.Birchall AJ, Lane AN. Anisotropic rotation in nucleic-acid fragments – significance for determination of structures from NMR data. Eur. Biophys. J. 1990;19:73–78. doi: 10.1007/BF00185089. [DOI] [PubMed] [Google Scholar]
- 106.Gabel F, Simon B, Sattler M. A target function for quaternary structural refinement from small angle scattering and NMR orientational restraints. Eur. Biophys. J. Biophys. Lett. 2006;35:313–327. doi: 10.1007/s00249-005-0037-3. [DOI] [PubMed] [Google Scholar]
- 107.Grishaev A, Wu J, Trewhella J, Bax A. Refinement of multidomain protein structures by combination of solution small-angle X-ray scattering and NMR data. J. Am. Chem. Soc. 2005;127:16621–16628. doi: 10.1021/ja054342m. [DOI] [PubMed] [Google Scholar]
- 108.Overbeek JTG, Wiersma PH. In: Electrophoresis. Bier M, editor. New York; 1967. pp. 1–52. [Google Scholar]
- 109.Stellwagen E, Stellwagen NC. Probing the electrostatic shielding of DNA with capillary electrophoresis. Biophys. J. 2003;84:1855–1866. doi: 10.1016/S0006-3495(03)74993-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Crothers DM, Drak J, Kahn JD, Levene SD. DNA bending, flexibility, and helical repeat by cyclization kinetics. Methods Enzymol. 1992;212:3–29. doi: 10.1016/0076-6879(92)12003-9. [DOI] [PubMed] [Google Scholar]
- 111.Barbic A, Zimmer DP, Crothers DM. Structural origins of adenine-tract bending. Proc. Natl Acad. Sci. USA. 2003;100:2369–2373. doi: 10.1073/pnas.0437877100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Record MT, Anderson CF, Lohman TM. Thermodynamic analysis of ion effects on the binding and conformational equilibria of protein and nucleic acids. Q. Rev. Biophys. 1978;11:103–178. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
- 113.Anderson CF, Record MT. Salt nucleic-acid interactions. Annu. Rev. Phys. Chem. 1995;46:657–700. doi: 10.1146/annurev.pc.46.100195.003301. [DOI] [PubMed] [Google Scholar]
- 114.Manning GS. Electrostatic free energies of spheres, cylinders, and planes in counterion condensation theory with some applications. Macromolecules. 2007;40:8071–8081. [Google Scholar]
- 115.Manning GS. Counterion condensation on charged spheres, cylinders, and planes. J. Phys. Chem. B. 2007;111:8554–8559. doi: 10.1021/jp0670844. [DOI] [PubMed] [Google Scholar]
- 116.Qian H, Schellman JA. Transformed Poisson-Boltzmann relations and ionic distributions. J. Phys. Chem. B. 2000;104:11528–11540. [Google Scholar]
- 117.Lane AN, Jenkins TC. Thermodynamics of nucleic acids and their interactions with ligands. Q. Rev. Biophys. 2000;33:255–306. doi: 10.1017/s0033583500003632. [DOI] [PubMed] [Google Scholar]
- 118.Han HY, Hurley LH, Salazar M. A DNA polymerase stop assay for G-quadruplex-interactive compounds. Nucleic Acids Res. 1999;27:537–542. doi: 10.1093/nar/27.2.537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Risitano A, Fox KR. Inosine substitutions demonstrate that intramolecular DNA quadruplexes adopt different conformations in the presence of sodium and potassium. Bioorg. Med. Chem. Lett. 2005;15:2047–2050. doi: 10.1016/j.bmcl.2005.02.050. [DOI] [PubMed] [Google Scholar]
- 120.Raymond E, Soria JC, Izbicka E, Boussin F, Hurley L, Von Hoff DD. DNA G-quadruplexes, telomere-specific proteins and telomere-associated enzymes as potential targets for new anticancer drugs. Invest. New Drugs. 2000;18:123–137. doi: 10.1023/a:1006373812586. [DOI] [PubMed] [Google Scholar]
- 121.Davis JT. G-quartets 40 years later: from 5′-GMP to molecular biology and supramolecular chemistry. Angew. Chem. Int. Ed. 2004;43:668–698. doi: 10.1002/anie.200300589. [DOI] [PubMed] [Google Scholar]
- 122.Phan AT, Kuryavyi V, Gaw HY, Patel DJ. Small-molecule interaction with a five-guanine-tract G-quadruplex structure from the human MYC promoter. Nat. Chem. Biol. 2005;1:167–173. doi: 10.1038/nchembio723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Pan BC, Shi K, Sundaralingam M. Crystal structure of an RNA quadruplex containing inosine tetrad: implications for the roles of NH2 group in purine tetrads. J. Mol. Biol. 2006;363:451–459. doi: 10.1016/j.jmb.2006.08.022. [DOI] [PubMed] [Google Scholar]
- 124.Fersht A. New York: W.H. Freeman & Co.; 1999. Structure and Mechanism in Protein Science. [Google Scholar]
- 125.Fang GW, Cech TR. The beta-subunit of oxytricha telomere-binding protein promotes g-quartet formation by telomeric DNA. Cell. 1993;74:875–885. doi: 10.1016/0092-8674(93)90467-5. [DOI] [PubMed] [Google Scholar]
- 126.Price CM, Cech TR. Telomeric DNA protein interactions of Oxytricha macronuclear DNA. Genes Dev. 1987;1:783–793. doi: 10.1101/gad.1.8.783. [DOI] [PubMed] [Google Scholar]
- 127.SantaLucia J. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl Acad. Sci. USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Kierzek E, Kierzek R. The thermodynamic stability of RNA duplexes and hairpins containing N-6-alkyladenosines and 2-methylthio-N-6-alkyladenosines. Nucleic Acids Res. 2003;31:4472–4480. doi: 10.1093/nar/gkg633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Antao VP, Lai SY, Tinoco I. A thermodynamic study of unusually stable RNA and DNA hairpins. Nucleic Acids Res. 1991;19:5901–5905. doi: 10.1093/nar/19.21.5901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Proctor DJ, Ma HR, Kierzek E, Kierzek R, Gruebele M, Bevilacqua PC. Folding thermodynamics and kinetics of YNMG RNA hairpins: specific incorporation of 8-bromoguanosine leads to stabilization by enhancement of the folding rate. Biochemistry. 2004;43:14004–14014. doi: 10.1021/bi048213e. [DOI] [PubMed] [Google Scholar]
- 131.Jelesarov I, Crane-Robinson C, Privalov PL. The energetics of HMG box interactions with DNA: thermodynamic description of the target DNA duplexes. J. Mol. Biol. 1999;294:981–995. doi: 10.1006/jmbi.1999.3284. [DOI] [PubMed] [Google Scholar]
- 132.Mergny JL, Lacroix L. Analysis of thermal melting curves. Oligonucleotides. 2003;13:515–537. doi: 10.1089/154545703322860825. [DOI] [PubMed] [Google Scholar]
- 133.Cantor CR, Schimmel PR. Biophysical Chemistry. Vol. III. San Francisco: W.H. Freeman & Co.; 1980. [Google Scholar]
- 134.Olsen CM, Gmeiner WH, Marky LA. Unfolding of G-quadruplexes: energetic, and ion and water contributions of G-quartet stacking. J. Phys. Chem. B. 2006;110:6962–6969. doi: 10.1021/jp0574697. [DOI] [PubMed] [Google Scholar]
- 135.Breslauer KJ. Extracting thermodynamic data from equilibrium melting curves for oligonucleotide order-disorder transitions. Methods Enzymol. 1995;259:221–242. doi: 10.1016/0076-6879(95)59046-3. [DOI] [PubMed] [Google Scholar]
- 136.Marky LA, Breslauer KJ. Calculating thermodynamic data for transitions of any molecularity from equilibrium melting curves. Biopolymers. 1987;26:1601–1620. doi: 10.1002/bip.360260911. [DOI] [PubMed] [Google Scholar]
- 137.Mergny JL, Lacroix L. Analysis of thermal melting curves. Oligonucleotides. 2003;13:515–537. doi: 10.1089/154545703322860825. [DOI] [PubMed] [Google Scholar]
- 138.Mergny JL, Phan AT, Lacroix L. Following G-quartet formation by UV-spectroscopy. FEBS Lett. 1998;435:74–78. doi: 10.1016/s0014-5793(98)01043-6. [DOI] [PubMed] [Google Scholar]
- 139.Rachwal PA, Fox KR. Quadruplex melting. Methods. 2007;43:291–301. doi: 10.1016/j.ymeth.2007.05.004. [DOI] [PubMed] [Google Scholar]
- 140.Herrera JE, Chaires JB. A premelting conformational transition in poly(dA)-Poly(dT) coupled to daunomycin binding. Biochemistry. 1989;28:1993–2000. doi: 10.1021/bi00431a006. [DOI] [PubMed] [Google Scholar]
- 141.Allen DL, Pielak GJ. Baseline length and automated fitting of denaturation data. Protein Sci. 1998;7:1262–1263. doi: 10.1002/pro.5560070524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Cooper A. Thermodynamic analysis of biomolecular interactions. Curr. Opin. Chem. Biol. 1999;3:557–563. doi: 10.1016/s1367-5931(99)00008-3. [DOI] [PubMed] [Google Scholar]
- 143.Prehoda KE, Mooberry ES, Markley JL. Pressure denaturation of proteins: evaluation of compressibility effects. Biochemistry. 1998;37:5785–5790. doi: 10.1021/bi980384u. [DOI] [PubMed] [Google Scholar]
- 144.Lumry R, Biltonen R. Validity of the ‘two-state’ hypothesis for conformational transitions of proteins. Biopolymers. 1966;4:917–944. doi: 10.1002/bip.1966.360040808. [DOI] [PubMed] [Google Scholar]
- 145.Wallimann P, Kennedy RJ, Miller JS, Shalongo W, Kemp DS. Dual wavelength parametric test of two-state models for circular dichroism spectra of helical polypeptides: anomalous dichroic properties of alanine-rich peptides. J. Am. Chem. Soc. 2003;125:1203–1220. doi: 10.1021/ja0275360. [DOI] [PubMed] [Google Scholar]
- 146.Haq I, Chowdhry BZ, Chaires JB. Singular value decomposition of 3-D DNA melting curves reveals complexity in the melting process. Eur. Biophys. J. 1997;26:419–426. doi: 10.1007/s002490050096. [DOI] [PubMed] [Google Scholar]
- 147.Hendler RW, Shrager RI. Deconvolutions based on singular value decomposition and the pseudoinverse: a guide for beginners. J. Biochem. Biophys. Methods. 1994;28:1–33. doi: 10.1016/0165-022x(94)90061-2. [DOI] [PubMed] [Google Scholar]
- 148.Ren J, Qu X, Trent JO, Chaires JB. Tiny telomere DNA. Nucleic Acids Res. 2002;30:2307–2315. doi: 10.1093/nar/30.11.2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Jaumot J, Escaja N, Gargallo R, Gonzalez C, Pedroso E, Tauler R. Multivariate curve resolution: a powerful tool for the analysis of conformational transitions in nucleic acids. Nucleic Acids Res. 2002;30:92. doi: 10.1093/nar/gnf091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Spolar RS, Record M.T., Jr Coupling of local folding to site-specific binding of proteins to DNA [see comments] Science. 1994;263:777–784. doi: 10.1126/science.8303294. [DOI] [PubMed] [Google Scholar]
- 151.Prabhu NV, Sharp KA. Heat capacity in proteins. Ann. Rev. Phys. Chem. 2005;56:521–548. doi: 10.1146/annurev.physchem.56.092503.141202. [DOI] [PubMed] [Google Scholar]
- 152.Chaires JB. Possible origin of differences between van't Hoff and calorimetric enthalpy estimates. Biophys. Chem. 1997;64:15–23. doi: 10.1016/s0301-4622(96)02205-3. [DOI] [PubMed] [Google Scholar]
- 153.Haq I, Chowdhry BZ, Jenkins TC. Calorimetric techniques in the study of high-order DNA-drug interactions. Methods Enzymol. 2001;340:109–149. doi: 10.1016/s0076-6879(01)40420-4. [DOI] [PubMed] [Google Scholar]
- 154.Balagurumoorthy P, Brahmachari SK. Structure and stability of human telomeric sequence. J. Biol. Chem. 1994;269:21858–21869. [PubMed] [Google Scholar]
- 155.Li W, Wu P, Ohmichi T, Sugimoto N. Characterization and thermodynamic properties of quadruplex/duplex competition. FEBS Lett. 2002;526:77–81. doi: 10.1016/s0014-5793(02)03118-6. [DOI] [PubMed] [Google Scholar]
- 156.Risitano A, Fox KR. Stability of intramolecular DNA quadruplexes: comparison with DNA duplexes. Biochemistry. 2003;42:6507–6513. doi: 10.1021/bi026997v. [DOI] [PubMed] [Google Scholar]
- 157.Antonacci C, Chaires JB, Sheardy RD. Biophysical characterization of the human telomeric (TTAGGG)4 repeat in a potassium solution. Biochemistry. 2007;46:4654–4660. doi: 10.1021/bi602511p. [DOI] [PubMed] [Google Scholar]
- 158.Majhi PR, Qi J, Tang CF, Shafer RH. Heat capacity changes associated with guanine quadruplex formation: an isothermal titration calorimetry study. Biopolymers. 2008;89:302–309. doi: 10.1002/bip.20918. [DOI] [PubMed] [Google Scholar]
- 159.Majhi PR, Qi JY, Tang CF, Shafer RH. Heat capacity changes associated with guanine quadruplex formation: an isothermal titration calorimetry study. Biopolymers. 2008;89:302–309. doi: 10.1002/bip.20918. [DOI] [PubMed] [Google Scholar]
- 160.Robertson AD, Murphy KP. Protein structure and the energetics of protein stability. Chem. Rev. 1997;97:1251–1267. doi: 10.1021/cr960383c. [DOI] [PubMed] [Google Scholar]
- 161.Holbrook JA, Capp MW, Saecker RM, Record MT. Enthalpy and heat capacity changes for formation of an oligomeric DNA duplex: interpretation in terms of coupled processes of formation and association of single-stranded helices. Biochemistry. 1999;38:8409–8422. doi: 10.1021/bi990043w. [DOI] [PubMed] [Google Scholar]
- 162.Rouzina I, Bloomfield VA. Heat capacity effects on the melting of DNA. 1. General aspects. Biophys. J. 1999;77:3242–3251. doi: 10.1016/S0006-3495(99)77155-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Rouzina I, Bloomfield VA. Heat capacity effects on the melting of DNA. 2. Analysis of nearest-neighbor base pair effects. Biophys. J. 1999;77:3252–3255. doi: 10.1016/S0006-3495(99)77156-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Gray RD, Chaires JB. Kinetics and mechanism of K+- and Na+-induced folding of models of human telomeric DNA into G-quadruplex structures. Nucleic Acids Res. 2008 doi: 10.1093/nar/gkn379. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Hazel P, Huppert J, Balasubramanian S, Neidle S. Loop-length-dependent folding of G-quadruplexes. J. Am. Chem. Soc. 2004;126:16405–16415. doi: 10.1021/ja045154j. [DOI] [PubMed] [Google Scholar]
- 166.Smarglasso N, Rosu F, Hsla W, Colson P, Baker ES, Bowers MT, De Pauw E, Gabelica V. G-Qaudruplex DNA assemblies: loop length, cation identity, and multimer formation. J. Am. Chem. Soc. 2008 doi: 10.1021/ja801535e. [Epub ahead of print; doi: 10.1021/ja80135e] [DOI] [PubMed] [Google Scholar]
- 167.Asensio JL, Lane AN, Dhesi J, Bergqvist S, Brown T. The contribution of cytosine protonation to the stability of parallel DNA triple helices. J. Mol. Biol. 1998;275:811–822. doi: 10.1006/jmbi.1997.1520. [DOI] [PubMed] [Google Scholar]
- 168.Mergny J-L, Gros J, De Cian A, Bourdoncle A, Rosu F, Saccà B, Guittat L, Amrane S, Mills M, Alberti P. In: Quadruplex Nucleic Acids. Neidle S, Balasubramanian S, editors. Cambridge: RSC Publishing; 2006. pp. 31–80. [Google Scholar]
- 169.Han H, Cliff CL, Hurley LH. Accelerated assembly of G-quadruplex structures by a small molecule. Biochemistry. 1999;38:6981–6986. doi: 10.1021/bi9905922. [DOI] [PubMed] [Google Scholar]
- 170.Wyatt JR, Davis PW, Freier SM. Kinetics of G-quartet-mediated tetramer formation. Biochemistry. 1996;35:8002–8008. doi: 10.1021/bi960124h. [DOI] [PubMed] [Google Scholar]
- 171.Risitano A, Fox KR. Influence of loop size on the stability of intramolecular DNA quadruplexes. Nucleic Acids Res. 2004;32:2598–2606. doi: 10.1093/nar/gkh598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Oliveberg M, Tan YJ, Fersht AR. Negative activation enthalpies in the kinetics of protein folding. Proc. Natl Acad. Sci. 1995;92:8926–8929. doi: 10.1073/pnas.92.19.8926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Oliveberg M, Tan YJ, Silow M, Fersht AR. The changing nature of the protein folding transition state: implications for the shape of the free-energy profile for folding. J. Mol. Biol. 1998;277:933–943. doi: 10.1006/jmbi.1997.1612. [DOI] [PubMed] [Google Scholar]
- 174.Chen SJ. RNA folding: conformational statistics, folding kinetics, and ion electrostatics. Annu. Rev. Biophys. 2008;37:97–214. doi: 10.1146/annurev.biophys.37.032807.125957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Ying L, Green JJ, Li H, Klenerman D, Balasubramanian S. Studies on the structure and dynamics of the human telomeric G quadruplex by single-molecule fluorescence resonance energy transfer. Proc. Natl Acad. Sci. USA. 2003;100:14629–14634. doi: 10.1073/pnas.2433350100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.Lee JY, Okumus B, Kim DS, Ha T. Extreme conformational diversity in human telomeric DNA. Proc. Natl Acad. Sci. USA. 2005;102:18938–18943. doi: 10.1073/pnas.0506144102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.Green JJ, Ying LM, Klenerman D, Balasubramanian S. Kinetics of unfolding the human telomeric DNA quadruplex using a PNA trap. J. Am. Chem. Soc. 2003;125:3763–3767. doi: 10.1021/ja029149w. [DOI] [PubMed] [Google Scholar]
- 178.Zhao Y, Kan Z, Zeng Z, Hao Y, Chen H, Tan Z. Determining the folding and unfolding rate constants of nucleic acids by biosensor. Application to telomere G-quadruplex. J. Am. Chem. Soc. 2004;126:13255–13264. doi: 10.1021/ja048398c. [DOI] [PubMed] [Google Scholar]
- 179.Schuck P. Reliable determination of binding affinity and kinetics using surface plasmon resonance biosensors. Curr. Opin. Biotechnol. 1997;8:498–502. doi: 10.1016/s0958-1669(97)80074-2. [DOI] [PubMed] [Google Scholar]
- 180.Schuck P. Use of surface plasmon resonance to probe the equilibrium and dynamic aspects of interactions between biological macromolecules. Ann. Rev. Biophys. Biomol. Struct. 1997;26:541–566. doi: 10.1146/annurev.biophys.26.1.541. [DOI] [PubMed] [Google Scholar]
- 181.Tanious FA, Nguyen B, Wilson WD. Biophysical Tools for Biologists: Vol 1 in Vitro Techniques. Vol. 84. San Diego: Academic Press; 2008. Biosensor-surface plasmon resonance methods for quantitative analysis of biomolecular interactions; pp. 53–77. [DOI] [PubMed] [Google Scholar]
- 182.Cantor CR, Schimmel PR. Biophysical Chemistry. San Francisco: W.H. Freeman; 1980. [Google Scholar]
- 183.Bardin C, Leroy JL. The formation pathway of tetramolecular G-quadruplexes. Nucleic Acids Res. 2008;36:477–488. doi: 10.1093/nar/gkm1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184.Schellman JA. Destabilization and stabilization of proteins. Q. Rev. Biophys. 2005;38:351–361. doi: 10.1017/S0033583505004099. [DOI] [PubMed] [Google Scholar]
- 185.Turner DH. Thermodynamics of base pairing. Curr. Opin. Struct. Biol. 1996;6:299–304. doi: 10.1016/s0959-440x(96)80047-9. [DOI] [PubMed] [Google Scholar]
- 186.SantaLucia J, Turner DH. Measuring the thermodynamics of RNA secondary structure formation. Biopolymers. 1997;44:309–319. doi: 10.1002/(SICI)1097-0282(1997)44:3<309::AID-BIP8>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- 187.Schroeder SJ, Burkard ME, Turner DH. The energetics of small internal loops in RNA. Biopolymers. 1999;52:157–167. doi: 10.1002/1097-0282(1999)52:4<157::AID-BIP1001>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 188.Schroeder SJ, Turner DH. Thermodynamic stabilities of internal loops with GU closing pairs in RNA. Biochemistry. 2001;40:11509–11517. doi: 10.1021/bi010489o. [DOI] [PubMed] [Google Scholar]
- 189.Chen G, Znosko BM, Jiao XQ, Turner DH. Factors affecting thermodynamic stabilities of RNA 3x3 internal loops. Biochemistry. 2004;43:12865–12876. doi: 10.1021/bi049168d. [DOI] [PubMed] [Google Scholar]
- 190.Powell SW, Jiang LH, Russu IM. Proton exchange and base pair opening in a DNA triple helix. Biochemistry. 2001;40:11065–11072. doi: 10.1021/bi010890a. [DOI] [PubMed] [Google Scholar]
- 191.Lane AN, Jenkins TC. Structures and properties of multi-stranded nucleic acids. Curr. Org. Chem. 2001;5:845–869. [Google Scholar]
- 192.Dong F, Olsen B, Baker NA. Correia JJ, Detrich HW. Biophsyical Tools for Biologists. Vol. 1. San Diego: Academic Press; 2008. pp. 844–871. [Google Scholar]
- 193.York DM, Yang WT, Lee H, Darden T, Pedersen LG. Toward the accurate modeling of DNA – the importance of long-range electrostatics. J. Am. Chem. Soc. 1995;117:5001–5002. [Google Scholar]
- 194.York DM, Darden TA, Pedersen LG. The effect of long-range electrostatic interactions in simulations of macromolecular crystals – a comparison of the Ewald and truncated list methods. J. Chem. Phys. 1993;99:8345–8348. [Google Scholar]
- 195.Darden TA, York DM, Pedersen LG. Particle mesh Ewald: an N log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 196.Ren PY, Ponder JW. Temperature and pressure dependence of the AMOEBA water model. J. Phys. Chem. B. 2004;108:13427–13437. [Google Scholar]
- 197.Ren PY, Ponder JW. Polarizable atomic multipole water model for molecular mechanics simulation. J. Phys. Chem. B. 2003;107:5933–5947. [Google Scholar]
- 198.Ren PY, Ponder JW. Consistent treatment of inter- and intramolecular polarization in molecular mechanics calculations. J. Comput. Chem. 2002;23:1497–1506. doi: 10.1002/jcc.10127. [DOI] [PubMed] [Google Scholar]
- 199.Dingley AJ, Grzesiek S. Direct observation of hydrogen bonds in nucleic acid base pairs by internucleotide (2)J(NN) couplings. J. Am. Chem. Soc. 1998;120:8293–8297. [Google Scholar]
- 200.Tanford C. Contribution of hydrophobic interactions to the stability of the globular conformation of proteins. J. Am. Chem. Soc. 1962;84:4240–4247. [Google Scholar]
- 201.Krueger AT, Kool ET. Model systems for understanding DNA base pairing. Curr. Opin. Chem. Biol. 2007;11:588–594. doi: 10.1016/j.cbpa.2007.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Schweitzer BA, Kool ET. Hydrophobic, non-hydrogen-bonding bases and base-pairs in DNA. J. Am. Chem. Soc. 1995;117:1863–1872. doi: 10.1021/ja00112a001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 203.Rachwal PA, Brown T, Fox KR. Sequence effects of single base loops in intramolecular quadruplex DNA. FEBS Lett. 2007;581:1657–1660. doi: 10.1016/j.febslet.2007.03.040. [DOI] [PubMed] [Google Scholar]
- 204.Shkel IA, Record MT. Effect of the number of nucleic acid oligomer charges on the salt dependence of stability (Delta G degrees(37)) and melting temperature (T-m): NLPB analysis of experimental data. Biochemistry. 2004;43:7090–7101. doi: 10.1021/bi036225e. [DOI] [PubMed] [Google Scholar]
- 205.Shkel IA, Tsodikov OV, Record MT. Asymptotic solution of the cylindrical nonlinear Poisson-Boltzmann equation at low salt concentration: analytic expressions for surface potential and preferential interaction coefficient. Proc. Natl Acad. Sci. USA. 2002;99:2597–2602. doi: 10.1073/pnas.032480699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 206.Spink CH, Chaires JB. Effects of hydration, ion release, and excluded volume on the melting of triplex and duplex DNA. Biochemistry. 1999;38:496–508. doi: 10.1021/bi9820154. [DOI] [PubMed] [Google Scholar]
- 207.Booth J, Brown T, Vadhia SJ, Lack O, Cummins WJ, Trent JO, Lane AN. Determining the origin of the stabilization of DNA by 5-aminopropynylation of pyrimidines. Biochemistry. 2005;44:4710–4719. doi: 10.1021/bi047561d. [DOI] [PubMed] [Google Scholar]
- 208.Qu XG, Chaires JB. Hydration changes for DNA intercalation reactions. J. Am. Chem. Soc. 2001;123:1–7. doi: 10.1021/ja002793v. [DOI] [PubMed] [Google Scholar]
- 209.Smirnov IV, Shafer RH. Electrostatics dominate quadruplex stability. Biopolymers. 2007;85:91–101. doi: 10.1002/bip.20609. [DOI] [PubMed] [Google Scholar]
- 210.Wilcox JM, Rempel DL, Gross ML. Method of measuring oligonucleotide-metal affinities: Interactions of the thrombin binding aptamer with K+ and Sr2+ Anal. Chem. 2008;80:2365–2371. doi: 10.1021/ac701903w. [DOI] [PubMed] [Google Scholar]
- 211.Wu YG, Tabata M. Effects of solvent composition and temperature on K+-18-crown-6 complexation in acetonitrile-water mixed solvents. J. Solut. Chem. 2004;33:777–795. [Google Scholar]
- 212.Liu Y, Zhang LJ, Li YM, Chen YT, Huang S, Meng J, Inoue Y, Ouchi M. Complexation thermodynamics of crown-ethers.4. Ring-enlargement effects upon cation complexation with dibenzo-18 to dibenzo-22-crown-6. Thermochimica Acta. 1995;253:93–101. [Google Scholar]
- 213.Niederhauser TL, Brown BR, Ziemer SP, Sargent JD, Woolley EM. Thermodynamics of complexation of aqueous 18-crown-6 with potassium ion: apparent molar volumes and apparent molar heat capacities of aqueous 18-crown-6 and of the (18-crown-6 plus potassium chloride) complex at temperatures (278.15 to 393.15) K, at molalities (0.02 to 0.3) mol center dot kg(-1), and at the pressure 0.35 MPa. J. Chem. Thermodyn. 2004;36:1067–1077. [Google Scholar]
- 214.Liu Y, Tong LH, Sun XQ, Wang DF, Hu HW. Complexation thermodynamics of bis(crown ether)S.3. Calorimetric titration of complexation of the etheric and esteric types of bis(crown ether)S with metal-cations. Acta Chim. Sinica. 1991;49:220–224. [Google Scholar]
- 215.Schultze P, Hud NV, Smith FW, Feigon J. The effect of sodium, potassium and ammonium ions on the conformation of the dimeric quadruplex formed by the Oxytricha nova telomere repeat oligonucleotide d(G(4)T(4)G(4)) Nucleic Acids Res. 1999;27:3018–3028. doi: 10.1093/nar/27.15.3018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 216.Hud NV, Schultze P, Sklenar V, Feigon J. Binding sites and dynamics of ammonium ions in a telomere repeat DNA quadruplex. J. Mol. Biol. 1999;285:233–243. doi: 10.1006/jmbi.1998.2327. [DOI] [PubMed] [Google Scholar]
- 217.Hud NV, Smith FW, Anet FAL, Feigon J. The selectivity for K+ versus Na+ in DNA quadruplexes is dominated by relative free energies of hydration: a thermodynamic analysis by H-1 NMR. Biochemistry. 1996;35:15383–15390. doi: 10.1021/bi9620565. [DOI] [PubMed] [Google Scholar]
- 218.Ida R, Wu G. Direct NMR detection of alkali metal ions bound to G-quadruplex DNA. J. Am. Chem. Soc. 2008;130:3590–3602. doi: 10.1021/ja709975z. [DOI] [PubMed] [Google Scholar]
- 219.Ma L, Iezzi M, Kaucher MS, Lam YF, Davis JT. Cation exchange in lipophilic G-quadruplexes: Not all ion binding sites are equal. J. Am. Chem. Soc. 2006;128:15269–15277. doi: 10.1021/ja064878n. [DOI] [PubMed] [Google Scholar]
- 220.Sket P, Plavec J. Not all G-quadruplexes exhibit ion-channel-like properties: NMR study of ammonium ion (non)movement within the d(G(3)T(4)G(4))(2) quadruplex. J. Am. Chem. Soc. 2007;129:8794–8800. doi: 10.1021/ja0710003. [DOI] [PubMed] [Google Scholar]
- 221.Podbevek P, Sket P, Plavec J. Nmr study of ammonium ion binding to d[G(3)T(4)G(4)](2) and d[G(4)(T(4)G(4))(3)] G-quadruplexes. Nucleosides Nucleotides Nucleic Acids. 2007;26:1547–1551. doi: 10.1080/15257770701545358. [DOI] [PubMed] [Google Scholar]
- 222.Tohl J, Eimer W. Interaction energies and dynamics of alkali and alkaline-earth cations in quadruplex-DNA-structures. J. Mol. Model. 1996;2:327–329. [Google Scholar]
- 223.Timasheff SN. Thermodynamic binding and site occupancy in the light of the Schellman exchange concept. Biophys. Chem. 2002;101:99–111. doi: 10.1016/s0301-4622(02)00188-6. [DOI] [PubMed] [Google Scholar]
- 224.Timasheff SN. Protein hydration, thermodynamic binding, and preferential hydration. Biochemistry. 2002;41:13473–13482. doi: 10.1021/bi020316e. [DOI] [PubMed] [Google Scholar]
- 225.Xie GF, Timasheff SN. The thermodynamic mechanism of protein stabilization by trehalose. Biophys. Chem. 1997;64:25–43. doi: 10.1016/s0301-4622(96)02222-3. [DOI] [PubMed] [Google Scholar]
- 226.Timasheff SN. The control of protein stability and association by weak-interactions with water – how do solvents affect these processes. Annu. Rev. Biophys. Biomol. Struct. 1993;22:67–97. doi: 10.1146/annurev.bb.22.060193.000435. [DOI] [PubMed] [Google Scholar]
- 227.Hansen PL, Podgornik R, Parsegian VA. Osmotic properties of DNA: critical evaluation of counterion condensation theory. Phys. Rev. E. 2001;6402 doi: 10.1103/PhysRevE.64.021907. [DOI] [PubMed] [Google Scholar]
- 228.Parsegian VA, Rand RP, Rau DC. Osmotic stress, crowding, preferential hydration, and binding: a comparison of perspectives. Proc. Natl Acad. Sci. USA. 2000;97:3987–3992. doi: 10.1073/pnas.97.8.3987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 229.Hill TL. Toronto: Dover; 1986. An Introduction to Statistical Thermodynamics. [Google Scholar]
- 230.Minton AP. Effect of a concentrated ‘inert’ macromolecular cosolute on the stability of a globular protein with respect to denaturation by heat and by chaotropes: a statistical-thermodynamical model. Biophys. J. 2000;78:101–109. doi: 10.1016/S0006-3495(00)76576-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 231.Rivas G, Fernandez JA, Minton AP. Direct observation of the self-association of dilute proteins in the presence of inert macromolecules at high concentration via tracer sedimentation equilibrium: theory, experiment, and biological significance. Biochemistry. 1999;38:9379–9388. doi: 10.1021/bi990355z. [DOI] [PubMed] [Google Scholar]
- 232.Rivas G, Stafford W, Minton AP. Characterization of heterologous protein-protein interactions using analytical ultracentrifugation. Methods. 1999;19:194–212. doi: 10.1006/meth.1999.0851. [DOI] [PubMed] [Google Scholar]
- 233.Miyoshi D, Karimata H, Sugimoto N. Hydration regulates the thermodynamic stability of DNA structures under molecular crowding conditions. Nucleos. Nucleot. Nucl. 2007;26:589–595. doi: 10.1080/15257770701490282. [DOI] [PubMed] [Google Scholar]
- 234.Miyoshi D, Matsumura S, Nakano S, Sugimoto N. Duplex dissociation of telomere DNAs induced by molecular crowding. J. Am. Chem. Soc. 2004;126:165–169. doi: 10.1021/ja036721q. [DOI] [PubMed] [Google Scholar]
- 235.Liu JH, Kouzine F, Nie ZQ, Chung HJ, Zichrini EF, Weber A, Zhao K, Levens D. The FUSE/FBP/FIR/TFIIH system is a molecular machine programming a pulse of c-myc expression. EMBO J. 2006;25:2119–2130. doi: 10.1038/sj.emboj.7601101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 236.Qin Y, Hurley LH. Structures, folding patterns, and functions of intramolecular DNA G-qaudruplexes found in eukaryotic promoter regions. Biochimie. 2008;90:1149–1171. doi: 10.1016/j.biochi.2008.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 237.Volker J, Blake RD, Delcourt SG, Breslauer KJ. High-resolution calorimetric and optical melting profiles of DNA plasmids: resolving contributions from intrinsic melting domains and specifically designed inserts. Biopolymers. 1999;50:303–318. doi: 10.1002/(SICI)1097-0282(199909)50:3<303::AID-BIP6>3.0.CO;2-U. [DOI] [PubMed] [Google Scholar]
- 238.Blake RD, Delcourt SG. Thermal stability of DNA. Nucleic Acids Res. 1998;26:3323–3332. doi: 10.1093/nar/26.14.3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 239.Phan AT, Leroy JL. Intramolecular i-motif structures of telomeric DNA. J. Biomol. Struct. Dyn. 2000:245–251. doi: 10.1080/07391102.2000.10506628. [DOI] [PubMed] [Google Scholar]
- 240.Gueron M, Leroy JL. The i-motif in nucleic acids. Curr. Opin. Struct. Biol. 2000;10:326–331. doi: 10.1016/s0959-440x(00)00091-9. [DOI] [PubMed] [Google Scholar]
- 241.Ahmed S, Kintanar A, Henderson E. Human telomeric C-strand tetraplexes. Nature Structural Biology. 1994;1:83–88. doi: 10.1038/nsb0294-83. [DOI] [PubMed] [Google Scholar]
- 242.Leroy JL, Gueron M, Mergny JL, Helene C. Intramolecular folding of a fragment of the cytosine-rich strand of telomeric DNA into an I-motif. Nucleic Acids Res. 1994;22:1600–1606. doi: 10.1093/nar/22.9.1600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 243.Phan AT, Mergny JL. Human telomeric DNA: G-quadruplex, i-motif and watson-crick double helix. Nucleic Acids Res. 2002;30:4618–4625. doi: 10.1093/nar/gkf597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 244.Cashman DJ, Buscaglia R, Freyer MW, Dettler J, Hurley LH, Lewis EA. Molecular modeling and biophysical analysis of the c-MYC NHE-III1 silencer element. J. Mol. Model. 2008;14:93–101. doi: 10.1007/s00894-007-0254-z. [DOI] [PubMed] [Google Scholar]
- 245.Li W, Miyoshi D, Nakano S, Sugimoto N. Structural competition involving G-quadruplex DNA and its complement. Biochemistry. 2003;42:11736–11744. doi: 10.1021/bi034168j. [DOI] [PubMed] [Google Scholar]
- 246.Li W, Wu P, Ohmichi T, Sugimoto N. Characterization and thermodynamic properties of quadruplex/duplex competition. FEBS Lett. 2002;526:77–81. doi: 10.1016/s0014-5793(02)03118-6. [DOI] [PubMed] [Google Scholar]
- 247.Kouzine F, Sanford S, Elisha-Feil Z, Levens D. The functional response of upstream DNA to dynamic supercoiling in vivo. Nat. Struct. Mol. Biol. 2008;15:146–154. doi: 10.1038/nsmb.1372. [DOI] [PubMed] [Google Scholar]
- 248.SantaLucia J, Hicks D. The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 2004;33:415–440. doi: 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
- 249.Bommarito S, Peyret N, SantaLucia J. Thermodynamic parameters for DNA sequences with dangling ends. Nucleic Acids Res. 2000;28:1929–1934. doi: 10.1093/nar/28.9.1929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 250.Gilson E, Geli V. How telomeres are replicated. Nat. Rev. Mol. Cell Biol. 2007;8:825–838. doi: 10.1038/nrm2259. [DOI] [PubMed] [Google Scholar]
- 251.Schaffitzel C, Berger I, Postberg J, Hanes J, Lipps HJ, Pluckthun A. In vitro generated antibodies specific for telomeric guanine-quadruplex DNA react with Stylonychia lemnae macronuclei. Proc. Natl Acad. Sci. USA. 2001;98:8572–8577. doi: 10.1073/pnas.141229498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 252.Paeschke K, Juranek S, Simonsson T, Hempel A, Rhodes D, Lipps HJ. Telomerase recruitment by the telomere end binding protein-beta facilitates G-quadruplex DNA unfolding in ciliates. Nat. Struct. Mol. Biol. 2008;15:598–604. doi: 10.1038/nsmb.1422. [DOI] [PubMed] [Google Scholar]
- 253.Colgin LM, Baran K, Baumann P, Cech TR, Reddel RR. Human POT1 facilitates telomere elongation by telomerase. Curr. Biol. 2003;13:942–946. doi: 10.1016/s0960-9822(03)00339-7. [DOI] [PubMed] [Google Scholar]
- 254.Xin HW, Liu D, Wan M, Safari A, Kim H, Sun W, O'Connor MS, Zhou SY. TPP1 is a homologue of ciliate TEBP-beta and interacts with POT1 to recruit telomerase. Nature. 2007;445:559–562. doi: 10.1038/nature05469. [DOI] [PubMed] [Google Scholar]
- 255.Hockemeyer D, Palm W, Else T, Daniels JP, Takai KK, Ye JZS, Keegan CE, de Lange T, Hammer GD. Telomere protection by mammalian Pot1 requires interaction with Tpp1. Nat. Struct. Mol. Biol. 2007;14:754–761. doi: 10.1038/nsmb1270. [DOI] [PubMed] [Google Scholar]
- 256.Tang J, Kan ZY, Yao Y, Wang Q, Hao YH, Tan Z. G-quadruplex preferentially forms at the very 3′ end of vertebrate telomeric DNA. Nucleic Acids Res. 2008;36:1200–1208. doi: 10.1093/nar/gkm1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 257.Salas TR, Petruseva I, Lavrik O, Bourdoncle A, Mergny JL, Favre A, Saintome C. Human replication protein a unfolds telomeric G-quadruplexes. Nucleic Acids Res. 2006;34:4857–4865. doi: 10.1093/nar/gkl564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 258.Martins C, Gunaratnam M, Stuart J, Makwana V, Greciano O, Reszka AP, Kelland LR, Neidle S. Structure-based design of benzylamino-acridine compounds as G-quadruplex DNA telomere targeting agents. Bioorg. Med. Chem. Lett. 2007;17:2293–2298. doi: 10.1016/j.bmcl.2007.01.056. [DOI] [PubMed] [Google Scholar]
- 259.Burger AM, Dai FP, Schultes CM, Reszka AP, Moore MJ, Double JA, Neidle S. The G-quadruplex-interactive molecule BRACO-19 inhibits tumor growth, consistent with telomere targeting and interference with telomerase function. Cancer Res. 2005;65:1489–1496. doi: 10.1158/0008-5472.CAN-04-2910. [DOI] [PubMed] [Google Scholar]
- 260.Hounsou C, Guittat L, Monchaud D, Jourdan M, Saettel N, Mergny JL, Teulade-Fichou MP. G-quadruplex recognition by quinacridines: a SAR, NMR, and biological study. Chemmedchem. 2007;2:655–666. doi: 10.1002/cmdc.200600286. [DOI] [PubMed] [Google Scholar]
- 261.Teulade-Fichou MP, Hounsou C, Guittat L, Mergny JL, Alberti P, Carrasco C, Bailly C, Lehn JM, Wilson WD. Molecular recognition of quadruplex DNA by quinacridine derivatives. Nucleos. Nucleot. Nucl. 2003;22:1483–1485. doi: 10.1081/NCN-120023016. [DOI] [PubMed] [Google Scholar]
- 262.Çetinkol OP, Engelhardt AE, Nanjunda RK, Wilson WD, Hud NV. Submicromolar, selective G-quadruplex ligands from one pot: thermodynamics and structural studies of human telomeric DNA binding by azacyanines. Chem. Bio. Chem. 2008;9:1889–1892. doi: 10.1002/cbic.200800234. [DOI] [PubMed] [Google Scholar]
- 263.Deng Y, Chan SS, Chang S. Telomere dysfunction and tunor suppression: the senescence connection. Nat. Rev. Cancer. 2008;8:450–458. doi: 10.1038/nrc2393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 264.Greider CW. Telomeres do d-loop-t-loop. Cell. 1999;97:419–422. doi: 10.1016/s0092-8674(00)80750-3. [DOI] [PubMed] [Google Scholar]
- 265.Baird DM. Telomere dynamics in human cells. Biochimie. 2008;90:116–121. doi: 10.1016/j.biochi.2007.08.003. [DOI] [PubMed] [Google Scholar]
- 266.Rahman R, Forsyth NR, Cui W. Telomeric 3′-overhang length is associated with the size of telomeres. Exp. Gerontol. 2008;43:258–265. doi: 10.1016/j.exger.2008.01.005. [DOI] [PubMed] [Google Scholar]
- 267.Rankin AM, Faller DV, Spanjaard RA. Telomerase inhibitors and ‘T-oligo’ as cancer therapeutics: contrasting molecular mechanisms of cytotoxicity. Anticancer Drugs. 2008;19:329–338. doi: 10.1097/CAD.0b013e3282f5d4c2. [DOI] [PubMed] [Google Scholar]
- 268.Amiard S, Doudeau M, Pinte S, Poulet A, Lenain C, Faivre-Moskalenko C, Angelov D, Hug N, Vindigni A, Bouvet P, et al. A topological mechanism for TRF2-enhanced strand invasion. Nat. Struct. Mol. Biol. 2007;14:147–154. doi: 10.1038/nsmb1192. [DOI] [PubMed] [Google Scholar]
- 269.Xu Y, Sato H, Shinohara K.-i, Komiyama M, Sugiyama H. T-loop formation by human telomeric G-quadruplex. Nucleic Acids Symp. 2007;41:243–244. doi: 10.1093/nass/nrm122. [DOI] [PubMed] [Google Scholar]
- 270.Gomez D, Wenner T, Brassart B, Douarre C, O’Donohue MF, El Khoury V, Shin-Ya K, Morjani H, Trentesaux C, Riou JF. Telomestatin-induced telomere uncapping is modulated by POT1 through G-overhang extension in HT1080 human tumor cells. J. Biol. Chem. 2006;281:38721–38729. doi: 10.1074/jbc.M605828200. [DOI] [PubMed] [Google Scholar]
- 271.de Lange T. T-loops and the origin of telomeres. Nat. Rev. Mol. Cell Biol. 2004;5:323–329. doi: 10.1038/nrm1359. [DOI] [PubMed] [Google Scholar]
- 272.Griffith JD, Comeau L, Rosenfield S, Stansel RM, Bianchi A, Moss H, de Lange T. Mammalian telomeres end in a large duplex loop. Cell. 1999;97:503–514. doi: 10.1016/s0092-8674(00)80760-6. [DOI] [PubMed] [Google Scholar]
- 273.Zhang YL, Crothers DM. Statistical mechanics of sequence-dependent circular DNA and its application for DNA cyclization. Biophys. J. 2003;84:136–153. doi: 10.1016/S0006-3495(03)74838-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 274.Muyldermans S, Dejonge J, Wyns L, Travers AA. Differential association of linker histones H1 and H5 with telomeric nucleosomes in chicken erythrocytes. Nucleic Acids Res. 1994;22:5635–5639. doi: 10.1093/nar/22.25.5635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 275.Smith CD, Smith SL, DeRisi JL, Blackburn EH. Telomeric protein distributions and remodeling through the cell cycle in Saccharomyces cerevisiae. Mol. Biol. Cell. 2003;14:556–570. doi: 10.1091/mbc.E02-08-0457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 276.Michishita E, McCord RA, Berber E, Kioi M, Padilla-Nash H, Damian M, Cheung P, Kusumoto R, Kawahara TLA, Barrett JC, et al. SIRT6 is a histone H3 lysine 9 deacetylase that modulates telomeric chromatin. Nature. 2008;452:492–U416. doi: 10.1038/nature06736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 277.da Silva MW. Geometric formalism for DNA quadruplex folding. Chem. Eur. J. 2007;13:9738–9745. doi: 10.1002/chem.200701255. [DOI] [PubMed] [Google Scholar]
- 278.Chen G, Wen JD, Tinoco I. Single-molecule mechanical unfolding and folding of a pseudoknot in human telomerase RNA. RNA. 2007;13:2175–2188. doi: 10.1261/rna.676707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 279.Tinoco I, Li PTX, Bustamante C. Determination of thermodynamics and kinetics of RNA reactions by force. Q. Rev. Biophys. 2006;39:325–360. doi: 10.1017/S0033583506004446. [DOI] [PMC free article] [PubMed] [Google Scholar]