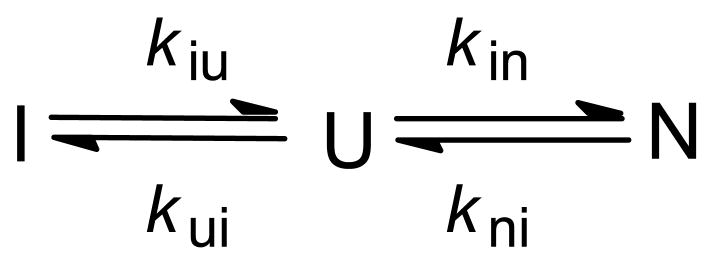Early Events in Protein Folding Explored by Rapid Mixing Methods

1. Introduction

Globular proteins often exhibit cooperative unfolding transitions in which only folded (native) and unfolded (denatured) molecules are populated at equilibrium.^1,2 This two-state behavior is thought to be a consequence of the fact that the native structure is stabilized by a large number of weak interactions, which are cooperative in nature, so that partially folded states are inherently unstable.³ Even when partially structured states accumulate as transient intermediates in kinetic experiments, these are generally not sufficiently stable to be observable under strongly denaturing equilibrium unfolding conditions. On the other hand, non-native states with spectroscopic and hydrodynamic properties intermediate between those of the fully native and unfolded states (the so-called molten-globule state) often accumulate under mildly denaturing conditions, such as acidic or basic pH.^4–6 In some cases, deviations from simple two-state behavior can also be observed in denaturant-induced or thermal unfolding equilibria.^6,7 Although a stable native state that is energetically well separated from denatured states is expected to favor rapid folding into a unique structure,^8,9 there is growing evidence that kinetic intermediates are very common, even in small, single-domain proteins.^10–14 Thus, conformational states distinct from both the fully native and unfolded populations are readily accessible for many proteins, making them structurally less cooperative than thought previously.

The study of protein folding pathways is more than an academic exercise. Insight into the structural, thermodynamic and kinetic properties of protein folding intermediates is critical for understanding a wide range of diseases that can be linked to aggregation of partially denatured or misfolded forms of proteins.^15–20 Issues related to protein stability and folding also play a central role in understanding the biological consequences of mutations²¹ and for designing proteins with new or modified functional properties.^22,23 Studies of protein folding mechanisms in vitro further provide the necessary framework for elucidating the folding of proteins in their cellular environments and other cellular processes, such as protein trafficking and degradation.^24,25

Theoretical models and computer simulations describe the process of protein folding in terms of a diffusive motion of a particle on a high-dimensional free energy surface.^26–28 This ‘landscape’ description of protein folding predicts that a protein can choose among a large number of alternative pathways, which eventually converge toward a common free energy minimum corresponding to the native structure. In contrast, the time course of protein folding monitored by optical and other experimental probes generally shows relaxation kinetics with one or a few exponential phases, which are adequately described in terms of a simple kinetic scheme with a limited number of populated states (the chemical kinetics description). These apparently conflicting models can be consolidated if the free energy surface is divided into several regions (basins) separated by substantial free energy barriers due to unfavorable enthalpic interaction or entropic factors (conformational bottlenecks). The protein can rapidly explore conformational space within each basin comprising a broad ensemble of unfolded or partially folded states, but has to traverse substantial kinetic barriers before entering another basin. This type of free energy surface can thus give rise to multi-exponential folding kinetics.

Progress in understanding dynamic and mechanistic aspects of protein folding has been closely linked with advances in kinetic methods. The development of commercially available stopped-flow instruments in the 1960’s^29,30 enabled the first quantitative kinetic studies of protein folding reactions.^31–37 The combination of quenched-flow methods, initially developed for the study of enzyme reaction mechanisms,³⁸ with hydrogen exchange labeling and NMR has proven to be particularly fruitful for the structural characterization of transient folding intermediates.^39–41 Dielectric and ultrasonic relaxation measurements gave early insight into the dynamics of helix-coil transitions in homo-polypeptides,^42,43 and more recent studies on model peptides, using laser-induced temperature-jump methods,⁴⁴ established that the time window for formation of isolated helices and β-hairpins ranges from about 50 ns to several μs.^45–48 Together with other laser initiation techniques^49,50 and dynamic NMR methods,^51,52 laser T-jump studies have also been a rich source of information on the dynamics of folding on the microsecond time scale (reviewed in refs ^53–56). In particular, a number of small proteins and domains were shown to undergo two-state folding/unfolding transitions with relaxation times as short as a few microseconds.^57–65 These fast-folding proteins are of interest not only in an effort to find the ultimate “speed limit” for protein folding,⁵⁶ but also serve as bench marks for computer simulations of protein folding, which have advanced to the stage where conformational transitions on the microsecond time scale can be described with atomic resolution.^61,66–69

The dynamics of secondary structure formation and two-state folding on the microsecond time scale has been reviewed extensively^53–55 and is not the main subject of this chapter. Instead, we will focus on recent advances in rapid mixing methods and their application to studies of early stages of protein folding, drawing mainly from work published since 1997. Solution mixing techniques have experienced a renaissance due to advances in mixer design and detection methods, which made it possible to extend the time resolution well into the microsecond time range.^70–73 Efficient turbulent mixers coupled with a variety of detection methods have yielded a wealth of information on early stages of protein folding.^{61,71,74–91} Although rapid mixing techniques cannot compete with the perturbation methods mentioned above in terms of time resolution, they remain the method of choice for studies of protein folding reactions far from the equilibrium transition region where intermediate states are most likely to accumulate.

2. Rapid Mixing Techniques for Protein Folding Studies

As with any complex reaction, time-resolved data are essential for elucidating the mechanism of protein folding. Even in cases where the whole process of folding occurs in a single step, which is the case for many small proteins,⁹² the kinetics of folding and unfolding provide valuable information on the rate-limiting step in folding, which, in analogy to chemical or enzymatic reaction mechanisms, is often described as an ensemble of transition states.⁹³ The effects of temperature and denaturant concentration give insight into activation energies and solvent-accessibility of the transition state ensemble,^1,94 and by measuring the kinetic effects of mutations, one can gain more detailed structural insight.^95–97 If the protein folding process occurs in stages, i.e., if partially structured intermediate states accumulate, kinetic studies can potentially offer much additional insight into the structural and thermodynamic properties of intermediate states and intervening barriers.^{10,14,98–101}

2.1. Turbulent Mixing

Most rapid mixing schemes rely on turbulent mixing to achieve complete mixing of two (or more) solutions. Mixers of various designs are in use ranging from a simple T-arrangements to more elaborate geometries, such as the Berger ball mixer.¹⁰² The goal is to achieve highly turbulent flow conditions in a small volume. The turbulent eddies thus generated can intersperse the two components down to the μm distance scale. However, the ultimate step in any mixing process relies on diffusion in order to achieve a homogeneous mixture at the molecular level. Given that the diffusion time t varies as the square of the distance r over which molecules have to diffuse, it takes a molecule with a diffusion constant D=10⁻⁵ cm²/s about 1 ms to diffuse over a distance of 1 μm (t=r²/D). Thus, the mechanical mixing step has to intersperse the two components on a length scale of less than 1 μm in order to achieve sub-ms mixing times. The onset of turbulence is governed by the Reynolds number, Re, defined as

$$Re=\rho vd/\eta$$ (1)

where ρ is the density (g/cm³), ν is the flow velocity (cm/s), d describes the characteristic dimensions of the channel (cm), and η is the viscosity of the fluid (e.g., 0.01 poise for water at 20 °C). To maintain turbulent flow conditions in a cylindrical tube, Re has to exceed values of about 2,000.

Turbulence is important not only for achieving efficient mixing, but also for maintaining favorable flow conditions during observation. In stopped-flow and quenched-flow experiments, turbulent flow insures efficient purging of the flow lines. In continuous-flow measurements, turbulent flow conditions in the observation channel lead to an approximate “plug flow” profile, which greatly simplifies data analysis compared to the parabolic profile obtained under laminar flow conditions. The time resolution of a rapid mixing experiment is governed not only by the mixing time, which in practice is difficult to quantify, but also the delay between mixing and observation. The effective delay between initiation of the reaction and the first reliably measurable data point is defined as the dead time, Δt_d. In both stopped- and continuous-flow experiments, any unobservable volume (dead volume), ΔV, between the point where mixing is complete and the point of observation contributes an increment Δt = ΔV/(dV/dt) to the dead time (dV/dt is the flow rate). Additional contributions to the effective dead time include the time delay to stop the flow and any artifacts that can obscure early parts of the kinetic trace.

Increasing the flow rate promotes more efficient mixing by generating smaller turbulent eddies, and yields shorter time delays Δt, and thus should lead to shorter dead times. However this trend does not continue indefinitely. Aside from practical problems due to back pressure and, in the case of stopped-flow measurements, various stopping artifacts, the time resolution of a rapid mixing experiment is ultimately limited by cavitation phenomena.¹⁰³ Under extreme conditions, the pressure gradients across turbulent eddies can become so large that the solvent begins to evaporate, forming small vapor bubbles that can take a long time to dissolve. The result is an intensely scattering plume that makes meaningful detection of the kinetic signal virtually impossible. Rapid mixing experiments involving large changes in denaturant concentration, which is often the case in studies of protein folding or unfolding, pose additional challenges related to the increase in solvent viscosity, which slows down the mixing process, convective flow due to density gradients across the mixer, and the heat of mixing, which can give rise to thermal artifacts.

To achieve efficient turbulent mixing conditions requires high flow rates and relatively large channel dimensions (the practical limit below which backpressure becomes prohibitive seem to lie around 100 μm), which can consume substantial amounts of material. An interesting alternative to turbulent mixing with improved sample economy uses hydrodynamic focusing to mix solutions under laminar flow conditions.^104,105 By compressing a fluid phase into a thin layer, the technique can potentially achieve mixing times in the low microsecond range. However, the slow onset of mixing has so far limited practical applications of hydrodynamic focusing to dead times near 1 ms.^73,106,107

2.2. Stopped-flow Methods

The simple, but versatile, stopped-flow technique, coupled with optical detection (typically fluorescence, absorbance or circular dichroism), has long been the primary source of kinetic insight into protein folding reactions.^{10,36,98,99,108,109} In a typical stopped-flow experiment, a few hundred μl of solution are delivered to the mixer via two syringes driven by a pneumatic actuator or stepper-motors. Flow rates in the range of 5 to 15 ml/s with channel diameters of the order of 1 mm insure turbulent flow conditions (Re>5,000). After delivering a volume sufficient to purge and fill the observation cell with freshly mixed solution, the flow is stopped abruptly when a third syringe hits a stopping block or a valve is closed. Commercial instruments can routinely reach dead times of a few ms. Recent improvements in mixer and flow-cell design by several manufacturers of stopped-flow instruments resulted in dead times well under 1 ms. The upper end of the time scale that can be reliably measured in a stopped-flow experiment is determined by the stability of the mixture in the flow cell, which is limited by convective flow or diffusion of reagents in and out of the observation volume. For slow reactions with time constants longer than a few minutes, manual mixing experiments are generally more reliable. Stopped-flow mixing is usually coupled with real-time optical observation using absorbance (UV through IR), fluorescence emission or circular dichroism (CD) spectroscopy. In addition, the stopped-flow technique has been implemented in conjunction with many other biophysical techniques, such as fluorescence lifetime measurements,^110,111 NMR,^112,113 and small-angle x-ray scattering.¹¹⁴ An extension of the stopped-flow technique makes use of two or more consecutive mixing steps in order to prepare the system in a particular initial state (double-jump stopped-flow), which can provide important information on kinetic mechanisms in protein folding.^85,115

The interpretation of stopped-flow data requires a careful calibration of the instrumental dead time by measuring a pseudo-first-order reaction tuned to the time scale of interest (i.e., a single-exponential process with a rate-constant approaching the expected dead time) and an optical signal matching the application. Common test reactions for absorbance measurements include the reduction of 2,6-dichlorophenolindophenol (DCIP) or ferricyanide by ascorbic acid.¹¹⁶ A convenient test reaction for tryptophan fluorescence measurements is the irreversible quenching of N-acetyltryptophanamide (NATA) by N-bromosuccinimide (NBS). For fluorescence studies in or near the visible range, one can follow the pH-dependent association of the Mg2+ ion with 8-hydroxyquinoline, which results in a fluorescent chelate,¹¹⁷ or the binding of the hydrophobic dye 1-anilino-8-naphlalene-sulfonic acid (ANS) to bovine serum albumin (BSA), which is associated with a large increase in fluorescence yield.¹¹⁸

2. 3. Continuous-flow Techniques

In a continuous-flow experiment, the reaction is again triggered by turbulent mixing, but, in contrast to stopped-flow, the progress of the reaction is sampled under steady-state flow conditions as a function of the distance down-stream from the mixer.^38,119 This avoids artifacts related to arresting the flow and makes it possible to use relatively insensitive detection methods. Thus, continuous-flow measurements can achieve shorter dead times compared to stopped-flow, but this comes at the expense of sample economy. Earlier versions of this experiment involved point-by-point sampling of the reaction profile while maintaining constant flow at high rates (several ml/s for a conventional mixer). The prohibitive amounts of sample consumed limited the impact of continuous-flow techniques until advances in mixer design made it possible to achieve highly efficient mixing at lower flow rates,^70,72,75,120 and an improved detection scheme allowed simultaneous recording of a complete reaction profile in a few seconds.⁷² These developments lowered both the dead time and sample consumption by at least an order of magnitude, and made routine measurements on precious samples with dead times as short as 50 μs possible.

In 1985, Regenfuss et al.⁷⁰ described a capillary jet mixer consisting of two coaxial glass capillaries with a platinum sphere placed at their junction. The reaction progress was monitored in a free-flowing jet, using conventional photography to measure fluorescence vs. distance from the mixer. Measurements of the binding kinetics of ANS to bovine serum albumin indicated that dead times less than 100 μs can be achieved with this mixer design. More recently, several laboratories reported continuous-flow resonance Raman and fluorescence studies of enzyme and protein folding reactions on the sub-millisecond time scale, using machined mixers with dead-times in the 100 μs range.^71,75,120 More widespread use of these methods has been hampered by a number of technical and experimental difficulties. Continuous-flow experiments involving a free-flowing jet^{70,75,120,121} are fraught with difficulties due to instability and scattering artifacts. The use of a conventional camera with high-speed monochrome film for fluorescence detection⁷⁰ is inadequate due to the low sensitivity of the film in the UV region, limited dynamic range and the non-linearity of the film response. Finally, prohibitive sample consumption makes continuous-flow experiments that record a kinetic trace one point at a time feasibly only for highly abundant proteins.^71,74,79,84

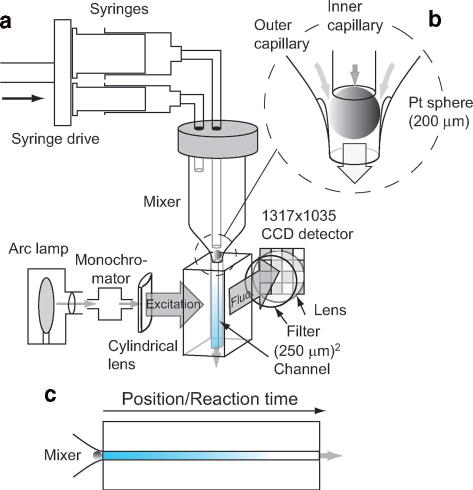
We were able to overcome many of these limitations by combining a highly efficient quartz capillary mixer, inspired by the design of Regenfuss et al.,⁷⁰ with a flow cell and an improved detection system involving a digital camera system with a UV-sensitized CCD detector.⁷² A diagram of the experimental arrangement is shown in Figure 1. For solution delivery, we use a motor-driven syringe pump (Update, Madison, WI), which injects the reagents to be studied at high rate into each of the two coaxial capillaries (typically using volume ratios of 1:5 or 1:10). The outer capillary consists of a thick-walled quartz tube, which is pulled to a fine tip (~200 μm i.d. at the end), using a glassblowing lathe or a simple gravity method. A smaller inner capillary (360 μm o.d., 150–180 μm i.d.) with a platinum sphere (~250 μm diameter) suspended at the tip is positioned inside the tapered end of the outer capillary. Solid glass rods fused to the inner wall of the outer capillary (tapering down to diameter of ~20 μm) prevent the sphere from plugging the outlet. The reagents are forced through the narrow gap between the sphere and the outer wall where mixing occurs under highly turbulent flow conditions. The mixture emerging is injected into the flow channel (250 μm × 250 μm) of a fused-silica observation cell joined to the outer capillary by means of a hemispherical ground-glass joint. Typical flow rates are 0.6 to 1.5 ml/s, resulting in linear flow velocities of 10 to 25 m/s through the 0.25×0.25 mm² channel of the observation cell.

Figure 1.

Continuous-flow capillary mixing apparatus in fluorescence mode. a Schematic of the solution delivery system, mixer, observation cell and optical arrangement. b Expanded view of the mixer. c Diagram illustrating continuous-flow measurement.

The reaction progress in a continuous-flow mixing experiment is measured by recording the fluorescence profile vs. distance downstream from the mixer. A conventional light source consisting of an arc lamp, collimating optics and monochromator, is used for fluorescence excitation. Relatively uniform illumination of the flow channel over a length of 10–15 mm is achieved by means of a cylindrical lens. A complete fluorescence vs. distance profile is obtained by imaging the fluorescent light emitted at a 90°angle onto the CCD detector of a digital camera system (Micromax, Roper Scientific, Princeton NJ) containing a UV-coated Kodak CCD chip with an array of 1317 × 1035 pixels. The camera is equipped with a fused silica magnifying lens and a high-pass glass filter or a band-pass interference filter to suppress scattered incident light. In a typical continuous-flow fluorescence experiment, a raw reaction profile, I_r(d), is obtained by averaging the emitted light intensity across the flow channel vs. the distance d downstream from the mixer. To account for the non-uniform distribution of incident light intensity, I_c(d), a matching intensity profile is recorded for a “fluorescent control” (e.g., dilution of the unfolded protein solution with denaturing buffer, or dilution of NATA with buffer without quencher). The scattering background, I_b(d), is measured by passing water (or buffer) through both capillaries. Distance is converted into time on the basis of the known flow rate and cross-sectional area of the flow channel (0.0625 mm² in our setup) and the length of the channel being imaged. Finally, a corrected fluorescence trace, fl_rel(t), is obtained by taking a ratio of the background-corrected reaction and control traces,

$$f{l}_{\mathit{rel}}=(I_r-I_b)/(I_c-I_b).$$ (1)

To estimate the dead time of the continuous-flow experiment, we routinely measure the pseudo-first-order NATA-NBS quenching reaction at a final NATA concentration of 40 μM and several NBS concentrations in the range 2–32 mM. Figure 2a shows a plot of the relative fluorescence, fl_rel, calculated according to eq 1, along with exponential fits (solid lines). Since fl-_rel = 1 corresponds to the unquenched NATA signal expected at t=0, the intercept of the fits with fl_rel = 1 indicates the time point t=0 where the mixing reaction begins. The delay between this point and the first data point that falls onto the exponential fit corresponds to the dead time of the experiment, Δt_d, which in this example is 50 ± 5 μs. In Figure 2b, the rate constants obtained by exponential fitting are plotted as a function of NBS concentration. The slope of a linear fit (solid line) yields a second-order rate constant for the NBS-induced chemical quenching of NATA of 7.9 × 10⁵ M⁻¹s⁻¹, which agrees well with the rate constant obtained from stopped-flow measurements at lower NBS concentration.¹²² Together with the linearity of the second-order rate plot (Figure 2b), this documents the accuracy of the continuous-flow measurement. Instrumental dead times can be substantially longer if one or both of the solutions contains a denaturant, such as guanidine hydrochloride (GuHCl) or urea at high concentration due to a combination of viscosity-dependent decreases in mixing efficiency and thermal mixing artifacts. Thus, it is important to calibrate mixer performance for each set of solution conditions and flow rates used, for example by including the appropriate denaturant and buffers in a NATA-NBS quenching experiment. A straightforward method for assessing mixing efficiency is to compare the reaction profile measured during continuous-flow mixing of NATA with water (under the appropriate buffer/denaturant conditions) with that of a pre-mixed solution at the same final NATA concentration. For an efficient mixer at sufficiently high flow rates, we find that the ratio of these flow profiles approaches unity within a fraction of a mm downstream of the mixing region (Figure 1). Alternatively, mixing efficiency could be assessed using a very fast reaction completed within the dead time, such as the quenching of tryptophan (or NATA) by sodium iodide. To detect any flow-related artifacts, such as caviation, we simply compare the flow profiles of a dilute NATA solution (introduced into both inner and outer capillary) recorded during continuous flow and immediately after stopping the drive.

Figure 2.

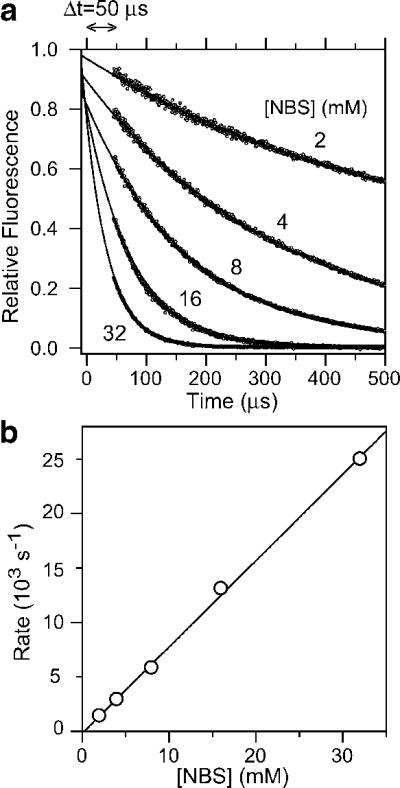
Continuous-flow measurements of the quenching of NATA fluorescence by NBS used to determine the experimental dead-time. a Plot of NATA fluorescence (>324 nm) vs. time at several NBS concentrations. b NATA-NBS reaction rates from exponential fitting of the data in panel a vs. NBS concentration. Linear regression (line) yields a second-order rate constant of 7.9 10⁵ M⁻¹ s⁻¹.

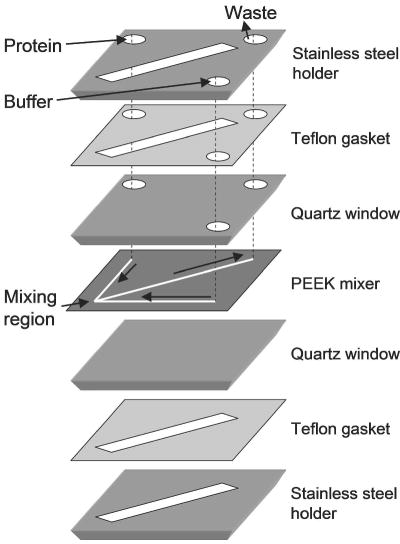
Although capillary mixers remain highly competitive in terms of mixing efficiency and dead time, some of the drawbacks of this design are the challenging manual manufacturing process, limited reproducibility and difficulty of cleaning after a blockage. Several groups have relied on various micromachining techniques to construct mixers consisting of thin (~100 μm) channels, often using a simple T-arrangement.^{71,75,79,84,91,123,124} A recent example is the microfluidic mixer design by Bilsel at al.⁹¹ illustrated in Figure 3. Using laser micromachining they introduced a series of fine (50–125 μm diameter) channels into a thin film (127 μm thick) made of a hard, chemically inert polymer (PEEK) sandwiched between two fused silica windows. The two inlet channels meet at a 90°angle with the outlet channel bisects the two, resulting in a large fluid momentum change that promotes turbulent mixing. Bilsel et al. incorporated this mixer in a laser-based optical setup capable of both steady-state and time-resolved fluorescence detection.⁹¹ Using the NATA-NBS quenching reaction (c.f. Fig. 2), they recorded a dead time of 50 μs, which is comparable to that obtained with our capillary mixer and shorter than those reported using other microfluidic mixers.

Figure 3.

Schematic of a microfluidic mixer designed by Bilsel et al.⁹¹. The 127-μm-thick mixer is sandwiched between quartz windows and is sealed in a stainless-steel holder using Teflon gaskets (1.6 mm thick). Solutions are delivered to and from the mixing region through holes in the upper layers (arrows). Reprinted with permission from ref 91. Copyright 2005 American Institute of Physics.

3. Detection Methods

A major strength of rapid mixing methods is that they can be readily combined with a wide range of detection methods. Data acquisition in the stopped-flow mode requires rapid sampling of the signal at intervals shorter than the dead time while continuous-flow experiments permit steady-state spectroscopic measurements for longer time intervals limited only by the capacity of the solution delivery system. Table 1 lists common detection methods used in rapid mixing studies of the kinetics of folding, which are illustrated in this section with selected examples.

Table 1.

Common detection methods used in rapid mixing studies of protein folding

Method	Probe	Properties Probed	Sensitivity
Fluorescence	Trp, Tyr	solvent shielding tertiary contacts (quenching)	+++
	ANS	Hydrophobic clusters, collapse	+++
	FRET	donor-acceptor distance	++
Absorbance	Trp, Tyr, cofactor	polarity, solvent perturbation	++
far-UV CD near-UV CD	peptide bond	secondary structure	−−
	Tyr, Trp, co-factor	side-chain packing, mobility	−−
IR, Raman	peptide bond cofactor	secondary structure metal coordination	+
SAXS	heavy atoms	size (Rg), shape	−
NMR, H/D exchange	labile hydrogens	H-bonding, solvent accessibility	−
EPR	unpaired electrons	environment of free radicals, paramagnetic metals	−

3.1. Tryptophan Fluorescence

The fluorescence emission properties of tryptophan and tyrosine side chains provide information on the local environment of these intrinsic chromophores. For example, a fully solvent-exposed tryptophan in the denatured state of a protein typically shows a broad emission spectrum with a maximum near 350 nm and quantum yield of ~0.14, similar to that of free tryptophan or its derivative, NATA. Burial of the tryptophan side chain in an apolar environment within the native state or a compact folding intermediate can result in a substantial blue-shift of the emission maximum (by as much as 30 nm) and enhanced fluorescence yield. These changes are a consequence of the decrease in local dielectric constant and shielding from quenchers, such as water and polar side chains. In other cases, close contact with certain (polar) side-chains gives rise to a decrease in fluorescence yield upon folding. Many polar amino acid side chains (as well as main chain amino groups) are known to quench tryptophan fluorescence, probably via excited-state electron or proton transfer.^125,126 Thus, the straightforward measurement of fluorescence intensity vs. folding or unfolding time can provide useful information on solvent accessibility and proximity to quenchers of an individual fluorescence probe. Complications due to the presence of multiple fluorophores can be avoided by using mutagenesis to replace any additional tryptophans.^127,128 Because Trp is a relatively rare amino acid, proteins with only one tryptophan are not uncommon; in the case of Trp-free proteins, a unique fluorophore can be introduced by using site-directed mutagenesis.^129,130

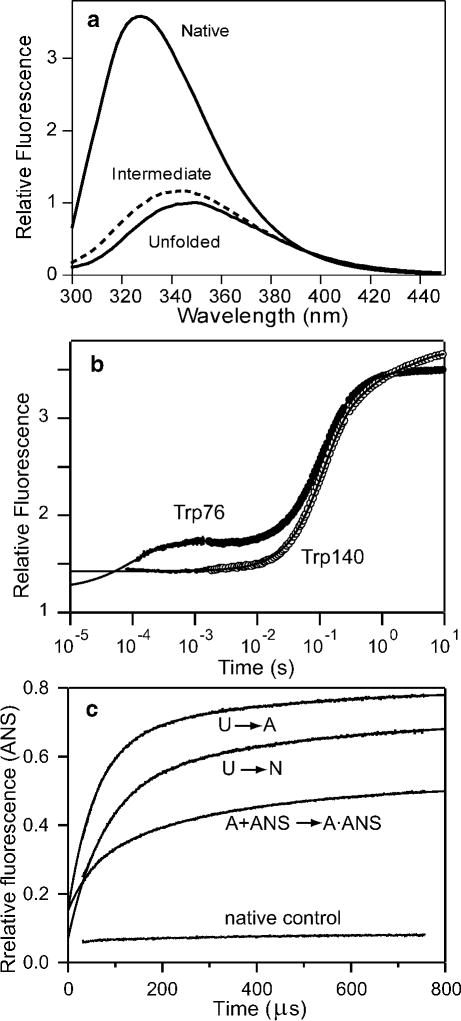
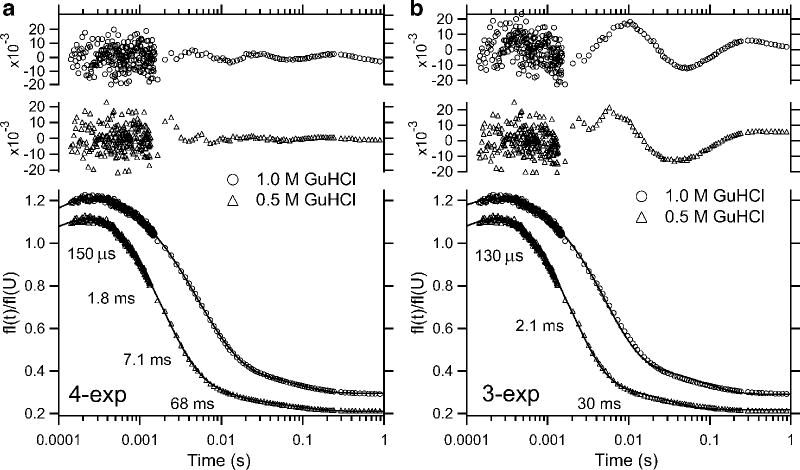
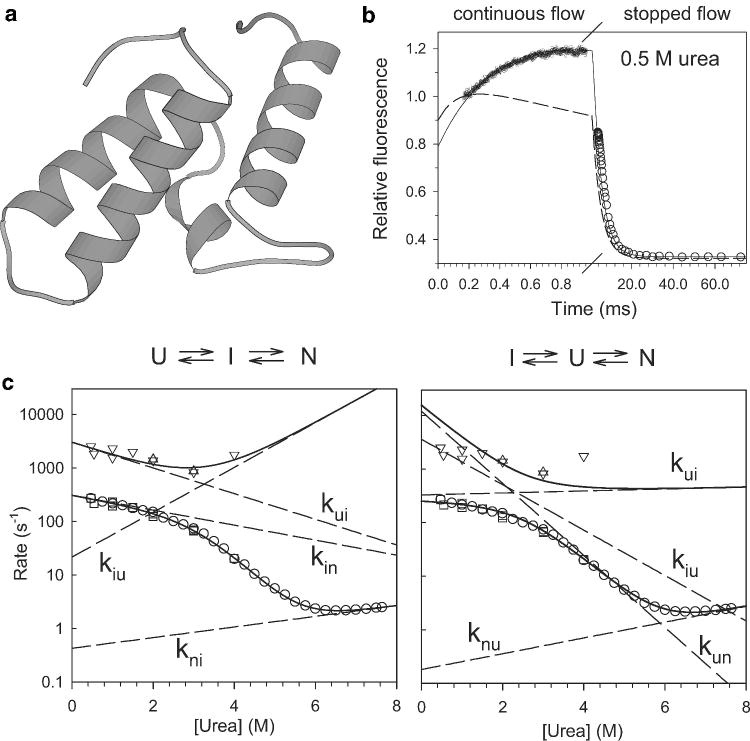
The use of tryptophan fluorescence to explore early stages of protein folding is illustrated in Figure 4, which shows results on staphylococcal nuclease (SNase) recently obtained in our laboratory.⁸⁷ A variant with a unique tryptophan fluorophore in the N-terminal β-barrel domain (Trp76 SNase) was obtained by replacing the single typtophan in wild-type SNase, Trp140, with His in combination with Trp substitution of Phe76. The fluorescence of Trp76 is strongly enhanced and blue-shifted under native conditions relative to the denatured state in the presence of urea (panel a), indicating that upon folding the indole ring of Trp76 moves from a solvent-exposed location to an apolar environment within the native structure. An intermediate state with a fluorescence emission spectrum similar to, but clearly distinct from the native state was detected in equilibrium unfolding experiments (dashed line in Figure 4a). In contrast to WT* SNase (P47G, P117G and H124L background), which shows no changes in tryptophan fluorescence prior to the rate-limiting folding step (~100 ms), the F76W/W140H variant shows additional changes (enhancement) during an early folding phase with a time constant of about 80 μs (Figure 4b). The observation that the main folding phase has essentially the same rate for both variants (10.4 s⁻¹ for WT* and 11.3 s⁻¹ for the Trp76 variant) indicates that the overall folding mechanism is not perturbed by the F76W/W140H mutations (the differential behavior at long times suggest that the mutations modulate a slow-folding species containing non-native peptide-bond isomers). Thus, the observed amplitude differences can be largely attributed to the fact that Trp76 reports on the rapid formation of a hydrophobic cluster in the N-terminal β-sheet region while the wild-type Trp140 is silent during this early stage of folding.

Figure 4.

Folding mechanism of SNase probed by tryptophan fluorescence. a Fluorescence emission spectra of the Trp76 variant of SNase under native and denaturing conditions (solid) and a folding intermediate populated at equilibrium (dashed). The spectrum of the intermediate was determined by global analysis of the fluorescence spectra as a function of urea concentration (pH 5.2, 15 °C). b Time-course of folding (triggered by a pH jump from 2 to 5.2) for wild-type SNase (Trp140) and a single-tryptophan variant (Trp76) measured by continuous-flow (< 10⁻³ s) and stopped-flow (> 10³ s) fluorescence. c ANS fluorescence changes during ANS binding/folding of Trp76 SNase measured by continuous-flow experiments at 15°C in the presence of 160 μM ANS. U → A: Salt concentration jump from 0 M to 1 M KCl at pH2.0; U → N: refolding induced by a pH-jump from 2.0 to 5.2; A+ANS → A•ANS: ANS binding kinetics in the presence of 1 M KCl at pH 2.0; native control: ANS binding kinetics under the native condition (pH 5.2). Adapted from ref 87 (Figures 3 and 5).

3.2. ANS Fluorescence

Valuable complementary information on the formation of hydrophobic clusters at early stages of folding can be obtained by using ANS as extrinsic fluorescence probe.^131–133 Figure 4c illustrates this with recent results on the Trp76 variant of SNase introduced above.⁸⁷ Continuous-flow measurements showed a major enhancement in ANS fluorescence during early stages of SNase folding to fully native conditions (U→N), and also during formation of the compact acid-denatured state of SNase (U→A). For comparison, we also measured the kinetics of ANS binding to the pre-formed A-state. While the rate of ANS binding to the A-state shows the linear dependence on ANS concentration characteristic of a second-order binding process, the rates observed during refolding reactions ending either in the native state or the A-state level off at ~120 μM ANS. The limiting ANS-independent rate at higher concentrations is thus due to an intramolecular conformational event that precedes ANS binding. The rate of this process closely matches that of the earliest phase detected by intrinsic fluorescence of Trp76 (Figure 4b), confirming that both processes reflect a common early folding step. This agreement confirms that ANS can serve as a faithful probe for detecting early folding intermediates. This is especially important in view of the fact that ANS has been shown to perturb the kinetics of late folding steps,¹³³ and is known to shift folding equilibrium transitions.¹³⁴

Maki et al.⁸⁷ also observed a major enhancement in ANS fluorescence during folding of WT* SNase with a time constant of 80 μs, which closely matches that of the Trp76 mutant. This further supports the notion that this rapid process reflects an intrinsic conformational event rather than being a consequence of the amino acid changes (F76W/W140H). Taken together, the tryptophan and ANS fluorescence data are consistent with the rapid accumulation of an ensemble of states containing a loosely packed hydrophobic core involving primarily the β-barrel domain. In contrast, the specific interactions in the α-helical domain involving Trp140 are formed only during the final stages of folding.

3.3. Fluorescence Energy Transfer

Fluorescence resonant energy transfer (FRET) can potentially give more specific information on the changes in average distance between fluorescence donors and acceptors. For example, horse cytochrome c (cyt c) contains an intrinsic fluorescence donor-acceptor pair, Trp59 and the covalently attached heme group, which quenches tryptophan fluorescence viaexcited-state energy transfer.¹³⁵ We have made extensive use of this property to characterize the folding mechanism of cyt c,^40,136,137 including the initial collapse of the chain on the microsecond time scale.^76,77

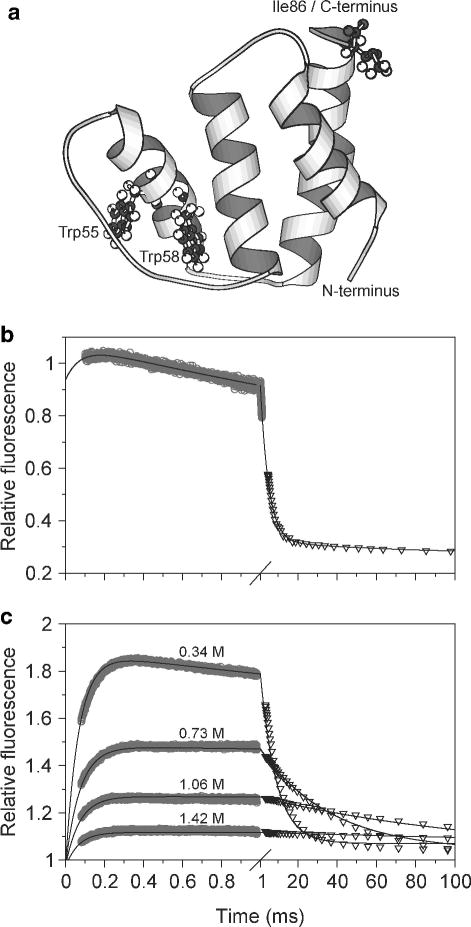
We recently combined ultrafast mixing experiments with FRET in order to monitor large-scale structure changes during early stages of folding of acyl-CoA binding protein (ACBP), a small (86-residue) four-helix bundle protein.⁸³ ACBP contains two tryptophan residues on adjacent turns of helix 3, which served as fluorescence donors. An AEDANS fluorophore covalently attached to a C-terminal cysteine residue introduced via mutagenesis was used as an acceptor (Figure 5a). Earlier equilibrium and kinetic studies, using intrinsic tryptophan fluorescence, showed a cooperative unfolding transition and single-exponential (un)folding kinetics consistent with an apparent two-state transition. Even when using continuous-flow mixing to measure intrinsic tryptophan fluorescence changes on the sub-ms time scale (Figure 5b), we found only minor deviations from two-state folding behavior. However, when we monitored the fluorescence of the C-terminal AEDANS group while exciting the tryptophans, we observed a large increase in fluorescence during a fast kinetic phase with a time constant of 80 μs, followed by a decaying phase with a time constant ranging about 10 ms to 500 ms, depending on denaturant concentration (Figure 5c). The large enhancement in FRET efficiency is attributed to a major decrease in the average distance between helix 3 and C-terminus of ACBP. The fact that the early changes are exponential in character suggests that the initial compaction of the polypeptide is limited by an energy barrier rather than chain diffusion. The subsequent decrease in AEDANS fluorescence during the final stages of folding is attributed to a sharp decrease in the intrinsic fluorescence yield of the two tryptophans due to intramolecular quenching. The specific side chain interactions responsible for quenching are established only in the close-packed native structure and are not present during the initial folding event. These observations indicate that the early (80 μs) folding phase marks the formation of a collapsed, but loosely packed and highly dynamic ensemble of states with overall dimensions (in terms of fluorescence donor-acceptor distance) similar to that of the native state.

Figure 5.

FRET-detection of an early folding intermediate in a helix-bundle protein, ACBP. a Ribbon diagram of ACBP, based on an NMR structure. The two tryptophan residues and the mutated C-terminal isoleucine are shown in ball and stick. The two lower panels show refolding kinetics of unmodified ACBP (b) and AEDANS-labeled ACBP,I86C (c) in pH 5.3 buffer containing 0.34 M GuHCl at 26 °C. In both panels data from continuous-flow (○) and stopped-flow (▽) experiments were matched and combined. Reprinted with permission from ref 83. Copyright 2002 National Academy of Sciences of the USA.

3.4. Continuous-flow Absorbance

Although fluorescence is inherently more sensitive, our capillary mixing instrument can also be adapted for continuous-flow absorbance measurements on the microsecond time scale. The fully transparent flow cell used for fluorescence measurements is replaced with a custom-made partially opaque absorbance flow cell of the same dimensions (0.25 mm path length). Relatively uniform illumination with minimal changes to the optical arrangement (see Figure 1) was achieved by using a scattering cell containing an opaque solution (non-dairy creamer works well). As in fluorescence measurements, a complete reaction profile can be recorded in a single 2–3 s continuous-flow run by imaging the flow channel onto the CCD detector. Using the reduction of DCIP by ascorbic acid as a test reaction,¹¹⁶ we measured dead times as short as 40 μs at the highest flow rate tested (1.1 ml/s).

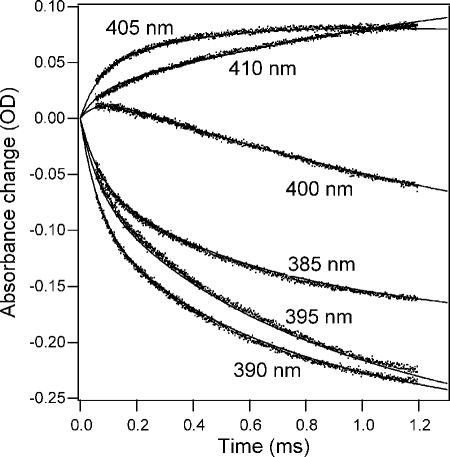
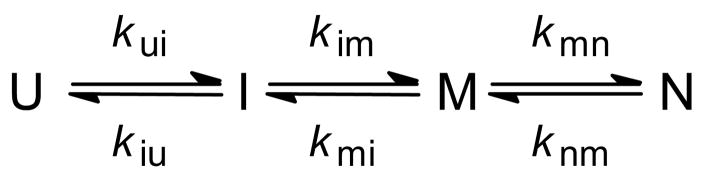
As a first application of absorbance-detected continuous-flow mixing, we measured the changes in heme absorbance in the Soret region (~360–430 nm) associated with the folding of oxidized horse cyt c.¹³⁸ The reaction was initiated by a rapid jump from pH 2, where the protein is fully unfolded, to pH 4.7, where folding occurs rapidly with minimal complications due to non-native histidine-heme ligands. A series of kinetic traces covering the time window from 40 μs to ~1.5 ms were measured at different wavelengths spanning the Soret region (Figure 6). A parallel series of stopped-flow experiments (data not shown) was performed under matching conditions to extend the data to longer times (2 ms to 10 s). Global fitting of the family of kinetic traces to sums of exponential terms yielded three major kinetic phases with time constants of 65 μs, 500 μs and 2 ms, respectively, consistent with accumulation of two intermediate species, I and M (Scheme 1), with absorbance properties distinct from both the initial (U) and final (N) states. In previous continuous-flow fluorescence measurements on horse cyt c,^76,77 we also observed three kinetic phases with very similar time constants, indicating that a basic four-state mechanism is sufficient to describe the folding process of cyt c in the absence of complications due to non-native heme ligation and other slow events, such as cis-trans isomerization of peptide bonds.

Figure 6.

Initial stages of refolding of acid-denatured oxidized cyt c at pH 5 monitored by continuous-flow absorbance measurements at different wavelengths spanning the Soret heme absorbance band. The lines represent a global fit of a four-state folding mechanism to the family of kinetic traces. Reprinted with permission from ref 138. Copyright 2004 Elsevier Inc.

Scheme 1.

3.5. Probes of Secondary Structure Formation

CD spectroscopy in the far-UV (peptide) region, which provides a measure of average secondary structure content of a protein,^139,140 has been an important tool for protein folding research (reviewed in refs ^{10,98,99,101,141,142}). Stopped-flow CD measurements on numerous proteins have shown that a substantial fraction of the overall change in the far-UV CD spectrum associated with refolding can appear within the instrumental dead time while changes in the near-UV region of the CD spectrum often do not occur until the late stage of folding.^143–150 Such observations have been generally interpreted in terms of a model involving the transient accumulation of early intermediates that appear native-like in terms of the CD-detectable secondary structure, but still unfolded in terms of the environment of aromatic side chains observed in the near-UV region of the CD spectrum. However, until recently the time resolution of stopped-flow CD measurements has been limited to the 10 ms range by the low inherent sensitivity of the technique and various flow artifacts, such as strain-induced birefringence. Akiyama et al.⁷⁹ were able to record CD at folding times as short as 400 μs by coupling an efficient turbulent mixer (T-design) with a commercial CD spectrometer. Their continuous-flow measurements of CD spectral changes in the far-UV region revealed the kinetics formation of (helical) secondary structure during early stages of folding of cyt c⁷⁹ and apomyoglobin.⁸⁹

Infrared spectroscopy is a promising alternative for monitoring acquisition of secondary structure during protein folding. The amide I band, which is dominated by backbone carbonyl stretching vibrations, is a valuable source of information on secondary structure,¹⁵¹ especially after recent work on peptides led to a firmer assignment of the spectral contributions of specific secondary structure types and degrees of hydration.¹⁵² However, the implementation of IR spectroscopy in conjunction with rapid mixing poses a series of technical challenges, including the problem of rapidly sampling a wide spectral range and the design of a flow cell with sufficiently short optical path-lengths to allow transmission of infrared light through the solvent. The need for protein concentrations in the mM range is another impediment. By interfacing a Fourier transform infrared (FTIR) spectrometer in rapid-scan mode with a stopped-flow mixer, it is possible to record complete IR spectra on transient states populated on the 10 ms time scale.^153–155 Marinkovic et al.¹²⁴ were able record transient IR spectra with a time resolution in the ms range by using a synchrotron as an IR radiation source in conjunction with a micro-fabricated mixer developed previously for resonance Raman studies⁷¹. In another recent paper Kimura et al. ¹⁵⁶ used FTIR-detected continuous-flow measurements to monitor helix formation in poly-L-glutamic acid in the sub-ms time range.

3.6. Small-angle X-ray Scattering

Small-angle X-ray scattering (SAXS) experiments can provide unique information on the molecular dimensions and shape of proteins, including dynamic ensembles of partially or fully denatured states.^157,158 In order to monitor size and shape changes during early stages of folding, several laboratories have combined synchrotron-based SAXS measurements with stopped-flow^114,159 or continuous-flow instruments,^84,89 as well as a novel hydrodynamic mixing method.^73,106 Akiyama et al.⁸⁴ constructed a mixer/flow-cell assembly with a dead time as short as 160 μs for continuous-flow SAXS measurements on a synchrotron. This challenging experiment enabled them to follow the changes in size (radius of gyration, R_g) and shape (pair distribution derived from scattering profiles) associated with refolding of cyt c,⁸⁴ myoglobin,⁸⁹ ribonuclease A (RNase A)¹⁶⁰ and single-chain monellin.¹⁶¹

3.7. Other Detection Methods

Continuous-flow measurements have been coupled with a number of other biophysical techniques, including resonance Raman spectroscopy⁷¹ and EPR.^80,162 In their pioneering work, Takahashi et al.⁷¹ used resonance Raman spectroscopy to monitor changes in heme coordination during folding of cyt c on the sub-milliscond time scale. Their findings confirmed and extended prior results on the involvement of heme ligation in folding of cyt c, based on stopped-flow absorbance and fluorescence measurements.^163–165 Grigoryants et al.⁸⁰ developed a unique capillary mixer for continuous-flow measurements in an EPR spectrometer. The short relaxation times (compared to NMR) of free radicals and paramagnetic metal centers makes it possible to record EPR signals on short-lived species. Scholes and colleagues have used this technique to measure the kinetics of folding of spin-labeled yeast cyt c on the sub-millisecond time scale.¹⁶²

4. Quenched-flow H/D Exchange Studies of Early Folding Events

Quenched-flow hydrogen exchange labeling experiments coupled with NMR analysis^{39–41,166–168} continue to be the main source of residue-specific structural information on folding intermediates.^82,169–174 Mass-spectrometric analysis has emerged as an alternative analytical technique for H/D exchange labeling studies of protein folding and other conformational changes.^175,176 H/D exchange labeling methods and their application to protein folding have been reviewed extensively.^{101,166,177–181} We will, therefore, limit our discussion to recent NMR-based H/D exchange studies aimed at the structural characterization of early folding intermediates.

4.1. A quenched-flow Method for H/D Exchange Labeling on the μs Time Scale

Most protocols for H/D exchange labeling rely on commercial quenched-flow equipment to carry out two or three sequential mixing steps, which limits the time resolution to a few milliseconds or longer. However, amide protons are often found to become protected from H/D exchange within the dead time of quenched-flow mixing (2–10 ms), indicating that hydrogen bonded structure can form on the sub-millisecond time scale.^{167,168,170,182–185}

Bökenkamp et al. ¹²³ described a quenched-flow device with substantially improved time resolution (~100 μs minimum delay between sequential mixing events). They constructed a series of mixers by etching 200 μm diameter channels into silicon chips, using a microfabrication method. Each chip contains a pair of T-mixers connected by a delay line of variable length. Solutions are delivered at flow rates sufficient for efficient turbulent mixing, using a BioLogic (Claix, France) quenched-flow apparatus.

We recently devised an alternative approach for extending quenched-flow measurements into the microsecond time range.¹³⁸ The device uses a quartz capillary mixer similar to that used for optical measurements (Figure 1), but without observation cell, in order to generate a homogeneous mixture of two solutions (e.g., unfolded protein and refolding/exchange buffer). The mixture emerges from the capillary as a fine (200 μm diameter) jet with a linear velocity of up to 40 m/s at the highest flow rate used (1.25 ml/s). A second mixing event can be achieved simply by injecting the jet into a test tube containing a third solution (quench buffer); the high flow velocity ensures very efficient mixing. To determine the dead time (i.e., the shortest delay between the two mixing events), we carried out a series of H/D exchange experiments on a pentapeptide (YGGFL). Rapid exchange of the backbone amide protons with solvent deuterons was achieved by mixing an H₂O solution of the peptide with D₂O buffered at basic pH (9.7). The exchange reaction was quenched by injecting the mixture into ice-cooled acetate buffer at pH 3. Under these quench conditions, the rate of exchange for some of the peptide NH groups (Gly3, Phe4 and Leu5) is sufficiently slow (10, 45 and 70 min, respectively) to determine their residual NH intensity by recording one-dimensional ¹H NMR spectra. To vary aging time the capillary was raised from direct contact with the quench solutions to a distance of about 40 mm corresponding to an upper time limit of ~1 ms. For Gly3 and Phe4, exponential fits of the decay in residual NH intensity with the incremented time delay yields exchange rates of 5,600 and 4,400 s⁻¹, respectively, in agreement with published intrinsic exchange rates.¹⁸⁶ Extrapolation of the fits up to the NH intensity expected at t=0 (measured in a separate control) indicates that the first measurement corresponds to an effective exchange time of 60 ± 10 μs, thus defining the dead time of the measurement.

4.2. H/D Exchange Labeling of Early Folding Intermediates

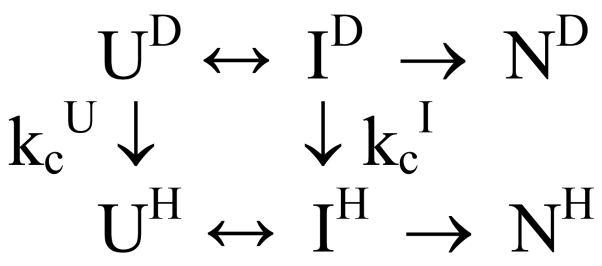
A straightforward, yet informative, technique for measuring amide protection patterns in early folding intermediates is the burst-phase labeling method, which is closely related to the competition method used in the first study of protein folding by NMR-detected H/D exchange.³⁹ In contrast to the pulse labeling protocol used for following the kinetics of protection at longer times (>5 ms), the competition method requires only two sequential mixing steps, which can be applied in rapid succession, using the capillary quenched-flow device.¹³⁸ For a three-state folding mechanism with a populated intermediate (K_UI>1), the competition experiment can be described by Scheme 2, where k_cU and k_cI are the exchange rates of a given NH group in the unfolded and intermediates states, respectively. k_c(U) corresponds to the intrinsic (chemical) exchange rate, k_c, estimated on the basis of model peptides.¹⁸⁶ If k_cI ≪ k_cU, i.e., the NH group is protected in the intermediate, the proton occupancy, Y_H, for a given amide proton will initially rise at a rate k_c+k_UI and approach at long times a steady-state level determined by the ratio of folding and exchange rates.³⁹ Under conditions where exchange and folding rates (k_UI) are comparable, both k_c and k_UI can, in principle, be determined from a series of experiments involving variation of the competition time at constant pH. However, a more straightforward experiment is to vary pH at a fixed competition time.³⁹ By minimizing the time period (competition time) during which the pH-dependent competition between folding and H/D exchange can occur, it is possible to measure protection factors in early intermediates, even if amide protons are only marginally protected.^167,168 In this burst-phase labeling scheme, proton occupancies, Y_H, are measured as a function of labeling pH, using a competition time of a few ms. Any shift in the Y_H vs. pH profile to higher pH, compared to that expected for an unprotected proton (measured in a control experiment in the presence of denaturant), provides an estimate for the effective protection from exchange due to accumulation of early intermediates within the competition time. If the I-state is a relatively stable (late) intermediate, the results are expressed in terms of protection factors, P = k_ex(U)/k_ex(I), where k_ex(U) and k_ex(I) are the effective exchange rates of a given amide protons in the unfolded population and intermediate state, respectively (see also ref 187). Although the model-peptide rates, k_c, can be used to estimate k_ex(U), it is more reliable to measure this rate under destabilizing conditions in order to account for any residual structure in the denatured state.¹⁶⁸ This modification greatly improves the accuracy of the results, making it possible to measure protection factors as small as 2 (since P = K_IU + 1, this corresponds to 50% population of a hydrogen-bonded species).

Scheme 2.

To study structure formation on the sub-ms time scale, one has to extend the competition experiment to pH values above 10 where intrinsic exchange times are of the order of 1 ms or less. Under such extreme conditions, we can no longer assume that the exchange reaction is limited by the intrinsic exchange rate, k_c (a limiting case commonly referred to as EX₂ exchange).¹⁸⁸ If k_c exceeds the rate of folding (k_UI), the rate of unfolding (k_IU) becomes rate-limiting for exchange (EX₁ exchange). Eq 2 is a more general steady-state rate expression that covers both EX₂ as well as EX₁ exchange conditions (assuming k_UI ≫ k_IU, k_c).^{173,188–190} In eq 2,

$${\text{Y}}_{\text{H}}(\text{pH})=1-\text{exp}(\frac{{\text{k}}_{\text{IU}}\times {\text{k}}_{\text{c}}\text{(pH)}}{{\text{k}}_{\text{IU}}+{\text{k}}_{\text{UI}}+{\text{k}}_{\text{c}}\text{(pH)}}\times {\text{t}}_{\text{p}})$$ (2)

k_UI and k_IU are the rates of formation and unfolding of the intermediate, respectively, k_c = k_c(U) is the intrinsic exchange rate from the unfolded state, and t_p is the duration of the exchange/folding competition time. This analysis assumes that k_c is the only pH-dependent rate, and that any direct exchange from the I-state (k_c(I) in Scheme 2) is negligible compared to k_c(U). The rates of formation and unfolding of intermediates are likely to become pH-dependent under very basic conditions, which may give rise to deviations from the behavior predicted by eq 2 at high pH. To describe situations with marginally stable conformational states (k_UI ~ k_IU), it is necessary to use the full double-exponential solution for a three-state kinetic mechanism.^173,188

4.3. Probing the Stability of Folding Intermediates by Pulse Labeling

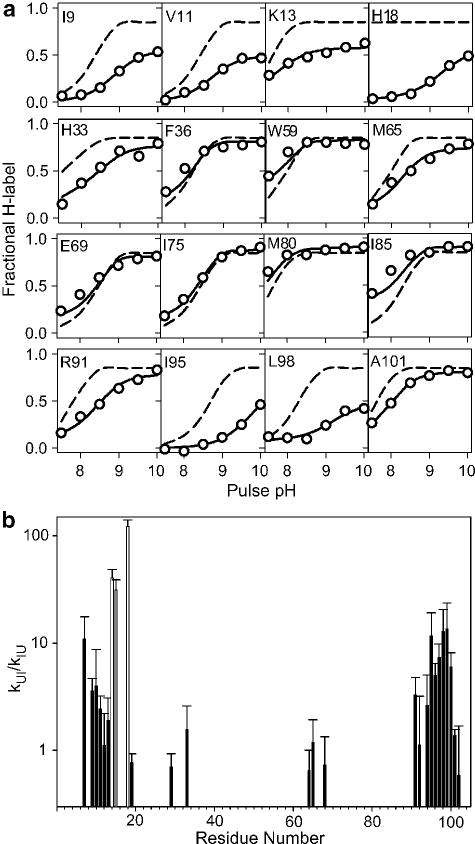
Residue-specific information on the structure and stability of intermediates populated at longer folding times (>ms) can be obtained by allowing the protein to fold for a fixed refolding time before applying a short labeling pulse at variable pH.^{170,173,182,190–192} This labeling protocol calls for three sequential timed mixing steps at accurately timed intervals ranging from a few ms to about 10 s, which can be achieved using commercially available quenched-flow instrumentation (shorter times are, in principle, accessible using a microfluidic device¹²³). Figure 7 illustrates this approach with recent results by Krishna et al.¹⁷³, who used a pulse pH variation strategy to characterize the structural and dynamic properties of a late intermediate populated during folding of cytochrome c. Previous pulsed hydrogen exchange studies have shown that this intermediate accumulates within about 10 ms of refolding at pH 6 or above, contains stable structure primarily in a pair of interacting N- and C-terminal α-helices and is stabilized by the presence of a non-native histidine-heme ligand.^40,163,164 The symbols in Figure 7a show the pH-dependent proton occupancy for selected residues monitored by 2D NMR analysis of samples that were exposed to a 50 ms labeling pulse at variable pH following a refolding delay of 100 ms.¹⁷³ The dashed lines indicate the pH profiles expected if a particular NH group were unprotected in the intermediate. For many residues, especially those in the N- and C-terminal regions of the protein, the observed labeling profiles are displaced toward higher pH, indicating that they are involved in stable hydrogen bonds that protect them from solvent exchange. Elöve and Roder¹⁹⁰ have previously reported similar behavior for a subset of residues that can be resolved by 1D NMR and concluded that the complex labeling curves were indicative of a heterogeneous population of molecules folding along parallel pathways. Krishna et al.¹⁷³ were able to fit the observed pH profiles quantitatively by using a generalized version of eq 2. Assuming that exchange occurs from the unfolded state at the intrinsic exchange rate k_c,¹⁸⁶ the model has only two free parameters, k_UI and k_IU, which reflect the dynamics and stability of individual hydrogen bonds. A plot of the equilibrium constant for formation of the I-state, K_UI = k_UI/k_IU, vs. residue number (Figure 7b) indicates that the structured regions of the intermediate (K_UI ≥1) are limited to the N- and C-terminal helices and a handful of intervening residues. The gray bars indicate residues (Cys14, Ala15 and His18) involved in residual hydrogen-bonded structure even under fully denaturing conditions.^163,168,193 The analysis of Krishna et al.¹⁷³ can account for the complex variation in the slope and saturation behavior of the data in terms of a transition from EX₂ (exchange-limited) to EX₁ (opening-limited) exchange kinetics. Thus, the ensemble of intermediates populated over the 10–100 ms time window appears to be more homogeneous than we thought initially.¹⁹⁰

Figure 7.

Characterization of an intermediate populated during folding of cytochrome c (pH 6, 10 °C).¹⁷³ a Fractional degree of labeling vs. pulse pH for a representative set of NH groups measured by 2D NMR analysis of refolding cytochrome c samples that were exposed to a 50 ms labeling pulse of increasing pH at a folding time of 100 ms. Solid lines represent a fit of the data yielding the rates of formation and unfolding of the intermediate state (see text). Dashed lines indicate the labeling profiles expected in the absence of structure. b Equilibrium constant for formation of the intermediate, K_UI = k_UI/k_IU, based on the fits of the labeling results in a. Values of K_UI ≥ 1 indicative of persistent hydrogen bonded structure are mainly found for residues in the N- and C-terminal helices. Cys 14, Ala15 and His 18 (gray bars) are protected even in the unfolded state. Adapted from ref 173 (Figures 3 and 4), with permission by the authors.

5. Early Intermediates in the Folding of Small Proteins

5.1. Stopped-flow Evidence for Rapid Folding Events

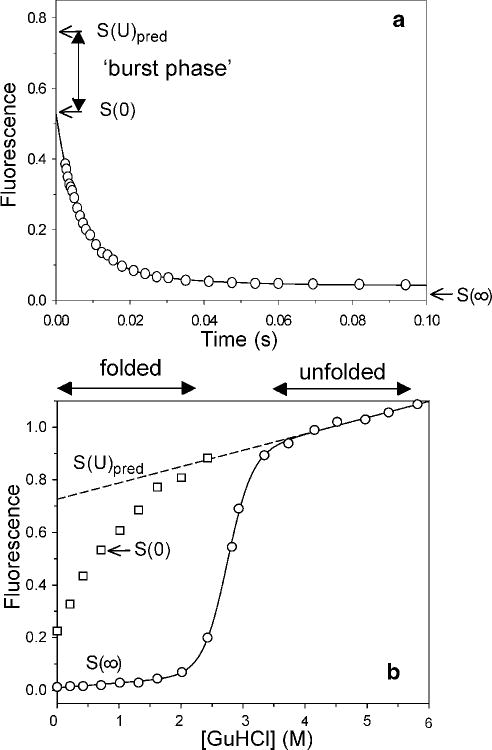
The first indications of protein folding events on the microsecond time scale came from stopped-flow experiments, which often show unresolved changes in optical signals occurring within the dead time of measurements.^{145,148,170,183,194–196} To illustrate this so-called burst-phase effect, Figure 8 shows the kinetics of refolding of horse cytochrome c (cyt c)¹³⁶ measured by stopped-flow fluorescence (panel a) along with equilibrium fluorescence data vs. denaturant concentration (panel b). The protein was unfolded by addition of 4.5 M GuHCl, which lies in the baseline region above the cooperative unfolding transition, and the refolding reaction was triggered by 6-fold dilution with buffer (0.1 M sodium acetate, pH 5), resulting in a final GuHCl concentration of 0.75 M, well within the folded baseline region. The data points in panel a were recorded by sampling the fluorescence emission above 325 nm (using a glass cutoff filter) at logarithmically spaced time intervals. The first time point corresponds to the instrumental dead time of 2.5 ms, which was calibrated using the NATA-NBS test reaction (see Figure 2). The observed kinetics on the ms time scale describes a double-exponential decay (solid line) comprising a major phase with time constants of ~8 ms and a minor one with a time constant of about 500 ms. Extrapolation of the observed kinetics back to t=0 yields the initial signal, S(0), which is compared in panel b (arrow) with the equilibrium unfolding transition plotted on the same fluorescence scale (relative to unfolded protein at 4.5 M GuHCl). The initial signal observed in this and a series of additional stopped-flow experiments at different final GuHCl concentrations is consistently below the relative fluorescence of the unfolded state, S_pred(U), predicted by linear extrapolation from the unfolded baseline region to lower GuHCl concentrations (dashed line in panel b). The difference between the predicted and observed initial amplitude, S_burst = S_pred(U) – S(0), reflects conformational events occurring within the dead time of the stopped-flow experiment (the so-called burst-phase amplitude). If the formation of intermediate(s) during the dead time is kinetically well resolved from slower folding steps, a pre-equilibrium is established between unfolded and intermediate states, whose stability can be estimated from the denaturant dependence of S_burst (provided that pre- and post-transition baseline values can be defined). Similar observations for many different proteins using various spectroscopic parameters gave clear evidence for the existence of rapid conformational events that cannot be resolved with conventional mixing techniques, and provided a strong incentive for the development of faster methods for triggering and observing structural changes during the first millisecond of refolding.^71,72

Figure 8.

Stopped-flow fluorescence evidence for an unresolved rapid process (burst phase) during folding of cyt c (pH 5, 10 °C). a Tryptophan fluorescence changes during refolding of acid-unfolded cytochrome c (pH 2, ~15 mM HCl) at a final GuHCl concentration of 0.7 M. The initial signal S(0) at t=0 (determined on the basis of a separate dead-time measurement) falls short of the signal for the unfolded state under refolding conditions, S_pred(U), obtained by linear extrapolation of the unfolded-state baseline (see dashed line in b). b Effect of the denaturant concentration on the initial (squares) and final (circles) fluorescence signal, S(0) and S(∞), measured in a series of stopped-flow refolding experiments at different final GuHCl concentration. Reprinted with permission from ref 138. Copyright 2004 Elsevier Inc.

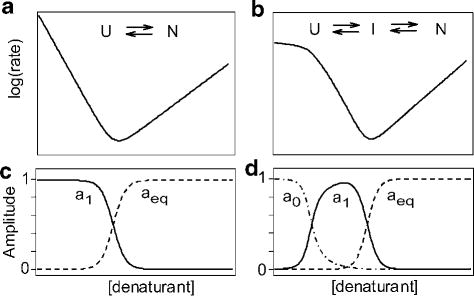
A second line of evidence supporting accumulation of early folding intermediates has been based on the dependence of folding rates on denaturant concentration (usually guanidine HCl or urea), as illustrated schematically in Figure 9. In the absence of populated intermediates, a logarithmic plot of the measured rate constant of folding, k_f, vs. denaturant concentration (panel a) often describes a V-shape with a decreasing linear dependence at denaturant concentrations below the midpoint of the unfolding transition (C_m), a minimum at C_m, and a linearly increase for the rate of unfolding at denaturant concentrations above C_m (hence the name “chevron plot”).^95,197,198 As illustrated by Figure 9b, accumulation of intermediate states prior to the rate-limiting folding step can give rise to a non-linear folding branch of the chevron plot, usually a downward curvature with decreasing denaturant concentration. The discovery of this so-called rollover effect is often attributed to Matouschek et al.,⁹⁶ who found that the chevron plot for barnase showed a pronounced curvature at low denaturant concentrations. However, Matthews and colleagues described similar complexities in the folding kinetics of the α-subunit of tryptophan synthase as early as 1981.¹⁹⁹ A quantitative connection between folding intermediates and the rollover effect was established be several groups in the mid-1990’s who used quantitative kinetic models to explain the curvature in the log(k_f) vs. [denaturant] dependence in terms of accumulation of an early (obligatory) folding intermediate.^195,200,201 Khorasanizadeh et al.¹⁹⁵ further showed that both the rollover and burst-phase effects can be modeled quantitatively by a three-state folding mechanism (Scheme 3) involving rapid formation of an intermediate prior to the rate-limiting formation of the native state. In this scenario, a partially folded state is sufficiently stable to become populated at low denaturant concentrations and limits the overall rate of folding, which gives rise to both deviation from linearity in the chevron plot (Figure 9b) and a drop in the observable kinetic amplitude of the main (rate-limiting) folding phase (Figure 9d). In many cases, the observed folding times at low denaturant concentrations approach values in the millisecond range, which rules out the possibility that the rate-limiting process represents cis/trans isomerization of a proline peptide bond.^37,202,203 Moreover, the amplitude behavior shown in Figure 9d where the fast kinetic phase is dominant at low denaturant concentrations (a_o approaching 1) and decreases in amplitude at the expense of the slow phase (a₁) is characteristic of a sequential folding process with an on-pathway intermediate. In contrast, slow isomerization steps, such as proline isomerization, that precedes the formation of the native state generally gain amplitude under destabilizing conditions approaching the midpoint of the unfolding transition.²⁰³

Figure 9.

Schematic log(rate) vs. [denaturant] plots (chevrons) for a two-state (a) and a three-state (b) folding/unfolding mechanism. The lower panels show the predicted amplitude for the main folding phases (a₁), the burst phase predicted for a three-state process (a₀ in panel d) and the equilibrium unfolding transition (a_eq).

Scheme 3.

In other cases, a complex dependence of folding or unfolding rates can occur even without appreciable population of intermediate states.¹³ For example, the rate of unfolding for several c-type cytochromes was found to level off at high denaturant concentrations, giving rise to a chevron plot with a highly non-linear unfolding branch.^{85,136,163,172,204,205} Sauder et al.²⁰⁴ were able to fit this behavior quantitatively on the basis of a kinetic model involving a poorly populated, but obligatory intermediate in unfolding, which leads to a change in the rate-limiting transition state under strongly destabilizing conditions. In the case of the cytochromes, this effect can be attributed to cleavage of the ligand bond between the sulfur of a methionine and the heme iron,^163,204 but a similar phenomenon has been reported for non-heme proteins. For example, Walkenhorst et al.²⁰⁶ used a mechanism involving a high-energy unfolding intermediate to explain the non-linearity observed in the unfolding kinetics of SNase. In a recent comprehensive survey of about 25 proteins, Sanchez and Kiefhaber¹³ showed that non-linear chevron plots are a common feature, even for proteins without detectable intermediates, and can be interpreted quantitatively in terms of sequential folding mechanisms with high-energy obligatory intermediates. Native-like intermediates can lead to curvature in the kinetics of unfolding while less ordered high-energy intermediates account for complexities in refolding. Although alternative models, such as a solvent-induced shift of a broad folding barrier,²⁰⁷ cannot be ruled out in every case, a three- or four-state mechanism is the simplest scenario and provides a consistent description of the effects of mutations and solvent conditions on the kinetics of folding and unfolding.

5.2. B1 Domain of Protein G

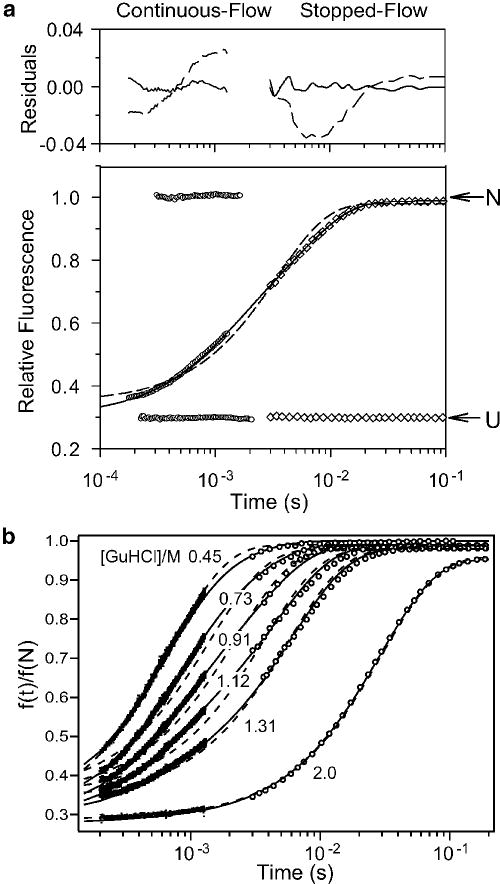
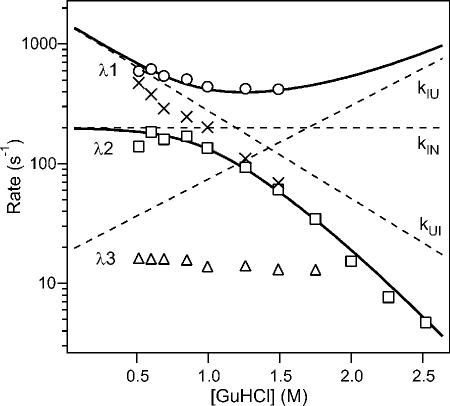
The observation of a burst-phase, such as that in Figure 8, suggested deviations from two-state behavior for many proteins. This list includes not only large proteins with over 100 residues, but also several smaller ones.^{10–12,101,129,208} An illustrative example is the 57-residues B1 domain of protein G (GB1), which is among the smallest globular protein domains that do not depend on disulfide bonds or metals for stabilization.²⁰⁹ Like many other small proteins,⁹² GB1 was initially thought to fold according to a two-state mechanism.²¹⁰ However, continuous-flow fluorescence measurements of the GB1 folding kinetics⁷⁸ showed clear deviations from the first-order (single-exponential) kinetics expected for a simple two-state process (Figure 10a). The time course of refolding from the guanidine-denatured state revealed a prominent exponential phase with a time constant of 600–700 μs followed by a second, rate-limiting, process with a time constant of 2 ms or longer, depending on denaturant concentration (Figure 10b). The fast phase dominates the kinetics at low denaturant concentrations and accounts for the total fluorescence change associated with the burial of Trp43 upon folding, including the previously unresolved burst-phase signal.²⁰⁸ In Figure 11, the rate constants obtained by fitting two exponential terms to the observed traces and the corresponding amplitudes are plotted vs. denaturant concentration. The biphasic kinetics of folding observed over a range of GuHCl concentrations can be modeled quantitatively on the basis of a three-state folding mechanism (Scheme 3), where I represents an ensemble of intermediate states with native-like fluorescence properties (i.e., Trp43 is buried). The dependence of elementary rate constants, k_ij, on denaturant concentration c (dashed lines in Figure 11) is governed by the following relationship

$$ln{k}_{\text{ij}}=ln{k_{\text{ij}}}^0+({m_{\text{ij}}}^{‡}/RT)\times c$$ (3)

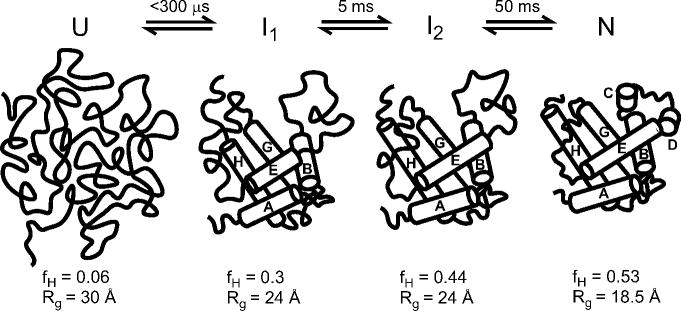
where k_ij⁰ represents the elementary rate constant in the absence of denaturant, and m_ij^‡ describes its dependence on denaturant concentration (kinetic m-value). The system of linear differential equations describing Scheme 3 were solved by determining the eigenvalues and eigenvectors of the corresponding rate matrix, using standard numeric methods.^211,212 Although a three-state kinetic mechanism can be solved analytically (e.g., ref 13), the rate-matrix approach has the advantage that it can be readily expanded to more complex first-order kinetic mechanisms. After optimizing the four elementary rate constants and corresponding m-values, the two observable rates (eigenvalues) and associated amplitudes predicted by the model (solid lines in Figures 11a and b) simultaneously fit both the observed rate profile (log(rate) vs. GuHCl concentration) and kinetic amplitudes at each denaturant concentration, as well as the midpoint and slope of the equilibrium unfolding transition (diamonds in panel b). The three-state mechanism explains the kinetic behavior at low (<1 M) and intermediate (1–3 M) GuHCl concentrations in terms of two distinct kinetic limits reminiscent of the EX₁ and EX₂ limits of hydrogen exchange.¹⁸⁸ At low denaturant concentration, the intermediate is stable and transiently populated (the free energy of I in Figure 11c is lower than that of U), and the rate of the slower folding phase approaches the elementary rate constant of the final folding step, k_IN. At the same time, the fast (sub-ms) folding phase gains amplitude at the expense of the slow (rate-limiting) phase. At intermediate denaturant concentrations, the intermediate is destabilized (Figure 11c) and no longer accumulates. However, if I is an obligatory intermediate, the observed folding rate approaches the limiting value k_f = K_UI × k_IN, where K_UI = k_UI / k_IU is the equilibrium constant of the U ⇔ I transition. Thus, the sharp decrease in the net folding rate as the denaturant concentration approaches the midpoint of the unfolding transition is explained in terms of the unfavorable U ⇔ I pre-equilibrium involving a high-energy intermediate.

Figure 10.

Folding kinetics of GB1 at pH 5.0, 20 °C, in the presence of 0.4 M sodium sulfate. Panel a shows a representative kinetic trace at 1.12 M GHCl monitored by continuous-flow (circles) and stopped-flow (diamonds) fluorescence along with controls for fully unfolded (U) and folded (N) solutions. Single- and double-exponential fits and residuals are shown with solid and dashed lines, respectively. Reprinted with permission from ref 78. Copyright 1999 Nature Publishing Group. Panel b shows a family of refolding traces at the final GuHCl concentrations indicated. Solid lines show the time course predicted on the basis of a three-state model (Scheme 3), using the following parameters: k_UI° = 2300 s⁻¹, m_UI^‡ = −0.6 kcal mol⁻¹M⁻¹, k_IU° = 70 s⁻¹, m_IU^‡ = 1.15 kcal mol⁻¹M⁻¹, k_IN° = 600 s⁻¹, m_IN^‡ = 0, k_NI° = 0.14, m_NI^‡ = 0.3 kcal mol⁻¹M⁻¹ (see Figure 11a, ref 78). The relative signals for the N-, I- and U-states were s_N = 0.29 ± 0.01, s_I = s_U = 0.98 ± 0.02. Dashed lines indicate a best “fit” of a two-state mechanism, using rate constants falling on a linear extrapolation of the chevron plot between 1.5 and 3 M GuHCl to lower denaturant concentrations (cf. ref 213).

Figure 11.

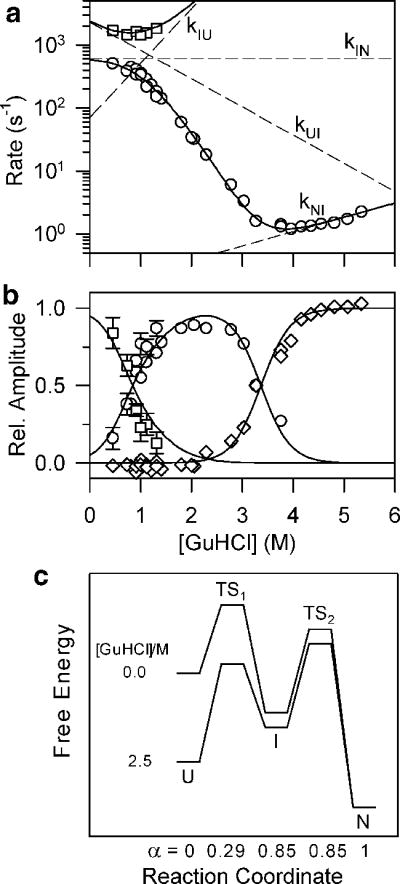
GuHCl-dependence of the rate constants (a) and kinetic amplitudes (b) of the fast (squares) and slow (circles) kinetic phases observed during folding of GB1. c Free energy diagrams for folding of GB1 under conditions where the intermediate, I is well populated (0 M) and unstable (2.5 M GuHCl). α represents the change in solvent-accessible surface area relative to the unfolded state U. Reprinted with permission from ref 78. Copyright 1999 Nature Publishing Group.

Three-state analysis of a complete set of kinetic data, such as that of GB1 reported by Park et al.,⁷⁸ provides a comprehensive description of the folding mechanism in terms of the size of the free-energy barriers separating the intermediate from the unfolded and native states (labeled TS₁ and TS₂ in Figure 11c) and the stability of the intermediate (ΔG = −RT ln (k_UI/k_IU). In addition, the denaturant-dependence of the four elementary rate constants provides valuable insight into the changes in solvent-accessible surface area associated with each transition. In Figure 11c, each state and intervening transition state is labeled with the corresponding α-value (sometimes called β_T in reference to Tanford¹) obtained by the cumulative kinetic m-values with respect to the total equilibrium m-value. According to this analysis, the initial barrier, TS₁, represents a well solvated ensemble of states (α =0.29) while both I and TS₂ are nearly as solvent-shielded as the native state (α =0.85). The relative changes in fluorescence associated with the two folding phases of GB1 provide additional insight into the structural properties of the intermediate. The large increase in fluorescence during the fast phase (Figure 11), which accounts for nearly all of the fluorescence change at equilibrium, indicating that Trp43 becomes largely buried already during the initial phase of folding. Given the central location of Trp43 at the interface between the C-terminal β-hairpin and the α-helix, this indicates that the intermediate contains a well-developed hydrophobic core.

Krantz et al. recently questioned the validity of our analysis and argued that the folding kinetics of GB1 should be modeled as a two-state process.²¹³ This implies that the complete time course of folding can be fitted by a single exponential. In contrast, we find that a satisfactory fit of our combined continuous- and stopped-flow data requires two exponential phases, while a single exponential fit leads to non-random residuals of the order of 10%, which is unacceptable, given the quality of the data (Figure 10a). It should be noted that the two phases differ sufficiently in rate (>3.5-fold) to make their separation unambiguous. This conclusion is strengthened by the absence of additional, slower phases in GB1, which contains no proline residues. Below 1 M GuHCl, where the slower phase of our double-exponential fit levels off (Figure 11a), the apparent rate obtained by single-exponential fitting continues to increase, approximating the linear chevron behavior of a two-state system (cf. Figure 9a). This phenomenon is explained by the fact that the approximate rate obtained by fitting a single exponential represents a weighted average of the rates obtained by double-exponential fitting (see section 5.3). Because the fast phase dominates at low and the slow phase at higher denaturant concentrations, the result is a relatively linear rate profile. We further note that the population of the intermediate becomes negligible at GuHCl concentrations approaching the transition region, resulting in an apparent two-state unfolding equilibrium. Thus, contrary to Krantz et al.,²¹³ the predicted equilibrium behavior cannot be used to discriminate between the two models. Finally, the folding kinetics of GB1 was found to be independent of protein concentration,²⁰⁸ indicating that intermolecular interactions are not involved in stabilizing the intermediate.

As a further validation of the three-state model, we used the elementary rate constants obtained by modeling the data in Figure 11a along with the relative fluorescence values for the various states (panel b) to predict the time course of folding. The fact that we can simultaneously reproduce all of the curves measured at different denaturant concentration (solid lines in Figure 10b) is a compelling demonstration that Scheme 3 is fully consistent with all observations (see refs ^87,206 for earlier applications of this global kinetic modeling approach). Alternative three-state mechanisms with nonproductive or nonobligatory intermediates lead to somewhat poorer fits of the data at low denaturant concentration, but cannot be ruled out definitively on the basis of available data (see section 6.4). However, a simple two-state mechanism with a linear chevron plot (cf. ref 213) leads to poor predictions of the observed time course of folding at all except the lowest and highest GuHCl concentrations for which we have both continuous- and stopped-flow data (dashed lines in Figure 10b).

5.3. Ubiquitin

The 76-residue α/β protein ubiquitin is another well-studied small protein for which three-state folding behavior has been reported under some conditions. Khorasanizadeh et al.^129,195 found deviations from two-state behavior in the folding kinetics of a tryptophan-containing ubiquitin variant (F45W mutant), including a downward curvature in the rate profile (log(rate) vs. [denaturant] plot) and a concomitant drop in the relative amplitude of the main folding phase at low denaturant concentration. They were able to account for both phenomena (rollover and burst phase) in terms of a three-state mechanism with an obligatory on-path intermediate (Scheme 3). As detailed above for GB1, this simple scheme explains the leveling-off of the rate constant and diminishing amplitude of the principal (rate-limiting) folding phase at GuHCl concentrations below 1 M. However, alternative explanations cannot be ruled out without direct observation of the inferred fast folding phase. Moreover, the uncertainty in the burst-phase amplitude is substantial if the main observable folding phase approaches the dead time of the kinetic experiment, which is the case for ubiquitin under stabilizing conditions. Krantz and Sosnick²¹⁴ remeasured the folding kinetics of F45W ubiquitin, using a stopped-flow instrument with a dead time of ~1 ms. They found a linear rate profile for the main folding phase and no indications of a burst phase, and concluded that our earlier evidence for a folding intermediate was based on fitting artifacts.

In an effort to settle this debate, we recently revisited the folding kinetics of F45W ubiquitin,¹⁴ combining continuous-flow fluorescence measurements with stopped-flow experiments with an improved dead time, which allowed us to continuously monitor the time course of folding from about 100 μs to 100 s (see Figure 12a for two representative kinetic traces). The initial increase in fluorescence relative to the GuHCl-unfolded state with a time constant τ₀ = 150 μs becomes more pronounced in the presence of sodium sulfate (data not shown) and is consistent with a decrease in the solvent accessibility of the fluorophore, Trp45, at an early stage of folding. However, further studies are required to determine whether this process reflects formation of a folding intermediate or a nonspecific collapse event. The subsequent fluorescence decay is attributed to intramolecular quenching of Trp45 fluorescence upon folding.²¹⁵ A thorough kinetic analysis, using multi-exponential fitting functions, indicates that a minimum of four distinct phases are required to obtain a satisfactory fit of the data over the 0.1 to 1 s time window (Figure 12a); a minor additional fluorescence decay at longer times has been attributed to proline isomerization.¹²⁹ In contrast, if we use only three exponentials (including one increasing and two decaying phases) to fit the data over the same time window, we obtain nonrandom residuals with amplitudes much larger than the scatter of the data points (Figure 12b). Under the most stabilizing conditions studied (0.5 M GuHCl), a satisfactory fit of the main fluorescence decay from 300 μs to 10 ms requires two distinct phases, λ₁ and λ₂, with time constants τ₁ = 1.8 and τ₂ = 7.1 ms, respectively. Another phase (τ₃ ~ 70 ms) is necessary to account for a minor decay observed between 20 and 200 ms. The fact that both the rate and amplitude of phase λ₃ are essentially independent of denaturant concentration points toward a heterogeneous process, perhaps involving a minor population of molecules containing non-native (cis) proline isomers. Although this process is clearly too fast to be assigned to proline isomerization, the presence of a cis peptide bond in a critical location may slow down a conformational folding step. A plot of the rate constants for the three decaying phases vs. GuHCl concentration (Figure 13) shows a pronounced rollover for λ₂ (squares) with a denaturant-independent regime below 0.75 M followed by a linear decrease above 1 M GuHCl, whereas λ₁ shows a shallow upward curvature. As in the case of GB1 (Figure 11), this behavior is fully consistent with a three-state mechanism (Scheme 3). Figure 13 also shows the apparent rates for the main decaying phase obtained by fitting only three exponentials (symbol x). Since they represent an average of λ₁ and λ₂ weighted according to the relative amplitudes, they continue to increase with decreasing GuHCl concentration below 1 M. Thus, the controversy whether an intermediate accumulates during folding of ubiquitin again boils down to a curve fitting issue. In our initial study, we detected only the slower process, λ₂, which exhibits the rollover and missing-amplitude effects indicative of a burst-phase intermediate.¹⁹⁵ By extending their stopped-flow measurements to shorter times (~1 ms), Krantz and Sonick²¹⁴ obtained a faster rate without apparent rollover corresponding to a weighted average of the two underlying processes. In a recent stopped-flow study, Went et al.²¹⁶ found that F45W ubiquitin exhibits three-state folding kinetics under some conditions (in the presence of GuHCl or urea plus salt) and two-state behavior under other conditions (in the presence of urea at low ionic strength). They further report that the folding rate for F45W ubiquitin shows moderate variation with protein concentration, suggesting that transient association may stabilize the intermediate. All of these observations, including our earlier findings on the effects of core mutations,¹⁹⁵ can be explained by the presence of a marginally stable intermediate, which affects the kinetics of folding only under sufficiently stabilizing conditions.

Figure 12.

Comparison of quadruple (a) and triple (b) exponential fitting of the kinetics of refolding of F45W ubiquitin at final GuHCl concentrations of 0.5 and 1.0 M (pH 5, 25 °C). Fluorescence traces measured in continuous- and stopped-flow experiments were normalized with respect to the unfolded protein in 6 M GuHCl. The residuals (top two traces in each panel) indicate that four exponentials are required to obtain a satisfactory fit of the data over the time window shown. Reprinted with permission from ref 14. Copyright 2005 Wiley-VCH.

Figure 13.

Expanded region of the rate profile (log rate vs. [GuHCl[) for the two main phases (circles and squares) and a minor slower phase (dtriangles) observed during folding of F45W ubiquitin (pH 5, 25 °C). The solid lines show the rates predicted by a three-state model, and the dashed lines indicate the elementary rate constants used. The X-symbols show the apparent rates obtained by triple-exponential fitting (Figure 10b). Reprinted with permission from ref 14. Copyright 2005 Wiley-VCH.

The examples presented in this and the preceding sections highlight some of the curve fitting problems that often plague the kinetic analysis of complex processes. Although any unimolecular system, irrespective of the number of states involved, can be described by a system of linear differential equations whose solution is a sum of exponential terms²¹¹, it is often difficult or impossible to determine the appropriate number of terms to be used in fitting an individual kinetic trace. While the problem can in principle be approached using Laplace transforms or maximum entropy methods, these require extremely high data quality to yield meaningful results. For example, in the case of ubiquitin (Figure 12), the residuals obtained with three exponentials are clearly not satisfactory, and addition of a fourth term seems well justified, but the residuals are still not perfect and could be improved further by introducing a fifth phase. However, at some point we are beginning to fit systematic errors, such as baseline drifts, digitization noise, stop artifacts, etc., which are inevitable especially in stopped-flow experiments. A related problem is that the number of apparent phases depends on the exact conditions used. For example, increasing concentrations of denaturant typically simplify the kinetics as folding intermediates are destabilized. At some (arbitrary) point one has to drop a phase, which leads to a discontinuity in amplitudes.

Many of the pitfalls of empirical data fitting can be avoided by “fitting” a kinetic mechanism globally to a whole family of kinetic traces recorded as a function of an extrinsic variable, such as denaturant concentration, stabilizing salts, temperature or pH. As illustrated above for the case of GB1 (section 5.2, Figure 10), this circumvents the problem of having to chose the order of the fitting function, and fully exploits both rate and amplitude information. However, for more complex systems (more than three states), it is nontrivial and very time consuming to explore alternative scheme in an effort to determine the minimal mechanism (i.e., the least complex one consistent with the data). We have in the past used similar strategies to elucidate the folding mechanism of SNase.^87,206 With as many as seven states populated along two parallel pathways, SNase is a far more challenging system than GB1, which tests the limits of our manual fitting procedures (numeric instabilities for certain combinations of rate constants have thus far prevented us from implementing the rate-matrix method in combination with nonlinear least-squares fitting algorithms).

5.4. Cytochrome c

Cyt c has played a central role in the development of new kinetic approaches for exploring early events in protein folding. The presence of a covalently attached heme group in this 104-residue protein (Figure 14a) serves as a useful optical marker, and its redox and ligand binding properties provide unique experimental opportunities for rapid initiation and observation of folding.^49,50,71 Its sole tryptophan residue, Trp59, is located within 10 Å of the heme iron (Figure 14a), resulting in efficient fluorescence quenching through a Förster-type energy transfer mechanism. Strongly denaturing conditions (e.g., guanidine HCl concentrations >4 M, or acidic pH at low ionic strength) result in a large increase in Trp59 fluorescence (up to ~60% of that of free tryptophan in water) indicative of an expanded chain conformation with an average tryptophan-heme distance greater than 35 Å.^75,135 While numerous studies have shown that folding of oxidized cyt c is accompanied by changes in coordination of the heme iron,^{40,71,136,148,163,164,217–219} these complications can be largely avoided by working at mildly acidic pH (4.5–5) where the protein is still stable, but histidine residues are protonated and no longer can bind to the heme iron,^74,163 or by mutation of His33, which is primarily responsible for non-native heme ligation.¹⁶⁵

Figure 14.

a Ribbon diagram of horse cytochrome c, based on the crystal structure²⁶⁶. b Refolding kinetics of acid-unfolded cyt c at pH 4.5, 22 °C measured by continuous-flow mixing, indicating heme-induced quenching of Trp59 fluorescence associated with chain collapse.⁷⁶ Inset: Arrhenius plot for the rates of the major (circles) and the minor (squares) submillisecond phases. Adapted from ref 76 (Figure 2).

Our capillary mixing apparatus⁷² enabled us to resolve the entire fluorescence-detected folding kinetics of cyt c, including the elusive initial collapse of the chain⁷⁶. Figure 14b shows the decay in Trp59 fluorescence observed during refolding of acid-unfolded cyt c (pH 2, 10 mM HCl) induced by a pH jump to native conditions (pH 4.5, 22 °C). The continuous-flow data covering the time range from about 50 μs to 1 ms are accurately described by a biexponential decay with a major rapid phase (time constant 59 ± 6 μs) and a minor process in the 500 μs range. This fit extrapolates to an initial fluorescence of 1.0 ± 0.05 (relative to the acid-unfolded protein) at t = 0, indicating the absence of additional, more rapid fluorescence changes that remain unresolved in the 50 μs dead time. By combining continuous-flow data with kinetic measurements on a conventional stopped-flow instrument, we were able to follow the time course of folding over six orders of magnitude in time.⁷⁶ An Arrhenius plot of the rate of the initial phase (Figure 14b, inset) yields an apparent activation enthalpy of 30 kJ/mol, which is significantly larger than that expected for a diffusion-limited process.²²⁰ In subsequent laser T-jump studies, Hagen, Eaton and colleagues^221,222 detected a relaxation process with similar rates and activation energy, confirming the presence of a free energy barrier between unfolded and collapsed conformations of cyt c.

In other continuous-flow experiments, we measured the kinetics of folding of cyt c starting from either the acid-unfolded (pH 2, 10 mM HCl) or the GuHCl-unfolded state (4.5 M GuHCl, pH 4.5 or pH 7), and ending under various final conditions (pH 4.5 or pH 7 and GuHCl concentrations from 0.4 to 2.2 M).⁷⁶ In each case, we observed a prominent initial decay in fluorescence with a time constant ranging from 25 to 65 μs. In particular, the rate of the initial phase, measured under the same final conditions (pH 4.5, 0.4 M GuHCl), was found to be independent of the initial state (acid- or GuHCl-unfolded). These observations clearly indicate that a common rate-limiting step is encountered during the initial stages of cyt c folding. The large amplitude of the initial phase (as much as 70% of the total change in fluorescence under strongly native conditions) is consistent with the formation of an ensemble of compact states, which was confirmed by more recent SAXS experiments.^84,106

Using their continuous-flow CD setup with a dead time of 400 μs, Akiyama et al.⁷⁹ were able to resolve the changes in the far-UV region of the CD spectrum associated with the second (τ~500 μs) and third (τ~2 ms) phase of folding of oxidized cyt c. The initial folding phase (τ ~60 μs) observed in our absorbance- and fluorescence-detected experiments (Figures 6 and 14), ^76,116 appears as a burst phase in their continuous-flow CD data. The CD signal prior to the 400 μs phase indicates that about 20% of the native α-helical structure is present at this stage. This helix content is comparable to that of the acid-unfolded state at pH 2 (which retains some residual helical structure), but lower than that of the guanidine-unfolded form. Thus, a small, but measurable, amount of helical secondary structure is present already during the initial collapse of the cyt c polypeptide chain. In a subsequent study, Akiyama et al.⁸⁴ used continuous-flow SAXS measurements on a synchrotron to follow the changes in radius of gyration (R_g) associated with the various stages of the cyt c folding reaction. Starting with the expanded acid-denatured state characterized by a radius of gyration, R_g, of 24 Å, they observed accumulation of a partially collapsed state (R_g = 20.5 Å) within the 160 μs dead time of their experiment. In a subsequent phase on the ms time regime, the protein passes through a second, more compact intermediate (R_g = 18 Å) before reaching the native state (R_g = 13.9 Å). These findings confirm that cyt c undergoes a partial chain collapse during the initial folding phase, which corresponds to the process on the 10–100 μs time scale detected via the heme-induced quenching of Trp59 fluorescence in our previous microsecond mixing measurements of Trp-heme fluorescence energy transfer (Figure 14)⁷⁶ and heme absorbance changes (Figure 6),¹³⁸ as well as recent T-jump experiments by Hagen and colleagues.^221,222

5.5. Apomyoglobin

Apomyoglobin (apoMb) is another important model protein that has been the subject of numerous studies focusing on early stages of folding.^{89,171,174,183,223–230} On extracting the heme, the apo-form of myoglobin, retains its tightly packed globular structure^226,231,232 along with seven α-helical segments (labeled A–E, G and H in Figure 15; the F-helix is disordered in the absence of the heme).

Figure 15.

Sequential four-state mechanism involving two partially structured ensembles, I₁ and I₂, in addition to the acid-unfolded (U) and native (N) states. Cartoons of various states apomyoglobin consistent with the fraction of helical residues (f_H) and radius of gyration (R_g) reported in ref 89. Cylinders indicate the approximate position of α-helices in the native state and possible arrangement of core helices in the intermediates consistent with amide protection data.¹⁷¹,¹⁷⁴

Uzawa et al.⁸⁹ recently capitalized on their unique capability of measuring secondary structure and molecular dimensions with submillisecond time resolution to explore the folding of horse apoMb. By combining continuous-flow CD measurements⁷⁹ with conventional stopped-flow data, the authors were able to measure the formation of helical secondary structure associated with the folding of acid-denatured apoMb (triggered by a rapid jump in pH from 2.2 to 6) over the time range from 300 μs to 1 s. The changes in the CD signal at 222 nm are consistent with a stepwise increase in helix content (expressed in terms of the fraction of helical residues, f_H) in three kinetic phases, including a major process occurring within the instrumental dead time (burst phase) and two observable phases with time constants of 5 and 50 ms, respectively. Continuous-flow SAXS measurements⁸⁴ under matching folding conditions showed a major collapse of the chain within the 300 μs dead time of the experiment, followed by a further decrease in chain dimensions during the final (50 ms) folding phase. Uzawa et al.⁸⁹ interpret their findings in terms of a four-state folding mechanism (Figure 15),²³³ based on their observation of three distinct folding phases, as well as previous kinetic data by Jamin et al.²²⁹. Figure 15 also shows cartoons of the various states populated during apoMb folding consistent with the recent information on size and secondary structure, as well as additional data on the location of stable helical segments obtained in previous NMR-based hydrogen exchange labeling studies.^171,183 The acid-unfolded state, U, contains only a small amount of α-helical structure detectable by CD and is significantly expanded compared to the native state. However, detailed NMR studies by Dyson, Wright and coworkers²³⁴ show clear deviations from the behavior expected for a random coil, including evidence for fluctuating residual secondary structure and restricted backbone motions. The high helix content of the I₁ intermediate (~60% of the native level) indicates that it contains helical segments in regions outside the A, G and H helix core observed in the initial pulsed hydrogen exchange study.¹⁸³ Likely candidates are the B and E helices, which, according to a more recent hydrogen exchange labeling study,¹⁷¹ are partially solvent-protected in an ensemble of early intermediates corresponding to I₁. Although these experiments cannot directly discriminate native and non-native interactions, there is recent evidence, based on the effect of mutations in the B-helix on amide protection patterns, indicating that the early intermediate contains primarily native-like helix-helix interactions.²³⁵ The shape information (pair distribution function) extracted from the SAXS measurements at early folding times further supports a bipartite structure with a compact core comprising the bulk of the chain and some disordered segments.⁸⁹ Interestingly, the five folded helices correspond to peaks in the hydrophobicity plot of the myoglobin sequence while the still unfolded C and D helices are among the most polar regions of the protein. The I₂ intermediate formed during a later stage of folding is characterized by a further increase in helix content to about 80% of the native level, which can be explained by an increase in the length of existing helices (amide protection data detect no newly formed helices at this time). However, the overall size and shape of the protein remains unchanged, consistent with a partially hydrated (swollen) conformation containing some disordered loops.

Together with previous T-jump evidence for very rapid conformational events,^224,227 the recent microsecond mixing results⁸⁹ demonstrate that major structural event, both in terms of molecular dimensions and helix formation, occur within the first few hundred microseconds of initiating the apoMb folding reaction. Although earlier folding times remain to be explored, secondary structure formation and chain compaction appear to be coupled during the early stages of folding. This conclusion is consistent with continuous-flow fluorescence results by Jamin et al.²²⁹ indicating that a partially structured equilibrium state with properties similar to the I₁ intermediate exhibits two-state folding/unfolding kinetics with a folding time of ~50 μs in the absence of denaturant (obtained by extrapolation of data in the presence of urea). Cyt c, the only other protein whose submillisecond folding kinetics has been followed by CD and SAXS, also shows a large decrease in overall dimensions on 100 μs time range,^73,76,84 but the helix content of the early intermediate is lower than that of apoMb.⁷⁹ Thus, the exact balance between chain compaction and secondary structure is likely to vary considerably from one protein to another.

6. Significance of Early Folding Events

6.1. Barrier-limited Folding vs. Chain Diffusion

In the preceding sections we discussed the folding kinetics of six proteins studied by microsecond mixing, GB1, cyt c, ubiquitin, ACBP, SNase and apoMb, all of which exhibit two or more distinct folding phases with major conformational changes occurring on the microsecond time scale.^{76,78,81,83,87} Other examples include cytochrome c₅₅₁ from Pseudomonas aeruginosa,⁸⁵ β-lactoglobulin,⁸² a Trp-containing variant of RNase A,⁸⁸ and the bacterial immunity protein Im7,⁸¹ which will be discussed further below. For several proteins (GB1, ubiquitin, Im7, β-lactoglobulin, SNase and RNase), we observed an increase in intrinisc fluorescence during the fast phase, which can be attributed to the burial of a tryptophan within an apolar environment. For three proteins (cyt c, cytochrome c₅₅₁ and ACBP), we measured a large increase in energy transfer efficiency during the fast phase, confirming that these early conformational events include a large-scale collapse of the polypeptide chain. Since all of these proteins require a few ms or longer for traversing the rate-limiting barrier for folding, there is no doubt that important conformational events, including a large-scale collapse of the chain, occur prior to the ultimate barrier in the acquisition of the native structure. In every case the initial phase follows an exponential time course, indicating that a discrete free energy barrier separates the ensemble of compact states from the more expanded ensemble of unfolded states. In contrast, if the collapse of the polypeptide chain were a continuous process governed by diffusive dynamics,⁸ one might expect non-exponential (‘distributed’) kinetics with a broad distribution of time constants.^26,236 In fact, Gruebele and colleagues^59,237,238 observed such distributed folding kinetics in temperature-jump experiments under conditions where folding can proceed downhill from a saddle point in the free energy surface. However, other theories predict that polymer collapse can be characterized by a single relaxation time²³⁹, and the observation of exponential kinetics may not always be a sufficient condition for the presence of an activation barrier.²⁴⁰ Nevertheless, the case for a barrier-limited process is strengthened considerably if the process also exhibits a significant activation enthalpy, as observed for cyt c.⁷⁶ Finally, comparison of the pH-induced folding traces of cyt c monitored by Trp59 fluorescence (Figure 14) and heme absorbance (Figure 6) indicates that the time constant of the initial phase is independent of the probe used (59 ± 6 μs by fluorescence compared to 65 ± 4 μs by absorbance). This observation strongly supports the presence of a barrier, since a diffusive collapse process is expected to lead to probe-dependent kinetics, as observed in a recent T-jump study.²³⁸

The existence of a prominent free energy barrier between expanded and compact states justifies the description of the initial folding events in terms of a model involving an early folding intermediate. The first large-scale conformational change during folding can, thus, be described as a reversible two-state transition. The finding that the rate of collapse in cyt c is insensitive to initial conditions⁷⁶ suggests that the barrier may represent a general entropic bottleneck encountered during the compaction of the polypeptide chain, which is consistent with the moderate activation enthalpy associated with the initial transition (Figure 14). Bryngelson et al.²⁶ classified this type of folding behavior as a ‘type I’ scenario where a free energy barrier arises because of the unfavorable reduction in conformational entropy, which can be compensated by favorable enthalpic and solvent interactions only during the later stages of collapse.

6.2. Chain Compaction: Random Collapse vs. Specific Folding

Although denatured proteins often retain far more structure than is expected for a random coil polymer,²⁴¹ they are substantially more expanded than the native state.²⁴² Therefore, the folding process must be accompanied by a net decrease in chain dimensions. However, there are persistent controversies surrounding the question whether chain contraction occurs prior to or concurrent with the rate-limiting folding step, and whether compact states are the result of random hydrophobic collapse or a more specific structural events.^{89,100,233,243–245} Our earlier conclusion that the optical changes on the submillisecond time scale (burst-phase events) seen for cyt c and many other proteins^10,101 reflect the formation of productive folding intermediates has been challenged by Englander and coworkers^244,246 on the basis of fluorescence and CD measurements on two heme-containing peptide fragments of cyt c (residues 1–65 and 1–80, respectively). Although the fragments are unable to assume a folded structure, they nevertheless show rapid (<ms) denaturant-dependent fluorescence and far-UV CD changes resembling the burst-phase behavior of the intact polypeptide chain (cf. Figure 8). Assuming that the fragments remain fully unfolded under all conditions, Sosnick et al.^244,246 concluded that both the optical properties of the fragments and the burst-phase changes seen during refolding of intact cyt c reflect a rapid solvent-dependent readjustment of the unfolded polypeptide chain rather than formation of partially folded states. However, this conclusion is inconsistent with our observation that refolding of both GuHCl- and acid-denatured cyt c is accompanied by an exponential fluorescence decay,⁷⁶ which indicates that the ensemble of states formed on the submillisecond time scale are separated by a free energy barrier from the unfolded states found immediately after adjustment of the solvent conditions. That these states are not just part of a broad distribution of more or less expanded denatured conformations is further supported by the observation of non-random amide protection patterns.¹⁶⁸ Apparently, both the full length and truncated forms of cyt c can assume a compact ensemble of states upon lowering of the denaturant concentration. This leads to the prediction that the fragments will also exhibit an exponential fluorescence change on a time scale similar to that of the intact protein⁷⁶ (40–60 μs at 22 °C and GuHCl concentrations of 0–0.4 M). This prediction was confirmed in a recent study by Qiu et al.,²²² who observed an exponential relaxation process with a time constant of 20–30 μs at room temperature and a substantial activation energy (60–70 kJ/mol) for the 1–65 and 1–80 fragments of cyt c, using a laser T-jump apparatus.

In a related paper on RNase A, Englander and colleagues²⁴⁷ reported that the GuHCl-dependence of the CD signal for the fully disulfide-reduced form closely matches the initial kinetic amplitude observed in stopped-flow refolding experiments on the protein with all four disulfide bonds intact. As in the case of the cyt c fragments, Qi et al.²⁴⁷ assumed that reduced RNase remains in a random denatured state even under nondenaturing solvent conditions, which needs to be explored further. As an alternative interpretation, we again suggest that both in the presence and absence of disulfide bonds, RNase A rapidly forms a nonrandom ensemble of states, which is consistent with the shallow, but distinctly sigmoidal GuHCl dependence of the far-UV CD signal.²⁴⁷ Since the native RNase A structure relies on disulfide bonds for its stability, folding of the reduced form cannot proceed beyond this early intermediate while the oxidized protein continues to fold to the native state. This scenario is consistent with recent a recent microsecond mixing study in which Kumura et al.¹⁶⁰ used CD and SAXS to early conformational events in oxidized and reduced RNas A.

The folding pathway of apomyoglobin as sketched in Figure 15 is a striking example of a complex folding mechanism where a series of conformational ensembles with increasing structural organization precede the final, rate-limiting, step in the acquisition of the native structure. The intermediate populated on the submillisecond time regime already contains a partially structured core giving rise to non-spherical contributions to the x-ray scattering profile, a distinctly helical far-UV CD component⁸⁹ and solvent-shielded amide protons in a cluster of interacting α-helices.²³⁵ These properties are far from random, arguing against the notion that rapid conformational changes may reflect a random collapse of the chain driven by non-specific hydrophobic interactions.²¹³ For all but the simplest proteins, the rate-limiting transition state for folding cannot be reached in a single, concerted step, resulting in transient accumulation of partially structured conformations. Rapid secondary structure formation and concomitant compaction of the chain, guided by a few critical tertiary contacts, may limit the conformational space to be searched during folding, providing the bias toward the native structure necessary for efficient folding on a relatively smooth energy surface.²⁶

6.3. Kinetic Role of Early Folding Intermediates

Several small proteins exhibit two-state behavior under certain conditions (e.g., elevated denaturant concentration, destabilizing mutations), but show evidence for populated intermediates (burst phase and/or nonlinear rate profiles) under other, more stabilizing, conditions.^{50,75,83,129,195,248–250} Thus, apparent two-state behavior can be considered a limiting cases of a multistate folding mechanism with unstable (high-energy) intermediates^13,195. On the other hand, there are many well documented examples of small proteins that show two-state folding behavior even under stabilizing conditions (reviewed in refs ^92,251). In several cases, the rate of folding at low denaturant concentrations was found to extend into the submillisecond time range and could be resolved only by methods such as NMR lineshape analysis,^51,252 electron transfer triggering,²⁵³ pressure-jump²⁵⁴ or T-jump techniques.⁵⁶

While these findings clearly indicate that many small proteins can fold rapidly without going through intermediates, there is little support for the notion that early intermediates slow down the search for the native conformation,^164,255,256 except in cases where they contain features inconsistent with the native fold, such as nonnative proline isomers, metal ligands^163,164,257 or intermolecular interactions.²⁵⁸ In fact, solution conditions that favor accumulation of intermediates, such as low denaturant concentrations or stabilizing salts, generally accelerate the overall rate of folding.¹⁰ Conversely, mutations that destabilize or abolish early intermediates often result in much slower rates of folding,^195,259,260 which is a strong indication that they are productive states. Although continuous-flow results are fully consistent with a sequential mechanism involving obligatory intermediates,^76,78,83,138 it has been difficult to rigorously demonstrate that early intermediates are obligatory states on a direct path to the native state (Scheme 3). Alternative mechanisms involving formation of nonproductive states (Scheme 4) or mechanisms with parallel pathways and non-obligatory intermediates (Scheme 5) can be ruled out only if (i) the two transitions are kinetically coupled (i.e., they have similar rates), (ii) both phases are directly observable and kinetically resolved, and (iii) the experimental probe used to monitor folding can discriminate native from intermediate and unfolded populations. Under these circumstances, the transient accumulation of an obligatory intermediate leads to a detectable lag in the appearance of the native population whereas an off-path intermediate gives rise to a rapid increase in the population of N during the initial phase. Clear evidence for such a lag phase was obtained in a stopped-flow fluorescence study on a proline-free variant of staphylococcal nuclease.²⁰⁶ On the other hand, a thorough kinetic analysis, using a double-jump protocol, indicated that a late intermediate during folding of lysozyme is non-obligatory.¹¹⁵ Other efforts to detect a lag phase during folding of interlukin-1β^261,262 and apoMb²³⁰ were inconclusive because of the disparate time scales of early and rate-limiting folding events. In order to determine the kinetic role of early folding intermediates, it is necessary to directly measure the population of native molecules on the submillisecond time scale, either by double-jump experiments or via a specific spectroscopic probe for the native state.

Scheme 4.

Scheme 5.

A particularly favorable protein for investigating the kinetic importance of early folding intermediates is the bacterial immunity protein Im7, an 86 residue protein with a simple four-helix bundle structure (Figure 16a). Radford and colleagues have previously shown that Im7 populates a hyperfluorescent intermediate during the 2.5 ms dead time of their stopped-flow instrument.²⁴⁹ However, the data could be fitted equally well to models involving either on- or off-pathway intermediates. Capaldi et al.⁸¹ extended these measurements into the microsecond time range, using our continuous-flow mixing instrument to detect the changes in fluorescence of a single tryptophan (Trp75) associated with folding under various conditions (Figure 16b). The initial increase in fluorescence above the level of the denatured state in 6 M urea over the 100 μs to 1 ms time range is consistent with the rapid formation of a compact state resulting in a solvent-shielded environment for Trp75. The native structure is formed within a few milliseconds or longer (depending on the final concentration of urea), which is accompanied by partial quenching of Trp75 fluorescence due to close contact with a histidine. The tight kinetic coupling of the two folding events, together with the distinct fluorescence properties of the three conformational states involved, allowed us to discriminate among various possible kinetic mechanisms. The time course of folding predicted by solving the kinetic equations corresponding to the on-path mechanism (Scheme 3) accurately describe the observed behavior (Figure 16b, solid line). By contrast, the off-pathway mechanism (Scheme 4) failed to reproduce the data, especially at low urea concentrations where the intermediate is well populated (Figure 16b, dashed line). The amplitude of the submillisecond folding phase predicted by the off-pathway mechanism was far too small to account for the initial increase in the signal associated with the formation of a hyperfluorescent intermediate. Likewise, the quality of the fits does not improve when a second, parallel pathway is introduced (Scheme 5) and deteriorates when more than 25% of the flux bypassed the intermediate. These findings were further confirmed by a more detailed analysis of the dependence of the two observable rate constants on urea concentration (Figure 16c).⁸¹ While Scheme 3 reproduces all of the kinetic data, there are major discrepancies in the rate of the fast phase predicted by Schemes 4 and 5, which can thus be ruled out.

Figure 16.

Kinetic mechanism of Im7 folding. a Ribbon diagram of Im7. b Representative kinetic trace measured by continuous-flow (●) and stopped-flow (○) fluorescence. The kinetics at this and all other urea concentrations measured is accurately predicted by on on-pathway mechanism (solid line) while schemes with off-pathway intermediates fail to reproduce the data (dashed line). c Observed (symbols) and predicted (solid lines) rates of folding and unfolding, based on mechanisms with on-pathway (left) and off-pathway (right) intermediates. Dashed lines indicate the corresponding elementary rate constants. Adapted from ref 81 (Figures 2 and 3).

By eliminating alternative mechanisms, we have, thus, been able to show that accumulation of a compact intermediate on the submillisecond time scale is a productive and obligatory event in folding of Im7.⁸¹ This supports the notion that rapid formation of compact states can facilitate the search for the native conformation. Interestingly, a recent mutational study revealed that the Im7 folding intermediate contains non-native tertiary interactions among the three major α-helices, A, B and D, while the short helix C forms only during the final stages of folding.²⁶³ Apparently, intermediates can be kinetically productive even if they contain some structural features not found in the final native state.

7. Conclusions and Implications

We have focused this review on recent developments in rapid mixing techniques coupled with improved biophysical techniques for monitoring conformational changes associated with early stages of protein folding. The findings clearly indicate that many proteins fold in stages with significant conformational events occurring within milliseconds of refolding, long before the rate-limiting step in formation of the native state. These early structural events can be attributed to accumulation of partially folded intermediates, which may act as stepping stones in finding the unique native conformation. Table 2 lists the time constants of the earliest folding phase measured by continuous-flow fluorescence for some of the proteins discussed in this chapter along with their size and structural type. While the number of proteins studied is still too small to warrant general conclusions, it is interesting to note that the initial folding times vary by an order of magnitude, but show no apparent correlation with protein size. This argues against the notion that the early stages of folding are dominated by a nonspecific hydrophobic polymer collapse, in which case the rate of the initial phase would depend primarily on the size of the hydrophobic core and would be insensitive to structural details.

Table 2.

Comparison of the time constant of the initial folding phase with protein size and secondary structure type for

Protein	No. of Residues	Structure type	Relative Contact Order1	Time Constant (μs)2	Reference
GB1	57	α/β	17.2%	600	78
ACBP	86	α	14.0%	80	83
Im7	87	α	10.6%	450	81
cyt c	104	α	11.1%	60	76
SNase	149	α/β	10.0%	753	87

¹The relative contact order was calculated using a web-based program at http://depts.washington.edu/bakerpg/contact_order/ (ref ²⁶⁴).

²Time constant of earliest kinetic phase detected in continuous-flow fluorescence measurements.

³Value for the F76W/W140H variant of SNase.

There appears to be no simple relationship between the time scale of early folding events and secondary structure content. For example, the β-sheet containing proteins, GB1 and SNase, are near opposite ends of the time range, and Im7 has a ~5-fold slower initial rate compared to the structurally similar ACBP. Thus, the individual structural and topological features have a profound effect already during early stages of folding. The rate of the early folding events also shows no apparent correlation with protein stability (e.g., ACBP and Im7 have similar stabilities, but are near opposite ends of the rate scale). The finding that the earliest detectable folding event in GB1 domain is an order of magnitude slower than that of cyt c may well be related to the fact that GB1 contains β-sheet structure while cyt c is primarily α-helical (Figure 14a). With its parallel pairing of β-strands from opposite ends of the chain, GB1 has a high relative contact order (a metric of fold complexity that was found to correlate with the logarithm of the folding time of proteins with two-state mechanisms²⁶⁴). Such a trend is not expected for proteins with multistate folding mechanisms, since the rate-limiting step in structurally and kinetically more complex proteins is likely to involve structural events unrelated to the overall fold, such as side chain packing and specific tertiary interactions. However, if compact early intermediates have a native-like chain topology, one might expect a correlation between the time constant of the initial phase and contact order. To test this prediction, we include in Table 2 the relative contact order calculated according to Plaxco et al.²⁶⁴ Some of the trends seen are consistent with this idea. For instance, cyt c and ACBP have low contact order and collapse much faster than GB1, which has the highest contact order among the proteins studied. The surprisingly fast initial phase of SNase (75 μs) in comparison to the much smaller GB1 (600 μs) may be related to the fact that the folding step in SNase detected by Trp76 and ANS fluorescence reflects a relatively local structural event within its antiparallel β-barrel domain, whereas the fluorescence of Trp43 in protein G may report on a more global conformational change involving the parallel pairing of N- and C-terminal β-strands. Finally, we note that several small proteins (or isolated domains of larger proteins) can complete the process of folding on a comparable time scale as the early stages of folding for some of the multi-state proteins discussed here^58,61,64,265 (see ref 56 for additional examples). The underlying conformational events may be similar, but the fast-folding two-state proteins can directly reach the native state in a concerted collapse/folding event while most proteins encounter additional steps after crossing the initial barrier.

Abbreviations

ACBP

acyl-CoA binding protein

AEDANS

5-((((2-iodoacetyl)amino)ethyl)amino)naphthalene-1-sulfonic acid

ANS

1-anilino-8-naphlalene-sulfonic acid

ApoMb

apomyoglobin

BSA

bovine serum albumin

CD

circular dichroism

CCD

charge coupled device

cyt c

cytochrome c

DCIP

2,6-dichlorophenolindophenol

EPR

electron paramagnetic resonance

FRET

fluorescence resonant energy transfer

FTIR

Fourier transform infrared

GB1

B1 domain of protein G

GuHCl

guanidine hydrochloride

H/D

hydrogen/deuterium

NATA

N-acetyltryptophanamide

NBS

N-bromosuccinimide

NMR

nuclear magnetic resonance

PEEK

polyetheretherketone

RNase

ribonuclease A

SAXS

small-angle X-ray scattering

SNase

staphylococcal nuclease

T-jump

temperature jump (laser-induced)

Biographies

Hong Cheng was born and raised in Shanghai, China. He received a B.Sc. degree (1983) from the Fudan University, Shanghai, China. After earning his Ph.D. in Physical Chemistry from the City University of New York in 1991 under the direction of Prof. William V. Sweeney, he moved to the University of Wisconsin at Madison as a postdoctoral research associate to study iron-sulfur proteins by using NMR under the direction of Prof. John L. Markley. In 1995 he moved to the Fox Chase Cancer Center where he currently is a staff scientist and manager of the NMR facility. The focus of his research is on protein structure, function and folding.

Kosuke Maki was born in Tokyo, Japan in 1969. He received his B.Sc. in physics from University of Tokyo in 1994 and his Ph.D. in physics from University of Tokyo in 1999 under the supervision of Prof. Kunihiro Kuwajima. He spent two years as a postdoctoral fellow in Prof. Masahiro Iwakura’s group at the Advanced Institute of Science and Technology (AIST), Japan. Then he worked with Prof. Heinrich Roder at the Fox Chase Cancer Center as a postdoctoral associate from 2001 to 2003, where he explored the mechanisms of protein folding, especially in the early stages of the folding by means of the ultrarapid mixing technique. In 2003, he rejoined Prof. Kunihiro Kuwajima’s group as a research associate where he continues to work on protein folding problems.

Heinrich Roder was born and raised in Switzerland. He studied Physics at the Federal Polytechnic (ETH) in Zürich and earned his Ph.D. in Biophysics under the direction of Prof. Kurt Wüthrich (1981). In 1984, following postdoctoral work with Prof. Hans Frauenfelder at the University of Illinois at Urbana, he joined the faculty of the Department of Biochemistry and Biophysics at the University of Pennsylvania in Philadelphia (Assoc. Prof. 1990; Adj. Prof. 1994). In 1991 he moved across town to the Fox Chase Cancer Center where he is currently a Senior Member and Chair of the Program in Biomolecular Structure and Function. Much of his research career has been devoted to the protein folding problem, focusing mainly on kinetic mechanisms and the role of intermediates. He made critical contributions to the development of NMR-based hydrogen exchange labeling methods and rapid mixing techniques.