Abstract
The catalytic cycle of an enzyme is frequently associated with conformational changes that may limit maximum catalytic throughput. In Escherichia coli dihydrofolate reductase, release of tetrahydrofolate (THF) product is the rate-determining step under physiological conditions and is associated with an ‘occluded’ to ‘closed’ conformational change. In this study, we demonstrate that in dihydrofolate reductase the ‘closed’ to ‘occluded’ conformational change in the product ternary complex (E:THF:NADP+) also gates progression through the catalytic cycle. Using NMR relaxation dispersion, we have measured the temperature and pH dependence of µs-ms timescale backbone dynamics of the ‘occluded’ E:THF:NADP+ complex. Our studies indicate the presence of three independent dynamic regions, associated with the active-site loops, the cofactor binding cleft, and the C-terminus and an adjacent loop, which fluctuate into discrete conformational substates with different kinetic and thermodynamic parameters. The dynamics of the C-terminal associated region is pH dependent (pKa < 6), but the dynamics of the active-site loops and cofactor binding cleft are pH independent. The active-site loop dynamics access a ‘closed’ conformation and the accompanying ‘closed’ to ‘occluded’ rate constant is comparable to the maximum pH independent hydride transfer rate constant. Together, these results strongly suggest that the ‘closed’ to ‘occluded’ conformational transition in the product ternary complex is a prerequisite for progression through the catalytic cycle and that the rate of this process places an effective limit on the maximum rate of the hydride transfer step.
Keywords: enzyme kinetics, NMR relaxation dispersion, pH-independent rate
INTRODUCTION
Many enzymes have evolved to the point where chemical bond-breaking and bond-making events are no longer rate limiting (1). Instead, conformational changes required to bind substrate, orient the reactants, or release products, may limit catalytic turnover (2). A comprehensive understanding of the limits on enzyme catalytic rates thus requires an understanding of both the chemical events at the active site and the physical processes that are required for catalytic turnover. Both considerations are important in de novo enzyme engineering and drug design efforts.
Escherichia coli dihydrofolate reductase (DHFR) is an excellent model system for understanding the role of protein dynamics in enzymatic catalysis. DHFR catalyzes the reduction of 7,8-dihydrofolate (DHF) through stereospecific hydride transfer from reduced nicotinamide adenine dinucleotide phosphate (NADPH) cofactor (3,4). The enzyme is both an anticancer and antimicrobial drug target and has been the subject of extensive structural (5), functional (6), and theoretical studies (7). Analysis of pre-steady state kinetics has demonstrated that E. coli DHFR cycles through five major states under physiological conditions (8): the holoenzyme (E:NADPH), the Michaelis complex (E:DHF:NADPH), and three tetrahydrofolate product complexes - the product ternary complex (E:THF:NADP+) formed immediately following hydride transfer, the product binary complex (E:THF) formed by dissociation of oxidized cofactor, and the product release complex (E:THF:NADPH). At physiological pH, the rate limiting step is the release of THF product from the E:THF:NADPH complex.
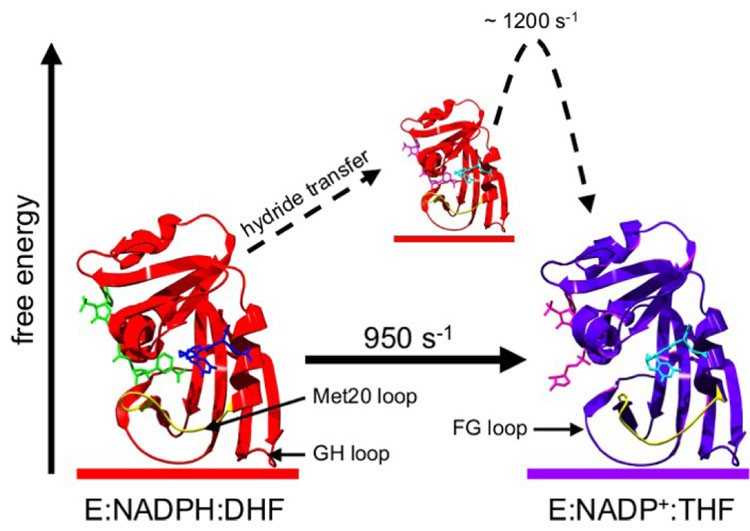
DHFR is a relatively small protein (159 residues) comprised of a mixed eight strand β-sheet flanked by four α-helices and several flexible loops. Extensive structural characterization of the enzyme revealed three major conformations in the crystalline state (5), although only the ‘closed’ and ‘occluded’ conformations have been observed under solution conditions (9). The ‘closed’ and ‘occluded’ conformations differ in the structure of the active-site Met20 loop. The ‘closed’ conformation, observed in the holoenzyme (E:NADPH) and the Michaelis model complexes (E:FOL:NADP+, E:DHF:NADP+) (9), is stabilized through hydrogen bonding interactions between the Met20 and FG loops (5). Following hydride transfer, the product ternary complex E:THF:NADP+ assumes an ‘occluded’ ground-state structure (Figure 1). The hydrogen bonds between the Met20 and FG loops break, and new hydrogen bonds are formed between the Met20 and GH loops to stabilize the ‘occluded’ conformation. In the ‘occluded’ conformation, the nicotinamide ring of the cofactor is sterically hindered from entering the active site, and thus, chemistry can only occur through a ‘closed’ conformation. The ‘occluded’ conformation is observed in the three product complexes of wild-type DHFR: E:THF:NADP+, E:THF, and E:THF:NADPH (9). The cycling between ‘closed’ and ‘occluded’ conformations is critical for progress around the enzymatic cycle. Mutations that disrupt either the ‘closed’ or ‘occluded’ conformations lead to decreases in hydride transfer rate and/or steady-state catalytic turnover (10–15).
Figure 1.
Conformational dynamics in E.coli dihydrofolate reductase govern catalytic turnover. Prior to hydride transfer, the Met20 loop is in a ‘closed’ conformation (left, PDB 1RX2), but adopts an ‘occluded’ conformation following hydride transfer (right, PDB 1RX4). The rate constant for the ‘closed-to-occluded’ transition in E:THF:NADP+ determined by R2 relaxation dispersion (21) is strikingly similar to the maximum pH-independent hydride transfer rate constant (8). NADPH, DHF, NADP+ and THF are colored green, blue, pink and cyan, respectively. The Met20 loop is highlighted in yellow.
We have used nuclear magnetic resonance (NMR) to study the dynamic properties of E.coli DHFR as it traverses its catalytic cycle (16–21). In particular, we have applied R2 relaxation dispersion spectroscopy to analyze the µs-ms timescale dynamics of DHFR at each step of the catalytic cycle (20,21). R2 relaxation dispersion is a measure of how well conformational exchange contributions (Rex) to the transverse relaxation rate constant (R2) can be suppressed by the 180° refocusing pulses in a Carr-Purcell-Meiboom-Gill (CPMG) pulse train (22,23). For two-site exchange between a lower energy conformation A and a higher energy conformation B, analysis of relaxation dispersion curves provides information on the kinetics of the conformational exchange between A and B (kex = kAB + kBA), the populations of states A and B (pA and pB), and the chemical shift difference (Δω) between sites A and B (24).
For E.coli DHFR, R2 relaxation dispersion experiments have shown that at each step of the catalytic cycle, the enzyme adopts a major substate represented by the X-ray structure of that intermediate (or of complexes that model the intermediate), and one or more minor substates that are structurally similar to either the next or prior intermediate in the catalytic cycle (21). In particular, the product ternary complex E:THF:NADP+ has an ‘occluded’ major substate, and a ‘closed’ minor substate that is structurally similar to the Michaelis model complex E:FOL:NADP+. Moreover, the rate constant determined from R2 relaxation dispersion (k ~ 1200 s−1) for the conversion of the higher energy ‘closed’ substate to the lower energy ‘occluded’ substate of E:THF:NADP+ is very similar to the maximum pH-independent hydride transfer rate constant (950 s−1) for conversion from substrate to product, suggesting that the pH independent rate constant may be limited by the ‘closed-to-occluded’ conformational change in E:THF:NADP+. In addition, dynamic processes were observed in the cofactor binding site due to fluctuations involving a minor substate that is similar in structure to the E:THF complex (21).
In this study, we have further explored the energy landscape of the E:THF:NADP+ complex by measuring µs-ms protein dynamics under a more extensive array of temperature and pH conditions. Our experiments reveal three separate dynamic events in the protein, and indicate that physical changes within the energy landscape of the product ternary complex are tightly linked to maximum rates of hydride transfer.
Materials and Methods
Protein purification and sample preparation
E.coli DHFR was expressed and purified according to previously established procedures (21). The ligands NADP+ and THF are light and/or oxygen sensitive and must be treated accordingly. Before sample preparation, buffer was thoroughly degassed through freeze-pump-thaw cycles using a vacuum apparatus, and ascorbic acid was added to act as an oxygen scavenger. The final samples contained 1 mM DHFR, 10 mM NADP+, 6 mM THF, 1 mM DTT, 25 mM KCl and 10% D2O in 70 mM KPi pH 6.1 – 7.6. The samples were placed in amberized NMR tubes, subjected to vacuum again, overlayed with argon and flame-sealed to prevent buffer re-oxidization. Under these conditions, the samples are stable for R2 relaxation dispersion measurements for ~ 1 week.
R2 relaxation dispersion experiments
15N R2 relaxation rates were measured at 1H spectrometer frequencies of 500 and 800 MHz using relaxation-compensated CPMG (Carr-Purcell-Meiboom-Gill) pulse sequences in a constant-time manner as previously described (20,22). The total relaxation time was 40 ms. The R2 relaxation dispersion data were fit simultaneously at the two frequencies using the in-house computer program GLOVE with the following series of equations describing conformational exchange between two sites, A and B:
| (1) |
in which,
| (2) |
| (3) |
where Ψ=kex 2−Δω2 , ζ= −2Δωkex(pA–pB), τcp is the time between successive 180° pulses in the CPMG pulse train, R2 0 is the R2 relaxation rate in the absence of conformational exchange, pA and pB are the populations of the ground- and excited-state conformations respectively (pA + pB = 1), and Δω is the chemical shift difference between substates A and B. Rate constants for the ground-to-excited state (kAB) and excited-to-ground state (kBA) transitions can be determined by pB·kex and pA·kex respectively. Residues generally fit into one of three clusters, including the active-site loops and other residues around the active-site, cofactor binding site, or the C-terminal associated region. Each cluster was fit with global kex and pApB values while allowing Δω values to vary for each residue. The clusters showed significantly different kex and pApB values (Table 1). In Supporting Information Table S1, we report Δω values following global fitting procedures. However, in a few select cases, χ2 global/χ2 individual > 2, so we report only the Δω value for the individual fit.
Table 1.
Kinetic and thermodynamic fitting parameters for wild-type E:THF:NADP+ 15N R2 relaxation dispersion curves at different pH and temperatures
| Cluster 1 – active site loops | Cluster 2 – cofactor binding cleft | Cluster 3 – C-term associated region | ||||
|---|---|---|---|---|---|---|
| kex (s−1) | pApB | kex (s−1) | pApB | kex (s−1) | pApB | |
| pH 7.6 | ||||||
| −294 K | 985 ± 23 | 0.008 ± 0.000 | n.d.1 | n.d.1 | 529 ± 142 | 0.013 ± 0.001 |
| −297 K | 1210 ± 55 | 0.010 ± 0.000 | 600 ± 118 | 0.019 ± 0.011 | 586 ± 50 | 0.015 ± 0.001 |
| −300 K | 1300 ± 47 | 0.014 ± 0.000 | 1700 ± 116 | 0.029 ± 0.017 | 550 ± 30 | 0.022 ± 0.001 |
| −303 K | 1624 ± 76 | 0.017 ± 0.001 | n.d.1 | n.d.1 | 666 ± 42 | 0.028 ± 0.001 |
| −306 K | 1832 ± 129 | 0.019 ± 0.002 | n.d.1 | n.d.1 | 700 ± 54 | 0.033 ± 0.001 |
| pH 7.0 | ||||||
| −297 K | 1352 ± 73 | 0.010 ± 0.001 | 598 ± 73 | 0.040 ± 0.015 | 532 ± 20 | 0.021 ± 0.001 |
| −300 K | 1470 ± 70 | 0.014 ± 0.001 | 1739 ± 53 | 0.028 ± 0.009 | 588 ± 15 | 0.025 ± 0.001 |
| pH 6.5 | ||||||
| −294 K | 913 ± 92 | 0.008 ± 0.000 | n.d.1 | n.d.1 | 662 ± 85 | 0.019 ± 0.002 |
| −297 K | 1280 ± 41 | 0.010 ± 0.001 | 558 ± 61 | 0.032 ± 0.006 | 521 ± 25 | 0.024 ± 0.001 |
| −300 K | 1350 ± 44 | 0.014 ± 0.001 | 1726 ± 212 | 0.028 ± 0.005 | 523 ± 19 | 0.028 ± 0.009 |
| −303 K | 1652 ± 488 | 0.016 ± 0.009 | n.d.1 | n.d.1 | 550 ± 65 | 0.031 ± 0.002 |
| pH 6.1 | ||||||
| −294 K | 949 ± 68 | 0.008 ± 0.000 | n.d.1 | n.d.1 | 419 ± 61 | 0.018 ± 0.002 |
| −300 K | 1500 ± 200 | 0.014 ± 0.001 | 1400 ± 320 | 0.025 ± 0.003 | 463 ± 40 | 0.032 ± 0.002 |
| −303 K | 1640 ± 108 | 0.018 ± 0.003 | n.d.1 | n.d.1 | 450 ± 40 | 0.038 ± 0.002 |
not determined; although conformational exchange is still apparent in the cofactor binding cleft, the R2 relaxation dispersion curves are not of sufficient quality to determine Δw, kex or pApB values
pH and temperature dependence of protein dynamics
R2 relaxation dispersion measurements were performed using four different pH conditions (pH 6.1, 6.5, 7.0 and 7.6) and up to five different temperatures (294, 297, 300, 303 and 306 K) (Table 1). Only the dynamics in the C-terminal associated region showed a dependence on pH.
The enthalpy (ΔH) and entropy (−TΔS) energy differences between the excited- and ground-state conformations can be estimated through the temperature dependence of the conformational exchange equilibrium constant using van’t Hoff analysis according to equation 4,
| (4) |
where K is equal to kBA/kAB. Reported errors are based on jackknife simulations (20,21). The activation barriers can be estimated using transition-state theory, according to equation 5,
| (5) |
where k is the rate constant measured from R2 relaxation dispersion (kAB), kB is Boltzmann’s constant, h is Plank’s constant, R is the universal gas constant, T is temperature, ΔS‡ is the entropy of activation and ΔH‡ is the enthalpy of activation.
An alternative to transition-state theory is the phenomenological Ferry law (25,26) that describes a lower energy barrier with a rough enthalpic surface according to equation 6,
| (6) |
where k is the rate constant measured from R2 relaxation dispersion (kAB), C is a constant, R is the universal gas constant, T is temperature, ΔH0‡ is the enthalpy of activation associated with the smooth Arrhenius-like barrier height and <H2>1/2 is the enthalpy due to the ruggedness of the barrier.
Results
Relaxation dispersion in the E:THF:NADP+ complex
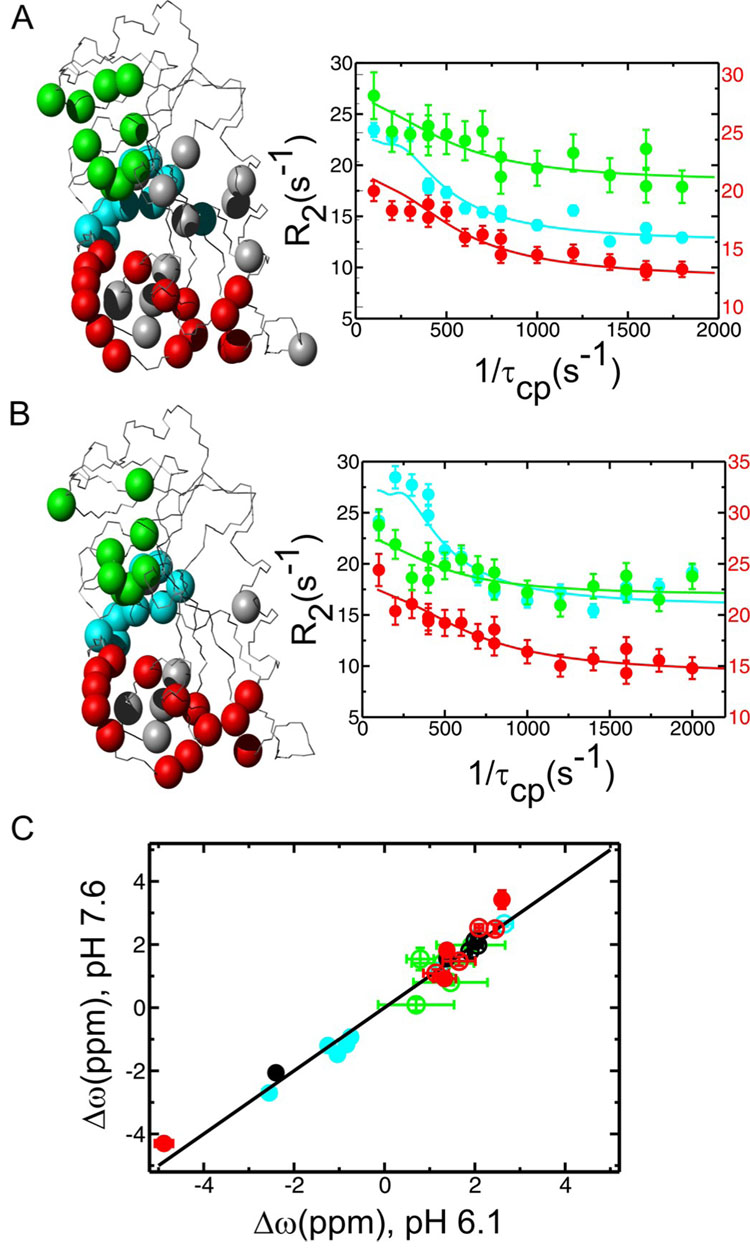
Relaxation dispersion curves were measured under a wide range of conditions using relaxation-compensated CPMG pulse sequences (22), as described in Materials and Methods. These data extend previous measurements performed at pH 7.6 and 300 K (21). Residues with conformational exchange were mapped to three regions; the active site loops (Met20, FG and GH loops), the cofactor binding cleft and the C-terminal associated region (residues 129–134 and 155–159) (Figure 2A). The kinetics and thermodynamics of the protein conformational fluctuations differ significantly between the three clusters. The kex (pb) values are 1300 ± 50 s−1 (1.4%), 1700 ± 120 s−1 (2.9%) and 550 ± 30 s−1 (2.2%) at pH 7.6 and 300 K for the active-site loops, cofactor binding cleft and the C-terminal associated region, respectively (Table 1). Since kex and pb values for each cluster are substantially different across several pH and temperature conditions (Table 1), we conclude that that the E:THF:NADP+ complex populates at least three independent higher energy substates as a result of conformational fluctuations.
Figure 2.
Conformational exchange as measured by R2 relaxation dispersion in the product ternary E:THF:NADP+ complex of DHFR at pHs 7.6 (A) and 6.1 (B). (A and B) Residues displaying conformational exchange (Rex) are highlighted as colored spheres on the E:THF:NADP+ structure (PDB 1RX4) according to the cluster to which they belong (red and grey – active-site loops and associated residues, green – cofactor binding cleft, blue – C-terminal associated region). Representative R2 relaxation dispersion curves from each dynamic cluster are shown on the right (red – Gly121, green – Thr46 and blue – Asp131). Data were collected at two external magnetic fields (1H 500 and 800 MHz), but only 800 MHz field data are shown here for clarity. R2 rate constants for the red Gly121 curves are plotted on the right-hand y-axis to improve clarity. (C) Higher energy substates observed at pH 6.1 and 7.6 are similar as indicated by the 1:1 linear correlation between the dynamic chemical shift differences (Δω) observed in the R2 relaxation dispersion experiments at the two pH conditions. Data points are color coded as above. Filled circles indicate that the sign of Δω could be determined for both pHs using an HMQC/HSQC comparison according to (51). Unfilled circles indicate that the sign could not be determined for one or both pH conditions.
pH Dependence of the Dynamic Events in E:THF:NADP+
To obtain further insights into the apparent correlation between the maximum hydride transfer rate and the rate of the conformational relaxation from the closed excited state to the occluded ground state of E:THF:NADP+, 15N R2 relaxation dispersion measurements were made for the E:THF:NADP+ complex under varying pH conditions ranging from pH 6.1 – 7.6. The dynamic events at the active-site loops and in the cofactor binding cleft are not dependent on pH. Similar residues showed dispersive behavior throughout the pH range (Figure 2b), and Δω values are nearly identical at each pH (Figure 2c and Supporting Information Table S1), suggesting that the identity of the higher energy substates corresponding to these dynamic events does not change significantly with pH. The kinetic (kex) and thermodynamic (pB) parameters for these dynamic events also remained relatively constant from pH 6.1 to 7.6 (Figure 3), and a change in temperature resulted in identical changes to these parameters under all pH conditions (Table 1).
Figure 3.
pH dependence of the conformational exchange kinetics in E:THF:NADP+ at 300 K. The rate constants for the excited-to-ground state transition (kBA) for the active-site loops, cofactor binding cleft and C-terminal associated region are plotted in red, green and blue, respectively. The dotted black curve is a simulation of the pH dependence of the hydride transfer rate constant with pKa 6.5 and pH-independent rate constant of 950 s−1 (at 298 K) (8).
In contrast, the dynamic process in the C-terminal associated region of DHFR was observed to be pH dependent with a pKa < 6 (Figure 3). As the pH decreased from 7.6 to 6.1, kex decreased and pb increased, but the Δω values remained identical (Supporting Information Table S1). This suggested that although the kinetics and thermodynamics of the dynamic process in the C-terminal region change with pH, the higher energy substate remains identical throughout the pH range of the experiments.
Temperature Dependence of the Dynamic Events in E:THF:NADP+
Measurements of R2 relaxation dispersion as a function of temperature can provide further insights into the conformational energy surface in terms of entropy and enthalpy contributions. The population (pB) of the higher energy substate associated with the dynamic event at the active site loops increases with temperature (Figure 4A). A van’t Hoff type analysis of this trend indicates that the higher energy ‘closed’ substate is enthalpically disfavored (ΔH = +13.9 ± 0.5 kcal/mol), but it is entropically favored (−TΔS = −11.2 ± 0.5 kcal/mol at 298 K) over the ‘occluded’ ground-state structure (ΔG(closed-occluded) = + 2.7 ± 0.5 kcal/mol at 298 K). Again, it should be noted that Δω values do not significantly change with temperature (Supporting Information Table S1), indicating that the identity of the higher energy substate remains the same over the entire pH and temperature range.
Figure 4.
Temperature dependence of the conformational exchange kinetics in E:THF:NADP+ at pH 7.6 for the (A) active-site loops and (B) C-terminal associated region. Rate constants for the excited-to-ground state (kBA; ■) and ground-to-excited state (kAB; ▲) transitions, and the equilibrium constant (kBA/kAB;●) are plotted. (C) Thermodynamic comparison of E:FOL:NADP+ and E:THF:NADP+ at 298 K. Thermodynamic barriers were calculated using transition-state theory according to Materials and Methods. Green, blue and red traces represent DG, DH and TDS respectively. E:FOL:NADP+ is a model for the Michaelis complex E:DHF:NADPH.
For the C-terminal associated residues, the higher energy substate is also enthalpically disfavored (ΔH = +15.5 ± 0.5 kcal/mol) and entropically favored (−TΔS = −13.1 ± 0.5 kcal/mol; ΔG = 2.4 ± 0.5 kcal/mol at 298 K) (Figure 4B). However, these values are significantly different from the values for the closed-occluded conformational change, again indicating the dynamic processes in the active-site loops and the C-terminal associated region are largely independent.
We have previously estimated the activation barrier associated with the ‘occluded-to-closed’ conformational change in E:FOL:NADP+ using transition-state theory (20). For E:FOL:NADP+, the calculated energy barrier has ΔG‡= 16.0 kcal/mol, ΔH‡= 21.2 kcal/mol and −TΔS‡= −5.1 kcal/mol at 298 K(20). In a similar manner, we calculated energy barriers for protein dynamics in the active-site loops (ΔG‡= 15.9 ± 0.5 kcal/mol, ΔH‡= 20.3 ± 0.5 kcal/mol, −TΔS‡= −4.4 ± 0.5 kcal/mol) and the C-terminal associated region (ΔG‡= 16.1 ± 0.4 kcal/mol, ΔH‡= 18.5 ± 0.4 kcal/mol, −TΔS‡= −2.4 kcal/mol) for E:THF:NADP+ at 298 K (Figure 4C). However, it should be noted that these values represent upper limits to the true activation parameters, considering the limitations of transition-state theory in describing multi-dimensional, diffusive events such as protein folding and conformational change (27,28).
An alternative to transition-state theory is the phenomenological Ferry Law (25,26) that incorporates a lower energy barrier with a rough enthalpic surface. While the accessible temperature range is too small to allow meaningful fits to this model, we estimate the enthalpy due to the ruggedness of the landscape (<H2>1/2) to be in the range 1.8 – 2.6 kcal/mol for both the active-site loop and C-terminal associated regions, assuming that the activation enthalpy associated with the smooth (Arrhenius-like) part of the barrier ΔH0 ‡= 0 – 10 kcal/mol. The estimated values of <H2>1/2 are in agreement with the ruggedness of the enthalpic barriers for collective protein motions involving multiple atoms and interactions determined for other systems (26,29).
DISCUSSION
In recent years, there has been renewed discussion about the role played by protein dynamics in enzyme catalysis (4,30). Enzymes must bind diverse ligands as they traverse their catalytic cycles, and thus, they undergo a variety of conformational changes as they bind substrate(s), catalyze the chemical step(s) and release products (2). At any stage of the catalytic cycle, these conformational changes may become rate-limiting. Recent results from NMR studies of protein dynamics in E.coli DHFR and other enzymes (20,21,31–34) suggest that limits to catalytic rates in enzymes are intimately related to conformational exchange rates measured by R2 relaxation dispersion. Although much progress has been made in small molecule and antibody catalysis, design efforts have failed to achieve the remarkable specificity and catalytic power of naturally occurring enzymes. This may be in part due to our inability to recapitulate the intricate orchestration of conformational changes involved in bio-catalysis.
E.coli DHFR has served as a model system to study the interplay between protein dynamics and enzyme function (3). NMR, computer simulations and single molecule studies have all indicated the importance of protein dynamics in the catalytic cycle of DHFR. For example, computer simulations have identified a ‘correlated network of coupled motion’ that acts to decrease the donor-acceptor distance for very efficient hydride transfer (35). Site-directed mutagenesis of residues within the network has confirmed their importance (35–37), and kinetic isotope effect (KIE) (38–40) and single molecule studies (41–43) of the WT and mutant-catalyzed reaction have further underscored the essential role of protein dynamics in gating the distance between hydride donor and acceptor atoms for catalytic function. Similar results have been found for other enzymes that catalyze hydrogen transfer, including alcohol dehydrogenase (44,45) and soybean lipoxygenase (46).
Outside of the catalytic step itself, protein dynamics play a critical role in binding substrates to and releasing products from DHFR. At physiological pH, the rate-limiting step is release of THF product from the product release complex E:THF:NADPH (12.5 s−1) (8). We have previously shown through R2 relaxation dispersion techniques that E:THF:NADPH accesses a higher energy substate structurally similar to E:NADPH with a rate constant of 13–18 s−1 (21). These results argue strongly that product release occurs through the higher energy substate, and thus, steady-state turnover is rate-limited by the ground state to excited substate conversion (kAB) in E:THF:NADPH.
Similarly, we have noted that the rate constant for the excited substate to ground state conversion (kBA) in E:THF:NADP+ is strikingly similar to the pH-independent maximum hydride transfer rate constant (21). Many of the residues that significantly change 15N chemical shift between the ‘closed’ and ‘occluded’ conformations of DHFR exhibit 15N R2 relaxation dispersion, and moreover, the dynamic chemical shifts (Δω) for these residues correspond to the ground-state chemical shift differences (Δδ) between ‘closed’ and ‘occluded’ conformations. These results indicate that the E:THF:NADP+ complex fluctuates between an ‘occluded’ ground state and a higher energy ‘closed’ substate. The present work adds significant new insights by showing that the rate of the ‘closed-occluded’ transition in E:THF:NADP+ is pH independent. Taken together, these and the previous results suggest that the rate at which the closed excited state formed immediately following hydride transfer relaxes to the occluded ground state of the E:THF:NADP+ product complex also places an effective limit on maximum enzymatic turnover. In effect, once hydride donor and acceptor atoms are properly positioned within the active site, hydride transfer is instantaneous (or at least khydride >> 950 s−1) (4) but the ‘closed’ E:THF:NADP+ complex must still collapse into the ground-state ‘occluded’ conformation before continuing through the catalytic cycle. It should be emphasized that the closed excited state measured using R2 relaxation dispersion does not result from back hydride transfer. The hydride transfer reaction is strongly pH-dependent (8) whereas kex for the closed-occluded conformational change is pH-independent, and the back reaction is very much slower (0.03 s−1) near neutral pH than the rate of formation of the closed excited state (kAB = 20 s−1).
Other regions within the E:THF:NADP+ complex also show significant conformational exchange, including the cofactor binding cleft and the C-terminal associated region. We have previously shown that the cofactor binding cleft accesses a conformation similar in structure to that found in E:THF, that is, a conformation without cofactor bound (21). The C-terminal associated region (residues 129–134, 155–159), unlike the cofactor binding cleft and active-site loops, shows dispersive behavior in every complex of DHFR so far studied. Although we do not have a relevant structural model for this dynamic event, it should be noted that the dynamic chemical shifts (Δω) are similar for all complexes in the catalytic cycle. In this context, these motions can be seen as ‘intrinsic dynamics’ (33) of the enzyme although the role of these motions, if any, is unknown. It is noteworthy that the kinetic (kex) and thermodynamic (pb) parameters for this dynamic event change depend on the ligand-bound state of the enzyme. For example, in the E:FOL:NADP+ complex kex is much higher (1010 s−1 at pH 6.8, 303 K) (20) than in the E:THF:NADP+ complex (kex = 550 s−1 at pH 6.5, 303 K). This is in contrast to the dynamics at the active-site loops where kex in E:FOL:NADP+ is much lower (477 s−1 at pH 6.8, 303 K) than that seen for E:THF:NADP+ (1650 s−1 at pH 6.5, 303 K). These differences may be related to the overall conformation of the enzyme (‘closed’ vs ‘occluded’) and/or the occupancy of the substrate/product binding pocket. The change from faster to slower C-terminal dynamics between E:FOL:NADP+ and E:THF:NADP+ may be important in the overall configuration energy of the enzyme, and may compensate for the change in dynamics observed in the active-site loops.
The motions of the three dynamic regions in the E:THF:NADP+ complex are independent. The three clusters yield different global kex and pB values, and show different pH and temperature dependence. Although the dynamics of the active-site loops and the cofactor binding cleft are pH independent, the dynamics of the C-terminal associated region are clearly pH dependent with pKa < 6. The C-terminal and active-site loop motion can also be differentiated based on temperature dependence and hence, on the enthalpy/entropy contributions to the overall Gibbs free energy. Thus, independent dynamic events can be differentiated based on their response to pH, temperature, mutagenesis and other solvent effects (e.g. solvent isotope effect (47,48), and these approaches can be used to further characterize protein motions in larger and more complex enzyme systems where multiple dynamics events are likely.
Enzymes are inherently dynamic, and changes in conformation are required for efficient substrate binding and product release. In this study, we have demonstrated that, in DHFR, the ‘closed-to-occluded’ conformational change associated with relaxation of the product ternary complex into its ground state following chemical reaction, occurs at a very similar rate as maximum hydride transfer. This may not be surprising if we consider that under physiological conditions, the rate-limiting step is not chemistry, but release of THF from the enzyme. Within this evolutionary context, hydride transfer needs only to be optimized to the same extent as the release of product from the E:THF:NADPH complex and the accompanying ‘occluded-to-closed’ conformational change, which in turn must be related back to the reverse ‘closed-to-occluded’ conformational change in E:THF:NADP+ and hydride transfer. In this manner, the kinetics and thermodynamics of the ‘closed-occluded’ transition (i.e. physical changes within the energy landscape of DHFR) intimately links, and ultimately dictates, both steady-state turnover and maximum hydride transfer. These findings are entirely consistent with the dynamic energy landscape view of enzyme catalysis (21,49,50)
Acknowledgements
We would like to thank John Chung and Gerard Kroon for helping with the NMR experiments, and Euvel Manapalaz and Linda Tennant for excellent technical expertise. This work was supported by grant GM75995 from the National Institutes of Health. DDB was the recipient of a Canadian Institutes of Health Research postdoctoral fellowship.
Footnotes
Supporting Information Available
There is one table containing dynamic chemical shift information from 15N R2 relaxation dispersion experiments and figures detailing full R2 relaxation dispersion results at 1H spectrometer frequencies of 500 and 800 MHz. This material is available free of charge via the Internet at http://pubs.acs.org
Abbreviations footnote: dihydrofolate reductase (DHFR), folic acid (FOL), dihydrofolate (DHF), tetrahydrofolate (THF), NADPH (nicotinamide adenine dinucleotide phosphate reduced form), NADP+ (nicotinamide adenine dinucleotide phosphate oxidized form), CPMG (Carr-Purcell-Meiboom-Gill), NMR (nuclear magnetic resonance), HSQC (heteronuclear single quantum correlation), HMQC (heteronuclear multiple quantum correlation)
References
- 1.Stroppolo ME, Falconi M, Caccuri AM, Desideri A. Superefficient enzymes. Cell Mol. Life Sci. 2001;58:1451–1460. doi: 10.1007/PL00000788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hammes GG. Multiple conformational changes in enzyme catalysis. Biochemistry. 2002;41:8221–8228. doi: 10.1021/bi0260839. [DOI] [PubMed] [Google Scholar]
- 3.Schnell JR, Dyson HJ, Wright PE. Structure, dynamics and catalytic function of dihydrofolate reductase. Ann. Rev. Biophys. Biomol. Struct. 2004;33:119–140. doi: 10.1146/annurev.biophys.33.110502.133613. [DOI] [PubMed] [Google Scholar]
- 4.Hammes-Schiffer S, Benkovic SJ. Relating protein motion to catalysis. Ann. Rev. Biochem. 2006;75:519. doi: 10.1146/annurev.biochem.75.103004.142800. [DOI] [PubMed] [Google Scholar]
- 5.Sawaya MR, Kraut J. Loop and subdomain movements in the mechanism of Escherichia coli dihydrofolate reductase: crystallographic evidence. Biochemistry. 1997;36:586–603. doi: 10.1021/bi962337c. [DOI] [PubMed] [Google Scholar]
- 6.Benkovic SJ, Fierke CA, Naylor AM. Insights into enzyme function from studies on mutants of dihydrofolate reductase. Science. 1988;239:1105–1110. doi: 10.1126/science.3125607. [DOI] [PubMed] [Google Scholar]
- 7.Hammes-Schiffer S. Quantum-classical simulation methods for hydrogen transfer in enzymes: a case study of dihydrofolate reductase. Curr. Opin. Struct. Biol. 2004;14:192–201. doi: 10.1016/j.sbi.2004.03.008. [DOI] [PubMed] [Google Scholar]
- 8.Fierke CA, Johnson KA, Benkovic SJ. Construction and evaluation of the kinetic scheme associated with dihydrofolate reductase from Escherichia coli. Biochemistry. 1987;26:4085–4092. doi: 10.1021/bi00387a052. [DOI] [PubMed] [Google Scholar]
- 9.Venkitakrishnan RP, Zaborowski E, McElheny D, Benkovic SJ, Dyson HJ, Wright PE. Conformational changes in the active site loops of dihydrofolate reductase during the catalytic cycle. Biochemistry. 2004;43:16046–16055. doi: 10.1021/bi048119y. [DOI] [PubMed] [Google Scholar]
- 10.Adams J, Johnson K, Matthews R, Benkovic SJ. Effects of distal point-site mutations on the binding and catalysis of dihydrofolate reductase from Escherichia coli. Biochemistry. 1989;28:6611–6618. doi: 10.1021/bi00442a012. [DOI] [PubMed] [Google Scholar]
- 11.Cameron CE, Benkovic SJ. Evidence for a functional role of the dynamics of glycine-121 of Escherichia coli dihydrofolate reductase obtained from kinetic analysis of a site-directed mutant. Biochemistry. 1997;36:15792–15800. doi: 10.1021/bi9716231. [DOI] [PubMed] [Google Scholar]
- 12.Miller GP, Benkovic SJ. Strength of an interloop hydrogen bond determines the kinetic pathway in catalysis by Escherichia coli dihydrofolate reductase. Biochemistry. 1998;37:6336–6342. doi: 10.1021/bi973065w. [DOI] [PubMed] [Google Scholar]
- 13.Miller GP, Benkovic SJ. Deletion of a highly motional residue affects formation of the Michaelis complex for Escherichia coli dihydrofolate reductase. Biochemistry. 1998;37:6327–6335. doi: 10.1021/bi972922t. [DOI] [PubMed] [Google Scholar]
- 14.Miller GP, Wahnon DC, Benkovic SJ. Interloop contacts modulate ligand cycling during catalysis by Escherichia coli dihydrofolate reductase. Biochemistry. 2001;40:867–875. doi: 10.1021/bi001608n. [DOI] [PubMed] [Google Scholar]
- 15.Rajagopalan PT, Lutz S, Benkovic SJ. Coupling interactions of distal residues enhance dihydrofolate reductase catalysis: mutational effects on hydride transfer rates. Biochemistry. 2002;41:12618–12628. doi: 10.1021/bi026369d. [DOI] [PubMed] [Google Scholar]
- 16.Epstein DM, Benkovic SJ, Wright PE. Dynamics of the dihydrofolate reductase folate complex: Catalytic sites and regions known to undergo conformational change exhibit diverse dynamical features. Biochemistry. 1995;34:11037–11048. doi: 10.1021/bi00035a009. [DOI] [PubMed] [Google Scholar]
- 17.Falzone CJ, Wright PE, Benkovic SJ. Dynamics of a flexible loop in dihydrofolate reductase from Escherichia coli and its implication for catalysis. Biochemistry. 1994;33:439–442. doi: 10.1021/bi00168a007. [DOI] [PubMed] [Google Scholar]
- 18.Osborne MJ, Schnell J, Benkovic SJ, Dyson HJ, Wright PE. Backbone dynamics in dihydrofolate reductase complexes: Role of loop flexibility in the catalytic mechanism. Biochemistry. 2001;40:9846–9859. doi: 10.1021/bi010621k. [DOI] [PubMed] [Google Scholar]
- 19.Schnell JR, Dyson HJ, Wright PE. Effect of cofactor binding and loop conformation on side chain methyl dynamics in dihydrofolate reductase. Biochemistry. 2004;43:374–383. doi: 10.1021/bi035464z. [DOI] [PubMed] [Google Scholar]
- 20.McElheny D, Schnell JR, Lansing JC, Dyson HJ, Wright PE. Defining the role of active-site loop fluctuations in dihydrofolate reductase catalysis. Proc. Natl. Acad. Sci. USA. 2005;102:5032–5037. doi: 10.1073/pnas.0500699102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- 22.Loria JP, Rance M, Palmer AG. A relaxation-compensated Carr-Purcell-Meiboom-Gill sequence for characterizing chemical exchange by NMR spectroscopy. J. Am. Chem. Soc. 1999;121:2331–2332. [Google Scholar]
- 23.Palmer AG, Kroenke CD, Loria JP. Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Methods Enzymol. 2001;339:204–238. doi: 10.1016/s0076-6879(01)39315-1. [DOI] [PubMed] [Google Scholar]
- 24.Palmer AG. Nmr probes of molecular dynamics: overview and comparison with other techniques. Annu. Rev. Biophys. Biomol. Struct. 2001;30:129–155. doi: 10.1146/annurev.biophys.30.1.129. [DOI] [PubMed] [Google Scholar]
- 25.Ferry JD, Grandine LDJ, Fitzgerald ER. The relaxation distribution function of polyisobutylene in the transition from rubber-like to glass-like behavior. J. Appl. Phys. 1953;24:911–921. [Google Scholar]
- 26.Denisov VP, Peters J, Hörlein HD, Halle B. Using buried water molecules to explore the energy landscape of proteins. Nature Struct. Biol. 1996;3:505–509. doi: 10.1038/nsb0696-505. [DOI] [PubMed] [Google Scholar]
- 27.Ansari A, Jones CM, Henry ER, Hofrichter J, Eaton WA. The role of solvent viscosity in the dynamics of protein conformational changes. Science. 1992;256:1796–1798. doi: 10.1126/science.1615323. [DOI] [PubMed] [Google Scholar]
- 28.Qian H. From discrete protein kinetics to continuous Brownian dynamics: a new perspective. Protein Sci. 2002;11:1–5. doi: 10.1110/ps.18902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mulder FA, Mittermaier A, Hon B, Dahlquist FW, Kay LE. Studying excited states of proteins by NMR spectroscopy. Nat. Struct. Biol. 2001;8:932–935. doi: 10.1038/nsb1101-932. [DOI] [PubMed] [Google Scholar]
- 30.Benkovic SJ, Hammes-Schiffer S. A perspective on enzyme catalysis. Science. 2003;301:1196–1202. doi: 10.1126/science.1085515. [DOI] [PubMed] [Google Scholar]
- 31.Beach H, Cole R, Gill ML, Loria JP. Conservation of µs-ms enzyme motions in the apo- and substrate-mimicked state. J. Am. Chem. Soc. 2005;127:9167–9176. doi: 10.1021/ja0514949. [DOI] [PubMed] [Google Scholar]
- 32.Kovrigin EL, Loria JP. Enzyme Dynamics along the Reaction Coordinate: Critical Role of a Conserved Residue. Biochemistry. 2006;45:2636–2647. doi: 10.1021/bi0525066. [DOI] [PubMed] [Google Scholar]
- 33.Eisenmesser EZ, Millet O, Labeikovsky W, Korzhnev DM, Wolf-Watz M, Bosco DA, Skalicky JJ, Kay LE, Kern D. Intrinsic dynamics of an enzyme underlies catalysis. Nature. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- 34.Wolf-Watz M, Thai V, Henzler-Wildman K, Hadjipavlou G, Eisenmesser EZ, Kern D. Linkage between dynamics and catalysis in a thermophilic-mesophilic enzyme pair. Nat. Struct. Mol. Biol. 2004;11:945–949. doi: 10.1038/nsmb821. [DOI] [PubMed] [Google Scholar]
- 35.Agarwal PK, Billeter SR, Rajagopalan PTR, Benkovic SJ, Hammes-Schiffer S. Network of coupled promoting motions in enzyme catalysis. Proc. Natl. Acad. Sci. USA. 2002;99:2794–2799. doi: 10.1073/pnas.052005999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Watney JB, Agarwal PK, Hammes-Schiffer S. Effect of mutation on enzyme motion in dihydrofolate reductase. J. Am. Chem. Soc. 2003;125:3745–3750. doi: 10.1021/ja028487u. [DOI] [PubMed] [Google Scholar]
- 37.Wong KF, Selzer T, Benkovic SJ, Hammes-Schiffer S. Impact of distal mutations on the network of coupled motions correlated to hydride transfer in dihydrofolate reductase. Proc. Natl. Acad. Sci. U. S. A. 2005;102:6807–6812. doi: 10.1073/pnas.0408343102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sikorski RS, Wang L, Markham KA, Rajagopalan PT, Benkovic SJ, Kohen A. Tunneling and coupled motion in Escherichia coli dihydrofolate reductase catalysis. J. Am. Chem. Soc. 2004;126:4778–4779. doi: 10.1021/ja031683w. [DOI] [PubMed] [Google Scholar]
- 39.Wang L, Goodey NM, Benkovic SJ, Kohen A. Coordinated effects of distal mutations on environmentally coupled tunneling in dihydrofolate reductase. PNAS. 2006;103:15753–15758. doi: 10.1073/pnas.0606976103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wang L, Goodey NM, Benkovic SJ, Kohen A. The role of enzyme dynamics and tunnelling in catalysing hydride transfer: studies of distal mutants of dihydrofolate reductase. Philos. Trans. R. Soc. Lond B Biol Sci. 2006;361:1307–1315. doi: 10.1098/rstb.2006.1871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rajagopalan PT, Zhang Z, McCourt L, Dwyer M, Benkovic SJ, Hammes GG. Interaction of dihydrofolate reductase with methotrexate: Ensemble and single-molecule kinetics. Proc. Natl. Acad. Sci. USA. 2002;99:13481–13486. doi: 10.1073/pnas.172501499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhang Z, Rajagopalan PT, Selzer T, Benkovic SJ, Hammes GG. Single-molecule and transient kinetics investigation of the interaction of dihydrofolate reductase with NADPH and dihydrofolate. Proc. Natl. Acad. Sci. U. S. A. 2004;101:2764–2769. doi: 10.1073/pnas.0400091101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Antikainen NM, Smiley RD, Benkovic SJ, Hammes GG. Conformation coupled enzyme catalysis: single-molecule and transient kinetics investigation of dihydrofolate reductase. Biochemistry. 2005;44:16835–16843. doi: 10.1021/bi051378i. [DOI] [PubMed] [Google Scholar]
- 44.Kohen A, Cannio R, Bartolucci S, Klinman JP. Enzyme dynamics and hydrogen tunnelling in a thermophilic alcohol dehydrogenase [see comments] Nature. 1999;399:496–499. doi: 10.1038/20981. [DOI] [PubMed] [Google Scholar]
- 45.Liang ZX, Lee T, Resing KA, Ahn NG, Klinman JP. Thermal-activated protein mobility and its correlation with catalysis in thermophilic alcohol dehydrogenase. Proc. Natl. Acad. Sci. USA. 2004;101:9556–9561. doi: 10.1073/pnas.0403337101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Knapp MJ, Rickert K, Klinman JP. Temperature-dependent isotope effects in soybean lipoxygenase-1: correlating hydrogen tunneling with protein dynamics. J Am. Chem. Soc. 2002;124:3865–3874. doi: 10.1021/ja012205t. [DOI] [PubMed] [Google Scholar]
- 47.Kovrigin EL, Loria JP. Characterization of the Transition State of Functional Enzyme Dynamics. J. Am. Chem. Soc. 2006;128:7724–7725. doi: 10.1021/ja061435a. [DOI] [PubMed] [Google Scholar]
- 48.Watt ED, Shimada H, Kovrigin EL, Loria JP. The mechanism of rate-limiting motions in enzyme function. PNAS. 2007;104:11981–11986. doi: 10.1073/pnas.0702551104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Swint-Kruse L, Fisher HF. Enzymatic reaction sequences as coupled multiple traces on a multidimensional landscape. Trends Biochem. Sci. 2008;33:104–112. doi: 10.1016/j.tibs.2007.12.001. [DOI] [PubMed] [Google Scholar]
- 50.Benkovic SJ, Hammes GG, Hammes-Schiffer S. Free-Energy Landscape of Enzyme Catalysis. Biochemistry. 2008;47:3317–3321. doi: 10.1021/bi800049z. [DOI] [PubMed] [Google Scholar]
- 51.Skrynnikov NR, Dahlquist FW, Kay LE. Reconstructing NMR spectra of "invisible" excited protein states using HSQC and HMQC experiments. J. Am. Chem. Soc. 2002;124:12352–12360. doi: 10.1021/ja0207089. [DOI] [PubMed] [Google Scholar]