The role of weakly polar and H-bonding interactions in the stabilization of the conformers of FGG, WGG and YGG

Abstract

The energetics of intramolecular interactions on the conformational potential energy surface of the terminally protected N-Ac-Phe-Gly-Gly-NHMe (FGG), N-Ac-Trp-Gly-Gly-NHMe (WGG) and N-Ac-Tyr-Gly-Gly-NHMe (YGG) tripeptides was investigated. To identify the representative conformations, simulated annealing molecular dynamics (MD) and density functional theory (DFT) methods were used. The interaction energies were calculated at the BHandHLYP/aug-cc-pVTZ level of theory. In the global minima, 10%, 31% and 10% of the stabilization energy come from weakly polar interactions, respectively, in FGG, WGG and YGG. In the prominent cases 46%, 62% and 46% of the stabilization energy is from weakly polar interactions, respectively, in FGG, WGG and YGG. On average, weakly polar interactions account for 15%, 34% and 9% of the stabilization energies of the FGG, WGG and YGG conformers, respectively. Thus, weakly polar interactions can make an important energetic contribution to protein structure and function.

INTRODUCTION

Ubiquitous weakly polar interactions are an important subset of non-covalent interactions in proteins where they play a crucial role in structure stabilization. They involve at least one aromatic residue (Ar) and include aromatic-aromatic (Ar-Ar), Ar-backbone (Ar-Bb), aromatic-sulfur (Ar-S) and CH-π interactions.^1,2

Both the secondary and tertiary structure of proteins can be stabilized by weakly polar interactions.³ Recently, it was shown that about half of the total stabilization energy (-218 kJ·mol^-1) of the so-called Trp-cage motif of the TC5b protein⁴ is from weakly polar interactions.⁵ It has also been shown that the tertiary fold of avian pancreatic polypeptide⁶ is solely stabilized by weakly polar interactions (-114 kJ·mol^-1) involving residues Phe20 and Tyr27.⁷

In short peptides, weakly polar interactions can constrain the conformation of side chains and stabilize local structures.^8-10 It was shown that inclusion of a Tyr residue induces weakly polar interactions in Ala-based α-helical structures and influences the electronic circular dichroism spectra of α-helices.¹¹ NMR measurements also indicated the proximity of the backbone to the Ar side chain¹² and when the conformational preferences of N-Ac-AAAAYA-NHMe amide were investigated using quantum chemical computations, it was shown that the tyrosyl side chain interacts with the backbone of the peptide in the most stable conformers.¹³ The individual Ar-Bb interaction energies were substantial in being notably close to the strength of an average H-bond (-20 kJ·mol^-1).

Conformations of tripeptides with protected and unprotected ends have also been investigated extensively.^14-19 Gas phase spectroscopic studies and quantum chemical computations of Phe-Gly-Gly and Trp-Gly-Gly are excellent examples where the combination of experimental and theoretical methods was proven to be invaluable.^15,17,18,20 However, results obtained with peptide models, which have unprotected N- and C-terminus are usually not appropriate to extrapolate the intrinsic behavior of polypeptide chains. They may be biased by specific interactions involving the unprotected N- and C-terminal groups of the models. Indeed, calculations of conformers of tripeptides were especially affected. In Phe-Gly-Gly, the global minimum is stabilized by a α-COOH-π interaction, which is statistically unlikely in proteins.¹⁷ In Trp-Gly-Gly the global minimum is stabilized by a bifurcated H-bond which involves the unprotected α-NH₂ group.^15,18 The most stable Tyr-Gly-Gly conformer has H-bonds, which involve the unprotected α-COOH group both as a donor and acceptor.¹⁹ All the above mentioned gas phase calculations yielded interactions which cannot exist in the interior of a protein since the N- and C-terminus are derivatized in peptide bonds. Adequate structural mimicking to preserve the effects of neighboring residues is particularly important in protein modeling.^14,16,21-26

Recently, several types of capping groups were tested in the computations of interaction energies of short peptide fragments and most accurate results were obtained with N-Ac and NHMe protecting groups, respectively, at the N- and C-terminal ends.^27-29 Furthermore, studies of the BHandHLYP functional, in describing weakly polar interactions³⁰ as well as π-stacked dispersion systems,³¹ revealed that it gives results close to those derived from high level MP2/CBS and CCSD(T)/CBS computations.

In this study, density functional theory³² (DFT) was used to elucidate the role of weakly polar interactions in the stabilization of N-Ac-Phe-Gly-Gly-NHMe (FGG), N-Ac-Trp-Gly-Gly-NHMe (WGG) and N-Ac-Tyr-Gly-Gly-NHMe (YGG) in aqueous phase.

METHODS

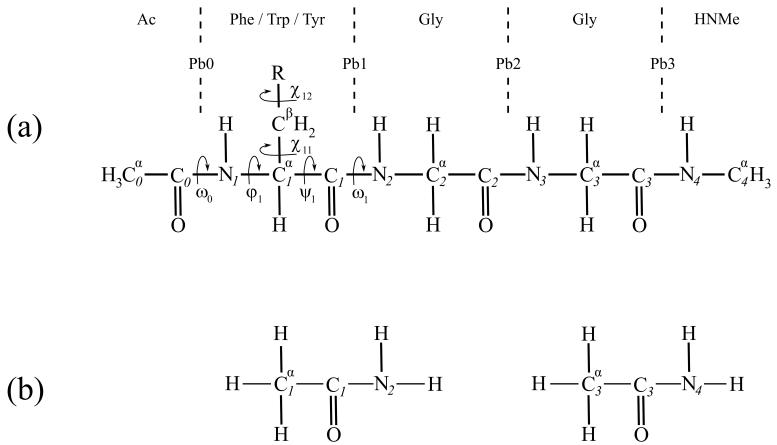
Figure 1a shows the chemical structures of the tripeptide models investigated here, represented as by Percel and associates.³³

Figure 1.

(a) the chemical structure of the investigated N-Ac, NHMe blocked tripeptides; the definitions of torsion angles are complied with the recommendation of ref 33, Pbi (i=0,1,2,3) designates the ith peptide bond. (b) acetamide fragments which used to calculate the interaction energy between peptide bonds (in this case Pb1 and Pb3).

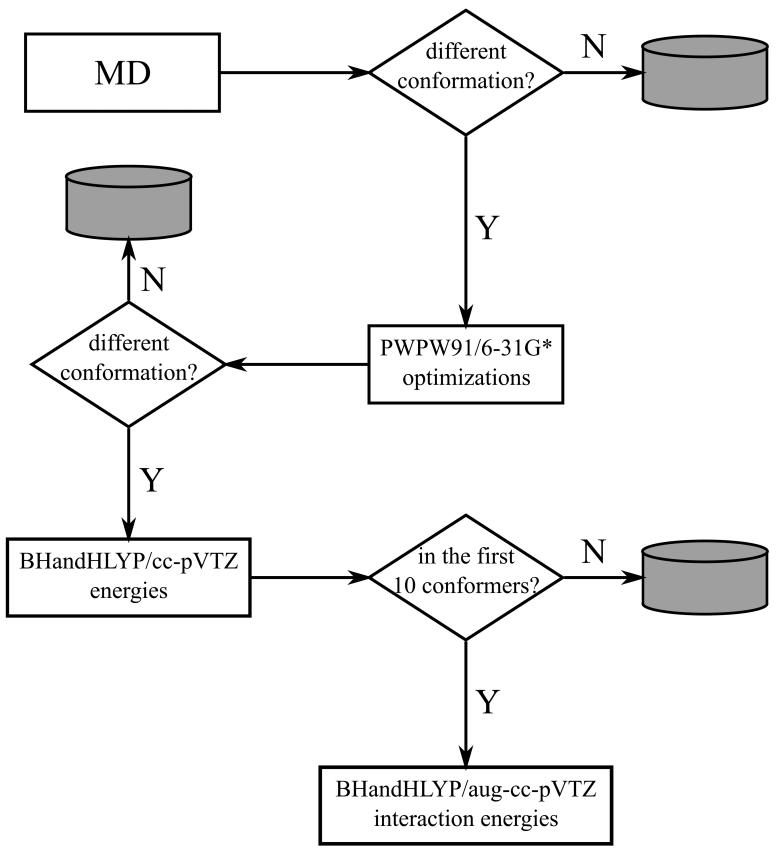
Scheme 1 illustrates the strategy used to identify the representative conformations of FGG, WGG and YGG. 1000 initial geometries per peptide were generated by aqueous-phase molecular dynamics (MD) simulations using in-house perl scripts and a simulated annealing protocol.³⁴ The simulated annealing calculations were performed as described before³⁵, except that the OPLS-AA/L force field was used. GB/SA implicit solvation³⁶ and stochastic dynamics were used to simulate the viscous drag of water (γ=91 ps^-1). After MD simulations, geometries were sorted and considered to be different if the root mean square deviation (RMSD) of non-hydrogen atoms were not less than 0.25 Å. The sorting procedure resulted in 328, 325 and 243 conformers for FGG, WGG and YGG, respectively.

Scheme 1.

Strategy used to determine representative conformations of FGG, WGG and YGG.

The structures obtained were further optimized at the PWPW91/6-31G* level of theory³⁷ in aqueous-phase using a self-consistent reaction field method with a Poisson-Boltzmann solver. DFT level optimized structures were sorted again according to the aforementioned criterion. 313, 311 and 229 conformers were obtained for FGG, WGG and YGG, respectively. Single-point, aqueous phase energy calculations were then performed with the BHandHLYP³⁸ functional using the cc-pVTZ basis set to obtain a more accurate energetic rank of the conformers.

BHandHLYP was expressed as:

$$0.5\cdot E_X^{\mathit{HF}}+0.5\cdot E_X^S+1.0\cdot E_C^{\mathit{LYP}}$$

where $E_X^{\mathit{HF}}$ and $E_X^S$ are the exact Hartree-Fock and the local Slater exchange functionals, respectively; $E_C^{\mathit{LYP}}$ is the Lee, Yang and Parr correlation functional.³⁹

The intramolecular interaction energies of the 10 most stable conformers were calculated at the BHandHLYP/aug-cc-pVTZ level of theory in aqueous phase. The recently developed rotation method^13,40 (RM) was used to calculate the Ar-Bb interaction energies; a brief outline of RM can be found in the Appendix section. In the present study, the original version of RM was used because DFT-based methods with large basis sets are less sensitive to the basis set superposition error (BSSE). Nevertheless, to prove this assumption, the conformer with the strongest Ar-Bb interaction energy (WGG 1), where the largest BSSE can be expected, was investigated with both methods using the BHandHLYP/aug-cc-pVTZ(-f) level of theory. Indeed, the difference between the interaction energies obtained with the original and extended RM was 0.2 kJ/mol, which is negligible. To calculate the Pb0-Pb2, Pb0-Pb3 and Pb1-Pb3 Bb-Bb interaction energies for both weakly polar and H-bonds, the peptide bonds were modeled as acetamide (Figure 1b). Acetamide was selected instead of N-methyl-acetamide to avoid the artificial close contacts and repulsive interactions between the saturating hydrogens. Nevertheless, in FGG and YGG the adequacy of acetamide was tested in Pb0-Pb3 interactions and no substantial differences were found between the results obtained with acetamide and with N-methyl acetamide (supplementary material, Table 1S). The counterpoise procedure (CP) was used to correct the basis set superposition errors.⁴¹ On the basis of the results of our and other’s recent benchmark studies,^30,31 the BHandHLYP functional was selected because it reliably reproduces high level ab initio results. Since the molecular geometries are usually less sensitive of the applied level of theory than are the electronic properties, the PWPW91 functional³⁷ was used in the optimizations due to its computational efficiency. Although, to assess the effects of the different functionals, the 10 lowest energy conformers (BHandHLYP/cc-pVTZ//PWPW91/6-31G*) were also optimized at the BHandHLYP/6-31G* level of theory. The PWPW91/6-31G* and BHandHLYP/6-31G* optimizations yielded chemically equivalent conformers (supplementary material, Figure 1S).

The MD calculations were performed with the TINKER package⁴² (ver. 4.2). The DFT calculations were conducted with the Jaguar package⁴³ (ver. 5.5 release 11, ver. 6.0 release 11, ver. 6.5 release 106). All computations were accomplished on a custom built 64bit dual AMD Opteron Linux (Fedora Core 3) cluster. Figures were prepared with Grace (http://plasma-gate.weizmann.ac.il/Grace/), Inkscape (http://www.inkscape.org/) and YASARA (http://www.yasara.org) packages.

RESULTS AND DISCUSSION

Aromatic-backbone interactions

Table 1 shows that, in general, the energies of interaction of the Ar groups are stronger with the larger C-terminal than the N-terminal backbone structures. The average C-terminal interaction energies are -2.6 kJ·mol^-1, -9.8 kJ·mol^-1 and -1.3 kJ·mol^-1, respectively, in FGG, WGG and YGG, whereas the values for the corresponding N-terminal backbone structures are -0.5 kJ·mol^-1, -1.0 kJ·mol^-1 and -0.3 kJ·mol^-1. Strongest Ar-Bb interactions, with an average interaction energy of -10.8 kJ·mol^-1, occur in the conformers of WGG. The individual Ar-Bb interaction energies for conformer 0 (the global minimum), conformer 1 and conformer 4 of WGG are stronger than the energy of a typical H-bond, which is ca. 20 kJ·mol^-1 in biological systems.⁴⁴ The above observations are in agreement with the results of a previous PDB search⁹ showing that Trp has the highest probability to be involved in Ar-Bb interactions. This may be due to the large aromatic indolyl-group.⁸

Table 1.

Ar-Bb interaction energies (kJ·mol^-1)

	FGG			WGG			YGG
conformer	N†	C‡	Total	N†	C‡	Total	N†	C‡	Total
0	0.2	0.0	0.2	0.0	-23.6	-23.6	-0.5	0.0	-0.5
1	-2.2	-3.0	-5.2	-1.6	-28.5	-30.1	-2.8	0.0	-2.8
2	-1.2	0.0	-1.2	-0.3	-2.5	-2.8	0.0	-2.9	-2.9
3	0.0	2.8	2.8	-1.9	-9.6	-11.5	0.0	-1.3	-1.3
4	0.0	-2.6	-2.6	-1.2	-19.8	-21.0	0.8	0.0	0.8
5	0.9	-15.4	-14.5	1.0	7.0	8.0	0.0	3.7	3.7
6	-2.8	-2.2	-5.0	-0.3	-11.5	-11.8	-0.9	0.0	-0.9
7	-0.7	0.0	-0.7	-2.8	-2.9	-5.7	-0.5	-14.6	-15.1
8	-0.3	0.0	-0.3	-2.8	-9.1	-11.9	0.9	0.0	0.9
9	0.7	-5.4	-4.7	0.0	2.6	2.6	0.0	1.9	1.9
average	-0.5	-2.6	-3.1	-1.0	-9.8	-10.8	-0.3	-1.3	-1.6

^†interaction energies between the aromatic side chain and the Ac-N₁H group (Figure 1a, Scheme 1S).

^‡interaction energies between the aromatic side chain and the Gly-Gly-NHMe and the C₁=O groups (Figure 1a, Scheme 1S).

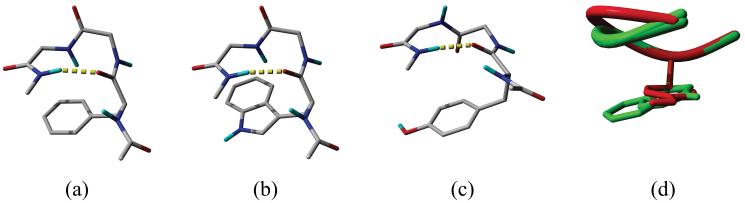
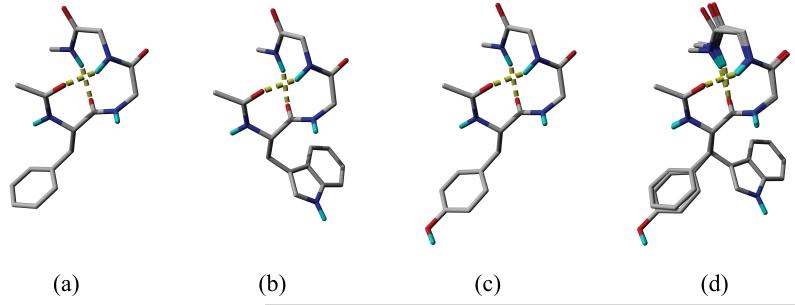
Conformer 5 of FGG, conformer 1 of WGG and conformer 7 of YGG, which have the largest Ar-Bb interaction energies, are depicted in Figure 2a, b and c, respectively. Each conformer is also stabilized by an H-bond in addition to the Ar-Bb interaction. In FGG and WGG the Ar-Bb interaction includes an N-H⋯π and an aromatic-peptide bond (Ar-Pb) interaction. N-H⋯π interactions are non-conventional hydrogen bonds.⁴⁵ In gas phase, their interaction energies range from -2 kJ·mol^-1 to -10 kJ·mol^-1 depending on their geometries; the optimal distance between the centroid of the aromatic ring and the N₃ hydrogen is about 3.6 Å.⁴⁵ This distance is 3.0 Å and 2.8 Å, respectively, in the conformers of FGG and WGG. The -13.1 kJ·mol^-1 energy difference between the conformers (-15.4 kJ·mol^-1 in FGG and -28.5 kJ·mol^-1 in WGG) is the consequence of the larger aromatic surface of the indolyl- than phenyl ring. The benzo part of the indolyl ring also interacts with the backbone and this is an extra interaction which is absent in FGG. In the WGG conformer, the pyrrol ring occupies the position of the phenyl ring of the FGG conformer as can be seen in Figure 2d.

Figure 2.

Conformers with the strongest Ar-Bb interactions. (a) conformer 5 of FGG, (b) conformer 1 of WGG, (c) conformer 7 of YGG; H-bonds are shown as yellow dashed tubes. (d) the superimposition of conformers depicted in (a) — green, (b) — green and (c) — red; the backbones are represented as ribbons. Aliphatic hydrogens are not shown.

In YGG, the Pb2 is rotated 180° from its position in FGG and WGG. Thus, instead of a N-H⋯π interaction a non-conventional O⋯H-C hydrogen bond⁴⁶ is formed (the distance between the hydrogen and the oxygen is 2.49 Å) while the Ar-Pb interaction is still present. The energy of the Ar-Bb interaction in YGG is -16.4 kJ·mol^-1 which is similar to that in FGG (-14.5 kJ·mol^-1). The energy of an O⋯H-C hydrogen bond is about half that of a N-H⋯π interaction.^46a Since another O⋯H-C interaction occurs between one of the C₄^α hydrogens and the hydroxyl oxygen in YGG (the O⋯H distance is 3.04 Å), the stronger N-H⋯π interaction in FGG is replaced by two O⋯H-C interactions in YGG, resulting in similar total interaction energies. Figure 2d shows the superimposed conformers. Due to the rotation of Pb2 of conformer 7 of YGG, the trace of the C^α atoms of YGG is different from those of FGG and WGG. However, the χ₁₂ angle of the YGG conformer (-89.2°) is also considerably different from those of FGG (-71.3°) and WGG (-71.8°) so that the curve traced by the C^α atoms is parallel to the aromatic side chain in all the three conformers.

Backbone-backbone interactions

The Bb-Bb intramolecular interaction energies are shown in Table 2. Most frequent and strongest Bb-Bb interactions are H-bonds which occur between the carbonyl-oxygen of residue i and amide-hydrogen of residue i+3 (C_i=O⋯H-N_i+3) assembling a 10-membered pseudo ring. The predominance of the β-type turn structures is in agreement with the conformational preferences of the N-Ac-Phe-Gly-Gly-NH₂ peptide chain shown by the spectroscopic studies of Mons and associates.^16,25 The energy of the H-bonds is between -16.5 kJ·mol^-1 and 21.2 kJ·mol^-1 with an average value of 19.4 kJ·mol^-1 which is similar to those observed or calculated by high level ab initio methods in biological structures.⁴⁴

Table 2.

Bb-Bb interaction energies (kJ·mol^-1)

	FGG			WGG			YGG
conformer	Pb0-Pb3†	Pb0-Pb2†	Pb1-Pb3†	Pb0-Pb3†	Pb0-Pb2†	Pb1-Pb3†	Pb0-Pb3†	Pb0-Pb2†	Pb1-Pb3†
0	-4.4	-18.5‡	-18.6	-3.0	-17.9	-19.7	-3.8	-18.1	-19.2
1	1.1	-20.3	-19.5	-0.8	-1.4	-19.7	-1.0	-21.1	-18.3
2	0.0	-20.6	-19.1	0.0	-20.1	-19.1	-3.1	-18.6	-19.1
3	-1.4	-20.9	-20.0	0.3	-3.7	-19.4	-2.7	-18.9	-19.8
4	-17.9	1.2	-2.2	-0.3	-0.6	-19.6	-5.2	-19.3	-19.2
5	-0.2	-1.5	-19.4	-6.8	-19.3	-19.9	-0.7	-21.1	-20.5
6	-1.5	-19.4	-2.9	-3.6	0.7	-19.3	-18.8§	-18.3§	-2.8
7	-1.8	-19.7	-2.9	-2.3	-19.4	-2.7	1.8	-3.2	-19.6
8	-1.2	-20.0	-3.5	-4.9	-3.1	-19.5	-0.4	-19.9	-16.5
9	1.2	-2.1	-18.3	-1.6	-21.2	-19.5	1.3	-21.2	-20.4
average	-2.6	-14.2	-12.6	-2.3	-10.6	-17.9	-3.3	-18.0	-17.5

^†the peptide bonds are modeled as acetamide (Figure 1b).

^‡interaction energies of H-bonds are shown in bold.

^§a bifurcated H-bond where the C₀ carbonyl oxygen is the acceptor atom and the N₃ and N₄ hydrogens are the donor atoms; a special fragmentation was used (Supplementary material, Figure 2S).

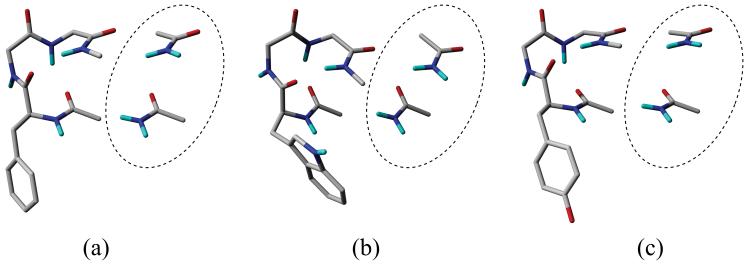
Nevertheless, several considerably strong weakly polar Bb-Bb interactions can be found between the zeroth and third peptide bonds (Pb0-Pb3). Figure 3 shows the conformers, which have strongest Pb0-Pb3 weakly polar Bb-Bb interactions. The strongest interaction energies are -4.4 kJ·mol^-1, -6.8 kJ·mol^-1 and -5.2 kJ·mol^-1, respectively, in FGG, WGG and YGG. It is remarkable that, in WGG, the Pb0-Pb2 H-bonds and Ar-Bb interactions compete; when a strong Ar-Bb interaction (Table 1, WGG total column) occurs then no Pb0-Pb2 H-bond can be found (Table 2, WGG Pb0-Pb2 column).

Figure 3.

Conformers with the strongest weakly polar Bb-Bb interactions; (a) conformer 0 of FGG, (b) conformer 5 of WGG, (c) conformer 4 of YGG. The appropriate acetamide models bordered by dashed ellipses were used to calculate the Bb-Bb interaction energies.

Decomposition of the intramolecular interaction energies

Table 3 shows the weakly polar, H-bonding and the total intramolecular interaction energies in the tripeptides. It can be seen that the average contribution of weakly polar interactions in FGG, WGG and YGG are 15%, 34% and 9%, respectively. Furthermore, in conformer 5 of FGG and conformer 7 of YGG the weakly polar contribution approaches that of the H-bonding. In both cases, 46% of the total intramolecular interaction energy comes from weakly polar interactions. Moreover, in several WGG conformers, the weakly polar interactions are the main source of stabilization (conformer 1, 4 and 8). In the most prominent case (conformer 1 of WGG) weakly polar interactions are responsible for 62% of the total intramolecular interaction energy.

Table 3.

Intramolecular interaction energies (kJ·mol^-1) in FGG, WGG and YGG

	FGG			WGG			YGG
conformer	wp†	H-bond	Total	wp†	H-bond	Total	wp†	H-bond	Total
0	-4.2	-37.1	-41.3	-26.6	-37.6	-64.2	-4.3	-37.3	-41.5
1	-4.1	-39.8	-43.9	-32.3	-19.7	-52.0	-3.8	-39.4	-43.3
2	-1.2	-39.7	-40.9	-2.8	-39.2	-41.9	-6.0	-37.7	-43.7
3	1.4	-41.0	-39.5	-14.9	-19.4	-34.3	-4.0	-38.7	-42.7
4	-3.6	-37.5‡	-41.1	-21.9	-19.6	-41.5	-4.4	-38.5	-42.9
5	-16.2	-19.4	-35.6	1.2	-39.2	-38.1	3.0	-41.7	-38.7
6	-9.4	-19.4	-28.7	-14.7	-19.3	-34.0	-3.7	-37.2§	-40.9
7	-5.3	-19.7	-25.0	-10.7	-19.4	-30.1	-16.5	-19.6	-36.1
8	-4.9	-20.0	-24.9	-19.9	-19.5	-39.4	0.5	-36.4	-35.9
9	-5.7	-18.3	-24.0	1.0	-40.7	-39.7	3.2	-41.6	-38.4
average	-5.3	-29.2	-34.5	-14.2	-27.4	-41.5	-3.6	-36.8	-40.4
	(15%)	(85%)	(100%)	(34%)	(66%)	(100%)	(9%)	(91%)	(100%)

^†weakly polar interaction energy

^‡includes the energy of a Pb1-Pb2 H-bond calculated by the rotation method (Supplementary material, Figure 3S).

^§includes the energy of a bifurcated H-bond calculated by a special fragmentation (Supplementary material, Figure 2S).

Weakly polar interactions also contribute to the stability of the global minima (Figure 4a, b and c) of the peptides. The backbones have the same fold (Figure 4d) and all global minima are stabilized by two H-bonds, which have almost the same strength; 37.1 kJ·mol^-1, 37.6 kJ·mol^-1 and 37.3 kJ·mol^-1, respectively, in FGG, WGG and YGG. weakly polar contributions are -4.2 kJ·mol^-1, -26.6 kJ·mol^-1 and -4.3 kJ·mol^-1, respectively, in FGG, WGG and YGG (Table 3). A remarkable difference is that in FGG and YGG, the aromatic side chain interacts with the N-terminal region, while in WGG it interacts with the C-terminal region (Figure 4a, b and c). Consequently, the χ₁₁ angles are similar in FGG and YGG, respectively, -59.5° and -63.1°, but they substantially differ from that in WGG; -178.0°. In FGG and YGG, the interaction between the aromatic ring and the N-terminal region is an N-H⋯π interaction. The distance between the N₁ hydrogen and the centroid of the aromatic ring is 3.40 Å and 3.47 Å, respectively, in FGG and YGG. The energies of these N-H⋯π interactions are close, -4.2 kJ·mol^-1 and -4.3 kJ·mol^-1 in FGG and YGG, respectively; they are about 10% of the total stabilization energy. In WGG the interaction with the larger C-terminal region includes an Ar-Pb1 and a C-H⋯π interaction; the distance between the midpoint of the C₁-N₂ bond and the centroid of the indolyl-ring is 3.94 Å and the distance between the closest C₂^α hydrogen and the centroid of the benzo-ring is 4.03 Å. The two interactions result in a considerably larger weakly polar interaction energy, -26.6 kJ·mol^-1, which accounts for 41% of the total stabilization energy of the WGG global minimum.

Figure 4.

Global minimum conformers; (a) FGG, (b) WGG, (c) YGG and (d) the superimposed global minima (the backbone and C_β atoms are superimposed). H-bonds are depicted as dashed yellow tubes; aliphatic hydrogens are not shown.

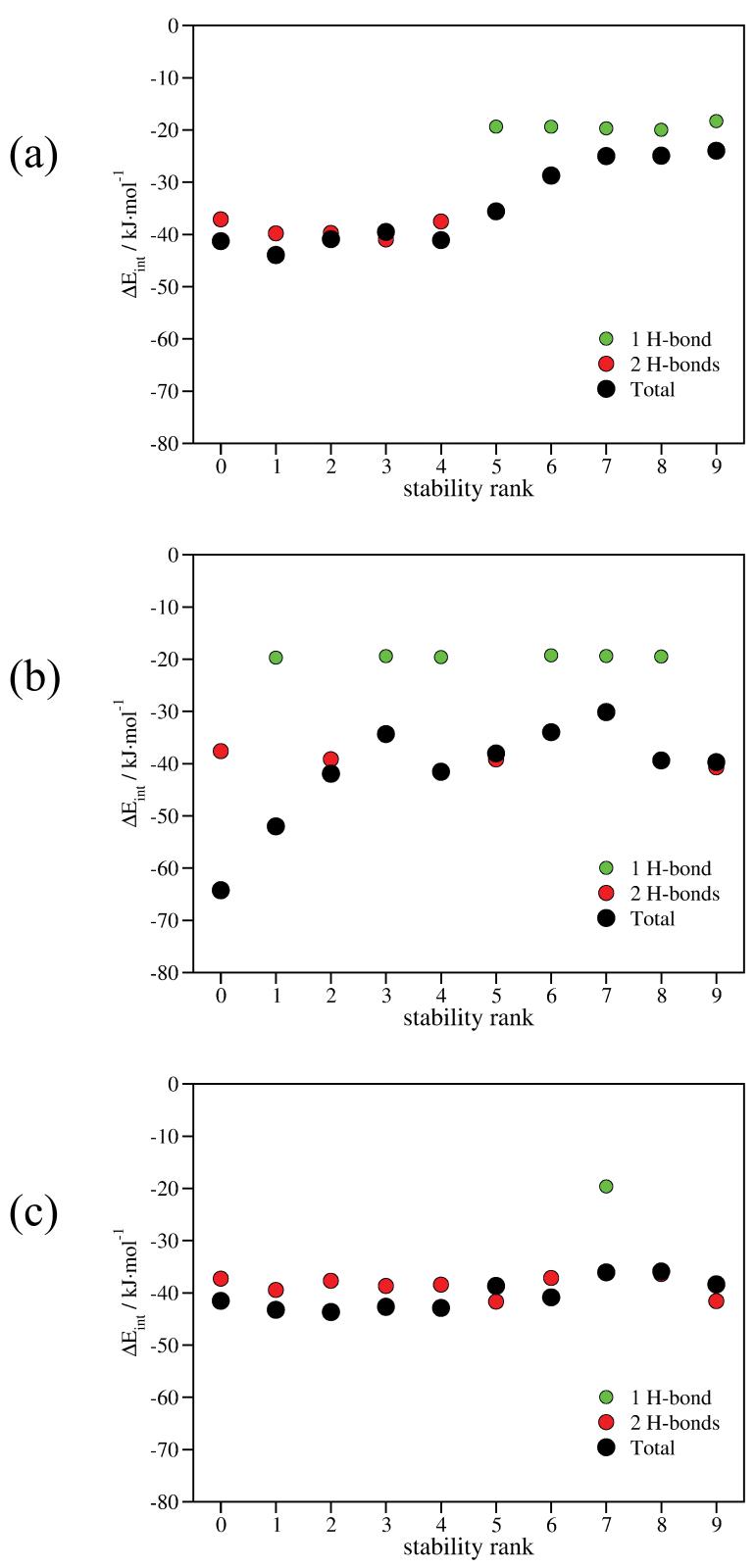
The intramolecular interaction energies of the individual conformers as a function of their stability rank are depicted in Figure 5. In FGG, the five most stable conformers contain two H-bonds, while the less stable ones contain one H-bond (Figure 5a, red and green circles). The contributions of H-bonds are fairly constant: 1 H-bond, ca. 20 kJ·mol^-1; 2 H-bonds, ca. 40 kJ·mol^-1. A more smooth, nearly monotone increasing curve can be obtained if the weakly polar interactions are also included (Figure 5a, black circles).

Figure 5.

The intramolecular interaction energies as a function of the stability rank of the conformers. (a) FGG, (b) WGG, (c) YGG. Green circles designate the H-bonding energies of conformers with 1 H-bond; red circles designate the H-bonding energies of conformers with 2 H-bonds; black circles designate the total (H-bonding + weakly polar) intramolecular interaction energies of the conformers.

It is clear that the relative stability of the WGG conformers can not be explained on the basis of the number or energies of H-bonds only (Figure 5b, red and green circles). The global minimum and the third, the sixth, the tenth most stable conformers include two H-bonds, while the others include just one H-bond. When weakly polar contributions are taken into account, a much better correlation can be obtained between the relative stability of the conformers and the magnitude of the intramolecular interaction energies (Figure 5b, black circles).

In YGG, nine of the ten most stable conformers include two H-bonds (Figure 5c, red circles). Nevertheless, the presence of conformer 7 with 1 H-bond can not be justified without weakly polar interactions. Although the role of weakly polar interactions is less important here, a better correlation can be obtained if they are also considered.

CONCLUSIONS

Ar-Bb, Bb-Bb weakly polar interactions together with H-bonds play a crucial role in the stabilization of the conformations of the investigated tripeptide models. The global minima are stabilized by H-bonds and Ar-Bb interactions. The backbones of the global minima have the same fold and H-bonding structure but due to the different weakly polar interactions the position of the side chain of Trp is substantially different from that of Phe and Tyr. In conformers with the strongest weakly polar interactions, the peptide backbone is parallel with the plane of the aromatic side chain. On average, 15%, 34% and 9% of the total stabilization energies of the FGG, WGG and YGG conformers, respectively, come from weakly polar interactions.

The energetics of weakly polar interactions in tripeptide models, investigated here, together with the common occurrence of these interactions in proteins clearly indicate that weakly polar interactions can make an important contribution to protein structure and function.

APPENDIX

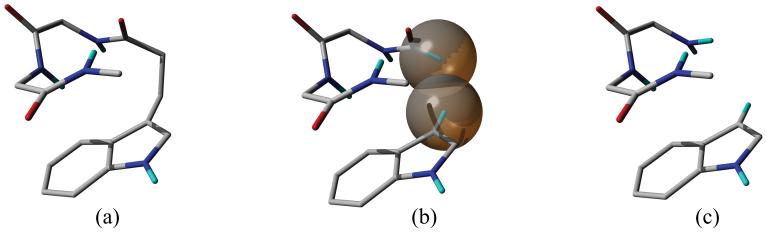
Both symmetry adapted perturbation theory (SAPT) and the so called supermolecular approach can be used to to calculate the energies of intermolecular interactions.⁴⁷ The supermolecular approach, in which the energy of interaction is obtained as the difference between the total energy of the complex and its constituents, is computationally more practical allowing the studies of larger systems. The central problem of the supermolecular approach is the introduction of the basis set superposition error (BSSE), which is the natural consequence of the incompleteness of the applied basis set. Nevertheless, the counterpoise (CP) procedure of Boys and Bernardi can be used to correct the BSSE.⁴¹ To use the supermolecular approach in calculating the energies of intramolecular interactions the molecule must be fragmented by breaking chemical bonds, removing original and introducing new saturating atoms. If the interacting parts of the molecule are separated by only a few atoms then it is possible that either (i) atoms, which have a substantial impact on the electronic structure, need to be removed (Figure 6c) or (ii) by retaining them, the saturating atoms will induce false repulsions (Figure 6b).

Figure 6.

The supermolecular approach; (a) the intact molecule, (b) the fragmented molecule after the removal of two CH₂ groups (the spheres represent the van der Waals surface of the saturating hydrogens), (c) the fragmented molecule after the removal of two CH₂ and a C=O group.

The rotation method (RM) was developed to avoid unphysical fragmentations.¹³,⁴⁰ In RM, the energy of an intramolecular interaction is approximated as the difference between the energies of the original conformation and a suitable reference conformation. The reference conformation in which one of the interacting groups is rotated into a non-interacting position differs in only one torsional angle from the original conformation.

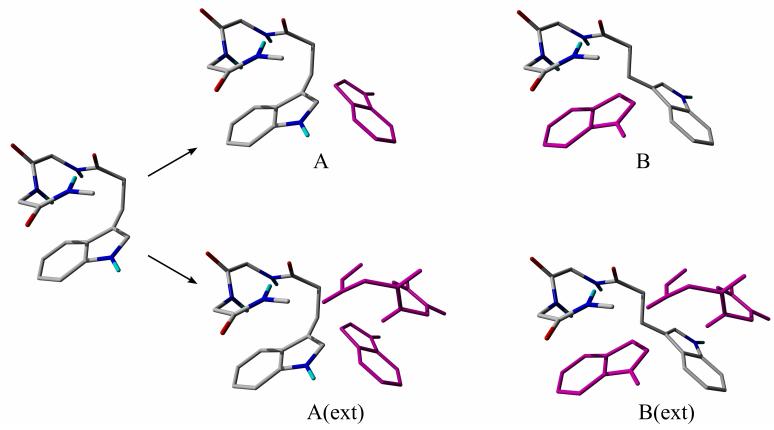
In its original formulation, to define the reference conformation, the smaller of the interacting groups was rotated and its basis functions were retained as ghost functions (Figure 7).¹³ However, it was proved that this version underestimates the BSSE and consequently overestimates the interaction energy.⁴⁸ The extended RM was developed to correct this deficiency.⁴⁰ In the extended RM, the basis functions of the larger group are also rotated to define ghost basis functions (Figure 7).

Figure 7.

The variants of the rotation method; ghost functions are depicted in magenta. Conformations A and A(ext) are the original structures with an Ar-Bb interaction, B and B(ext) are the reference structures. In the original and the extended version of the rotation method the energy of interaction is calculated as E_A-E_B and E_A(ext)-E_B(ext), respectively. E_X is the total energy of the appropriate molecular system shown in the figure.

An obvious drawback of RM is that if the studied system is too “crowded” then a non-interacting reference conformation can hardly be created. Nevertheless, this shortcoming may be avoided by removing the molecular parts which do not affect the interacting groups. Another drawback of it is that due to the increased number of basis function computationally is more demanding than the appropriate supermolecular approach with fragmentation.

It was demonstrated that the interaction energies derived from the extended rotation method are in agreement with those obtained with the appropriate supermolecular approach.⁴⁰ Thus, when the interacting groups in a molecule are too close, the rotation method is recommended for calculating the intramolecular interaction energies. Nevertheless, the supermolecular approach with fragmentation is always preferred to the rotation method unless it generates artificial interactions.