Abstract
Cardiac alternans, a beat-to-beat alternation in action potential duration (at the cellular level) or in ECG morphology (at the whole heart level), is a marker of ventricular fibrillation, a fatal heart rhythm that kills hundreds of thousands of people in the US each year. Investigating cardiac alternans may lead to a better understanding of the mechanisms of cardiac arrhythmias and eventually better algorithms for the prediction and prevention of such dreadful diseases. In paced cardiac tissue, alternans develops under increasingly shorter pacing period. Existing experimental and theoretical studies adopt the assumption that alternans in homogeneous cardiac tissue is exclusively determined by the pacing period. In contrast, we find that, when calcium-driven alternans develops in cardiac fibers, it may take different spatiotemporal patterns depending on the pacing history. Because there coexist multiple alternans solutions for a given pacing period, the alternans pattern on a fiber becomes unpredictable. Using numerical simulation and theoretical analysis, we show that the coexistence of multiple alternans patterns is induced by the interaction between electrotonic coupling and an instability in calcium cycling.
I. INTRODUCTION
Sudden cardiac death, attributable to unexpected ventricular arrhythmias, is one of the leading causes of death in the US and kills over 300,000 Americans each year [1]. The induction and maintenance of ventricular arrhythmias has been linked to single-cell dynamics [2, 3]. In response to an electrical stimulus, cardiac cells fire an action potential [4], which consists of a rapid depolarization of the transmembrane voltage (Vm) followed by a much slower repolarization process before returning to the resting value (Fig. 1). The time interval during which the voltage is elevated is called the action potential duration (APD). The time between the end of an APD and the beginning of the next one is called the diastolic interval (DI). The time interval between two consecutive stimuli is called the basic cycle length (BCL). When the pacing rate is slow, a periodic train of electrical stimuli produces a phase-locked steady-state response, where each stimulus gives rise to an identical action potential (1:1 pattern). When the pacing rate becomes sufficiently fast, the 1:1 pattern may be replaced by a 2:2 pattern, so-called electrical alternans [5, 6], where the APD alternates between short and long values. Recent experiments have established a causal link between alternans and the risk for ventricular arrhythmias [7–9]. Therefore, understanding mechanism of alternans is a crucial step in detection and prevention of fatal arrhythmias.
FIG. 1.
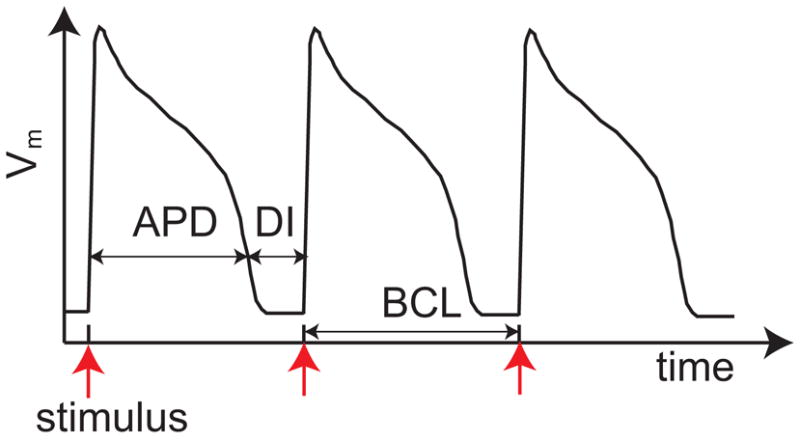
Schematic action potential showing the response of the transmembrane voltage to periodic electrical stimuli.
Cellular mechanisms of alternans have been much studied. Summaries on this topic can be found in recent review articles by Shiferaw et al. [10] and Weiss et al. [11]. At the cellular level, cardiac dynamics involves bidirectional coupling between membrane voltage (Vm) dynamics and intracellular calcium (Cain) cycling. During an action potential, the elevation of Vm activates L-type Ca currents ICa to invoke the elevation of [Cain], which in turn triggers Ca release from the sarcoplasmic reticulum (SR), a procedure known as calcium-induced-calcium release (CICR) [12]. The Vm → Cain coupling satisfies graded release, where a larger DI leads to an increase in the Ca release at the following beat since it allows more time for L-type Ca channels to recover. On the other hand, Ca release from the SR affects the APD in two folds: to curtail the APD by enhancing the inactivation of L-type Ca currents ICa; and to prolong the APD by intensifying Na+/Ca2+ exchange currents INaCa. Therefore, depending on the relative contributions of ICa and INaCa, an increase in Ca release may either shorten the APD (negative Cain → Vm coupling) or lengthen the APD (positive Cain → Vm coupling) [13–15]. There exist two main cellular mechanisms of alternans. Firstly, alternans may be attributed to steep APD restitution [5], which is due to a period-doubling instability in the Vm dynamics. In this case, Cain transient alternans, as a slave variable, is induced because Vm regulates [Cain] via the L-type Ca currents and the sodium-calcium exchange currents. Secondly, alternans may be caused by a period-doubling instability in Cain cycling, which is associated with a steep relationship between the sarcoplasm reticulum (SR) release and SR load [16, 17]. In this case, APD alternans is a secondary effect via Cain → Vm coupling. For ease of reference, we call the first mechanism APD-driven alternans and the second Ca-driven alternans. Interestingly, APD and Cain transient alternans can be electromechanically (E/M) in phase or out of phase [18, 19]. In E/M in-phase alternans, a long-short-long APD pattern corresponds to a large-small-large [Cain] pattern, See Fig. 2 (a). In contrast, in E/M out-of-phase alternans, a long-short-long APD pattern corresponds to a small-large-small [Cain] pattern, See Fig. 2 (b). When alternans happens in isolated cells, the bidirectional coupling between APD and Cain transient determines the relative phase of APD and Cain transient alternans. In particular, APD-driven alternans always leads to E/M in-phase alternans whereas Ca-driven alternans is E/M in phase for positive Cain → Vm coupling and out of phase for negative Cain → Vm coupling [13–15].
FIG. 2.
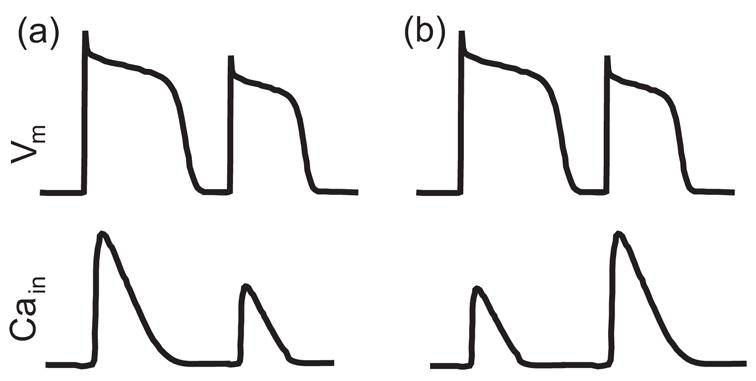
Schematic illustration of electromechanically in-phase (a) and out-of-phase (b) alternans.
The mechanism of alternans in multicellular tissue is more complicated since it involves electrotonic coupling and conduction velocity restitution. Of particular interest is a phenomenon called spatially discordant alternans, in which different regions of the tissue alternate out of phase. Discordant alternans is arrhythmogenic because it forms a dynamically heterogeneous substrate that may promote wave break and reentry [2, 3]. To study the spatiotemporal patterns of alternans, Echebarria and Karma derived amplitude equations that are based on APD-driven alternans [20, 21]. These amplitude equations not only are capable of quantitative predictions but also provide insightful understandings on the arrhythmogenic patterns. In a recent article, Dai and Schaeffer [22] analytically computed the linear spectrum of Echebarria and Karma’s amplitude equations for the cases of small dispersion and long fibers.
Spatial patterns of alternans have been investigated in experiments [7, 23–25]. Recently, Aistrup et al. [26] used single-photon laser-scanning confocal microscopy to measure Ca signaling in individual myocytes. They found that Ca alternans is spatially synchronized at low pacing rates whereas dyssynchronous patterns, where a number of cells are out of phase with adjoining cells, arise when the pacing rate increases. Aistrup et al. also observed subcellular alternans at fast pacing, where Ca alternans is spatially dyssynchronous within a cell. Using simulations of 1-d homogeneous tissue, Sato et al. [15] found that, in cardiac fibers with negative Ca→Vm coupling, Ca alternans reverses phase over a length scale of one cell whereas, in fibers with positive Ca→Vm coupling, Ca alternans changes phase over a much larger length scale. They interpreted this difference by showing that negative Ca→Vm coupling tends to desynchronize two coupled cells while positive Ca→Vm coupling tends to synchronize the coupled cells.
Motivated by the aforementioned experimental and theoretical work, this paper aims to explore spatial patterns of cardiac alternans. Through extensive numerical simulations, we find that complex spatial patterns of Ca alternans with phase reversals in adjacent cells can happen in homogeneous fibers with both negative and positive Ca→Vm couplings. Most surprisingly, we find that the spatiotemporal pattern of cardiac alternans is not determined by the pacing period alone. Specifically, when calcium-driven alternans develops in multicellular tissue, there coexist multiple spatiotemporal patterns of alternans regardless of the length of the fiber, the junctional diffusion of Ca, and the type of Ca→Vm coupling. We further investigate the mechanism that leads to the coexistence of multiple alternans solutions. Our analysis shows that multiple alternans solutions are induced because of the interaction between electrotonic coupling and an instability in Cain cycling.
II. MODEL DESCRIPTION
A. Membrane dynamics
We adopt a model of membrane dynamics that combines the calcium dynamics model developed by Shiferaw et al. [27] and the canine ionic model by Fox et al. [28]. In the following, we will refer to this model as the Shiferaw-Fox model. Detailed formulations of the model can be found in [27, 29]. The Shiferaw-Fox model has adopted two sets of parameters in the calcium dynamics to account for negative and positive Cain →Vm couplings. Besides the phase difference, the two sets of parameters also produce alternans at different values of BCL. Using Shiferaw’s default parameters, we find alternans happens at BCL ≈ 401 ms for negative Cain → Vm coupling and BCL ≈ 323 ms for positive Cain → Vm coupling. Fig. 3 shows the bifurcation diagrams in APD and peak value of [Cain] for negative Cain → Vm coupling. The bifurcation diagrams for positive Cain → Vm coupling are similar and thus are not shown here. We note that, in simulations of isolated cells using the Shiferaw-Fox model, alternans solutions do not depend on the initial condition nor on the pacing history. However, as we will show in the following, fibers based on the Shiferaw-Fox model possess multiple alternans solutions, which are sensitive to the initial condition and the pacing protocol.
FIG. 3.
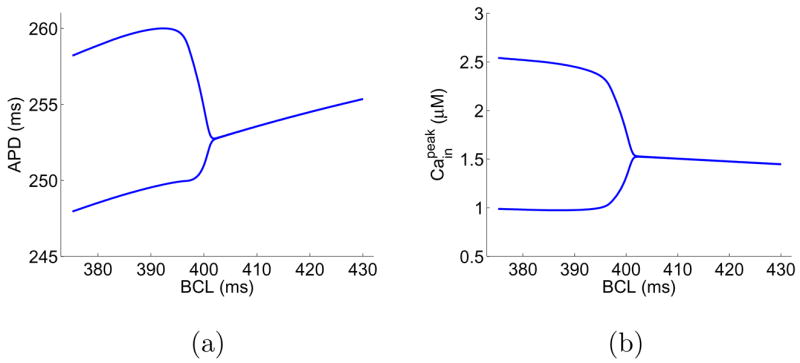
Bifurcation diagrams of an isolated cell using the Shiferaw-Fox model.
B. Simulation of fiber models
We study paced, homogeneous fibers, which can be modeled using the cable equation:
| (1) |
where υ represents Vm, D = 5 ×10−4 cm2/ms represents the effective diffusion coefficient of υ in the fiber, Cm = 1 μF/cm2 represents the transmembrane capacitance, Iion is the total ionic current, and Iext represents the external current stimulus. The ionic current Iion is computed using the Shiferaw-Fox model. The current stimulus has duration 1 ms and amplitude 80 μA/μF. This paper studies fibers of various lengths. For two coupled cells, we pace the left cell. For longer fibers, we pace the leftmost few cells to ensure propagation. For example, the leftmost 5 cells are paced in simulating a fiber of 100 cells. The cable equation (1) is solved using the finite difference method with a space step of Δx = 0.015 cm and time step of Δt = 0.1 ms. No-flux boundary conditions are imposed at both ends of the fiber [27, 29].
C. Pacing protocols
To study the onset and development of alternans, we pace both single cells and fibers of various lengths with several pacing protocols, which are briefly described below.
In the downsweep protocol [30], the cell/fiber is paced periodically with period BCL until it reaches steady state. Then, the pacing period is reduced by ΔB and the procedure is repeated many times. Note that this protocol is also known as dynamic pacing protocol [31].
The perturbed downsweep protocol, proposed by Kalb et al. [30], can be regarded as a perturbation to the downsweep protocol. At each pacing period BCL, the cell/fiber is first paced N beats to reach steady state. Then, a longer pacing period is applied at the N+1st pacing, after which the original pacing period is applied for 10 beats to allow the tissue to recover its previous steady state. Next, a shorter pacing period is applied and followed by 10 beats of the original pacing period. Finally, the pacing period is reduced by ΔB and the procedure is repeated.
To explore the possibility for multiple alternans solutions, we set up certain initial condition and pace the tissue with period BCL to reach steady state, a process we call direct pacing.
To explore the origin of an alternans pattern, we use the upsweep protocol [30], which is a reversed downsweep protocol.
III. SPATIOTEMPORAL PATTERNS OF ALTERNANS: NUMERICAL EXPLORATION
We simulate fibers using the Shiferaw-Fox model with both negative and positive Cain → Vm couplings under various conditions. Default parameters in Shiferaw’s code [29] are used unless otherwise specified. Despite quantitatively significant differences, we find both types of couplings lead to the coexistence of multiple alternans solutions. For clarity, we start with the results for negative Cain → Vm coupling and defer the results for positive Cain → Vm coupling in a later subsection.
A. Coexistence of multiple solutions
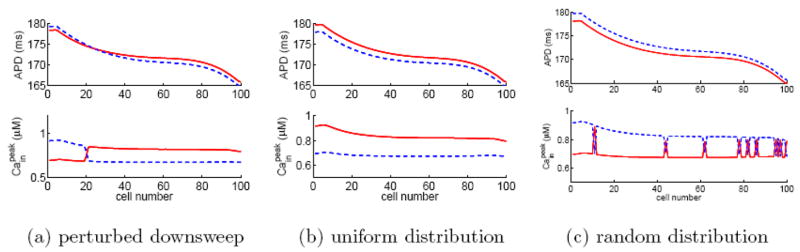
We first consider a homogeneous fiber of 100 cells with negative Cain → Vm coupling. To our surprise, numerical simulations show that when the fiber is in alternans, there coexist multiple solutions for a given pacing period. For example, Fig. 4 shows 6 selected solutions of alternans for the fiber paced at BCL=375 ms. Here, the steady-state solutions in panels (a–c) are obtained using the downsweep protocol with step size ΔB=1 ms, 2 ms, and 25 ms, respectively. The pacing protocols are started from BCL=500 ms in (a) and (c) and from BCL=499 ms in (b). We note that the solution of a downsweep protocol is not influenced by the initial condition at the starting, long BCL; instead, the solution is sensitive to the step size ΔB. The steady-state solutions in panels (d–f) are obtained by pacing the fiber at BCL=375 ms with prescribed initial conditions for 200 beats, the so-called direct pacing. The initial condition of the fiber in panel (d) is uniform, i.e., all cells are assigned the same resting voltage, gating variables, and ionic concentrations. The initial condition in panel (e) is same as that in (d) except that [Cain] is assigned to be 0.54 μM for the first 35 cells and 0.66 μM for the remaining cells. Interestingly, this initial condition leads to a steady-state [Cain] pattern, which, besides the phase reversal between cells 35 and 36, has another phase reversal between cells 11 and 12. The initial condition in panel (f) is the same as that in (d) except that [Cain] is randomly assigned for cells on the fiber according to a uniform distribution in the interval of 0.45 μM to 0.75 μM. In all protocols, we pace the fiber for 200 beats at each BCL and plot the last 10 beats at BCL=375 ms. The simulation results in Fig. 4 demonstrate that the alternans on a fiber is not solely determined by the pacing period. Instead, the solution is sensitive to the pacing protocol and the initial condition. It is worth noting that, besides the solutions shown in Fig. 4, there exist many other solution patterns. In particular, there exist many complex patterns similar to Fig. 4 (f). In the following, we will verify whether the phenomenon is influenced by the length of the fiber, junctional Ca diffusion, or Cain →Vm coupling.
FIG. 4.
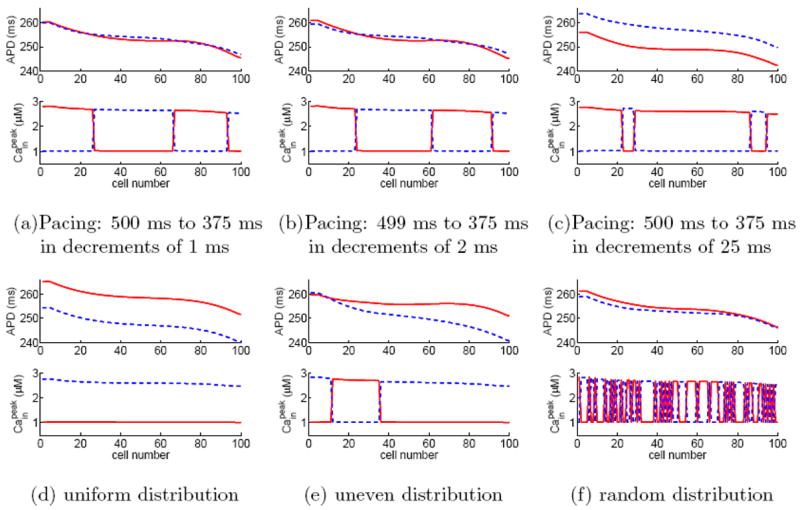
(Color online) Six selected alternans solutions for a homogeneous fiber of 100 cells with negative Ca→Vm coupling when paced at BCL=375 ms. Panels (a)–(c) are obtained using down-sweep protocols from 500 ms to 375 ms in steps of 1, 2, and 25 ms, respectively. Panels (d)–(f) are obtained by directly pacing at BCL=375 ms with different initial distributions in Cain, see text for details. To verify if a solution reaches steady state, we plot the last 10 beats of the simulation results, where odd beats are represented by red solid lines and even beats by blue dashed lines. The coincidence of all odd beats and that of all even beats confirm that the solution is indeed in steady state.
B. Influence of the length of the fiber
We repeat the numerical simulations for fibers of various lengths and find that the phenomenon persists regardless of the length of the fiber. Probably, the most illuminating example is a “fiber” of two coupled cells. Denoting the voltage at cell 1 as V1 and that at cell 2 as V2, we can simulate the two coupled cells by integrating the following equations [32]
| (2) |
| (3) |
Note that only cell 1 is paced in this case. Using various pacing protocols and initial conditions, we find the two coupled cells can have spatially desynchronized (Fig. 5 (a)) and synchronized (Fig. 5 (b)) alternans. Note that in the desynchronized pattern, APD in both cells exhibit a beat-to-beat variation of a few hundredth of ms, which is impossible to observe in experiments.
FIG. 5.
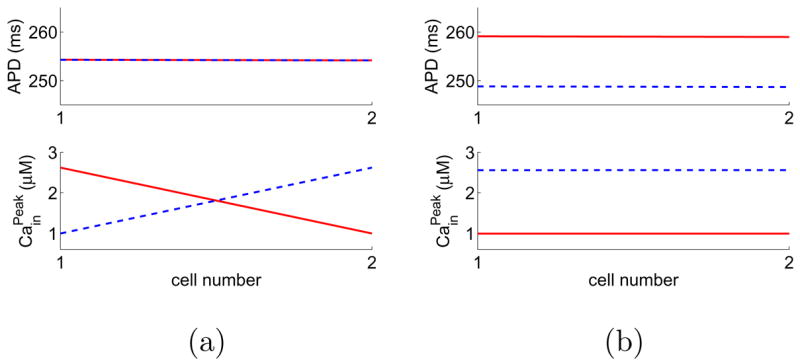
(Color online) A “fiber” of two cells with negative Ca→Vm coupling can have both spatially desynchronized and synchronized alternans solutions. The pacing period is 375 ms. The last 10 beats of the steady-state solutions are plotted, where odd beats are represented by red solid lines and even beats by blue dashed lines.
C. Influence of junctional Ca diffusion
The original Shiferaw-Fox model does not include the diffusion of Ca between neighboring cells [33]. Physiologically, there exists gap junctional Ca diffusion although its magnitude is several orders lower than voltage diffusion [34, 35] and thus is typically neglected in cardiac modeling. One may wonder whether including junctional Ca diffusion will affect the simulation results. To answer this question, we introduce junctional Ca diffusion to the Shiferaw-Fox model by modifying the equation governing [Cain] as follows [32]:
| (4) |
where Ci represents [Cain], Dc = 3 ×10−9 cm2/ms is the Ca diffusion coefficient [34, 35], Zc is the valence of Ca, F is the Faraday constant, R is the gas constant, T = 300 K is the temperature, and Ic represents the Cain currents in the Shiferaw-Fox model. With this modification, we repeat the numerical simulations and find there still exist multiple alternans solutions.
For example, Fig. 6 shows three selected solutions for a homogeneous fiber of 100 cells paced at BCL=375 ms. Figures 6 (a) and (b) are obtained using downsweep protocols same as those in Fig. 4 (b) and (c), respectively. Figure 6 (c) is obtained using a random initial distribution in [Cain] (cf. Fig. 4 (f)). Comparing results in Figs. 4 and 6 shows that the coexistence of multiple solutions is not influenced by junctional Ca diffusion.
FIG. 6.
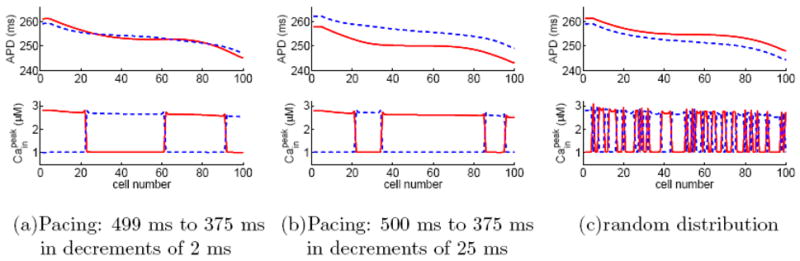
(Color online) Three selected alternans solutions for a homogeneous fiber model, where junctional Ca diffusion is included. The cells have negative Ca→Vm coupling and the pacing period is 375 ms. Panels (a) and (b) are obtained using downsweep protocols and panel (c) is obtained by direct pacing with random initial distribution of Cain. The last 10 beats of the steady-state solutions are plotted, where odd beats are represented by red solid lines and even beats by blue dashed lines.
D. Influence of Cain →Vm coupling
Simulations show that fibers with positive Cain →Vm coupling also possess multiple alternans solutions. For example, Fig. 7 shows 3 selected solutions for a homogeneous fiber of 100 cells with positive Cain →Vm coupling, paced at BCL=300 ms. Figure 7 (a) is obtained via a perturbed downsweep protocol, where the step size is ΔB=25 ms and a long and a short perturbations of ±20 ms are applied at each BCL, see section 2 for details of the perturbed downsweep protocol. Figures 7 (b) and (c) are obtained by directly pacing the cell at BCL=300 ms using a uniform and a random initial distributions in [Cain], respectively.
FIG. 7.
(Color online) Three selected alternans solution in a homogeneous fiber of 100 cells with positive Ca→Vm coupling. The pacing period is 300 ms in all panels. Panel (a) is obtained using a perturbed downsweep protocol. Panels (b) and (c) are obtained by direct pacing with with initial uniform distribution and random distribution of Cain, respectively. (See text for details.) The last 10 beats of the steady-state solutions are plotted: odd beats are red solid and even beats are blue dashed.
We simulate two coupled cells with positive Cain → Vm coupling and find that alternans can be both spatially synchronized and spatially desynchronized, see Fig. 8. In Figs. 5 and 8, values of APD are almost identical in the two cells because conduction time across a cell’s length is negligible. Thus, these examples indicate that the coexistence of multiple solutions does not depend on steep CV restitution. We note that, using a downsweep protocol with step size of 2 ms, Sato et al. [15] also studied alternans in two coupled cells. They observed the desynchronized solution for negative Cain → Vm coupling and the synchronized solution for positive Cain → Vm coupling. Using numerical simulation, Sato et al. showed that negative Cain → Vm coupling tends to desynchronize two coupled cells whereas positive Cain → Vm coupling tends to synchronize them. Thus, we hypothesize that the synchronized solution for negative Cain → Vm coupling and the desynchronized one for positive coupling are induced by electrotonic coupling, which will be verified in the next section.
FIG. 8.
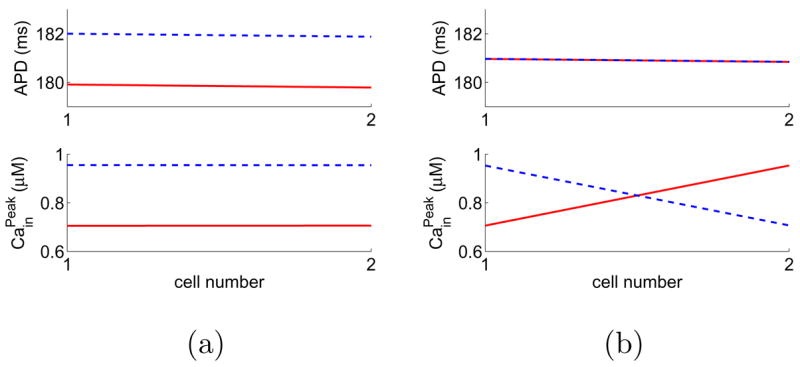
(Color online) A “fiber” of two cells with positive Ca→Vm coupling can have both spatially synchronized and desynchronized alternans solutions. The pacing period is BCL= 300 ms. The last 10 beats of the steady-state solutions are plotted: odd beats are red solid and even beats are blue dashed.
IV. ORIGIN OF THE INDETERMINACY
A. Numerically tracing an alternans solution
The coexistence of multiple alternans solutions in a fiber is surprising because the underlying cell’s model possesses a supercritical period-doubling bifurcation, describing a transition from a unique 1:1 solution to a unique alternans solution (Fig. 3). The transition to alternans in a fiber appears to be more complicated. First, when paced at sufficiently large values of BCL, a fiber has a single 1:1 solution, regardless of the initial condition. However, as shown in the previous section, the fiber can develop multiple patterns of alternans. Therefore, it is interesting to ask how different alternans patterns are related to one another and how they are connected to the 1:1 solution. To address these questions, we utilize the upsweep protocol to trace the “origins” of different alternans solutions. Starting at BCL=375 ms from a pattern in Fig. 4, we increase BCL by 1 ms every 200 beats until the alternans solution either changes to a different alternans pattern or becomes a 1:1 pattern. Then, we mark that value of BCL as the “starting” point for the studied alternans pattern. Under this protocol, each solution in Fig. 4 transforms into another alternans solution at a starting BCL shown in Table I. Specifically, pattern (a) “starts” at BCL=416 ms and patterns (b)-(f) start at BCL values between 402 and 405 ms. Further numerical simulations show that the fiber first undergoes alternans at BCL=425 ms. This is counterintuitive because, in the underlying cell’s model, the onset of alternans occurs at 401 ms (cf. Fig. 3). Since alternans solutions in the fiber can occur earlier than alternans in the single-cell model, we hypothesize that these solutions are induced from the interaction between cellular dynamics and electrotonic coupling (induced alternans). We further hypothesize that alternans may also result from the intrinsic instability mechanism that leads to alternans in the underlying cellular model (intrinsic alternans). Noticing that the spatially concordant alternans in pattern (d) starts at BCL=402 ms, near the onset of alternans in the single-cell model, we hypothesize the concordant alternans is a result of intrinsic alternans.
TABLE I.
Origins of the alternans patterns in Fig. 4.
| pattern | (a) | (b) | (c) | (d) | (e) | (f) |
| starting BCL (ms) | 416 | 405 | 404 | 402 | 403 | 404 |
Using upsweep protocols, we also trace the origins of the alternans in Fig. 5 for the two coupled cells. Numerical simulations show that the desynchronized solution in Fig. 5 (a) stops at BCL=405 ms and the synchronized solution in Fig. 5 (b) stops at BCL=401 ms. Moreover, we also find that different alternans solutions for fibers with positive Cain → Vm coupling stop at different values of BCL. Thus, the bifurcation structure for a fiber is much more complicated than that for a single cell. Moreover, the numerical results suggest that the multiple alternans patterns born from different bifurcations are due to the interaction between electrotonic coupling and instability in calcium cycling.
B. Bifurcation Mechanism
Shiferaw et al. showed that the bidirectional Vm/Ca coupling in the Shiferawox can be captured by a 2-d mapping model [13]. The work of Shiferaw et al. provides a theoretical framework for understanding various experimental observations including electromechanically in-phase/out-of-phase alternans and quasi-periodic oscillations of voltage and calcium. Here, we follow their approach and take a mapping model in the following form [36],
| (5) |
| (6) |
where An, Dn, and Cn represent the APD, DI, and peak [Cain] concentration of nth beat, respectively. By definition, it follows that Dn =BCL−An, see Fig. 1. Function f stands for the APD resitution. The second term in Eq. (5) accounts for the influence of [Cain] on APD. Negative Cain → Vm coupling corresponds to γ < 0 and positive coupling to γ > 0. Due to graded release, μ has to be positive [15]. Function g determines the relation between Ca concentrations in two consecutive beats.
Using map (5, 6), we will show how the interaction between electrotonic coupling and instability in calcium cycling leads to multiple alternans patterns in fibers. Since the analysis below does not depend on the forms of f and g, we do not specify their forms here. Instead we present numerical examples based on concrete forms of f and g in the Appendix. The numerical examples there show that fiber models based on the map (5, 6) are able to reproduce the phenomena observed in simulations of the Shiferaw-Fox model.
1. Bifurcation for single cells
Using a mapping model similar to (5,6), Shiferaw et al. [13] carried out a bifurcation analysis to show how different alternans solutions in single cells arise as a result of Vm/Ca coupling. Here, we briefly review that analysis, which serves as a starting point to understand bifurcation for fibers. To this end, consider a paced cell described by map (5,6). A 1:1 solution is a fixed point of the map and its stability is determined by the Jacobian matrix:
| (7) |
where f′ measures the slope of the APD restitution and g′ measures the slope of the [Cain] relation, and all derivatives are evaluated at the fixed point.
The strength of Vm/Ca coupling varies among species [13]. In this paper, we assume a weak coupling between Vm dynamics and Ca cycling, which allows easy analysis and yields insight on the instability mechanisms in cardiac cells as well as in fibers. To this end, we assume γμ ≪ f′, g′ in the following. Using a perturbation technique [37], we find the eigenvalues of J to first order in γμ are
| (8) |
Since γμ is small, one can see that a period-doubling bifurcation occurs if one of the slopes, f′ or g′, becomes sufficient large (compared to 1). Thus, if the bifurcation is caused by increasing in f′, we say the alternans is APD driven. On the other hand, it is called a Ca-driven alternans if the bifurcation is due to increasing in g′. For simplicity, if alternans is APD driven, we assume g′ remains small and will not induce dynamic instability for all physiologically interesting parameter regimes; and vice versa.
APD-driven alternans
In case of APD-driven alternans, it follows that f′ > g′. To first order in γμ, the unstable eigenvector is
| (9) |
which is in phase in APD and [Cain]. Therefore, APD-driven alternans is electromechanically in phase.
Calcium-driven alternans
In case of Ca-driven alternans, it follows that g′ > f′. To first order in γμ, the unstable eigenvector is
| (10) |
For positive Cain → Vm coupling, it follows that γ > 0 and thus alternans is electromechanically in phase. On the other hand, for negative Cain →Vm coupling, it follows that γ < 0 and thus alternans is electromechanically out of phase.
2. Bifurcation for two coupled cells
To understand the bifurcation mechanism for fibers, we start with the extreme case of two coupled cells. Denoting the locations of the cells by x1 and x2, we represent the APD, DI, and [Cain] of cell i for the nth beat as An (xi), Dn (xi), and Cn (xi), respectively. Following Fox et al. [38], we account for electrotonic coupling between the cells using weighted averaging:
| (11) |
| (12) |
| (13) |
| (14) |
where
| (15) |
and ρ(0) and ρ(1) are the weighting functions. Here, we have neglected the effect of dispersion due to conduction velocity restitution since the “fiber” is short and thus the influence of conduction restitution to APD is insignificant. On the time scale of one APD, Vm diffuses on a spatial scale of a few tens of cells [20]. Thus, the coupling in APD between two neighboring cells is strong. As a result, ρ(0) ≈ ρ(1) and ρ(0) + ρ(1) = 1. Therefore, we let ρ(0) = 1/2 + ε and ρ(1) = 1/2 − ε, where 0 < ε ≪ 1. For a 1:1 solution, the two cells have the same values of APD and [Cain]. Thus, the Jacobian matrix can be written as
| (16) |
where all derivatives are evaluated at the 1:1 solution.
Using perturbation theory [37], we find the eigenvalues to first order in γμ and ε are
| (17) |
Note that the first two eigenvalues are the same as those for the case of single cells (cf. Eq. 8). Thus, they are due to intrinsic membrane dynamics. The last two eigenvalues are induced by the electrotonic coupling as manifested by the small coupling parameter ε.
APD-driven alternans
For APD-driven alternans, the intrinsic bifurcation is the only mechanism to produce alternans. The corresponding eigenvector to first order in γμ and ε is
| (18) |
Thus, APD-driven alternans tends to be electro-mechanically in phase and spatially synchronized.
Calcium-driven alternans
For Ca-driven alternans, bifurcation can happen intrinsically when g′ + γμg′/(g′ − f′) = 1 (intrinsic bifurcation). Bifurcation can also be induced by electrotonic coupling when g′+ 2 ε γμ = 1 (induced bifurcation). To first order in γμ and ε, the eigenvector corresponding to the intrinsic bifurcation is
| (19) |
To first order in γμ and ε, the eigenvector corresponding to the induced bifurcation is
| (20) |
Therefore, while the intrinsic bifurcation gives birth to a spatially synchronized solution, the induced bifurcation leads to a spatially desynchronized pattern. And the electromechanical phase is determined by the sign of γ.
Subtracting the intrinsic eigenvalue from the induced one yields γμ (g′(g′ − f′) − 2ε), which has the same sign as γ since g′ > f′(Ca-driven alternans) and μ > 0 (graded release). If γ < 0, the induced eigenvalue is more negative; therefore, the spatially desynchronized pattern, born from the induced bifurcation, occurs before the spatially synchronized pattern, born from the intrinsic bifurcation. On the other hand, if γ > 0, the intrinsic eigenvalue is more negative; therefore, the spatially desynchronized pattern occurs after the spatially synchronized pattern. The analysis is in agreement with numerical simulations of the Shiferaw-Fox model using upsweep protocols. Therefore, when BCL is continuously decreased from a 1:1 solution, it is more likely to observe the spatially synchronized solution for the positive Cain →Vm coupling case whereas it is more likely to observe spatially desynchronized pattern in the negative Cain →Vm coupling case. This is probably why Sato et al. observed different solution patterns for negative and positive Cain →Vm couplings in their downsweep simulations.
The conclusion based on two coupled cells may be extended to short fibers; however, we expect long fibers have more complicated phenomena than presented here. In particular, because the dispersion effect may play an important role in long fibers as shown by Echebarria and Karma [20, 21] and by Dai and Schaeffer [22]. Nevertheless, the simple case sheds light on the effect of electrotonic coupling, the difference between APD and Ca-driven alternans, and the difference between negative and positive Cain →Vm couplings.
3. Understanding bifurcation for fibers
For Ca-driven alternans in fibers, we start with the extreme case of μ = 0. As can be seen from the cellular model (5,6), in this case, Cain dynamics becomes independent of Vm dynamics. Because Cain dynamics is not influenced by electrotonic coupling, when alternans develops in a fiber, cells can arbitrarily choose their phases in [Cain]. Depending on the initial conditions, Ca alternans on a fiber can take different spatial patterns. When μ is small but nonzero, [Cain] in different cells are weakly coupled due to feedback of Vm dynamics and electrotonic coupling. If this weak coupling does not suppress the coexistence of multiple solutions, the alternans pattern will become sensitive to initial conditions and pacing protocols. Under certain pacing protocols, Cain alternans on a fiber may possess a complex pattern with multiple phase reversals, as shown in Figs. 4 (f), 6 (c), and 7 (c). In these examples, the spatial patterns of APD are much less complex, which is because APD on the fiber is an averaging effect over many cells due to the fast diffusion of Vm [20, 21]. As a result of electrotonic coupling, different spatial patterns of Cain alternans may correspond to similar spatial patterns of APD. Moreover, as shown in simulations of the Shiferaw-Fox model (see Figs. 4, 6, and 7) and of the mapping model (see Fig. 10 in Appendix), spatial dyssynchrony in Cain alternans may induce spatially discordant APD alternans, which verifies the hypothesis of Aistrup et al. [26].
FIG. 10.
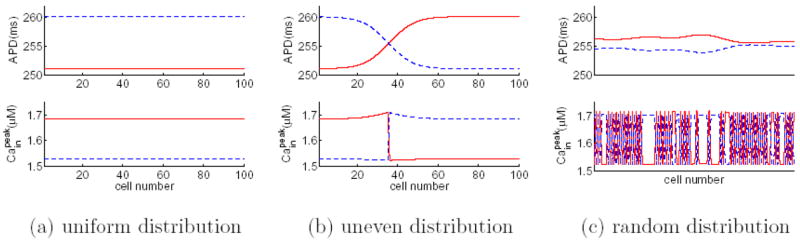
(Color online) Simulation of the coupled-maps model: three selected alternans solutions for a homogeneous fiber of 100 cells with negative Ca→Vm coupling. The pacing period is 375 ms in all panels. Panel (a) starts from a uniform initial distribution in Cain. Panel (b) starts from an initial condition, where Cain is set to be 1.5 μM in the first 35 cells and 1.7 μM in the remaining cells. Panel (c) starts from a random initial distribution in Ca. The last 10 beats of the steady-state solutions are plotted, where odd beats are represented by red solid lines and even beats by blue dashed lines.
V. SUMMARY AND DISCUSSION
Using numerical simulation and theoretical analysis, we have investigated spatiotemporal patterns of calcium-driven alternans. The main finding is that although alternans of an isolated cell is solely determined by the pacing period, the solution in a fiber is sensitive to pacing protocols and initial conditions. To the author’s knowledge, this is the first report on the coexistence of multiple alternans solutions for cardiac fibers. We have further verified that the coexistence of multiple alternans solutions is independent of the length of the fiber, junctional Ca diffusion, and the type of Cain →Vm coupling. Since multiple solutions also exist for fibers of as few as a couple of cells, the phenomenon does not require steep conduction velocity restitution. Another interesting observation is that complex patterns of Cain alternans with multiple phase reversals in neighboring cells may arise in a homogeneous fiber with both negative and positive Cain →Vm couplings. The simulation results also verify the hypothesis of Aistrup et al. that spatially desynchronized Ca signaling may lead to spatially discordant APD alternans [26].
We have also explored the bifurcation mechanism for the coexistence of multiple solutions. Numerical simulations and symbolic bifurcation analyses trace the onset of multiple alter-nans patterns to a number of bifurcations induced by the interaction between electrotonic coupling and an instability in calcium cycling. The bifurcation here bears similiarity to that of a ring model. For example, Courtmanche et al. [39] used the Beeler-Reuter model [40] to show that, when the length of the ring is reduced, there is an infinite-dimensional Hopf bifurcation, which gives birth to an infinite number of quasi-periodic solutions. Since the Beeler-Reuter model does not account for intracellular calcium cycling, it will be interesting to investigate how calcium-induced alternans propagates in a ring.
Simulations in this paper lead to another interesting observation—the onset of altrenans in a fiber does not occur at the same value of BCL as that in the underlying single-cell model, a phenomenon against the common wisdom. This counter-intuitive observation indicates that one can not directly relate behavior of fibers to that of single cell models. Another intriguing example about the differences between alternans in fibers and alternans in single cells is presented in the work of Cherry and Fenton [41], who analyzed two models of canine ventricular myocytes: the Fox-MchHarg-Gilmour (FMG) model [28] and the Hund-Rudy (HR) model [42]. Simulations of both models show that the bifurcation structures for fibers are different than those for the corresponding single cells (see Fig. 5 in [41]). Most interestingly, the HR 0d model (a single cell) shows alternans for BCL between 180 and 230 ms whereas the HR 1d model (a 1.25 cm-long fiber) does not undergo alternans for all values of BCL studied. Examples in [41] as well as examples in the current paper show that stability of a fiber may not be inferred from stability of the single cell model and vice versa.
Results in this paper are based on numerical simulations and hypothesized mapping models. Here, we describe potential experiments to verify the numerical observations. Probably, the simplest experiment would measure the spatial patterns of APD or Ca alternans on a fiber under various pacing protocols. It is well know that in vitro experiments suffer non-stationary drifts due to tissue dying. However, this is a slower process compared to typical experimental protocols, which last a few tens of minutes. Moreover, time constant of cardiac tissue is on the order of a few tens of seconds [30]. Therefore, it is possible to conduct multiple well-designed protocols in a time interval when tissue dynamics remains stationary. Other related experiments include the work of Fenton [43], where action potential is measured using microelectrode at a cell in a slice of paced dog epicardium tissue. Fenton showed that the onset and the form of alternans at the measured cell depend on the pacing history. While Fenton’s observations may be attributable to factors such as cardiac memory, the coexistence of multiple alternans patterns in cardiac tissue may be another contributing element.
As pointed out by Qu and Weiss [44], because Cain instability and Vm instability are always being regulated by each other, it remains a challenge to identify the sources of instabilities in cardiac experiments. Recent work by Sato et al. [45] and by Jordan and Christini [46] have developed theoretical criteria to assess the relative contributions of Vm and Cain dynamics in inducing cardiac alternans. The coexistence of multiple alternans patterns observed here may provide another possible criterion for this purpose. If the phenomenon was verified in experiments, it will raise questions in detection of alternans. New theories will also be needed to understand the development of different alternans patterns to ensure better prediction and control of spatiotemporal alternans.
Acknowledgments
The author would like to thank David Schaeffer, Daniel Gauthier, Wanda Krassowska, and Kevin Gonzales for their insightful comments. Particular thanks go to Yohannes Shiferaw for providing a Fortran code of the Shiferaw-Fox model and for answering many technical questions regarding the model. The author is also grateful to Daisuke Sato and Alain Karma for their useful discussions during the KITP miniprogram on cardiac dynamics. The author would like to thank the anonymous reviewers for their thoughtful comments and constructive suggestions. Support of the National Institutes of Health under grant 1R01-HL-72831 is gratefully acknowledged.
APPENDIX A: SIMULATION OF THE MAPPING MODEL
Here, we present numerical examples for single cells and for fibers using the mapping model (5, 6). For simulation purpose, we let f(Dn) = α(1 − β e−Dnτ and g (Cn) = −s (Cn − Ccrit) − Cmin. Inspired by the results of Shiferaw et al. (Fig. 10 (d) in [27]), we choose the slope s in g to be , where θ = tanh (k (C − Ccrit)). To produce numerical results, we adopt the following set of parameters: α = 500 ms, β = 0.62; τ = 500 ms, γ = −30 ms/μM, μ = 0.0025 μM=ms, Ccrit = 1.6 μM, Cmin = 1.25 μM, s1 = −2.5, s2 = 0.01, and k = 10 μM−1. Note that we have arbitrarily chosen a negative value of γ although a positive value of γ will produce similar phenomena. Moreover, we make the magnitude of γμ small to simulate weak Vm/Cain coupling.
1. Alternans for single cells
With the chosen parameters, map (5, 6) gives birth to alternans through a period-doubling bifurcation at B = 410.958 ms, see the bifurcation diagrams in Fig. 9. For this simple model, it can be analytically shown that, for a given BCL, the cell has either a unique 1:1 solution or a unique alternans solution. However, as we will see below, a fiber has multiple alternans solutions induced from electrotonic coupling.
FIG. 9.
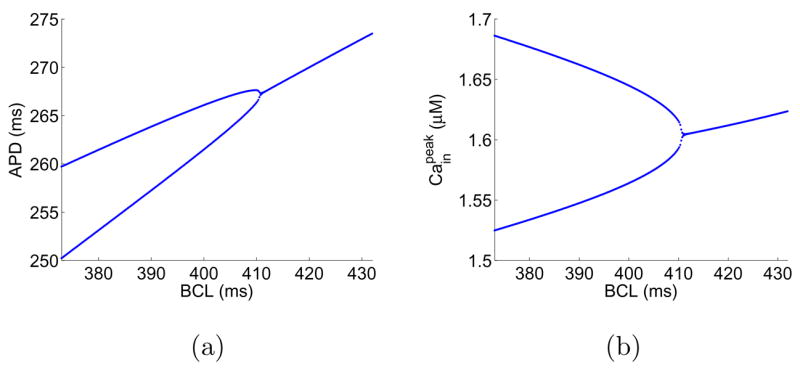
Bifurcation diagrams of the map (5, 6) with negative Vm/Ca coupling.
2. Alternans for fibers
Based on the mapping model (5, 6) for single cells, we construct a coupled-maps model to simulate fibers. Coupled-maps models have been used by a few authors to study propagation of action potential [38, 47–49]. Here, we follow that approach. Specifically, we consider a fiber consisting of M identical cells, located at xi, i = 1, 2, … M. The distance between two neighboring cells is denoted by Δx. At cell xi, APD and DI are related by the following equation:
| (A1) |
where Tn+1 (xi) is the time interval between two consecutive activations of site xi. The time Tn+1 (xi) is determined by the propagation time from the pacing site to xi, that is,
| (A2) |
where Vn (xi) stands for the conduction velocity. We adopt a conduction velocity from Fox et al. [48]: Vn (xi) = Vmax (1 − exp (− (Dn (xi) + β)/δ)) with parameters Vmax = 0.72 cm/ms, β = 17.408, and δ = 14. To account for the effect of electrotonic coupling, we modify the weighted averaging formula in Fox et al. [38] as follows:
| (A3) |
where Ān+1 (xj) = n(Dn (xj)) + γ (Cn+1 (xj) − Ccrit) and w (j) = exp (−0.0067 j2). The equation for [Cain] reads
| (A4) |
Simulations of the coupled-maps model (A1–A4) show that the alternans pattern on a fiber depends on the pacing history, a phenomenon consistent with that observed in simulations of the Shiferaw-Fox model. For example, Fig. 10 shows 3 selected solutions for a homogeneous fiber of 100 cells paced at B=375 ms. Panels in Fig. 10 have different initial conditions in [Cain]. Panel (a) starts from a uniform initial distribution. Panel (b) starts from an initial condition, where [Cain] is set to be 1.5 μM in the first 35 cells and 1.7 μM in the remaining cells. Panel (c) starts from a random initial distribution. Thus, the coupled maps model is able to reproduce the coexistence of multiple alternans solutions as observed in the Shiferaw-Fox model.
References
- 1.http://www.americanheart.org/.
- 2.Karma A. Electrical alternans and spiral wave breakup in cardiac tissue. Chaos. 1994;4:461–472. doi: 10.1063/1.166024. [DOI] [PubMed] [Google Scholar]
- 3.Garfinkel A, Kim YH, Voroshilovsky O, Qu Z, Kil JR, Lee MH, Karagueuzian HS, Weiss JN, Chen PS. Preventing ventricular fibrillation by flattening cardiac restitution. Proc Natl Acad Sci USA. 2000;97:6061–6066. doi: 10.1073/pnas.090492697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Plonsey R, Barr RC. Bioelectricity: A Quantitative Approach. Kluwer; New York: 2000. [Google Scholar]
- 5.Nolasco JB, Dahlen RW. A Graphic Method for the Study of Alternation in Cardiac Action Potentials. Journal of Applied Physiology. 1968;25:191–196. doi: 10.1152/jappl.1968.25.2.191. [DOI] [PubMed] [Google Scholar]
- 6.Panfilov A. Spiral breakup as a model of ventricular fibrillation. Chaos. 1998;8:57–64. doi: 10.1063/1.166287. [DOI] [PubMed] [Google Scholar]
- 7.Pastore JM, Girouard SD, Laurita KR, Akar FG, Rosenbaum DS. Mechanism linking T-wave alternans to the genesis of cardiac fibrillation. Circulation. 1999;99:1385–1394. doi: 10.1161/01.cir.99.10.1385. [DOI] [PubMed] [Google Scholar]
- 8.Bloomfield DM, Bigger JT, Steinman RC, Namerow PB, Parides MK, Curtis AB, Kaufman ES, Davidenko JM, Shinn TS, Fontaine JM. Microvolt T-wave alternans and the risk of death or sustained ventricular arrhythmias in patients with left ventricular dysfunction. J Am Coll Cardiol. 2006;47:456–463. doi: 10.1016/j.jacc.2005.11.026. [DOI] [PubMed] [Google Scholar]
- 9.Shusterman V, Goldberg A, London B. Upsurge in T-wave alternans and nonalternating repolarization instability precedes spontaneous initiation of ventricular tachyarrhythmias in human. Circulation. 2006;113:2880–2887. doi: 10.1161/CIRCULATIONAHA.105.607895. [DOI] [PubMed] [Google Scholar]
- 10.Shiferaw Y, qu Z, Garfinkel A, Karma A, Weiss JN. Nonlinear Dynamics of Paced Cardiac Cells. Ann NY Acad Sci. 2006;1080:376–394. doi: 10.1196/annals.1380.028.x. [DOI] [PubMed] [Google Scholar]
- 11.Weiss JN, Karma A, Shiferaw Y, Chen P-S, Garfinkel A, Qu Z. From Pulsus to Pulseless: The Saga of Cardiac Alternans. 2006;98:1244–1253. doi: 10.1161/01.RES.0000224540.97431.f0. [DOI] [PubMed] [Google Scholar]
- 12.Endo M. Calcium release from the sarcoplasmic reticulum. Physiol Rev. 1977;57:71–108. doi: 10.1152/physrev.1977.57.1.71. [DOI] [PubMed] [Google Scholar]
- 13.Shiferaw Y, Sato D, Karma A. Coupled dynamics of voltage and calcium in paced cardiac cells. Phys Rev E. 2005;71:021903. doi: 10.1103/PhysRevE.71.021903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shiferaw Y, Karma A. Turing Instability mediated by voltage and calcium diffusion in paced cardiac cells. PNAS. 2006;103:5670–5675. doi: 10.1073/pnas.0511061103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sato D, Shiferaw Y, Garfinkel A, Weiss JN, Qu Z, Karma A. Spatially Discordant Alternans in Cardiac Tissue: Role of Calcium Cycling. Circulation Research. 2006;99:520–527. doi: 10.1161/01.RES.0000240542.03986.e7. [DOI] [PubMed] [Google Scholar]
- 16.Chudin E, Goldhaber J, Garfinkel A, Weiss J, Kogan B. Intracellular Ca(2+) dynamics and the stability of ventricular tachycardia. Biophysics Journal. 1999;77:2930–2941. doi: 10.1016/S0006-3495(99)77126-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Díaz ME, O’Neill SC, Eisner DA. Sarcoplasmic Reticulum Calcium Content Fluctuation Is the Key to Cardiac. Circulation Research. 2004;94:650–656. doi: 10.1161/01.RES.0000119923.64774.72. [DOI] [PubMed] [Google Scholar]
- 18.Rubenstein DS, Lipsius SL. Circulation. 1995;91:201. doi: 10.1161/01.cir.91.1.201. [DOI] [PubMed] [Google Scholar]
- 19.Walker ML, Rosenbaum DS. Cardiovasc Res. 2003;57:599. doi: 10.1016/s0008-6363(02)00737-x. [DOI] [PubMed] [Google Scholar]
- 20.Echebarria B, Karma A. Instability and Spatiotemporal Dynamics of Alternans in Paced Cardiac Tissue. Phys Rev Lett. 2002;88:208101. doi: 10.1103/PhysRevLett.88.208101. [DOI] [PubMed] [Google Scholar]
- 21.Echebarria B, Karma A. Amplitude equation approach to spatiotemporal dynamics of cardiac alternans. doi: 10.1103/PhysRevE.76.051911. to appear in PRE. [DOI] [PubMed] [Google Scholar]
- 22.Dai S, Schaeffer DG. Spectrum of a linearized amplitude equation for alternans in a cardiac fiber. in process. [Google Scholar]
- 23.Choi BR, Salama G. Simultaneous maps of optical action potentials and calcium transients in guinea-pig hearts: mechanisms underlying concordant alternans. J Physiol. 2000;529:171–188. doi: 10.1111/j.1469-7793.2000.00171.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pruvot EJ, Katra RP, Rosenbaum DS, Laurita KR. Role of calcium cycling versus restitution in the mechanism of repolarization alternan. Circ Res. 2004;94:1083–1090. doi: 10.1161/01.RES.0000125629.72053.95. [DOI] [PubMed] [Google Scholar]
- 25.Katra RP, Pruvot E, Laurita KR. Intracellular calcium handling heterogeneities in intact guinea pig hearts. Am J Physiol Heart Circ Physiol. 2004;286:H648–H656. doi: 10.1152/ajpheart.00374.2003. [DOI] [PubMed] [Google Scholar]
- 26.Aistrup GL, Kelly JE, Kapur S, Kowalczyk M, Sysman-Wolpin I, Kadish AH, Wasserstrom JA. Pacing-induced Heterogeneities in Intracellular Ca Signaling, Cardiac Al-ternans, and Ventricular Arrhythmias in Intact Rat Heart. Circulation Research. 2006;99:65–73. doi: 10.1161/01.RES.0000244087.36230.bf. [DOI] [PubMed] [Google Scholar]
- 27.Shiferaw Y, Watanabe M, Garfinkel A, Weiss J, Karma A. Model of intracellular calcium cycling in ventricular myocytes. Biophys J. 2003;85:3666–3686. doi: 10.1016/S0006-3495(03)74784-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fox JJ, McHarg JL, Gilmour RF. Ionic mechanism of electrical alternans. Am J Physiol. 2002;282:H516–H530. doi: 10.1152/ajpheart.00612.2001. [DOI] [PubMed] [Google Scholar]
- 29.A Fortran code of the Shiferaw-Fox model was made by Yohannes Shiferaw and is available at http://www.csun.edu/~yshiferaw/shiferaw.html.
- 30.Kalb SS, Dobrovolny HM, Tolkacheva EG, Idriss SF, Krassowska W, Gau-thier DJ. The restitution portrait: a new method for investigating rate-dependent restitution. J Cardiovasc Electrophysiol. 15:698–7. doi: 10.1046/j.1540-8167.2004.03550.x. [DOI] [PubMed] [Google Scholar]
- 31.Riccio ML, Koller ML, Gilmour RF., Jr Electrical restitution and spatio-temporal organization during ventricular fibrillation. Circulation Research. 1999;84:955–963. doi: 10.1161/01.res.84.8.955. [DOI] [PubMed] [Google Scholar]
- 32.W. Krassowska, unpublished.
- 33.In models without junctional diffusion, [Cain] in neighboring cells are indirectly coupled through their dependence on the voltage.
- 34.Bers DM. Excitation-Contraction Coupling and Cardiac Contractile Force (Developments in Cardiovascular Medicine) Kluwer; Boston: 2001. [Google Scholar]
- 35.Allbritton NL, Meyer T, Stryer L. Range of Messenger Action of Calcium Ion and Inositol 1,4,5-Trisphosphate. Science. 1992;258:1812–1815. doi: 10.1126/science.1465619. [DOI] [PubMed] [Google Scholar]
- 36.Yohannes Shiferaw, Daisuke Sato, and Alain Karma, private communication.
- 37.Nayfeh AH. Perturbation Methods. John Wiley Interscience; New York: 1973. [Google Scholar]
- 38.Fox JJ, Riccio ML, Hua F, Bodenschatz E, Gilmour RF., Jr Spatiotemporal Transition to Conduction Block in Canine Ventricle. Circulation Research. 2002;90:289–296. doi: 10.1161/hh0302.104723. [DOI] [PubMed] [Google Scholar]
- 39.Courtemanche M, Glass L, Keener JP. Instabilities of a Propagating Pulse in a Ring of Excitable Media. Physical Review Letters. 1993;70:2182–2185. doi: 10.1103/PhysRevLett.70.2182. [DOI] [PubMed] [Google Scholar]
- 40.Beeler GW, Reuter H. Reconstruction of the Action Potential of Ventricular Myocardial Fibres. J Physiol. 1977;268:177–210. doi: 10.1113/jphysiol.1977.sp011853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Cherry EM, Fenton FH. A Tale of Two Dogs: Analyzing Two Models of Canine Ventricular Electrophysiology. Am J Physiol Heart Circ Physiol. 2007;292:H43–H55. doi: 10.1152/ajpheart.00955.2006. [DOI] [PubMed] [Google Scholar]
- 42.Hund TJ, Rudy Y. Rate Dependence and Regulation of Action Potential and Calcium Transient in a Canine Cardiac Ventricular Cell Model. Circulation. 2004;110:3168–3174. doi: 10.1161/01.CIR.0000147231.69595.D3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fenton F. Beyond Slope One: Alternans Suppression and Other Understudied Properties of APD Restitution. KITP Miniprogram on Cardiac Dynamics, Kavli Institute for Theoretical Physics; Santa Barbara, CA. July 28, 2006. [Google Scholar]
- 44.Qu Z, Weiss JN. The chicken or the egg? Voltage and calcium dynamics in the heart. Am J Physiol Heart Circ Physiol. 2007;293:H2054–H2055. doi: 10.1152/ajpheart.00830.2007. [DOI] [PubMed] [Google Scholar]
- 45.Sato D, Shiferaw Y, Qu Z, Garfinkel A, Weiss JN, Karma A. Inferring the cellular origin of voltage and calcium alternans from the spatial scales of phase reversal during discordant alternans. Biophys J. 2007;92:L33–L35. doi: 10.1529/biophysj.106.100982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Jordan PN, Christini DJ. Characterizing the contribution of voltage- and calcium-dependent coupling to action potential stability: implications for repolarization alternans. Am J Physiol Heart Circ Physiol. 2007;293:H2109–H2118. doi: 10.1152/ajpheart.00609.2007. [DOI] [PubMed] [Google Scholar]
- 47.Fox JJ, Gilmour RF, Jr, Bodenschatz E. Conduction Block in One-Dimensional Heart Fibers. PRL. 2002;89:198101–1. doi: 10.1103/PhysRevLett.89.198101. [DOI] [PubMed] [Google Scholar]
- 48.Fox JJ, Riccio ML, Drury P, Werthman A, Gilmour RF., Jr Dynamic mechanism for conduction block in heart tissue. New Journal of Physics. 2004;5:101.1–101.14. 2003.09. [Google Scholar]
- 49.Otani NF. Theory of action potential wave block at-a-distance in the heart. PRE. 2007;75:021910. doi: 10.1103/PhysRevE.75.021910. [DOI] [PubMed] [Google Scholar]