Predicting helix orientation for coiled-coil dimers

Abstract

The alpha-helical coiled coil is a structurally simple protein oligomerization or interaction motif consisting of two or more alpha helices twisted into a supercoiled bundle. Coiled coils can differ in their stoichiometry, helix orientation and axial alignment. Because of the near degeneracy of many of these variants, coiled coils pose a challenge to fold recognition methods for structure prediction. Whereas distinctions between some protein folds can be discriminated on the basis of hydrophobic/polar patterning or secondary structure propensities, the sequence differences that encode important details of coiled-coil structure can be subtle. This is emblematic of a larger problem in the field of protein structure and interaction prediction: that of establishing specificity between closely similar structures. We tested the behavior of different computational models on the problem of recognizing the correct orientation - parallel vs. antiparallel - of pairs of alpha helices that can form a dimeric coiled coil. For each of 131 examples of known structure, we constructed a large number of both parallel and antiparallel structural models and used these to asses the ability of five energy functions to recognize the correct fold. We also developed and tested three sequenced-based approaches that make use of varying degrees of implicit structural information. The best structural methods performed similarly to the best sequence methods, correctly categorizing ∼81% of dimers. Steric compatibility with the fold was important for some coiled coils we investigated. For many examples, the correct orientation was determined by smaller energy differences between parallel and antiparallel structures distributed over many residues and energy components. Prediction methods that used structure but incorporated varying approximations and assumptions showed quite different behaviors when used to investigate energetic contributions to orientation preference. Sequence based methods were sensitive to the choice of residue-pair interactions scored.

Introduction

The alpha-helical coiled coil has long served as a model for studying the relationship between protein sequence and structure. The coiled coil consists of a bundle of supercoiled helices that are encoded by a 7-residue sequence repeat of the form [abcdefg]_n. With a and d positions hydrophobic and e and g positions usually polar or charged, a “sticky” stripe winds its way around an individual helix, dictating the formation of a twisted helical bundle (Figure 1a and b). Because of this simple relationship, the coiled-coil fold is one of the easiest protein structures to predict. Numerous programs have been developed to detect the presence of coiled-coil forming segments in sequences, and these exhibit respectable sensitivity and specificity.^1-4 However, few methods exist to predict the variety of topologies found in coiled-coil structures.^4-6 Helix content can vary from 2 to 7 helices, and helix orientation can be parallel or antiparallel. Structures can be homo- or hetero-oligomeric, and the helices can align axially in different ways. Thus, the “coiled coil” is really a large family of structures that share many properties but exhibit different topological characteristics.⁷

Figure 2.

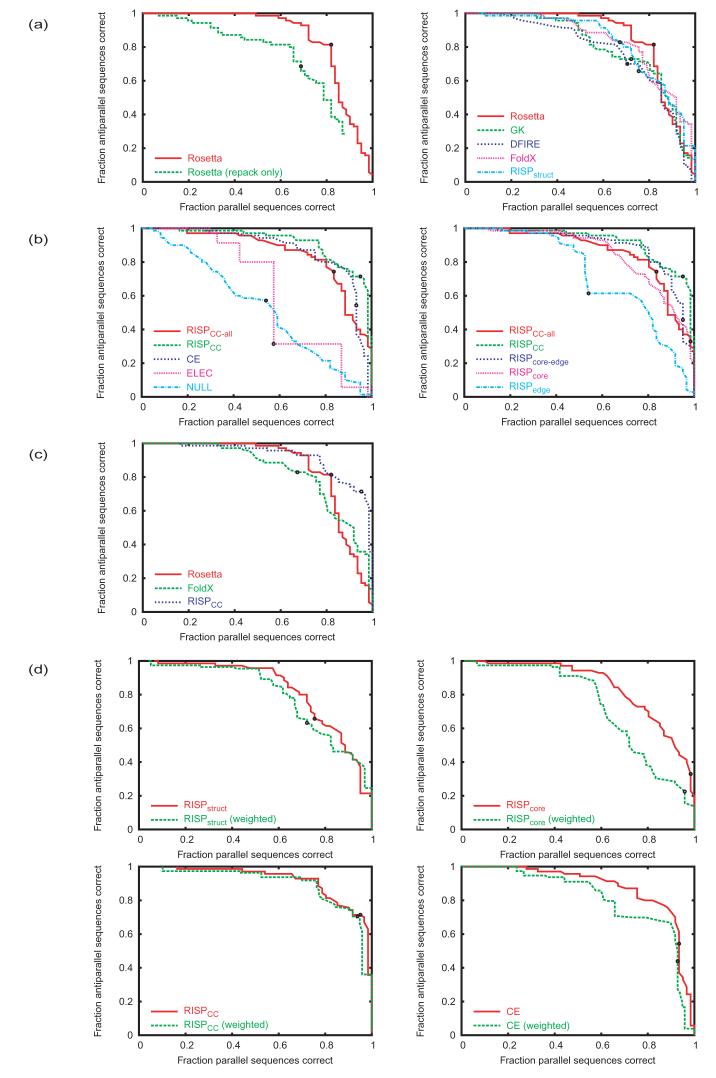
Parallel vs. antiparallel discrimination performance of different methods. The fraction of antiparallel structures correctly predicted is plotted versus the fraction of parallel structures correctly predicted. Curves were generated by varying E_cut = E_AP - E_P. A structure was predicted to have an antiparallel orientation if the energy of the antiparallel state was lower than that of the parallel state plus E_cut. If this energy was higher, the orientation was predicted as parallel. E_cut = 0 denoted by black dot. (a) Comparison of ESMs. At left, a comparison of Rosetta evaluated on structures without (repacked only) or with (repacked, min) structural relaxation. At right, all candidate ESMs evaluated using relaxed structures. (b) Comparison of ISMs. At left, candidate ISMs including NULL control; at right, several variants of the RISP model. (c) Comparison of best ESM and ISM models. (d) Comparison of the performance on the test set (red) and the performance when hetero- and homodimer results are weighted equally (green). Clockwise from top left, the panels are for RISP_stuct, RISP_core, CE and RISP_CC.

The difficulty of predicting coiled-coil structure lies in differentiating what can be subtle distinctions in interactions. For example, it has been reported for several designed coiled coils that changing a single a- or d-position residue can lead to a change or loss of oligomerization specificity.^8-10 Small changes in sequence can also alter helix orientation preferences. In the work of Oakley et al., moving a buried Asn residue by 7 positions in one helix and 3 in its partner helix was sufficient to switch a designed coiled coil from a parallel to an antiparallel orientation.¹¹ Lumb and Kim found that a buried Asn can establish both oligomerization and helix orientation specificity.¹² Perhaps surprisingly, this sensitivity to small sequence changes appears to hold for many native sequences as well. Mutation of an Asn residue at an a position of the yeast transcription factor GCN4 leads to loss of oligomerization specificity in that coiled coil,¹³ and changing 2 residues in the antiparallel coiled-coil dimer of Bcr can give either a mixture of antiparallel higher-order helical assemblies or trimers, depending on the mutations.¹⁴ This plasticity of coiled-coil structure in response to mutation makes the problem of fold recognition challenging. Much of the signal that is typically used to discriminate one structure from another in prediction, including patterns of predicted secondary structure and preferences of residues for different degrees of burial, is of little or no use in classifying coiled coils by type because these properties are largely the same in many of the competing structures. This situation also arises in other structure-prediction problems, where target and decoy structures must be resolved that sometimes include “mirror-image” variants containing the correct secondary structure elements arranged incorrectly with a reversed overall chirality.^15,16

Despite these challenges, some progress has been made on the problem of predicting coiled-coil interaction preferences from sequence. Several methods have been proposed for discriminating dimers from trimers. Simulations have successfully captured oligomeric preferences, and sequence-based programs have been developed for making predictions on novel coiled coils.^4,5,17 However, these were developed over a decade ago, using extremely small sets of known coiled-coil examples, and frequently fail on additional test cases that are available today. More recently, several methods have been developed to predict interacting partners among the bZIP transcription factors - an important protein family in which dimerization is mediated by a parallel coiled coil.^6,18-21 Relatively little is known about determinants of coiled-coil helix orientation, however. Various strategies have been used to design coiled coils that specifically adopt a parallel or antiparallel orientation, such as electrostatic charge patterning or the manipulation of a- and d-position polar residues or shape complementarity.^11,22-27 Alanine in core positions has been proposed to contribute to antiparallel specificity in coiled coils.²⁸ But in general, it is difficult to recognize sequence patterns that may specify helix orientation in native sequences. Analyzing features that determine orientation specificity via mutagenesis is often confounded by the fact that key residues may encode other types of specificity as well. For example, when probing the possible role of d-position Glu in determining the orientation preference of the Bcr coiled-coil domain, mutation to Leu led to the formation of trimers and other higher-order oligomers, as mentioned above.¹⁴

In this paper, we describe the performance of several types of computational models on the problem of predicting coiled-coil orientation. Due to the relatively small number of coiled coils with known orientation preference, learning strategies such as those that have been used in other motif recognition problems are not readily applicable.^1,29-32 Instead, we relied on structural models to evaluate coiled-coil orientation. We developed both explicit structural models and sequence-based models in which our use of structure was implicit. “Out-of-the-box” methods of both types did not perform very well, but small adjustments that took advantage of coiled-coil properties significantly improved the results.

Results

We tested several methods for predicting whether two sequences that can form a coiled coil will assemble as a parallel or an antiparallel dimer. For simplicity, we considered pairs of sequences of equal length that can be fully overlapped in both parallel and antiparallel orientations, i.e., those sequences that are “blunt ended” when aligned both ways. This test is akin to biochemical assays that can measure the relative stability of these two conformations,^11,33 although it avoids complexities that can be introduced by non-dimer states. An important feature of our calculations is that they do not require an accurate treatment of a dissociated and/or unfolded reference state (because the common unfolded state cancels), and therefore represent a best-case scenario for computational prediction.¹⁸ Significant additional challenges, such as predicting the correct axial alignment of helices, and determining that two sequences will form a dimer rather than some other type of oligomer, must be overcome to develop a general coiled-coil structure prediction method.

Our assessment of different methods used a database of parallel and antiparallel coiled-coil dimers of known structure. To assemble this database, dimers were identified using the program SOCKET,³⁴ which detects the knobs-into-holes side-chain packing that characterizes coiled-coil interfaces. Additionally, SOCKET was used to determine the coiled-coil heptad assignment (abcdefg). Because SOCKET also detects knobs-into-holes packing in non-coiled-coil structures, such as 4-helix bundles and helical sheets,^34,35 these were manually removed. We also included several sequences from the human bZIP family of coiled coils^21,36 in order to increase the number of parallel heterodimers in the database. In total, 61 parallel and 70 antiparallel examples with low sequence similarity and length >= 18 residues were selected and defined as our test set. We made the assumption that the coiled-coil motif itself is sufficient to encode the observed helix orientation for these structures. This may not always be true, and it is less likely to be true for short sequences that are part of a more complex fold. It is also less likely to be true for coiled coils that are highly buried. Nevertheless, local determination of helix orientation has been confirmed experimentally for a small number of cases in the literature, and it is likely to be true for the majority of our examples.^14,37-40 Due to the limited number of available structures, there are biases in the data set. In particular, the parallel structures include more homodimers and the antiparallel structures more heterodimers. This affected the performance of some methods, as discussed below. A summary of the structures that make up the database is provided in Table I and a detailed list is available in Supplemental Table S1.

Table I.

Test set of coiled-coil dimers of known orientation

	Sequence Pairs	Avg. Length (range) in residues	Number of intramolecular coiled coils	Avg (range) fraction exposed SASAa	Avg (range) RMSD to closest ideal Crick backbone (Å)b
Parallel	61
		32.9 (18-75)		0.71 (0.24 - 0.95)	0.72 (0.29-2.5)
Homodimer	49		0
		32.9 (18-40)		0.80 (0.67 - 0.91)	0.57 (0.35-1.0)
Heterodimer	12		0
Antiparallel	70
		25.0 (18-40)		0.59 (0.33 - 0.89)	0.51 (0.21-1.0)
Homodimer	19		0
		22.5 (18-53)		0.58 (0.16 - 0.83)	0.60 (0.28-2.4)
Heterodimer	51		45

Data for seven bZIP coiled coils without structures not included in averages.

^aFraction exposed is the ratio of the solvent-accessible surface area (SASA) of the coiled coil as observed in the crystal structure to the SASA of the isolated coiled coil. SASA calculated using NACCESS.⁶⁸

^bRMSD to the closest ideal Crick backbone is the difference between the crystal structure and the best-fitting Crick ideal structure. Data for all structure is shown in Supplemental Figure S1.

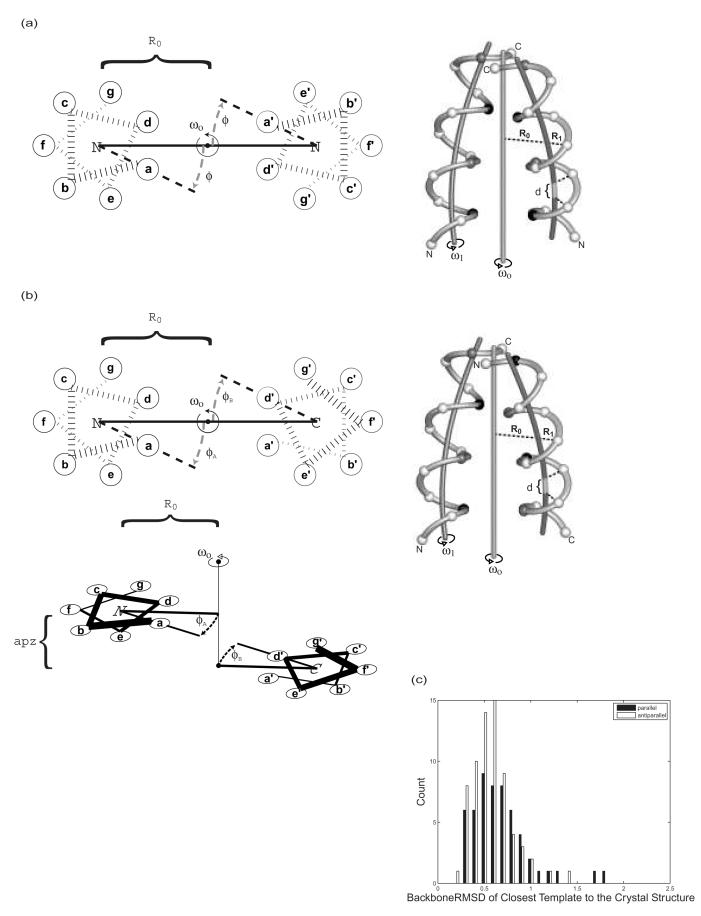
We tested two general categories of methods. The first required explicit models of structure for each orientation. The experimentally determined structure was available for the correct orientation for most of the sequences, but to simulate a real prediction problem we did not use this structure in our evaluations. Instead, models of both parallel and antiparallel complexes were predicted for each dimer. To generate idealized parallel backbones, we used a parameterization first developed by Crick in 1953 and subsequently adapted for use with modern molecular modeling programs by Harbury et al.^41,42 To describe antiparallel coiled-coil backbones, we introduced two new parameters into the Crick parameterization (see Methods). We then generated 120 ideal parallel and 81 ideal antiparallel backbones that spanned the parameter space of the dimeric coiled-coil test set (Supplemental Figures S1-4). The backbone RMSD between each native structure and its closest idealized backbone was in the range of 0.25-1.8 Å, with all but 12 structures within 1.0 Å (Figure 1c).

The other class of methods that we tested was based on sequence and did not require structural modeling. These approaches took advantage of characteristics of the coiled coil, such as the heptad repeat and extensive experimental characterization of interfacial residue-residue interactions that are important for dimer stability and specificity. We used this information to select interchain pairs of heptad positions that were scored based upon the residues at those positions, thus using structural information implicitly. We refer to the two different types of approaches as ESMs and ISMs, for explicit or implicit structural models, respectively.

These two classes of models have different strengths and weaknesses. The ISMs are much faster to evaluate and can easily incorporate experimental data about relevant heptad pairs and interaction energies. However, they make strong assumptions about the independence of pair-wise interactions and may obscure potentially significant details of atomic interactions necessary for modeling orientation specificity. ESMs provide advantages for analysis and interpretation of the physical basis of the overall interaction. Finally, ESMs are more generalizable in that they can potentially be applied equally to any structure; ISMs must be created specifically for the structure to be modeled.

Performance of explicit structure models

Predicting helix orientation using ESMs involved three steps: (1) generating large numbers of parallel and antiparallel dimer backbones, (2) modeling each sequence pair on each backbone, and (3) selecting the lowest-energy model. The first step was carried out using the coiled-coil parameterizations described above. The second step was carried out using Rosetta, or a combination of Rosetta and CHARMM (see below).^43-45 The third step gave rise to differences between models, with each ESM named according to the energy function used at this stage.

In a preliminary set of calculations, we tested two structure-prediction methods for use in step 2. Initially, Rosetta was simply used to place side chains into preferred conformations on each of 81 parallel and 120 antiparallel idealized Crick backbones. When Rosetta was used to select the lowest-energy structure and orientation for each pair of sequences (corresponding to step 3), this procedure predicted the orientation of 42/61 parallel sequences and 48/70 antiparallel sequences correctly. In the second approach, all Rosetta-repacked backbones were relaxed via minimization using the CHARMM param19 force field.⁴⁵ Rosetta evaluation of these relaxed structures gave strikingly better results, improving the prediction rate to 50/61 (82%) of parallel sequences and 57/70 (81%) of antiparallel sequences. The performance of these models is shown in Figure 2a (left panel). Results are plotted as the fraction of antiparallel sequences predicted correctly vs. the fraction of parallel sequences predicted correctly. Because including minimization in step 2 significantly improved performance, this protocol was adopted in all remaining calculations, for all ESMs. Using this approach, the predicted structures for the correct orientation provided a good approximation of the real structures, with backbone RMSD values in the range 0.4-2.2 Å (all but 7 within 1.5 Å) and χ-angle recovery rates only slightly lower than can be achieved on the native structure (Supplemental Table S2).

Figure 3.

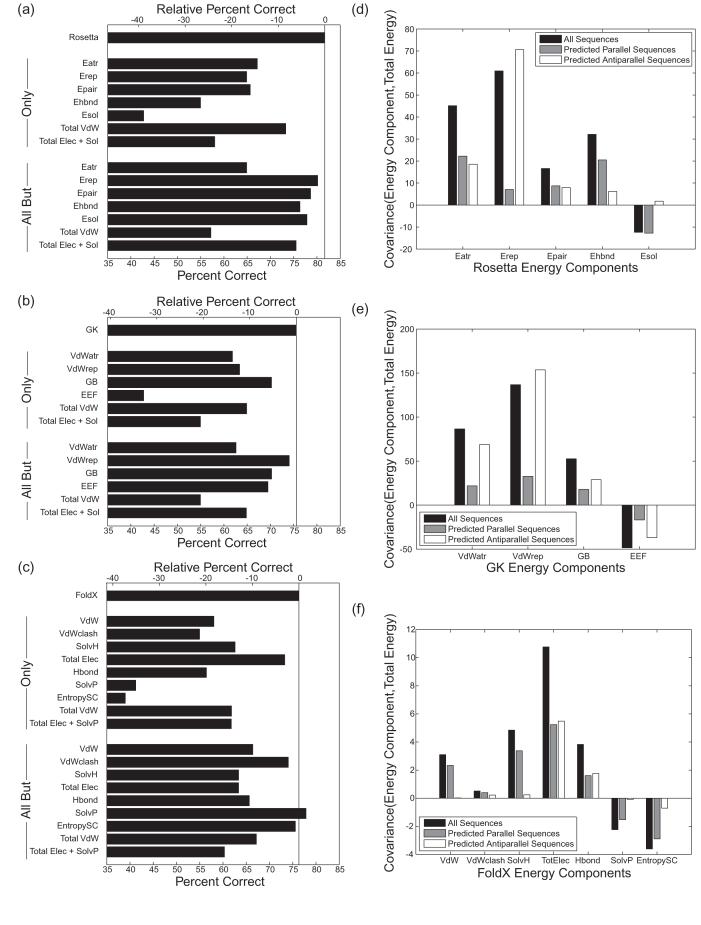
Overview of prediction performance and component analysis. All predictions were made using E_cut = 0.(a) Predictions clustered by method and example. Color (red: parallel, blue: antiparallel) denotes orientation prediction, and intensity (bright to dark) corresponds to the score of that prediction (ΔE), binned into deciles, where darker color indicates low rank (ΔE close to zero). CRYSTAL column denotes orientation in the x-ray structure. (b-e) Prediction results for subsets of sequences, re-clustered. Color scheme as in (a). CRYSTAL column denotes known orientation. Remaining columns are energy terms contributing to overall orientation predictions for the best ESM and ISM methods. Terms favoring parallel orientation are red; those favoring antiparallel are blue. Intensity is in units of sigma (standard deviation of all energy components on all test sequences for a given prediction method), capped at 2.5 σ. In (b-e), energy terms are shown for examples with: (b) the largest absolute magnitude Rosetta Erep, (c) the largest absolute magnitude Rosetta Eatr, (d) the largest FoldX electrostatic components, and (e) paired a-a’ Asn residues in the parallel orientation. N indicates that the sequence pair contains Asn at one or more a-a’ positions in the parallel orientation; I indicates that the sequence pair contains an Ile pair at d-d’ in the parallel orientation. FoldX, Rosetta, and GK energy components are described further in the Methods and in Supplemental Table S3.

Models GK, FoldX, DFIRE and RISP used different potentials to select the lowest-energy structures. Model GK, developed by Grigoryan et al.,¹⁸ is based on the CHARMM param19 force field⁴⁵ and includes van der Waals interactions and a combination of EEF1 desolvation⁴⁶ and generalized Born screening of electrostatic interactions. This model previously showed good performance predicting coiled-coil binding partners.¹⁸ GK describes similar physical terms to those captured by Rosetta, but it is more physical, with no statistical terms or empirical weighting. It performed slightly less well on orientation prediction than Rosetta. FoldX is a scoring function developed by Guerois et al.⁴⁷ It consists of physically descriptive terms weighted to predict experimental mutation free energies of primarily large-to-small mutations. Its performance was intermediate between that of Rosetta and GK (Figure 2a).

DFIRE and RISP are statistical potentials derived from the frequencies of interactions in the PDB.⁴⁸ They were applied to coiled-coil structures by scoring pairs of atoms or residues that met certain criteria. DFIRE is an atom-based potential that has been reported to predict protein-protein complex affinities accurately from experimental structures.⁴⁸ On our orientation-prediction test, it performed slightly worse than GK. RISP is a Residue-based Interfacial Statistical Potential consisting of 210 weights for scoring pairs of inter-chain residues that fall within a distance cutoff; it is very similar to the residue-based potential developed by Lu et al.⁴⁹ Applied to the relaxed structure set as RISP_struct, it performed relatively poorly (Figure 2a).

To address test-set bias, we approximated the performance expected if there were equal proportions of homo- and heterodimers in the parallel and antiparallel test sets. This was done by calculating the average performance on homodimeric and heterodimeric examples, weighted equally, for each orientation class, at each E_cut value (E_cut is defined in Figure 2). Figure 2d shows that RISP_struct was quite sensitive to this adjustment. This potential favored homodimers, and some of its success in predicting parallel structures was a result of this bias. The DFIRE, Rosetta, FoldX and GK potentials, on the other hand, performed similarly in the two tests.

Performance of implicit structure models

In our ISM models, the energy of a structure is expressed as a sum of contributions from pair-wise residue interactions. The models differ from one another in the choice of pairs and/or the weights assigned to them. Our selection of residue pairs took advantage of the known heptad register of the test-set structure. Heptad assignment for coiled-coil sequences with unknown structures can be made using programs such as Paircoil.^1,3 We considered only interactions among the a,d, e, and g residues that make up the coiled-coil dimer interface. A summary of the notation and residue pairs for all ISM models is shown in Table II. To approximate the RISP_struct method using an ISM, we scored seven pairs involving residues that commonly satisfy the RISP_struct distance cutoff. These pairs were assigned their RISP weights, giving method RISP_CC-all. Like RISP_struct, RISP_CC-all did not perform very well (Figure 2b). Interestingly, however, when we scored only 5 types of interactions for each coiled-coil orientation, giving model RISP_CC, the performance was much better and rivaled that of the best ESM methods (Figure 2c). The pairs in RISP_CC include those that have been described many times as being important for coiled-coil associations (i.e. a-a’, d-d’ and g-e’ for parallel^50-53 and a-d’, g-g’ and e-e’ for antiparallel⁵⁴ ) as well as core-to-edge terms (g-a’ and d-e’ for parallel and a-e’, d-g’ for antiparallel) that have been investigated in some systems and that were previously predicted to be important.^18,55,56 Further reduction of the number of pairs, i.e. using only core a-a’, d-d’ (parallel) or a-d’ pairs (antiparallel), giving model RISP_core, or only edge g-e’ or g-g’ (parallel) or e-e’ (antiparallel) pairs, giving RISP_edge, degraded performance (Figure 2b).

Table II.

Summary of pair terms used in ISM models

Model	Parallel	Antiparallel
ELEC	g-e’	g-g’ e-e’
CE	a-a’ g-e’	a-d’ g-g’ e-e’
RISPcore	a-a’ d-d’	a-d’
RISPedge	g-e’	g-g’ e-e’
RISPcore-edge	a-a’ d-d’ g-e’	a-d’ g-g’ e-e’
RISPCC	a-a’ d-d’ g-e’ g-a’ d-e’	a-d’ g-g’ e-e’ a-e’ d-g’
RISPCC_all	a-a’ d-d’ g-e’ g-a’ d-e’ a-d’ d-a’	a-d’ g-g’ e-e’ a-e’ d-g’ d-d’ a-a’

A prime (’) designates a residue on the opposite helix. All interaction pairs listed involve structurally adjacent sites on opposite helices. For edge interactions where there may be some ambiguity as to what pair is indicated, the interactions are as follows: g-e’ pairs in parallel coiled coils are between a g residue and the e residue of the next (mor C-terminal) heptad of the opposite helix; n antiparallel coiled coils g-g’ pairs are between a g residue and the g residue of the previous (more N-terminal) heptad of the opposit helix and e-e’ pairs are between an e residue and the e residue of the next (more C-terminal) heptad of the opposite helix.

Given the success of model RISP_CC, we tested model CE. This model includes the same heptad-position pairs, but draws weights, where possible, from experimentally reported interaction energies. These include weights for a-a’ and g-e’ interactions in the parallel orientation, taken from coupling energies measured in the Vinson laboratory. Weights for a-d’ interactions in the antiparallel orientation were taken from measurements by Hadley et al.⁵⁷ This model also did well, despite the limited number of available measurements (Figure 2b). The performance of two control models is also shown in Figure 2b. Model ELEC scores only thee- and g-position electrostatic complementarity and did not provide good parallel vs. antiparallel discrimination. We also illustrate the performance of a null model in which weights were assigned to the restricted set of pairs randomly.

Of the ISM models, RISP_core and CE showed significant amounts of homodimer bias, i.e. their performance was worse when we weighted the homo- and heterodimer results equally (Figure 2d). For RISP_core, this effect came from more favorable weights for a-a’ and d-d’ homotypic interactions than heterotypic interactions. This bias was somewhat surprising, as the RISP energy function was designed to minimize such effects by excluding cases where a residue interacts with a symmetry-related copy of itself in the training set. Increasing the number of pair terms to make the RISP_CC model, e.g. by adding edge and core-edge interactions that occur between positions not related by symmetry, diluted this effect, and the overall bias decreased (Figure 2d). The CE model is based on a much smaller number of terms than the RISP models, and so homodimer bias here is likely a result of unequal numbers of weights available for scoring homo vs. heterodimers.

Analysis

The performance of all methods on all examples indicates that some structures are easier to predict than others. For 23 dimers (18%), all 8 methods predicted the correct orientation, and for 74 dimers (56%), at least 6 out of 8 methods were correct. Seventeen structures (13%) were predicted correctly by three or fewer methods. Some of the examples that are rarely predicted correctly may contradict our assumption that the PDB reflects the structure that coiled-coil fragments would adopt in isolation. For example, 1OV9, VicH H-NS histone-like protein, consists of an antiparallel coiled coil flanked by N-terminal swap domains that pack against it; any influence on helix orientation from these domains was not considered in our models. Another example is 1X75, DNA gyrase subunit A, in which an intramolecular antiparallel coiled coil is packed against a large structured loop. Again, structural elements that we did not model may contribute to the observed orientation.

The various prediction methods work very differently, as is evident when comparing their performance on subsets of the test complexes. Figure 3a clusters both methods and examples by the similarity of predicted orientation preferences. Classifying all methods as statistics-based (DFIRE, RISP_struct and RISP_CC), knowledge-based (ELEC, CE) or pseudo-physical (Rosetta, GK, FoldX) shows that the knowledge-based potentials are least similar to the other methods and also not closely related to one another. The simple ELEC model had poor performance overall (Figure 2b). Figure 3a shows that much of this poor performance resulted from the model’s frequent failure to make a prediction (gray boxes), due to equivalent attractive and repulsive charge-charge interactions in both orientations. There are also examples where ELEC made a strong, yet incorrect, prediction. Model CE performed much better than ELEC; in overall prediction rate it was similar to the very good RISP_CC(also an ISM). Yet, the clustering in Figure 3a shows that CE is not at all similar to the other ISMs in terms of how orientation is assigned for specific sequences. This is understandable, as CE and RISP are based on completely different methods of deriving pair-wise scoring weights (experiments vs. PDB frequency analysis). Comparisons of ELEC, CE, and RISP_CC further illustrate how three types of terms (edge interactions involving e and g positions, core interactions involving a and d positions, and core-to-edge interactions) are all important (Supplementary Figure S5a). The inclusion of these heptad-position pairs in RISP_CC (absent from ELEC or CE) help to account for its better performance. Finally, it is interesting that the RISP_struct and RISP_CC methods cluster quite tightly, despite significant differences in their prediction performances, underscoring their basis in the same contact potential.

Figure 4.

Energy component contributions to performance. (a-c) The performance of each component or sum of components was considered alone (Only) or was excluded from the total (All But). The lower axis shows absolute performance and the upper axis shows performance relative to the total energy. (a) Rosetta components as described in the methods with Total VdW including Eatr + Eref, and Total Elec + Sol including Epair + Esol. (b) GK energy components as described in the methods with Total VdW including VdWatr + VdWrep, and Total Elec + Sol including GB + EEF. (c) FoldX energy components as described in the methods with Total Elec including Elec + HDipole + Eleckon, Hbond including SideHbond + BackHBond, Total VdW including VdW + VdWclash and Total Elec + SolvP including Elec + HDipole + Eleckon + SolvP. (d-f) Histograms illustrating how different components of the energy functions co-vary with the overall predicted E_parallel - E_antiparallel values. Only energy terms with strong covariances are shown. Covariance for all sequences is shown in black, for sequences predicted to be parallel in gray, and for sequences predicted to be antiparallel in white. (d) Rosetta components are the same as in (a). (e) GK energy components are the same as in (b). (f) FoldX energy components are the same as in (c) with TotElec the same as Total Elec.

Differences among the structure-based methods can be dissected using component analysis, which potentially offers insights into physical determinants of helix orientation. For 5 methods (the ISMs CE and RISP_CC and the ESMs FoldX, Rosetta and GK), we broke the predicted energy differences into their component terms for all of the examples in the test set. Figures 3b-e show subsets of these (all examples are included in Supplemental Figure S5b). For the ESMs, we also examined the predictive power of individual components, as well as the co-variation of individual energy-term differences with the total parallel vs. antiparallel energy difference. These data are summarized in Figure 4 (descriptions of components are included in Supplemental Table S3).

Figure 5.

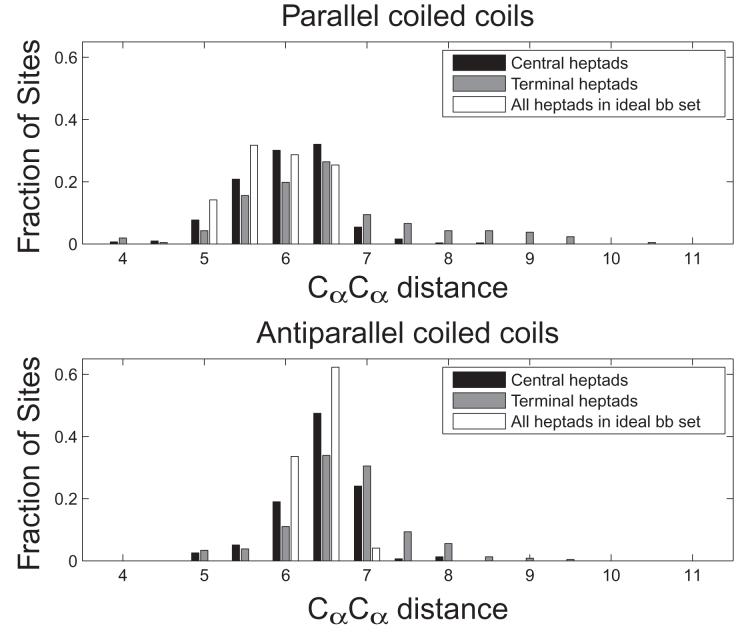
Distribution of C_α-C_α distances for core residues in parallel and antiparallel coiled coils. All C_α-C_α distances between core residues (a-a’, d-d’ in parallel and a-d’ in antiparallel) were binned by distance. For the test-set structures, residues were divided into two sets: Central heptads (black) include positions that are not the first or last seven residues of a coiled-coil helix, and terminal heptads (gray) include residues that are the first or last seven in a coiled-coil helix. All core positions of the ideal backbone set are binned together and shown in white.

Figure 4 panels a-c illustrate the contributions of different energy terms to prediction performance. The prediction accuracy of each important term when used alone is shown, along with the effect of removing terms individually from the total energy. The Rosetta terms Eatr and Erep, which together give the total van der Waals energy, gave reasonable prediction performance when used alone (73%). Although the Rosetta electrostatics terms were poorly predictive in isolation, they significantly enhanced overall performance (removing them reduced performance from 82% to 76%). Interestingly, FoldX relied much more on a single type of term. The electrostatics term alone gave 73% prediction performance (just 3% below that of the FoldX total energy). Removing this term from the total energy reduced performance to 63%. The GK model is more similar to Rosetta than to FoldX, although it describes a more important role for electrostatics than Rosetta does. Interestingly, omitting the repulsive van der Waals energy contribution from the total energy had little effect on the performance of any of the models. Note, however, that repulsive van der Waals terms were included when selecting the most appropriate backbone structure, and may contribute significantly in this way.

The strong predictive ability of the Rosetta van der Waals energy and the FoldX electrostatics terms suggests that these complementary descriptors could possibly be combined to give a better-performing model. However, we observed that linear combinations of these two terms performed worse than Rosetta on the test set. Extensive fitting of multiple terms to give optimal performance is not appropriate, given that the limited size of the test set restricts our ability to do rigorous cross-validation testing.

Co-variation is another way to assess which energy terms are most important for making predictions. Seeking physical insights, we used this approach to explore whether component terms contribute differently to the total energy depending on whether the final prediction is parallel or antiparallel. For both Rosetta and GK, the van der Waals energy terms co-varied strongly with the total energy (Figures 4d and e). The largest contribution came from the repulsive term, and interestingly, steric clashes were more important for examples predicted to be antiparallel than for those predicted to be parallel. Other Rosetta and GK terms, including those that describe electrostatic and solvation contributions, were smaller and exhibited less dramatic differences between parallel and antiparallel predictions. The FoldX electrostatic terms co-varied to a significant extent with the total energy (Figure 4f), consistent with the analysis of Figure 4c. However, the FoldX energy terms that differed most between parallel and antiparallel predictions were the van der Waals energy (VdW), solvation terms (SolvP and SolvH) and side-chain entropy contribution (entropySC); these each showed stronger co-variation with the total energy for parallel predictions than for antiparallel. The observations for all three energy functions described above are consistent with parallel structures being packed more tightly than antiparallel, such that van der Waals interactions are more attractive, side-chain motions are more restricted, desolvation is greater, and clashes are more likely in the parallel orientation.

Figure 3 panels b-e further emphasize differences between the methods and also support the characterization of parallel and antiparallel structures suggested by the co-variation analysis. Figure 3b illustrates cases where differences in steric repulsion between parallel and antiparallel structures were important, as reflected by a large magnitude for the Rosetta Erep term. The GK model also recognized an effect from repulsive van der Waals interactions for these examples. All but one of the cases with large Erep terms were predicted to be antiparallel by Rosetta and GK, most of them correctly so. Further analysis revealed that 11 out of 13 such examples, including 2 incorrect predictions, had Ile residues paired at d-d’ positions in the parallel structures; this is an interaction that is known to lead to unfavorable sterics for some well-studied parallel coiled-coil dimers.^51,58 The examples in Figure 3b were treated differently by FoldX, RISP_CC, and CE than by Rosetta and GK, as is expected because the former energy functions do not include a strongly repulsive steric term. Despite this, RISP_CC and FoldX performed well on these structures. These methods capture the influence of poor packing due to steric clashes using other terms, in an overall balance that gives correct results.

Because steric clashes involving Ile residues are a candidate motif for determining orientation, we examined all such examples in the test set. There are 18 complexes in which two Ile residues were paired at d-d’ when modeled in the parallel orientation. Rosetta correctly predicted 10 out of 10 of the antiparallel coiled coils, and only 3 of 8 of the parallel. Notably, all 8 of these parallel-orientation paired Ile residues are in terminal heptads. From the crystal structures, it is clear that the helices often fray slightly towards the ends of the supercoil to accommodate these β-branched residues (Figure 5). Such fraying is not included in our idealized backbone models. To compensate for this, we tested models in which each coiled-coil heptad, or each residue, contributed its minimum energy when evaluated over all backbones. This provided a way for the radius of the supercoiled bundle to effectively vary, potentially accounting more accurately for the local context of key interactions. However, this did not improve overall performance. FoldX, which does not contain a strong repulsive term, did slightly better at predicting these structures, with 5 out of 8 parallel structures predicted correctly but only 9 out of 10 antiparallel structures correct.

Figure 6.

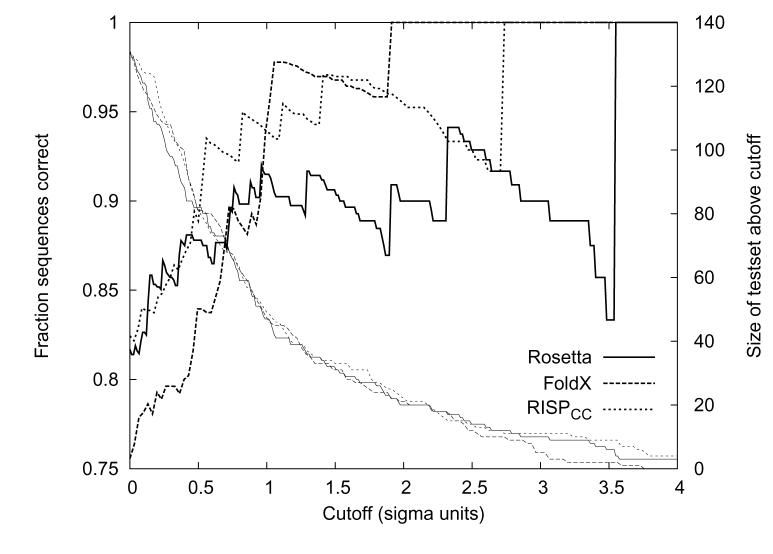
Performance as a function of increasing the gap requirement. Performance was evaluated only for those examples with ǀEparallel - Eantiparallelǀ > x*σ and is plotted (thick lines, left axis) as a function of x. The size of the test set at each value of x is plotted using thin lines and the right axis.

Figure 3c highlights examples where there was a substantial difference in the Rosetta attractive van der Waals component between the parallel and antiparallel states. In these examples, this component favored the parallel orientation most of the time and indeed, complexes with large values of this term were mostly parallel. Similar patterns are seen in the CE and RISP_CC COREatr terms, in the FoldX VdW and SolvH terms and, to a lesser extent, in the GK Eatr term. Favorable packing was offset in most models by solvation penalties, presumably because polar residues were more buried in better-packed structures. Thus, clear preferences for the antiparallel structure showed up in the FoldX SolvP and Rosetta Esol terms for examples in this panel, and, to a lesser extent, in the GK EEF term. These trends support a model where closer packing and more burial (both favorable hydrophobic burial and unfavorable polar burial) can be achieved in the parallel orientation relative to the antiparallel orientation.

Differences in electrostatics between orientations were predicted to be important by some models. For FoldX, electrostatics terms co-varied most strongly with the total energy (Figure 4f). Figure 3d shows examples that had large contributions from FoldX electrostatics (Elec, HDipole and Eleckon); these terms more often favored antiparallel structures. The GK potential also showed some of the FoldX trends for these examples, but the overall importance of electrostatics relative to other terms was reduced. Finally, electrostatics contributed very little to the Rosetta potential, which uses a combination of a statistically derived term (Epair) and an orientation-dependent hydrogen bond term (Ehbnd) to account for electrostatic effects.

Figure 4d shows a preference for parallel coiled coils in the Rosetta hydrogen bonding term, which we suspected could include a contribution from Asn residues. A preference for paired, hydrogen-bonding Asn residues at a-a’ positions in parallel coiled coils has been well documented and described as a determinant of coiled-coil orientation and alignment.^11,12,21 We explored whether this effect was evident in our data. Among all 131 sequence pairs tested, there were 28 examples where two Asn residues could be paired at a-a’ sites in a parallel model. Of these, 27 were from parallel structures and only one was from an antiparallel structure (Figure 3e). At least in our test set, therefore, the potential to pair Asn residues at a-a’ is a strong indicator of a parallel orientation. This is recognized by models CE and RISP_CC. CE includes a strong preference for Asn-Asn pairing, as determined experimentally,⁵³ and its influence was clear in the CE COREatr term. RISP_CC also assigns a favorable weight to this term, reflected in its COREatr term.

However, the structure-based prediction methods did not show a strong energy component pattern typifying paired Asn groups. No single term dominated the predictions for these structures, although many seemed to be determined by more favorable packing in the parallel than in the antiparallel orientation. Further analysis at the residue level using Rosetta revealed that Asn hydrogen bonding favored the parallel state for only 16 out of 27 parallel examples, and the total energy of Asn residues at paired a-a’ positions favored the parallel state in only 14 out of 27 cases. Nevertheless, 23 of 27 parallel dimers containing a pair of Asn residues were predicted correctly by Rosetta, similar to the performance on all sequences. Thus, although Asn pairs at a-a’ positions correlate strongly with a parallel orientation in the test set, the Rosetta method did not rely heavily on this interaction to make correct predictions. This is consistent with previous observations by Grigoryan et al.¹⁸ that the experimental preference for Asn-Asn over Asn-Val a-a’ pairs in coiled-coil dimers is difficult to capture using these types of methods.

Confidence

To explore whether the predicted energy differences between parallel and antiparallel models can be used as a measure of confidence, we modified our scheme such that a structure was assigned as parallel (or antiparallel) only if the absolute energy difference ǀE_antiparallel - E_parallelǀ was greater than some cutoff. Increasingly stringent cutoffs left larger numbers of test set examples unclassified. Figure 6 illustrates the tradeoff between performance and the number of classifiable structures. For the three best-performing methods, the number of predicted structures falls off quickly as performance improves. A gain of 10% prediction accuracy requires predicting between 40-60% of the test set as “unknown”. Thus, although it is possible to improve the confidence of the predictions by imposing a larger energy gap, this comes at a very severe penalty.

Figure 1.

Crick parameterization of parallel and antiparallel coiled coils. (a-b) Schematic illustrating parameters used to describe (a) parallel and (b) antiparallel backbone geometries. For each wheel diagram, the heptad positions are indicated in lowercase letters and the direction of the chain is indicated by whether the N or C terminus is out of the page. For the structural diagram, the a and a’ positions are shown in black, the d and d’ positions in gray, and the rest in white. (c) Distribution of the backbone RMSD (N, Cα, and C atoms) for the native crystal structures in the test set to the closest ideal structure in the backbone sets. For every example, an idealized model with an RMSD of less than 1.8 Å was available for selection as a template.

Discussion

Our results illustrate that coiled-coil helix orientation prediction is not a trivial problem. Standard methods, applied either at the sequence or structure level, do not give good performance. Nevertheless, refinement of these approaches can provide effective predictors. For our ESMs, we found that allowing structural flexibility was important. To increase the probability that an appropriate backbone was available for each complex, each dimer was modeled on 120 different parallel and 81 different antiparallel templates. This was critical; ultimately 52 parallel and 44 antiparallel backbones were used to construct the minimum-energy structures of both orientations for the 131 complexes modeled. Although we found in post-analysis that a much smaller set of backbones could provide the same total prediction performance, it would have been difficult to determine in advance which scaffolds these should be. Thus, although it may be possible to capture backbone variability more efficiently than we have done here (e.g. by using a better-targeted backbone library or some different approach), we have found that it is important to model flexibility to achieve good results. We also found that small amounts of structural relaxation following rigid-backbone/rotameric side-chain repacking were important. Comparing the performance of Rosetta on ideal vs. minimized backbones (Figure 2a) illustrates the significance of energetically costly clashes that can be removed relatively easily with minimization.

Analysis of the complexes for which ESMs gave incorrect predictions suggested that our models do not yet include sufficient structural plasticity. In particular, we found that our parallel dimer models cannot accommodate pairs of Ile residues at d-d’ positions. This is consistent with earlier observations by Harbury et al. that β-branched residues confer a preference for trimers or tetramers over dimers when located at the d position of parallel homo-oligomers.¹³ In native parallel structures, relatively rare Ile residues at d positions towards the end of the coiled-coil chain are accommodated by fraying of the ends (Figure 5). In contrast to this, the backbones on which we modeled these coiled coils were uniform over the length of the sequence. Incorporating greater local structural variation may be important for improving performance in the future, although our attempts to approach this in a systematic way have not succeeded so far. For now, knowledge that the structure-based methods can fail in cases where there are terminal-heptad β-branched clashes can guide appropriate use of these methods.

In the absence of more structural sampling, softening the steric repulsive term is a way to approximate structural variability. However, it is not easy to modify the ESMs to accommodate small clashes, because such clashes can be important for determining the correct helix orientation. For example, softening the repulsive terms in Rosetta or GK to accommodate Ile pairs at terminal d positions may prevent the proper identification of clashes elsewhere. Interestingly, FoldX lacks such a rigid repulsive term, yet is still able to correctly predict the orientation of many sequences that contain these paired residues (Figure 3b). Overall, our analyses support a model in which packing constraints are more demanding on parallel than on antiparallel backbones. Features of this model are captured differently by different methods. Models that include steric repulsion use this to predict that certain structures are antiparallel. Yet models that lack these terms can nevertheless recognize better packing in other ways. For FoldX, energy decomposition shows a role for the surface-area based van der Waals and hydrophobic solvation terms in favoring parallel structures. However, for sequences with large clashes (as assessed by Rosetta Erep differences), the preference of these terms for the parallel state is reduced or even reversed (Figure 3b). This illustrates that despite a lack of explicit steric repulsion, FoldX can still recognize poor packing that arises in structure prediction of the incorrect orientation.

The models used here, although all quite successful for the task of prediction, do not reach a significant consensus about what sequence features and energy terms are most critical for specific cases. RISP_CC, FoldX, and Rosetta are based on different sets of assumptions, and each model includes many parameters that are not derived rigorously from physical principles. GK is a more physical model, and although it may be more informative in component analysis, it did not perform quite as well. Thus, although structure-based models supposedly work by accurately capturing physical phenomena, the large extent to which they differ in their particulars here leaves this premise in doubt (Figures 3 and 4). Our results suggest that despite good performance, caution should be observed when attempting to gain physical insight from individual energy terms in structure-based, yet highly parameterized, calculations. This is especially true given that these methods are optimized to recapitulate native structures and mutational energies, rather than to reproduce individual physical components.

Testing of various ISMs also led to interesting results. The performance of these methods was very sensitive to the choice of interfacial pairs that were scored. In particular, scoring all pairs of residues that satisfied a 4.5 Å distance cutoff in explicitly modeled structures was not effective (model RISP_struct). Scoring all pairs of residues that could potentially be within 4.5 Å, based on sequence and known coiled-coil dimer structures, was also not effective (model RISP_CC-all). Strikingly, however, when just 5 types of pairs were included for each orientation, performance was very good (RISP_CC). The key pairs included those that have been highlighted by many biochemical experiments over the past 10-15 years. In particular, Vinson and colleagues have quantified contributions of a-a’, d-d’ and g-e’ pairs in parallel bZIP coiled coils,^50-53 and there is an approximate structural correspondence between these and the a-d’, g-g’ and e-e’ pairs of antiparallel coiled coils, which have been less investigated.⁵⁴ The core-to-edge terms (g-a’ and d-e’ for parallel and a-e’, d-g’ for antiparallel) provide a slight but detectable improvement in performance (Supplementary Figure S5a). Interestingly, including the core-core terms (a-d’ in parallel or a-a’, d-d’ in antiparallel structures) significantly degraded performance, despite recent observations by Hadley et al. that these can be significant in some antiparallel structures.⁵⁹ These results suggest that fold-recognition techniques applied to protein complexes, e.g. as are implemented in programs such as InterPreTS and Multiprospector,^60-62 could be improved if strategies for identifying critical specificity-determining residues in different folds were available. A significant disadvantage of some of the ISMs is that they exhibit a parallel bias for homodimeric structures. It is unlikely that this preference has a physical justification, as it is not supported by the best performing ESM models. Therefore, the use of ISMs to predict coiled-coil orientation may be subject to systematic errors that favor structures in which residues interact with adjacent copies of themselves. This effect is also likely to show up in other related ISM applications.

Our results illustrate that several different types of computational approaches are capable of discriminating parallel from antiparallel coiled-coil helix alignments with reasonable accuracy. By far the most efficient of these are the sequence-based methods, which are easily scalable to evaluate candidate interactions at the proteomic scale. Structure-based methods are less prone to biases, however, and these methods could also be scaled up for some types of applications. Our recently developed cluster-expansion methodology, in which a simple expression for energy as a function of sequence can be fit to the results of more expensive calculations, is a promising way of approaching this problem.^63,64 However, significant challenges remain before accurate tertiary/quaternary annotation can be provided for novel coiled-coil sequences. Techniques must be developed that can recognize the correct set of interacting helices and their appropriate stoichiometry. When sequences are of different lengths, the correct axial alignment must also be selected. Our demonstration of helix-orientation prediction in a rigorously chosen subset of examples represents an important and necessary component of this larger-scale genomic annotation problem.

Methods

Coiled-coil database

Parallel and antiparallel coiled-coil dimer structures were obtained by applying SOCKET to the EMBL Protein Quaternary Structure (PQS) database downloaded on April 12, 2007.³⁴ Structures returned by SOCKET were filtered to exclude those shorter than 18 residues as well as those with a discontinuous heptad assignment. A manual filtering step was used to exclude non-coiled-coil structures, such as certain portions of helix bundles, helix sheets and other extended knobs-into-holes assemblies.³⁵ The GCN4 coiled-coil family was overrepresented in this set; several sequences containing point mutations were removed. Finally, due to the significant minority of parallel heterodimeric coiled-coil crystal structures, we added seven sequence pairs from the human bZIP family, for which the helix orientation and alignment can be determined by sequence alignment^21,36 : ATF7+MAFK, ATF2+FOS, CREBPA+JUN, CEBPbeta+CEBPalpha, ATF1+CREM, CEBPgamma+ATF4 and the ATF1 homodimer. All complexes contained two chains of the same length and were completely overlapping (i.e. had “blunt” ends) in both parallel and antiparallel orientations. The final set consisted of 61 parallel and 70 antiparallel coiled coils.

Crick Parameterization

To describe and generate parallel coiled-coil dimer backbones, we used the parameterization originally proposed by Crick and subsequently implement by Harbury et al. as a user routine in CHARMM.^41,42 This parameterization has been shown to closely mimic the geometry of several parallel coiled coils.⁴¹ Additionally, using our parallel coiled-coil test set, we found that this idealized parameterization can be fit to a set of 54 native backbones with C_α RMSD values ranging from 0.25 to 2.5 Å, and with 46 of 54 backbones having an RMSD less than 1.0 Å (supporting data in Supplemental Figure S1).

We modified the Crick/Harbury approach to describe and generate antiparallel coiled-coil backbones. As in the fitcc program (Personal Communication Tom Alber; Author Mark Sales http://ucxray.berkeley.edu/∼mark/fitcc.html), we used the fact that the C_α trace of the antiparallel coiled coil has approximately the same symmetry properties as the parallel coiled coil. The two relevant exceptions are that a symmetry-breaking axial shift can occur between the two chains, and the ϕ values that describe the angle of side chains relative to the helix-helix interface need not be the same on both chains. We modified the coiled-coil parameterization to account for these differences by introducing two new parameters. Parameter apz_i captures the helical shift as described above, and parameter ϕ is replaced with an independent value for each helix: ϕ_A and ϕ_B. We re-write the parameterization for antiparallel coiled coils as:

$$\begin{array}{cc}\hfill & CC\left(\tau \right)=EC\prime \left(\tau \right)+H\left(\tau \right)\hfill \\ \hfill & E({\omega }_0\tau ,\alpha ,0)=\left(\begin{array}{ccc}\hfill \cos \left({\omega }_0\tau \right)\hfill & \hfill -\sin \left({\omega }_0\tau \right)\cos \left(\alpha \right)\hfill & \hfill 0\hfill \\ \hfill \sin \left({\omega }_0\tau \right)\hfill & \hfill \cos \left({\omega }_0\tau \right)\cos \left(\alpha \right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sin \left(\alpha \right)\hfill & \hfill \cos \left(\alpha \right)\hfill \end{array}\right)\hfill \\ \hfill & C\prime =\left(\begin{array}{c}\hfill R_1\cos ({\omega }_1\tau +{\varphi }_i)\hfill \\ \hfill R_1\sin ({\omega }_1\tau +{\varphi }_i)\hfill \\ \hfill ap{z}_i\hfill \end{array}\right)\hfill \\ \hfill & H\left(\tau \right)=\left(\begin{array}{c}\hfill R_0\cos \left({\omega }_0\tau \right)\hfill \\ \hfill R_0\sin \left({\omega }_0\tau \right)\hfill \\ \hfill d\cos \left(\alpha \right)\hfill \end{array}\right)\hfill \\ \hfill & \text{where}\sin \left(\alpha \right)=\frac{R_0{\omega }_0}{d}\hfill \end{array}$$

Here R₀ is the superhelical radius, ϕ_i are phase angles that locate the residues on the superhelical backbone trace, and ω₀ is the superhelical frequency. α is the helix-crossing angle, R₁ is the α-helix radius and ω₁ is the α-helix frequency. As described above,apz_i is an axial helical offset that is set to 0 for chain A, and is non-zero for other chains. As for the parallel coiled coil, we generate chains by constructing them using this equation and rotating them into position about the superhelical axis. This antiparallel parameterization was coded as a user-defined energy routine in CHARMM, as for the parallel parameterization.

We used the Crick parameterization both to fit idealized backbones to native structures and to generate de novo backbones. To fit a native structure, we optimized superhelical parameters, as well as two external parameters that locate the coiled coil in the laboratory frame. It is important that the superhelical axis of the native coiled coil be aligned with the z-axis of the parameterization above. The superhelical axis of a parallel coiled coil can be well approximated as the rotational axis that maximizes superposition of one helix onto another. However, this is not the case for antiparallel coiled coils. For these, we found the best alignment by adjusting the internal Crick parameters, along with two Euler rotations and three translational degrees of freedom, using a process similar to that of the fitcc program. The center of mass of the helix was translated to the origin, and then the coiled coil was approximately oriented using two vectors defined by connecting the first and last C_α atom of each helix. The average of these two vectors was aligned with the z-axis. Starting from this position, the rest of the Crick parameters, along with two Euler angles and translations in three dimensions, were optimized using Matlab’s constrained minimization algorithm⁶⁵ to minimize the RMSD of the native helix to the closest ideal Crick helix. Given this superhelical alignment, antiparallel Crick parameters were fit in CHARMM by minimizing the energy with respect to these parameters as well as a rotation about the superhelical axis and a translation with respect to this axis. The energy minimized was proportional (with constant 25 kcal/Ų) to the sum of the distances squared of all C_α atoms from the ideal Crick C_α-atom positions.

Generation of backbones

All structures were generated via minimization under a potential that included the user defined Crick energy as well as van der Waals interactions, bond length, bond angle, dihedral and improper dihedral energy terms, and a hydrogen bonding potential, all defined by the param19 force field.⁴⁵ Parameters R₁, ω₁ and d, which describe α-helix geometry, were set to 2.26 Å, 4π/7 radians per residue and 1.52 Å respectively.⁴¹ Other parameters were sampled as follows. The parallel set contained 120 structures with R₀ values of 4.7, 4.8, 4.9, 5.0, 5.1 and 5.2 Å, ϕ values of 0.25, 0.30, 0.35, and 0.40 radians, and ω₀ values of -0.055, -0.06, -0.065, and -0.70 radians. The antiparallel set contained 81 structures with R₀ values of 4.8, 4.9 and 5.1 Å,ω₀ of -0.050, -0.060 and -0.070 radians, ϕ_A, ϕ_B pairs (in radians) of (0.412, 0.395), (0.422, 0.384), (0.432, 0.374) and apz_i values of 1.5, 2.0 and 2.5 Å. These values span the space of native parallel and antiparallel sequences, as illustrated in Supplementary Figures S2-S3. ϕ_A, ϕ_B values were sampled as pairs due to correlations between these in native structures (Supplemental Figure S4).

Evaluation of structures

Sequences were repacked on 201 parallel + antiparallel rigid backbones using Rosetta with default parameters and expansion of the first and second dihedral angles in the rotamer library.⁴⁴ The energy of these repacked structures was recorded to provide the Rosetta energy. Repacked structures were then converted to CHARMM 19 atom types and minimized using CHARMM with param19 EEF1 parameters and topology.^45,46 The energy function used in minimization included van der Waals; EEF1 solvation; distance-dependent-dielectric electrostatics with dielectric constant of 4r; bond length, angle, dihedral angle, and improper dihedral molecular mechanics energy; hydrogen bond energy; and the Crick user energy. Minimization was done with 1000 steps of steepest decent followed by 1000 steps of adopted-basis Newton-Raphson. These minimized structures were then re-evaluated using five ESM energy functions.

Energy functions — ESMs

All Crick-minimized backbones were evaluated with each ESM. The lowest energy structure in each orientation was used to determine the energy difference. All structures were held fixed during evaluation.

The Rosetta energy was calculated using the same energy function as for repacking. All energy terms were included in the final score; however, the structure-independent reference state canceled in the final analysis. Energy components labeled in the figures for Rosetta are: Eatr - attractive van der Waals; Erep - repulsive van der Waals; Epair - statistical pair electrostatics; Ehbnd - hydrogen bonding; Esol - solvation; and Edun - Dunbrack statistical energy.

Model GK uses the physical energy function described by Grigoryan and Keating.¹⁸ Briefly, the energy function consists of three terms. First, a van der Waals energy term includes atomic radii from CHARMM param19.⁴⁵ Second, an electrostatics energy term combines Coulombic interaction energy in a uniform dielectric of 4 with Generalized Born (GB) screening to account for transfer into an external dielectric of 80 and an internal dielectric of 4. Perfect Born radii for use in the GB formulae were calculated using PEP.⁶⁶ Finally, a desolvation energy term is included from the EEF1 function in CHARMM.⁴⁶ Energy components labeled in the figures for GK are: VdWatr and VdWrep - attractive and repulsive van der Waals; GB - screened Coulombic interaction energy; EEF - EEF1 solvation component.

The DFIRE statistical potential was applied by using binding energies computed using the dcomplex executable, as obtained from the Zhou lab.⁴⁸

The FoldX energy was calculated with FoldX version 2.5.2 obtained from the Serrano laboratory.^47,67 We used the “Stability” command with all options set to their default values. All energy terms contributed to the final score. Energy components labeled in the figures for FoldX are: VdW - van der Waals; VdWclash - van der Waals clash; Elec+HDipole+Eleckon - sum of electrostatic, helix-dipole electrostatic and electrostatic k_on; SideHBond+BackHBond - sum of side-chain and backbone hydrogen bonding; SolvP - polar solvation energy; SolvH - hydrophobic solvation energy; and EntropySC+EntropyMC - sum of side-chain and backbone entropy.

RISP (Residue-based Interfacial Statistical Potential) was derived using the framework outlined by Lu et al.⁶² It was based on protein complexes from the QS50 database at 3dcomplex.org,⁶⁸ which consists of PDB entries filtered to exclude all complexes with greater than 50% sequence identity. We further excluded all structures showing significant sequence homology (BLAST E < 10^-10) to structures in our coiled-coil test set. An interface between two chains was defined as the set of all residues with any heavy atom within 4.5 Å of the other chain. Interfaces containing 5 or fewer residues were excluded. To reduce the observed bias of the derived potential towards favoring homodimeric interactions, interfaces were excluded if they contained two or more residues making contact with copies of themselves on other chains. The final database consisted of 2,864 interfaces containing 105,287 residues. Pair-wise residue scores were computed according to:

$$P(i,j)=-\log \frac{N_{\mathit{obs}}(i,j)}{N_{\exp }(i,j)}$$

where N_obs(i, j) is the number of contacts observed between residues i and j in the training database and N_exp(i, j) is the product of the mole fractions of residues i and j in the database multiplied by the total number of residues in the database. This reference state performed better at orientation discrimination compared to a reference state based on the mole fraction of residues occurring in solvent-exposed positions.⁶² The RISP potential was applied to modeled coiled-coil structures as a sum of pair-wise residue contact scores. Contacts were determined according to the same criteria used in the development of the potential.

Energy functions - ISMs

A null control model (NULL) was developed by assigning random scores between +1 and -1 to all possible amino acid pairs at a-a’, d-d’, and g-e’ (parallel) or a-d’, e-e’, and g-g’ (antiparallel) positions.

Model ELEC assigns all occurrences of g-e’ (parallel) or g-g’ + e-e’ (antiparallel) E-R, R-E, K-E or E-K pairs a weight of -1, while E-E, R-R, R-K, K-R, K-K, D-E, E-D and D-D pairs are given a weight of +1.

The CE model is constructed using 48 experimentally determined coupling energies for each orientation. For parallel coiled coils, coupling energies were obtained from references Krylov et al.⁵⁰ and Acharya et al.⁵² For antiparallel coiled coils, we computed coupling energies fora-d’ residue pairs from the △G values of Hadley et al. as double mutant thermodynamic cycles relative to alanine.⁵⁷ Because no published data are available for antiparallel interactions involving g and e residues, we applied the analogous values from the Krylov study to the antiparallel pairs g-g’ and e-e’.

To apply RISP to sequence data, we predefined pairs of heptad positions to be scored. Different models included different pairs, as follows: RISP_core included core interactions: a-a’, d-d’ (parallel) and a-d’ (antiparallel) pairs. RISP_edge included edge interactions: g-e’ (parallel) and g-g’, e-e’ (antiparallel) pairs. RISP_core,edge included the pairs in both RISP_core and RISP_edge. RISP_CC included all pairs from RISP_core,edge as well as the core-edge pairs g-a’, d-e’ (parallel) and a-e’, d-g’ (antiparallel). Finally, the RISP_all model further included the pairs d-a’ (parallel) and a-a’, d-d’ (antiparallel). These lists are summarized in Table II. Energy components used in Figure 3 for RISP_CC are: COREatr/rep — all core-core interactions; EDGEatr/rep — all edge-edge interactions; CEatr/rep — all core-edge interactions. Based on analyses of coiled-coil crystal structures, RISP_all corresponds to selecting all pairs with the potential to be in contact according to the 4.5 Å criterion used to develop RISP.