Biomechanical ordering of dense cell populations

Abstract

The structure of bacterial populations is governed by the interplay of many physical and biological factors, ranging from properties of surrounding aqueous media and substrates to cell–cell communication and gene expression in individual cells. The biomechanical interactions arising from the growth and division of individual cells in confined environments are ubiquitous, yet little work has focused on this fundamental aspect of colony formation. We analyze the spatial organization of Escherichia coli growing in a microfluidic chemostat. We find that growth and expansion of a dense colony of cells leads to a dynamical transition from an isotropic disordered phase to a nematic phase characterized by orientational alignment of rod-like cells. We develop a continuum model of collective cell dynamics based on equations for local cell density, velocity, and the tensor order parameter. We use this model and discrete element simulations to elucidate the mechanism of cell ordering and quantify the relationship between the dynamics of cell proliferation and the spatial structure of the population.

Morphogenesis is a highly important theme in both biology and nonequilibrium physics. The fundamental issue is to understand how the local interactions of elementary components lead to collective behavior and the formation of highly organized systems. In nature, this self-organization can lead to significant selective advantages for living organisms and is found on many levels, from biomolecules and single cells to schools of fish and herds of animals. Recent findings indicate that bacteria actively migrate toward surfaces and small enclosed spaces, where they form high-density microcolonies to facilitate quorum sensing (1). To resist environmental stresses, some species of bacteria form biofilms (2–4), which are commonly present in both natural environments (including living tissues, soils, and aquatic systems) and on synthetic surfaces (such as industrial piping and device implants). Generally, the collective dynamics of such cell populations involve a complex interplay of various physical, chemical, and biological phenomena such as chemotaxis (5), motility (6), cell–cell signaling (7), adhesion (8), and gene regulation (9).

An important unexplored consequence of the formation of high-density bacterial colonies is spatial organization caused by the “contact biomechanics” arising from cellular growth and division. At low density, communication among cells occurs mainly through chemotaxis, but as bacteria aggregate and form dense communities, direct biomechanical interaction plays an increasingly strong role in colony organization. Although previous studies have explored the complex signaling mechanisms involved in the early stages of biofilm formation, the biomechanics of direct cellular contacts have received little attention. To address this issue, we focus here on the essential structure and dynamics of a growing 2D colony of nonmotile bacteria within a controlled microfluidic environment. In isolating this aspect of colony development, we are able to develop a precise quantitative understanding of the role of biomechanical interactions in the formation of highly organized bacterial colonies. We combine experimental observations and analysis with discrete element simulations (DES) and theoretical modeling to provide a multiscale description of cell colony growth. Our results reveal how cell growth and colony expansion trigger the formation of the orientational (nematic) order in the population, which, in turn, affects the mechanical and biochemical properties of the colony.

Results

To explore the biomechanical effects of bacterial colony growth, we used nonmotile Escherichia coli that possess a rod-like structure with a length-to-diameter ratio that varies between two and five depending on the age of the cell (Fig. 1 A–C). The cells were loaded into a custom-designed microfluidic device containing a long and narrow open channel (30 × 500 × 1 μm³) where a monolayer of cells could grow under constant environmental conditions. The colony structure was recorded every 2 min by using time-lapse microscopy and subsequently analyzed by using specially designed segmentation and tracking software. Further details of the experimental protocol can be found in supporting information (SI) Text. After extraction from the images, cell positions and orientations were used to compute coarse-grained density, velocity, and orientation fields. The degree of orientation was characterized by the orientational order parameter, Q = [<cos 2φ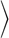² + <sin 2φ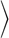²]^1/2, where φ is the angle between the cell axis and the channel axis, and brackets denote averaging over the whole system. This order parameter ranges from 0 for a completed disordered colony to 1 for a colony that is completely aligned (see SI Text).

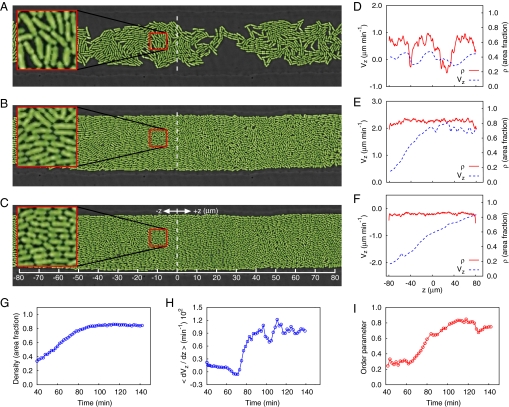
Fig. 1.

Experimental results for bacterial growth and ordering from an evenly distributed low-density seeding of cells. (A–C) Three snapshots of E. coli monolayer growth and ordering in a quasi-2D open microfluidic cavity taken at 60, 90, and 138 min from the beginning of the experiment. (D–F) Velocity and density profiles along the channel corresponding to the snapshots to the left. (G–I) Time traces of mean density, velocity gradient, and order parameter.

We characterized colony growth and ordering in an open channel microchemostat (Figs. S1 and S2). Initially, a small number of randomly oriented cells were spread throughout the channel (data not shown), and a slow flow of medium with negligible drag force on the cells was supplied (10). Constrained by the narrow 1-μm height of the microfluidic channel and lacking flagella, the bacteria remained motionless during the initial growth phase. After about three generations (60 min; Fig. 1 A and D), the cells began to mechanically push each other and generate a macroscopic expansion flow. At that time, the colony still remained disordered, as demonstrated by the low value of the order parameter (Q ≈0.2; Fig. 1I). At a later stage (90 min; Fig. 1 B and E), the density in the left part of the field of view reached a close packing regime, so the expansion flow amplified to accommodate cell proliferation. Based on a measurement of the gradient of the flow velocity along the channel (dV_z/dz ≈0.023 min⁻¹), we estimate the cell doubling time at this stage to be t_d = ln2[dV_z/dz]⁻¹ ≈30 min, which agrees well with the typical log-phase division period of E. coli. The increasing outgoing flux at this point was accompanied by a rapid orientation of cells along the direction of flow as indicated by the appreciable growth of the order parameter (Fig. 1I). Eventually, a quasi-stationary regime was established, with nearly constant density and velocity gradient and a high degree of cell orientation along the channel axis (138 min; Fig. 1 C and F). At this stage, the expansion velocity gradient had decreased by around half (dV_z/dz ≈0.012 min⁻¹), corresponding to a slower cell doubling time of ≈60 min. This finding corroborates earlier evidence of the slowing of cell growth rate in response to high mechanical pressure (11), although we note that other factors such as a decrease in nutrient concentration or an increase in waste concentration could be acting in conjunction. At this final stage, the cells in the chambers are nematically ordered along the axis of the channel, which coincides with the direction of the expansion flow. Our main conjecture from this experiment is that the nematic ordering of cells is driven by the self-generated growth-induced expansion flow. It is in marked contrast with thermal systems such as liquid crystals and polymers, where nematic ordering is driven by steric exclusion of rod-like molecules and a corresponding entropy maximization (12).

To understand the mechanism of cell ordering during colony growth, we first developed a continuum model of the colony dynamics derived from the general equations of nematodynamics (13) suitably generalized to include the effects of cell growth and division (see SI Text). These equations describe the temporal evolution of coarse-grained density, ρ(x, z, t), velocity, v = (v_x, v_z)(x, z, t), pressure, p(x, z, t), and tensor order parameter, Q(x, z, t), characterizing local cell orientation. We assume that the cell density grows exponentially at a rate α and that this growth does not have a direct effect on local orientation because offspring maintain the orientation of their mother cell just after division. However, the exponential increase in cell mass increases the pressure within the colony, which generates an expansion flow that leads to cell ordering. For flows in long channels, the continuum model may be formulated in terms of dynamical equations for the amplitudes of the coarse-grained fields (model A; see Fig. 2 and Materials and Methods).

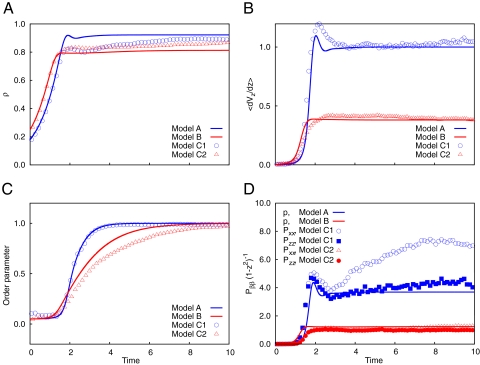
Fig. 2.

Comparison of continuum and DES modeling of the bacterial growth. Shown are time traces of the amplitudes of density (A), velocity gradient (B), order parameter (C), and stress components for constant growth rate (D) (A = 2.0; models A and C1) and pressure-dependent growth rate (A = 4.0; models B and C2). Results of the continuum modeling are indicated by lines, and results of the DES simulations are indicated by symbols. Parameters of continuum models A and B are: L = 1, P = 10, s = 0.4, ρ_c^d = 0.62, ρ_c⁰ = 0.7, B = 1, μ = 8, α₀ = 1, p_c = 1.6.

To accommodate the constant cellular growth rate, α, the expansion flow in the asymptotic regime must have a longitudinal velocity profile v(z) = αz (in dimensional form). This velocity profile is driven by a parabolic pressure distribution, p = αL²/μ(1 − z²/L²), where L is the half-length of the channel and μ is the friction coefficient, thus the pressure in the middle of the channel (z = 0) scales as L² and for long channels may reach high values. There is experimental evidence that high pressure affects cell function and in particular can slow down or stop cell growth (11). This effect, in turn, helps to alleviate the pressure buildup in large colonies. We also observed a significant slowdown of the cell growth at the late stage of the colony development (see above). To incorporate this effect, we replaced the constant cell growth rate, α, in the model by α₀[1 − (p/p_c)²], with a certain critical value of pressure, p_c, at which cell growth terminates (model B). This model leads to similar dynamics; however, saturation occurs at much smaller values of pressure and velocity gradient in the bulk of the colony (Fig. 2). We discuss a possible implication of this effect below.

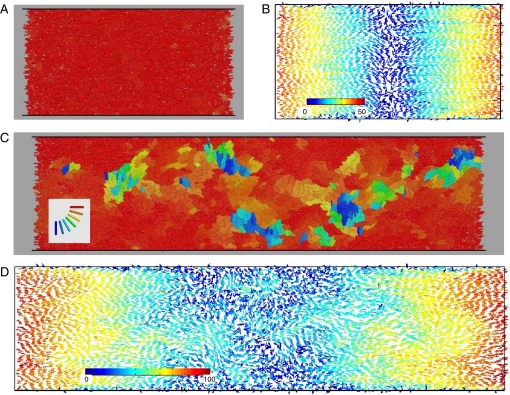
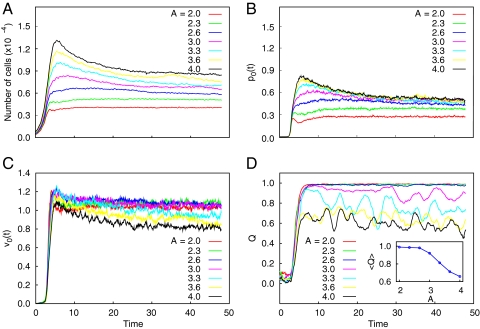
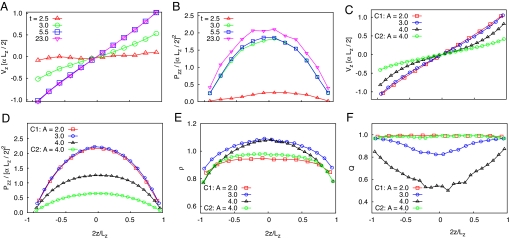
Continuum models aid in understanding the basic biomechanical mechanisms of cell–cell interaction and ordering and can guide our intuition in designing engineered biofilms. However, to make quantitative predictions, a more detailed description of biofilm structure is needed. To augment the experiments and calibrate our continuum models, we carried out detailed DES of the cell dynamics and interactions (models C1 and C2 for constant and pressure-dependent growth rates, respectively; see SI Text and Figs. S3 and S4). We used DES to explore the effect of channel length on colony ordering (Fig. 3). For simulations within a short channel, complete order was established, with almost all cells oriented along the channel (Fig. 3A). However, for simulations within a long channel, the population remained in a disordered state characterized by large “swirls” (Fig. 3C). This difference can also be seen in velocity profiles obtained by coarse-graining the velocities of individual cells (Fig. 3 B and D). In Fig. 3 arrow color indicates the magnitude of the velocity field, from blue (low) to red (high). Also, we observe that the velocity averaged over the cross-section of the cavity is a linear function of the distance from the center of the cavity. This linear elongational flow is consistent with mass conservation, which stipulates that local cell growth must be balanced by mass expansion toward the open ends of the channel, where the resulting velocity gradient is equal to the cell growth rate, α. Fig. 4 illustrates the evolution of the population size, pressure in the middle section, mean velocity gradient, and mean order parameter in DES of colony growth in open channels of different aspect ratios ranging from A = 2 to A = 4 for the pressure-independent growth model. These plots show the transition from a highly ordered regime in short channels (A < 3) to a partially disordered asymptotic regime in long channels (A > 3). Fig. 5 depicts the profiles of flow parameters averaged across the channel cross-section (velocity, pressure, density, order parameter) plotted against channel length for different system aspect ratios. As seen in Figs. 3–5, there is a clear transition from a completely ordered stationary regime in short channels (Q → 1) to a partially disordered stationary regime in longer channels with a minimum near the middle of the channel (Q ≈ 0.6 … 0.8). The nature of this transition is presently unknown but is apparently related to the high values of pressure in the middle of the cavity and the corresponding strong expansion flow. Indeed, in our simulations of a modified system in which the cellular growth rate was not constant but pressure-dependent, high nematic order was observed in both short and long channels.

Fig. 3.

DES of the ordering dynamics in channels with different aspect ratios. (A) Orientation of individual cells (color-coded) in the system with A = 2.0 and a constant growth rate (model C1). (B) Velocity field for the same case as in A, where unit velocity vectors show the velocity direction for each cell and colors (from blue to red) correspond to the velocity magnitude (from low to high). (C) The same as A, but for a twice longer system (A = 4.0). Defects of the orientation are constantly created in the middle of the channel and advected by the flow toward the open boundaries. (D) The same as B, but for a twice longer system (A = 4.0). The flow is no longer laminar, and there is no apparent correlation between orientation and velocity magnitude.

Fig. 4.

DES of bacterial growth for the pressure-independent growth condition (model C1) in channels with different aspect ratios, varying in the range A = 2–4. For each aspect ratio, we show the time evolution of the total number of cells within the channel (A), the pressure in the middle of the channel (B), the mean velocity gradient (C), and the averaged order parameter (D). (D Inset) The decay of the asymptotic value of the order parameter with the aspect ratio, A. Time is measured in units of the inverse growth rate.

Fig. 5.

Spatiotemporal dynamics of bacterial growth generated by using DES. (A and B) Evolution of profiles of velocity and pressure along the channel in the short system (A = 2). (C–F) Stationary profiles of the velocity, pressure, density, and order parameter for channels of different aspect ratios: A = 2, 3, 4 for the case of constant growth rate (model C1) and A = 4 for the case of pressure-dependent growth rate (model C2).

To test the validity of the continuum modeling, we compared the results of the DES (models C1 and C2) with models A and B. Fig. 2 shows the results of this comparison for simulations in a short channel with pressure-independent growth (models A and C1) and in a long channel with pressure-dependent growth (models B and C2). Except for replacing the constant growth rate, α, by α₀[1 − (p/p_c)²], all parameters were kept the same. In both cases, the continuum model provides a good description of the colony dynamics, indicating that the cell density grows at a similar rate and saturates near the close-packed limit (Fig. 2A). However, both the pressure and the ensuing expansion flow in the pressure-dependent growth case (models B and C2) are almost two times smaller (Fig. 2 B and D), and the cellular ordering is proportionally slower (Fig. 2C). Interestingly, pressure-dependent growth leads to the isotropization of local stresses, as evidenced in Fig. 2D. This effect may be attributed to the ability of slower-growing cells to better adjust to local contact stresses.

Discussion

In natural environments, bacterial colonies often grow from a few cells or even a single cell. In this case, the colony has a well defined boundary that expands during cell growth. Although it is a more difficult system for continuum modeling, we performed experiments and DES to test the ordering mechanism. Our results show that rapid ordering occurs in this case as well (see SI Text and Fig. S5). Because colony dynamics are essentially nonuniform, a proper continuum description should go beyond the ordinary differential equation model presented above. We anticipate that many interesting issues will arise naturally in this context, including ordering front propagation, coarsening, and defect formation. However, the analysis of these phenomena goes beyond the scope of this publication.

In summary, we have shown that purely biomechanical short-range interactions can lead to highly ordered structures in a growing bacterial population. Our central finding is that the nematic ordering of cells is mediated by the expansion flow generated by cellular growth. This phenomenon is fundamentally different from the nematic transition in liquid crystals and polymers (13) and vibrated granular rods (14, 15), where ordering is primarily driven by the combination of steric exclusion and fluctuations. The mechanism of the ordering transition reported here is related to cell growth and therefore should be ubiquitous in “living granular matter.” However, as there are a number of other factors that affect the collective dynamics of cellular colonies in natural environments (adhesion, motility, chemotaxis, etc.), a determination of the relative importance of biomechanical ordering within this larger context awaits future studies.

Materials and Methods

Microfluidics.

The design of the microfluidic device used in these experiments was adapted from the Tesla microchemostat design developed in ref. 10 for use with Saccharomyces cerevisiae. Modifications were made to support imaging monolayers of E. coli, including lowering the cell chamber height from 4 μm to 1 μm to match the cylindrical diameter of cells of the K-12 MG1655 strain, lowering the delivery channel height from 12 μm to 3 μm to maintain equivalent flow splitting between the cell chamber and the bypass channel, and dividing the cell trapping region into three channels for simultaneous observation of isolated colonies (Fig. S1A). Devices were fabricated in the University of California at San Diego Integrated Technology Laboratory using standard soft lithography techniques (16–19). Photomasks were drawn in FreeHand MX (Macromedia), printed onto transparency film by CAD/Art Services, and mounted onto borosilicate glass plates (McMaster-Carr). Master molds were created by first spin-coating SU-8 2000 negative photoresists (MicroChem) upon clean silicon wafers to appropriate depths by using a Headway PWM32 programmable spinner and then patterning with a UV contact mask aligner (HTG). Replica molds were created from master molds by mixing PDMS/Sylgard 184 (Dow Corning) in a 10:1 (elastomer base/curing agent) ratio, degassing in a vacuum desiccator at −1 atm for 1 h, and curing in place over the master at 80°C for 2 h. After removal of the PDMS monolith, chips were sectioned, bored at the fluidic ports, cleaned with HPLC-grade methanol, and permanently bonded to clean no. 1½ coverslips (Corning) via exposure to O₂ plasma at 30 W for 1 min in a 500-II Plasma Asher (Technics Plasma).

Time-Lapse Microscopy.

All images were acquired with an Orca-ER cooled CCD camera (Hamamatsu Photonics) mounted on a Diaphot TMD epifluorescent inverted microscope (Nikon) outfitted with fluorescence excitation and emission filter wheels (CFP/YFP/DsRed filter set 86006; Chroma Technology), an XY motorized stage with fine-focus control (Prior Scientific), and Uniblitz VS35 high-speed shutters (Vincent Associates). In each experiment, a microfluidic device was mounted to the stage and then wetted by using a solution of 0.1% TWEEN 20 surfactant (Sigma–Aldrich) in LB media. Thermal control was maintained by connecting high-volume fluidic channels fabricated into the device to a reciprocating heated water bath. Cells were loaded into the device from the cell port by directing high flow both from the cell port and the media port to the waste port. Upon trapping a single cell in each channel, flow past the cell chamber was reversed and slowed to 1–2 μm/s such that fresh nutrients were delivered from the media port via a combination of diffusion and advection without physically disturbing the cells. Flow was consistently directed from the media port throughout the loading and running process to minimize contamination and device clogging. During run time, images of cell growth were collected at ×100 in the transmitted channel every 2–3 min over ≈4–6 h. To capture a complete profile of the system at each time point, three slightly overlapping images were acquired for subsequent stitching into a 1 × 3 montage. Image acquisition and XY scanning were automated via a custom application written in LabVIEW (National Instruments), while focus was maintained throughout the experiment by manual adjustment. After each imaging session, positions and orientations of individual cells were determined by using a custom image segmentation software suite written in IDL (ITT Visual Information Solutions).

Continuum Modeling.

For the description of the expansion flow in a straight open channel of length 2L, we can assume that all fields depend only on time and coordinate −L < z < L along the channel. The equations of nematodynamics adapted for a growing cell colony have the form: (see SI Text)

where q is the zz component of the tensor order parameter (which in the 1D case coincides with the magnitude, Q), v is the z component of the cell velocity, α is the cell growth rate, μ is the bottom friction coefficient (we assume that the friction force is proportional to the cell velocity and independent of the orientation), and the pressure, p, satisfies the constitutive relation

This relation implies that the pressure is exponentially small for ρ < ρ_c (parameter s is large), and exponentially large for ρ > ρ_c.^‖ The close-packing density, ρ_c, is itself a function of the order parameter, q, where more ordered populations have higher close-packing densities. We model this dependency by the relation, ρ_c = ρ_c^d + (ρ_c^o − ρ_c^d)q², where ρ_c^d and ρ_c^o are critical densities of disordered and ordered rods, respectively. The dimensionless parameter B describes the rate of ordering driven by the velocity gradient.

These equations admit a solution with nonstationary but uniform density and order parameter along the channel and linear and parabolic longitudinal profiles of velocity and pressure, respectively. The amplitudes of these fields satisfy the following dynamical equations:

where v = v₀(t)z, p = p₀(t)[1 −(z/L)²], and p₀ = P exp[s(ρ − ρ_c(q))]. This system with α = α₀ = const comprises the basic dynamical model of bacterial growth and ordering (model A). Model B differs from model A in that the cell growth rate, α, depends on the pressure, p, as α = α₀[1 − (p/p_c)²]. Time traces of the density, the velocity gradient along the channel, the order parameter, and the pressure predicted by the models are depicted in Fig. 2. In agreement with our experimental observations, the density of cells initially grows exponentially and then saturates near the random close-packing density. At this time, the pressure grows rapidly and triggers an expansion flow. After emergence of the expansion flow, the order parameter begins to grow, with the system eventually reaching a final state characterized by a density approaching the close-packed density of completely ordered rods and an order parameter, Q, close to 1.

We note that extensive work has already been performed on the role of shear flow in the isotropic-nematic transition in liquid crystals (see, for example, ref. 20). However, in ordinary liquid crystals, thermodynamic entropic effects play the primary role in molecule ordering, and the shear flow only modifies the transition. In the biological realm, cells have zero effective thermodynamic temperature, and therefore entropic alignment is absent. Furthermore, cell growth produces not shear but expansion flow, which as we show here leads to the rapid ordering of cells.

DES.

To simulate the motion, growth, and interaction of bacteria, we model every cell as a horizontal rod (spherocylinder) moving within a 2D space. The motion of a cell is affected both by elastic and frictional forces exerted by the walls of the microfluidic chamber and by interactions with other cells. To compute these forces, we use a variant of the soft particle molecular dynamics simulation technique (21), which calculates forces from the overlaps between particles. The interaction between overlapping spherocylinders is modeled as the interaction between viscoelastic virtual spheres of the same diameter as the spherocylinders, centered at the closest points between the axes of the spherocylinders such that the cylinders are in contact whenever the virtual spheres are. The normal forces between virtual spheres are computed by using the Hertzian model, and the tangential frictional forces are computed by using dynamic Coulomb friction. Each cell also experiences a frictional force and a torque that are proportional to the cell linear and angular velocities, respectively. These forces simulate cellular interaction with the top and bottom surfaces in a shallow microfluidic channel.

Over time, the length of a cell grows exponentially until it reaches a critical value. At this point, the cell divides into two daughter cells, which continue to grow independently. This process of growth and division repeats for each cell, resulting in an exponential growth of the population. We assume that cells divide when their length reaches a maximal length, l_m, which is drawn from a Gaussian distribution near a fixed length, l₀, with a coefficient of variation of 0.3. The sizes of the two daughter cells are taken from a peaked distribution near l_m/2 to avoid spurious synchronization of cell division events. The growth rate, α, of the cells is constant in model C1 and depends on the pressure (sum of normal components of the stress tensor acting on the individual cell) in model C2. In all models, we neglect the influence of media flow. Further description of these algorithms can be found in SI Text.

Note Added in Proof.

After submission of this paper, the results of a similar investigation were reported by Cho et al. (22).