Dissociation of minor groove binders from DNA: insights from metadynamics simulations

Abstract

We have used metadynamics to investigate the mechanism of noncovalent dissociation from DNA by two representatives of alkylating and noncovalent minor groove (MG) binders. The compounds are anthramycin in its anhydrous form (IMI) and distamycin A (DST), which differ in mode of binding, size, flexibility and net charge. This choice enables to evaluate the influence of such factors on the mechanism of dissociation. Dissociation of IMI requires an activation free energy of ∼12 kcal/mol and occurs via local widening of the MG and loss of contacts between the drug and one DNA strand, along with the insertion of waters in between. The detachment of DST occurs at a larger free energy cost, ∼16.5 or ∼18 kcal/mol depending on the binding mode. These values compare well with that of 16.6 kcal/mol extracted from stopped-flow experiments. In contrast to IMI, an intermediate is found in which the ligand is anchored to the DNA through its amidinium tail. From this conformation, binding and unbinding occur almost at the same rate. Comparison between DST and with kinetic models for the dissociation of Hoechst 33258 from DNA uncovers common characteristics across different classes of noncovalent MG ligands.

INTRODUCTION

In the last decades, many complexes between DNA and drugs targeting the minor groove (MG) have been extensively studied using experimental biophysical techniques as well as molecular simulations (1–13). In contrast, the structural determinants and relative energies playing a role in molecular recognition have been poorly characterized (14–20), despite their relevance for rational drug design (21,22). Recognition is known to be a complex process that may involve several steps before formation of the most stable adduct: both noncovalent (17,19,23) and covalent (16,24) binders may exploit mechanisms like one-dimensional sliding within the MG and translocation among different sites (involving binding and dissociation) (10,25–28). In particular, the importance of dissociation for the selectivity and the affinity of different MG binders has been pointed out by several experimental studies (17,18,23,29,30). Such an experimental effort has not been accompanied yet by a thorough theoretical investigation, which would be certainly fundamental to address the mechanism and the energetics of detachment at a molecular level.

Dissociation of a ligand from DNA generally occurs on a time scale not reachable by standard molecular dynamics (MD) simulations; thus, enhanced-sampling methods are needed to perform such an investigation. Fortunately, in the last years the development of novel methods to accelerate rare events (31), along with the increased reliability of force fields (32–36) and simulation protocols (37,38), enabled nonequilibrium dynamics of complex biological systems to be characterized (39–43). Among them, metadynamics (44) has been largely used to identify mechanisms of and to extract free energies associated with biologically relevant processes (45–47). In particular, the technique has been successfully applied to get insights on aspects of the molecular recognition of proteins by small ligands (48,49), while, to the best of our knowledge, it has never been exploited to investigate the dynamics of ligand/DNA systems.

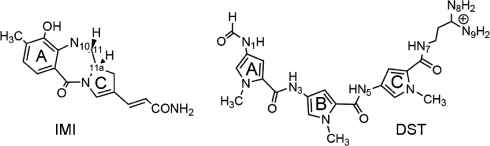
In this work, the first computational study is presented on the dissociation of MG binders from DNA, as one of the key events of the translocation among different sites [notice that the binding mechanism of the intercalating agent daunomycin has recently been described (20)]. Within the framework of classical MD, we have used metadynamics to explore the influence of size, flexibility and charge of the compounds on the detachment mechanism. The comparison has been performed on two representatives of noncovalent and covalent MG binders which differ in the properties listed above, considering their noncovalent adducts with DNA duplexes. The prototype of noncovalent binders is distamycin A (50) (hereafter DST, Scheme 1), which is positively charged, quite flexible and highly selective towards AT-rich tracts (51,52), due to H-bonding between its amide nitrogens and N3(A) and/or O2(T) of DNA (22,53–55). The alkylating agent is anthramycin (56,57), here considered in its most reactive anhydrous form (10,58) (hereafter IMI, Scheme 1). In contrast to DST, anthramycin is neutral, rather rigid, and manifests only a modest preference towards PuG*Pu triplets (59), the asterisk indicating the alkylated guanine. Both compounds have shown to exert an antitumoral action by interfering with transcription (6,54,60–62) and replication (57,63,64) processes, and their derivatives are currently undergoing clinical trials as anticancer drugs (65–72).

Scheme 1.

Besides the general motivation outlined above, additional reasons have guided our choice of the compounds. First, structural information of the drug/DNA noncovalent complexes is available: the X-ray structure of the complexes between DST and duplexes d[GGCCAATTGG]₂ and d[CGCAAATTTGCG]₂ has been solved (51,52), whilst that of a noncovalent complex between IMI and the 14-mer d[5′-CAACGTTGGCCAAC-3′]₂ has been recently modeled by the authors (10,28), starting from the experimental structure of the covalent complex (56). Second, the dissociation rate constant of DST from the 10-mer d[GCGATTAGCG]₂ (which is the same duplex used in our simulations) has been derived from stopped-flow experiments (19), enabling the direct comparison between calculated and experimental activation free-energy barriers of the process. Since the duplex d[GCGATTAGCG]₂ is not palindromic, the two possible binding orientations of DST have been considered to pinpoint their possible influence on the escaping process.

Our calculations provide a microscopic picture of the dissociation of the two molecules, along with the free energy surfaces (FESs) associated with the process. To identify relevant conformations and to estimate more accurately the associated free energies, the lowest free-energy path (LFEP) (73), which is equivalent to an intrinsic reaction coordinate (IRC) and gives the minimum cost path of detachment, has been evaluated on the FESs. Such an approach has been successfully used in previous works on biochemical relevant processes (74–76).

Our simulations pinpoint relevant similarities and differences between the dissociation mechanisms of the two compounds. Additionally, our results are in good agreement with the available kinetic data extracted from stopped-flow experiments for DST (19), furnishing molecular-level details on the dissociation that are not available to experiment. Finally, the comparison of the mechanism we found for DST with a kinetic model proposed for the binding/unbinding of the dye Hoechst 33258 suggests the existence of very similar recognition routes followed by different classes of MG binders.

MATERIALS AND METHODS

Systems

The DST•d[5′-GCGATTAGCG-3′]₂ (in bold the binding sequence) complex was built by taking the ligand from the X-ray structure of its adduct with the duplex d[GGCCAATTGG]₂ [PDB code 1JTL (51)], and by building the 10-mer using the nucgen module of AMBER (77,78). Since the DNA sequence is not palindromic, two nonequivalent orientations of the ligand inside the MG were considered. In one (hereafter called DST•DNA), the amidinium group of DST is in contact with the tract d[A₇G₈]₂; in the second pose (hereafter DST•DNA′), the same group is close to the tract d[G₃A₄]₂. Both orientations resulted in stable adducts after 6 ns of MD simulations (vide infra). The initial structure of the noncovalent complex IMI•d[5′-CAACGTTGGCCAAC-3′]₂ was extracted from a previous MD simulation (10). There the adduct was built starting from the X-ray structure of the covalent complex between anthramycin and the 10-mer d[5′-CCAACGTTG*G-3′]₂ [PDB code 274D (56)], the asterisk labeling the covalently modified base. The binding sequence assumed as starting configuration in the present work is adjacent to that in the covalent complex, and has been shown to be a more stable free-energy minimum (28). In addition, 6 ns long simulations were performed of the free-standing duplexes d[5′-GCGATTAGCG-3′]₂ and d[5′-CAACGTTGGCCAAC-3′]₂, as well of the ligands IMI and DST, in solution.

Parameterization

The PARMBSC0 refinement of the parm99 force field (32,33) was used for the parameterization of the oligonucleotide moieties, while force field parameters for IMI were taken from ref. (10). Parameters for DST were calculated following the standard AMBER procedure, using the gaff force field (79), except for the charges, which were evaluated according to the RESP approach: the ligand was firstly optimized at the HF/6-31G(d) level up to a convergence in energy of 10⁻⁵ AU using the Gaussian03 (80,81) package. The CPCM (82) implicit solvent model was employed to mimic the presence of the solvent, in order to avoid formation of intramolecular H-bonds due to the in vacuo conditions. A second restrained optimization was then performed at the same level of theory but in vacuo, and the electrostatic potential map generated by the molecule was then calculated [this protocol ensure to extract atomic charges consistent with the AMBER force field (83)]. From the potential the atomic RESP (84) charges were derived using the antechamber module of the AMBER package (78).

MD calculations

The neutrality of the systems was achieved through the addition of sodium counter-ions (18 in DST•DNA and in the corresponding simulation of the free-standing duplex; 22 in IMI•DNA and in the corresponding simulation of the free-standing duplex; 1 in the simulation of the free-standing DST) modeled with the AMBER-adapted Aqvist (85) potential. Resulting structures were solvated within a monoclinic box containing 10 246 (DST•DNA), 9827 (DST•DNA′), 6719 (d[5′-GCGATTAGCG-3′]₂), 13 611 (IMI•DNA), 8723 (d[5′-CAACGTTGGCCAAC-3′]₂), 3278 (IMI) and 4097 (DST) water molecules, described by the TIP3P (86) potential. Periodic boundary conditions were applied. The initial sizes of the boxes were 60 × 84 × 69 ų, 57 × 80 × 69 ų, 57 × 56 × 69 ų, 75 × 80 × 72 ų, 59 × 80 × 62 ų, 47 × 47 × 48 ų and 52 × 52 × 52 ų in DST•DNA, DST•DNA′, d[5′-GCGATTAGCG-3′]₂, IMI•DNA, d[5′-CAACGTTGGCCAAC-3′]₂, IMI and DST respectively. This choice ensures that the minimum distance between solute images is >25 Å during the whole dissociation process.

Electrostatic interactions were treated using the particle mesh Ewald (37) (PME) algorithm with a real space cutoff of 10 Å, the same as for van der Waals interactions. The pair list was updated every 10 steps, and Lincs constraints (87) were applied to all bonds involving hydrogen atoms, permitting a time step of 2 fs. NPT conditions were achieved by coupling the systems to the Nosé–Hoover (88,89) thermostat (τ = 1 ps) and the Andersen–Parrinello–Rahman (90,91) barostat (τ = 1 ps).

The systems were equilibrated using the following computational procedure: (i) structural optimization of the solvent, using the conjugate gradient algorithm; (ii) energy minimization of the entire system, using the same convergence criteria as in (i); (iii) linear heating of the system up to 300 K in 100 ps, while imposing harmonic restraints on the solute (k = 5 kcal/Ų); (iv) 5 ns of constant temperature–pressure (T = 300 K, P = 1 atm). This temperature, although lower than that of the human body, is virtually the same at which the available kinetic measurements in vitro have been performed, i.e. 298 K (19).

Starting structures for metadynamics were taken from the last nanosecond of MD, selecting those with the lowest RMSD with respect to the average structure of the solute (also calculated within the last nanosecond). The MG width of DNA was defined by taking the distances between sugar C4′ atoms, and calculated with the program Curves (92–94). All simulations were carried out using a modified version of the GROMACS (95–97) package implemented with metadynamics (46).

Metadynamics

Dissociation of the ligands was investigated by metadynamics (44), a method to compute free energies and to accelerate rare events. The algorithm is based on a dimensional reduction: a set of collective variables (CVs) s_i (i = 1,…, N_CVs), function of the coordinates of the system x = {x₁, x₂,…, x_N}, where N is the number of particles, is evolved with a standard MD supplemented by a history-dependent potential, discouraging the system from visiting previously sampled conformations. In the standard implementation the history-dependent potential is built-up by Gaussians of N_CVs-th dimension, height w and widths δs_i (i = 1,…, N_CVs), deposed at time intervals τ_G along the CVs trajectory. In the limit of a long metadynamics run, the sum of these penalty terms tends to compensate exactly the underlying FES in the reduced space, permitting a reconstruction of the FES explored up to time t (98).

The CVs used here to describe IMI and DST dissociation are:

1. The distance d_CMs between the centers of mass of the ligand and of the DNA tracts d[GTTGG]₂ and d[CATTAC]₂ (for IMI and DST, respectively). A similar choice of CVs has been applied, e.g. in ref. (49).

2. The number of hydrophobic contacts n_hph between nonpolar carbons on the ligand and on the bases covered by the ligand in the starting structure, modeled as a coordination number:

   1

   The parameters a and b have values of 6 and 12, respectively, while r₀ = 6 Å accounts for the typical carbon–carbon distance (4/4.5 Å) and the thermal motions’ amplitude (1.5/2 Å). A similar CV has been used in refs (48, 99).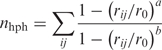

3. The number n_hb of H-bonds between the ligand and the bases that it covers in the starting structure, described also by Equation (1) with a = 8, b = 12 and r₀ = 2.5 Å. A similar CV has been chosen in refs (45, 46).

The choice of the Gaussian parameters is crucial. Here, the height w has been chosen following both theoretical suggestions and previous experience on similar problems (47,49,98), to be ∼0.024 kcal/mol (0.1 kj/mol) and ∼0.072 kcal/mol (0.3 kj/mol) for IMI and DST, respectively. Concerning the widths of the Gaussians, as a rule of thumb they should be ∼1/3 of the typical fluctuations of the CV during a free MD (49); following this rule, we have chosen δs_CMs = 0.5 Å, δs_hph = 6 and δs_hb = 1 in the case of IMI, δs_CMs = 0.5 Å, δs_hph = 6 and δs_hb = 3 for DST. The time interval between two successive Gaussian depositions was set to 0.5 ps in all the simulations.

FESs for IMI•DNA and DST•DNA were calculated as a function of (d_CMs, n_hph) and (d_CMs, n_hb); in addition, simulations were performed in which the three CVs were kept active. In every metadynamics run, the dissociation event was observed after a few nanoseconds (see Supplementary Table S1). In the case of DST•DNA′, we initially used d_CMs and n_hb as active variables: as we obtained dissociation mechanism and a free-energy landscape similar to those found in DST•DNA (vide infra), no additional simulations were performed. The activation free energies associated with the detachments were extracted by stopping the summation over Gaussians just after the complete detachment of the drug (49). Notice that no estimation of the binding free energy has been done in the present work. This would require (even in the presence of additional restraints) a more extensive simulation, and goes beyond the scope of the present article. It is also worth pointing out that the bias introduced by metadynamics has been shown to unaffect a proper reconstruction of the entropy, which converges as fast as the free energy and has the same accuracy (100).

For the sake of clarity, we show here only the free-energy profiles as a function of d_CMs and n_hph in case of IMI•DNA and as a function of d_CMs and n_hb in case of DST•DNA. The average error associated with these free-energy profiles was evaluated as in ref. (48) after rescaling each CV to the size of the free energy well S* in the corresponding direction (98). Here, we used S*_CMs ≈ 0.2 nm, S*_hph ≈ 40 in the case of IMI•DNA, S*_CMs ≈ 0.3 nm, S*_hb ≈ 20 in the case of DST•DNA (and DST•DNA′), which gave of 1.6 and 2.2 kcal/mol, respectively.

LFEPs and structural/energetical analyses

The LFEP, which is the equivalent of the IRC at finite temperature, has been calculated on the FESs following the methodology of ref. (73). It has been shown that relevant minima, intermediates and transition states for the process under study can be identified along this path (74–76). To extract structural and energetic information on the process, a cluster analysis using the algorithm described in ref. (101) with a cutoff of 1.5 Å has been performed on the ensemble of configurations corresponding to relevant points along the LFEP. For each ensemble of structures, a dominant cluster has been found which is larger in size at least one order of magnitude with respect to the others. For this reason, the structural parameters and the contributions to the free energy were calculated by averaging over each principal cluster only. The free energy along the LFEP has been dissected into the following sources: (i) van der Waals and Coulomb energies, evaluated using the terms in the AMBER force field; (ii) entropy and free energy of hydration, evaluated as ΔC_p·ln(T/386) kcal/mol/T and ΔC_p(T − 295) kcal/mol (5,102). The heat capacity changes ΔC_p are calculated as ΔC_p = 0.32·ΔA_np − 0.14·ΔA_p cal/mol/K, where ΔA_np and ΔA_p are the variations in the hydrophobic (nonpolar) and hydrophilic (polar) surface areas, respectively (102).

It is worthy to point out that while calculated free energies are sufficiently accurate to enable comparison with experimental data, contributing sources have usually larger SDs, and will be used here only for qualitative comparison.

RESULTS

In this section, we analyze the mechanism of dissociation of IMI and DST from their respective DNA duplexes. In addition, we report the associated free energy barriers, as well as the changes in interaction energy, hydration and structure of the complexes. For DST, we considered both the orientations of the ligand within the MG (systems DST•DNA and DST•DNA′, see Supplementary Figure S1). Because of the similar mechanism and energetics of detachment found in the two systems, here we present results only for DST•DNA. The profile and the relevant differences in free energies associated with the detachment of DST in DST•DNA′ are collected in the Supplementary Material (Figure S2), along with a movie of the process (see ‘movie_DST_flip.mpg’ in the Supplementary Material). A small summary of our findings on DST•DNA′ is reported at the end of this section.

The free-energy surfaces were calculated as a function of variety of collective variables (or reaction coordinates), using the metadynamics method (44). Here, we report the free-energy surfaces G(d_CMs, n_hph) for IMI•DNA and G(d_CMs, n_hb) for DST•DNA, where d_CMs is the distance between the centers of mass of the ligand and of the DNA tracts it covers, n_hph the number of hydrophobic contacts, and n_hb the number of hydrogen bonds (the latter have been modeled through a coordination number, see section “Materials and Methods”). A virtually identical dissociation mechanism resulted from additional metadynamics simulations, in which different combinations of CVs were purposely selected (see section “Choice of the CVs” and the Movies in the Supplementary Material).

Before presenting in detail our main results, we would like to remark the following general points:

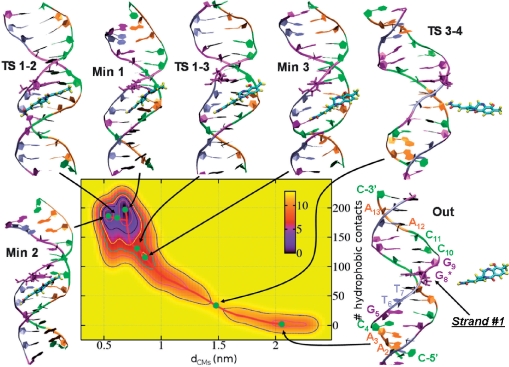
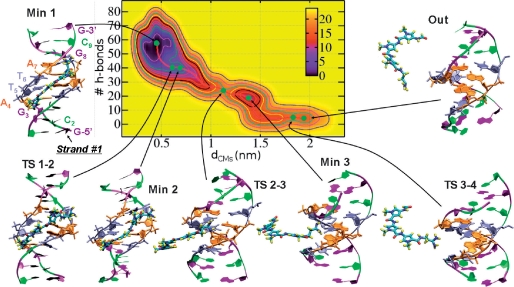
• Since we were interested in estimating the free-energy barriers of dissociation, simulations have been stopped once the ligand is completely detached from the DNA duplex. Thus, in conformations labeled as ‘Out’ in Figures 1 and 2, referring to the unbound state, the duplexes and the ligands do not have necessarily the structure of the correspondingly equilibrated free-standing systems (for example, residual interface waters could be present that have not yet relaxed). To compare the energetics of the systems (and, in particular the structural changes of the duplexes along the process) with respect to an equilibrated reference state, we have performed additional simulations of duplexes and ligands in solution. These simulations will be labeled as ‘Free’ in the following, the meaning being clear from the context (e.g. the free energy of hydration of IMI•DNA will be referred to the sum of those of IMI and DNA, while the structural distortions of the DNAs along the LFEP will be referred to the values extracted from the simulation of the free-standing duplexes).

• We have followed the conformational changes undergone by the duplexes and the ligands upon dissociation. In particular, we have analyzed bending, variations in the MG width and changes in the interbase-pair parameters twist, roll and tilt of the duplex. Although the DNA is undergoing significant structural changes in the process, the distortions turn out to be quite localized, and the duplexes always stay closer to B- than A-DNA form, without featuring overall bending. For this reason, we refer the reader interested in a discussion of local conformational changes and of their connection to kinks in the helical axis and/or changes in the MG width, to the Supplementary Information (Figures S5–S8).

Figure 1.

Free-energy surface G(d_CMs n_hph) associated with the dissociation of IMI from DNA. A LFEP (red line) is also shown connecting relevant minima and transition states (whose representative structures are also shown by green filled circles). Isosurfaces are drawn one per 2 kcal/mol. Labeling of nuclebases is indicated in the ‘Out’ configuration.

Figure 2.

Free-energy surface G(d_CMs n_hb) associated with the detachment of DST from DNA. Labeling of nucleobases is indicated in the ‘Min 1’ configuration. See Figure 1 for further details.

We start with the description of the dissociation of IMI from DNA. When not specified, all the values and the comparisons are referred to the absolute minimum (labeled ‘Min1’) of each system.

IMI

The initial structural model has been taken from the final configuration of a previous MD simulation (10) of the adduct IMI•d[5′-CAACGTTG*GCCAAC-3′]₂. In this configuration, the binding site of IMI, located in d[5′-TTG*-3′]₂, does not coincide with its alkylation site d[5′-TG*G-3′]₂: indeed, this structure corresponds to that found in ref. (10) after sliding of IMI along the MG, and it has been shown to be a minimum along the sliding pathway (28).

The FES G(d_CMs n_hph) corresponding to the dissociation of IMI, the associated LFEP and the relevant conformations of the complex are collected in Figure 1. There are two virtually isothermic global minima, separated by a small barrier of ∼3 kcal/mol (Table 1). In the first (Min1, the absolute minimum), located at d_CM ≈ 0.68 nm, n_hph ≈ 199, the drug is bound at the tract d[5′-TTG*-3′]₂ and stabilized by van der Waals and Coulomb interactions (Table 2); on average, a single H-bond is formed, involving bases G7, A21 and the hydroxyl group and N₁₀ of IMI.

Table 1.

Free energies (kcal/mol) associated with relevant configurations which define the LFEP in IMI•DNA (top) and DST•DNA (bottom, see also Figures 1 and 2)

IMI•DNA	Min 1	TS 1-2	TS 1-3	Min 2	Min 3	TS 3-4
dCMs, nhph	0.68, 199	0.61, 186	0.69, 133	0.54, 188	0.86, 117	1.47, 35
ΔG	0.0	3.0	6.7	0.7	5.7	12.3
DST•DNA	Min 1	TS 1-2	Min 2	TS 2-3	Min 3	TS 3-4
dCMs, nhb	0.45, 57	0.61, 40	0.69, 40	1.13, 24	1.38, 19	1.84, 5.3
ΔG	0.0	5.4	4.5	17.8	10.2	17.2

Values are calculated with respect to the absolute minimum (Min1).

Table 2.

Selected quantities (SD in brackets) calculated for the relevant conformations along the LFEPs of IMI•DNA (between IMI and tract d[5′-CGTTGGC-3′]₂, top) and DST•DNA (between DST and tract d[5′-CGATTAGC-3′]₂, bottom)

IMI•DNA	Min 1	TS 1-2	TS 1-3	Min 2	Min 3	TS 3-4
Coulomb	−8.4 (2.5)	−7.3 (2.4)	−4.8 (3.0)	−7.9 (2.4)	−2.9 (2.3)	−2.3 (1.3)
Van der Waals2	−38.1 (3.4)	−37.7 (4.9)	−22.2 (3.5)	−38.0 (4.3)	−19.4 (2.4)	−6.2 (2.2)
# H-bonds	0.9 (0.6)	0.7 (0.5)	0.5 (0.8)	0.7 (0.5)	0.2 (0.7)	0.0 (0.2)
TΔShyd	4.7 (9.8)	4.7 (9.8)	4.7 (9.8)	4.7 (9.1)	2.5 (9.8)	0.2 (9.1)
ΔGhyd	−5.0 (10.5)	−5.0 (10.5)	−3.4 (10.5)	−5.0 (9.7)	−2.6 (10.5)	−0.2 (9.7)
# H2OIMI	9.0 (1.7)	9.1 (1.6)	11.0 (2.3)	8.8 (1.7)	12.4 (2.2)	13.4 (2.4)
# H2Od[5′- CGTTGGC -3′]2	6.6 (1.3)	6.7 (1.1)	7.2 (1.1)	6.7 (1.2)	8.9 (1.2)	10.6 (1.0)
DST•DNA	Min 1	TS 1-2	Min 2	TS 2-3	Min 3	TS 3-4
Coulomb	−35.4 (5.3)	−20.6 (2.8)	−23.5 (5.6)	−20.8 (3.7)	−13.9 (5.2)	−18.2 (1.2)
Van der Waals2	−75.3 (4.6)	−59.5 (4.5)	−56.1 (2.4)	−21.1 (4.0)	−12.2 (2.3)	−0.9 (2.1)
# H-bonds	3.9 (1.0)	1.7 (0.8)	1.7 (0.8)	1.5 (0.7)	1.5 (0.7)	1.0 (0.2)
TΔShyd	13.1 (9.1)	11.6 (10.6)	9.4 (8.3)	5.3 (11.3)	3.3 (9.8)	0.5 (5.4)
ΔGhyd	−13.9 (9.7)	−12.3 (11.3)	−9.9 (8.9)	−5.8 (12.1)	−3.4 (10.5)	−0.5 (6.3)
# H2ODST	11.4 (1.9)	16.4 (1.9)	18.0 (1.5)	18.9 (3.2)	19.8 (2.5)	22.3 (3.7)
# H2Od[5′-CGATTAGC-3′]2	5.4 (0.8)	8.9 (1.6)	12.5 (0.7)	10.7 (1.1)	12.5 (1.1)	15.3 (1.3)

The Coulomb and van der Waals energies are reported in Kilocalories per mole (the values of Coulomb and van der Waals interaction energies in ‘Out’ are respectively 0.1 and 0.4 kcal/mol in IMI•DNA, and 0.1, 0.1 kcal/mol in DST•DNA). These are very approximate values and they are reported here only for qualitative comparisons. The hydration entropies (times the temperature) and hydration free energies are calculated as in ref. (102) and referred to the unbound system (i.e. to the sum of the same quantities extracted from simulations of free-standing duplexes and free ligands in solution). The number of intermolecular H-bonds and the number of waters within the first hydration shells of the ligand and of DNA tracts d[5′-CGTTGGC-3′]₂ (IMI) or d[5′-CGATTAGC-3′]₂ (DST) are also reported.

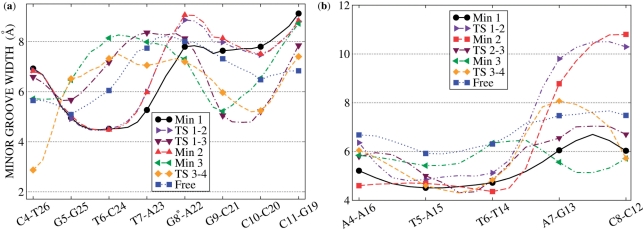
Min2 differs from Min1 only for a local deformation of the DNA duplex (the MG widens by ∼1 Å in the tract d[5′-TG*G-3′]₂, Figure 3a) rather than for a different position of the drug into the MG (Supplementary Figure S3). Consistently, these states feature very similar drug/DNA interaction strengths and hydration properties (Table 2). The two minima are separated by a transition state TS1-2 of ∼3 kcal/mol; in the conformation associated with TS1-2, the whole MG width profile virtually overlaps to that found in Min2 (Figure 3a), suggesting that this opening is related to the transition from Min1.

Figure 3.

Variations in the MG width along relevant conformations of the LFEP: (a) IMI•d[5′-CGTTG*GCC-3′]₂; (b) DST•d[5′-ATTAG-3′]₂.

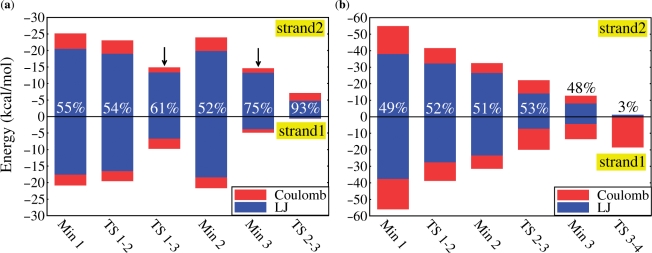
Detachment of the drug starts at TS1-3, which corresponds to a free energy of ∼7 kcal/mol. Here, the tract d[5′-TTG*-3′]₂ opens and a few water molecules intercalate between IMI and strand #1 (which contains the alkylating guanine, see Figure 1 and Supplementary Figure S2). Accordingly: (i) the free energy of hydration ΔG_hyd, calculated relatively to the unbound configurations, increases (Table 2); (ii) drug/DNA van der Waals interactions weaken, in particular those involving strand #1 (Figure 4a).

Figure 4.

Interaction energies between the drugs and selected tracts along each DNA strand. The fraction of the total LJ + Coulomb interaction energy between ligand and strand #2 is also shown as a percentage. (a) IMI with d[5′-C₄GTTG*GC₁₀-3′] (strand #1) and d[5′-C₁₈GTTG*GC₂₄-3′] (strand #2). Arrows indicate configurations where waters enter the region between IMI and strand1 (see also Supplementary Figure S4), weakening hydrophobic interactions; (b) DST with the tracts d[5′-C₂GATTAGC₉-3′] (strand #1) and d[5′-G₁₁CTAATCG₁₉-3′] (strand #2). In contrast to IMI, DST interactions with the two strands are almost identical in strength during the entire unbinding process.

The next point along the LFEP after TS1-3 is the metastable minimum Min3, associated with a ΔG of ∼6 kcal/mol: more waters enter the region between the drug and strand #1, so that the ligand lays now on strand #2 (Figure S4). The relief of the steric hindrance due to the DNA backbone permits a slight relaxation of IMI, which can be quantified through the values of the dihedral angles between benzene and pyrrol rings and between the pyrrol and the CONH₂ tail (Dihe1 and Dihe2, respectively in Supplementary Table S2).

From Min3, dissociation proceeds through the highest transition state, TS3-4, found at d_CM ≈ 1.47 nm, n_hph ≈ 35, and corresponding to a ΔG^‡ of ∼12 kcal/mol. In this conformation, the principal axis of the drug is almost perpendicular to that of the DNA. IMI keeps a weak contact with the duplex through its hydrophilic tail, but does not form H-bonds, and its head (A in Scheme 1) is completely solvated. From this conformation, the complete dissociation of the ligand takes place (conformation ‘Out’).

Concerning structural distortions of the duplex along the detachment route, its RMSDs increases up to >2 Å with respect to Min1 (Supplementary Table S2). Despite this, the RMSD with respect to canonical B-DNA remains lower than that from A-DNA form. In addition, the RMSD with respect to the average structure of the free-standing DNA (‘Free’) is almost constant around 2 Å during the process. As found for the structure of IMI, no evidences of significant changes compared to Min1 are present.

Summarizing, dissociation of IMI occurs through the following steps: the drug first loses contacts with strand #1, allowing waters to insert in between (TS1-3, Min3), then it experiences a complete detachment crossing a transition state in which its head leaves the MG (TS3-4), while the tail keeps small residual interactions with the DNA. The effective calculated barrier for the exit of the drug is ∼12 kcal/mol, and no additional stable states are found along the LFEP apart from the absolute minimum Min1.

DST

The starting complex has been built by manually docking the ligand, taken from the X-ray structure of the adduct DST•d[GGCCAATTGG]₂, on the 10-mer d[GCGATTAGCG]₂ (see section “Materials and Methods” for details on the setup of the system). Note that this is the same duplex used in the stopped-flow experiments of ref. (19) (see section “Materials and Methods”). The FES G(d_CMs n_hb) corresponding to ligand dissociation, the LFEP and the relevant conformations adopted by the complex are shown in Figure 2. The bound conformation is associated with a single broad minimum (Min1) centered at d_CMs ≈ 0.45 nm, n_hb ≈ 57, in which the drug binding mode is very similar to that observed in the X-ray structure of ref. (51): (i) the pyrrol rings A and B (Scheme 1) are slightly rotated with respect to each other to match the curvature of the groove. To quantify the distortion, we have defined the dihedral angles between pyrrol rings A and B (Dihe1 in Scheme 1), B and C (Dihe2) and between the amidinium tail and ring C (Dihe3). The Dihe1 and Dihe2 have values of ∼20°, as in the X-ray structure (51), while Dihe3 changes by ∼180°. However, this change does not affect the orientation of the diamino group with respect to the MG, and thus the interaction network (Supplementary Table S3); (ii) DST influences asymmetrically the MG width, wider at the 3′ end of strand #1 (Figure 3b), whereas it does not have an effect on the structural parameters of the duplex (Supplementary Table S3), as in the X-ray structure; (iii) approximately four H-bonds on average are formed between the ligand and the DNA duplex (Table 2). As in the X-ray structure (51), these involve mostly the nitrogen donors of the ligand and atoms O2 and N3 on the nucleobases. According to the above comparisons, our model reproduces the main features revealed by the X-ray structure.

The complex is mainly stabilized by van der Waals interactions between DST and the DNA backbone (Table 2), although electrostatic interactions are also relevant, specially between the charged amidinium tail of the drug and the tract d[5′-AG-3′]₂ (data not shown). As expected from its larger size and contact surface area, DST makes significantly stronger interactions with the DNA than IMI.

The detachment process starts at the transition state TS1-2 (ΔG^‡ = 5.4 kcal/mol). Here, the drug is significantly distorted: the amidinium tail points outside the MG floor, causing a widening of the MG in the neighboring region, and the complex gains ∼10 waters within the first hydration shell (Table 2). Consistently, the average number of DST–DNA H-bonds decreases, as well as the van der Waals and the electrostatic interactions. In Min2 (ΔG = 4.5 kcal/mol), the drug assumes a configuration intermediate between that of Min1 and TS1-2. The total interaction energy is practically the same as in TS1-2, and a few additional waters enter the hydration shell of ligand and DNA.

From the very shallow minimum Min2, the detachment occurs through the highest transition state along the LFEP, TS2-3 (ΔG^‡ ≈ 18 kcal/mol). Here DST loses contacts with the MG floor, but it is still bound to the DNA backbone: the ligand ‘follows’ the strands of the duplex, while its charged tail remains into the groove (Figure 2). This loss of (mainly hydrophobic) contacts between the ligand and the MG walls is mirrored by a significant decrease of van der Waals interactions, while leaving unaltered the other nonbonded interactions and the number of waters within first hydration shells (Table 2). As the main body of DST exits the MG, this latter recovers the same width as in Min1. The ligand also assumes a conformation quite similar to that in Min1.

TS2-3 is followed by the intermediate state Min3, in which the main ligand axis is almost perpendicular to that of the DNA, and the positive charge on the amidinium tail of DST favorably interacts with the negative electrostatic potential of AT-rich tracts (8,103). Both electrostatic and van der Waals interactions slightly weaken with respect to TS2-3, while the number of H-bonds between the ligand and the duplex does not change. Although the solvation free-energy change is significant compared to the previous minimum Min2, the number of waters within the first hydration shells of DST and d[5′-CGATTAGC-3′]₂ is fairly similar to that found there (Table 2). This might be due to two compensating factors: (i) the narrowing of the MG (Figure 3b), which causes a decrease of the value of the SASA, contrasting the increase of the same due to the dissociation of the main DST body; (ii) the burying of the charged amidinium tail of DST, which counterbalances the complete solvation of DST rings and polar hydrogens. In regard to the structure of the ligand, the rings are almost planar with respect to each other and Dihe3 also recovers a value very similar to that found in Min1 (Table S3).

From Min3 the ligand exits the MG (configuration ‘Out’) passing through TS3-4 (ΔG^‡ ∼7 kcal/mol with respect to Min3 and ∼17 kcal/mol relative to Min1), where it is stabilized by electrostatics interactions with strand #1 (Figures 2 and 3b). In this conformation, both DNA and DST gain a few water molecules in their hydration shells with respect to Min3, and the hydration free energy is essentially zero as compared to the unbound configuration.

As found for IMI, during the whole process the DNA remains closer to the canonical B-DNA conformation than to A-DNA, whereas the structure of DST undergoes significant changes (Supplementary Table S3). With respect to Min1 the RMSD of the duplex remains at 1.5–2 Å, while its value with respect to ‘Free’ decreases along the minima from Min1 to Out.

Summarizing, dissociation of DST proceeds in three steps: (i) the amidinium tail partially rearranges and breaks its H-bonds with DNA; (ii) DST pyrrol rings become solvated, while the positively charged tail anchors the drug to MG; (iii) the ligand tail detaches. The effective activation free energy is ∼18 kcal/mol, and the free-energy barrier for the complete DST detachment (from Min3 to Out) is almost identical to that found for the reverse path from Min3 to Min2 (ΔG ∼ 7 kcal/mol).

We close this section by reporting our results for DST•DNA′, in which the ligand is bound in the MG with a reverse orientation with respect to that in DST•DNA (see Supplementary Figure S1). Interestingly, the effective free-energy barrier for dissociation is ∼16.5 kcal/mol, very similar to the value of ∼18 kcal/mol in DST•DNA. Also, the mechanism of detachment is essentially the same: the aminidium tail of the ligand is the last group to lose contact with the duplex; there is an intermediate state in which this group is within the MG, the rest of the ligand being solvated; from this intermediate, the free-energy barriers associated with binding and unbinding are very similar, although their value is lower than that extracted from the simulations on DST•DNA (see Supplementary Figure S2).

Choice of the CVs

As for any method based on dimensional reduction, the free energy extracted from metadynamics may depend significantly on the choice of the CVs. Although this selection should be driven by chemico-physical intuition, it is ultimately arbitrary. For this reason, we have tested the reliability of our findings on the molecular mechanism by performing two additional simulations with different sets of active variables for each system. Namely, we have: (i) exchanged the set of active CVs, i.e. d_CMs n_hb for IMI•DNA and d_CMs, n_hhp for DST•DNA; (ii) activated all the three CVs. We are aware that these CVs cannot be totally uncorrelated; however, such a correlation can affect in principle every choice of CVs function of geometric coordinates.

Finally, including additional CVs (internal degrees of freedom of the drugs, Euler angles, etc.) is in principle possible, but at the price of somehow loosing, at least within the framework of the standard metadynamics approach used in the present work, a simple (yet accurate) description of the process.

Notably, the mechanism of dissociation proceeds in the very same way with all the chosen CVs (see Movies in the Supplementary Material). In particular, in each simulation the hydrophilic/charged tail is the last group of the ligand to lose contact with the MG. This indicates that the sets of CVs we have used to accelerate the dynamics of dissociation are able to catch the relevant slow motions associated with the process. In addition, the activation free energies calculated as a function of d_CMs, n_hb for IMI•DNA (∼11 kcal/mol) and d_CMs, n_hhp for DST•DNA (∼22 kcal/mol) are, within the errors, comparable with those calculated as a function of the original CVs (see results in the previous paragraphs). Based on these supplementary tests, we believe that the main features of IMI and DST dissociation from DNA have been captured by our free-energy profiles in Figures 1 and 2.

DISCUSSION AND CONCLUSIONS

In this work, we have used classical MD-based metadynamics to characterize the dissociation of anthramycin [a representative of alkylating agents (57,64)] and DST [a prototype of sequence-readers based on H-bond matching (22,104)] from their noncovalent complexes with DNA.

The calculated effective free-energy barriers associated with the removal of DST from DNA do not depend severely on the orientation of the ligand within the MG. Indeed, the values are ∼18 kcal/mol in DST•DNA and ∼16.5 kcal/mol in DST•DNA′, both in good agreement with the value of 16.6 kcal/mol extracted within the Arrhenius theory from stopped-flow experiments (19). The effective free-energy barrier for IMI detachment is significantly lower, ∼12 kcal/mol. Although no experimental kinetic data are available for IMI, the value is consistent with the fact that this ligand has lower molecular weight, contact surface area and number of H-bonds donors/acceptors compared to DST. Indeed, DST needs to disrupt a larger pattern of H-bonds, electrostatic and hydrophobic interactions to detach from its target DNA than IMI (Table 2). In addition, different entropy changes upon dissociation—not specifically evaluated here—may contribute to the different barrier heights. In fact, the gain in configurational entropy upon dissociation should be larger for DST, due to its enhanced internal flexibility compared to IMI. However, the number of waters entering the hydration shells of ligand and DNA after dissociation is certainly smaller in IMI•DNA. These waters are more ‘structured’ than the bulk ones and contribute to lower the entropy of the solvent.

At the mechanistic level, our calculations highlight the relevant common features and the striking differences in the dissociation by the two ligands. Although the finding that for both drugs the hydrophobic interactions provide the main contribution to DNA affinity was somehow expected, it is interesting that the hydrophilic tails of the ligands (Scheme 1) leave the MG at last in both complexes. Note that this result is independent of choosing the number of H-bonds or hydrophobic contacts as an active CV. Concerning the differences, we found that only in DST•DNA the dissociation goes through a stable intermediate (Min3 in Figure 2, Min2 in Supplementary Figure S2), in which the positively charged amidinium tail of DST complements the negative electrostatic potential of the d[ATTA]₂ tract. From this minimum, dissociation and reassociation are equally probable. Such an intermediate was not detected by stopped-flow experiments (19); however, since this state is trapped between relatively low barriers (∼7 kcal/mol in DST•DNA and only ∼3 kcal/mol in DST•DNA′) with consequently high escaping rates, we suggest that it may be present but it has not been experimentally resolved. Thus, we believe that not only our study is in accordance with available measurements, but it also reveals molecular details of the mechanism not easily accessible to the experiment.

In contrast to DST, one TS only characterizes the escaping of IMI from the MG. The lack of stable intermediates is possibly due to the fact that the tail of the molecule, although polar, is neutral; thus, it is not able to establish electrostatic interactions with the negative potential of the MG (tract d[5′-TTG*-3′]₂) equally strong as DST (see Table 2). In addition, the MG locally widens around the drug allowing for hydration of the whole region between IMI and one strand. Widening and enhanced hydration trigger the dissociation of IMI also in the additional metadynamics simulations performed with different sets of CVs. In contrast, no intermediate or metastable states featuring the presence of water molecules between the ligand and a single DNA strand were identified in DST•DNA or DST•DNA′ (Figure 4). This is probably due to the stronger intermolecular interactions this ligand establishes with the duplex with respect to IMI, which renders less likely insertion and stabilization of waters between ligand and DNA strands.

Although the duplexes undergo significant structural changes along the dissociation paths, the distortions remain quite localized in both systems, and the duplexes always stay closer to B- than A-DNA form, without featuring overall bending. This is in agreement with the suggestions proposed by Lavery and Sklenar (92), who pointed out that variations in local parameters like roll and tilt do not necessary induces global distortion in the helix.

In an effort at identifying common features among the mechanism of dissociation by different classes of MG binders, we compare our results for DST with the available kinetic data (23) for the dye Hoechst 33258 (HST, Supplementary Chart S1) (105), which is the prototype of MG noncovalent binders containing benzimidazole groups. A kinetic model proposed by Breusegem et al. (23) invokes the presence of a bound intermediate, structurally different from the fully bound complex, and from which the rates of binding and dissociation are very similar. This situation is extremely reminiscent of our findings for DST: an intermediate featuring the ligand partially bound to the DNA duplex exists, for which the free energy barriers for association or dissociation are very similar.

To the best of our knowledge, the present computational study provides the first molecular-level characterization of the mechanism of dissociation from DNA by the representatives of two classes of pharmacologically relevant MG binders. The agreement between the calculated and experimentally available barriers for one of those (DST) confirms the reliability of metadynamics to estimate free-energy barriers and to obtain mechanistic insights into the process (47–49,74). Some of the mechanistic aspects appear to be shared with the structurally different noncovalent MG binder, Hoechst 33258 (17), which is the prototype of MG binders containing benzimidazoles. These similarities suggest the existence of common mechanisms among different non-covalent MG binders.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Cybersar Project, Grant Nr.: 20/13703. Funding for open access charge: SISSA/ISAS, Trieste.

Conflict of interest statement. None declared.