The whole alignment and nothing but the alignment: the problem of spurious alignment flanks

Abstract

Pairwise sequence alignment is a ubiquitous tool for inferring the evolution and function of DNA, RNA and protein sequences. It is therefore essential to identify alignments arising by chance alone, i.e. spurious alignments. On one hand, if an entire alignment is spurious, statistical techniques for identifying and eliminating it are well known. On the other hand, if only a part of the alignment is spurious, elimination is much more problematic. In practice, even the sizes and frequencies of spurious subalignments remain unknown. This article shows that some common scoring schemes tend to overextend alignments and generate spurious alignment flanks up to hundreds of base pairs/amino acids in length. In the UCSC genome database, e.g. spurious flanks probably comprise >18% of the human–fugu genome alignment. To evaluate the possibility that chance alone generated a particular flank on a particular pairwise alignment, we provide a simple ‘overalignment’ P-value. The overalignment P-value can identify spurious alignment flanks, thereby eliminating potentially misleading inferences about evolution and function. Moreover, by explicitly demonstrating the tradeoff between over- and under-alignment, our methods guide the rational choice of scoring schemes for various alignment tasks.

INTRODUCTION

Figure 1 displays some genomic alignments from the popular UCSC genome browser (http://genome.ucsc.edu/) (1). The alignments are ‘optimal local alignments’, i.e. genomic subsequence–subsequence alignments maximizing an alignment score (2,3). Because the rigorous Smith–Waterman–Gotoh algorithm for optimal alignment is relatively slow, fast heuristic methods like FASTA and BLAST have been developed (4,5). The genomic alignments in Figure 1 were made with a BLAST variant called BLASTZ (6,7).

Figure 1.

A likely overalignment between fugu mtDNA and a human nuclear insertion of mitochondrial DNA. The figure displays four pairwise alignments, of a 200-bp stretch of human chromosome 2 to the fugu, dog, rat and mouse genomes, taken from the UCSC genome browser (version hg18). The light gray bars on the right represent mtDNA from the four organisms; the darker bars on the left, nuclear DNA. Note that the mtDNA alignments extend beyond the right-hand edge of the figure.

In Figure 1, a region from human chromosome 2 aligns to mitochondrial DNA (mtDNA) from fugu, dog, rat and mouse. Probably, chromosome 2 harbors a recent nuclear insertion of mtDNA (NUMT), of which there are many in the human genome (8). The dog, rat and mouse alignments all terminate at precisely the same location in the NUMT sequence, indicating a putative end of the NUMT in chromosome 2. The fugu alignment extends 85 bp farther to the left, however, suggesting the erroneous extension of a ‘true alignment’ into an unrelated sequence.

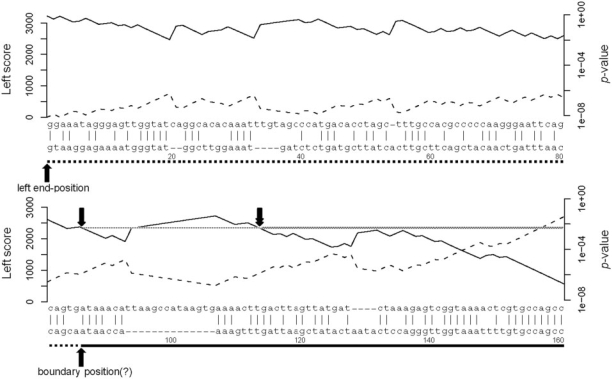
Figure 2 shows a part of the fugu alignment from Figure 1 in detail. The dashed line plots the cumulative alignment score (labeled ‘Left score’ on the y-axis to the left). For every pair of aligned letters, the cumulative score adds a score from a scoring matrix, and for each alignment gap, it subtracts a penalty score. Starting from the left end-position of the optimal local alignment, the cumulative alignment score never drops below zero—necessarily so, else the alignment score would not be maximal—but the score remains close to zero for about the first 85 bp. The proximity to zero is a hint that the flank of the fugu alignment is not trustworthy.

Figure 2.

Overalignment P-values for the start of the fugu–human alignment in Figure 1. The upper sequence is from the fugu mitochondrial chromosome, and the lower sequence is from human chromosome 2. (The alignment extends further to the right than shown in Figure 2.) The solid line under the human sequence indicates the region aligning to the dog, rat and mouse mtDNA; the dotted line, the putative spurious left flank starting at the boundary position (marked with ‘?’, to indicate its putative nature). The dashed line shows the cumulative alignment score, starting with zero at the left, using the HoxD55 matrix with GOP = 400, GEP = 30. The solid line shows the probability of obtaining this score or greater by alignment of two random sequences, from the formula P ≈ ce^λy for the cumulative alignment score y. The single downward arrow indicates the P-value P at the boundary position, between 10⁻² and 10⁻³. Trimming the left flank at P-value P requires trimming to the rightmost occurrence of the P-value P, indicated by the downward double arrow. (As an aside, the alignment would still match reasonably well if it moved the first seven human bases after the boundary position to the other end of the large gap, perhaps supporting the undependability of the alignment to the left of the downward double arrow).

In Figures 1 and 2, for each gap of size k, BLASTZ reduced the cumulative score by 400 + 30 k, a so-called ‘affine gap penalty’ with gap opening penalty (GOP) of 400 and gap extension penalty (GEP) of 30. BLASTZ used the HoxD55 matrix for the fugu DNA alignment, and the HoxD70 matrix for the mammalian DNA alignments (Table 1). For reference, Table 2 lists some typical scoring schemes for DNA and protein alignments. The HoxD70 matrix (and presumably also HoxD55) derives from aligned segments of human and mouse DNA (9). Unlike simple match/mismatch scoring schemes, the HoxD matrices apply lesser penalties to transitions (A↔G and C↔T) than to transversions [although simple match/mismatch scoring schemes might be more appropriate for species not exhibiting transition–transversion bias (10)]. Similarly, the BLOSUM scoring matrices reflect the substitution frequencies found in blocks from protein alignments (11). (Each number, e.g. 45 in BLOSUM45, refers to a percent identity threshold, so lower thresholds increase the dissimilarity of the letter pairs contributing to the substitution frequencies.)

Table 1.

The HoxD55 and HoxD70 scoring matrices

HoxD55					HoxD70
	A	C	G	T	A	C	G	T
A	91	−90	−25	−100	91	−114	−31	−123
C	−90	100	−100	−25	−114	100	−125	−31
G	−25	−100	100	−90	−31	−125	100	−114
T	−100	−25	−90	91	−123	−31	−114	91

Table 2.

Over-alignment parameters for some common scoring schemes

Matrix	GOP	GEP	λ	c	E(length)	P(length = 0)	Comments
BLOSUM45	15	2	0.203	0.674	6.72	0.490
BLOSUM50	10	2	0.141	0.714	22.89	0.369	FASTA 3.5 default
BLOSUM62	7	2	0.239	0.700	7.80	0.483	WU BLAST 2.0 default
BLOSUM62	11	1	0.267	0.669	5.53	0.532	NCBI BLAST 2.2.17 default
BLOSUM62	11	2	0.299	0.645	2.96	0.589
BLOSUM62	10	4	0.309	0.633	2.37	0.605	Matcher default
BLOSUM62	9.5	0.5	–	–	–	–	Water, Supermatcher default
BLOSUM80	10	1	0.300	0.609	2.81	0.611
HoxD55	400	30	0.00592	0.802	23.50	0.330	UCSC genome alignments
HoxD70	400	30	0.00908	0.694	4.53	0.486	BLASTZ v7 default
+1/−1	2	1	0.916	0.997	2.30	0.602
+1/−3	5	2	1.332	1.000	0.36	0.736	NCBI BLAST 2.2.17 default
+2/−3	5	2	0.593	0.790	0.87	0.666	NCBI BLAST website default
+5/−4	12	4	0.133	0.789	10.80	0.351	FASTA 3.5, Matcher default
+5/−4	0	10	0.0765	0.9294	40.51	0.226	WU BLAST 2.0 default
+5/−4	9.5	0.5	–	–	–	–	Water, Supermatcher default

Protein parameters are for Robinson-Robinson frequencies. DNA parameters are for 60% AT.

*Dashes represent that simulations were unable to determine whether the scoring scheme was in the local regime.

Statistical P-values (or E-values) can discriminate biologically interesting alignments from chance sequence similarities. Unfortunately, current P-values evaluate only entire alignments. If applied, even though the alignment flank in Figure 1 appears spurious, the P-values would indicate (probably correctly) that the fugu alignment is biologically interesting. Clearly, it would be useful to be able to control the risk of overextending a true pairwise sequence alignment and to identify potentially spurious alignment flanks.

Accordingly, given an alignment scoring scheme and a set of background letter frequencies, we calculate the distribution of how far a ‘true alignment’ extends into a flanking pair of random sequences. For several DNA scoring schemes, by considering NUMTs with known edges, we demonstrate the practical tradeoff between the risks of over- and under-alignment. Finally, for various scoring schemes, we calculate the score distribution of alignment extensions occurring by chance alone, thereby calculating the overalignment P-values pertinent to spurious alignment flanks. Thus, our quantitative results permit a rational basis for choice of scoring schemes for balancing the risks of over- and under-alignment.

METHODS

We used crude Monte Carlo sampling to generate 10 000 pairs of pseudo-random sequences of fixed length 400. We also generated pseudo-random sequences with importance sampling. The importance sampling technique determines random sequence lengths dynamically. It is faster than crude Monte Carlo and can usually compute the statistical parameters for local alignment in real time (i.e., within 1 s) (12). We quantified the probability of zero flank length, the average flank length and the overalignment parameters c and λ (from the approximate P-value formula P ≈ ce^λyfor a flank score y). The simulation errors for c and λ were estimated from the so-called ‘splitting method’ (Park,Y., Sheetlin,S. and Spouge,J.L., 2008, manuscript in preparation); and for the probability of zero flank length and the average flank length, from standard errors. In Supplementary dataset 1, empty fields indicate that simulations were unable to confirm that the corresponding scoring schemes were in the local regime, making computation of the overalignment parameters infeasible. [The Results section indicates why a practical scoring scheme must be in the local regime. As a scoring scheme moves out of the local regime, a phase transition occurs, making the sequence lengths in importance sampling increase to infinity (13).]

To explain the probability of zero flank length and the average flank length in detail, consider a high-scoring true alignment containing two sequences, and concatenate each of the two sequences to a random flank sequence. If the maximal scoring alignment of the concatenated true and flank sequences included no flank sequences, the flank length was 0: there was no overextension. If over-extension occurred, then the flank length is the number of letters the maximum alignment contains from the first concatenated flank sequence.

To identify recent human NUMTs, we aligned the human mitochondrial genome to the human nuclear genome (UCSC version hg18) using NCBI BLAST 2.2.17 with options -p blastn -e 1e-10 -m 9 -F ‘m D’. We then kept BLAST hits that matched gaps in either the hg18/rheMac2 or hg18/panTro2 alignment nets from UCSC, allowing up to 5-bp difference between the edge of the BLAST hit and the edge of the gap.

To test various scoring schemes, the human NUMTs were aligned to mtDNA from mouse (UCSC version mm9), fugu (UCSC version fr2) and the inshore hagfish Eptatretus burgeri (Refseq NC_002807.1) (14), using an implementation of the Smith–Waterman algorithm (‘water’ from EMBOSS 5.0.0) (15). Figures 2–6 were created with R (www.R-project.org).

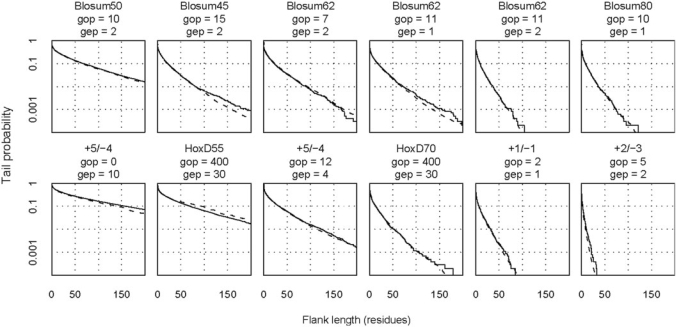
Figure 3.

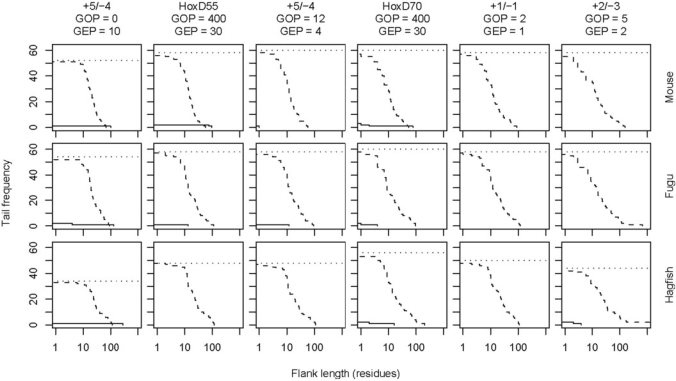
Probability distributions for the length of overalignment into random sequences. The solid lines show distributions obtained from alignment of 10 000 random sequence pairs (using the variant of the Needleman–Wunsch algorithm mentioned in the Results section). The dashed lines show distributions predicted by importance sampling. The top row refers to protein sequences with Robinson–Robinson frequencies, and the bottom row refers to DNA with 60% AT. The abbreviations are GOP (gap opening cost), GEP (gap extension cost), and + X/−Y (match score/mismatch score).

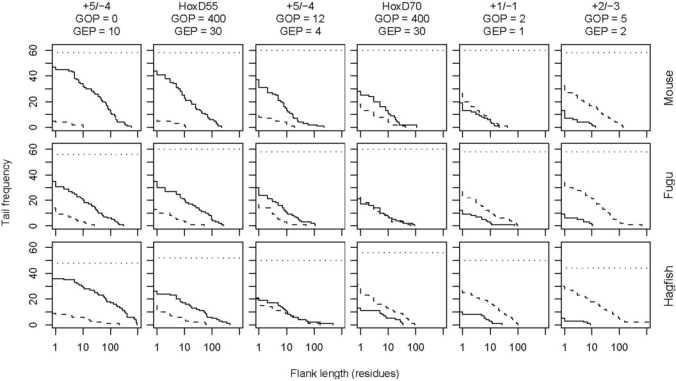
Figure 4.

Tradeoff between over- and under-alignment. These graphs refer to Smith–Waterman alignments of mouse, fugu and hagfish mtDNA to 31 human NUMTs with 1000 bp of flanking sequence on either side. The 62 endpoints of the NUMTs are known to within ±5 bp. The solid lines show the distribution of overalignments, and the dashed lines show the distribution of underalignments. We discarded alignments not overlapping the NUMT at all: the horizontal dotted lines indicate the number of endpoints remaining for consideration.

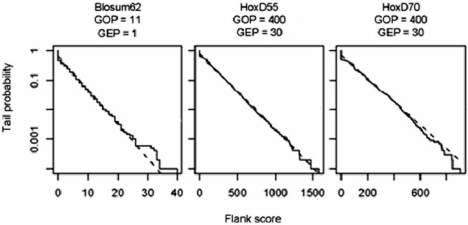
Figure 5.

Probability distributions for the scores of overalignments into random sequences. The solid lines show score distributions from alignment of 10 000 random sequence pairs (using the variant of the Needleman–Wunsch algorithm mentioned in the Results section). The dashed lines show distributions predicted by the formula P ≈ ce^λy. Table 2 contains the values of the overalignment parameters c and λ. The dotted lines are the distributions of the maximum left score, as described in the Results section.

Figure 6.

Tradeoff between over- and under-alignment after trimming flanks with P > 0.01. These graphs refer to the same alignments as in Figure 4. This time, however, the alignments were shortened at either end by removing flanks with P > 0.01. In a few cases, the trimming removed the entire alignment: we discarded these cases from consideration.

RESULTS

We generated pseudo-random sequences to determine how far typical alignment scoring schemes spuriously overextend alignments into neighboring unrelated sequences. Random protein sequences reflected the standard Robinson–Robinson (16) amino acid frequencies; random DNA sequences, the human genome average frequency of 60% AT. To mimic extension from a true alignment, a variant of the Needleman–Wunsch algorithm optimized the score over all alignments starting (possibly with gaps) at the beginning of the two sequences but ending anywhere. For a given pair of random sequences, after finding a constrained alignment with the maximal score, we recorded its flank length, which is the number of residues aligned in the first random sequence. We estimated flank length distributions, both by ‘crude Monte Carlo sampling’ (the name for brute-force simulation in statistics), which generates letters independently from the appropriate background frequencies, and by a well-accepted, more efficient but complicated procedure called ‘importance sampling’ (see Methods section for more details) (12).

Figure 3 plots the flank length distributions for several scoring schemes; Table 2 lists the expected lengths and probabilities of length = 0. Although the distributions vary widely, the crude Monte Carlo and importance sampling estimates agree closely. Among protein scoring schemes, BLOSUM50 with GOP = 10 and GEP = 2 has an expected flank length of 23 and probability 0.1 of a flank length exceeding 65. Thus, sizeable overextensions are likely with this scoring scheme. The other protein scoring schemes in Figure 3 are much more restrained: for instance, BLOSUM62 with GOP = 11 and GEP = 1 has an expected flank length of 5.5 and probability 0.1 of a flank length exceeding 17. However, there is always a small probability of getting large flanks: BLOSUM62 with GOP = 11 and GEP = 1 has probability 0.01 of a flank length exceeding 69. Since it is common to perform hundreds or even millions of alignments, these probabilities are not negligible. The flank lengths for NCBI BLAST can be roughly halved by increasing the gap extension penalty to 2.

The flank length distributions for popular DNA scoring schemes vary even more widely. The +5/−4 scheme with GOP = 0 and GEP = 10 is severely prone to overextension, with an expected flank length of 41 and probability 0.1 of a flank length exceeding 141. Surprisingly here, the gap extension penalty is twice the match score, perhaps highlighting the importance of a large gap opening penalty in restraining overextension. Surprisingly also, even with the same gap penalties, and despite apparent similarity, the HoxD55 matrix is much more prone to overextension than HoxD70. Because the HoxD55 scheme with GOP = 400 and GEP = 30 has an expected flank length of 24 and probability 0.1 of a flank length exceeding 94, overextensions like the one in Figure 1 are probable. On the other hand, the default schemes for NCBI BLAST are extremely restrained: the +2/−3 scheme with GOP = 5, GEP = 2 has only probability 0.01 of a flank length exceeding 8, and the +1/−3 scheme is, of course, even more conservative.

Because local alignments of random sequences should not extend to include most of the sequence length, practical scoring systems are constrained to have reasonably strong mismatch and gap penalties. Despite extensive simulation, we were unable to verify that the default scoring schemes in two EMBOSS programs, Water and Supermatcher (but not Matcher) satisfied this constraint for sequences with 60% AT (15). [In technical terms, practical scoring systems must be in the ‘local regime’ (13), which depends also on the letter frequencies in random sequences. In other words, a scoring system might be in the local regime for GC-rich DNA, but not for AT-rich DNA. Although a few approximate analytical studies are extant (17,18), simulations are generally required to show that a scoring system is in the local regime. We could not verify that the Water and Supermatcher scoring systems were in the local regime.]

Mismatch and/or gap penalties restrain overextension, but there is of course a tradeoff: if penalties are too high, alignments fail to include weakly similar subsequences. Because the tradeoff depends on the nature of weak biological similarities, we studied it in real biological sequences, by examining alignments of mtDNA to recent human NUMTs. Because NUMTs are unrelated DNA insertions with well-defined edges, they serve our purposes particularly well. As described in the Methods section, we identified 31 recent NUMTs. The 31 NUMTs, with 1000 bp of flanking sequence on either side (Supplementary dataset 2), were then aligned to mtDNA from mouse, fugu and hagfish (a borderline vertebrate), representing three levels of divergence.

Figure 4 shows the length distribution of overalignments, where the alignment extends past the edge of the NUMT, and underalignments, where the alignment ends before the edge of the NUMT, for six scoring schemes. Although the default scheme of NCBI BLAST (+2/−3 with GOP = 5, GEP = 2) is indeed resistant to overalignment, it pays for this with a strong tendency for underalignment. On the other hand, the most aggressive scoring schemes (+5/−4 with GOP = 0, GEP = 10 and HoxD55 with GOP = 400, GEP = 30) exhibit the least underalignment, but excessive overalignment. The default scheme of BLASTZ (HoxD70 with GOP = 400, GEP = 30) offers a good balance between under- and overalignment, especially for the level of divergence between human and fugu mtDNA. (To avoid misunderstanding, note that on average, human and fugu mtDNA are much less divergent than human and fugu nuclear DNA.) In general, conservative scoring schemes provide a better balance for closely related sequences, and aggressive schemes for divergent sequences. If one desires a simple match/mismatch scoring scheme, then +1/−1 with GOP = 2, GEP = 1 offers a reasonable balance for a wide range of problems, being somewhat more conservative than the BLASTZ default.

A judicious choice of scoring scheme can make large overextensions infrequent, but it does not prevent them completely. Thus, we need to identify overextensions when they occur. Figure 2 suggests that long overextensions have relatively low scores. Thus, given the score distribution for alignments extending from true alignments into random sequences, a P-value (the probability of a chance flank with equal or greater score) could help identify spurious alignment flanks.

Given a true alignment, a spurious alignment flank is approximately the alignment of two random sequences starting from the final aligned letter pair in the true alignment. [To test robustness of our results by varying the nature of the true alignment, we simulated long sequence pairs under the hybrid alignment model of related sequences (19), and then concatenated random unrelated sequences to the aligned sequences. Results remained essentially unchanged (data not shown).] Under the approximation, the contribution to the alignment score from the flank is equivalent to a quantity known as the ‘global maximum score’ (20). The global maximum score y has a P-value P ≈ ce^λy, where c is a fixed constant and λ is the so-called ‘Gumbel scale parameter for local alignment’. Analytical formulas for c and λ are known only for gapless alignment (21), but importance sampling techniques can estimate c and λ very efficiently for gapped alignment (see Methods section). Crude Monte Carlo sampling confirmed the accuracy of P-values from importance sampling (Figure 5).

Table 2 gives values of λ and c for sixteen scoring schemes; Supplementary dataset 1 gives values for many other scoring schemes. Figure 2 illustrates how the formula P ≈ ce^λyconverts a given flank score into an overalignment P-value. In the bottom row of Figure 2, the cumulative score reaches a minimum value of 515, at the end of the large gap in the lower sequence. Because P ≈ ce^λy ≈ 0.038 (c = 0.802, λ = 0.00592 and y = 515), and because the UCSC fugu–human data include many thousands of individual alignments, we expect many spurious extensions with P-values of this magnitude.

Then, how can we use the overalignment P-value to strengthen inferences from alignments? Figure 2 plots the flank P-value against the alignment position with a solid line. After exclusion of the largest flank with P-value P, 1−P becomes a lower bound for the (theoretical) probability that on that flank, the remaining alignment does not involve two random sequences. (The inference might seem feeble, but it is the only inference possible from any alignment P-value).

In bioinformatics, P-values usually flag biological similarities, so this statement might seem counterintuitive. The overalignment P-value, however, aims to exclude biologically spurious flanks, to increase the dependability of the remaining alignment. Several intervals on a flank alignment might have the same score (and thus, the same overalignment P-value), however. Which interval should we exclude?

To introduce some relevant subtleties, consider the boundary position between the true and flank alignments in Figure 2. Consider now the left end-position of the maximal local alignment. Let the ‘left scores’ be the successive cumulative global alignment scores within the flank, starting from the left end-position and moving rightward (as shown by the dotted line in Figure 2). Now, reverse direction and consider the ‘right scores’ (not shown in Figure 2), which are successive cumulative global alignment scores starting from the boundary position and moving leftward. Because the left end-position is the end of the maximal local alignment, it achieves the maximum right score, which we denote here by M. Fortunately, the P-value 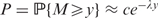for the maximum right score M is known from other work (20).

Because the alignment score for any interval remains the same under sequence reversal, the left score at the boundary position is also M. Because we know the left end-position of an optimal local alignment but not the boundary position, to exclude a boundary position with a left score M = y, we must exclude every position with left score y. In Figure 2, e.g. we must exclude the rightmost position with left score y, indicated by the downward double arrow. As an intuitive justification, consider every alignment position with left score y. All intervening alignment intervals have a score of 0, which does nothing for our confidence that they represent parts of a biologically interesting alignment.

One should bear in mind that statistical significance does not always reflect biological significance, however. Various rules of thumb can estimate biological significance from BLAST E-values, e.g. PSI-BLAST iterations retain sequences with a statistical E-value of 0.005. Figure 2 suggests that for overalignment P-values, statistical and biological significance are similar, but further practical experience is required to confirm this point.

To increase confidence in an alignment, an investigator could trim the alignment flanks with the overalignment P-value, but trimming also involves a tradeoff: overalignment becomes less frequent but underalignment becomes more frequent. The P-value threshold used for trimming flanks should therefore reflect the subjective penalties assigned to over- and under-alignment. Figure 6 shows the same mtDNA-NUMT alignments as Figure 4, but after removing flanks with P > 0.01. As expected, overalignment decreases but underalignment increases. In particular, underalignments of length around 10 bp are frequent, because true alignments are likely to extend for a few bases into nearby sequences. Since the overalignment P-values for short extensions are near 1.0, no solid judgment is possible about a few residues at the end of any alignment.

Based on these results, we do not recommend routine trimming of alignment flanks, particularly because well-balanced scoring schemes rarely produce large overextensions. Rather, programs should include the P-value of flanks, so investigators can know how often a random flank produces the indicated alignment. In the case of low-quality alignments of transcription factor binding sites, for example, investigators can then regard any flanks with large P-values with appropriate suspicion.

DISCUSSION

Two essential messages emerge from our study: (i) appropriate scoring schemes can help avoid overextension of alignments, and (ii) alignment tools should indicate overalignment P-values. Our results (particularly Figure 4) indicate the critical importance of choosing an appropriate scoring scheme to balance the risks of over- and under-alignment.

The appropriateness of a scoring scheme might not be immediately obvious: HoxD70 and HoxD55 (Figures 3 and 4), e.g. are superficially similar scoring matrices, but they differ greatly in the overalignment of unrelated sequences. Since most users accept the default values in alignment software, the onus is on developers to choose good defaults. Our results provide invaluable guidance on defaults for avoiding alignment overextension. The two most aggressive DNA scoring schemes shown in Figures 3 and 4 (+5/−4 with GOP = 0, GEP = 10 and HoxD55 with GOP = 400, GEP = 30) should probably not be used. The BLASTZ default (HoxD70 with GOP = 400, GEP = 30) is well suited to aligning vertebrate DNA, as one would hope. Very conservative schemes, such as the defaults for NCBI BLAST, are appropriate for aligning very similar sequences. For similar sequences, more aggressive schemes (such as +1/−1 with GOP = 2, GEP = 1 for DNA) also appear to perform well, but more conservative schemes should perform even better, by reducing the small but unnecessary risk of overextension in such cases. A less conservative default is appropriate to a general purpose tool such as BLAST, however, particularly the BLAST variant, discontiguous megablast, which is useful for finding distant similarities.

While it is easy to change scoring schemes, it is more difficult to annotate alignments with the corresponding overalignment P-values. We considered the possibility of a postprocessing tool for annotation with overalignment P-values, but there are two difficulties: such a tool needs to know the scoring scheme, and alignments themselves come in a bewildering variety of formats. Both of these problems would disappear if alignment programs calculated overalignment P-values. The only difficulty entailed in the calculation is to provide alignment programs with the parameters λ and c in the P-value approximation P ≈ ce^λy. Accordingly, Supplementary dataset 1 contains a table of λ and c for a limited selection of scoring schemes and residue abundances, and software for calculating λ and c is available at http://www.ncbi.nlm.nih.gov/CBBresearch/Spouge/Software/.

Our analysis has examined spurious alignment flanks, but not spurious internal regions. In fact, Smith–Waterman and related local alignment algorithms can include arbitrarily poor internal segments in alignments (22). In practice, tools such as BLAST mitigate the problem with algorithms like X-drop, insisting that any segment of the alignment exceed a (negative) threshold score. On the other hand, the BLASTZ default probably does not mitigate the problem, because its X-drop parameter is so large.

There are some alternative approaches to detecting and avoiding inaccurate subalignments. Mevissen and Vingron (23) assign a ‘reliability index’ to every residue pair in a maximal-scoring alignment, using the score of the best alternative alignment that does not include the residue pair. More recently, Lunter et al. (24) used detailed evolutionary models and posterior decoding to improve the accuracy of genome alignment, and to predict the probability that individual alignment columns are correct. Both of these approaches are related to centroid alignment, used by Miyazawa (25) to improve alignment accuracy, and recently championed by Lawrence (26,27). All such methods involve changing the alignment algorithm, however, which impedes their wider adoption, and a probabilistic alignment tool with the speed and flexibility of BLAST has yet to be developed. Furthermore, the reliability estimates are a step away from true reliability: the index of Mevissen and Vingron requires calibration, and the posterior probabilities of Lunter et al. reflect a model of sequence evolution and thus are not necessarily accurate. Our study, in contrast, addresses a more specific problem, but one of practical importance, and it provides a straightforward solution.

Finally, to illustrate the impact of alignment overextension, consider the proportion of spurious extensions in the UCSC human–fugu genome alignment, which includes 189,888 individual alignments, covering 49,912,422 bp of the human genome. Since the average flank length is 24 (Table 2), and each alignment has two ends, according to our estimates, 9,114,624 (18%) of the aligned human sequence is spurious, and the longest overextension is probably close to 1000 bp. The reality is almost certainly worse than the estimate, which assumes random sequences, and ignores the effects of repeats, isochores, etc.

SUPPLEMENTARY DATA

Supplementary data are available at NAR Online.

FUNDING

Intramural Research Program of the National Library of Medicine at the National Institutes of Health partially. Funding for open access charge: NLM, NIH.

Conflict of interest statement. None declared.