Abstract
We focused on a region encompassing a major maize domestication locus, Tb1, and a locus involved in the flowering time variation, Dwarf8 (D8), to investigate the consequences of two closely linked selective sweeps on nucleotide variation and gain some insights into maize geographical diffusion, through climate adaptation. First, we physically mapped D8 at ∼300 kb 3′ of Tb1. Second, we analyzed patterns of nucleotide variation at Tb1, D8, and seven short regions (400–700 bp) located in the Tb1–D8 region sequenced on a 40 maize inbred lines panel encompassing early-flowering temperate and late-flowering tropical lines. The pattern of polymorphism along the region is characterized by two valleys of depleted polymorphism while the region in between exhibits an appreciable amount of diversity. Our results reveal that a region ∼100 kb upstream of the D8 gene exhibits hallmarks of divergent selection between temperate and tropical lines and is likely closer than the D8 gene to the target of selection for climate adaptation. Selection in the tropical lines appears more recent than in the temperate lines, suggesting an initial domestication of early-flowering maize. Simulation results indicate that the polymorphism pattern is consistent with two interfering selective sweeps at Tb1 and D8.
AN increasing number of genome-scan studies combining the availability of large genomic data sets and statistical tools have contributed to the discovery of genes or genomic regions involved in adaptive evolution (Wright et al. 2005; Borevitz et al. 2007; Williamson et al. 2007). Along with the development of genome scans, a growing number of studies are identifying confounding factors that are misleading for our interpretation of the data. Many of these factors are related to demography. For instance, Currat et al. (2006) demonstrated that the patterns observed at two genes associated with brain development and previously reported as being a target of adaptive evolution (Evans et al. 2005; Mekel-Bobrov et al. 2005) can in fact be generated by an initial structured population undergoing a spatial population expansion. Other confounding factors such as biased gene conversion (BGC) have also been recently pinpointed. For instance, Galtier and Duret (2007) revealed that the pattern identified as a typical signature of adaptive evolution by Pollard et al. (2006) is in fact the result of GC-biased gene conversion, demonstrating that BGC can mimic the effects of an accelerated rate of substitution. Several methods to correct for these confounding factors are becoming available (reviewed in Tenaillon and Tiffin 2008). However, our ability to detect selection ultimately depends on the selection features (intensity, timing, and initial allele frequency) as well as the surrounding genomic characteristics such as the local mutation and recombination rate (linkage disequilibrium).
Cultivated plants have been subjected to recent and intense human selection, leaving large genomic imprints (Palaisa et al. 2003; Clark et al. 2004; Olsen et al. 2006), their archaeological history is well documented, and access to genetic data from their wild relatives facilitates inferences on their demographic history. The use of genome scans in cultivated plants to identify genomic regions involved in domestication and breeding therefore appears promising. In addition, because linkage disequilibrium (LD) decays within a few hundred base pairs in allogamous species such as maize (Remington et al. 2001; Tenaillon et al. 2001), association mapping using candidate regions identified from the genome scans should lead to the identification of sites physically close to the targets of selection. A number of genome-scan studies applied to the search for adaptive evolution in domesticated plants have successfully led to the identification of candidate regions (Casa et al. 2005; Wright et al. 2005; Yamasaki et al. 2005; Caicedo et al. 2007).
On the other hand, Teshima et al. (2007) recently demonstrated that these studies also miss a number of selected loci, in particular those involving selection on recessive alleles and/or from standing genetic variation. In addition, because plant domestication and adaptation likely involve the fixation of beneficial mutations in short time periods (Caicedo et al. 2007), the occurrence of sweep interference may be common and contribute to reducing our power to detect selection. Patterns generated by interfering sweeps have been described in a few theoretical (Kim and Stephan 2003; Chevin et al. 2008) and empirical works (Kirby and Stephan 1995). Results from these studies predict that selection at two closely linked loci could influence the surrounding neutral polymorphism pattern in a manner that could not be predicted by the plain addition of two hitchhiking effects (Kim and Stephan 2003; Chevin et al. 2008). In particular, when beneficial alleles are initially carried by different chromosomes and depending on the selection coefficients and the timings of the selective sweeps, a less marked reduction of diversity in the region is expected in between the sweeps. Finally, while LD decays rapidly in maize, causative sites can involve cis-acting regulatory regions as distant as ∼60–∼70 kb from the identified candidate genes, as described for Tb1 and Vgt1 (Clark et al. 2004; Salvi et al. 2007). It is therefore essential to study the surrounding patterns of LD before inferring a causative site as the target of selection.
Maize (Zea mays ssp. mays) exhibits amazing phenotypic and genetic diversity and has the broadest cultivation range among cultivated plants. An analysis of genomewide SSR diversity among the whole range of American maize and three wild teosinte (Z. mays) subspecies demonstrated the single domestication of maize from Z. mays ssp. parviglumis (Matsuoka et al. 2002) 6000–10,000 years ago. The precise location of the progenitor population is likely the Balsas river valley in Mexico (Matsuoka et al. 2002). Several studies conducted in the 1990s (Doebley et al. 1990; Doebley and Stec 1991, 1993) revealed that only few major quantitative trait loci (QTL) were involved in morphological differences between maize and teosintes. Among the genes underlying these QTL, the Tb1 gene is involved in plant architecture and is responsible for the reduced tillering of maize compared to teosintes (Doebley et al. 1997). By analyzing the patterns of Tb1 nucleotide variation among maize and teosintes (Z. mays ssp. parviglumis), the pioneer work of Wang et al. (1999) revealed that the selection footprint at the Tb1 gene is restricted to the 5′-noncoding region, arguing for a high recombination rate and the possibility of recurrent crosses with wild individuals during the domestication process. Clark et al. (2004) further demonstrated that the selective sweep on Tb1 5′-noncoding region encompasses a 60- to 90-kb region that was later shown to include a cis-regulatory region playing a central role in the realization of the cultivated phenotype (Clark et al. 2006).
The relatively quick expansion of maize cultivation through the Americas required that maize adapt in a short time frame to new environmental conditions. Among numerous adaptive traits, flowering time is central because it allows the adjustment of plant cycle to favorable climate conditions as well as the avoidance of abiotic stresses such as drought or cold. Flowering time is a quantitative trait determined by many genes. Maize accessions exhibit a great variability for this trait in a geographically dependent manner (Camus-Kulandaivelu et al. 2006). On the basis of QTL meta-analysis, Chardon et al. (2004) showed that ∼60 QTL are involved in the variation of this trait in maize. However, only very little is known about the molecular basis of these QTL. So far, only two genes have been identified: Dwarf8 (D8), for which several polymorphisms correlate with quantitative variation in flowering time (Thornsberry et al. 2001; Andersen et al. 2005; Camus-Kulandaivelu et al. 2006), and Vgt1, a cis-acting regulatory element that underlies a major flowering-time QTL (Salvi et al. 2007; Ducrocq et al. 2008).
When considering the general framework of plant domestication modalities, comparison of domestication syndromes in grasses suggests that the genes facilitating the harvest have been selected before those increasing yield (Buckler et al. 2001). First-selected genes should therefore include those responsible for plant architecture, seed size, and shattering as well as flowering time. This hypothesis is supported for maize by the work of Jaenicke-Després et al. (2003), which suggests that the Tb1 domesticated allele was already fixed in maize as early as 4400 years ago while selection on the grain quality gene Su1 was still ongoing. The selective history of D8 is less known than that of Tb1. Allelic frequencies at D8 differ between maize genetic groups, suggesting diversifying selection (Camus-Kulandaivelu et al. 2006). Moreover, since D8 also exhibits a selection imprint in teosintes (Tenaillon et al. 2004) and because of the importance of flowering time as a domestication trait (Buckler et al. 2001), it is likely that D8, like Tb1, has been selected in the very early history of cultivated maize.
D8 is located only 1 cM away from Tb1, at an unknown physical location and may have therefore been affected by selection acting at Tb1 during domestication. Because both genes are “textbook” examples and located so close together, they offer an ideal model to investigate the patterns of nucleotide variation and LD generated by closely linked selective events. Moreover, the Tb1–D8 region appears promising to gain insights into the maize diversification history from its center of origin. To undertake the study of the Tb1–D8 region, we first physically mapped D8 and defined six short regions (400–700 bp) located between Tb1 and D8. Second, to study the nucleotide variation patterns, we sequenced Tb1, D8, the six short regions, and an additional short region located in the 5′ region of Tb1 in a subset of 40 maize lines representing both tropical and temperate diversity. Third, we measured the association between several SNPs of the Tb1–D8 region and the variation of flowering time within a 375-maize-line association panel. Finally, to clarify the mechanisms that lead to the polymorphism patterns observed in the Tb1–D8 region, we used a simulation-based approach to compare our observed patterns to predicted patterns under contrasted scenarios of occurrence of a D8 favored allele in a given population (temperate or tropical).
MATERIALS AND METHODS
Dwarf8 physical mapping:
The relative physical location of D8 from Tb1 was assessed using bacterial artificial chromosome (BAC) clones. Tb1 is anchored by an SSR marker (umc1082) in contig 57 of the “Maize Agarose FPC Map” (http://www.genome.arizona.edu/fpc/maize/). This contig includes 1809 BACs covering a 12,000-kb region. Among those BACs, we chose 105 BACs constituting a minimum tilling path that covers a large region 3′ and 5′ of Tb1 (a list of the BACs is available in supplemental Table S1). We PCR amplified a fragment containing a D8 insertion–deletion (D8idp) on all selected BACs as described in Camus-Kulandaivelu et al. (2006). Two overlapping BACs, namely c0435E06 and c0329M07, led to amplification using this protocol. Both were located 320 ± 12.3 kb, 3′ of Tb1.
Marker identification:
We identified short regions (400–700 bp) localized between Tb1 and D8, using BACs and BAC ends mapped on the Maize Agarose FPC Map (Cone et al. 2002) and for which sequences were available at http://www.ncbi.nlm.nih.gov/. For BAC ends, we elongated the available sequences by blasting them using either NCBI (http://www.ncbi.nlm.nih.gov/blast/bl2seq/wblast2.cgi) or the assembled Z. mays sequences (http://maize.tigr.org/). Among these short regions, we chose four of them (d801, d802, b188, and t1p3) according to three criteria: (i) the short region was single copy; the PCR amplification led to a single PCR product and the sequence presented no known homology with existing sequences in the NCBI database (http://www.ncbi.nlm.nih.gov/BLAST/); (ii) the sequences of the short regions presented one or several SNPs between two inbred lines (B73 and W85, supplemental Table S2); and (iii) selected short regions were as evenly spaced as possible. Because a large region 3′ of Tb1 remained uncovered by those four short regions, we performed the subcloning and partial sequencing of two BACs (b0410G15 and b0488E10). Among the 96 sequences produced, we chose two additional short regions (f03 and g05) according to the criteria described above. Both markers were localized 145.4 ± 20.5 kb, 3′ of Tb1. However, because of the lack of additional physical mapping information, we were not able to precisely identify their relative position. Finally, we chose a short region 5′ of Tb1 (tb58) previously described (Clark et al. 2004). Figure 1 summarizes the physical location and the amplification size of Tb1, D8, and the seven short regions selected as markers. We use the term “markers” in the rest of the text to name the short regions that were chosen and further sequenced.
Figure 1.—
Relative physical positions of the markers and the genes (circles). The origin of the x-axis corresponds to the position of Tb1 and approximate distances between the markers and the origin are indicated in kilobases along the dashed lines. The shaded box indicates the length of 1 cM. Sequence lengths in base pairs excluding gaps are indicated in parentheses. The relative position of f05 and g03 could not be determined using the available physical map. Horizontal gray arrows indicate the markers that were positioned at the intersection of two BACs and corresponding numbers (in gray) indicate the width of the interval in which they are located. Markers or genes encompassing ORFs are indicated by solid circles.
Plant material:
We sampled DNA sequence diversity from a large panel of 40 maize inbreds whose origins were previously inferred both from SSR markers using the STRUCTURE software and from pedigree data. The 40 inbreds belong to two different inbred groups characterized by contrasted flowering time: the early-flowering Northern Flint group (20 inbreds) and the late-flowering tropical group (20 inbreds). All inbreds chosen from the Northern Flint group encompassed the early-flowering allele at D8, based on a 6-bp indel (Camus-Kulandaivelu et al. 2006), while inbreds chosen from the tropical group encompassed the late-flowering allele at D8. These inbreds were chosen because they could unambiguously be attributed to one of the above defined groups but also because they covered the range of diversity observed in each group. A more detailed description of the material is given in supplemental Table S2.
Sequencing:
We PCR amplified the seven selected markers (d801, d802, b188, t1p3, f03, g05, and tb58), a 2.7-kb region in Tb1 (encompassing part of the 5′-UTR, the coding region, and part of the 3′ region), and a 1-kb fragment of D8 (including the 5′-UTR and a small part of the coding region) on a panel of 40 inbreds. The PCR primers were designed using the Primer3 program (Rozen and Skaletsky 2000). A list of PCR primers and conditions is available (supplemental Table S3). Tb1 was amplified according to Tenaillon et al. (2001). Direct sequencing using ABI Dye terminator sequencing kits (Applied Biosystems, Foster City, CA) followed PCR amplification after ethanol precipitation. The products were sequenced and analyzed on ABI3130XL sequencers (Applied Biosystems). D8 and the markers were amplified from a sister genus of Zea, Tripsacum dactyloides, using the same primers and PCR conditions. However, among the markers, we managed to obtain PCR products and sequences from T. dactyloides for only three of them: d801, d802, and f03. T. dactyloides being potentially heterozygous, a PCR template was cloned into pGEM-T vector (Promega, Madison, WI) prior to sequencing. Concerning tb58, Tb1, and D8, many sequences from our sample of 40 inbreds were already available in databases (supplemental Table S2). Available and produced sequences were assembled and aligned into contigs in Staden v.5.1 (Staden 1996) and manually corrected in BioEdit v.4.8.8 (Hall 1999). Coding regions in D8 and Tb1 were assigned according to previously described open reading frames (ORFs) (Doebley et al. 1997; Thornsberry et al. 2001). We searched for ORFs for all markers using BLAST (http://www.ncbi.nlm.nih.gov/BLAST/). Only two markers had ORFs: d801 had homologies with a putative zinc-finger protein expressed in rice (Os03g0706900) over 104 amino acids and d802 had homologies with a rice expressed sequence tag (EST) Os03g0707200 over 37 amino acids. ORF information (supplemental Table S4) was used to estimate diversity on synonymous and nonsynonymous sites.
Polymorphism description:
The per-site standard estimates of nucleotide diversity, the average number of segregating sites, Watterson's θ (Watterson 1975), and the average number of pairwise differences, π (Nei 1987), were obtained for all sites and silent sites using DNAsp v.4.1 (Rozas et al. 2003).
Differentiation:
The differentiation between groups (Northern Flint and tropical) was measured by Gst and Fst and its significance was tested with Snn using DNAsp v.4.1. Gst is the ratio between the estimated haplotype diversity within groups over the estimate of the total haplotype diversity (Nei 1973). It considers each haplotype as a different allele and hence does not take into account the level of divergence between haplotypes. In contrast, Fst is the ratio between the estimated nucleotide diversity within groups over the estimate of the total nucleotide diversity (Hudson et al. 1992). Snn (i.e., nearest neighbor statistic) is a measure of how often the nearest neighbors of sequences are found in the same group (Hudson 2000). We assessed Snn significance, using a 1000-replicate permutation test. Besides differentiation estimates, haplotype networks can help in visualizing divergence by creating a minimum spanning tree that depicts the relationships between haplotypes: each line connecting two haplotypes represents the number of changes between them. Such networks were built using Tassel 1.9.5 (Bradbury et al. 2007). Finally, we used Strobeck's S statistic (Strobeck 1987) to detect deviation of the number of observed haplotypes from the neutral model.
Selection:
We tested for deviations from the neutral expectations with Tajima's D statistic, Fu and Li's F*, and D* using DNAsp v.4.1 (Rozas et al. 2003). A significant negative value of Tajima's D indicates an excess of rare variants as expected under positive and negative selection. A significant positive Tajima's D value, at the opposite, indicates an excess of high-frequency variants as expected under balancing selection or under population structure. We performed an additional test requiring an outgroup species (T. dactyloides): the HKA test. It is based on the comparison of the ratios of polymorphism over divergence (estimated from the outgroup) between multiple markers, ideally, one candidate marker against several control (neutral) markers (Hudson et al. 1987). Eleven control loci previously sequenced in a collection of nine tropical and Dent inbred lines (Tenaillon et al. 2001) were included in our HKA analyses. Because only tropical and Dent lines were sequenced for control loci, we performed the HKA test only within the tropical group. We tested each of our candidates for which an outgroup was sequenced (d801, d802, and f03) against these control loci. We performed the multilocus HKA test on the basis of a maximum-likelihood approach (Wright and Charlesworth 2004). This approach tests for neutrality at the candidate locus and gives an estimate, k, that measures the degree to which diversity is increased or decreased by selection. To test for neutrality at each candidate locus independently, we considered three neutral models including the 11 control loci and d801, d802, or f03. For each of these marker sets, we compared the likelihood value obtained under the neutral model with the likelihood value obtained under a nested model accounting for selection at one of the candidate loci (d801, d802, or f03). We performed additional likelihood-ratio tests on nested models including d801 and f03 as candidate loci for selection. The neutral model considered (model A) includes 11 control markers and 2 candidates (13 neutral loci in total). See Table 1 for a detailed comparison of the tests performed.
TABLE 1.
Likelihood-ratio tests of neutrality of silent polymorphisms at loci d801 and f03 in tropical lines
|
kb
|
|||||
|---|---|---|---|---|---|
| Name: model (locus under selection) | Comparison | LR stat. (d.f.)a | P-value | d801 | f03 |
| A: neutral (none) | 1 | 1 | |||
| B: selection (d801 and f03) | B vs. A | 8.41 (2) | 0.0149 | 0.177 | 0.396 |
| C: selection (d801) | C vs. A | 4.97 (1) | 0.0257 | 0.144 | 1 |
| B vs. C | 3.44 (1) | 0.0637 | |||
Eleven neutral loci previously sequenced in a common sample of nine tropical and Dent lines were taken as control loci (Tenaillon et al. 2001).
Likelihood-ratio statistic (degrees of freedom).
k measures the degree of diversity reduction caused by selection.
In addition, we used a simulation approach, successfully applied to maize data at the Tb1 locus (Przeworski 2003). It models a complete selective sweep using the coalescent framework and provides a joint posterior distribution of the selection coefficient (s) and the time in generations since the fixation of the favored allele (Tgen = 4NT). Similarly to Przeworski (2003), we set the population size (N) to 500,000 and the distance to the selected site, k, to 1 unit. The estimate of the mutation rate in the Tb1 region, 3.1 × 10−8/site/generation, was provided in a recent study by Clark et al. (2005). We estimated the recombination rate as 3.3 × 10−8/site/generation by the ratio of the estimated genetic distance between Tb1 and D8 (1 cM = 1% recombination) over the estimated physical distance of ∼300 kb. The resulting recombination estimate was close to the estimate used in a previous study, 1.35 × 10−8 (Przeworski 2003). We chose default parameters for ɛ = 0.1 and Mɛ = 1000 simulations (see Przeworski 2003 for a description of these parameters).
Simulations:
We used Monte Carlo simulations to evaluate the effects of two evolutionary scenarios on the patterns of polymorphism of the Tb1–D8 region. Camus-Kulandaivelu et al. (2006) suggest that D8 has been subjected to diversifying selection in relation to climate adaptation, its early allele being beneficial in the Northern Flint (NF) population and its late allele being beneficial in the tropical population. We therefore considered a single maize population—that could be either the tropical or the NF population—and included positive selection at two genetically linked loci, a domestication locus (locus 1) and a flowering-time locus (locus 2). The two scenarios differed in the mode and time of introduction of a new favored flowering-time allele at locus 2 in the maize population considered. Scenarios were simulated using a slightly modified version of the model developed by Chevin et al. (2008) that was specifically designed to study sweep interference among partially linked loci. Chevin et al.'s (2008) approach models the forward evolution of virtual chromosomes bearing neutral markers positioned along a genetic map (positions are expressed in centimorgans) under the infinite-site model of mutation and allows for recombination between and within markers. At any stage, some sites within the simulated region may be subjected to selection. Time of arrival of a beneficial mutation as well as its position within a marker and the corresponding selection coefficient are determined by the user.
Using this framework, we simulated the evolution of six neutral markers (DNA stretches of ∼500 bp), two of which include one selected site. The genetic map was defined relative to the position of the first selected site (locus 1), such that it had position 0 cM. The second selected site was located at 0.5 cM (locus 2), and the selection coefficient was set for both markers to 0.05 as determined for Tb1 by Olsen et al. (2006). Three other markers were located in between the two selected markers (0.125, 0.25, and 0.375 cM) while one marker was located outside this interval at position 0.75 cM and served as a control.
Because of both population size limitation and computational time inherent to forward simulations, we could not take into account demography and considered a constant maize population size, Na, of 1000 diploid individuals consistent with the ancestral maize population size (Tenaillon et al. 2004; Wright et al. 2005). To mimic the sampling of the initial maize population from among the teosinte genetic pool, the initial polymorphism of each neutral marker was generated using ms, a coalescent-based program that produces sequences drawn within a population at Wright–Fisher equilibrium (Hudson 2002). For each marker, we performed 1000 ms runs simulating the evolution of 2000 sequences (1000 diploid individuals) with a recombination rate 4rNa = 4.10−3 and a mutation parameter θa = 4μNa = 3.5, which roughly corresponds to what is observed on maize markers of length 500 bp (Tenaillon et al. 2004). The forward phase was initiated at the beginning of the selection at locus 1, starting from the polymorphisms generated with ms. The per-site mutation rate during the forward phase was set to μ = θa/(4Na × 500) = 1.75 × 10−6 and the intralocus recombination rate to 10−6 while the interlocus recombination was determined by the genetic distance between the markers.
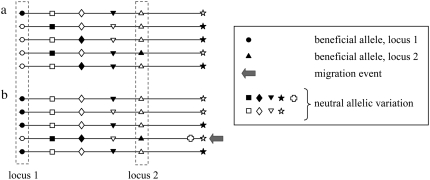
The forward simulation started with a low frequency of the cultivated locus 1 allele in the population, consistent with the strong signature of selection found in the 5′ region of Tb1 (Wang et al. 1999; Clark et al. 2004). The results were conditioned on fixation at both locus 1 and locus 2; therefore, five identical haplotypes carrying the favored allele were initially introduced to prevent a loss by drift in the early generations. This procedure is justified since, conditional on its final fixation, a beneficial mutation rises quickly in frequency, and thus there is negligible opportunity for mutation or recombination to occur on the haplotype that carries it (Barton 1998). The mode and time of occurrence of the favored flowering-time allele (locus 2) differed between the two scenarios (Figure 2):
In the “simultaneous scenario,” the locus 2 favored allele was introduced on a randomly chosen haplotype at a low frequency simultaneously to the domesticated allele at locus 1. Selection acted on both favored alleles since the beginning of the simulations. Similarly to the haplotype carrying the beneficial locus 1 allele, the haplotype carrying the beneficial flowering-time allele (locus 2) was introduced in five identical copies. In a rare case (probability of 0.0025), the same haplotype carried both favored alleles.
In the “migration scenario,” the beneficial locus 2 allele was introduced by migration from the ancestral population after the fixation of the locus 1 cultivated allele. Migration was modeled as a single event introducing five copies of a single haplotype from the ancestral population. The migrant haplotype was chosen from the initial sequence population at the end of the ms process.
Figure 2.—
Scenarios considered in the simulations involving interfering sweeps at two loci, a domestication locus (locus 1) and a flowering-time locus (locus 2): (a) the “simultaneous scenario”, where both beneficial alleles appear at low frequency and are simultaneously selected; and (b) the “migration scenario,” where the beneficial locus 2 allele is introduced from the ancestral population (teosinte) after the fixation of the locus 1 beneficial allele among maize. Symbols stand for the markers located along the simulated genetic map. Solid and open symbols represent different alleles. Solid alleles at locus 1 and locus 2 are beneficial and selected.
Besides these two scenarios, we also modeled selection at a single locus (locus 1).
Simulations where one of the selected alleles was lost by drift were ignored. We performed 1000 repeats for each of the five scenarios and stopped each simulation at the fixation of both locus 1 and locus 2 favored alleles. For each marker and for each 1000 repeats of each scenario, we measured the nucleotide diversity, π (Nei 1987) on 20 sequences randomly selected among the 2000 simulated sequences. π-values were averaged across repeats and 95% confidence intervals (C.I.) were determined.
Association mapping at b188 and d801:
We studied the association between the polymorphisms at two markers (b188 and d801) and flowering-time variation on a large panel of 375 inbred lines previously described by Camus-Kulandaivelu et al. (2006). We analyzed 13 biallelic polymorphisms, including 3 SNPs and 4 insertion–deletion polymorphisms (IDPs) at b188, and 3 SNPs and 2 IDPs at d801, as well as the 6-bp IDP (D8idp) located in the D8 gene and previously shown to be associated with flowering-time variation (Thornsberry et al. 2001; Andersen et al. 2005; Camus-Kulandaivelu et al. 2006). All these polymorphisms are referred to, hereafter, as candidate SNPs. Flowering time was evaluated under long-day conditions as days to pollen shed expressed in thermal time (Ritchie and Nesmith 1991), and adjusted means were estimated for each inbred line over a two locations by two replicates by 15 plant rows experiment as described by Camus-Kulandaivelu et al. (2006). The association mapping was first performed using a linear model, hereafter “model Q,” which corrects for population structure (Pritchard et al. 2000a). Model Q was tested using the GLM procedure and the ss3 option in SAS (SAS 1989). Population structure was inferred from 55 genomewide SSR loci, using STRUCTURE software (Pritchard et al. 2000b) in a previous work by Camus-Kulandaivelu et al. (2006). On the basis of goodness-of-fit criteria, the number of groups was estimated to be five and 10 runs of STRUCTURE were performed, leading to 10 matrices of group memberships. For the sake of comparison with Camus-Kulandaivelu et al.'s (2006) results, we analyzed the phenotype–genotype associations under each of the 10 five-group structures. Second, we used a mixed model (“model Q + K”), correcting for both population structure (using the highest goodness-of-fit structure matrix) and kinship (Yu et al. 2006). Kinship was inferred from Loiselle et al.'s (1995) coefficient, using SpageDi (Hardy and Vekemans 2002). The Q + K model analysis was performed using TASSEL software (Bradbury et al. 2007) and we consider the candidate SNP and population structure as fixed effects and the inbred line effect as random. Although population structure and kinship were calculated with the same SSR data set, the use of this model is justified because (i) it has been shown that these two measures of long-range LD do not capture the same part of phenotype–genotype associations (Yu et al. 2006; Zhao et al. 2007) and (ii) the association panel used is known to contain related maize lines (Camus-Kulandaivelu et al. 2007). Finally, to determine whether b188 or d801 candidate SNPs each explains an independent part of flowering-time variation as compared to D8idp, we used a linear model (“model Q + IDP”) that corrects for population structure and tested for the effect of D8idp and an additional candidate SNP, using the GLM procedure and the ss3 option in SAS (SAS 1989). Linkage disequilibrium among those 13 candidate SNPs was estimated as r2 (squared correlation coefficient) (Hill and Robertson 1968) between all pairs of sites and tested using Fisher's exact tests.
RESULTS
Patterns of nucleotide diversity:
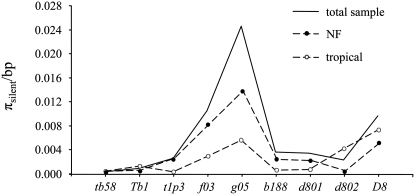
The nucleotide diversity as measured by πsilent exhibits a contrasted pattern of variation along the Tb1–D8 region (Figure 3) in the entire sample of 40 lines and within the two genetic groups (tropical and Northern Flint). πsilent-values (supplemental Table S5) are <0.0035 at tb58, Tb1, and t1p3 as well as at b188 and d801, while they reach their maximum at f03 and g05. Considering the whole sample, a 33- and a 77-fold increase in diversity is observed between the markers tb58 and f03, and tb58 and g05, respectively. The higher level of diversity at f03 and g05 as compared to Tb1 and t1p3 is lower but remains substantial (from 4-fold up to 28-fold). Similarly, the increase in diversity at f03 and g05 as compared to b188 and d801, respectively, is notable (∼6-fold increase). In contrast, at D8, tropical lines and to a lower extent NF recover an appreciable amount of diversity (maximum πsilent-value of 0.0072 in the tropical group at D8). Overall, the pattern of πsilent along the Tb1–D8 region exhibits two valleys of depleted polymorphism, suggesting the existence two selective events affecting the two maize groups in both (i) the tb58–Tb1 region consistent with maize domestication and (ii) the b188–d801 region.
Figure 3.—
Nucleotide diversity as estimated by the per-base estimate at silent sites: πsilent. Because we have only rough estimates of the physical distance between the loci, we arranged them at equal distances in their order of appearance along chromosome 1. The relative position of f03 and g05 was chosen arbitrarily. NF, Northern Flint.
Patterns of differentiation:
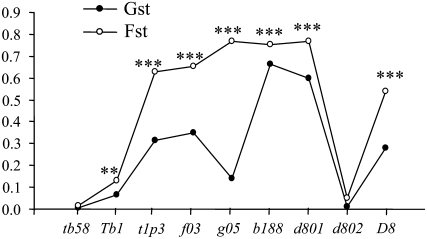
Just like πsilent, nucleotide (Fst) and haplotype (Gst) differentiation exhibit a contrasted pattern of variation along the Tb1–D8 region (Figure 4). Gst and Fst exhibit low values at tb58, Tb1, and d802 (Gst values range from −0.004 to 0.049, and Fst values from 0.000 to 0.118). The Snn values are not significant at both tb58 and d802 but are significant at Tb1 (P < 0.01). On the contrary, elevated values of Gst and Fst were obtained for t1p3, f03, b188, d801, and D8, indicating a high level of differentiation between NF and tropical lines at these markers. For all these markers, Snn values are highly significant (P < 0.0001). Among them, b188 and d801 exhibit the highest level of differentiation (Gst = 0.655 and Fst = 0.746 for b188, Gst = 0.587 and Fst = 0.761 for d801). The only notable difference between Gst and Fst behavior is at g05. Indeed, g05 exhibits the highest Fst value among all sequenced markers (0.761) while its Gst value is moderate (0.128). Haplotype networks (data not shown) further revealed that sequences at markers t1p3, f03, g05, b188, and d801 are divided into two main haplotypic groups reflecting the sample subdivision into NF and tropical lines while the haplotypic structure becomes more complex at D8. The high level of diversity within the two haplotypic groups at g05 is such that each inbred line forms a single haplotype resulting in elevated Fst while the Gst value remains low.
Figure 4.—
Haplotype (Gst) and nucleotide differentiation (Fst) between the Northern Flint and the tropical inbred lines. Significance of Snn values is indicated above Fst values (**P < 0.01, ***P < 0.0001).
Overall, the weak level of differentiation between NF on one hand and tropical lines on the other, at tb58 and Tb1 (Figure 4), results from the presence of a single cultivated haplotype in this region. In contrast, the high level of differentiation observed for other markers (Figure 4) is due to the coexistence of two main haplotypic groups with contrasted allele frequencies in the NF and the tropical lines. The particularly low level of diversity within the two haplotypic groups in the b188–d801 region suggests divergent selection acting in this region.
Testing for selection in the Tb1–D8 region:
Figure 5 (see also supplemental Table S5) shows the Tajima's D variation pattern along the Tb1–D8 region in NF and tropical and the combined sample of NF and tropical lines. The tropical sample is characterized by negative Tajima's D values along the entire region, with minimum and significant values of −2.145 (P < 0.05) and −2.296 (P < 0.01) at f03 and g05, respectively. Similarly, Fu and Li's D* and F* statistics (supplemental Table S5) exhibit negative and significant values at f03 and g05 in the tropical sample (g05, D* = −3.58 and F* = −3.72; f03, D* = −2.87 and F* = −3.08). The NF sample, in contrast, exhibits nonsignificant D values for all nine markers. A similar pattern across the region is observed for the NF sample, using D* and F*. Using the combined sample of NF and tropical lines, which led to a substantial gain of power, we found negative and significant values of Tajima's D at Tb1 (P < 0.05) and d802 (P < 0.01) as well as a significant haplotypic test for tb58 (P < 0.05) and Tb1 (P < 0.01), revealing a significant deficit of haplotypes at both of these markers.
Figure 5.—
Tajima's D values for the Northern Flint lines (NF), the tropical lines, and the combined sample of NF and tropical lines. Tajima's D significance is indicated (*P < 0.05, **P < 0.01).
Tajima's D values on the combined sample of NF and tropical lines are also informative regarding the level of differentiation between both groups (Figure 5). In fact, an excess of common variants and correspondingly elevated Tajima's D values are expected in regions of high differentiation. We did find elevated values (>1) for t1p3, f03, g05, b188, d801, and D8, with significant values of 2.98 at g05 (P < 0.01) and of 2.20 at f03 (P < 0.05), consistent with their high level of genetic diversity (πsilent, Figure 3) and differentiation (Fst, Figure 4).
A multilocus HKA maximum-likelihood-based method was applied to test for selection in the tropical sample at three markers, d801, d802, and f03 for which an outgroup sequence was available. Besides explicitly testing for selection at defined candidate loci, this approach also allows us to estimate a parameter k that quantifies the degree to which the diversity is increased or decreased by the effect of selection. We included 11 control markers sequenced in a previous study (Tenaillon et al. 2001) on a sample of nine tropical and Dent lines and the same outgroup (T. dactyloides). Models involving selection at either d801 or f03 alone performed significantly better than the neutral model (P = 0.0084 for d801 and P = 0.0294 for f03), selection at d801 being stronger with a lower associated value of k (k = 0.114) than selection at f03 (k = 0.288). In contrast, no evidence of selection was detected at d802 (P = 0.0815). We further tested nested models involving either selection at loci d801 and f03 (model B) or selection at d801 only (model C). As shown in Table 1, the model involving selection at both d801 and f03 performed significantly better than the neutral model (A). The lack of significance between models B and C (P = 0.0637), although borderline, seems to indicate that the model involving selection at d801 only is the most parsimonious. We obtained similar results by running for each model two additional independent Markov chains starting with different seeds, which overall indicates a good convergence of the chain. These results suggest that d801 has been under selection or, more likely, linked to a target of selection in the tropical lines. The absence of selection at d802 in the tropical sample as detected by the multilocus HKA may indicate that d802 is farther away from the target of selection than d801, consistent with its slightly higher level of nucleotide diversity (Figure 3) and its low level of differentiation between the NF and the tropical lines (Figures 4 and 5).
To refine our search of selection footprints in the tropical and the NF sample, respectively, and, in particular, to gain precision on the estimation of the intensity of selection (s) as well as on the time since fixation of the beneficial allele at the target regions (T), we used a coalescence-based method developed by Przeworski (2003). Outputs of the program provide the percentage of simulations among 1000 with T ≤ 0.2. According to Przeworski (2003), an elevated value (>99%) is indicative of a recent selective sweep. Our results support the recent fixation (consistent with the domestication known date) of a beneficial allele around tb58 (Table 2) in the tropical and in the NF sample, as well as a recent selective sweep near b188 and d801 within the tropical lines. d802 exhibits a clear pattern of selection in the NF sample, consistent with its negative Tajima's D value (Figure 5), while no recent selective event in the b188–d801 region was identified. Indeed, at b188 and d801, only 63.9 and 55.4% of simulations had a value of T ≤ 0.2 in the NF sample as compared to 99 and 99.5% in tropical lines (Table 2).
TABLE 2.
Percentage of simulations among 1000 with T ≤ 0.2
| Loci | NF | Tropical |
|---|---|---|
| tb58 | 93.1 | 99.8 |
| f03 | 97.8 | 97.2 |
| b188 | 63.6 | 99 |
| d801 | 55.4 | 99.5 |
| d802 | 100 | 96.6 |
| d8b | NAa | 40.6 |
| Region 1 | 93 | NAa |
| Region 2 | 89.2 | 97.9 |
This criterion was arbitrarily chosen according to Przeworski (2003). A high percentage of simulations (>99%) is indicative of a recent selective sweep.
Not available.
Because of computer limitation, we were not able to compute d8 for the NF. We therefore decided to arbitrarily divide d8 into two regions ranging from 1 to 848 (region 1) and from 849 to 1357 (region 2) and computed independently each region for the NF and the tropical lines, respectively.
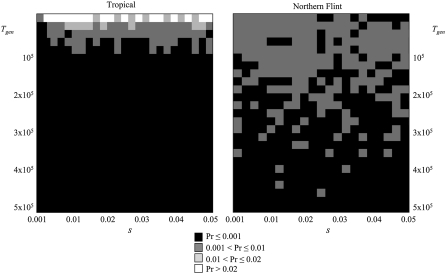
Differences in selective patterns between tropical and NF lines at b188 are further illustrated in Figure 6. Figure 6 presents the associated probabilities from the joint posterior distribution of Tgen (time since fixation of a beneficial allele in generations) and s (the selection coefficient) for the tropical and the NF sample. Higher probabilities are obtained for Tgen < 9000 generations as compared to Tgen > 9000 in the tropical sample, while in the NF sample, values were spread over the whole grid of time values explored and never reached >1%, again suggesting no recent fixation of a beneficial allele in the NF sample at b188. We obtained similar graphs with d801 (data not shown). From these data, it was difficult to infer any “most probable” s value associated within the range explored. It is, however, clear that elevated s values are compatible with our data in the tropical sample.
Figure 6.—
Sample from the joint posterior distribution at locus b188 of Tgen (= 4NT), the time in generations since the fixation of the beneficial allele, and s, the selection coefficient of the favored allele, respectively, in Northern Flint lines (right) and tropical lines (left). As indicated in the key, solid areas indicate a low probability of observing the values among 1000 simulations while shaded areas indicate higher probabilities.
Association mapping at d801 and b188:
Markers d801 and b188 exhibit a strong signal of divergent selection between the NF and the tropical lines, although selection at these loci is likely older in the NF sample than in the tropical sample. They hence unexpectedly appear as interesting candidate loci for variation in flowering time in maize. To verify this prediction, we undertook an association genetic analysis between the variation in flowering time and the SNPs located in b188 and d801 on a 375-maize-line panel described by Camus-Kulandaivelu et al. (2006). According to Camus-Kulandaivelu et al. (2006), this panel is structured into five genetic groups (NF, European Flint, Stiff stalk, Dent, and tropical). Association studies correcting for population structure (Q) or both population structure and kinship (Q + K) gave very similar results: all SNPs in b188 and D801 are significantly associated with flowering time (see P in Table 3). When correcting for multiple testing in model Q (Padj), two SNPs in b188 (B173 and B316) and a single SNP in d801 (D218) are still associated with flowering time. Interestingly, in all models, D8idp, a polymorphism in the D8 coding region previously identified as associated to variation in flowering time (Thornsberry et al. 2001; Andersen et al. 2005; Camus-Kulandaivelu et al. 2006), was never significant. We found very strong (r2 > 0.6) and highly significant LD among all SNPs in b188 and d801 markers (Figure 7), B173 and B316 being in total linkage. In contrast, pairwise LD values between D8idp and either b188 or d801 SNPs were much lower (0.2 < r2 < 0.4). When considering both population structure and D8idp as covariates to test an additional SNP from either b188 or d801 in a single model (model Q + IDP, Table 3), we found that B173, B316, or D218 SNPs explain a borderline significant part of flowering-time variation (0.05 < Psnp < 0.10) that is not already explained by D8idp. The reciprocal is not true; the specific part of flowering-time variation explained by D8idp was never significant (Pidp > 0.20) when taking both population structure and one b188 or d801 SNP as a covariate.
TABLE 3.
Association between polymorphisms at b188, d801, and D8 loci and variation in flowering time in a panel of 375 inbred lines
| Model Qa
|
Model Q + Kb
|
Model Q + IDPc
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Locus | SNP | Paveraged | Pe | Padjf |
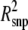 g (%) g (%) |
Pe |
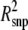 g (%) g (%) |
Pidph | Psnpi |
| b188 | B17 | 0.012 | 0.016 | 0.103 | 0.88 | 0.019 | 0.48 | 0.378 | 0.230 |
| B173 | 0.002 | 0.001 | 0.001 | 1.55 | 0.003 | 0.70 | 0.608 | 0.056 | |
| B263 | 0.012 | 0.016 | 0.117 | 0.88 | 0.019 | 0.48 | 0.378 | 0.230 | |
| B272 | 0.011 | 0.014 | 0.079 | 0.92 | 0.017 | 0.50 | 0.378 | 0.230 | |
| B291 | 0.011 | 0.014 | 0.066 | 0.92 | 0.017 | 0.50 | 0.378 | 0.230 | |
| B316 | 0.002 | 0.001 | 0.002 | 1.60 | 0.003 | 0.80 | 0.608 | 0.056 | |
| B472 | 0.065 | 0.023 | 0.188 | 0.79 | 0.020 | 0.52 | 0.220 | 0.268 | |
| d801 | D14 | 0.025 | 0.031 | 0.340 | 0.74 | 0.046 | 0.32 | 0.607 | 0.218 |
| D50 | 0.021 | 0.028 | 0.284 | 0.76 | 0.041 | 0.33 | 0.598 | 0.206 | |
| D151 | 0.019 | 0.025 | 0.225 | 0.79 | 0.039 | 0.34 | 0.598 | 0.206 | |
| D218 | 0.013 | 0.013 | 0.050 | 0.98 | 0.014 | 0.49 | 0.550 | 0.098 | |
| D262 | 0.021 | 0.028 | 0.264 | 0.76 | 0.041 | 0.33 | 0.598 | 0.206 | |
| D8 | D8idp | 0.101j | 0.136 | 0.869 | 0.35 | 0.065 | 0.32 | ||
A general linear model controlling for population structure.
A mixed model controlling for both population structure and kinship.
A general linear model that corrects for population structure and tests for the effect of D8idp (see footnote h) and an additional SNP (see footnote i).
Average SNP P-value over all 10 matrices for a five-group population structure.
SNP P-value considering the most likely population structure.
SNP P-value adjusted for multiple tests from 10,000 permutations (TASSEL software).
Part of the phenotypic variance explained by the SNP factor.
P-value for D8idp including a SNP as a covariate.
P-value for each SNP including D8idp as a covariate.
Average P-value reported in Camus-Kulandaivelu et al. (2006).
Figure 7.—
Linkage disequilibrium (LD) in the Tb1–D8 region in a panel of 375 maize inbred lines. LD is estimated as the squared coefficient of correlation (r2) among biallelic SNPs in b188 (B17–B472) and d801 (D14–D262) markers, and the D8 gene (D8idp SNP), and tested using Fisher's exact tests. The shaded squares located in the top diagonal of the matrix represent the r2 values between pairs of SNPs while those located in the bottom diagonal represent the corresponding P-values.
The phenotypic effect of the early and late alleles at the SNP B173 or B316 of the b188 marker was further investigated. Qualitatively, we first observed that the effect of a given allele on flowering time was consistent among groups. Second, among groups, variation of the late allele frequency correlated positively with average flowering time (r = 0.87, P < 0.05). Therefore, variation in allele frequencies at B173 or B316 seems clearly adaptive, which suggests that one of the sites within b188 or nearby in the zone displaying strong linkage disequilibrium with this site is involved in flowering-time variation. The estimated contribution of B173 or B316 to flowering-time variation (R2) ranged from 0.70 to 1.60%, depending on the model considered (Table 3). However, because the variation in allele frequency is also clearly associated with the population structure, by erasing the structure effect in the analysis, we may also discard part of the allele effect. The estimated effect should hence be considered as the lower bound, while the estimated effect without taking population structure into account (R2 = 10.3%) would define the effect upper bound. In terms of degree days (dd), the estimated effect without accounting for population structure corresponds to 109.4 dd while the effect inferred under the Q model corresponds to 44.2 dd.
Monte Carlo simulations:
Because the pattern of polymorphism observed in the Tb1–D8 region (Figure 3) is striking with its pick of diversity in between the two targets of selection, we used forward simulations to explore evolutionary scenarios that could be compatible with such a peculiar pattern. On the basis of our biological knowledge of domestication, we tested two contrasted scenarios (Figure 2) involving two sweeps, one located at a domestication locus (locus 1) and one located at a close genetic distance (0.5 cM) at a flowering-time locus (locus 2). Besides these two scenarios, we also modeled selection at a single locus (locus 1). Our results are presented in Figure 8.
Figure 8.—
Polymorphism patterns produced by one sweep located at position 0 (a) and two interfering sweeps located at positions 0 (locus 1) and 0.5 (locus 2), as modeled under the “simultaneous scenario” (b) and the “migration scenario” (c). At each marker (solid circle), π was estimated on 20 randomly chosen simulated sequences and averaged over 1000 repeats (solid lines); dotted lines indicate the 95% confidence interval.
In the case where only locus 1 (marker at position 0) was selected (Figure 8a), we observed the typical selective sweep pattern previously described by Przeworski et al. (2005) with a substantial reduction of diversity (π = 0.00069) combined with negative Tajima's D values (data not shown) at the selected locus. A gradual return to neutral expectations is observed when moving toward the marker at position 0.75 cM (π = 0.00498).
In the simultaneous scenario, the locus 2 favored allele was introduced at low frequency and selected simultaneously to the domesticated allele at locus 1. In the majority of the simulations (1995 of 2000), the locus 2 favored allele was not initially carried by the haplotype bearing the locus 1 domesticated allele. The sequences located at locus 1 and locus 2 display, on average, the lowest diversity of the region with reduced 95% confidence intervals (Figure 8b). The markers located in between the selected sites exhibit a higher level of diversity. In particular, the marker located in the middle of the selected sites (position 0.25 cM) has, on average, the highest π-value (0.00305) that corresponds to an approximately fourfold increase. This level of diversity is slightly higher than the one observed at the marker located outside the region at position 0.75 cM (π = 0.00271), consistent with the results described in Chevin et al. (2008) under fairly similar conditions.
In the migration scenario, the locus 2 favored allele was introduced at low frequency by migration from the teosinte population subsequently to the fixation of the locus 1 favored allele. The polymorphism pattern generated by this scenario is similar to that observed in the simultaneous scenario with an approximately threefold increase in diversity at the marker located in between the selected loci.
Overall, interfering sweeps lead to “bell” patterns similar to the one observed in the Tb1–D8 (Figure 3) region and we were not able to discriminate between the diversity patterns produced under the two scenarios.
DISCUSSION
Because the Tb1–D8 region bears two important genes, a domestication gene (Tb1) and a candidate for climate adaptation (D8), within a restricted interval of ∼300 kb as determined by our analysis (Figure 1), it offers a unique opportunity both to investigate the patterns of variation generated by interfering sweeps and to gain insights into maize expansion history from its domestication center.
Our results first confirm the selective event in the Tb1–tb58 region during maize domestication. The very low level of differentiation coupled with a close examination of the sequence alignment reveals the presence of a unique cultivated haplotype for Tb1 and tb58 (Figure 4), consistent with a single domestication event (Wang et al. 1999). Note the sensitivity of the Snn test that detects a significant differentiation between NF and tropical at Tb1. Additionally, our results clearly validate the existence of a second target of selection, roughly located in the b188–D8 region. Indeed, the molecular evolution pattern around D8 cannot result from a single selective sweep at Tb1–tb58 during maize domestication. There is some evidence in the literature that D8 is under selection in maize (Tenaillon et al. 2001, 2004) and, more importantly, that some polymorphisms within D8, such as D8idp, associate significantly with the variation of flowering time (Thornsberry et al. 2001; Andersen et al. 2005; Camus-Kulandaivelu et al. 2006). However, it seems from our data that the region upstream of D8 encompassing b188 and d801 exhibits a strong signal of divergent selection in relation to climate adaptation in tropical and NF material. Several arguments support this hypothesis: b188 and d801 have a very low amount of polymorphism in both samples (Figure 3) together with a very high level of differentiation between tropical and NF lines due to the occurrence of two major haplotypes (Figure 4). Consistently, both markers also exhibit elevated Tajima's D values in the combined sample of NF and tropical lines although not significant ones (Figure 5). Their reduced level of diversity (Figure 3) likely affects our ability to detect a significant differentiation using Tajima's D. Multiple HKA tests further reveal selection at d801 (Table 1).
Altogether, our results are consistent with divergent selection between NF and tropical lines in a region ∼100–150 kb upstream of D8. We studied the phenotypic effect of individual SNPs located within the two markers d801 and b188, using the maize inbred lines panel described by Camus-Kulandaivelu et al. (2006). Three SNPs showing significant and strong linkage disequilibrium between each other (r2 > 0.8) are significantly associated with flowering time (Table 3), i.e., SNPs B173 and B316 in b188 and SNP D218 in d801. For each SNP, a given allele is consistently associated with a given phenotypic effect within all groups of origin (data not shown). Finally, a strong among-group correlation between B173 or B316 late allele frequency and phenotypic variation (r = 0.87, P < 0.05) was also observed. In contrast, association between the D8idp polymorphism located in the D8 gene itself was only close to significance (P = 0.065) in the mixed model (Table 3) and presents weak linkage disequilibrium with the three flowering-associated SNPs of b188 and d801 (Figure 7). These results strongly support the role of the region upstream of D8 in the genetic determination of flowering-time variation in maize.
Because of intensive LD in the region, it is, however, impossible from our data to infer a causative SNP responsible for flowering-time variation. Still, it is interesting to note that similarly to Tb1, the causal mutation may be located several kilobases upstream of the D8 gene and may act through a cis-regulatory mechanism. Alternatively, because we found a strong homology between d801 and a putative zinc-finger protein expressed in rice, another gene/regulatory region of another gene than D8 itself may be involved in the determination of flowering time. Note that this putative rice protein encompasses a conserved RING-finger domain, responsible for DNA binding and oligomerization (Liu et al. 1999). In plants, genes containing such a RING-finger domain are known to be involved in many functions including photoperiodic response (Chen and Ni 2006) and tolerance to cold (Dong et al. 2006), high temperatures (Zeba et al. 2006), and drought (Ko et al. 2006).
The phenotypic effect of the b188–d801 region seems clear from our association genetic results but explains at the most 1.60% of flowering-time variation. Because flowering time is strongly structured according to geographical origin (Camus-Kulandaivelu et al. 2007), the part of flowering-time variance absorbed by the genetic structure component in our models is high and likely results in an underestimation of associated SNP effects. Nevertheless, this region likely involves variation with relatively small phenotypic effects, which can be observed in a model of stabilizing selection with a slow-moving optimum (Kopp and Hermisson 2007). In practice, our results are therefore consistent with an adaptation accompanied by a progressive climate change and/or a slow migration.
Using Przeworski (2003)'s approach, we obtained contrasted patterns of selection in NF and tropical lines (Table 2 and Figure 6). The most straightforward interpretation of our data is that selection in the tropical sample is more recent than selection in the NF sample. We must, however, consider two alternative explanations. First, the target of selection could be farther away from the studied region in the NF than in the tropical lines. This hypothesis implies that two different regions are involved in flowering-time determinism in each group: a region around b188 and d801 for the tropical group and a region around d802 in the NF group. Indeed, d802 harbors the lowest diversity level and the most severe footprint of selection in the NF sample [100% of simulations, T < 0.2 (Table 2)]. We consider this interpretation as unlikely first because it requires the presence of two loci involved in the control of flowering time within a very restricted region of ∼110 kb and second because the Tajima's D values are consistently negative along the whole region in the tropical lines in contrast to what is observed in the NF sample. Moreover, the differentiation between the NF and the tropical material is very low at d802 (Figures 4 and 5). As a second alternative explanation, we considered that tropical lines could have undergone a more severe bottleneck than NF lines, consistent with the reduced level of diversity observed along the region in the tropical sample. We used the 55 microsatellites dispersed throughout the genome and previously genotyped in the NF and the tropical lines used in this study (Camus-Kulandaivelu et al. 2006) to evaluate the genomic level of diversity in both samples. We used three measures of diversity: Nei's heterozygosity, H (Nei 1987), the number of alleles (all), and the Garza and Williamson (G–W) index (Garza and Williamson 2001). Low values of the G–W index are indicative of recent bottlenecks (Garza and Williamson 2001). We found neither evidence for a depleted level of diversity in the tropical as compared to the NF sample (H = 0.475, all = 3.20 in the NF and H = 0.596, all = 4.18 in the tropical sample) nor evidence for a more severe/recent bottleneck in the tropical sample as compare to the NF sample (average G–W index calculated among 55 microsatellite loci = 0.33 and 0.32 in the NF and the tropical samples, respectively). In fact, the genomic level of diversity was somehow lower in the NF sample, consistent with a previous study (Doebley et al. 1986) reporting a reduced diversity of NF American landraces as compared to Mexican landraces. Therefore the differences in the patterns of nucleotide variation that we observed between the NF and the tropical samples cannot be explained by a more severe bottleneck in the tropical sample, but likely result from a recent selection of the late-flowering allele.
A more recent selection in the tropical material than in the NF supports the “highland hypothesis,” according to which maize first diversified in the Mexican highlands before reaching the lowland areas (Smith 1998, 2001; Freitas et al. 2003). On the basis of results at the key flowering-time locus Vgt1, Ducrocq et al. (2008) hypothesized that tropical lowland maize differentiated from a pool of variable highland maize via selection on late-flowering alleles, allowing for a longer life cycle and therefore higher yield in the warm and wet lowland areas. Several lines of evidence showing that both NF and Mexican highland maize are genetically closer to teosinte than tropical maize support our findings. For instance, NF bears at a high frequency a Sugary1 haplotype that is found in present teosintes as well as in a 2000-year-old cob from New Mexico (Jaenicke-Després et al. 2003). In contrast, this haplotype is very rare in other cultivated maize varieties (Jaenicke-Després et al. 2003). Similarly, the 6-bp deletion located in D8, D8idp, is found at high frequency in NF while it is very rare in tropical maize except in Andean landraces and in some Mexican highland varieties (Camus-Kulandaivelu et al. 2006). According to Freitas et al. (2003), these Andean landraces are the relics of the early Mexican highland varieties' expansion in South America. NF also exhibits some particular “ancestral” phenotypic characteristics such as the presence of well-developed tillers and long husks (Brown and Anderson 1947) as well as a very particular system for kernel exposure apparently derived from the spikelet structure, similar to what is observed in the wild teosinte Z. mays ssp mexicana (Galinat 1988). Finally, Matsuoka et al. (2002) pinpointed the basal position of current highland Mexican landraces in an SSR-based maize distance tree. Altogether, these observations suggest that NF is closely related to the first domesticated Mexican highland maize, consistent with the highland hypothesis. It is interesting in regard to recent data showing that the Balsas river valley region, in which the maize is supposed to have been originally domesticated (Matsuoka et al. 2002), was possibly a cooler and drier herbaceous environment at the time of domestication since it underwent a major climatic and ecological change 9000–11,000 years ago, turning progressively into a warm and wet tropical forest (Piperno and Flannery 2001).
The patterns of polymorphism in the Tb1–D8 region in the NF and the tropical groups are characterized by a reduced and comparable diversity level at both target genes (Tb1 and d801) as compared to the region in between (notably at markers f05 and g03) that exhibits a higher level of diversity. We simulated evolutionary scenarios (Figure 2) that we considered biologically relevant for the occurrence of the flowering-time favored allele (either the early-flowering-time allele in the NF group or the late-flowering-time allele in the tropical group). Both involved interfering sweeps at two genetically linked loci located 0.5 cM apart, a domestication locus (locus 1, located in the Tb1–tb58 region), and a flowering-time locus (locus 2, located in the d801–b188 region). Because in those two scenarios beneficial alleles are not associated within the same haplotype at the beginning of selection (except for a handful of simulations in the simultaneous scenario), they potentially drag along different neutral alleles in their neighboring regions. This situation generates an increased level of diversity and number of intermediate-frequency mutations in the region in between the two selected sites (Figure 8, b and c), relative to a single sweep and even sometimes to the neutral expectation (Chevin et al. 2008). Interestingly, this effect is slightly stronger when both alleles are selected simultaneously (simultaneous scenario) rather than successively (migration scenario).
Although confidence intervals are wide (Figure 8), the observed “bell” pattern in our simulations under both scenarios is consistent with our data. In other words, the favored allele at the flowering locus, presumably the first one selected being the early-flowering allele, may have been either selected simultaneously to the favored allele at the Tb1 domestication locus or alternatively brought by migration from the wild teosinte gene pool. Following our previous interpretation, i.e., early-flowering maize were the first to be domesticated, a scenario involving a simultaneous selection of the early-flowering allele and the Tb1 cultivated allele in a cold and dry area (highland hypothesis) followed by a selection of the tropical allele brought by migration after the fixation of the early-flowering allele would be the most consistent in regard to our data. Obviously this interpretation is somehow speculative because the model is simplistic. A more comprehensive method may involve the use of approximate Bayesian computing to jointly estimate the underlying parameters of selection and assess the relative likelihoods of the various models. Yet, the complex scenario we wished to study (involving selection at two linked loci) did not allow an efficient coalescent treatment. Although we are aware of the model limitation, we think that the patterns observed in the Tb1–D8 region are consistent with interference between two selective sweeps. Such a pattern likely obscures positive selection imprints in the region in between selected loci because of the elevated polymorphism level. Our results illustrate previous theoretical work suggesting that selection acting at two closely linked loci could influence the surrounding neutral polymorphism pattern in a manner that could not be predicted by the plain addition of two hitchhiking effects (Chevin et al. 2008; Kim and Stephan 2003) and that it can lead to mistaking strong positive selection for neutrality or even balancing selection (Chevin et al. 2008). Here, using the fine-scale polymorphism pattern in a previously characterized candidate region, we further show that the presence of two interfering sweeps can provide valuable information about the adaptive history of the species, in a way that cannot be revealed by two unlinked selective sweeps. Because the adaptive process of domestication likely involves the fixation of beneficial mutations in short time periods following a drastic environment shift rather than a constant supply of favored mutations (Orr 1998), the occurrence of sweep interference may not be negligible and the resulting patterns of variation may be misleading in our search for footprints of adaptive evolution (Chevin et al. 2008), adding a new layer to the theoretical challenges brought by the increase of genomic data.
Acknowledgments
We are grateful to V. Combes and D. Madur for providing the DNA samples as well as to D. Madur for providing the sequences from the association genetic panel. We thank J.-B. Veyrieras and B. Gouesnard for helpful discussions, S. Santoni for hosting L.C.K. in his lab, and A. Censi for his precious help in finding ORFs. Anonymous reviewers contributed to improve the manuscript by providing thoughtful comments. This study was supported by the Agence National de la Recherche (ANR-05-JCJC-0067-01 to M.I.T.). Sequencing was also funded by the Institut National de Recherche Agronomique (INRA) (DGAP-AOSG-2006) and the Promaïs program “diversité cornés” to A.C., and L.C.K. was supported by a Ph.D. fellowship from INRA and the Languedoc–Roussillon region.
References
- Andersen, J. R., T. Schrag, A. E. Melchinger, I. Zein and T. Lubberstedt, 2005. Validation of Dwarf8 polymorphisms associated with flowering time in elite European inbred lines of maize (Zea mays L.). Theor. Appl. Genet. 111 206–217. [DOI] [PubMed] [Google Scholar]
- Barton, N. H., 1998. The effect of hitch-hiking on neutral genealogies. Genet. Res. 72 123–133. [Google Scholar]
- Borevitz, J. O., S. P. Hazen, T. P. Michale, G. P. Morris, I. R. Baxter et al., 2007. Genome-wide patterns of single-feature polymorphism in Arabidopsis thaliana. Proc. Natl. Acad. Sci. USA 104 12057–12062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradbury, P. J., Z. Zhang, D. E. Kroon, T. M. Casstevens, Y. Ramdoss et al., 2007. TASSEL: software for association mapping of complex traits in diverse samples. Bioinformatics 23 2633–2635. [DOI] [PubMed] [Google Scholar]
- Brown, W. L., and E. Anderson, 1947. The Northern Flint corns. Ann. Mo. Bot. Gard. 34 1–28. [Google Scholar]
- Buckler, E. S. IV, J. M. Thornsberry and S. Kresovich, 2001. Molecular diversity, structure and domestication of grasses. Genet. Res. 77 213–218. [DOI] [PubMed] [Google Scholar]
- Caicedo, A. L., S. H. Williamson, R. D. Hernandez, A. Boyko, A. Fledel-Alon et al., 2007. Genome-wide patterns of nucleotide polymorphism in domesticated rice. PLoS Genet. 3 1745–1756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camus-Kulandaivelu, L., J.-B. Veyrieras, D. Madur, V. Combes, M. Fourmann et al., 2006. Maize adaptation to temperate climate: relationship between population structure and polymorphism of Dwarf8 gene. Genetics 172 2449–2463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camus-Kulandaivelu, L., J.-B. Veyrieras, B. Gouesnard, A. Charcosset and D. Manicacci, 2007. Evaluating the reliability of Structure outputs in case of relatedness between individuals. Crop Sci. 47 887–892. [Google Scholar]
- Casa, A. M., S. E. Mitchell, M. T. Hamblin, H. Sun, J. E. Bowers et al., 2005. Diversity and selection in sorghum: simultaneous analyses using simple sequence repeats. Theor. Appl. Genet. 111 23–30. [DOI] [PubMed] [Google Scholar]
- Chardon, F., B. Virlon, L. Moreau, M. Falque, J. Joets et al., 2004. Genetic architecture of flowering time in maize as inferred from quantitative trait loci meta-analysis and synteny conservation with the rice genome. Genetics 168 2169–2185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, M. J., and M. Ni, 2006. RFI2, a RING-domain zinc finger protein, negatively regulates CONSTANS expression and photoperiodic flowering. Plant J. 46 823–833. [DOI] [PubMed] [Google Scholar]
- Chevin, L.-M., S. Billiard and F. Hospital, 2008. Hitchhiking both ways: effect of two interfering selective sweeps on linked neutral variation. Genetics 180 301–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark, R. M., E. Linton, J. Messing and J. F. Doebley, 2004. Pattern of diversity in the genomic region near the maize domestication gene tb1. Proc. Natl. Acad. Sci. USA 101 700–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark, R. M., S. Tavare and J. Doebley, 2005. Estimating a nucleotide substitution rate for maize from polymorphism at a major domestication locus. Mol. Biol. Evol. 22 2304–2312. [DOI] [PubMed] [Google Scholar]
- Clark, R. M., T. Nussbaum Wagler, P. Quijada and J. Doebley, 2006. A distant upstream enhancer at the maize domestication gene tb1 has pleiotropic effects on plant and inflorescent architecture. Nat. Genet. 38 594–597. [DOI] [PubMed] [Google Scholar]
- Cone, K. C., M. D. McMullen, I. V. Bi, G. L. Davis, Y. S. Yim et al., 2002. Genetic, physical, and informatics resources for maize on the road to an integrated map. Plant Physiol. 130 1598–1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currat, M., L. Excoffier, W. Maddison, S. P. Otto, N. Ray et al., 2006. Comment on “Ongoing adaptive evolution of ASPM, a brain size determinant in Homo sapiens” and “Microcephalin, a gene regulating brain size, continues to evolve adaptively in humans”. Science 313 172a. [DOI] [PubMed] [Google Scholar]
- Doebley, J., and A. Stec, 1991. Genetic analysis of the morphological differences between maize and teosinte. Genetics 129 285–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doebley, J., and A. Stec, 1993. Inheritance of the morphological differences between maize and teosinte: comparison of results for two F2 populations. Genetics 134 559–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doebley, J., M. M. Goodman and C. W. Stuber, 1986. Exceptional genetic divergence of Northern Flint corns. Am. J. Bot. 73 64–69. [DOI] [PubMed] [Google Scholar]
- Doebley, J., A. Stec, J. Wendel and M. Edwards, 1990. Genetic and morphological analysis of a maize-teosinte F2 population: implications for the origin of maize. Proc. Natl. Acad. Sci. USA 87 9888–9892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doebley, J., A. Stec and L. Hubbard, 1997. The evolution of apical dominance in maize. Nature 386 485–488. [DOI] [PubMed] [Google Scholar]
- Dong, C. H., M. Agarwal, Y. Y. Zhang, Q. Xie and J. K. Zhu, 2006. The negative regulator of plant cold responses, HOS1, is a RING E3 ligase that mediates the ubiquitination and degradation of ICE1. Proc. Natl. Acad. Sci. USA 103 8281–8286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ducrocq, S., D. Madur, J.-B. Veyrieras, L. Camus-Kulandaivelu, M. Kloiber-Maitz et al., 2008. Key impact of Vgt1 on flowering time adaptation in maize: evidence from association mapping and ecogeographical information. Genetics 178 2433–2437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans, P. D., S. L. Gilbert, N. Mekel-Bobrov, E. J. Vallender and J. R. Anderson, 2005. Microcephalin, a gene regulating brain size, continues to evolve adaptively in humans. Science 309 1717. [DOI] [PubMed] [Google Scholar]
- Freitas, F. O., R. Bendel, R. G. Allaby and T. A. Brown, 2003. DNA from primitive maize landraces and archeological remains: implications for the domestication of maize and its expansion through South America. J. Archeol. Sci. 30 901–908. [Google Scholar]
- Galinat, W. C., 1988. The teosinte progenitors of corn as tools for its improvement. Forty-Third Annual Corn and Sorghum Research Conference, University of Massachusetts, Waltham, MA, pp. 180–193.
- Galtier, N., and L. Duret, 2007. Adaptation or biased gene conversion? Extending the null hypothesis of molecular evolution. Trends Genet. 23 273–277. [DOI] [PubMed] [Google Scholar]
- Garza, J. C., and E. G. Williamson, 2001. Detection of reduction in population size using data from microsatellite loci. Mol. Ecol. 10 305–318. [DOI] [PubMed] [Google Scholar]
- Hall, T. A., 1999. BioEdit: a user-friendly biological sequence alignment editor and analysis program for windows 95/98/NT. Nucleic Acids Symp. Ser. 41 95–98. [Google Scholar]
- Hardy, O. J., and X. Vekemans, 2002. SPAGeDi: a versatile computer program to analyse spatial genetic structure at the individual or population levels. Mol. Ecol. Notes 2 618–620. [Google Scholar]
- Hill, W. G., and A. Robertson, 1968. Linkage disequilibrium in finite populations. Theor. Appl. Genet. 38 226–231. [DOI] [PubMed] [Google Scholar]
- Hudson, R. R., 2000. A new statistic for detecting genetic differentiation. Genetics 155 2011–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson, R. R., 2002. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18 337–338. [DOI] [PubMed] [Google Scholar]
- Hudson, R. R., M. Kreitman and M. Aguade, 1987. A test of neutral molecular evolution based on nucleotide data. Genetics 116 153–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson, R. R., M. Slatkin and W. P. Maddison, 1992. Estimation of levels of gene flows from DNA sequence data. Genetics 132 583–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaenicke-Després, V., E. S. Buckler, IV, B. D. Smith, M. T. P. Gilbert, A. Cooper et al., 2003. Early allelic selection in maize as revealed by ancient DNA. Science 302 1206–1208. [DOI] [PubMed] [Google Scholar]
- Kim, Y., and W. Stephan, 2003. Selective sweeps in the presence of interference among partially linked loci. Genetics 164 389–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirby, D. A., and W. Stephan, 1995. Multi-locus selection and the structure of variation at the white gene of Drosophila melanogaster. Genetics 144 635–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ko, J. H., S. H. Yang and K. H. Han, 2006. Upregulation of an Arabidopsis RING-H2 gene, XERICO, confers drought tolerance through increased abscisic acid biosynthesis. Plant J. 47 343–355. [DOI] [PubMed] [Google Scholar]
- Kopp, M., and J. Hermisson, 2007. Adaptation of a quantitative trait to a moving optimum. Genetics 176 715–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, L. S., M. J. White and T. H. MacRae, 1999. Transcription factors and their genes in higher plants—functional domains, evolution and regulation. Eur. J. Biochem. 262 247–257. [DOI] [PubMed] [Google Scholar]
- Loiselle, B. A., V. L. Sork, J. Nason and C. Graham, 1995. Spatial genetic structure of a tropical understory shrub, Psychotria officinalis (Rubiaceae). Am. J. Bot. 82 1420–1425. [Google Scholar]
- Matsuoka, Y., Y. Vigouroux, M. M. Goodman, J. Sanchez, G. E. Buckler et al., 2002. A single domestication for maize shown by multilocus microsatellite genotyping. Proc. Natl. Acad. Sci. USA 99 6080–6084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mekel-Bobrov, N., N. S. L. Gilbert, P. D. Evans and E. J. Vallender, 2005. Ongoing adaptive evolution of ASPM, a brain size determinant in Homo sapiens. Science 309 1720. [DOI] [PubMed] [Google Scholar]
- Nei, M., 1973. Analysis of gene diversity in subdivided populations. Proc. Natl. Acad. Sci. USA 70 3321–3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei, M., 1987. Molecular Evolutionary Genetics. Columbia University Press, New York.
- Olsen, K. M., A. L. Caicedo, N. Polato, A. McClung, S. McCouch et al., 2006. Selection under domestication: evidence for a sweep in the rice Waxy genomic region. Genetics 173 975–983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr, H. A., 1998. The population genetics of adaptation: the distribution of factors fixed during adaptive evolution. Evolution 52 935–949. [DOI] [PubMed] [Google Scholar]
- Palaisa, K. A., M. Morgante, M. Williams and A. Rafalski, 2003. Contrasting effects of selection on sequence diversity and linkage disequilibrium at two phytoene synthase loci. Plant Cell 15 1795–1806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piperno, D. R., and K. V. Flannery, 2001. The earliest archaeological maize (Zea mays L.) from highland Mexico: new accelerator mass spectrometry dates and their implications. Proc. Natl. Acad. Sci. USA 98 2101–2103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard, K. S., S. R. Salama, N. Lambert, M.-A. Lambot, S. Coppens et al., 2006. An RNA gene expressed during cortical development evolved rapidly in humans. Nature 443 167–172. [DOI] [PubMed] [Google Scholar]
- Pritchard, J. K., M. Stephens, N. Rosenberg and P. Donnelly, 2000. a Association mapping in structured populations. Am. J. Hum. Genet. 67 170–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard, J. K., M. Stephens and P. Donnelly, 2000. b Inference of population structure using multilocus genotype data. Genetics 155 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Przeworski, M., 2003. Estimating the time since fixation of a beneficial allele. Genetics 164 1667–1676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Przeworski, M., G. Coop and J. D. Wall, 2005. The signature of positive selection on standing genetic variation. Evolution 59 2312–2323. [PubMed] [Google Scholar]
- Remington, D. L., J. M. Thornsberry, Y. Matsuoka, L. M. Wilson, S. R. Whitt et al., 2001. Structure of linkage disequilibrium and phenotypic associations in the maize genome. Proc. Natl. Acad. Sci. USA 98 11479–11484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie, J. T., and D. S. Nesmith, 1991. Temperature and crop development, pp. 5–29 in Modeling Plant and Soil Systems, edited by J. Hanks and J. T. Ritchie. ASA, CSSA, SSSA, Madison, WI.
- Rozas, J., J. C. Sanchez-DelBarrio, X. Messeguer and R. Rozas, 2003. DnaSP, DNA polymorphism analyses by the coalescent and other methods. Bioinformatics 19 2496–2497. [DOI] [PubMed] [Google Scholar]
- Rozen, S., and J. Skaletsky, 2000. Primer 3 on the WWW for general users and for biologist programmers, pp. 365–386 in Bioinformatic Methods and Protocols: Methods in Molecular Biology, edited by S. Krawetz and S. Misener. Humana Press, Totowa, NJ. [DOI] [PubMed]
- Salvi, S., G. Sponza, M. Morgante, D. Tomes, X. Niu et al., 2007. Conserved noncoding genomic sequences associated with a flowering-time quantitative trait locus in maize. Proc. Natl. Acad. Sci. USA 104 11376–11381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SAS, 1989. SAS/STAT User's Guide. SAS Institute, Cary, NC.
- Smith, B. D., 1998. The Emergence of Agriculture. W. H. Freeman, New York.
- Smith, B. D., 2001. Documenting plant domestication: the consilience of biological and archeological approaches. Proc. Natl. Acad. Sci. USA 98 1324–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staden, R., 1996. The Staden sequence analysis package. Mol. Biotechnol. 5 233–241. [DOI] [PubMed] [Google Scholar]
- Strobeck, C., 1987. Average number of nucleotide differences in a sample from a single subpopulation: a test for population subdivision. Genetics 117 149–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenaillon, M. I., and P. L. Tiffin, 2008. The quest for adaptive evolution: a theoretical challenge in a maze of data. Curr. Opin. Plant Biol. 11 110–115. [DOI] [PubMed] [Google Scholar]
- Tenaillon, M. I., M. C. Sawkins, A. D. Long, R. L. Gaut, J. F. Doebley et al., 2001. Patterns of DNA sequence polymorphism along chromosome 1 of maize (Zea mays ssp mays L.). Proc. Natl. Acad. Sci. USA 98 9161–9166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenaillon, M. I., J. U'Ren, O. Tenaillon and B. S. Gaut, 2004. Selection versus demography: a multilocus investigation of the domestication process in maize. Mol. Biol. Evol. 21 1214–1225. [DOI] [PubMed] [Google Scholar]
- Teshima, K. M., G. Coop and M. Przeworski, 2007. How reliable are empirical genomic scans for selective sweeps? Genome Res. 16 702–712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornsberry, J. M., M. M. Goodman, J. Doebley, S. Kresovich, D. Nielsen et al., 2001. Dwarf8 polymorphisms associate with variation in flowering time. Nat. Genet. 28 286–289. [DOI] [PubMed] [Google Scholar]
- Wang, R. L., A. Stec, J. Hey, L. Lukens and J. Doebley, 1999. The limits of selection during maize domestication. Nature 398 236–239. [DOI] [PubMed] [Google Scholar]
- Watterson, G. A., 1975. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 7 256–276. [DOI] [PubMed] [Google Scholar]
- Williamson, S. H., M. J. Hubisz, A. G. Clark, B. A. Payseur, C. D. Bustamante et al., 2007. Localizing recent adaptive evolution in the human genome. PLoS Genet. 3 901–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, S. I., and B. Charlesworth, 2004. The HKA test revisited: a maximum-likelihood-ratio test of the standard neutral model. Genetics 168 1071–1076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, S. I., I. V. Bi, S. G. Schroeder, M. Yamasaki, J. F. Doebley et al., 2005. The effects of artificial selection on the maize genome. Science 308 1310–1314. [DOI] [PubMed] [Google Scholar]
- Yamasaki, M., M. I. Tenaillon, I. V. Bi, S. G. Schroeder, H. Sanchez-Villeda et al., 2005. A large-scale screen for artificial selection in maize identifies candidate agronomic loci for domestication and crop improvement. Plant Cell 17 2859–2872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu, J., G. Pressoir, W. H. Briggs, I. V. Bi, M. Yamasaki et al., 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 38 203–208. [DOI] [PubMed] [Google Scholar]
- Zeba, N., M. Ashrafuzzaman and C. B. Hong, 2006. Molecular characterization of the Capsicum annuum RING zinc finger protein 1 (CaRZFP1) gene induced by abiotic stresses. J. Plant Biol. 49 484–490. [Google Scholar]
- Zhao, K. Y., M. J. Aranzana, S. Kim, C. Lister, C. Shindo et al., 2007. An Arabidopsis example of association mapping in structured samples. PLoS Genet. 3 e4. [DOI] [PMC free article] [PubMed] [Google Scholar]