Dynamical Analysis on Gene Activity in the Presence of Repressors and an Interfering Promoter

Abstract

Transcription is regulated through interplay among transcription factors, an RNA polymerase (RNAP), and a promoter. Even for a simple repressive transcription factor that disturbs promoter activity at initial binding of RNAP, its repression level is not determined solely by the dissociation constant of transcription factor but is sensitive to timescales of processes in RNAP. We first analyze the promoter activity under strong repression by a slow binding repressor, in which case transcription events occur in bursts, followed by long quiescent periods while a repressor binds to the operator; the number of transcription events, bursting, and quiescent times are estimated by reaction rates. We then examine interference effect from an opposing promoter, using the correlation function of initiation events for a single promoter. The interference is shown to de-repress the promoter because RNAPs from the opposing promoter most likely encounter the repressor and remove it in case of strong repression. This de-repression mechanism should be especially prominent for the promoters that facilitate fast formation of open complex with the repressor whose binding rate is slower than ∼1/s. Finally, we discuss possibility of this mechanism for high activity of promoter PR in the hyp-mutant of λ-phage.

INTRODUCTION

The regulation of the activity of a particular gene involves a complex interplay between a promoter, an RNA polymerase (RNAP), and one or several transcription factors (TF) (1,2). Ignoring the internal dynamics associated with transcription initiation, the probability for obtaining a successful RNAP elongation initiation can be estimated from an equilibrium unbinding ratio of TF (3,4). When internal steps in transcription initiations become sizeable we need to consider the race between these steps and the kinetics of TF binding.

The binding/unbinding rates of TF to bind to an operator is critically influenced by competitive nonspecific bindings (5,6). Recent measurements of in vivo dynamics in an Escherichia coli cell finds that a single Lac repressor needs between 60 and 360 s to locate its operator (6). For TFs whose copy number is ∼10–100 per cell, a cleared operator can remain free for up to ∼30 s. In comparison, RNAP transcription initiation rates varies considerably, and can be as fast as 1.8 transcription initiations per s for a certain ribosomal promoter (7). Therefore, there is room for effects associated to the race between first bindings of a TF or an RNAP once the promoter is cleared.

In a number of both prokaryotic and eukaryotic systems, the promoter activity are not only influenced by TF, but are also modulated by interfering promoters (8–15). For example, the regulation between lytic and lysogenic maintenance promoters in the P2 class of bacteriophages involves transcription interferences (TI) as well as TFs that repress the promoter activities (11). In λ-phages, the initial lysis-lysogeny decision is modulated by TI between the promoter PRE activated by CII and the promoter PR repressed by CI.

Dodd et al. (15) presented a framework to deal with TI and multiple TFs, using an assumption about fast equilibrium reactions of TF-binding and closed complex formation. In this article, we develop a formalism that deals with the competition between timescales of TF binding/unbinding and transcription initiation process, and examine the effect of interference.

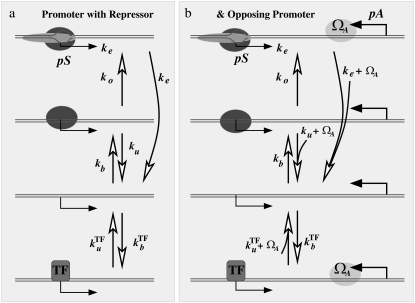
Fig. 1 shows a single promoter pS with an operator site for a repressive TF (left panel), and with a convergent promoter pA (right panel). For both cases, we illustrate the three basic steps of transcription initiation: 1), RNAP reversible binding to form a closed complex; 2), irreversible transition to open complex; and 3), initiation of transcription elongation. The rates for these three steps are promoter-dependent (16–18). As for the initial binding, given the fact that the maximum activity for ribosomal promoters reaches 1.8 transcription events per s (7), the time needed for an RNAP to diffuse to a promoter cannot be longer than ∼0.5 s. Regarding the later steps where RNAP forms an open complex and subsequently initiates transcription to leave the promoter, their timescales may vary a great deal from one promoter to another (19–23).

FIGURE 1.

(a) Model of promoter pS with a single TF that represses the promoter by competitive binding to an operator that overlaps with the promoter. The promoter activity is given in terms of the three-step model of Hawley and McClure (16) and Buc and McClure (17) for transcription initiation, with indicated transition rates for formation of closed complex, that of open complex, and elongation. (b) Same as in panel a, but with addition of a convergent promoter that interferes with both RNAP binding to pS and with binding of TF.

In the following, we will investigate in detail how these timescales play together to determine the extent to which a promoter is sensitive to repressors and to clearance due to the interference by elongating RNAPs from other promoters (note that a Java applet for the promoter model with a transcription factor is available at http://cmol.nbi.dk/models/dynamtrans/dynamtrans.html).

MODELS

We study the promoter activity under influence of TF and TI based on mathematical analysis on simple models of promoter in the following three levels. Our goal is to understand regulation of the three-step model for transcription initiation originally proposed by Hawley and McClure (16) and Buc and McClure (17), but we also analyze its simplified versions, i.e., the single-step and two-step models. The comparison of these three levels of models gives us intuitive understanding of the promoter behavior.

Three models for elongation initiation

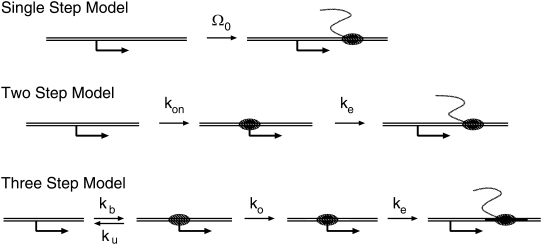
Let us start by describing the bare models with neither TF nor TI (Fig. 2).

FIGURE 2.

Schematic illustrations for the single-step model, the two-step model, and the three-step model of the elongation initiation.

Single-step model

The single-step model of transcription initiation is the model where the whole process is dominated by a slowest step, thus its elongation initiation is represented by a simple Poissonian process with the rate Ω₀.

Two-step model

In the two-step model, the transcription initiation consists of two steps: first, RNAP binds to the promoter site with the on-rate k_on; second, it initiates elongation with the rate k_e. The transcription initiation rate for the overall process Ω₀ is given by (14)

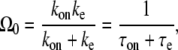(1)

with

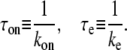(2)

The last expression of Eq. 1 simply shows that the average interval of elongation initiation 1/Ω₀ is the sum of the two times: τ_on, the time for RNAP to form the on-state, and τ_e, the time to start elongation in the on-state.

Three-step model

In the three-step model, two states within the RNAP binding state are differentiated: the one with closed DNA complex and the other with open DNA complex. The transition between the RNAP unbinding state (off-state) and the RNAP binding state with closed DNA is reversible, and characterized by the binding rate k_b and the unbinding rate k_u. When RNAP is in the closed complex state, the transition to the open state is irreversible with the rate k_o. Finally, the open complex is followed by elongation initiation with the rate k_e. This three-step model of transcription initiation was originally proposed by Hawley and McClure (16) and Buc and McClure (17).

The three-step model reduces to the two-step model with the effective on-rate 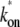given by

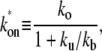(3)

in the case where the off-state and the closed DNA binding state are in equilibrium. This is fulfilled when the initial reversible process of RNAP binding/unbinding is faster than the other processes: k_b, k_u ≫ k_o, and k_e (14). The effective on-rate 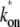in Eq. 3 can be understood as the open rate k_o reduced by the equilibrium expectation of being unbound.

The overall elongation rate Ω₀ for the three-step model has been shown (14) to be

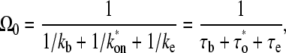(4)

with

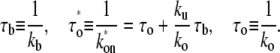(5)

The time 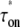is the time for the system to form an open complex after an RNAP binds to form a closed state for the first time. It is the sum of the two times: 1), τ_o, the time to form an open complex without unbinding; and 2), the binding time τ_b multiplied by the average number of times of RNAP unbindings before forming an open complex, k_u/k_o (a detailed explanation of mathematical interpretation is given in the Appendix). Note that this expression is not limited to the case where the two-step approximation is valid; it also holds for a general case.

In the above discussion, we have ignored the self-occlusion effect, where the next RNAP cannot bind to the operator site until the previous RNAP goes away from it. If we include this self-occlusion effect, the bare activity Ω_so should be

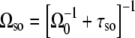(6)

with τ_so being the time that RNAP needs to clear the promoter.

Transcription factor

For each of these models, we consider the effect of a repressive transcription factor (TF), which we assume completely prevents RNAP from binding while it binds to the operator site. It is also assumed that RNAP binding to the promoter site prevents TF from binding to the operator site. The binding and unbinding rates of TF are denoted by 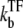and 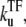respectively.

We will study, in particular, the strong repression regime, i.e., the dissociation ratio 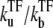is small. In such a case, TF binds for most of the time, preventing transcription initiation, but once a TF falls off, the promoter is free to initiate a burst of transcription elongations until another TF binds to the operator site (Fig. 3 b).

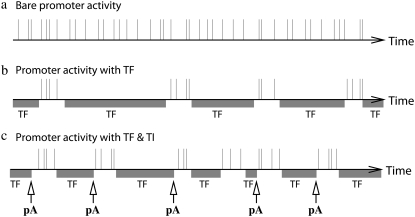
FIGURE 3.

Schematic diagrams for the time sequence of a promoter activity for a bare promoter (a), a promoter with TF regulation (b), and a promoter with TF under TI (c). The vertical lines represent the times when transcriptions are initiated. The shaded intervals labeled as TF represent the time intervals when a TF bounds to the operator site, thus the promoter cannot initiate transcription. Under the TF regulation, the transcription bursts take place when a TF does not bind. The arrows indicate the times when interfering RNAPs from pA arrive at pS and remove both TF and RNAP at pS; TI triggers transcription bursts.

Transcription interference

The effect of transcription interference (TI) on the promoter pS is examined by exposing it to transcribing RNAPs from another promoter pA in parallel (9) or in convergent (8,11) configuration (the latter case is illustrated in Fig. 1 b). The interfering promoter pA is characterized by the transcription initiation rate Ω_A and the initiation interval distribution p_A(τ). The RNAPs from pA are assumed to clear both the promoter and the operator sites of pS (sitting duck interference) and to occlude them while passing. This causes bursts of transcription events after the interference until another TF binds (Fig. 3 c).

There are several additional complications related to TI.

1. The RNAP sitting at the operator and the TF at the promoter of pS may not simply fall off by the interfering RNAP from pA, but may block it (i.e., “roadblock” effect).

2. Between the promoter and the operator, there should be time difference for the “sitting duck” interference and the occlusion to take place because they extend over a certain finite size and are in different locations along the DNA.

3. The interference may also take place through collision with an RNAP from pA after an RNAP from pS starts elongation.

4. The interference between pS and pA should be mutual; namely, pS can also interfere in the pA activity while pA interferes with pS.

In the case where pS and pA are in a parallel configuration, the collision effect (complication 3) and mutual interference (complication 4) do not exist. Even in a converging configuration, the collision effect is not significant when the distance between pS and pA is short, i.e., the traveling time between the two promoters is much shorter than the activity interval of the promoters. As for the mutual interference, the effect of pS on pA is negligible when the activity Ω_A of pA is much larger than the activity Ω of pS.

These effects of 1–4 introduce further complications in the problem, but note that we are going to ignore all of them in the following.

OUTLINE OF THEORY

The quantity we are going to examine is the averaged elongation initiation rate, or activity of pS, under the influence of TF and TI. Under the repression by TF, a promoter initiates transcription events in bursts and we will see how TI can activate the promoter. This effect can be prominent especially when the TF repression is strong and the timescale for TF is slow. In this section, we outline the theory. Detailed derivations of formulas are given in Supplementary Material, Data S1.

Single promoter property

As tools for the analysis, we use the following two functions: 1), p(τ), the probability distribution for time intervals between subsequent elongation initiation events; and 2), C(t), the averaged time-dependent rate of elongation initiation after both the promoter and the operator sites are cleared. We first examine p(τ) and C(t) for pS without TI, but under the effect of TF.

The average elongation rate Ω without TI is the inverse of the average elongation interval, thus it is related with p(τ) as

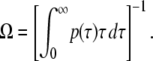(7)

The time-dependent elongation rate C(t) is actually a correlation function of elongation initiations without TI because it can be regarded as a probability density of initiation at the time t, provided there was an initiation at t = 0. This can be directly calculated from p(τ). For large t, C(t) approaches the promoter strength Ω,

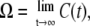(8)

because the effect of the initiation at t = 0 lasts only a finite time.

Effect of transcription interference

Now, we consider transcription interference (TI). Under the influence of interfering promoter pA, the promoter pS and its operator site are assumed to be cleared every time an RNAP from pA passes, and the activity of pS will change as C(t) after that. Thus the time-averaged activity during the interval of length τ is given by

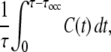(9)

where we have included the occlusion time τ_occ. The occlusion time τ_occ(= 1∼2 s) is the time during which the pS promoter cannot bind a new RNAP due to a transcribing RNAP from pA. Note that τ_occ = (r + ℓ)/v is the time needed for an RNAP from pA to transcribe across the pS promoter (length r + ℓ ∼105 bp and speed v estimated to be 50 bp/s (14)). This effect is not included in the correlation function C(t), because the correlation function defined here is a single promoter property.

The overall average activity of pS is the average of Eq. 9 over the interval distribution of pA, namely, p_A(τ). It is important to notice, however, that this average is not with the weight p_A(τ) itself but with the weight proportional to p_A(τ)τ because the probability that a given time falls in the interval of length τ is proportional to p_A(τ)τ, not p_A(τ). Therefore, the final expression for the elongation rate under TI is

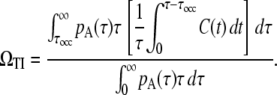(10)

The occlusion effect by RNAP from pA is explicitly included as a finite τ_occ, but the self-occlusion effect, that the RNAP from pS blocks its own promoter site pS, should be included in the correlation function C(t) if it is considered.

In addition to ignoring 1), roadblock effect; 2), time difference between the promoter and the operator; 3), RNAP collision; and 4), mutual interference, we will further approximate pA as Poissonian, namely,

(11)

and also ignore the occlusion time by putting τ_occ = 0, and the self-occlusion effects.

Evaluation of p(τ) and C(t)

By assuming each elementary process, such as binding, unbinding, elongation, etc., to be a Poissonian process with a given rate, we can obtain analytic expressions for p(τ) and C(t), from which we can calculate the overall elongation rate Ω for pS for various situation without TI. Using these functions, the elongation activity under the influence of TI is estimated from Eq. 10 with τ_occ = 0.

Detailed derivation of mathematical formulas is given in Data S1. In the following, we will describe results obtained from those analytic expressions.

RESULTS

We present the numerical evaluations of our expressions for various situations to clarify dynamical effects of TF and TI on the promoter activity.

Activity of a bare promoter

Let us start by comparing the three models in a bare form, i.e., without TF and TI.

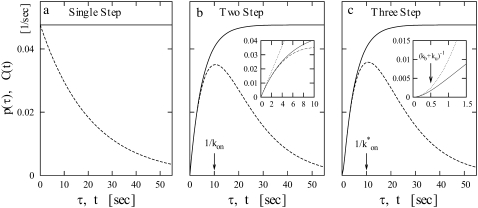
Fig. 4 shows the elongation initiation interval distribution p(τ) (dashed lines) and the time-dependent activity C(t) after the promoter site have been cleared by the competing activities (solid lines). The parameters are chosen for the three-step model, and those for the two-step and the single-step models are determined to match them with the three-step model using Eqs. 3 and 4, namely, k_on = 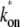and k_e to give the same overall activity Ω₀ for all the cases.

FIGURE 4.

The interval distribution p(τ) (dashed lines) and the time-dependent elongation rate C(t) (solid lines) for the single-step (a), the two-step (b), and the three-step model (c). The parameters for the three-step model are k_b = 1 s⁻¹, k_u = 1 s⁻¹, k_o = 0.2 s⁻¹, and k_e = 0.1 s⁻¹, which gives the average elongation rate Ω₀ = (1/k_b + 1/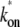 + 1/k_e)⁻¹ = 1/21 s⁻¹ and the effective on-rate 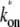≡ k_o/(1 + k_u/k_b) = 0.1 s⁻¹. The parameters for the two-step model are determined so that they behave similarly, i.e., the on-rate k_on = 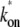and the elongation rate in the on-state 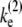for the two-step model given by 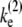= (1/Ω₀ – 1/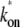)⁻¹. The insets show the behaviors at t ≈ 0 with the asymptotic curves (dotted lines).

In the single-step model, the elongation initiation is Poissonian, and the interval distribution p(τ) is a simple exponential with the elongation rate Ω₀. As there will be no correlations between subsequent initiations, the activity C(t) is given by the constant Ω₀.

In the two-step model, p(τ) and C(t) rise linearly from zero as k_onk_e t (the inset in Fig. 4 b). This is because the RNAP has to bind to the promoter site with the rate k_on before it initiates elongation with the rate k_e. The difference from the single-step model is seen in the timescale t ≲ min(1/k_on, 1/k_e). The two-step model reduces to the single-step model in the case either k_e ≪ k_on or k_e ≫ k_on, but these two cases show quite different behaviors in reaction to TF, as we can see in the following subsections.

In the three-step model, the promoter goes through two states after RNAP binding. Therefore p(τ) and C(t) increases initially as (1/2) k_bk_ok_et² at t ≈ 0 (the inset in Fig. 4 c). In the case of fast equilibration in the initial transition (k_b, k_u ≫ k_o), the three-step model reduces to the two-step model with an effective on-rate 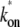given by Eq. 3.

In general, the main feature of an increased number of intermediate RNAP-promoter states causes an initial rise of p(τ) and consequently C(t) to be of increasing order in τ or t. Also the peak in p(τ) becomes sharper, which in principle could give a nonmonotonic behavior of C(t). For any realistic parameters, however, we find monotonic C(t) for the promoters without TF.

Activity of regulated promoter by TF

We now consider a promoter which is regulated by a TF that acts as repressor as illustrated in Fig. 1 a. Under strong repression by a slow binding TF, transcription events occur in bursts with quiescent periods of the length

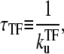(12)

when a TF binds to the operator and suppresses the activity. We will see that the general expressions of promoter activity Ω_TF repressed by TF can be put in the form that allows direct interpretation in terms of transcription burst. We evaluate the time-dependent activity C(t) for various parameters under the influence of TF, whose binding and unbinding rates are 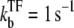with 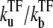= 0.1, 0.01, and 0.001. C(t) values without TF and with TF, which never unbinds, i.e., 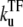= 0, are also plotted for comparison (dashed lines).

Single-step model

The TF effect on the single-step model is rather straightforward. The expression for C(t) is given by

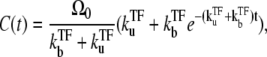(13)

which is plotted in Fig. 5 a. Immediately after the promoter is cleared at t = 0, the promoter activity recovers to the bare value Ω₀, but the initial high activity decreases as a TF binds at t ∼ 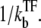In the latter stage, the transcription initiation is determined by the equilibrium probability of having a free promoter, 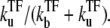Therefore, C(t) shows an exponential decrease from the initial bare activity Ω₀ to the repressed level of averaged activity,

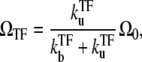(14)

FIGURE 5.

The time-dependent activity profile C(t) with TF for the single-step (a) and the two-step models with k_on = 0.1 s⁻¹ (b) and 1 s⁻¹ (c). The bare activity is one transcription initiation per 20 s: Ω₀ = 1/20 s⁻¹. For each case, we show five curves: the un-repressed case without TF (top, dashed lines); the repressed cases by TF with the binding rate and the unbinding rate 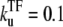s⁻¹ (top, solid lines); 0.01 s⁻¹ (middle, solid lines); 0.001 s⁻¹ (bottom, solid lines); and with TF that never unbinds (bottom, dashed lines). The arrows indicate C_max given by Eq. 22 and t_pl given by Eq. 23 for the two-step models. For the single-step model in panel a, the RNAP activity is limited only by a binding event once every 20 s. For the case in panel b of the two-step model, each step takes 10 s, while in the case of panel c, where the on-rate is fast, the overall activity limited by an elongation initiation time of 19 s.

for t ≫ 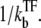Note that this simple equilibrium repression formula in Shea and Akers (3) for transcription repression holds only for the single-step model. More subtle competition comes into the problem for the two- and three-step models, as we will see below.

It is interesting to see that the equilibrium formula in Eq. 14 can be also put in the form

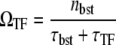(15)

with

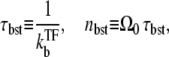(16)

and τ_TF defined in Eq. 12. This allows direct interpretation in terms of transcription burst; τ_bst and n_bst are the typical timescale and the number of transcription events, respectively, of a single transcription burst, and τ_TF is the typical timescale of the quiescent period between the bursts with TF bound to the operator. The expression in Eq. 15 represents that the average promoter activity Ω_TF is given by the number of transcription events in a burst n_bst divided by the time interval between the consecutive bursts, τ_bst + τ_TF. Note that Eq. 15 itself is valid in the general case, and is not limited to the case where the transcription events occurs in burst, namely, the promoter is strongly repressed by a slow binding TF.

Two-step model

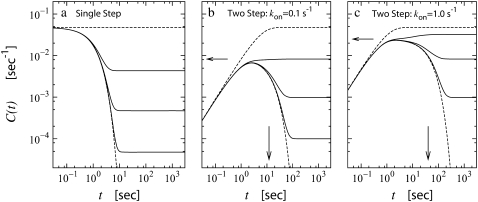
The situation is a little more complicated for the two-step model. In Fig. 5, b and c, two cases are shown: one with k_on = 0.1 s⁻¹ and the other with k_on = 1 s⁻¹. In the first case, the timescales of the two transitions, the on-rate and the elongation rate, are same, but in the second case, the on-rate is much faster than the elongation rate. The elongation rate k_e are chosen to give the same bare activity Ω₀ for the two cases.

The general behavior of C(t) is that 1), first it increases as k_onk_et until TF starts binding; 2), then it reaches a plateau value; and 3), finally it goes to the steady activity Ω_TF averaged over a long time.

The time-averaged activity with TF is given by

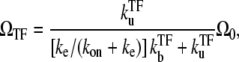(17)

with Ω₀ being the bare activity of the two-step model (Eq. 1). Note that the repression factor by TF, i.e., Ω_TF/Ω₀, is given by the equilibrium formula (Eq. 14) only when k_e ≫ k_on. In the other limit, TF cannot repress the promoter as one might expect from the dissociation constant of TF,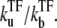

This time-averaged activity (Eq. 17) can be also expressed in the same form with Eq. 15,

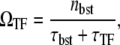(18)

but n_bst and τ_bst are given by

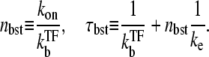(19)

Here, n_bst can be understood as the number of transcription events in a burst before a TF binds to the operator because 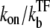is the winning ratio of RNAP to TF for binding. The bursting time τ_bst is the sum of the binding time of TF, 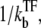and the elongation time, 1/k_e, multiplied by the number of transcription events. Again, this expression is valid in the general case, although it is interpreted best in the bursting situation.

In the strong repression limit where the bursting time is negligible compared with the quiescent time, we have

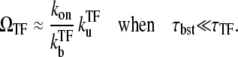(20)

Note that the time-averaged activity in this limit does not depend on the elongation rate k_e in the on-state. This is because the timescale is set by the slowest rate 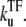The promoter produces a burst of n_bst(= k_on/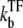) transcription events while a TF is not bound, but once a TF binds, it has to wait a time 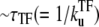for TF to unbind.

In the case 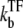≫ k_e ≫ 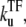the plateau becomes a maximum; C(t) can be approximated as

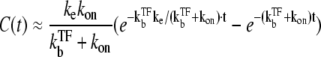(21)

for t ≲ 1/k_e × 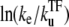(see Data S1). From this expression, we can estimate the maximum value C_max as

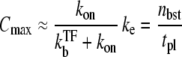(22)

with the plateau time

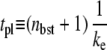(23)

for the time region

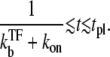(24)

The time-dependent activity C(t) shows the maximum value after the promoter site is clarified. The maximum value (Eq. 22) can be understood as k_e times branching-probability to the on-state 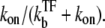This and Eq. 20 show that the promoter repression by TF is determined by the competition between TF and RNAP for binding to DNA, namely, between the binding rates 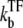and k_on. Therefore, even if the bare activity is the same, the repression by a TF can be quite different. This can be seen in Fig. 5: k_on = 0.1 s⁻¹ (Fig. 5 b) and 1 s⁻¹ (Fig. 5 c) with the same Ω₀ = 0.05 s⁻¹. The repression in Fig. 5 c is ∼10 times weaker than that in Fig. 5 b, because k_on is 10 times faster.

After TF falls off from the operator site, the promoter produces a burst of n_bst(= 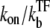) transcription events, on average, before another TF binds. Note that t_pl ≈ τ_bst in the case k_on ≫ 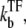namely, n_bst ≫ 1.

Three-step model

In the full three-step model, the RNAP have to pass through a closed DNA complex state first. The transition between this closed complex state and the off-state is reversible, but its rates can be relatively fast compared with the transition rates of the following steps. The fast initial binding process tends to make TF repression less efficient. This has been verified by measurements on promoters with strong RNAP binding affinity (23).

The general expression for the time-averaged activity with TF is again given by

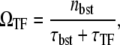(25)

with

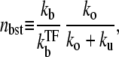(26)

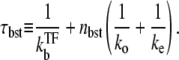(27)

The number of transcription events in a burst n_bst is now given by the winning ratio 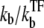of RNAP to TF multiplied by the branching ratio k_o/(k_o + k_u) in the closed state to the open state. The bursting time τ_bst is the sum of the TF binding time 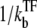and the time needed for elongation after RNAP binding to the promoter multiplied by the number of transcription events. Note that the bare activity Ω₀ in Eq. 4 can be expressed as

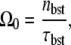(28)

which also holds for the other two models.

It is easy to see from Eqs. 4 and 25 that the repression factor Ω_TF/Ω₀ is given by the equilibrium formula (Eq. 14) only when k_e, k_o ≫ k_b, and 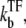namely, the internal timescales are negligible. Note that the expression in Eq. 25 can be put also in Michaelis-Menten form using (effective) dissociation constants (see Appendix).

In the strong repression limit where the bursting time is negligible, it is easy to see that

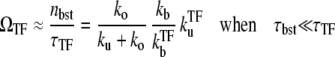(29)

from Eqs. 25 and 26. This reduces to Eq. 20 with k_on replaced by 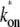of Eq. 3, in the case of a weakly bound closed complex (k_u ≫ k_b, k_o), because 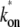≈ k_ok_b/k_u in this limit.

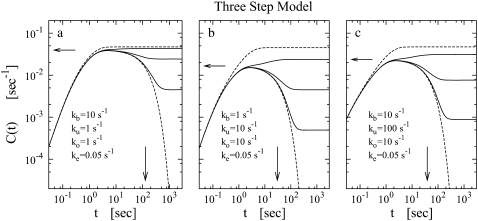
Fig. 6 shows the time-dependent activity profiles for three promoters whose bare activities are similar, but have different closed-complex formation transition rates. The first two cases, Fig. 6, a and b, are for the same 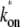= 0.909 s⁻¹, but for the last case, Fig. 6 c, 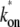= 0.0545 s⁻¹. One see that the promoters respond differently to repression by a TF. The arrows show the maximum value C_max of Eq. 22 with the plateau time

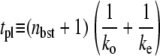(30)

and n_bst for the three-step model.

FIGURE 6.

The time-dependent activity profile C(t) with TF for the three-step models. For each case, we show five lines: the un-repressed case without TF (top, dashed lines); the repressed cases by TF with the binding rate 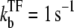and the unbinding rate 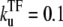s⁻¹ (top, solid lines); 0.01 s⁻¹ (middle, solid lines); 0.001 s⁻¹ (bottom, solid lines); and with TF that never unbinds (bottom, dashed lines). The arrows indicate C_max given by Eq. 34 and t_pl given by Eq. 30. For all cases, the bare activity is Ω₀ ≈ 0.05 s⁻¹, but we focus on the promoters with fast open complex formation, namely, the larger effective on-rate 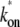= 10/11 s⁻¹. The case in panel a corresponds with a strong closed complex binding k_u/k_b ≪ 1, whereas panels b and c deals with a weakly binding RNAP. The difference between panels b and c illustrates the effect of a 10-times faster RNAP binding rate to the promoter.

Schematic description for time-dependent activity

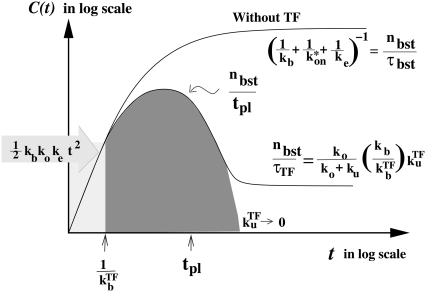
With all these results, Fig. 7 summarizes the behavior of time-dependent activity C(t) for the promoter with fast initial binding/unbinding under the strong but slow TF repression

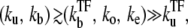(31)

where we have a typical bursting of transcription events with

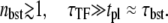(32)

After the clarification of the promoter and operator sites, the activity increases initially as

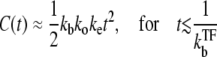(33)

until TF starts binding.

FIGURE 7.

Schematic activity profile of a promoter, with and without a TF that acts as a repressor by occluding the promoter site. Without repressor the promoter activity is set by the time that the promoter takes to pass through the three steps to initiate elongation, whereas a repressor reduces the final promoter activity to the extent proportional to the dissociation ratio 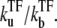Shortly after the promoter clearance, the activity recovers to reach the maximum value n_bst/t_pl until t ≲ t_pl. This can be much higher than the steady activity n_bst/τ_TF when t_t1 ≪ τ_TF, i.e., the promoter is strongly repressed (τ_TF ≫ t_p1, τ_bst) by a slow binding 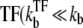or n_bst ≫ 1).

Then, it reaches the (maximum) plateau value:

(34)

Finally, C(t) diminishes down to the long time-averaged steady value with TF,

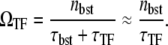(35)

From Eqs. 34 and 35, the enhancement factor f_enh by which the promoter can be activated after the clearance of the site is given by

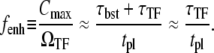(36)

This expression formalizes our original discussion: one obtains large relative peak activity when TF repression is strong, (τ_bst, t_pl) ≪ τ_TF, but slow 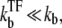namely, n_bst ≫ 1. The promoters with shorter internal-time 1/k_o + 1/k_e have larger relative peak activity, and therefore they will be more prone to de-repression by TI.

Interfering with regulated promoter activity

We now consider the interfering promoters pS and pA where pA is relatively strong in comparison with pS, and pS is strongly repressed by a slow TF. In this case, the average activity Ω_TI is given by Eq. 10, using the time-dependent activity C(t) without TI and the elongation interval distribution p_A(τ) of pA.

In the following, we ignore the occlusion time τ_occ by RNAP from pA; This should not be bad for the promoter whose activity is ≲0.1 s⁻¹, but may not be so good for a more active promoter. For p_A(τ), we will use the exponential distribution (Eq. 11), which corresponds to the single-step Poissonian promoter pA.

The expression for Ω_TI in Eq. 10 basically gives the average of C(t) over the typical timescale of pA, which is 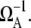Therefore, if you look at Ω_TF as a function of Ω_A, then Ω_TI would show a maximum at Ω_A ∼ 1/t_max in the case that C(t) has a maximum at t ≈ t_max.

Two-step model

We can obtain the explicit expression for Ω_TI, which can be approximated as

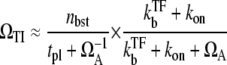(37)

for 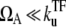in the regime 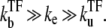Here, n_bst is the number of transcription events in a burst defined in Eq. 19, and t_pl is the plateau time (Eq. 23). This expresses the activity of the de-repressed two-step promoter in terms of the product of two factors. The first factor corresponds to the averaged activity for the bursting whose interval is given by t_pl + 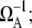this factor represents the de-repression by the interference through removal of TF by RNAP from pA before it dissociates by itself. The second factor represents the suppression by removing the open complex, i.e., “sitting duck” interference.

The expression in Eq. 37 shows a maximum

(38)

which corresponds to Eq. 22. The promoter activity is actually increased by the transcription interference. The enhancement factor, or the ratio Ω_TI,max/Ω_TF, is the same as in Eq. 36.

Three-step model

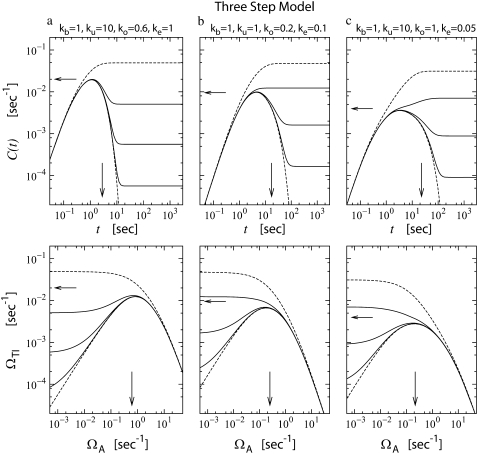
We cannot write down a compact expression, but Fig. 8 shows Ω_TI versus Ω_A (lower panels) along with the corresponding C(t) (upper panels) for the three-step model with different parameter values. One can see the correspondence between the upper and lower panels: The activity as function of Ω_A approximately resembles the activity profiles at time t ∼ 1/Ω_A plotted in corresponding upper panels. Notice also that the potential activation by a convergent promoter is largest for large k_o and k_e, as expected from Eq. 36. Finally, the relative effect of de-repression can be very large, in the case of very slow dissociation rate for the transcription factor.

FIGURE 8.

The time-dependent activity profile C(t) with TF (upper plots) and the average activity Ω_TI with TF and TI versus Ω_A (lower plots) for the three-step models. For each case, we show five lines: the un-repressed case without TF (top, dashed lines); the repressed cases by TF with the binding rate 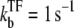and the unbinding rate 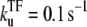(top, solid lines); 0.01 s⁻¹ (middle, solid lines); 0.001 s⁻¹ (bottom, solid red lines); and with TF that never unbinds (bottom, dashed lines). The arrows indicate C_max given by Eq. 34 and t_pl given by Eq. 30 for the upper plots, or Ω_TI,max and Ω_A by Eq. 38 with k_on replaced by 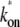and n_bst and t_pl replaced by Eqs. 26 and 30 of the three-step model for the lower plots. Notice that the activity, at a given level of pA activity, reflects the average activity of the promoter up to a cutoff time of 1/Ω_A.

SUMMARY AND DISCUSSION

We have presented a mathematical framework that expresses the dynamics of a promoter in the model of Hawley and McClure (16) and Buc and McClure (17). The formalism opens for discussion the promoter activity with TFs and TIs by an interfering promoter, and allows us to deal with the interplay between these elements.

In our formalism, the activity of a single promoter is characterized by the correlation function C(t), which represents the averaged time-dependent activity after the transcription initiation at t = 0. Any modifications to the activity of the single promoter, such as that by TF, are taken into account through the correlation function C(t). On the other hand, the effects from an interfering promoter punctuates the promoter/operator activity with the timescale of transcription initiation from the interfering promoter. This is represented by the expression in Eq. 10.

We have studied the effects of a repressive TF on the promoter activity. The general expressions for the promoter activity can be put in the form that is associated with the transcription burst, namely, a burst of n_bst transcription events during the bursting time τ_bst followed by a quiescent period of the length τ_TF. This is actually what happens in the case of a strongly repressed promoter by a slow binding TF. It should be noted that the equilibrium formula in Eq. 14 for the promoter activity repressed by TF is not valid unless the timescales of internal processes are negligible compared with binding/unbinding times of RNAP, because a TF competes with RNAP for binding to DNA.

Under the TI considered in this article, an interfering RNAP simply clears both the promoter and operator sites. If the promoter is strongly repressed by a TF, such interference is most likely to relieve the promoter out of repression, and interrupts the quiescent period to shorten to 1/Ω_A when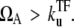

EXPERIMENTAL OBSERVATIONS

Let us discuss experimental relevance of our theoretical results for transcription burst and its modification by transcription interference.

Transcription bursts

Experimentally, bunched promoter activities have been seen in several eukaryotic systems involving TFs (26,27), and they have been interpreted to occur in response to transformation in heterochromatin states, or as a result of a promoter approaching transcription factories (28). For prokaryotes, bunched activities have only been observed for the promoter P_lac/ara under the fully induced condition (29), and has been interpreted without TF (30).

On the other hand, transcription bursts induced by activators have been examined in models and experiments on the yeast GAL1-promoter (31), considering transcription activation by the TATA-binding protein. The operator position has been also shown to influence the “bunchiness” of a promoter (32).

To the best of our knowledge, transcription bursts due to repressor, as analyzed in this article, have not yet been observed experimentally.

Transcription interference

We have, at present, no direct experimental evidences for the possibility of de-repression by TI. Its biological relevance, however, could be widespread in phage and E. coli. Convergent promoters are common regulatory motifs for all temperate phages with a CII-like protein, and ∼100 examples of convergent promoters have been also found in E. coli (14).

To show how TI with de-repression could help us to understand a biological system, let us discuss the hyp-mutant of λ; this system is intriguing because of its high production of Cro in the lysogeny and its enhanced immunity against infection of other λ-phages (33,34). Its DNA configuration resembles that in Fig. 1 b and the parameters in Fig. 8 are matched to this system. Therefore, the maximal repression case there corresponds to the case of the promoter PR in λ repressed by the factor of ∼500 due to CI (35,36) (A. Ahlgen-Berg and I. Dodd, 2008, private communication). The strength of hyp-PRE is not known, but Fig. 8 suggests that PR in lysogen could be de-repressed by the factor 10∼30 due to TI from hyp-PRE, provided that open complex formation is fast and that CI binds to OR relatively slowly. This could explain, at least, a part of the large amount of Cro found in the lysogeny of the hyp-mutant.

Another example is the O_R3O_R2O_R3 mutant, which has been also found to show stable lysogens (38), even though it is expected to be producing Cro 10∼30 times more than a normal λ (4), as in the case of the hyp-mutant. Such similarity, i.e., the stable lysogens under the high production of Cro, between the O_R3O_R2O_R3 and the hyp-mutant, leads us to speculate that the remarkable robustness of the lysogens (39) of these phages should be rooted in the same unknown mechanism.

Experimental proposal

Burst activity should be most directly monitored by a real-time observation, but also can be examined quantitatively from the number distribution of mRNA in a cell. This may be obtained if one can take snapshots of an assembly of cells from which the number of mRNA contained in each cell can be counted. The reaction rate constants for RNAP and TF should be able to be estimated from the mRNA distribution.

For example, from the distribution, one can calculate the Fano factor ν, which is the ratio of the variance to the average

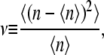(39)

with n being the number of mRNA in a cell. This Fano factor can be directly compared with our estimate of the number of transcription events in a burst n_bst. In the bursting situation with n_bst ≫ 1, the Fano factor should be given by n_bst if the quiescent periods follow Poissonian process and are much longer than the bursting periods,

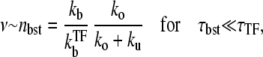(40)

but is smaller than that if the burstings are not sufficiently separated,

(41)

In the case n_bst ≪ 1, we would have ν ∼ 1 because each elongation initiation follows the Poissonian process. The full information of the distribution allows us more detailed comparison with our analysis.

Another experiment we can propose is to construct DNA with a promoter exposed to a library of interfering promoters with varying strength Ω_A, preferably in a parallel configuration to avoid RNAP collisions. Suppose the promoter is highly repressed by TF with unknown parameters. By examining how the promoter is de-repressed by the interfering promoters, the off-rate of TF can be estimated as the lower limit of Ω_A that de-represses the promoter.

Simplifications in this treatment

Before concluding, let us discuss some of the effects we have ignored in this treatment.

Roadblock

In our analysis of TI, we have assumed that RNAP always displaces TF without roadblock effect, but it is known that some TFs are roadblocks to RNAP. Roadblocks are most commonly reported in the in vitro experiments (40–42), whereas presence of elongation factors often allow RNAP to pass the roadblock in the in vivo situations (42,43). Reports on in vivo roadblocks is at present limited to the transcription factor LacI and the restriction enzyme EcoRI (44). It has been reported that some roadblocks may be translocated, being pushed by two or more RNAPs (44). If two consecutive RNAPs are required to dislocate a TF, the activity of interfering promoter Ω_A in Eq. 37 should be replaced by the effective activity, which is half of the original activity, Ω_A/2. This reduction factor of one-half should be further reduced in the case where a blocked RNAP may fall off before the second one arrives to give a push.

Another possibility for RNAP not removing the TF is that RNAP simply passes the TF without displacing it; the repressor simply does not leave the vicinity of the operator, therefore, the repressor maintains its function until it falls off by itself. This kind of situation has actually been observed when an RNAP reads through a nucleosome, displacing only parts of the histone complex (45,46). For some TFs, one could imagine mixed situations, where the TF is displaced but remains in physical proximity during the RNAP passage.

TFs such as CI in phage 186 (11) and CI in λ on OR (A. Ahlgen-Berg and I. Dodd, 2008, private communication) do not act as roadblocks, but are removed—which, we presume, is the more common situation.

Time difference for the promoter and the operator

The interfering RNAPs clear/occlude the promoter pS first, and then the operator in the convergent configuration, but in the opposite order in the parallel configuration. The time-difference of the effects for the two sites depends on the distance between the two sites. If the binding times of TF or RNAP are comparable or shorter than this time-difference, we have to take this into account, which makes the situation favorable to the promoter (or operator) in the convergent (or parallel) configuration.

RNAP collision

The RNAP from pS may be removed, even after it starts elongating, by colliding with the RNAP from pA. This effect is particularly profound when the distance between pS and pA is large. It has been found that the collision effect becomes substantial for convergent promoters with the pS-pA distance being ∼v/(2Ω_A), where v(∼50 bp/s) is the transcription elongation speed (14). For the parallel configuration of promoters, the collision effect does not exist.

Occlusion time

The occlusion time τ_occ, the time that the promoter pS is occluded by passing the RNAP from pA, was neglected. This has been also considered in Sneppen et al. (14), and they found that pS is influenced substantially by occlusion only when the activity of pA is stronger than 0.1 s⁻¹.

Mutual interference

In the convergent configuration of promoters, not only does pA interfere with pS, but pS also interferes with pA. Such mutual interference effects are likely to be important in switching mechanisms between equally strong convergent promoters, such as the convergent promoters PR and PRE of λ-phage in the early stages of infection. Full analytical treatment on the mutual interference is not easy in the general case, but stochastic simulations (14) and the four-world approximation analysis (15) have been performed. In this analysis, we consider the highly repressed promoter pS; thus the interference of pS on pA should be negligible. In the case of the parallel configuration, this effect does not exist.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX: PROMOTER ACTIVITY IN MICHAELIS-MENTEN FORM

Since the process of transcription initiation can be regarded as an enzyme reaction, our results for the averaged promoter activity in the three-step model can be put in the form of Michaelis-Menten kinetics.

Let us start by the bare activity without TF. The binding rate k_b of RNAP should be proportional to the density of RNAP,

(42)

with a reaction constant κ_b. Then, the bare activity (4) can be written as

(43)

with the maximum activity

(44)

and the effective dissociation constant for RNAP

(45)

TF has been introduced as a competitive inhibitor in our model. Its binding rate can be expressed as

(46)

with the TF density as [TF] and the reaction constant 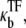then the dissociation constant for TF is given by

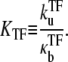(47)

With these parameters, the expression in Eq. 25 for the averaged activity with TF is written as

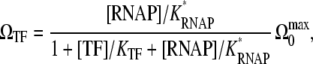(48)

which is in the standard form of Michaelis-Menten kinetics with a competitive inhibitor.