CONFORMATIONAL FLEXIBILITY AND STRAND ARRANGEMENTS OF THE MEMBRANE-ASSOCIATED HIV FUSION PEPTIDE TRIMER PROBED BY SOLID-STATE NMR SPECTROSCOPY

Abstract

The human immunodeficiency virus (HIV) fusion peptide (HFP) is the N-terminal apolar region of the HIV gp41 fusion protein and interacts with target cell membranes and promotes membrane fusion. The free peptide catalyzes vesicle fusion at least to the lipid mixing stage and serves as a useful model fusion system. For gp41 constructs which lack the HFP, high-resolution structures show trimeric protein and suggest that at least three HFPs interact with the membrane with their C-termini in close proximity. In addition, previous studies have demonstrated that HFPs which are cross-linked at their C-termini to form trimers (HFPtr) catalyze fusion at a rate which is 15−40 times greater than non-cross-linked HFP. In the present study, the structure of membrane-associated HFPtr was probed with solid-state nuclear magnetic resonance (NMR) methods. Chemical shift and intramolecular ¹³CO-¹⁵N distance measurements show that the conformation of the Leu-7 to Phe-11 region of HFPtr has predominant helical conformation in membranes without cholesterol and β strand conformation in membranes containing ∼30 mol% cholesterol. Interstrand ¹³CO-¹³CO and ¹³CO-¹⁵N distance measurements were not consistent with an in-register parallel strand arrangement but were consistent with either: (1) parallel arrangement with adjacent strands two-residues out-of-register; or (2) antiparallel arrangement with adjacent strand crossing between Phe-8 and Leu-9. Arrangement (1) could support the rapid fusion rate of HFPtr because of placement of the apolar N-terminal regions of all strands on the same side of the oligomer while arrangement (2) could support the assembly of multiple fusion protein trimers.

Enveloped viruses such as human immunodeficiency virus (HIV) are surrounded by a membrane and infect cells through fusion between the viral membrane and the target cell membrane (1, 2). This process is mediated by envelope proteins which traverse the viral membrane (3). For HIV, the gp41 envelope protein has a ∼170-residue ectodomain region which lies outside the viral membrane and contains a N-terminal ∼20-residue apolar “fusion peptide” (HFP). The HFP interacts with the target cell membrane and plays an essential role in membrane fusion (4). Peptides composed of the HFP sequence induce fusion between large unilamellar vesicles (LUVs) and between erythrocytes (5, 6). There are similar mutation/fusion activity relationships for HFP-induced fusion and HIV-induced fusion which suggests that HFP is a useful model system to understand some aspects of viral/target cell fusion (7-10). There is also evidence for participation of other regions of gp41 in membrane fusion (11-14). There are atomic-resolution structures of the “soluble ectodomain” of gp41 which does not contain the ∼30 N-terminal residues of gp41 (including the HFP) (2, 15-19). These structures are believed to correspond to the conformation after fusion has occurred and perhaps during some fusion steps (20). The gp41 molecules form a trimer in the soluble ectodomain structure with the three N-termini in close proximity at the end of an in-register helical coiled-coil. It has therefore been hypothesized that during viral/target cell fusion, at least three HFPs insert into the target cell membrane with their C-termini in close proximity. There is some antibody-based evidence for this hypothesis (21).

A variety of experimental methods have shown that membrane-associated HFP can assume either helical or nonhelical structure (5, 7, 22-32). Models for the helical structure have been developed based on nuclear magnetic resonance (NMR), electron spin resonance (ESR), infrared (IR), and circular dichroism (CD) data, as well as computer simulations (33-39). A β hairpin model for non-helical structure has been proposed based on IR and surface activity measurements in membranes (40).

Fluorescence, ESR, IR, and solid-state NMR data also suggest that the nonhelical HFPs in membranes form oligomeric structures (10, 41-44). These oligomeric structures may be important as evidenced by envelope protein trimerization and by experiments and modeling which indicate that the fusion site contains multiple trimers and a corresponding high HFP concentration (17, 18, 45). Additionally, the V2E mutation in gp41 dominantly interferes with HIV fusion and infectivity and suggests that oligomeric HFP is important in viral/target cell fusion (8, 10).

In an effort to mimic the oligomeric HFP topology suggested by the gp41 soluble ectodomain structures, HFP oligomers in dimeric (HFPdm) and trimeric form (HFPtr) have been synthesized with chemical cross-linking at their peptide C-termini. Cross-linking was accomplished with either cysteine or lysine residues. Comparative measurements were made between HFPdm and HFPtr and monomeric HFP (HFPmn) (28, 46). All three constructs contained additional C-terminal lysines to inhibit intermolecular self-association in aqueous solution and buffer conditions were found with minimal self-association. The rate of peptide-induced intervesicle lipid mixing was 15−40 times higher for HFPtr relative to HFPmn and suggests that oligomeric HFP topology plays a significant role in membrane fusion. The HFPdm rate was intermediate between the rates of HFPmn and HFPtr. Enhanced fusogenicity has also been observed for other oligomeric constructs which contain fusion peptides and support the hypothesis that oligomeric fusion peptide topology is one factor which contributes to fusion (47-49).

Solid-state NMR structural experiments have been carried out on membrane-associated HFPmn, HFPdm, and HFPtr. Backbone ¹³C carbonyl chemical shift and 2D exchange measurements suggest a predominant β strand conformation for HFPmn associated with membranes whose lipid headgroup and cholesterol composition is comparable to that found in host cells of the virus (25). In addition, the Phe-8 carbonyl chemical shift of HFPdm and HFPtr in the same host cell-like membrane composition is upfield of the random coil value and is more consistent with β strand conformation than with helical conformation (28, 46). For HFPtr associated with membranes which do not contain cholesterol, the Phe-8 chemical shift is downfield of the random coil value and is more consistent with helical conformation. In the present study, membrane-associated HFPtr was investigated using solid-state NMR methods including ¹³C chemical shifts and ¹³C-¹⁵N distance measurements to probe local peptide conformation and ¹³C-¹³C and ¹³C-¹⁵N distance measurements to probe interpeptide β strand arrangement. It had previously been proposed that the increased lipid mixing rate induced by β strand HFPdm and HFPtr was related to predominant parallel strand arrangement enforced by the C-terminal cross-linking (28). For this arrangement, the apolar N-terminal regions of the three strands would be on the same side of the oligomer and the resulting large apolar volume would cause significant membrane perturbation and rapid fusion rate. This structure would differ from the mixture of parallel and antiparallel arrangements observed for membrane-associated HFPmn (43). In this paper, an in-register parallel strand model for HFPtr was tested using a solid-state NMR ¹³CO-¹³CO distance measurement approach which had been previously applied to probe structure in β amyloid fibrils (50, 51).

The ¹³C-¹⁵N distances were determined with the rotational-echo double-resonance (REDOR) technique which is an approach to measure heteronuclear dipolar couplings under magic angle spinning (MAS) (52-60). MAS reduces solid-state NMR linewidths and increases signal-to-noise and the dipolar coupling d_CN depends on r_CN distance as (r_CN)⁻³. The ¹³C-¹³C distances were determined with a constant-time double-quantum build-up with finite pulses (fpCTDQBU) technique which is an approach to measure homonuclear dipolar couplings under MAS (51, 61-65). The dipolar coupling d_CC depends on r_CC distance as (r_CC)⁻³. This fpCTDQBU method is a finite pulse variant of the CTDQBU technique developed by Bennett et al. and incorporation of finite pulses increases the signal-to-noise, as will be discussed in the Results section (64). The utility of finite pulses was first demonstrated by Ishii in the related constant-time finite-pulse radiofrequency-driven recoupling (fpRFDR-CT) method and the two techniques are robust methods for determination of d_CC with weak dependences on chemical shift differences, chemical shift anisotropy (CSA), resonance offset, spin relaxation, and rf inhomogeneity (51, 65).

Quantitative analysis of the REDOR and fpCTDQBU data requires explicit computer simulation of the experiments as a function of molecular geometry parameters. The SIMPSON computer program was used for this purpose and allows input of the geometric parameters as well as the NMR parameters used in the experiment (66). The HFPtr results in the present paper also rely on careful calibration of the REDOR and fpCTDQBU experiments with model compounds for which the ¹³C-¹⁵N and ¹³C-¹³C distances are known and comparable to distances in HFPtr structural models.

MATERIALS AND METHODS

Materials

Rink amide resin and Wang Resin were purchased from Advanced Chemtech (Louisville, KY). N-α-fluorenylmethoxycarbonyl (FMOC)-N'-ε-4-methyltrityl-l-lysine (FMOC-Lys(Mtt)) was purchased from Calbiochem-Novabiochem (La Jolla, CA), and FMOC amino acids and FMOC-β-Ala-Wang resin were obtained from Peptides International (Louisville, KY). For the labeled peptide syntheses, labeled amino acids were purchased from Icon Services Inc (Summit, NJ) and were FMOC-protected using literature methods (67, 68). In addition, FMOC-1-¹³C glycine was purchased from Sigma-Aldrich (St. Louis, MO). 1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-rac-(1-glycerol) (POPG), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE), 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-L-serine (POPS), phosphatidylinositol (PI), sphingomyelin, 1,2-di-O-tetradecyl-sn-glycero-3-phosphocholine (DTPC), 1,2-di-O-tetradecyl-sn-glycero-3-phospho-rac-(1-glycerol) sodium salt (DTPG), and 1,2-di-O-phytanyl-sn-glycero-3-phosphoethanolamine (DPhPE) were purchased from Avanti Polar Lipids (Alabaster, AL). N-(2-hydroxyethyl)piperazine-N'-2-ethanesulfonic acid (HEPES) was obtained from Sigma-Aldrich (St. Louis, MO). The buffer solution used in the study contained 5 mM HEPES (pH 7.0) with 0.01% NaN₃.

HFPtr synthesis

The “HFPtr-L7_CF11_N” fusion peptide trimer was synthesized with sequence (AVGIGALFLGFLGAAGSTMGARSWKKKKKK)₃-A_β and with a ¹³CO label at Leu-7 and a ¹⁵N label at Phe-11 on each strand. The related “HFPtr-F8_CL9_N” trimer was synthesized with sequence (AVGIGALFLGFLGAAGSTWMGARSKKKKKK)₃-A_β and with a ¹³CO label at Phe-8 and a ¹⁵N label at Leu-9 on each strand. Residues in the N-termini of HFPtr correspond to the 23 N-terminal residues (sequence AVGIGALFLGFLGAAGSTMGARS) of the LAV_1a strain of the HIV-1 gp41 envelope fusion protein. HFPtr synthesis began with coupling of FMOC-Lys(Mtt) and activated β-Ala-Wang resin (46). A lysine trimer backbone was then formed with coupling of FMOC-Lys(Mtt) followed by coupling with N-α-FMOC-N'-ε-tert-butoxycarbonyl-l-lysine (FMOC-Lys(Boc)). Prior to the second and third couplings, the Mtt group on the lysine side chain was removed with 1% trifluoroacetic acid (TFA) in dichloromethane (DCM). The rest of the trimer was then synthesized using a peptide synthesizer (ABI 431A, Foster City, CA) equipped for standard FMOC chemistry. Cleavage of HFPtr from the resin was done in a 3 h reaction with a mixture of TFA-H₂O-phenol-thioanisole-ethanedithiol in a 33:2:2:2:1 volume ratio and purification was done with reversed-phase HPLC and a preparative C₁₈ column (Vydac, Hesperia, CA) and a water-acetonitrile gradient containing 0.1% TFA. Mass spectroscopy was used for peptide identification.

N-acetyl-L-leucine (NAL)

1-¹³C, N-¹³C doubly labeled NAL (D-NAL) was synthesized as a setup compound for fpCTDQBU experiments (69). Synthesis of D-NAL began with addition of 1-¹³C, ¹⁵N leucine to glacial acetic acid and heating to 100 °C. 1-¹³C acetic anhydride was then added, the solution was cooled to 80 °C, and water was added to react with any excess acetic anhydride. The D-NAL product was washed with cyclohexane, and the cyclohexane was subsequently removed under vacuum. Residual solvents were removed by water aspirator vacuum, drying in a vacuum dessicator and dissolution in water followed by lyophilization. Solution ¹H and ¹³C NMR confirmed the identity, purity and labeling of D-NAL. The NAL sample for solid-state NMR was prepared by aqueous dissolution of a 1:9 mixture of D-NAL and unlabeled NAL (ICN, Aurora, OH) followed by slow evaporation of the water. The polycrystalline solid was ground with a mortar and pestle. The intramolecular ¹³C-¹³C distance of D-NAL in the crystal is 3.1 Å (70).

Glycyl-L-phenylalanyl-L-phenylalanine (GFF)

Doubly labeled GFF (D-GFF) was synthesized with¹³CO labels at Gly-1 and Phe-3 and was a model compound for the fpCTDQBU experiments. D-GFF synthesis began with dissolution of FMOC-1-¹³C-Phe in a N-methylpyrrolidone (NMP)/DCM mixture followed by 2 h coupling of the amino acid to unsubstituted Wang resin using a mixture of 1.0 M N,N'-dicyclohexylcarbodiimide in NMP and 0.1 M 4-dimethylaminopyridine in dimethylformamide. Unreacted amino groups on the resin were benzoylated with benzoic anhydride. Standard FMOC chemistry was used for the remaining synthesis with 4 h and 8 h coupling times for FMOC-Phe and FMOC-1-¹³C-Gly, respectively. D-GFF was cleaved from the resin in a 3 h reaction with a mixture of TFA-water-phenol in a 33:2:2 volume ratio and precipitated by addition of t-butyl methyl ether (TBME). The yellowish-white precipitate was washed with TBME, centrifuged, lyophilized, dissolved in water, and passed through a 4−8 μm filter. After slow evaporation of the water, colorless and needle-like D-GFF hemihydrate crystals were harvested. A small aliquot of the crystals was dissolved in dimethylsulfoxide-d₆ and subsequent ¹H and ¹³C NMR spectroscopy confirmed the purity and labeling of D-GFF. The solid-state NMR sample of GFF was prepared by aqueous dissolution of D-GFF and unlabeled GFF (Sigma-Aldrich) in a 1:49 ratio followed by slow evaporation of solvent. The polycrystalline solid was ground with a mortar and pestle. The intramolecular ¹³C-¹³C distance of D-GFF in the crystal is 5.40 Å (71).

I4 peptide

A 17-residue acetylated and amidated “I4” peptide with sequence Ac-AEAAAKEAAAKEAAAKA-NH₂ was synthesized with a ¹³CO label at Ala-9 and a ¹⁵N label at Ala-13. The solid-state NMR I4 peptide sample was lyophilized from aqueous solution and is predominantly (83 ± 6%) α helical at Ala-9 (72). The two labeled nuclei should have a ¹³C-¹⁵N internuclear distance of ∼4.1 Å in the helical structure.

Lipid preparation

HFPtr samples were prepared using three lipid/cholesterol mixtures: (a) “PC-PG” had POPC and POPG in a 4:1 mol ratio and has a headgroup composition similar to that used in previous fusion peptide and fusion protein biophysical studies (73-76); (b) “LM3” had POPC, POPE, POPS, sphingomyelin, PI, and cholesterol in a 10:5:2:2:1:10 mol ratio and reflects the lipid headgroup and cholesterol composition of cells infected by HIV (77, 78); and (c) “LM3e” had DTPC, DTPG, DPhPE and cholesterol in a 9:3:3:10 mol ratio and was similar to LM3 in lipid headgroup and cholesterol composition but contained ether-linked rather than ester-linked lipids to eliminate natural abundance lipid ¹³CO signals. Lipid and cholesterol powders were dissolved in chloroform. The chloroform was removed under a stream of nitrogen followed by overnight vacuum pumping. Lipid dispersions were formed by addition of 5 mM pH 7.0 HEPES buffer followed by homogenization with 10 freeze-thaw cycles. Large unilamellar vesicles (LUVs) were prepared by extrusion through a filter with 100 nm diameter pores (79).

Solid-state NMR sample preparation

The samples were made in a manner similar to that used for doing functional fusion assays (46). HFPtr (0.1−0.2 μmol as determined by A₂₈₀) was dissolved in ∼2 mL of 5 mM HEPES buffer and LUVs (∼30 μmol total lipid) were prepared in ∼2 mL of buffer. The peptide and LUV solutions were mixed and kept at room temperature overnight followed by ultracentrifugation at 35000 rpm for 5 h at 4 °C. The peptide/lipid pellet formed after ultracentrifugation was transferred by spatula to a 4 mm diameter MAS NMR rotor. Unbound HFPtr is predominantly monomeric under these conditions and does not pellet. For the HFPtr and other samples, the rotor volume of ∼40 μL was filled.

Solid-state NMR spectroscopy

Experiments were done on a 9.4 T spectrometer (Varian Infinity Plus, Palo Alto, CA) using a MAS probe in double resonance ¹³C/¹H configuration for fpCTDQBU experiments and in triple resonance ¹³C/¹H/¹⁵N configuration for REDOR experiments. Relative to the triple resonance configuration, the double resonance configuration has 1.5 times higher ¹³C sensitivity. The NMR detection channel was tuned to ¹³C at 100.8 MHz, the decoupling channel was tuned to ¹H at 400.8 MHz, and for REDOR the third channel was tuned to ¹⁵N at 40.6 MHz. ¹³C shifts were externally referenced to the methylene resonance of adamantane at 40.5 ppm which allowed direct comparison with ¹³C shifts of proteins in aqueous solution (80, 81). ¹⁵N shifts were referenced to (¹⁵NH₄)₂SO₄ at 20 ppm. Experiments used a MAS frequency of 8000 ± 2 Hz and spacers were used to restrict samples to the central 2/3 rotor volume (∼40 μL) in which rf field variation was less than 10%.

Experiments were performed at −50 °C rather than room temperature in order to achieve more efficient cross-polarization (CP) and greater signal per ¹³C nucleus. There are similar ¹³C backbone chemical shifts at both low temperature and room temperature, suggesting that cooling the sample does not cause significant peptide structural changes (29). The ¹H, ¹³C and ¹⁵N pulse lengths and the CP matching condition were approximately obtained by running direct pulse and CP experiments on adamantane and (¹⁵NH₄)₂SO₄. Further parameter optimization was made with model compounds. Recycle delays were between 1 and 2 s.

REDOR spectroscopy

The “all-but-one ¹⁵N π pulse” version was used to suppress natural abundance ¹³C signals and selectively detect the labeled Phe-8 ¹³CO signal of HFPtr-F8_CL9_N (27, 52). An initial 2 ms CP was done with a ramped 40−50 kHz ¹³C rf field and a ∼60 kHz ¹H rf field and was followed by a 1 ms dephasing period and then ¹³C detection. A single ∼50 kHz ¹³C refocusing π pulse was placed at the midpoint of the dephasing period, and two-pulse phase-modulation (TPPM) ¹H decoupling of ∼90 kHz was applied during dephasing and detection (82). The ¹³C transmitter was set to ∼155 ppm and the ¹⁵N transmitter was set to ∼115 ppm. An “S₀” and an “S₁” acquisition were obtained. The dephasing period during the S₁ acquisition contained a 40 kHz ¹⁵N π pulse at the midpoint and at the end of each rotor cycle except for the fourth and the eighth cycles. XY-8 phase cycling (0, 90, 0, 90, 90, 0, 90, 0) was used for the ¹⁵N pulses (83). The ¹⁵N pulses disrupted averaging of the ¹³C-¹⁵N dipolar coupling by MAS and led to selective attenuation of the Phe-8 ¹³CO signal. The S₀ acquisition did not contain ¹⁵N pulses and ¹³C-¹⁵N dipolar coupling was efficiently averaged by MAS and did not lead to ¹³C signal attenuation. The selective spectrum of Phe-8 ¹³CO was obtained by subtracting the S₁ signal from the S₀ signal.

¹³CO-¹⁵N distances were measured with an “alternating ¹⁵N/¹³C π pulse” version of REDOR (53, 84). For the S₁ acquisition, the dephasing period of length τ_i included a ∼40 kHz ¹⁵N π pulse at the midpoint of each rotor cycle and a ∼50 kHz ¹³C π pulse at the end of each rotor cycle except for the last cycle. The S₀ acquisition did not include ¹⁵N π pulses during the dephasing period. TPPM ¹H decoupling of ∼90 kHz was applied during dephasing and detection. ¹³C signals were attenuated by ¹³C-¹⁵N dipolar coupling in the S₁ acquisition but not in the S₀ acquisition. Spectra were acquired for different τ_i and the difference between the ¹³CO S₀ and S₁ signal intensities divided by the S₀ signal intensity (ΔS/S₀)_i was the experimental parameter used to determine ¹³CO-¹⁵N dipolar couplings and distances. XY-8 phase cycling was used for the ¹⁵N π pulses and for all of the ¹³C π pulses except the final pulse. Individual S₀ or S₁ transients were added with phase cycling: ¹H π/2, 0, 180, 0, 180; ¹H CP, 90, 90, 90, 90; ¹³C CP 270, 270, 180, 180; final ¹³C π pulse, 270, 270, 180, 180; receiver, 180, 0, 90, 270.

The S₀ signal intensity of the I4 peptide was used to optimize ¹H π/2, ¹H decoupling, ¹³C π, and CP rf fields, and the ΔS/S₀ values of the I4 peptide were used to optimize the ¹⁵N π rf field.

fpCTDQBU spectroscopy

The NMR sequence has the form CP_90+ζ – (fpRFDR)_L – π/2_ζ – π/2₀ – (fpRFDR)_M – π/2₁₈₀ – π/2₉₀ – (fpRFDR)_N – acquisition where L, M, and N refer to the number of rotor cycles in each fpRFDR period and the other subscripts refer to the rf phases (64). Generation of transverse ¹³C magnetization during CP was followed by fpRFDR periods which contained finite ¹³C π pulses and during which the magnetization may be reduced by net ¹³C-¹³C dipolar coupling. The transverse magnetization was then detected during the acquisition period. For each value of ζ = 0, 90, 180, and 270, a distinct spectrum was obtained. The π/2₁₈₀ - π/2₉₀ pulse pair served to refocus ¹³C-¹³C dipolar coupling so that there was no net coupling over the period which began N rotor cycles prior to the pulse pair and ended at the beginning of acquisition. For ζ = 90 or 270, there was similarly no net dipolar coupling over the period which began after CP and ended L rotor cycles after the π/2_ζ - π/2₀ pulse pair. By contrast, for ζ = 0 or 180, there was net dipolar coupling during the dephasing period of duration τ_i = 2L × τ_R where τ_R is the rotor period. For each value of τ_i, S₀ and S₁ signals were acquired with S₀ = S_ζ=90 + S_ζ=270 and S₁ = S_ζ=0 + S_ζ=180. The parameter (ΔS/S₀)_i was calculated as in the REDOR experiment and served as the experimental constraint for determination of ¹³C-¹³C dipolar couplings and distances.

A single value of M and a single value of L + M + N were used for all τ_i values in a given experiment. The transverse magnetization therefore evolved for a single “constant-time” for all τ_i and the contribution to (ΔS/S₀)_i from effects other than the ¹³C-¹³C dipolar couplings was approximately independent of τ_i (85). Experiments were initially attempted with the non-constant-time and higher signal-to-noise sequence CP_90+ζ – (fpRFDR)_L – π/2_ζ – π/2₀ – (fpRFDR)_L – acquisition but the (ΔS/S₀)_i values obtained with this sequence for model compounds fitted poorly to simulations based on known ¹³CO-¹³CO distances. Constant-time was critical for quantitative interpretation of the data.

Other experimental details included: (1) the ¹³C transmitter was set to ∼177 ppm; (2) the CP period had 2 ms duration, ramped 40−50 kHz ¹³C rf field and a ∼54 kHz ¹H rf field; (3) ¹³C π/2 pulses had ∼43 kHz rf field; (4) fpRFDR periods had one ¹³C π pulse every two rotor cycles and the pulse was centered in the two cycle increment; and (5) continuous-wave ¹H decoupling at ∼95 kHz and ∼60 kHz were applied during the fpRFDR and acquisition periods, respectively. XY-8 phase cycling was used for fpRFDR π pulse train and the other pulses had phases: ¹H π/2, 180, 0, 0, 180; ¹H CP, 90, 90, 90, 90; ¹³C CP 270, 180, 270, 180. The corresponding values of ζ were 0, 90, 180, 270. Calibration of rf fields was done using the D-NAL sample. Both the D-NAL and D-GFF samples were used to study the effects of “finite” ¹³C π pulses, i.e. pulses with longer duration and concomitant smaller rf field.

Experimental data analysis

Integration of signal intensities in the isotropic carbonyl regions of the S₀ and S₁ spectra for a particular dephasing time τ_i yielded values denoted as S_0i. and S_1i. (ΔS/S₀)_i^exp is a normalized dephasing parameter:

$${\left(\frac{\Delta S}{S_0}\right)}_i^{exp}=\frac{S_{0i}-S_{1i}}{S_{0i}}=1-\frac{S_{1i}}{S_{0i}}$$ (1)

For each pair of S_0i, S_1i spectra, an experimental uncertainty σ was calculated as the root mean squared deviation of integrated intensities in 24 regions of the spectra without signal. The uncertainty in (ΔS/S₀)_i^exp is denoted σ_i^exp and was calculated (86):

$${\sigma }_i^{exp}=\frac{\sigma }{S_{0i}}\sqrt{1+\frac{{S_{1i}}^2}{{S_{0i}}^2}}=\frac{\sigma S_{1i}}{S_{0i}}\sqrt{\frac{1}{{S_{1i}}^2}+\frac{1}{{S_{0i}}^2}}$$ (2)

Determination of distances between labeled nuclei relies on comparision of (ΔS/S₀)_i^exp and (ΔS/S₀)_i^sim where sim ≡ simulated. The (ΔS/S₀)_i^sim only consider the labeled spins whereas (ΔS/S₀)_i^exp has contributions from natural abundance nuclei and other effects. The (ΔS/S₀)_i^exp values were therefore adjusted to remove these other contributions and the resulting corrected (ΔS/S₀)_i ^cor values were compared to (ΔS/S₀)_i^sim to obtain distances between labeled nuclei. We briefly discuss determination of (ΔS/S₀)_i ^cor for the REDOR measurements on the HFPtr-L7_CF11_N samples. The Supporting Information section provides a detailed description of the derivation of (ΔS/S₀)_i^cor for all of the samples and experiments.

Determination of (ΔS/S)_i^cor relies on consideration of contributions to S₀ and S₁ from ¹³CO nuclei in different environments. The following parameters/approximations are used for REDOR of HFPtr-L7_CF11_N: (1) There is 99% labeling of the Leu-7 ¹³CO and Phe-11 ¹⁵N sites. S₁ = S₀ for a labeled Leu-7 ¹³CO in a peptide strand with a Phe-11 ¹⁴N. (2) S₁ = 0 for a labeled Leu-7¹³CO separated by one or two bonds from a natural abundance ¹⁵N at Phe-8 or Leu-7. The Leu-7 S₁ is not affected by other natural abundance ¹⁵N. (3) S₁ = 0 for natural abundance backbone ¹³COs at Gly-10 or Phe-11 which are separated by one or two bonds from the labeled Phe-11 ¹⁵N. S₁ = S₀ for other natural abundance backbone ¹³CO sites. Criteria (1) and (2) are based on the close distance (≤ 2.5 Å) and consequent strong (≥ 200 Hz) dipolar coupling of ¹³CO and ¹⁵N nuclei separated by one or two bonds.

As described in the Supporting Information section, an expression for (ΔS/S₀)_i^cor can be derived:

$${\left(\frac{\Delta S}{S_0}\right)}_i^{cor}=\frac{1-U_C+n{A}_C}{(1-U_C-U_N-2B_N)}{\left(\frac{\Delta S}{S_0}\right)}_i^{exp}-\frac{2A_C+2A_N}{(1-U_C-U_N-2A_N)}$$ (3)

where U_C and U_N are the fractional abundances of Leu-7 ¹²CO and Phe-11 ¹⁴N, respectively, A_C and A_N are the fractional ¹³C and ¹⁵N natural abundances, respectively, and n is the average number of unlabeled CO sites per peptide strand. For the HFPtr samples, values of U_C, U_N, A_C, A_N, and n are 0.01, 0.01, 0.011, 0.0037, and 29.33, respectively. Eq. 3 leads to (ΔS/S₀)_i^cor /(ΔS/S₀)_i^exp ratios of ∼1.3. The value of σ ^cor_i was calculated by multiplying σ ^exp_i by the prefactor for (ΔS/S₀)_i^exp in Eq. 3 (86).

Simulations

(ΔS/S₀)_i^sim were calculated as a function of internuclear distances between two or three labeled nuclei and as a function of τ_i. The simulations were done with the SIMPSON program and incorporated the MAS frequency and the ¹³C and ¹⁵N rf fields, pulse lengths, timing, and phases, as well as ¹³C resonance offsets and CSA principal values and axis directions (66). The REDOR simulations were based on a single ¹³CO/¹⁵N spin pair and did not consider the ¹⁵N chemical shift or CSA. The fpCTDQBU simulations were based on either two or three ¹³CO nuclei and did not consider ¹⁵N spins. In the experiments, the effects of ¹H and ¹⁴N spins were largely removed by ¹H decoupling, constant-time, and/or MAS, and these spins were not incorporated in any of the simulations.

Orientation-dependent simulation input parameters included ¹³CO CSA principal values, the Euler angles which relate the ¹³CO CSA principal axis system(s) to a fixed crystal axis system, and the Euler angles which relate the ¹³CO-¹⁵N or ¹³CO-¹³CO internuclear vectors to the crystal axis system. Although distance determination by REDOR and fpCTDQBU experiments is not strongly dependent on these parameters, an effort was made to use reasonable values for the parameters. The (δ₁₁, δ₂₂, δ₃₃) CSA principal values for the I4 Ala-9, HFPtr-L7_CF11_N/PC-PG Leu-7, and HFPtr-L7_CF11_N/LM3e Leu-7 ¹³COs were set to (246, 203, 86), (248, 202, 85) and (242, 195, 83) ppm, respectively, and were based on experimentally measured isotropic chemical shifts and literature CSA values (87). For GFF, the Gly-1 and Phe-3 CSA principal values were (255, 168, 91) and (243, 193, 106) ppm, respectively, and were determined by fitting experimental centerband and spinning sideband intensities with the Herzfeld-Berger method (88).

The Euler angles which relate a ¹³CO CSA principal axis system to the crystal axis system can be considered in terms of the relative orientation of the principal axis system and the ¹³CO chemical bonds and the structure and orientation of the molecule relative to the crystal axes. For I4 Ala-9, HFPtr Leu-7, and GFF Gly-1 ¹³COs, the principal axis/chemical bond orientations were: (1) the δ₃₃ axis perpendicular to the peptide plane; and (2) the δ₂₂ axis tilted 130° from the CO-N bond (87). GFF Phe-3 has COO⁻ rather than amide functionality and its δ₃₃ axis was perpendicular to the OCO plane and its δ₁₁ axis bisected the OCO angle (89, 90).

The crystal frame Euler angles for the ¹³CO principal axis systems and the internuclear vectors were calculated using a Mathematica program whose inputs were atomic coordinates from high-resolution structures and the previously detailed ¹³CO CSA principal axis directions. The atomic coordinates for GFF were obtained from its crystal structure while for parallel β strand and antiparallel β strand structures, coordinates were obtained respectively from the crystal structure of cutinase (PDB file name 1cex) and from the crystal structure of human gamma-D crystalline R58H mutant (PDB file name 1h4a) (71, 91, 92). The latter two structures have been refined to 1.0 and 1.15 Å resolution, respectively. For REDOR simulations of the I4 and HFPtr-L7_CF11_N/PC-PG samples, the Ala-56 CO and Glu-60 N coordinates of cutinase were used. These residues are in a helical region of cutinase and the labeled ¹³CO chemical shifts of the two solid-state NMR samples correlate with helical conformation. The REDOR simulation of the HFPtr-L7_CF11_N/LM3e sample used coordinates of Leu-114 CO and Gly-118 N in a β strand region of cutinase because the ¹³CO shift of this sample correlated with β strand conformation. The two-spin fpCTDQBU simulation of the HFPtr-L7_CF11_N/LM3e sample used cutinase Ile-37 CO and Ala-116 CO coordinates, and the three-spin fpCTDQBU simulation of the HFPtr-L7_CF11_N/LM3e sample used cutinase Ile-37 CO, Ala-116 CO and Thr-144 CO coordinates. In cutinase, these are in-register residues in a parallel β strand region and this was our initial structural model for β strand HFPtr.

Signal-to-noise

Experiments and simulations were carried out to assess the effect of the ¹³C π rf field on the GFF fpCTDQBU signal-to-noise ratio. Comparison was made between the experimentally-based signal-to-noise parameter:

$${\left(\frac{Signal}{Noise}\right)}_i^{cor}=\frac{{\left(\frac{\Delta S}{S_0}\right)}_i^{cor}}{{\sigma }_i^{cor}}$$ (4)

and simulation:

$${\left(\frac{Signal}{Noise}\right)}_i^{sim}=\frac{{\left(\frac{\Delta S}{S_0}\right)}_i^{sim}}{{\sigma }_i^{sim}}=\frac{\frac{S_{0i}^{sim}-S_{1i}^{sim}}{S_{0i}^{sim}}}{\frac{k}{S_{0i}^{sim}}\sqrt{1+{\left(\frac{S_{1i}^{sim}}{S_{0i}^{sim}}\right)}^2}}=\frac{S_{0i}^{sim}-S_{1i}^{sim}}{k\sqrt{1+{\left(\frac{S_{1i}^{sim}}{S_{0i}^{sim}}\right)}^2}}$$ (5)

where k is an adjustable parameter to provide overall comparison between (Signal/Noise)_i^cor and (Signal/Noise)_i^sim values for a set of τ_i.

Fitting of internuclear distances

The distance between labeled nuclei was determined by χ² fitting:

$${\chi }^2={\chi }^2\left(d\right)=\sum _{i=1}^T\frac{{\left({\left(\frac{\Delta S}{S_0}\right)}_i^{cor}-{\left(\frac{\Delta S}{S_0}\left(d\right)\right)}_i^{sim}\right)}^2}{{\left({\sigma }_i^{cor}\right)}^2}$$ (6)

where T is the number of τ_i and d is the dipolar coupling. In units of Å, the ¹³C-¹³N distance r_CN = (3110 Hz/d_CN)^1/3 and the ¹³C-¹³C distance r_CC = (7720 Hz/d_CC)^1/3 (93). The best-fit d is the one for which χ² has global minimum value χ²_min and the uncertainty σ_d is set by the values of d corresponding to χ² = χ²_min + 1 (86). According to statistics theory, the most likely value of χ²_min is the number of degrees of freedom of the fit, ν, and ν = T−1 in the REDOR and fpCTDQBU analyses (94). The χ²_min values in the fittings were close to ν and were consistent with reasonably accurate evaluation of the σ ^cor_i in Eq. 6.

RESULTS

¹³CO chemical shifts

Liquid-state and solid-state NMR studies on proteins have shown an empirical correlation between the ¹³CO chemical shift and local conformation with higher shifts correlating with helical structure and lower shifts correlating with β strand structure (81, 95, 96). In the present study, ¹³CO shifts at Leu-7 and Phe-8 were measured for membrane-associated HFPtr and it was observed that there is a strong dependence of shifts on membrane composition. The Phe-8 chemical shift in membrane-associated HFPtr-F8_CL9_N was specifically detected using REDOR filtering (Fig. 1a,b) and peak shifts of 178.4 and 172.5 ppm were observed in PC-PG and LM3 membranes, respectively. These values correlate with database distributions of Phe ¹³CO shifts for helical (177.1 ± 1.4 ppm) and β strand (174.2 ± 1.6 ppm) conformations (81). As displayed in Fig. 1c, the REDOR-filtered peak Leu-7 ¹³CO shift in HFPtr-L7_CF11_N/PC-PG was 178.8 ppm. This shift agreed better with the database distribution of Leu ¹³CO in helical conformations (178.5 ± 1.3 ppm) than with the distribution in β strand conformations (175.7 ± 1.5 ppm).

Figure 1.

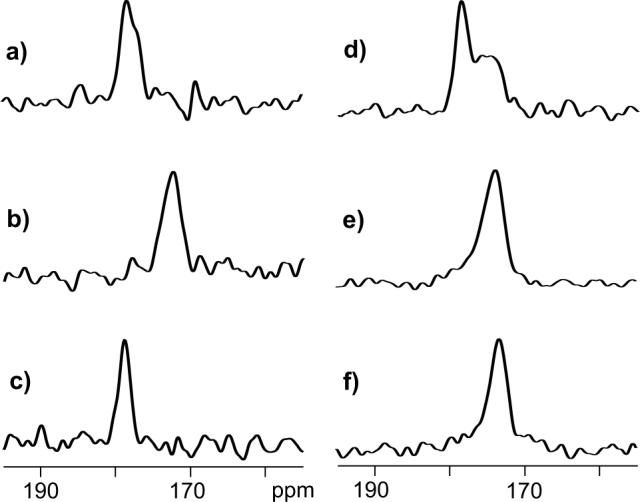
¹³C spectra of HFPtr-F8_CL9_N associated with (a) PC-PG and (b) LM3 membranes and of HFPtr-L7_CF11_N associated with (c, d) PC-PG, (e) LM3, and (f) LM3e membranes. The HFPtr:lipid mol ratio was ∼0.003 in the samples used to obtain spectra a and b and ∼0.007 in the samples used to obtain spectra c-f. Spectra a, b, and c are REDOR-filtered with τ_i = 1.0, 1.0, and 32.25 ms, respectively, and have ¹³CO peak chemical shifts of 178.4 (Phe-8), 172.5 (Phe-8), and 178.8 ppm (Leu-7), respectively. Spectra d, e, and f are REDOR S₀ spectra with 32.25 ms dephasing period and have ¹³CO peak chemical shifts of 178.6 ppm, 173.8 ppm, and 173.4 ppm, respectively. Each spectrum was processed with 100 Hz Gaussian line broadening and baseline correction. The MAS frequency was 8000 Hz and the numbers of scans used to obtain spectra a, b, c, d, e, and f are 118784, 132864, 46048, 23024, 21760, and 98720, respectively.

In the HFPtr-L7_CF11_N/LM3 sample, there were relatively small values of ΔS/S₀₀ and the Leu-7 ¹³CO peak was not observed in the REDOR-filtered spectrum. REDOR S₀ spectra were therefore used to obtain additional chemical shift information for the HFPtr-L7_CF11_N samples. The S₀ spectrum of the HFPtr-L7_CF11_N/PC-PG sample (Fig. 1d) is a combination of a sharper signal peaked at 178.6 ppm and a broader signal centered near 176 ppm. Comparison with the REDOR-filtered spectrum (Fig. 1c) suggests that the downfield signal is primarily due to the labeled Leu-7 ¹³CO while spin-counting and published spectra of ¹³CO labeled lipid samples suggest that the upfield signal is primarily due to natural abundance lipid ¹³CO (28). For the HFPtr-L7_CF11_N/LM3 sample (Fig. 1e), there is a single signal which is a superposition of intensity from the labeled Leu-7 and natural abundance lipid ¹³COs with a smaller contribution from natural abundance HFPtr ¹³COs. The HFPtr-L7_CF11_N/LM3e sample contains ether-linked rather than ester-linked lipids with consequent elimination of natural abundance ¹³CO lipid signals in the spectrum (Fig. 1f). The HFPtr-L7_CF11_N/LM3e spectrum is narrower than the HFPtr-L7_CF11_N/LM3 spectrum but the peak shift of the LM3e spectrum (173.4 ppm) is very similar to the peak shift of the LM3 spectrum (173.8 ppm) and suggests that the HFPtr conformation is insensitive to ether- vs. ester-linked lipids. The peak shifts are more consistent with Leu chemical shifts in β strand conformations (175.7 ± 1.5 ppm) than in helical conformations (178.5 ± 1.3 ppm).

Overall, the Leu-7 and Phe-8 peak HFPtr ¹³CO chemical shifts correlate with local helical conformation in PC-PG and with β strand conformation in LM3 and LM3e. Other studies of HIV and influenza fusion peptides suggest that the absence of cholesterol in PC-PG and its presence in LM3 and LM3e is an important determinant of peak chemical shifts and local conformations (27, 76).

¹³CO-¹⁵N distances

HFPtr-L7_CF11_N conformation was probed more quantitatively with REDOR determination of the distance between the labeled Leu-7 ¹³CO and Phe-11 ¹⁵N nuclei. If the Leu-7 to Phe-11 region has regular α helical conformation, the distance will be ∼4.1 Å while if the region has regular β strand conformation, the distance will be ∼11 Å. These distances correspond to dipolar couplings (d_CN) of ∼45 Hz and ∼3 Hz, respectively.

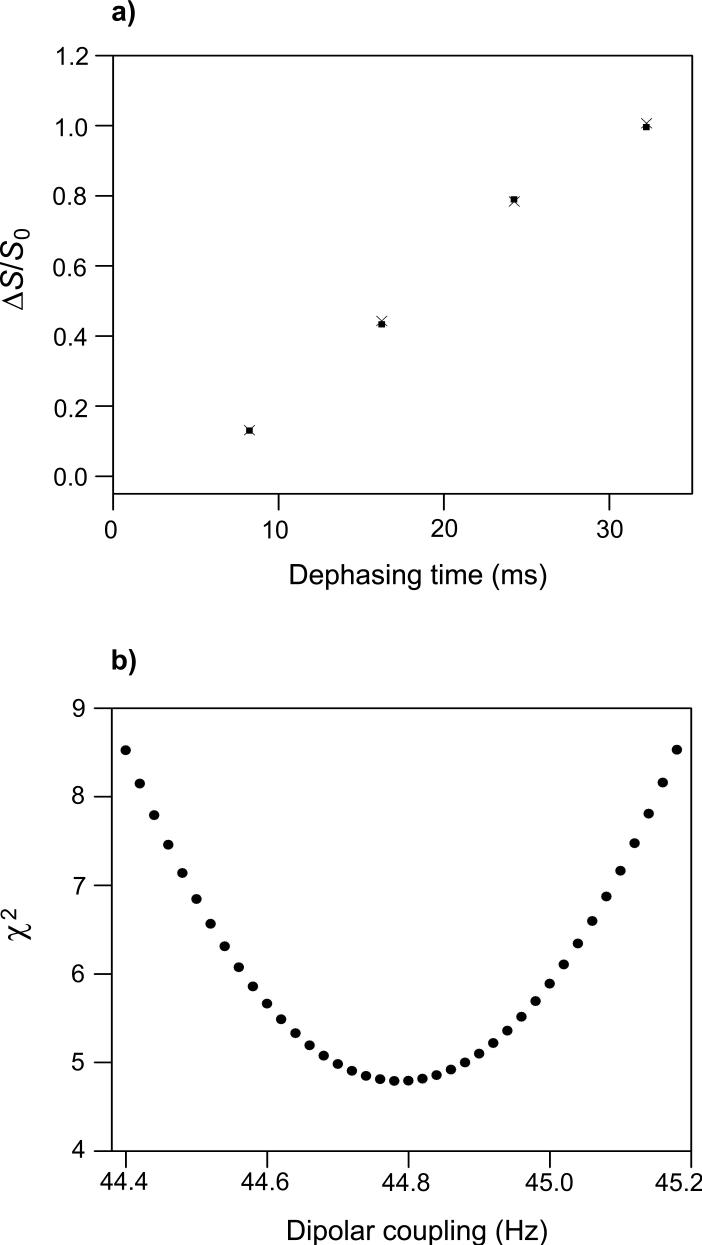
The REDOR experiment was first validated using the helical I4 peptide with Ala-9 ¹³CO and Ala-13 ¹⁵N labels (Fig. 2a, b and Fig. 3). As τ_i was increased from 8.25 to 32.25 ms, there was a regular decrease in S_1i^exp/S_0i^exp values and concomitant increase in (ΔS/S₀)_i^exp values. Using the approach and equations described in the Materials and Methods and Supplemental Material sections, the (ΔS/S₀)_i^cor were calculated from the (ΔS/S₀)_i^exp and then fitted to the (ΔS/S₀)_i^sim calculated for an array of d_CN values. The resulting d_CN = 44.78 ± 0.22 Hz and r_CN = 4.110 ± 0.007 Å are consistent with α helical structure between Ala-9 and Ala-13 and serve to validate the REDOR experiment.

Figure 2.

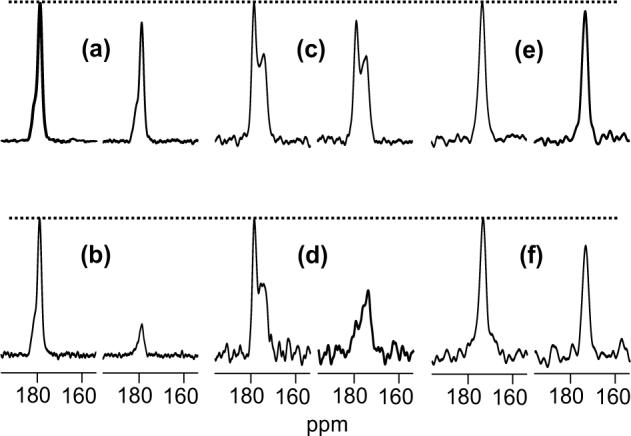
¹³C REDOR spectra of the (a, b) I4 peptide and HFPtr-L7_CF11_N associated with (c, d) PC-PG and (e, f) LM3e membranes. For each lettered pair of spectra, the S₀ spectrum is on the left and the S₁ spectrum is on the right. The MAS frequency = 8000 Hz, τ_R = 125 μs, and τ_i = 8.25 ms (spectra a, c, e) or τ_i = 32.25 ms (spectra b, d, f). Dotted lines are drawn at the peak S₀ intensities. The I4 spectra were processed with 50 Hz Gaussian line broadening, the HFPtr spectra were processed with 100 Hz Gaussian line broadening, and baseline correction was applied to all spectra. The numbers of scans used to obtain each spectrum in panels a, b, c, d, e, and f are 32, 32, 37710, 23024, 40528, and 98720, respectively.

Figure 3.

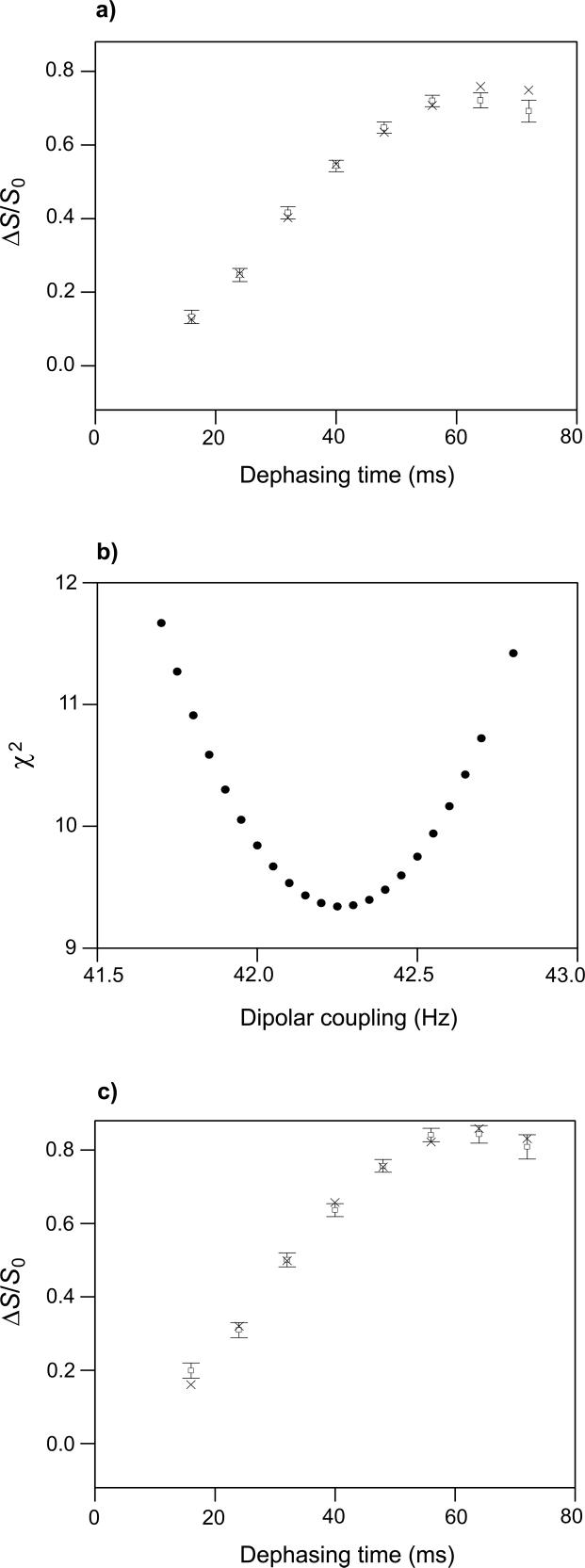
(a) REDOR (ΔS/S₀)_i^cor (filled squares) and (ΔS/S₀)_i^sim (crosses) vs. dephasing time for the I4 peptide. Each (ΔS/S₀)_i^cor was based on a (ΔS/S₀)_i^exp determined by integrations of 1 ppm regions in the S₀ and S₁ spectra. The integration region was centered at 178.8 ppm which is the peak shift in the S₀ spectra. For each τ_i, there were 64 total (S₀ + S₁) scans. The values of σ ^cor_i are ∼0.005 and the heights of the black squares are approximately equal to the average value of 2 × σ ^cor_i. (b) A plot of χ² vs. d_CN yields d_CN = 44.78 ± 0.22 Hz which corresponds to r_CN = 4.110 ± 0.007 Å for the Ala-9 ¹³CO/Ala-13 ¹⁵N labeled pair. The uncertainty was determined using the approach described in the Materials and Methods section. The (ΔS/S₀)_i^sim values in plot a were calculated with the best-fit d_CN.

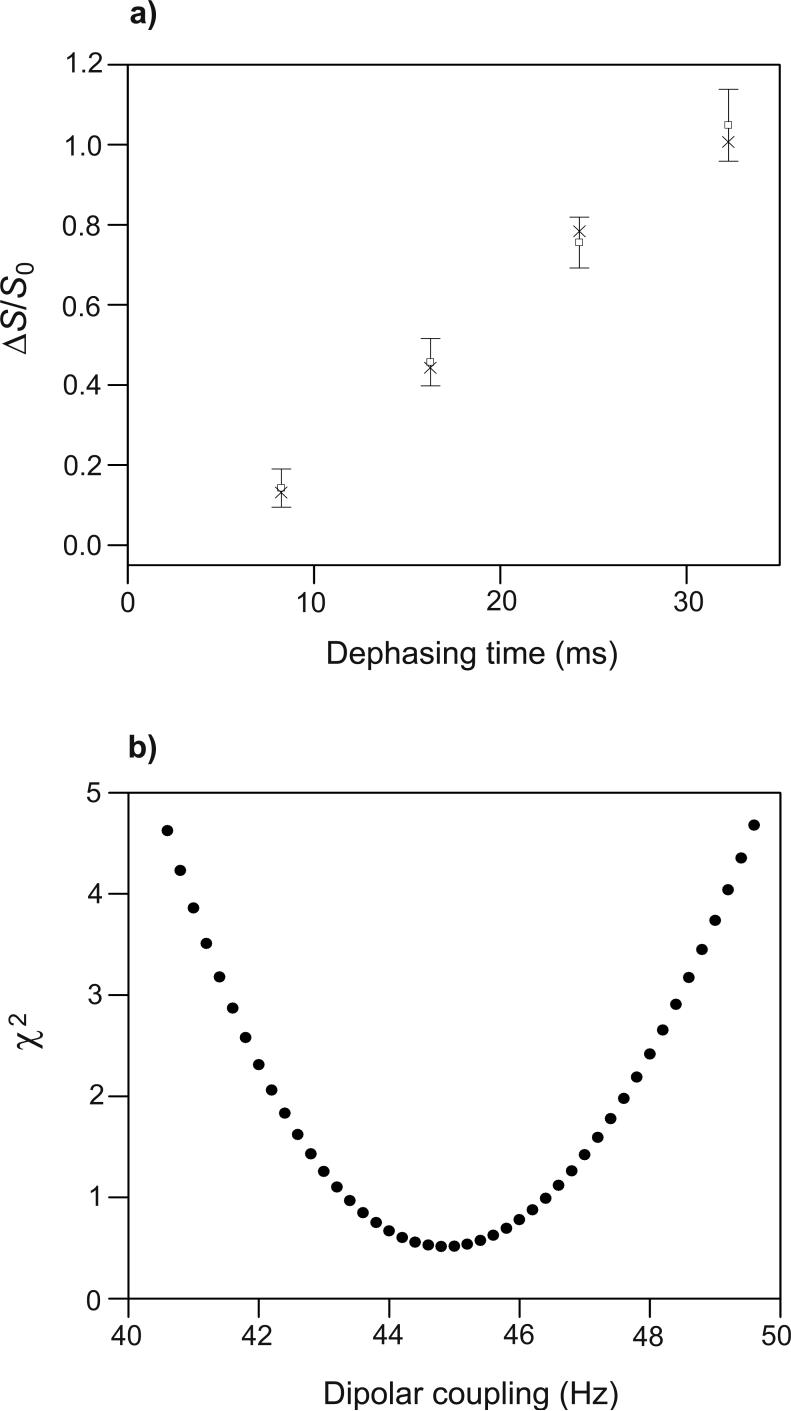
REDOR experiments were then performed on the HFPtr-L7_CF11_N/PC-PG sample. For the Leu-7 ¹³CO peak at 178.6 ppm, spectra with τ_i at 8.25 and 32.25 ms yielded S_1i^exp /S_0i^exp values which were in semi-quantitative agreement with the S_1i^exp/S_0i^exp values from the I4 sample (Fig. 2a-d). In the HFPtr spectra, the upfield natural abundance lipid ¹³CO signals near 175 ppm have (S_1i^exp/S_0i^exp ∼ 1 for all τ_i which is consistent with the expected large ¹³CO-¹⁵N distances and corresponding small d_CN values for these nuclei. Fitting of the Leu-7 (ΔS/S₀)_i^cor to (ΔS/S₀)_i^sim yielded d_CN = 44.8 ± 2.4 Hz and r_CN = 4.11 ± 0.08 Å for the Leu-7 ¹³CO/Phe-11 ¹⁵N labeled pair (Fig. 4). These values are consistent with α helical structure between the labeled nuclei and correlate with the previously discussed downfield Leu-7 ¹³CO chemical shift.

Figure 4.

(a) REDOR (ΔS/S₀)_i^cor (open squares with error bars) and (ΔS/S₀)_i^sim (crosses) vs. dephasing time for the HFPtr-L7_CF11_N/PC-PG sample. Each (ΔS/S₀)_i^cor was based on a (ΔS/S₀)_i^exp determined from spectral integrations over a 1 ppm region centered at 178.6 ppm, the Leu-7 ¹³CO peak chemical shift. The total (S₀ + S₁) numbers of scans used to obtain the (ΔS/S₀)_i^cor values for τ_i = 8.25, 16.25, 24.25, and 32.25 ms were 75420, 52832, 41568, and 46048, respectively. (b) A plot of χ² vs. d_CN yields d_CN = 44.8 ± 2.4 Hz which corresponds to r = 4.11 ± 0.08 Å for the Leu-7 ¹³CO/Phe-11 ¹⁵N labeled pair. The (ΔS/S₀)_i^sim values in plot a were calculated with the best-fit d_CN.

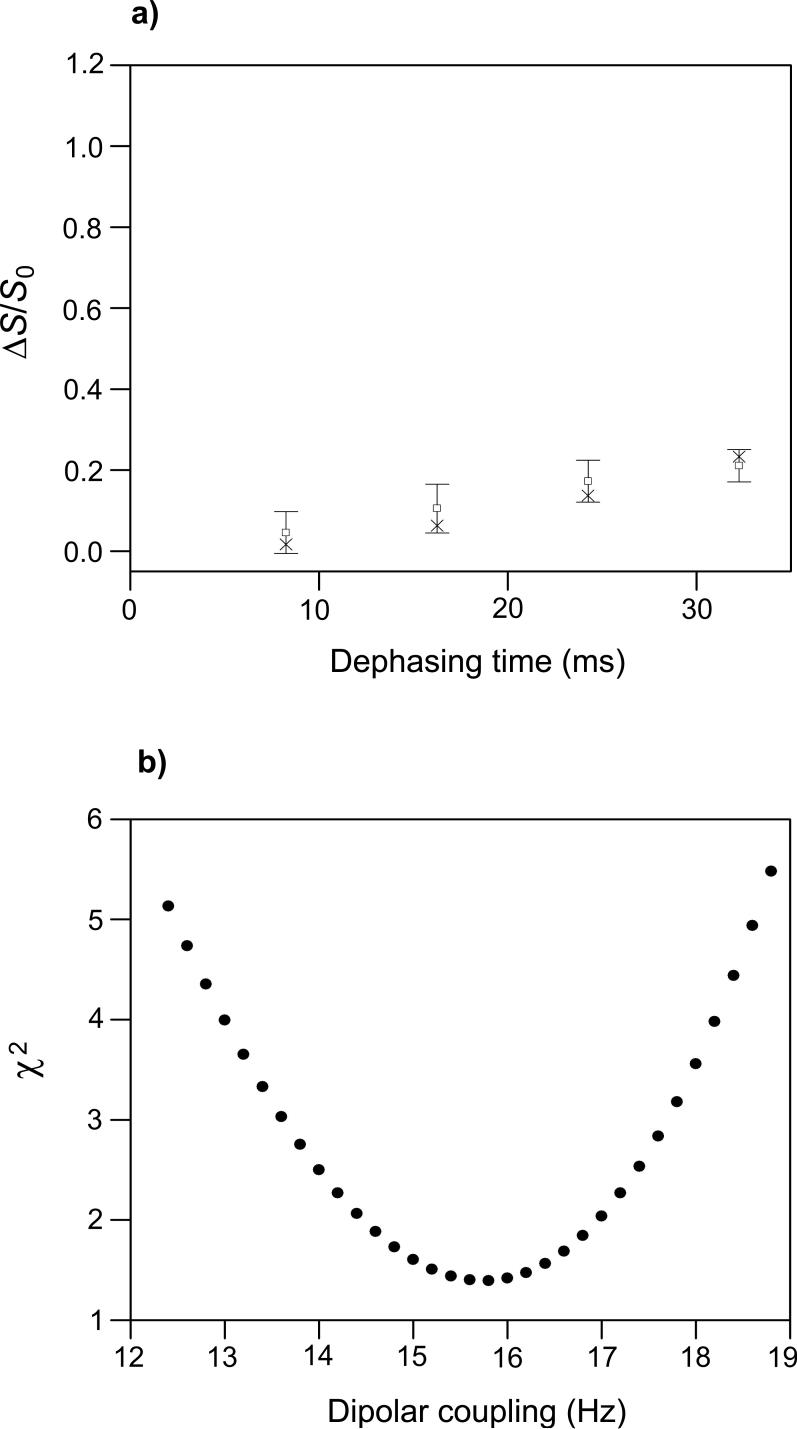
REDOR spectra of the HFPtr-L7_CF11_N/LM3e sample yielded S_1i^exp/S_0i^exp values which were significantly smaller than the S_1i^exp/S_0i^exp values for the I4 sample and suggest that the region between Leu-7 and Phe-11 has non-helical conformation (Fig. 2a, b, e, f). Fitting of (ΔS/S₀)_i^cor to (ΔS/S₀)_i^sim yielded d_CN = 15.8 ± 1.8 Hz which corresponds to r_CN = 5.8 ± 0.3 Å for the Leu-7 ¹³CO/Phe-11 ¹⁵N labeled pair (Fig. 5). This distance is longer than the ∼4.1 Å distance expected in a α helical conformation and shorter than the ∼11 Å distance expected in a β strand conformation. This result is discussed after presentation of the fpCTDQBU analyses; briefly, structural models suggest that the REDOR data reflect an interpeptide distance and provide information about the register of residues in adjacent β strands.

Figure 5.

(a) REDOR (ΔS/S₀)_i^cor (open squares with error bars) and (ΔS/S₀)_i^sim (crosses) vs. dephasing time for the HFPtr-L7_CF11_N/LM3e sample. Each (ΔS/S₀)_i^cor was based on a (ΔS/S₀)_i^exp determined from spectral integrations over a 1 ppm region centered at 173.4 ppm, the peak shift in the S₀ spectra. The total (S₀ + S₁) numbers of scans used to obtain the (ΔS/S₀)₀^cor values for τ_i = 8.25, 16.25, 24.25, and 32.25 ms were 81056, 76288, 172512, and 197440, respectively. (b) A plot of χ² vs. d_CN yields d_CN = 15.8 ± 1.8 Hz which corresponds to r_CN = 5.8 ± 0.3 Å for the Leu-7 ¹³CO/Phe-11 ¹⁵N labeled pair. The (ΔS/S₀)_i^sim values in plot a were calculated with d_CN = 15.8 Hz.

¹³CO-¹³CO distances

An in-register parallel β strand model for the HFPtr-L7_CF11_N/LM3e sample was tested with fpCTDQBU measurements of adjacent interstrand Leu-7 ¹³CO/Leu-7 ¹³CO dipolar couplings and distances. If the model is correct, the distance will be ∼4.8 Å with d_CC ∼ 70 Hz.

The fpCTDQBU experiment was first validated using the GFF sample for which there is a ∼2% fraction of D-GFF molecules with ¹³CO labels at Gly-1 and Phe-3. D-GFF has an intramolecular ¹³CO/¹³CO distance of 5.40 Å and d_CC ∼ 49 Hz. The GFF fpCTDQBU spectra have Phe-3, Phe-2 and Gly-1 ¹³CO peaks at 180.3, 176.4, and 170.9 ppm, respectively (Fig. 6a-d). As τ_i was increased from 16 to 80 ms, there was a general decrease in S_1i^exp/S_0I^exp values for the Phe-3 and Gly-1 peaks. This is consistent with the ∼65% contribution to these signals from D-GFF molecules for which there is significant Gly-1 ¹³CO/Phe-3 ¹³CO dipolar coupling. By contrast, the Phe-2 peak has S_1i^exp/S_0i^exp ∼ 1 for all τ_i which is consistent with the ∼98% contribution to this signal from unlabeled GFF molecules for which there are large ¹³CO/¹³C distances and corresponding small d_CC values.

Figure 6.

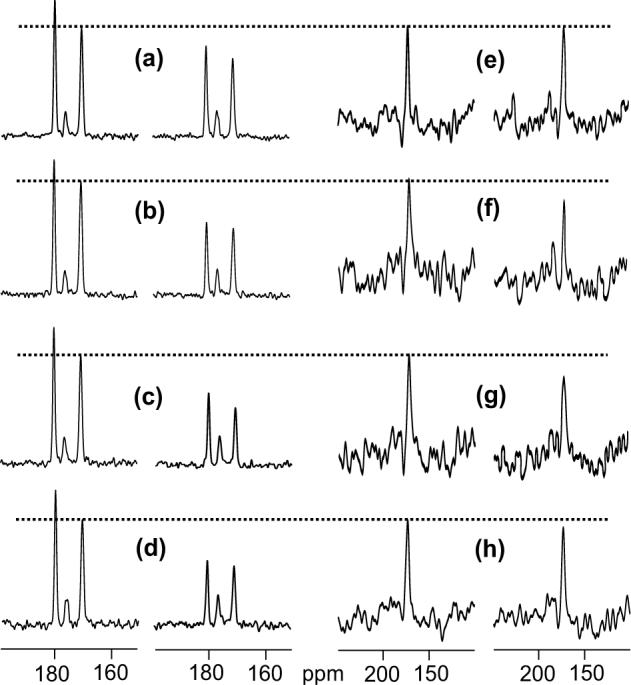
fpCTDQBU spectra of (a-d) the GFF sample and (e-h) the HFPtr-L7_CF11_N/LM3e sample. For each lettered pair of spectra, the S₀ spectrum is on the left and the S₁ spectrum is on the right. The MAS frequency = 8000 Hz, τ_R = 125 μs, the ¹³C π pulse rf field = 10 kHz, M = 336, and the total constant-time = (L + M + N) × τ_R = 84 ms. The values of L, N, and τ_i are: 128, 208, 32 ms (spectra a, e); 192, 144, 48 ms (spectra b, f); 256, 80, 64 ms (spectra c, g); 320, 16, 80 ms (spectra d, h). From left-to-right, each GFF spectrum has Phe-3, Phe-2 and Gly-1 ¹³CO peaks at 180.3, 176.4, and 170.9 ppm, respectively. For each set of GFF and HFPtr spectra with the same τ_i, a dotted line is drawn at the peak S₀ intensities of Gly-1 (GFF) and Leu-7 (HFPtr). The GFF spectra were processed with 50 Hz Gaussian line broadening, the HFPtr spectra were processed with 250 Hz Gaussian line broadening, and baseline correction was applied to all spectra. For some of the HFPtr spectra, there is a small glitch at ∼178 ppm which is due to DC offset in the data. The total numbers of scans used to obtain each spectrum in panels a, b, c, d, e, f, g, and h are 10240, 10240, 10240, 8192, 77056, 80736, 102432, and 152064, respectively.

As the magnitude of the constant-time parameter increases, transverse relaxation causes a decrease in ¹³CO signal intensity for all values of τ_i and consequent lower signal-to-noise ratio. It was therefore desirable to use the smallest constant-time which allowed observation of the full (ΔS/S₀)_i buildup for a ∼5 Å ¹³CO-¹³CO distance. Because RFDR is affected by ¹³C pulse duration, an investigation was made of the effect of the ¹³C π pulse rf field on the (ΔS/S₀)_i buildup rate and signal-to-noise ratio of the GFF sample (65). For the Gly-1 ¹³CO signal, smaller ¹³C π pulse rf fields yielded faster buildup in both experiment and simulation (Fig. 7a) but also led to smaller S₀ and S₁ signal intensities, perhaps because of larger resonance offsets and poorer refocusing of chemical shift evolution. A ¹³C π pulse rf field of ∼10 kHz gave the best overall (ΔS/S₀)_i buildup rate and signal-to-noise ratio (Fig. 7b). Good agreement between (ΔS/S₀)_i ^cor and (ΔS/S₀)_i^sim at 10 and 43 kHz fields was obtained using d_CC = 42 Hz. Good agreement between experimental and simulated signal-to-noise ratios at 10 kHz field was obtained using a single value of k (Eq. 5) while at 43 kHz field, this k value resulted in simulated signal-to-noise ratios about double those observed in experiment. Because the ¹³C π pulses at 43 kHz field are shorter than those at 10 kHz field, the 43 kHz experimental pulses are more poorly approximated by the ideal rectangular pulses of the simulations. This may result in poorer refocusing performance of the 43 kHz experimental ¹³C π pulses and lower signal-to-noise ratios relative to simulation.

Figure 7.

Dependence of fpCTDQBU of GFF Gly-1 ¹³CO on ¹³C π pulse rf field: (a) (ΔS/S₀)_i^cor and (ΔS/S₀)_i^sim vs. dephasing time; and (b) signal-to-noise ratio of (ΔS/S₀)_i^cor and (ΔS/S₀)_i^sim vs. dephasing time. The MAS frequency = 8000 Hz, δ_{13C transmitter} = 175.7 ppm, M = 336, and the constant-time = 84 ms. The symbol legend is: squares, cor, 10 kHz ¹³C π pulse rf field; crosses, sim, 10 kHz field; diamonds, cor, 43 kHz field; circles, sim, 43 kHz field. Uncertainties are displayed for the cor points in plot a and lines are drawn between like symbols in plot b. Each (ΔS/S₀)_i^cor was based on a (ΔS/S₀)_i^exp determined from spectral integrations over a 0.5 ppm region centered at the Gly-1 ¹³CO peak chemical shift. Each (ΔS/S₀)_i^cor value was determined using intensities from 4096 total (S₀ + S₁) scans. The S_0i^sim and S_1i^sim were calculated with d_CC = 42 Hz which yielded the best overall agreement between (ΔS/S₀)_i^cor and (ΔS/S₀)_i^sim values. The value of k (Eq. 5) was set to give the best agreement at 10 kHz field between the sim and cor signal-to-noise ratios.

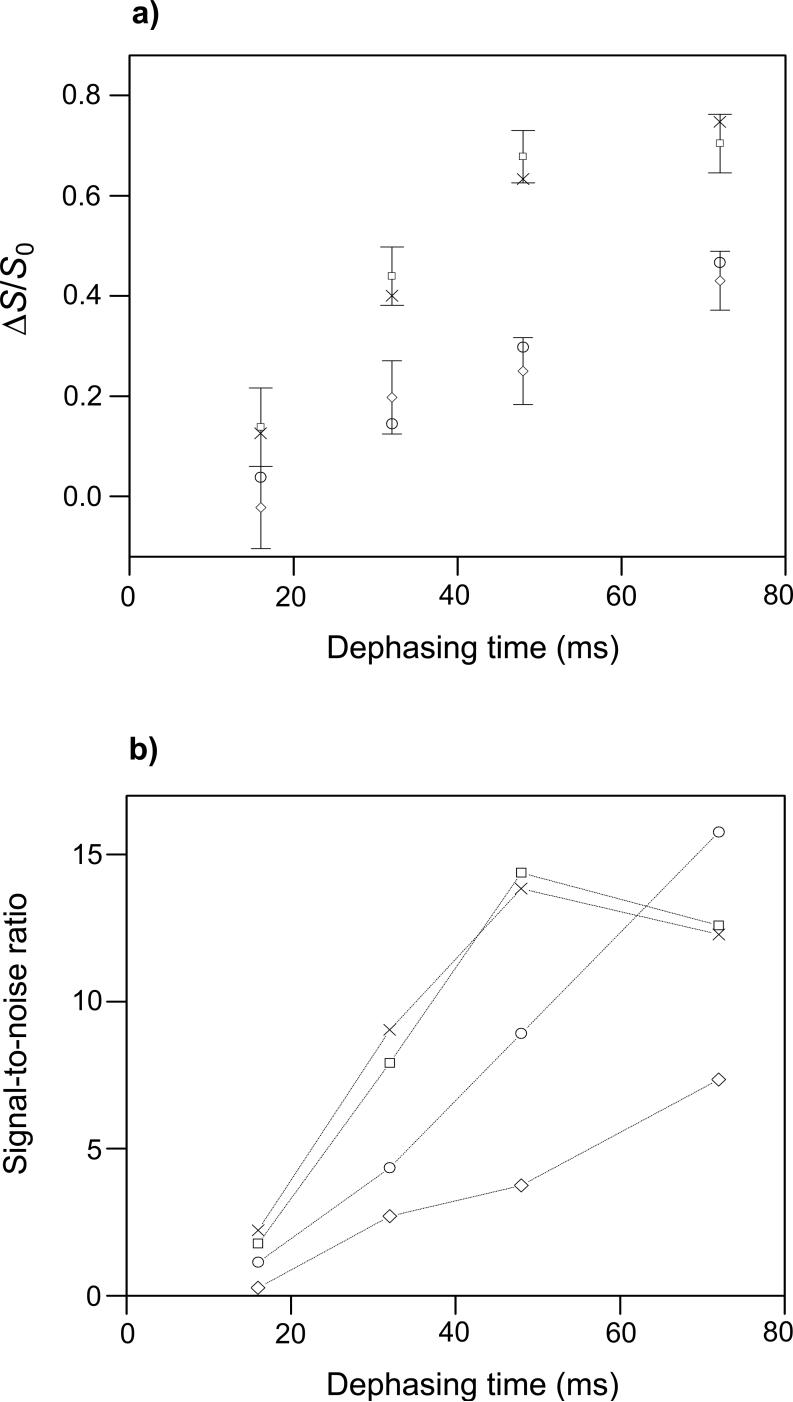
Subsequent fpCTDQBU experiments were done with a 10 kHz ¹³C π pulse rf field. Fig. 8 displays comparison and fitting of GFF Gly-1 ¹³CO (ΔS/S₀)_i ^cor and (ΔS/S₀)_i ^sim over a wide range of τ_i. The analysis focused on Gly-1 ¹³CO because it is has carbonyl rather than carboxyl functionality and is thus more relevant to the HFPtr sample. The fitting yielded d_CC = 42.3 ± 0.5 Hz and corresponding r_CC = 5.67 ± 0.02 Å for the Gly-1 ¹³CO/Phe-3 ¹³CO labeled pair. Variation of ¹³CO CSA axis orientations relative to the GFF atomic geometry did not greatly affect (ΔS/S₀)_i^sim and the fitted values of d_CC. For example, different sets of (ΔS/S₀)_i^sim were calculated with each set having a randomly generated principal axis orientation. Each set of (ΔS/S₀)_i^sim was then fitted to (ΔS/S₀)_i^cor and the resulting d_CC was always within a range of 37−47 Hz.

Figure 8.

(a) fpCTDQBU (ΔS/S₀)_i^cor (open squares with error bars) and (ΔS/S₀)_i^sim (crosses) vs. dephasing time for GFF Gly-1 ¹³CO. The MAS frequency = 8000 Hz, the ¹³C π pulse rf field = 10 kHz, δ_{13C transmitter} = 175.7 ppm, M = 336, and the constant-time = 84 ms. Each (ΔS/S₀)_i^cor was based on a (ΔS/S₀)_i^exp determined from spectral integrations over a 0.5 ppm region centered at the Gly-1 ¹³CO peak chemical shift. Each (ΔS/S₀)_i^cor value for τ_i = 16, 24, 32, 40, 48, 56, and 64 ms was determined using intensities from 20480 total (S₀ + S₁) scans and the (ΔS/S₀)_i^cor value for τ_i = 72 ms was determined using intensities from 16384 total scans. (b) A plot of χ² vs. d_CC yields d_CC = 42.3 ± 0.5 Hz which corresponds to r_CC = 5.67 ± 0.02 Å for the Gly-1/Phe-3 labeled pair. The (ΔS/S₀)_i^sim values in panel a were calculated with d = 42.3 Hz. (c) Plot of (ΔS/S₀)_i^cor(open squares with error bars) and (ΔS/S₀)_i^sim (crosses) calculated with d_CC = 49 Hz which corresponds to r_CC = 5.40 Å, the Gly-1 CO/Phe-3 CO distance in the X-ray structure. The (ΔS/S₀)_i^cor were fitted to (ΔS/S₀)_i^sim as a function of the D-GFF:unlabeled GFF ratio and the displayed (ΔS/S₀)_i^cor were calculated with the best-fit value of the ratio (1:71) for which χ² = 7.

In Fig. 8a, the only systematic disagreement between (ΔS/S₀)_i^cor and (ΔS/S₀)_i^sim occurs at large values of τ_i for which (ΔS/S₀)_i^cor decreases more rapidly than (ΔS/S₀)_i^sim. The best-fit r_CC is ∼5% larger than the 5.40 Å crystallographic distance (71). Uncertainty in the D-GFF:unlabeled GFF ratio in the sample is one possible reason for this discrepancy because this ratio affects the (ΔS/S₀)_i^exp → (ΔS/S₀)_i^cor conversion (cf. Materials and Methods and Supporting Information). The potential effect of this uncertainty was tested by calculation of (ΔS/S₀)_i^sim with d = 49 Hz (r_CC = 5.40 Å) and then fitting (ΔS/S₀)_i^cor to (ΔS/S₀)_i^sim as a function of the D-GFF:unlabeled GFF ratio (Fig. 8c). Good fits were obtained with ratios of ∼1:70 which is close to the ratio of ∼1:50 derived from weights of D-GFF and unlabeled GFF in the sample and by the ratio of the Gly-1:Phe-2 ¹³CO intensities. Overall, the GFF studies demonstrate that ¹³C-¹³C distances in the ∼5 Å range can be reasonably accurately determined with the fpCTDQBU method.

The fpCTDQBU spectra of the HFPtrL7_CF11_N/LM3e sample are displayed in Fig. 6e-h. Relative to the Gly-1 and Phe-3 ¹³CO peaks in the GFF spectra (Fig. 6a-d), the HFPtr spectra have larger S_1i/S_0i ratios which are consistent with a d_CC smaller than in D-GFF and a Leu-7 ¹³CO/Leu-7 ¹³CO distance longer than that in D-GFF. The τ_i = 32, 48, and 64 ms points were fitted in the context of a “two-spin” or a “three-spin” model (Fig. 9). The 80 ms point was not included in the fitting because of the systematic disagreement between (ΔS/S₀)_i^cor and (ΔS/S₀)_i^sim at large values of τ_i in the GFF analysis (Fig. 8a). The two-spin (three-spin) model has two (three) adjacent in-register parallel β strands and the simulations are based on two (three) ¹³COs, each of which is at the same residue position in its respective strand. The interstrand distance and corresponding d_CC value were input parameters for the simulations. In the three-spin model, the two outside strands were always equidistant from the central strand.

Figure 9.

fpCTDQBU (ΔS/S₀)_i^cor and (ΔS/S₀)_i^sim vs. dephasing time for the HFPtr-L7_CF11_N/LM3e sample. The MAS frequency = 8000 Hz, the ¹³C π pulse rf field = 10 kHz, δ_{13C transmitter} = 178.4 ppm, M = 336, and the constant-time = 84 ms. The (ΔS/S₀)_i^cor values are open squares with error bars. Each (ΔS/S₀)_i^cor was based on a (ΔS/S₀)_i^exp determined from spectral integrations over a 1 ppm region centered at 173.4 ppm, the peak shift in the S₀ spectra. The total (S₀ + S₁) numbers of scans used to obtain the (ΔS/S₀)_i^cor values for τ_i = 32, 48, and 64 ms were 154112, 161472, and 204864, respectively. The (ΔS/S₀)_i^sim values were calculated with two-spin and three-spin models in plots a and b, respectively. In plot a, the up triangles, crosses, and down triangles correspond to d_CC = 10, 15 and 20 Hz, respectively and in plot b, they correspond to d_CC = 8, 13, and 18 Hz, respectively. The best-fit values of d_CC are ∼15 Hz and ∼13 Hz for the two-spin and three-spin models, respectively, and correspond to interstrand Leu-7 ¹³CO-¹³CO distances of 8.0 Å and 8.4 Å. Reasonable upper limits on d_CC in the two-spin and three-spin models are ∼20 Hz and ∼18 Hz respectively, and correspond to distances of 7.3 Å and 7.5 Å.

The fitting is based on three points with relatively large uncertainties and visual comparison was used to assess best-fit d and its uncertainty. The best-fit values of d_CC in the two-spin and three-spin models are ∼15 Hz and ∼13 Hz, respectively, and correspond to r_CC of 8.0 Å and 8.4 Å. Reasonable upper limits on d_CC in the two-spin and three-spin models are ∼20 Hz and ∼18 Hz, respectively, and correspond to r_CC of 7.3 Å and 7.5 Å. The lower limits on d_CC and upper limits on r_CC are more difficult to assess because of the uncertainties in (ΔS/S₀)>_i^cor and weak dependence of (ΔS/S₀)_i^sim on d_CC at small values of d_CC. Overall, experimental values of d_CC and r_CC do not support the in-register parallel β model for which d_CC ∼ 70 Hz and _rCC ∼ 4.8 Å.

Strand arrangement models

Fig. 10 displays three models: (a) parallel β strand with all strands in-register; (b) parallel β strand with adjacent strands two residues out-of-register; and (c) antiparallel β strand with adjacent strand crossing between Phe-8 and Leu-9. Each model is shown with three strands although we do not have information about the numbers of strands in the LM3e-associated HFPtr oligomer. Table 1 displays Leu-7 CO/Phe-11 N and interstrand Leu-7 CO/Leu-7 CO distances from REDOR and fpCTDQBU experiments and from the models. The model distances are averages for parallel strand regions of cutinase and antiparallel strand regions of human gamma-D crystalline R58H mutant whose crystal structures have been refined to 1.0 Å and 1.15 Å, respectively (91, 92).

Figure 10.

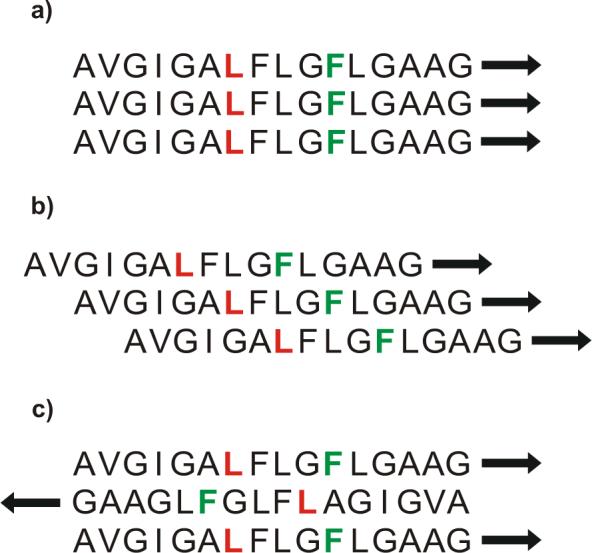
Structural models for strand arrangements of LM3e-associated HFPtr: (a) parallel in-register; (b) parallel with adjacent strands two-residues out-of-register; and (c) antiparallel with adjacent strand crossing between Phe-8 and Leu-9. The first sixteen residues of each strand are displayed, the ¹³CO labeled Leu-7 are colored red, and the ¹⁵N labeled Phe-11 are colored green.

Table 1.

Experimental and Model Distances^a

	rCN (Å)b	rCC (Å)c
Experiment	5.8(3)	8.2(9)
Parallel in-register modeld	11.0(3)	4.8(2)
Parallel out-of-register modele	6.5(3)	8.2(3)
Antiparallel modelf	6.1(3)	8.5(3)

^aEach model distance was determined from a region of a high-resolution crystal structure which has the same strand arrangement as the model. Several interatomic distances were measured in this region. An average distance is reported in the table as well as the standard deviation in units of 0.1 Å in parentheses.

^bLeu-7 CO/Phe-11 N distance.

^cInterstrand Leu-7 CO/Leu-7 CO distance.

^dModel distances were determined from the region of the cutinase protein corresponding to residues 34−39, 113−120, and 143−148.

^eAdjacent strands are two-residues out-of-register. Model distances were determined from the cutinase protein.

^fAdjacent strands cross between Phe-8 and Leu-9. Model distances were determined from the region of the human gamma-D crystalline R58H mutant protein corresponding to residues 2−7, 14−18, and 34−38.

There are significant differences between the experimental distances and in-register parallel strand model distances. The experimental Leu-7 ¹³CO/Phe-11 ¹⁵N distance is ∼6 Å which is much shorter than the ∼11 Å intrastrand or interstrand distance in the model. The lower limit on the experimental interstrand Leu-7 ¹³CO/Leu-7 ¹³CO distance is >7 Å and is significantly longer than the 4.8 Å distance in the model.

Distances in the out-of-register parallel strand and antiparallel strand models are more consistent with the experimentally-derived distances. There are ∼6 Å interstrand Leu-7 CO/Phe-11 N distances because of the strand registers in the models. In addition, the interstrand Leu-7 CO/Leu-7 CO distances are ∼8 Å. Calculations of REDOR and fpCTDQBU (ΔS/S₀)_i^sim for the two models agreed reasonably well with (ΔS/S₀)_i^cor. The data were more poorly fit by other strand arrangement models.

Further experiments are required to distinguish between the two models. For example, we recently observed Ala-6 ¹³C/Gly-10 ¹³C crosspeaks in 2D spectra of LM3-associated HFP which was uniformly ¹³C labeled at Ala-6 and Gly-10 (97). The crosspeaks were generated by magnetization exchange due to proton-driven spin diffusion which typically occurs between ¹³C nuclei separated by < 6 Å. For the out-of-register parallel and antiparallel models, the closest distance between Ala-6 and Gly-10 ¹³Cs is ∼7.1 Å and ∼4.5 Å, respectively, and the spectra are more consistent with the antiparallel model. Future experiments could be based on the REDOR approaches used to recently elucidate strand arrangements in the PG-1 antimicrobial peptide (59).

A turn structure in the Leu-7 to Phe-11 region could also be consistent with the experimental Leu-7 CO/Phe-11 N distance. Although this possibility cannot be definitively ruled out, measurements of ¹³C chemical shifts for nuclei in this region of LM3-associated HFP are all consistent with β strand conformation (29, 97). We also note the possibility of populations of distinct strand arrangements which would necessitate fitting REDOR and fpCTDQBU signals with populations of distinct spin geometries.

In summary, the REDOR and fpCTDQBU data are consistent with a parallel strand arrangement with adjacent strands two-residues out-of-register and with an antiparallel arrangement whose adjacent strand crossing is between Phe-8 and Leu-9. The data are not consistent with an in-register parallel strand arrangement.

DISCUSSION

Conformational plasticity

The structural plasticity of membrane-associated viral fusion peptides has been observed by several groups using a variety of experimental probes, and it is known that they can exist in helical or nonhelical forms (7). Other investigators have developed structural models for the helical form of the peptides based principally on liquid-state NMR, ESR, and IR data (33, 38, 39, 73, 74). IR and solid-state NMR studies of the β strand form of HFP and its oligomeric constructs have shown parallel strand arrangement, anti-parallel strand arrangement and a mixture of parallel and antiparallel arrangements (26, 43, 44). In the present study, the structure of membrane-associated HFPtr was explored with solid-state NMR methods including chemical shift, heteronuclear distance, and homonuclear distance measurements. The data suggest that the region of HFPtr between Leu-7 and Phe-11 is α helical when associated with membranes without cholesterol and is β strand when associated with membranes which have a lipid headgroup and cholesterol composition similar to that of host cells of the virus. These results are consistent with our observations that for a single FP:lipid mol ratio, cholesterol favors formation of the β strand conformation of fusion peptides (27, 76, W. Qiang and D. P. Weliky, unpublished experiments). This conformational difference has been seen both at room temperature as well as at the −50 °C temperature of the experiments in this paper (29). The observed fusion peptide conformations appear to be equilibrium rather than kinetically-trapped structures (98).

The presence of cholesterol in membranes is known to increase the lateral molecular packing density and membrane tensile strength, decrease in-plane elasticity and permeability of water through the membrane, and promote formation of the “liquid-ordered phase” (99-104). This phase is characterized by a rapid lateral molecular translational diffusion coefficient similar to that of the “liquid-disordered” phase and high configurational order of the lipid acyl chains similar to that of the “solid-ordered” phase (104, 105). These latter phases exist for non-cholesterol containing membranes at higher and lower temperature, respectively. Fluorescence data suggest that HFPmn in its helical form inserts more deeply into the membrane than HFPmn in its β strand form (106). The higher molecular packing density in the cholesterol-containing membranes may make HFPtr insertion more difficult and thus favor a more surface-associated β strand form.

Because the rapid fusion rate of HFPtr is observed both for vesicles which contain cholesterol and for vesicles which do not contain cholesterol, one reasonable hypothesis is that both the helical and β strand structures of HFPtr are highly fusogenic (46). Other investigators have proposed that the peptide structure responsible for fusion is irregular and may be transient (107, 108). Although the present paper does not directly address these issues, it is noted: (1) cholesterol-associated structural variation is also observed for the influenza virus fusion peptide (27, 76); and (2) pH-triggered fusion can be observed both for helical influenza fusion peptide bound to non-cholesterol containing membranes and for β strand influenza fusion peptide bound to cholesterol-containing membranes (109). These results argue in favor of fusogenic activity of both helical and β strand structures. Lentz and coworkers have proposed that fusion peptides catalyze fusion by filling void spaces in nonbilayer fusion intermediates and that this function can be done by peptides in either helical or β strand conformation (110). Our results are consistent with this model and two fusogenic conformations may allow the virus to fuse with a wider variety of membrane compositions. Membranes of uninfected host cells of the virus contain ∼30 mol% cholesterol and there is some depletion of cholesterol in these membranes after HIV infection (77, 78). The HIV membrane contains ∼45 mol% cholesterol and there is some evidence that HIV fuses with cholesterol-rich regions of host cell membranes (111).

The 15−40 fold higher rate of HFPtr-induced lipid mixing relative to HFPmn is observed both with PC-PG vesicles for which the final HFPtr conformation is helical and with LM3 vesicles for which the final conformation is β strand. For either conformation, there is a higher local concentration of peptide strands at the membrane surface with HFPtr than with HFPmn and this larger concentration could cause greater perturbation of the membrane and provide a general model for the increased fusion rate of HFPtr. Other possible differences between HFPtr and HFPmn are their depths and angles of membrane insertion as well as the arrangement and interactions of individual helices or strands.

Strand arrangement

Previous solid-state NMR REDOR data for HFPmn associated with cholesterol-containing membranes were consistent with a mixture of parallel and antiparallel strand arrangements (43). A predominant parallel strand arrangement is an appealing structural model to explain the increased fusion rate of β strand HFPtr because it places the apolar N-terminal regions of the strands close to one another and thereby provides a larger apolar volume to perturb the membrane. The solid-state NMR data of this paper are consistent with a parallel model with adjacent strands two-residues out of register.

The data are also consistent with antiparallel strands with adjacent strands crossing between Phe-8 and Leu-9. For this antiparallel arrangement, the sixteen N-terminal apolar residues (A1 to G16) could form a hydrogen-bonded β strand oligomer and the more polar C-terminal residues would be outside the hydrogen-bonded oligomer. If residues A1-G16 form a single β strand without turns, then a structural building block could be based on two HFPtr molecules “A” and “B”. The A₁, A₂, and A₃ strands would run in the same direction (as enforced by the cross-linking) and the B₁, B₂, and B₃ strands would run in the opposite direction. An antiparallel interleaved arrangement could be A₁B₃A₂B₂A₃B₁; i.e. residues in strand B₃ are hydrogen bonded to residues in strands A₁ and A₂. This antiparallel structure would place the bulky C-terminal regions of the HFPtr molecules on either side of the oligomer and could allow more efficient assembly of multiple HFPtr trimers at the membrane surface with consequent greater membrane perturbation and fusion rate. The total number of strands in a hydrogen-bonded oligomer may not be large as evidenced by poor room-temperature cross-polarization and the inferred high molecular mobility (29).

For membrane-associated HFPmn, IR data from several groups support an antiparallel strand arrangement (26, 30, 110, 112). However, IR data on constructs which contain the first 34 or 70 residues of gp41 support an in-register parallel strand arrangement (44). These latter constructs contain the 23-residues of HFPmn as well as an additional 11 or 47 C-terminal residues. The variation in strand arrangements among the constructs may be due to sequence or cross-linking differences (113).

Accurate measurement of weak couplings

Model compound results in this paper provide insight into the accuracy with which solid-state NMR determines weak couplings and long internuclear distances in peptides and proteins with selective isotopic labeling. This is a significant issue because most structurally interesting distances are long. After consideration of fractional labeling, natural abundance nuclei, and the population of molecules with random coil structures, the I4 REDOR data were fit well to d_CN of 44.8 Hz and r_CN of 4.11 Å. The latter value agrees quantitatively with r_CN of a α helix which is the predominant conformation of the I4 peptide.

After consideration of fractional labeling and natural abundance nuclei, the GFF fpCTDQBU data were fit well to d_CC of 42.3 Hz and r_CC of 5.67 Å. These values are respectively ∼15% smaller and ∼5% larger than the crystallographic values. Possible contributions to this discrepancy include: (1) vibrational averaging of d_CC through the large numbers of bonds between the two labeled nuclei; and (2) inaccuracy in the D-GFF:unlabeled GFF ratio. Overall, the experiment was a robust measure of d_CC and r_CC.

Incorporation of finite π pulses in the fpCTDQBU experiment resulted in higher ΔS/S₀ buildup rate and signal-to-noise. To our knowledge, previous application of fpRFDR sequences for distance determination has typically been done at high (≥ 20 kHz) MAS frequencies with the exception of work by Chan et al. on ³¹P-³¹P distances in phosphate compounds (114). The present work demonstrates application of fpRFDR at moderate spinning frequencies to measurement of structurally interesting and weak (<50 Hz) ¹³C-¹³C dipolar couplings. This is significant for membrane-associated peptides and proteins because it is often desirable to work at smaller protein:lipid ratio and therefore larger volume rotors with concomitant slower MAS frequencies. It was also found that constant-time was required to obtain interpretable RFDR data. Constant-time reduces signal intensity so reasonably high decoupling and judicious choice of the constant-time value were critical to obtain satisfactory data for the HFPtr sample. The fpCTDQBU sequence of the present study relies on the intensity difference of two spectra as a function of dephasing time while the related fpRFDR-CT method relies on the intensity of a single spectrum as a function of dephasing time (51, 65). The fpRFDR-CT technique may therefore yield data with higher signal-to-noise.

ABBREVIATIONS

CD

circular dichroism

CP

cross-polarization

CSA

chemical shift anisotropy

d_CC

¹³C-¹³C dipolar coupling

d_CN

¹³C-¹⁵N dipolar coupling

DCM

dichloromethane

D-GFF

doubly labeled GFF

D-NAL, 1-¹³C

N-¹³C doubly labeled NAL

DTPC

1,2-di-O-tetradecyl-sn-glycero-3-phosphocholine

DTPG

1,2-di-O-tetradecyl-sn-glycero-3-phospho-rac-(1-glycerol) sodium salt

DPhPE

1,2-di-O-phytanyl-sn-glycero-3-phosphoethanolamine

ESR

electron spin resonance

FMOC

9-fluorenylmethoxycarbonyl

fpCTDQBU

constant-time double-quantum build-up with finite pulses

fpRFDR-CT

constant-time finite-pulse rf-driven recoupling

GFF

glycyl-L-phenylalanyl-L-phenylalanine

HEPES

N-(2-hydroxyethyl)piperazine-N'-2-ethanesulfonic acid

HIV

human immunodeficiency virus

HFP

HIV fusion peptide

HFPdm

HIV fusion peptide dimer

HFPmn

HIV fusion peptide monomer

HFPtr

HIV fusion peptide trimer

HPLC

high-performance liquid chromatography

IR

infrared

LM3

lipid mixture 3

LM3e

ether-linked lipid mixture 3

LUV

large unilamellar vesicle

MAS

magic angle spinning

NAL

N-acetyl-L-leucine

NMP

N-methylpyrrolidone

NMR

nuclear magnetic resonance

PC-PG

4:1 POPC:POPG mixture

PDB

Protein Data Bank

PI

phosphatidylinositol

POPC

1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine

POPE

1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine

POPG

1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-rac-(1-glycerol)

POPS

1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-L-serine

rf

radio frequency

r_CC

¹³C-¹³C distance

r_CN

¹³C-¹⁵N distance

REDOR

rotational-echo double resonance

RFDR

radio frequency-driven recoupling

SIMPSON

simulation program for solid-state NMR spectroscopy

TBME

t-butyl methyl ether

TFA

trifluoroacetic acid

TPPM

two-pulse phase-modulation

2D

two-dimensional