Theory, analysis, and interpretation of single-molecule force spectroscopy experiments

Abstract

Dynamic force spectroscopy probes the kinetic and thermodynamic properties of single molecules and molecular assemblies. Here, we propose a simple procedure to extract kinetic information from such experiments. The cornerstone of our method is a transformation of the rupture-force histograms obtained at different force-loading rates into the force-dependent lifetimes measurable in constant-force experiments. To interpret the force-dependent lifetimes, we derive a generalization of Bell's formula that is formally exact within the framework of Kramers theory. This result complements the analytical expression for the lifetime that we derived previously for a class of model potentials. We illustrate our procedure by analyzing the nanopore unzipping of DNA hairpins and the unfolding of a protein attached by flexible linkers to an atomic force microscope. Our procedure to transform rupture-force histograms into the force-dependent lifetimes remains valid even when the molecular extension is a poor reaction coordinate and higher-dimensional free-energy surfaces must be considered. In this case the microscopic interpretation of the lifetimes becomes more challenging because the lifetimes can reveal richer, and even nonmonotonic, dependence on the force.

Mechanical forces play an increasingly recognized role in biology at the molecular level. Many biological macromolecules have a load-bearing function in living cells. Proteins such as titin in the skeletal and cardiac muscle sarcomere, fibronectin in the extracellular matrix, and spectrin in erythrocytes provide resistance under mechanical stress. Other biomolecules such as higher-order nucleic acid complexes are unraveled in a controlled way by mechanical forces before being processed by polymerases, helicases, and ribosomes (1).

The controlled application of mechanical forces on single molecules provides a powerful tool to study their structure, dynamics, and function. Remarkable advances in single-molecule manipulation have made it possible to measure the forces and strains that develop during many processes in a cell in real time. Moreover, the exertion of external forces modify these processes in a controlled way (2). In such experiments, a molecule or molecular complex is attached to an atomic force microscope (AFM) or laser optical tweezer, often through flexible molecular linkers. Pulling at a constant speed or at a constant force builds up mechanical tension, eventually culminating in a molecular transition such as ligand-receptor dissociation (3,4), unfolding of a protein (5–10), or unzipping of nucleic acids (11,12). When performed at constant force, these experiments directly probe the force-dependent lifetime of the system, τ(F). In contrast, the distribution of rupture forces measured in experiments at a constant pulling speed needs to be processed to provide information about τ(F).

The standard theory of irreversible rupture induced by an external time-dependent force treats rupture as the crossing of a free-energy barrier and is based on the assumption that the process is quasi-adiabatic. Quasi-adiabaticity implies that the characteristic time of relaxation of the system in the unruptured state is much faster than that of the escape over the barrier. The rate at which the external force is ramped up should thus not be too high. The probability S(t) that the system is still intact at time t then satisfies the first-order rate equation $\dot{S}(t)\equiv dS/dt=-S(t)/\tau (F(t))$, where we ignore fluctuations (13) in the time-dependent external force F(t). The distribution of rupture forces, p(F), is related to the distribution of lifetimes by $-\dot{S}dt=p(F)dF$ and is given by

where Ḟ is the force loading rate. It can be verified that ${\displaystyle {\int }_0^{\infty }p(F)dF=1}$. If a stiff molecular system is pulled by a spring with spring constant κ_s moving at a velocity υ, then F(t)=κ_s υ t and $\dot{F}={\kappa }_s\upsilon$ is proportional to υ and independent of F. However, if intervening flexible linkers are present in the experimental setup, the loading rate becomes a function of the force itself, $\dot{F}=\dot{F}(F)$ (14–17).

The widely used analysis of dynamic force spectroscopy data (18,19) employs the above expression in conjunction with Bell's phenomenological formula (20) for the force-dependent lifetime, ${\tau }_{\text{Bell}}(F)={\tau }_0\exp (-\beta F{x}^{‡})$, where the intrinsic lifetime τ₀ and the distance between the bound and transition states x^‡ are the parameters of the system in the absence of the applied force, and β⁻¹ = k_BT. When the loading rate is independent of force, the rupture-force distribution can be found analytically. Within the framework of the phenomenological approach, the mean rupture force [or alternatively, the maximum of p(F)] is predicted to be a linear function of the logarithm of the loading rate (21), whereas the variance of the rupture force is essentially independent of the loading rate (22).

With the increasing dynamic range of experiments, deviations from this predicted behavior have been observed. The assumption in Bell's formula, that the well-to-barrier distance x^‡ is independent of force, cannot be true for all forces. In one dimension the barrier and the well must move closer as the force increases, because they eventually merge at a critical force when the barrier to rupture vanishes.

Recently (22), we have made the phenomenological model, based on Bell's assumption, more realistic while retaining its mathematical simplicity. By applying Kramers theory to a variety of simple free-energy profiles (13,23), we obtained analytic expressions for the force-dependent lifetime, the rupture-force distribution, and its mean and variance that contain the Bell–Evans results as a special case. Our formalism contains a single additional parameter, namely the apparent free energy of activation, and predicts that both the logarithm of the lifetime at constant force and the mean rupture force are nonlinear functions of the force and the logarithm of the loading rate, respectively.

Explicit expressions for the rupture-force distributions enable the use of powerful maximum-likelihood or Bayesian inference methods in the analysis of experiments (22). We have recently applied this approach to experiments in which DNA hairpins were unzipped in a nanopore under applied voltage (24).

Here, we develop an alternate approach to extract kinetic information from force-spectroscopy experiments, which is easier to implement in practice. Our formalism is based on a relation between constant-speed and constant-force experiments. We validate the formalism by applying it to nanopore unzipping of DNA hairpins, and then use it to analyze the unfolding of a protein under mechanical force. Our approach allows one to easily account for the effect of linkers. We then describe how the lifetime τ(F) can be interpreted in microscopic terms. We conclude by developing a theory in which the pulling coordinate is not assumed to be a good reaction coordinate, and show that the general formalism to extract τ(F) still applies but the interpretation of τ(F) is more involved.

Results and Discussion

Relation Between Constant Speed and Constant Force Experiments.

Eq. 1 expresses the rupture-force distribution in terms of the loading rate and the lifetime at constant force. It can be readily inverted to get the lifetime in terms of the rupture-force distribution and loading rate (22),

This relation shows how rupture-force histograms p(F) measured at different loading rates Ḟ (right-hand side of Eq. 2 can be directly transformed into the force dependence of the lifetime τ(F) (left-hand side of Eq. 2) measurable in constant-force experiments. This mapping follows directly from the quasi-adiabatic assumption (22,26) and is independent of the nature of the underlying free-energy surface. Eq. 2 predicts that data obtained at different loading rates must collapse onto a single master curve that determines the force dependence of τ(F) over a wider range of forces than may be readily available from constant-force experiments. If the data do not collapse, then Eq. 1 does not hold and the time course of the kinetics at constant force is expected to be more complex than single-exponential.

From Eq. 2 one can obtain an approximate but quite general relationship between the lifetime at a force equal to the mean rupture force and the variance of the rupture-force distribution,

This relation can be derived from Eq. 2 by setting F = 〈F〉 and approximating p(F) by a normalized Gaussian distribution with the exact mean and variance. Although the true distributions are not well described by a Gaussian over the entire range of forces, it turns out that this approximation is quite good near the mean. Indeed, the same functional relation, with a numerical coefficient that differs by <10%, can be derived from the highly non-Gaussian rupture-force distributions (22) that correspond to τ(F) in Eq. 5 below. Whereas Eq. 3 gives an estimate for the τ(F) over a narrower range of F than does Eq. 2, it should prove useful if the data permit estimates of only the mean and variance. For datasets with substantial outliers it may be preferable to use $\tau (\langle F\rangle )\approx \frac{3}{4}\delta F/\dot{F}(\langle F\rangle )$, where δ F = F₃ − F₁ is the interquartile range (i.e., 25% of the rupture forces are higher than F₃ and 25% are lower than F₁).

The above results immediately suggest a very simple approach to the analysis of single-molecule data obtained from constant-velocity pulling experiments. If there are sufficient data to construct reasonably “smooth” rupture-force histograms, one can replot these by transforming them into τ(F) following Eq. 2. If limited data allow estimates of only the mean and the variance (or, more robustly, the interquartile range), one can use Eq. 3 to estimate τ(F) over a narrower range of forces.

If flexible molecular linkers are present, Ḟ is a function of F in a constant speed experiment. As shown in Methods, if the pulling apparatus is a harmonic spring with force constant κ_s, moving with velocity υ, and the flexible linker can be described by a worm-like chain (WLC), the force-dependent loading rate Ḟ is accurately given by

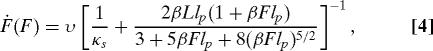where L is the contour length and l_p the persistence length of the WLC linker. The analogous expression for a freely jointed chain has recently been given by Ray et al. (17). The result in Eq. 4 can be used in Eq. 2 to account for the effect of linkers with constant contour length. After this correction, the resulting lifetimes should be the same as those measured in constant-force experiments on the same construct, even though the presence of the linker can influence this lifetime (25).

Application to Experiments.

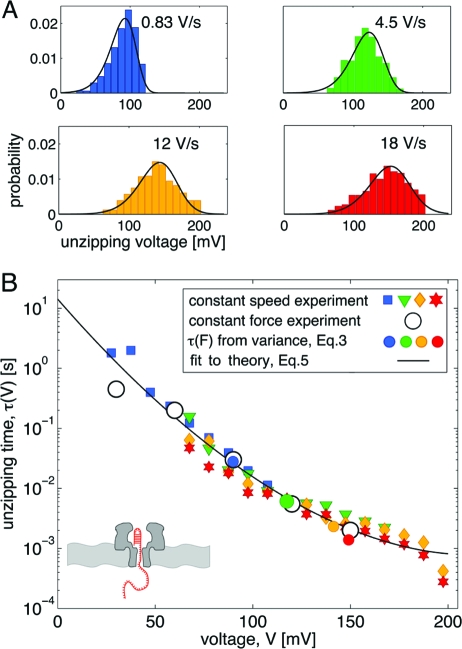
We now demonstrate the utility of Eqs. 2 and 3 by applying them to two experimental datasets. We first validate the methodology by comparing the results for the unzipping of DNA hairpins in a nanopore to those obtained previously by using the full power of the maximum-likelihood method (24). In nanopore force spectroscopy, an applied electric field is used to drive a charged polymer such as DNA through a membrane channel (27,28). The unzipping events are detected by monitoring the increase in the ionic current through the pore. In these experiments, the applied voltage plays the role of the mechanical force. Thus, “rupture-force histograms” are histograms of the unzipping voltage, and the “pulling speed” is the rate at which the voltage is ramped up. In contrast to our previous analysis (24) that fitted all the data (28 histograms), we here use only four selected histograms (Fig. 1A) for voltage-ramp speeds from 0.83 V/s to 18 V/s to show that the procedure also works with a smaller, more typical dataset. Fig. 1B shows the transformation of these histograms to the voltage-dependent lifetime τ(V) using Eq. 2 (see Methods for details). Fig. 1B provides a dramatic illustration of the utility of Eq. 2 for this system. Not only do the τ(V) obtained from histograms at different ramp speeds overlap, but there is also excellent agreement with results obtained independently at constant voltage. Moreover, the τ(V) obtained from the mean and variance by using Eq. 3 are also found to agree with the constant-voltage experiments.

Fig. 1.

Unzipping of DNA hairpins in a nanopore. Experimental data from ref. 28. (A) Unzipping voltage histograms at various voltage-ramp speeds. Black lines are the predicted voltage histograms with parameters extracted from the least-squares fit of Eq. 5 to the collapsed histograms, as shown in B. (B) Lifetime τ(V) of the DNA hairpin as a function of the applied voltage V. The lifetime is obtained by transforming the rupture-voltage histograms (filled symbols, colors as in A) according to Eq. 2. Note the excellent agreement with the lifetimes measured directly at constant voltage (open circles)

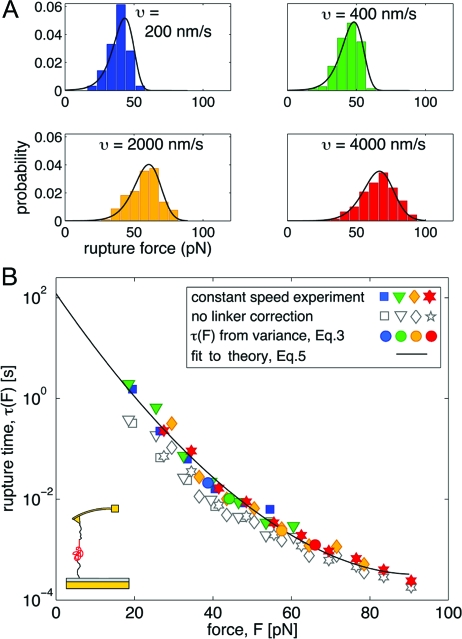
We will now apply the formalism to an AFM protein unfolding experiment. Schlierf and Rief (10,29) measured the unfolding of the immunoglobulin-like domain 4, ddFLN4, from the Dictyostelium discoideum F-actin cross-linker filamin at pulling speeds ranging from υ = 200 nm/s to 4,000 nm/s. The experiments probed the unfolding of a single subunit, ddFNL4, and the analysis is thus not complicated by the combinatorics of having multiple identical domains in the construct. The resulting rupture-force histograms and their transformation by using Eq. 2 are shown in Fig. 2. From the results with correction for the influence of the WLC linker [using Ḟ from Eq. 4 with the WLC parameters L = 79 nm and l_p = 0.5 nm, and κ_s = 4.9 pN/nm from (29)] and without a correction (using Ḟ =κ_sυ), it is evident that the linkers have the most prominent effect at low forces. Indeed, Eq. 4 shows that the effective stiffness is dominated by linkers in the low-force regime, and by the pulling spring in the high-force regime. Fig. 2 also shows that the estimates from the mean and variance of the rupture-force distributions using Eq. 3 agree with the τ(F) from the histogram transformation. Although in this case one does not have independent measurements at constant force, the validity of Eq. 2 is strongly supported by the fact that the histograms, collected over pulling speeds that differ by a factor 20, collapse onto a single master curve.

Fig. 2.

Unfolding of a protein with AFM. Experimental data from ref. 10. (A) Rupture-force histograms at various pulling speeds. Black lines are the predicted rupture-force distributions, Eq. 1, with the parameters of the least-squares fit of Eq. 5 to the collapsed histograms in B. (B) Lifetime τ(F) as a function of the applied force F, obtained by transforming the force histograms in A according to Eq. 2 (filled symbols; colors as in A) with the loading rate Ḟ(F) given by Eq. 4. Open symbols show the transformed histograms without linker correction.

Interpretation of τ(F).

Now that we have been able to extract the force dependence of the lifetime from rupture-force histograms obtained at different loading rates, we turn to the problem of interpreting this dependence in microscopic terms. Let us assume that rupture can be described as escape from a deep one-dimensional free-energy well. For several simple one-dimensional free-energy profiles, the lifetime τ(F) calculated from Kramers theory can then be written as (22):

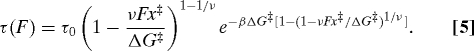In this expression, x^‡ is the distance to the transition state, τ₀ is the lifetime, and Δ G^‡ is the apparent free-energy of activation in the absence of an external force. The scaling factor ν specifies the nature of the underlying free-energy profile (22): ν = 1/2 corresponds to a harmonic well with a cusp-like barrier, or equivalently a harmonic barrier with a cusp-like well; ν = 2/3 corresponds to a potential that contains linear and cubic terms; for ν = 1 Bell's formula is recovered. Equation 5 was derived for forces at which a significant barrier (several k_B T) still exists and it is thus valid only when the force is below a critical force at which the barrier vanishes, F<Δ G^‡/νx^‡. We suggest least-squares fitting ln τ(F) by using Eq. 5 with several values of ν to estimate τ₀, x^‡, and Δ G^‡. If these parameters are insensitive to ν over a ν range that results in a good fit, they can be considered to be independent of the precise nature of the free-energy surface and thus meaningful.

Let us now validate this procedure by applying it to the nanopore-unzipping experiments. It is clear from Fig. 1B that the lifetime depends nonlinearly on the voltage (force) and thus cannot be fit by Bell's formula. By least-squares fitting the data in Fig. 1B with Eq. 5, we find that τ₀ = 14.3 s, V^‡ = 11.1 mV, and Δ G^‡ = 11.9 k_BT for ν = 1/2, whereas τ₀ = 9.6 s, V^‡ = 12.8 mV, and Δ G^‡ = 10.4 k_BT for ν = 2/3. The resulting fit with ν=1/2 is shown in Fig. 1B; the fit with ν=2/3 (not shown) is comparable. How well do these parameters reproduce the original rupture-force histograms? The solid lines in Fig. 1A are the predicted force histograms, obtained by plotting the rupture-force distributions (22) with the parameters extracted from the least-squares fit of Eq. 5 to the collapsed data as described above. It can be seen that both the fit to the collapsed data (Fig. 1B) and the prediction of the force histograms (Fig. 1A) are more than satisfactory, and the extracted parameters are relatively insensitive to ν. In addition, these parameters are close to those previously obtained (24) by applying a more involved global maximum-likelihood method (τ₀ = 20 s, V^‡ = 9.9 mV, and Δ G^‡ = 11.9 k_BT for ν = 1/2, and τ₀ = 8.3 s, V^‡ = 12.7 mV, and Δ G^‡ = 10.5 k_BT for ν=2/3). Thus, in this case, the procedure described here gives essentially the same information as our previous more sophisticated one, but is considerably simpler to implement.

Let us now apply the same procedure to the τ(F) data for protein unfolding in Fig. 2B corrected for linker effects (filled symbols). By least-squares fitting with Eq. 5 we find that τ₀ = 120 s, x^‡ = 1.1 nm, and Δ G^‡ = 15.0 k_BT for ν=1/2, whereas τ₀ = 213 s, x^‡ = 1.1 nm, and Δ G^‡ = 14.7 k_BT for ν=2/3. The solid line in Fig. 2B shows the fit for ν=1/2. We predicted the rupture-force histograms by numerical integration of Eq. 1 with Eq. 5 for τ(F) and Eq. 4 for Ḟ. These predicted histograms, shown by solid lines in Fig. 2A, agree well with the experimental histograms. We note that the parameters produced by least-squares fit of the data in Fig. 2B compare favorably with those reported by Schlierf and Rief (10), τ₀ = 100 s, x^‡ = 1.1 nm, and Δ G^‡ ≈ 19 k_BT, which were obtained in a different and more involved way. We also note that the intrinsic lifetimes obtained by least-squares fitting the data without linker correction (open symbols), τ₀ = 5 s for ν=2/3 and τ₀ = 10$ s for ν=1/2, differ by an order of magnitude from the lifetimes obtained by fitting the data corrected for the linker effect.

Generalization of Bell's Formula in the Framework of Kramers Theory

Interpretation of the force-dependent lifetime data, τ(F), with Eq. 5 is based on particular models of the free-energy profile. We will now show that the force-dependent lifetime data, τ(F), can be used to extract microscopic information independent of the form of the underlying free-energy profile. We will assume that (i) the pulling coordinate is a good reaction coordinate, which is the case when the dynamics along the pulling coordinate is slower than that along any other coordinate, and (ii) one can use Kramers theory of diffusive barrier crossing. As shown in Methods, the following expression can be derived from Kramers high-barrier theory for the force-dependent lifetime:

where we have introduced the notation 〈x^‡(F)〉 to denote the difference in the average positions of the transition state and the bound state along the pulling coordinate as a function of force. An immediate corollary of this relation is that the slope of ln τ(F) vs. F is a direct measure of how the distance between bound state and transition state changes with force. Equation 6 is the generalization of Bell's formula within the framework of Kramers theory, reducing to Bell's formula when 〈 x^‡(F)〉 is independent of F, with the minor difference that our result involves the difference between average locations rather than extrema.

Eq. 6 shows that Bell's formula is accurate only for sufficiently low forces. As the force increases, the distance to the transition state decreases, as can be seen by examining the behavior of any smooth one-dimensional potential. Consequently, Bell's formula is a lower bound to the force-dependent lifetime, τ_Bell(F)≤τ(F), and its uncritical use can lead to significant errors in the estimated intrinsic lifetime τ₀ and the distance to the transition state x^‡.

Multidimensional Free-Energy Surfaces.

At first-sight, Eq. 6 appears to provide a model-independent way to extract microscopic information from pulling experiments, assuming a single transition state. However, this relation only applies if the dynamics along the pulling coordinate is slower than that along any other coordinate, which may not be true in general. Therefore, we will now explore what happens when the pulling coordinate $x$ is not a good reaction coordinate. Interestingly, if the lifetimes at constant force are exponential, then the transformation (Eq. 2) of rupture-force histograms should be valid irrespective of the quality of x as a coordinate. The interpretation of the resulting τ(F), however, becomes more involved.

The simplest extension of the above theory treats pulling on a two-dimensional free-energy surface (31). Let us assume that, in addition to the pulling coordinate, x, there exists another coordinate, Q, that is the true reaction coordinate. Although at this stage Q is unspecified, for the sake of concreteness it is convenient to think of Q as the fraction of native amino acid contacts, which has been shown to be a good reaction coordinate for protein folding (32,33).

In the presence of a force F, the free-energy surface now has the form G(x,Q)= G₀(x,Q)−Fx [supporting information (SI) Fig. S1], where G₀ is the intrinsic surface. If the dynamics is assumed to be diffusive, one can calculate the lifetime by using Langer's multidimensional generalization of Kramers theory (34):

where H(H^‡) is the matrix of second derivatives at the minimum (transition state) and τ₊ is the positive root of the secular equation det(I + τ DH^‡)=0, where I is the unit matrix and D the matrix of diffusion coefficients.

Whereas this procedure is straightforward in principle, it is unnecessary if the dynamics along the pulling coordinate is much faster than along Q. This must be the case indeed if Q is a good reaction coordinate as we are assuming here. One can then integrate out the pulling coordinate and consider the dynamics only along Q in the presence of the appropriate force-dependent potential of mean force. Thus, in this limit, the problem becomes one-dimensional, and one can again apply Kramers theory to a free-energy profile that now depends on Q rather than x.

To make this explicit, let us consider the following two-dimensional free-energy surface where the potential along the pulling coordinate is purely harmonic,

In the context of protein unfolding, G₀(Q) would be a bistable potential with minima at low Q (the unfolded state) and at high Q (the folded state). At each value of Q, the free energy along the pulling coordinate (e.g., the end-to-end distance) is harmonic with curvature ω²(Q) and minimum x₀(Q). Thus, in this model unfolding can never occur along x at fixed Q, which is quite realistic based on the G(x,Q) surface obtained for protein-folding models (35). In general, x₀(Q) could either increase or decrease with Q (depending on whether the ends of a protein are close or far apart in the folded state).

Now if the dynamics along x is much faster than along Q, then we need to consider dynamics only along Q in the presence of an effective potential of mean force,

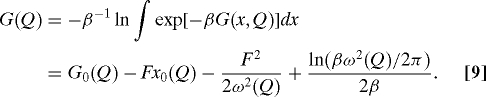To find the force-dependent lifetime, we can use Kramers theory in conjunction with this potential in exactly the same way as for G(x)=G₀(x)−Fx, where the x was assumed to be a good reaction coordinate.

However, the result of these two procedures can be quite different and the multidimensional point of view can lead to a much richer behavior of τ(F) as a function of F. The crucial difference is that the potential of mean force in Eq. 9 does not simply contain a −Fx term, as previously when x was assumed to be a good reaction coordinate. x₀(Q) need not be a linear function of Q, so that the distance x₀(Q^‡(F))−x₀(Q_w(F)) between the extensions at the transition state and in the free energy well need not always be positive and could even change sign. As a consequence, in some cases low forces may actually slow down rupture rather than accelerate it. In addition, the potential of mean force along Q now depends on the square of the force with an amplitude that is given by the width of the end-to-end distribution as a function of Q. Therefore, even if x₀(Q) is constant and the pulling and reaction coordinates are perpendicular, τ(F) depends on F² unless ω²(Q) is constant. Thus, even in this simple two-dimensional model, the force dependence of τ(F) can be more complex than that predicted not only by Bell's formula but also by our expression in Eq. 5. Such behavior has already been observed in protein-unfolding simulations (36), and should be found experimentally as further advances in single-molecule experimental techniques allow both lower- and higher-force regimes to be explored. In fact, in experiments, so-called catch-bonds have been reported in which force initially slows down rupture, before accelerating it at high force (37,38). Our multidimensional generalization indeed allows for the possibility of such nonmonotonic τ(F).

Concluding Remarks

We have described, implemented, and validated a remarkably simple method to directly determine force-dependent lifetimes τ(F) from rupture-force histograms collected at different pulling speeds. An important advantage of our procedure is that it eliminates the need to make model-dependent assumptions about the fiunctional form of τ(F) to analyze rupture-force histograms. We have shown how to account for the influence of flexible molecular linkers so that the resulting lifetimes are the same as those that would be obtained from experiments at constant force on the same construct. Equation 2, which transforms the rupture-force histograms into τ(F), is valid if the rupture-force kinetics at constant force is essentially single-exponential. If this is not the case, data collected at different loading rates would generally not collapse onto a single master curve. Although we explicitly considered irreversible rupture, the formalism is applicable to both forward and reverse transitions, as long as they can be separated, say based on the molecular extension.

Once the force dependence of the lifetime is obtained, either directly from constant-force measurements or by transforming the rupture-force histograms, one is faced with the problem of how to interpret it in microscopic terms. The simplest procedure is to use our formula (22) given in Eq. 5, which contains a single additional parameter compared with Bell's phenomenological expression, namely the apparent free energy of activation. We have shown that if the pulling coordinate is a good reaction coordinate, then, independent of the form of the free-energy profile, τ(F) is completely determined by the force dependence of the distance between the average locations of the transition state and bound state, Eq. 6. Finally, we explored the possibility that, although a good one-dimensional reaction coordinate does exist, it is not the pulling coordinate. In this case, the effective free-energy profile turns out to depend on the external force in a more complex way, leading to a richer (and possibly nonmonotonic) dependence of the lifetime on the force.

Methods

Force Dependence of the Loading Rate.

Suppose that a cantilever with spring constant κ_s moving with velocity V is connected via a flexible linker to the molecule of interest. By using simple force balance, it can readily be shown that the loading rate is given by v/Ḟ=1/κ_s+dI(F)/dF, where l(F) is the force-dependent extension of the linker (16). For a worm-like chain, L is approximately the solution of F=[4l/L−1−(1−l/L)⁻²]/(4β l_p) (39). To obtain the simple analytic expression for Ḟ given in Eq. 4, we calculated the first two terms in the low-force expansion of dl/dF as well as its behavior as F→∞, and constructed a Padé-like expression that interpolates between these limits and is accurate to within ∼ 3.5%.

Transformation of Rupture-Force Histograms into τ(F).

Consider a rupture-force histogram containing N bins of width ΔF that starts at F_o and ends at F_N=F₀+NΔ F. Let the number of counts in the ith bin be C_i, resulting in a height h_i=C_i/(N_totΔ F) with N_tot the total number of counts. Then for k=1, 2, …

Generalization of Bell's Formula by Using Kramers Theory.

Consider diffusive dynamics on a one-dimensional free-energy surface, G(x)=G₀(x)−Fx, where x is the pulling coordinate and G₀ is the free-energy profile in the absence of force. The lifetime is given by the general form of Kramers high-barrier approximation, $\tau (F)=D^{-1}{\displaystyle {\int }_{‡}{e}^{\beta G(x)}dx{\displaystyle {\int }_w{e}^{\mathrm{-\beta }G(x^{\prime })}d{x}^{\prime }}}$, where D is the diffusion coefficient and the integrals are taken over the barrier and well regions of G(x), respectively. For high barriers, the integrals are insensitive to the precise location of the point that divides the well from the barrier. Taking the derivative of the logarithm of τ(F) with respect to F, we have

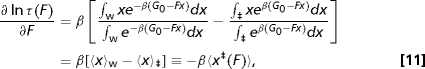where 〈x〉_w and 〈x〉_‡ are the force-dependent average values of x in the well and barrier regions, evaluated with Boltzmann and inverse-Boltzmann weights, respectively. Integration of both sides with respect to F results in Eq. 6.