Probing the origin of tubulin rigidity with molecular simulations

Abstract

Tubulin heterodimers are the building blocks of microtubules, a major component of the cytoskeleton, whose mechanical properties are fundamental for the life of the cell. We uncover the microscopic origins of the mechanical response in microtubules by probing features of the energy landscape of the tubulin monomers and tubulin heterodimer. To elucidate the structures of the unfolding pathways and reveal the multiple unfolding routes, we performed simulations of a self-organized polymer (SOP) model of tubulin. The SOP representation, which is a coarse-grained description of chains, allows us to perform force-induced simulations at loading rates and time scales that closely match those used in single-molecule experiments. We show that the forced unfolding of each monomer involves a bifurcation in the pathways to the stretched state. After the unfolding of the C-term domain, the unraveling continues either from the N-term domain or from the middle domain, depending on the monomer and the pathway. In contrast to the unfolding complexity of the monomers, the dimer unfolds according to only one route corresponding to the unraveling of the C-term domain and part of the middle domain of β-tubulin. We find that this surprising behavior is due to the viscoelastic properties of the interface between the monomers. We map precise features of the complex energy landscape of tubulin by surveying the structures of the various metastable intermediates, which, in the dimer case, are characterized only by changes in the β-tubulin monomer.

The mechanical properties of microtubules (MTs) play crucial roles in processes such as cell division and matrix remodeling induced by mechanical loading of connective tissues. Because of their dynamic instability, i.e., stochastic alternation of slow growth and rapid shrinking phases between MTs and soluble tubulin subunits, MTs are able to transport chromosomes and other cellular organelles inside the cell (1). Blockage of dynamic instability by drugs such as taxol, which reduce the flexibility of the MT structure, promotes mitotic arrest and leads to cell death (2, 3). This behavior makes MTs a main target for cancer drugs (2), but efforts to design effective drugs are hampered, in part, by the lack of clear understanding of the microscopic origin of MT instability and of the MT behavior under tension (4).

MTs are hollow cylinders, with large persistence lengths (5), composed of protofilaments aligned in parallel and joined laterally through mostly electrostatic contacts (6). Each protofilament consists of α-β tubulin dimers assembled in a head-to-tail fashion and joined noncovalently by hydrophobic and polar bonds along the longitudinal axis of the filament. The plus end of a MT is composed of β-tubulin (β-tub), whereas the minus end consists of α-tubulin (α-tub). During interphase, the minus end is attached to the centrosome, whereas the plus end has a GTP cap that contains at least one layer of GTP β-tub (4, 7). In addition, whereas both ends undergo polymerization and depolymerization during dynamic instability, the changes evolve at faster rates at the plus end (8).

The requirements of both rigidity for efficient transport of organelles and flexibility for dynamic growth make MTs an intriguing example of the role played by mechanical stability in the life of the cell. Experiments found that, in vivo, such a delicate balance is maintained because of a variety of factors that modulate the dynamic instability of MTs: GTP hydrolysis (3, 9), molecular motors such as Kin-13 and other microtubule-associated proteins (MAPs), and cofactors such as E and B, which increase the depolymerization rate (10, 11); MAPs such as CLIP-170, which stabilize the MT lattice preventing catastrophes (12); and katanin and spastin, which sever MTs (13). However, in vitro MT dynamic instability occurs under modest conditions: either as a result of GTP hydrolysis (14) or under cold denaturation even in a nonhydrolyzable GMPCPP MT variant (9). Therefore, decoding the role played by the above factors in controlling MT assembly and disassembly requires the understanding of dynamic instability of the pure MT lattice, because this is the substrate over which all their regulatory action is exerted (7).

Cellular factors such as molecular motors, katanin, and spastin induce depolymerization by applying forces on MTs (10, 13). Experiments and theory (15, 16) also showed that MTs are subject to permanent tension due to their dynamic instability, and that additional forces act on MTs when external mechanical perturbations are applied to cells (17, 18). Therefore, to understand MT dynamic instability, it is important to find the range of forces that induce their depolymerization or severing and to uncover the location and extent of the accompanying structural changes. Here, we report results from amino acid level computational investigations of the MT subunits under force. Although the ultimate goal is to understand the force response of the full MT, detailed molecular-level investigations of the MT lattice are not computationally feasible. Our current studies are a step toward this goal. The study of subunits is important for understanding the details of dynamic instability also because MT assembly seems to occur almost exclusively via single-subunit rather than via oligomer addition (7). In Discussion, we relate our study to the behavior of exposed dimers at depolymerizing ends of MTs and to general results pertaining to MT behavior.

Significant progress has been made in understanding the viscoelastic properties of MTs treated as polymeric ensembles of rigid units (19–21), as worm-like chains (WLC) (5) or elastic shells (22, 23). Computational studies (24–26) revealed roles for loops in the stabilization of the MT lattice structure, and that both energetic and entropic factors contribute to the formation of stable arrangements of protofilaments in a MT. However, no details are known about the kinetics of the conformational changes in tubulin dimers when MTs are under tension. Because of their large size and complex tertiary structure, which lead to metastable intermediates, the study of the dynamics of tubulin monomers and of the dimer is challenging. Single-molecule techniques are particularly useful for probing the free-energy landscape of such challenging biomolecules (27–29). Experiments using atomic force microscopy (AFM) (5), scanning force microscopy (SFM) (22), and optical tweezers (7) have been used to probe the mechanical properties of MTs. The SFM study revealed that MTs respond linearly to indentation forces up to ≈400 pN followed by a nonlinear response regime to forces up to ≈1,000 pN. The presence of these forces, which exceed the critical forces of 50–300 pN found in proteins (27, 28), indicates that MTs have unusually large bending rigidity. Because the tubulin subunits have high stiffness (2 GPa) (16), we hypothesize that the deformation of the tubulin heterodimers is responsible for the nonlinear force regime.

We employ molecular simulations of a self-organized polymer (SOP) model (30) to explore the complex unfolding pathways of tubulin subunits at AFM experimental loading rates. Previously, SOP allowed us to unravel the details of the force-unfolding scenarios in the GFP in perfect agreement with experimental findings (29, 30). Our current work shows that, even though both α- and β-tub monomers exhibit complex unfolding behaviors, the dimer follows a unique unraveling pathway under a variety of force conditions. We find that this dramatic shift in the response to tension is the result of an interplay between tension propagation in the structure and the strength of the heterodimer interface.

Results

To evaluate the role played by each component of the dimer (monomers and interface) in the response to tension, we first studied the force behavior of the dimer building blocks, the α and β monomers. This Aufbau-like approach is similar to the one used (31) to probe the strength and the kinetics of tertiary interactions in a RNA complex. Because the structures of the individual tubulin monomers appear unstable in the absence of cofactors (16, 32), and contacts between nonidentical protein subunits can lead to alterations in their mechanical response compared with the isolated monomers (33), the mechanical stability of the heterodimer can be more than the sum of the behavior of its monomers.

Each monomer consists of three domains: the N-term domain from positions 1 to 215, the middle domain from 216 to 384, and the C-term domain from 385 to the C terminus end of the chain (6). The N-term domain consists of six helices (H1 to H6) and six strands (S1 to S6). The N-term domain is connected to the middle domain, which is the taxol-binding domain in β-tub, by the middle helix H7. The middle domain includes helices H7 to H10 and strands S7 to S10. The C-term domain, which contains the MAPs binding sites, spans helices H11 and H12.

Forced Unfolding of Tubulin Monomers Occurs by Bifurcation of Pathways.

To unravel the complexity of the unfolding pathways in tubulin monomers, we performed simulations using the SOP model at two pulling speeds (Methods). From simulations of a large number of trajectories [see supporting information (SI) Table S1), we found that each monomer exhibits a bifurcation in unfolding resulting in two pathways.

Unfolding of α-Tub.

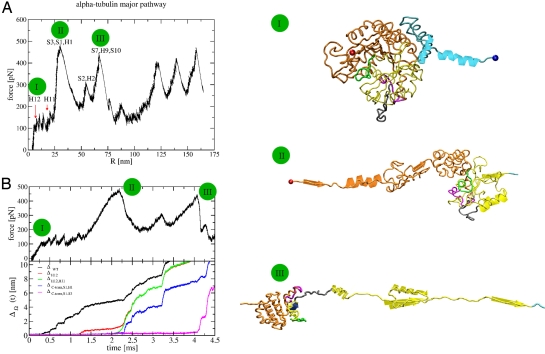
The force extension curves (FECs), depicting the evolution of the force in the chain vs. the extension (R) of the chain, for α-tub on both pathways show multiple peaks (Fig. 1A for the main path and Fig. S1 for the minor path) with similar force values. The major pathway appears in 62% of the 18 lower pulling speed trajectories and in 90% of the 10 faster pulling speed trajectories. To assign the structural changes that accompany the changes in force, we have determined the dynamical changes in the root mean square distances (rmsds) with respect to the intact Protein Data Bank (PDB) (34) structure and with various secondary structures removed. By comparing Δ_WT(t) and Δ_H12(t), we can infer the time when H12 rips from the intact structure by the jump in Δ_WT(t), whereas Δ_H12(t) would remain flat. Here, Δ_WT(t) is the rmsd in relation to the 1tub structure and Δ_H12(t) is the rmsd with respect to the folded structure with H12 removed (see ref. 29 and Methods for details). The graphs in Fig. 1B depict the time evolution of the force in the chain and the corresponding behavior of the various Δ_Ω along the major pathway at v = 19 μm/sec. H12 starts to open at t ≈ 0.35 msec as indicated by a small abrupt increase in Δ_WT. This event is followed by a series of stepwise jumps of ≈3Å in Δ_WT indicating that H12 unfolds noncooperatively. Similarly, comparison of Δ_H12 and Δ_H12H11 shows (Fig. 1B) an increase in Δ_H12 at t ≈ 1.25 msec corresponding to the unfolding of H11. Next, at t ≈ 2.2 msec, S1, H1, and S3 from the N-term domain unravel simultaneously under a force of ≈480 pN, which leads to an increase of 22 nm in R. Right afterward (at t ≈ 2.4 msec), H2 and S2 also unfold. At t ≈ 4 msec, S7, H9, and S10 unravel, increasing R by 23 nm. At the same time, H10, S8, and S9 detach from the rest of the structure while still being folded. After this event, the rmsds of the WT and the various substructures increase greatly and are accompanied by the deformation of the still folded structure. Applying the procedure detailed in (29, 30), we find that at this time in excess of 55% of the hydrophobic residues are exposed to the solvent. As a result, additional intermediates, which are resolvable in simulations, would have lifetimes too short for experimental detection. Thus, our simulations predict that, along the major pathway of α-tub, there are five detectable peaks that correspond to intermediates α-tubI1 = α-tubΔH12, α-tubI2 = (α-tubI1,ΔH11), α-tubI3 = (α-tubI2,Δ[S1,H1,S3]), where the square brackets indicate that all of the structures S1, H1, and S3 rip simultaneously, α-tubI4 = (α-tubI3,Δ[S2,H2]), and α-tubI5 = (α-tubI4,Δ[S7,H9,S10]).

Fig. 1.

Major unfolding pathway for α−tub. (A) The FEC is on the left. The C-term domain unfolds first, indicating that this is the most flexible region of the molecule. Pictures of unraveling conformations at three stages (marked with green circles on the FEC) are shown on the right. Elements that unravel are in diagram representation. The colors are: cyan, C-term domain; yellow, middle domain; orange, N-term domain; red sphere, N-term end; blue sphere, C-term end; magenta, taxol-binding pocket; gray, M-loop; green, T7-loop. The segment (S8,H10,S9) (depicted as a whole in III) opens only at the very end. For clarity, some unfolded parts are not shown. (B) Time-dependent changes in the force (Upper) and [ΔΩ(t)] (Lower). [ΔΩ(t)] indicates changes in structural elements. Ω in the black, red, green, blue, and magenta curves corresponds to WT, H12, C-term domain (both H12,H11) (S1,H2), and (S2,H2,S3), respectively. All of the snapshots were produced with VMD (42).

The unfolding pathway in the remaining trajectories differs from the one above (Fig. S1). The difference between the two pathways arises in the fifth peak, which now corresponds to the unfolding, at t ≈ 4.1 msec, of H3. The other elements that open are S4 and H4 at t ≈ 4.5 msec, and S5 at t ≈ 4.8 msec. Therefore, the increase in R in the fifth peak is 27 nm. Any additional peaks will not be discernible experimentally, because the structure deforms. Thus, in the minor pathway, we predict that there should be five discrete metastable intermediates, namely, α-tubI1 to α-tubI4 from above, and α-tubI5 = (α-tubI4,Δ[H3−S5]).

We find that both pathways start with the opening of the C-term domain, followed by the unraveling of the first α-helix and β-strand (H1 and S1) and strand S3 from the N-term end of the chain. The bifurcation in unfolding, which occurs after S2 and H2 unfold as well, is characterized by the continuation of unraveling from the N-term domain along the minor pathway and by a switch to unraveling from the middle domain along the major pathway.

Unfolding of β-Tub.

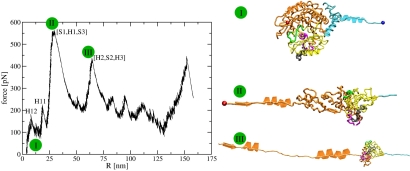
The FECs for β-tub on both pathways, at v = 19 μm/sec, show multiple peaks (Fig. 2 for main pathway and Fig. S2 for minor pathway). The major pathway appears in 94% of the 16 lower pulling speed trajectories and 95% of the 20 faster pulling speed trajectories. Fig. S3 depicts the time evolution of the force in the chain and the corresponding behavior of the various Δ_Ω functions along the major pathway. In the major pathway, H12 opens cooperatively at t ≈ 0.5 msec followed, at t ≈ 1.1 msec, by the unraveling of H11. Next, at t ≈ 2.3 msec, S1, H1 and S3 at the N-term end of the chain unfold under the maximal force of ≈550 pN leading to an increase of 22 nm in R. At t ≈ 4 msec, H2, S2 and H3 unfold. Additional intermediates present in the computational FEC would not to be detectable experimentally. Thus, our simulations predict that, for the major pathway of β-tub, there are four detectable peaks corresponding to intermediates β-tubI1 = β-tubΔH12, β-tubI2 = (β-tubI1,ΔH11), β-tubI3 = (β-tubI2,Δ[S1,H1,S3]), and β-tubI4 = (β-tubI3,Δ[H2,S2,H3]).

Fig. 2.

Major unfolding pathway of β-tub. The FEC is in the left. The right depicts unfolding snapshots using the convention in Fig. 1.

The unfolding pathway in the remaining trajectories differs from the major pathway (Fig. S2). The difference between the pathways arises in the third peak, which now corresponds, beyond the unfolding of S1, to the detachment, at t ≈ 2.2 msec, of the middle domain from the rest of the structure, and the unfolding of the S7 to H9 segment and of S9 and S10 elements under a 560 pN force. These unfolding events lead to a gain of 23 nm in R. The split of the structure between the N-term and the middle domain is accompanied, at t ≈ 2.8 msec, by the unfolding of the T7 loop and the H8 helix, which increase R by ≈9 nm. Additional peaks will not be discernible experimentally. Thus, in the minor pathway we predict that there are four intermediates, namely, β-tubI1, β-tubI2 from above, β-tubI3 = (β-tubI2,Δ[S1,S7−H9,S9,S10]), and β-tubI4 = (β-tubI4,ΔH8).

In short, both pathways start with the opening of the C-term domain, followed by the unraveling of the first β-strand from the N-term end of the chain. The bifurcation, occurring after this point, leads to the continuation of the unraveling of the chain from the N-term end (i.e., from H1) along the major pathway and to a switch to unfolding from the loop connecting the middle domain with the N-term domain in the minor pathway.

Comparison between the FECs of the two monomers reveals that the first peaks corresponding to both pathways in α-tub and to the major pathway in β-tub are almost identical. Among the common structural segments are the loop connecting H1 with S2, which opens between the third and fourth peaks of the FEC, together with S3, which opens during the highest force peak, and H2, which unwinds during the fourth peak. These elements form lateral contacts with another tubulin subunit in a protofilament (35). Therefore, our finding, in agreement with previous studies (24), that they are mechanically flexible in both monomers is likely to be a requirement for the formation of the lateral contacts in protofilaments.

We also found that H3 of β-tub, which forms the longitudinal interactions between dimers in protofilaments (35), is more flexible than H3 of α-tub. For example, although in β-tub H3 opens along the major pathway, in α-tub, it opens only during the minor path. This asymmetry in the behavior of H3 between the two monomers is probably required to achieve the optimal orientation of the longitudinal contacts.

Forced Unfolding of the Tubulin Heterodimer Occurs by a Unique Pathway.

The topology of the dimer involves, in addition to the 6 domains of the monomers, an extensive interface with 92 nonbonded contacts between the monomers. Therefore, care needs to be used when conducting pulling studies of the dimer. First, because tension propagates mainly through covalent bonds, we used a cross-linked mutant designed following recent experiments (31) to circumvent some of the problems in probing interfaces (36). Operationally, we simulated a dimer where the C-term end of α-tub is linked to the N terminus of β-tub through a long (31 positions) and flexible linker built (37) such as not to disrupt the dimer conformation. Second, to account for the influence of the point of application of force on the occurrence of a pathway, we pulled the dimer in three different ways (Methods). From simulations of a number of trajectories (Table S1), we found that the heterodimer exhibits a unique unfolding pathway independent of the pulling speed and the manner of application of force.

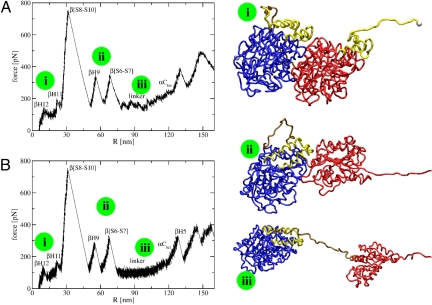
The dimer FEC presents multiple peaks (Fig. 3A for v = 19 μm/sec). Fig. S4 depicts the time evolution of the force in the dimer and of the various Δ_Ω functions along the unfolding pathway. The unfolding starts when H12 from β-tub opens cooperatively at t ≈ 0.47 msec. Next (at t ≈ 0.6 msec), H11 from β-tub unravels. After a substantial delay, at t ≈ 2.5 msec, S10, S9, S8, and H10 from β-tub unravel. The force required to unfold these elements is very large (750–800 pN). This is followed, at t ≈ 3.2 msec, by the unfolding of H9 from β-tub and, at 3.8 msec, by the unfolding of the S6 to S7 segment also from β-tub. At t ≈ 4 msec, the linker opens noncooperatively in over 1.5 msec. Afterward, the dimer ceases to exist. Thus, our simulations predict that there are five detectable peaks along the pathway of unfolding of the tubulin dimer. They correspond to intermediates dimerI1 = β−tub ΔH12, dimerI2 = (dimer I1,β−tub ΔH11), dimerI3 = (dimerI2,β−tub Δ[S8−S10]), dimerI4 = (dimerI3,β−tub ΔH9), and dimerI5 = (dimerI4,β−tub Δ[S6−S7]).

Fig. 3.

FECs for the unfolding pathway in the α−β dimer. (A) Fast pulling speed conditions. (B) Slow pulling speed simulations. Pictures of the molecules at different stages (marked with green circles on the FECs) are shown on the right. The colors are: blue, α-tub; golden, linker; red, β-tub; yellow, C-term domains from both monomers; white spheres, C-term end of β-tub and N-term end of α-tub.

In conclusion, the unraveling starts in the β-tub with the opening of the C-term domain, followed by the unfolding of the S8 to S10 segment from the middle domain. The last detectable step corresponds to the unraveling of the S6 to S7 elements, which connect the middle domain with the N-term domain. Therefore, when the linker that connects the two monomers opens, only the C-term domain and most of the middle domain of β-tub are unfolded.

Discussion

In this study, we dissect the unfolding paths and intermediate structures of MT subunits. The major mechanical unfolding event in both monomers and the tubulin dimer proceeds from an intermediate structure tub ΔH12,ΔH11, where the two α-helices that constitute the C-term domain are detached from the rest of the structure. From here, the unfolding occurs via additional intermediates that depend on the system and on the pulling speed. We find that our FECs deviate from a WLC behavior, because interactions between the elements that unravel lead to unfolding intermediates. Such intermediates usually induce deviations from the all-or-none entropic elasticity behavior predicted by the WLC model (28).

The unfolding of α-tub in the dimer occurs only after the dimer interface unravels. Because this behavior is preserved even along trajectories where the force is applied directly at the N-term end of the α-tub (Fig. S5), the absence of this pathway cannot be attributed to the lack of tension propagation in the dimer. In addition, this is not an artifact of the linker. An advantage of the linker is that, because it covalently binds the monomers, it enhances the propagation of the applied force from one monomer to the other. A disadvantage is that its flexibility leads (38) to an increase in the unfolding force of α-tub. However, in the WT dimer, the C-term end of α-tub is free and has reduced coordination with the rest of the structure. As a result, this chain end cannot align along the direction of the applied force and will remain folded. Simulations of the dimer performed without the linker and according to the three pulling set-ups from Methods yielded the same pathway of unfolding and range of forces as in the presence of the linker (data not shown).

The reason why the unfolding of the dimer never starts from α-tub is the presence of the dimer interface. Both unfolding paths in α-tub start with the opening of the C-term domain, followed by the unraveling of the N-term domain. The loop connecting the two helices at the C-term end of α-tub is buried at the dimer interface, which increases its stability (24). The interface includes also the fragments S2, H2, and S3, which open in the third and fourth peaks of the α-tub FEC. Therefore, because of the stabilization provided by the interface, opening of α-tub is unlikely while the interface is still formed. Based on these findings, we propose that stabilization of the C-term end of β-tub by reduction of its solvent accessibility similarly to the burial of the C-term domain of α-tub in the dimer interface can prevent the unfolding of the dimer under forces smaller than 200 pN. Our proposal is supported by the fact that MAPs with a role in the stabilization of the protofilament structure bind to the C-term domain (35).

The dimer unfolds following the same pathway regardless of the manner of application of force. However, along trajectories where the force is applied only to the N-term end of the α monomer, there is, compared with the other two pulling setups, an increase in the critical force (Fig. S5). For example, the force required to open H12 increases from ≈130 to ≈250 pN. The increase in force is because of a delay in tension propagation. The value of the critical force that unfolds a given segment is proportional to k v τ, where τ is the characteristic time for force to reach the protein segment and k v is the loading rate (38). When the force is applied at the N-term of α-tub, instead of the C-term of β-tub, it takes longer to propagate to the H12 helix of β-tub (τ ≈ 0.35 msec when applied at C-term of β-tub and τ ≈ 0.7 msec when applied to N-term of α-tub). Consequently, the force to unravel this helix increases as well.

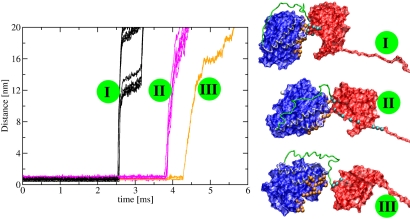
The 800 pN maximal force required to open the dimer exceeds the maximal forces in the α (400 pN) or the β monomer (500 pN). The interface between the monomers is responsible for this 300–400 pN force increase. A recent survey of rupture forces in >30 protein pairs (36) revealed values between 10 and 1,000 pN. The value of ≈300–400 pN obtained in our simulations for the rupture of the dimer interface is most similar to the force required to break interactions between adhesion molecules and their ligands (39). Following the time evolution of the 92 intermonomer contacts, we discovered that the interface opens in three steps, where each step is characterized by the simultaneous unzipping of a set of contacts (Fig. 4). Comparison with Fig. S4 indicates that the interface is completely broken after the dimerI5 intermediate. The first set of contacts to break, at t ≈ 2.5 msec, consists of 56 contacts (63%) between positions in either S9 or H10 in β-tub and the T5 loop in α-tub. This finding correlates very well with the fact that in the corresponding peak from the FEC, dimerI3, S9, and H10 unravel. This first set consists also of contacts between positions in the loop connecting H10 with S10 in β-tub and the C-term end of helix H11 in α-tub (positions 393–398). The second set of contacts, opening at t ≈ 3.8 msec, consists of 28 contacts (30%) between either the T7 loop or the helix H8 from β-tub and positions from loops in the N-term domain of α-tub. Additionally, contacts between the loop connecting H8 with S7 in β-tub and the loop between H11 and H12 in α-tub break at this time. Shortly afterward, i.e., at t ≈ 4.0 msec, the remaining 8 contacts open. At this time the contacts between the N terminus end of β-tub and the loop between S3 and H3 in α-tub break. A consequence of our findings is that the dimer is able to withstand unusually large forces up to 800 pN before undergoing major conformational changes. This conclusion reinforces our proposal that the nonlinear part of the force regime in the SFM experiments on MTs (22) is because of nonlinear elastic deformations in the tubulin dimers. Also, our result that the enhanced resistance to force of the heterodimer is largely due to interface contacts is likely to be generic. For example, experiments found that, during chemical denaturation, the first unfolding event is the dissociation of the heterodimer into monomers (40) and the structures of the monomers can be damaged in this process (32).

Fig. 4.

Evolution of contacts at the dimer interface during dimer unfolding. On the left, we plot the distance between selected contact residues from the α- and β-tub vs. time. The contacts unzip in 3 steps (colored in black, magenta, and orange). The corresponding dimer structures are depicted in surface representation on the right. The colors are: blue, α-tub; green, linker; red, β-tub; yellow, C-terminal regions of both monomers; white spheres, C-term end of β-tub and N-term end of α-tub; orange spheres, residues from the α-tub involved in the interface contacts; cyan spheres, residues from the β-tub involved in the interface contacts.

In our simulations, only a part of β-tub unravels before the breaking of the dimer interface. We predict that a similar behavior will be found in exposed dimers at the plus end of MTs. Our prediction is based on two arguments. First, because the lateral contacts between β-tub monomers in adjacent protofilaments involve mostly the M-loop between S7 and H9 (6, 25) and, in our simulations, this loop unravels only after the dimer interface opens, the additional stability conferred by the MT lattice to the M-loop will preserve the order of unfolding events leading to the opening of the interface. The second reason is based on the stable and extensive longitudinal contacts between dimers from the same protofilament. Because these contacts are formed at the α-tub end of the dimer, which remains unperturbed in all of the dimer simulations, they will not alter the unraveling of β-tub in the MT lattice compared with the soluble dimer case.

As mentioned above, MT growth and depolymerization proceed predominantly from the plus end. This is especially true in MTs from mitotic spindles, which are under increased tension (2). Our results can shed light on the advantages of the asymmetry between the ends of MTs. Because the depolymerization phase is favored under tension (16), it should occur with highest frequency from the end that responds fastest to force. Our simulations show that this is always β-tub, i.e., the plus end of the MTs. Consequently, we propose that MTs can act as mechanical force sensors.

Methods

SOP Model.

We used a topology-based model for tubulin in which each amino acid in the PDB entry 1tub is represented by its C_α atom (30). The total energy function for a conformation, specified in terms of the coordinates {r_i} (i = 1,2,… N), where N is the number of residues is

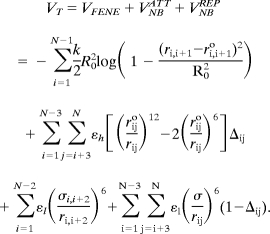The distance between two neighboring interaction sites i and i + 1 is r_i,i+1 and r_i,i+1^o is its value in the native structure. The finite extensible nonlinear elastic (FENE) potential (first term in Eq. 1) describes the backbone chain connectivity. The second term in Eq. 1 accounts for the interactions that stabilize the native state. If the noncovalently linked beads i and j for i−j >2 are within a cut-off distance R_C (i.e., r_ij<R_C) then Δ_ij = 1. If r_ij>R_C, then Δ_ij = 0. A uniform value for ε_h, which specifies the strength of the nonbonded interactions, is assumed. All nonnative interactions (third and fourth terms in Eq. 1) are repulsive (see Table S2 for the value of the parameters in the energy function).

Simulations.

We performed Brownian dynamics simulations at T = 300K (41) to generate the mechanical unfolding trajectories. To estimate the simulation time scale, we used 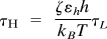with τ_L = 2 ps and ζ = 50τ_L−¹ for the overdamped limit. Following the typical AFM experimental setup, the C-terminal end of each monomer was stretched at two constant pulling speeds (v = 1.9 μm/s and v = 19 μm/s) while keeping the N-terminal end fixed. The cantilever spring constant was k_s = 35 pN/nm, which is in the range of (1–100) pN/nm used in the AFM experiments. For the dimer simulations we used three different pulling setups: (i) pulling at the C-term end of β-tub while keeping the N-term end of α-tub fixed; (ii) pulling at the N-term end of α-tub while keeping the C-term end of β-tub fixed; and (iii) pulling at both the N-term end of α-tub and C-term end of β-tub at the same time with the same pulling speed and in opposite directions. The simulations corresponding to the first setup were conducted at the two pulling speeds from above, while the remaining set-ups were carried out only at the higher pulling speed.

Assigning Structures of Intermediates by Comparing Global and Partial rmsds.

We compared the time-dependent changes in the global [Δ_WT(t)] partial rmsds [Δ_Ω(t)] to compute the time when a secondary structural element detaches from the folded tubulin structure. Here, Δ_WT(t) for a conformation at t is calculated with respect to the PDB structure of tubulin while Δ_Ω(t) is calculated with respect to the folded structure in which the secondary structural element Ω is removed (29). By varying Ω we can pinpoint the structure and the lifetimes of specific intermediates.