ESPD: a pattern detection model underlying gene expression profiles

Abstract

Motivation

DNA arrays permit rapid, large-scale screening for patterns of gene expression and simultaneously yield the expression levels of thousands of genes for samples. The number of samples is usually limited, and such datasets are very sparse in high-dimensional gene space. Furthermore, most of the genes collected may not necessarily be of interest and uncertainty about which genes are relevant makes it difficult to construct an informative gene space. Unsupervised empirical sample pattern discovery and informative genes identification of such sparse high-dimensional datasets present interesting but challenging problems.

Results

A new model called empirical sample pattern detection (ESPD) is proposed to delineate pattern quality with informative genes. By integrating statistical metrics, data mining and machine learning techniques, this model dynamically measures and manipulates the relationship between samples and genes while conducting an iterative detection of informative space and the empirical pattern. The performance of the proposed method with various array datasets is illustrated.

1 INTRODUCTION

DNA arrays provide simultaneous readouts for the expression levels of thousands of genes in samples (DeRisi et al., 1996). Innovative techniques to efficiently and effectively analyze these rapidly growing data are required, which will have a significant impact on the field of bioinformatics.

The raw array images are transformed into gene expression matrices where the rows usually represent genes and the columns represent samples. It is meaningful to cluster both genes and samples in gene expression data (Brazma and Vilo, 2000). Co-expressed genes can be grouped based on their expression patterns (Eisen et al., 1998) and in such gene-based clustering, the genes are treated as the objects, while the The samples can be partitioned into homogeneous groups and each group may correspond to a particular macroscopic phenotype, such as the present or absent clinical syndromes or cancer types (Golub et al., 1999). Thus, sample-based clustering regards the samples as the objects and the genes as the attributes. To group samples to reveal their macroscopic phenotypes is regarded as the process of empirical sample pattern detection.

In typical array datasets, the volume of genes and the number of samples are very different, e.g. 10¹–10² samples versus 10³–10⁴ genes. Gene- and sample-based methods therefore face very different challenges. Techniques that are effective for gene-based clustering, e.g. CAST (Ben-Dor et al., 1999), MST (Xu et al., 2002), HCS (Hartuv and Shamir, 2000), and CLICK (Shamir and Sharan, 2000), are not necessarily adequate for analyzing samples.

The existing methods of grouping samples fall into two major categories: supervised analysis and unsupervised analysis. The supervised approach assumes that phenotype information is attached to the samples and that biological samples are labeled, e.g. as being diseased versus normal. The major supervised analysis methods include the neighborhood analysis (Golub et al., 1999), the support vector machine (Brown et al., 2000), the tree harvesting method (Hastie et al., 2001), the decision tree method (Zhang et al., 2001), the genetic algorithm (Li et al., 2001), the artificial neural networks (Khan et al., 2001), a variety of statistical approaches (Jiang et al., 2001; Thomas et al., 2001) and rank-based methods (Park et al., 2001). In these methods, a subset of samples is used as the training set to select a small percentage of informative genes (around 50–200) which manifest the phenotype distinction of the training samples: finally, the whole set of samples is classified based on the selected informative genes.

We will focus on unsupervised sample pattern detection which assumes no phenotype information being assigned to any sample. Since the initial biological identification of sample phenotypes has been slow, typically evolving through years of hypothesis-driven research, automatically discovering sample pattern presents a significant contribution in array data analysis (Golub et al., 1999). Unsupervised sample pattern detection is much more difficult than supervised manner because the training set of samples, which can be utilized as a reference to guide informative gene selection, is not available. Many mature statistical methods such as t-test, Z-score (Thomas et al., 2001), and Markov filter (Xing and Karp, 2001) cannot be applied without the phenotypes of samples being known in advance. Thus identifying informative genes and empirical partition of samples become very challenging problems.

In this paper, we tackle the problem of unsupervised sample pattern detection by developing a novel analysis model called empirical pattern detection (ESPD) which includes a series of statistics-based metrics and iterative adjustment. We claim the following contributions.

• A formalized problem statement of ESPD of sparse high-dimensional datasets is proposed. Major differences from traditional clustering or recent subspace clustering problems are elaborated.

• A series of statistics-based metrics incorporated in unsupervised empirical pattern discovery are introduced. These metrics delineate local pattern qualities to coordinate between sample pattern discovery and informative genes selection.

• An iterative adjustment algorithm is presented to approach the optimal solution. The method dynamically manipulates the relationship between samples and genes while conducting an iterative adjustment to approximate the informative space and the empirical pattern simultaneously.

• An extensive experimental evaluation over real datasets is presented. It shows that our method is both effective and efficient and outperforms the existing methods.

The remainder of this paper is organized as follows. Section 2 gives the problem description and the pattern quality metrics while the algorithm is presented in Section 3. Experimental results appear in Section 4. The related work and concluding remarks are in Section 5.

2 THEORY AND METHODS

2.1 Problem statement

Let 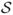= {s₁, s₂, …, s_m} be the set of samples and 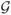= {g₁, g₂, …, g_n} be the set of genes. The data matrix can be represented as 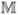= {w_i,j |i = 1 ~ n, j = 1 ~ m}(n ≫ m), where w_i,j corresponds to the value of the sample s_j on gene g_i.

Problem

Given a data matrix 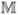and the number of samples’ phenotypes 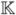, our goal is to find 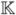mutually exclusive groups of the samples matching their empirical phenotypes and to find the set of genes which manifests the meaningful pattern.

Examples

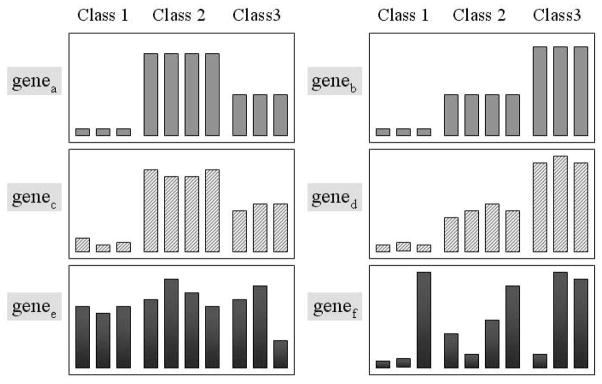
Figure 1 is a simplistic illustration of the gene expression patterns in an array dataset with three empirical phenotypes ( 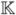= 3), labeled as ‘Class 1’, ‘Class 2’ and ‘Class 3’. The goal of analyzing such datasets is to discover these three classes of the samples and to identify a set of genes that manifests this class structure. In Figure 1, gene_a and gene_b show the idealized expression patterns: there are no noise and the expression levels of the genes are low for one class of samples, intermediate for another class and high for the third class. Gene_c and gene_d include noise but the genes expression patterns are quite similar to gene_a and gene_b and the variance is relatively small. Because such genes provide ‘good’ information for correctly grouping samples, they are regarded as informative genes. The gene expression patterns of gene_e and gene_f are noisy, have high variance and cannot be used to distinguish between sample classes. Genes with such patterns are called non-informative genes.

Fig. 1.

Examples of the gene expression patterns across three sample classes. The first 3 samples belong to Class 1, the second 4 samples to Class 2 and remainder to Class 3.

Definition 1

Each group of a partition of samples is called a base. The partition of samples matching the empirical phenotypes of the samples is called samples’ empirical pattern. Thus the empirical sample pattern is formed by 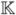intra-similar and well-separated bases.

Definition 2

An informative gene is a gene which manifests empirical sample pattern. Thus, each informative gene should display approximately invariant signals in each base and highly differential signals for the samples in different bases. The whole set of informative genes is called informative space.

Challenges

The real world applications are complex. The values within data matrices are all unlabeled real numbers and an obvious boundary between informative genes and non-informative genes is not readily accessible. The following two major reasons make it very hard to detect the empirical sample pattern and informative space by unsupervised methods.

• The volume of genes is very large while the number of samples is very limited. No distinct class structures of samples can be properly detected by the existing techniques (e.g. density based approaches).

• Most of the genes collected are not informative. A small percentage <10% (Golub et al., 1999) of genes that manifest phenotypic sample patterns are buried in a large amount of noise. This makes it difficult to construct an informative space.

2.2 Statistics-based metrics

We use a series of statistics-based metrics to capture the pattern steadiness within each base and dissimilarity between different bases to detect the empirical pattern and to search the informative space.

Let S_y ⊆ be a base, G_x ⊆ be a subset of genes, and M_x,y = {w_i,j| i ∈ G_x, j ∈ S_y} be the corresponding sub-matrix with S_y projected on G_x.

2.2.1 Intra-pattern-steadiness

Definition 3

The intra-pattern-steadiness of a base projected on a set of genes is measured by the average row variance [indicated by ℛ (x, y)] of the corresponding sub-matrix.

The general formula is

$$\begin{array}{l}\Re (x,y)=\frac{1}{\mid G_x\mid }\sum _{i\in G_x}\frac{{\sum }_{j\in S_y}{(w_{i,j}-{\overline{w}}_{i,S_{\gamma }})}^2}{\mid S_y\mid -1},\\ =\frac{1}{\mid G_x\mid ·(\mid S_y\mid -1)}\sum _{i\in G_x}\sum _{j\in S_y}{(w_{i,j}-{\overline{w}}_{i,S_y})}^2,\end{array}$$ (1)

where w̄_i,Sy = (Σ_j∈Sy w_i,j)/|S_y|, is the mean value of samples in S_y. The variance of each row measures the variability of a given gene within the base. Low average row variance value indicates that the expression of a group of genes is relatively invariant. Thus the lower the average row variance, the stronger the pattern-steadiness exhibited by the gene group across the samples in the base.

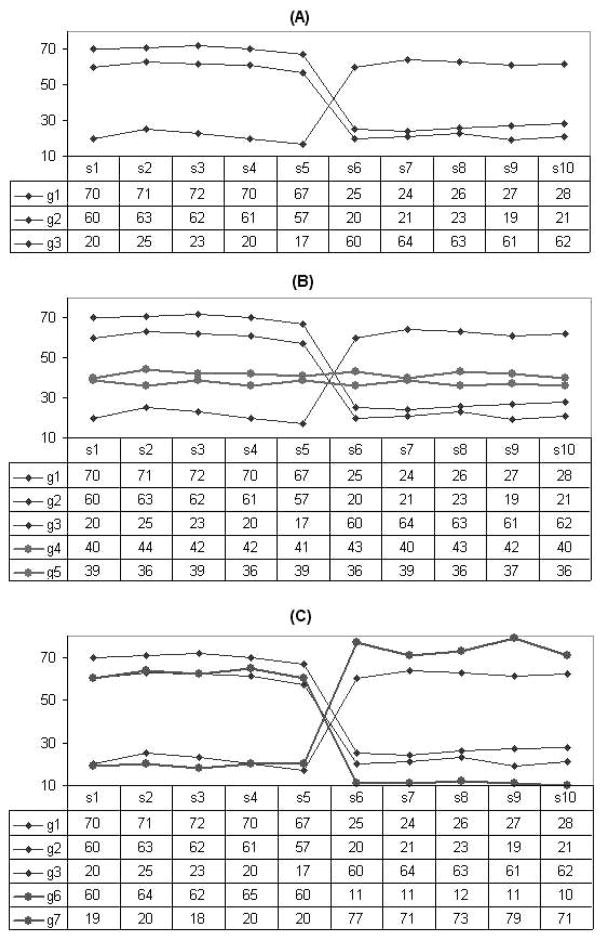
In Table 1, we compare the effect of average row variance with two typical local pattern similarity metrics such as the residue (used by Yang et al., 2002) and mean squared residue (used by Cheng and Church, 2000). Figure 2 shows two sets of genes over a base of six samples. All above measurements are calculated on these two bases. The smaller the values of the metrics, the more similar the genes. Both residue and mean squared residue strongly suggest that the genes in Figure 2A are more similar to each other than the genes in Figure 2B. However, the genes in Figure 2B display approximately invariant signals on the base and are more informative than genes in Figure 2A for manifesting the empirical sample pattern. Only the average row variance is adequate for intra-pattern-steadiness metric.

Table 1.

Comparision of different pattern similarity for the synthetic datasets of Figure 2

Measurement	Data (A)	Data (B)
Residue	0.20	0.45
Mean squared residue	0.05	0.40
Average row variance	339.07	5.30

Fig. 2.

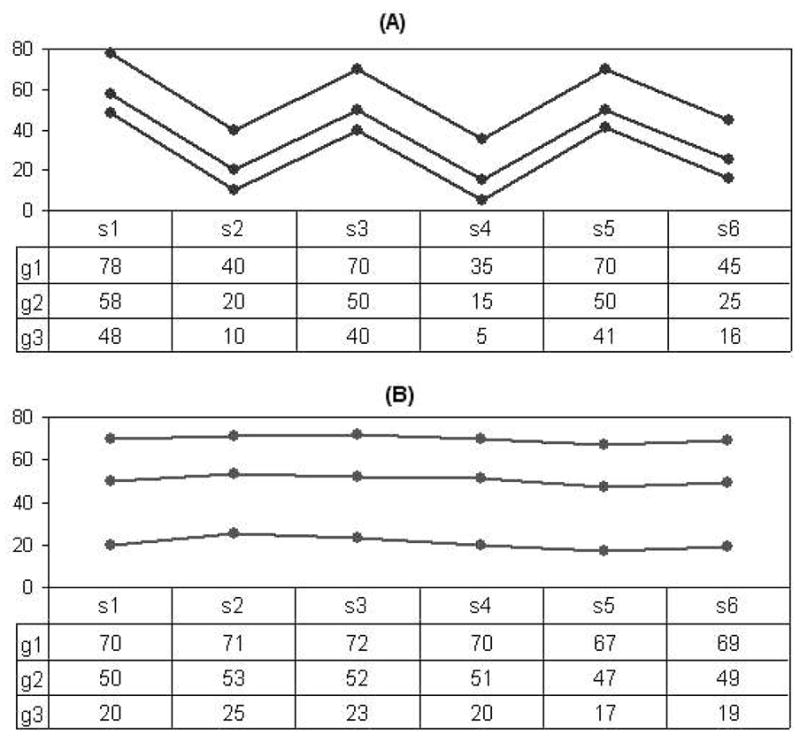
An example showing the performance of the intra-pattern-steadiness metric.

2.2.2 Inter-pattern-divergence

Definition 4. Inter-pattern-divergence of two different bases (denoted as S_y and S_y′) projected on the same subset of genes (denoted as G_x ) is measured by the average block distance [indicated by (x, y, y′))] which is expressed by the following formula:

$$\mathfrak{D}[(x,y,y^{\prime }])=\frac{{\sum }_{i\in G_x}\mid {\overline{w}}_{i,S_y}-{\overline{w}}_{i,S_y^{\prime }}\mid }{\mid G_x\mid },$$ (2)

where w̄_i,Sy is the mean value of samples in S_y on gene i and w̄_{i, S′y} is the mean value of samples in S′_y on gene i. The average block distance is normalized by |G_x| to avoid the possible bias due to the volume of genes.

2.2.3 Pattern quality

Definition 5

The pattern quality of a sample partition which contains 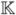bases ({S_y1, S_y2,…, S_y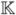}) on a set of genes G_x is measured by the reciprocal of the accumulation of the pairwise square-root of intra-pattern-steadiness divided by inter-pattern-divergence between each pair of bases.

The formula for this pattern quality (Ω) is:

$$\mathrm{\Omega }=\frac{1}{{\sum }_{S_y,S_{y^{\prime }}}\frac{\sqrt{\Re (x,y)+\Re (x,y^{\prime })}}{\mathfrak{D}(x,(y,y^{\prime }))}},$$ (3)

where S_y ∩ S_y′ = ∅.

The purpose of pattern discovery is to identify the empirical pattern where the patterns inside each base are steady and the divergence between each pair of bases is large. As indicated by Equation 3, a large value of pattern quality is expected for qualifying empirical pattern and informative genes.

Figure 3 shows three gene sets on the same set of samples of two bases, the horizontal axis shows the samples. Table 2 gives the intra-pattern-steadiness, inter-pattern-divergence and pattern quality measurements of the datasets shown in Figure 3. The dataset in Figure 3A includes three genes which manifest the pattern reflected by the two bases. The dataset in Figure 3B includes all genes within (A) plus two more genes (g4 and g5) which show low variance within each base. The new genes show less divergence between two bases so that they do not manifest the pattern. The overall pattern quality therefore become lower, thus the two new genes should not be included into the informative space. The dataset in Figure 3C is also constructed from Figure 3A by adding two more genes (g6 and g7) which show both low variance and large divergence. Table 2 shows the overall pattern quality become higher (from 14.27 to 15.35), thus the pattern became better by including them (g6 and g7) into the informative space. Therefore the dataset in Figure 3C is the best among these three datasets measured by pattern quality.

Fig. 3.

An example showing the effect of the pattern quality metric. Samples s1–s5 belong to one base and s6–s10 are in the other base.

Table 2.

The intra-pattern-steadiness, inter-pattern-divergence and pattern quality values for the datasets of Figure 3

Measurement	Data (A)	Data (B)	Data (C)
Intra-pattern-steadiness	4.25	3.44	4.52
Inter-pattern-divergence	41.60	25.20	46.16
Pattern quality	14.27	9.61	15.35

From these definitions, the problem of ESPD can be formalized as:

Input

1. m samples 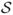= {s₁, s₂,…, s_m}, each measured by n-dimensional genes 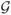= {g₁, g₂,…, g_n};

2. the number of phenotypes .

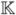Output

A 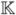-partition of samples (empirical pattern) and a subset of genes (informative space) such that the pattern quality (Ω) of the partition projected on the gene subset is maximized.

3 ALGORITHM

In general, the ESPD problem is NP-hard. An approach for obtaining a globally optimal solution is to try every possible 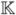-partitions of the samples, identify corresponding informative genes for each partition and then choose the best one by comparing the pattern quality values. However, this method yields a very inefficient algorithm.

We will present an iterative pattern adjustment algorithm to approach the optimal solution. The algorithm starts with a random partition (formed by 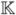bases) of samples and a subset of genes as the candidate of the informative space, then iteratively adjusts the partition and the gene set toward the optimal pattern.

3.1 Preliminaries

The algorithm maintains two basic elements, a state and the corresponding adjustments. The state of the algorithm describes the following items:

• A partition of samples {S_y1, S_y2,…,S_y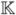}. Each S_yj is a base which satisfies S_yi∩S_yj = ∅ (y_i ≠ y_j) and $\mathcal{S}={\cup }_{i=1}^{\mathbb{K}}{S}_{y_i}$.

• A set of genes G_x ⊆ 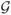which is a candidate for the the informative space.

• The pattern quality (Ω) of the state is calculated based on the partition on G_x.

An adjustment is an indivisible action for a sample or a gene which can change the current state of the algorithm. An adjustment of a state is one of the following:

• for a gene g_i ∉G_x, insert g_i into G_x ;

• for a gene g_i ∈ G_x, remove g_i from G_x ;

• for a sample s_j ∈ S_y′, move s_i to base S_y″, where S_y′ ≠ S_y″.

To measure the effect of an adjustment to a state, we calculate the quality gain of the adjustment as the change of the quality, i.e., ΔΩ = Ω′ − Ω, where Ω and Ω′ are the quality of the states before and after the adjustment, respectively.

Now, the goal becomes, given a starting state, we try to apply a series of adjustments to reach a state such that the pattern quality is maximized. The algorithm records a best state, in which the highest pattern quality so far is achieved.

3.2 An iterative adjustment approach

The algorithm (the pseudo-code shown in Fig. 4) consists of two phases: initialization and iterative adjustment. During the initialization phase, an initial state is randomly created and the corresponding pattern quality (Ω) value is computed.

Fig. 4.

The pseudo-code of the iterative adjustment approach.

During each iteration of the adjustment phase, all genes and samples are examined one by one. Each gene can be either inserted or removed from the current state. The corresponding quality gain (ΔΩ) is calculated. For each sample, there are ( 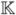− 1) possible movements, i.e. the sample can be moved to one of the other ( 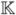− 1) groups. The quality gain is calculated respectively. The movement with the largest quality gain is chosen as the adjustment of the sample. The adjustment of a gene or sample will be conducted if ΔΩ is positive. If ΔΩ is negative, the adjustment will be conducted with a probability p = exp[ΔΩ/(Ω × T (i))].

The algorithm is sensitive to the order of gene and sample adjustments in each iteration. To give every gene or sample a fair chance, all possible adjustments are randomized at the beginning of each iteration.

The probability function p has two components. The first component, ΔΩ/Ω is the fractional decrease of pattern quality. Greater fractional decrease results in less probability the adjustment being performed. The second component, T (i), is a decreasing simulated annealing (Kirkpatrick et al., 1983) function where i is the iteration number. When T (i) is large at the beginning, p will be close to 1 and the adjustment has high probability to be conducted. As the iteration goes on, T (i) becomes smaller and the probability p will also become less. In our implementation, we set T (0) = 1 and T (i) = 1/(1 + i), which is a slow annealing function.

As indicated by Kirkpatrick et al. (1983), a simulated annealing search can reach the globally optimal solution as long as the simulated annealing function is slow enough and there are sufficient number of iterations. The upper bound of the number of iterations is the total number of possible solutions. However, for real applications, we should consider the trade-off between running time and optimal solution. Thus, we set the termination criterion as whenever in an iteration, no positive adjustment can be obtained. Once the iteration stops, the partition of samples and the candidate gene set in the best state will be output.

The time complexity of this method is dominated by the iteration phase. The time to compute Ω at the beginning is in O(m × |G_x |). In each iteration, the time complexity depends on the calculation of Ω′ for the possible adjustments. Since Equations (1)–(3) are all accumulative, we can simplify the formula by only computing the changed part of the metrics. It can be proved that the time cost of computing Ω′ is O(m) for each gene, and O(m · n) for each sample. There are n genes and m samples involved in each iteration. Therefore, the algorithm’s time complexity is O(n · m² · I), where I is the number of iterations.

4 EXPERIMENTS AND RESULTS

In this section, we will report an extensive performance evaluation of the proposed algorithm, using various real-world gene expression datasets.

4.1 The array datasets

• The multiple sclerosis datasets—The multiple sclerosis (MS) dataset consists of array-derived gene expression profiles that were provided by our collaborators in the Department of Pharmaceutical Sciences and in the Department of Neurology. The dataset contains two pair-wise group comparisons of interest. The first data subset, ‘MS versus Controls’, contains array data from 15 MS samples and 15 age and sex-matched controls while the second subset is referred to as ‘MS-IFN’ because it contains array data from 14 MS samples prior to and 24 h after interferon-β (IFN) treatment. Each sample is measured over 4132 genes.

• The leukemia datasets—The leukemia datasets are based on a collection of leukemia patient samples reported in Golub et al. (1999). It contains measurements corresponding to acute lymphoblastic leukemia (ALL) and acute myeloid leukemia (AML) samples from bone marrow and peripheral blood. Two matrices are involved: one includes 38 samples (27 ALL versus 11 AML, denoted as G1), and the other contains 34 samples (20 ALL versus 14 AML, denoted as G2). Each sample is measured over 7129 genes.

• The hereditary breast cancer dataset—The hereditary breast cancer dataset is from Hedenfalk et al. (2001). They reported on a microarray experiment concerning the genetic basis of breast cancer. Tumors from 22 women were analyzed, three types of samples are included in one data matrix: 7 of the women known to have the BRCA1 mutation, 8 known to have BRCA2 and 7 being labeled ‘Sporadics’. Each sample is measured over 3226 genes.

• The SRBCT dataset—Khan et al. (2001) studied the diagnose of the small, round blue-cell tumors (SRBCTs). SRBCTs include rhabdomosarcoma (RMS), Burkitt lymphomas (BL, a subset of Hodgkin lymphoma), neuroblastoma (NB), and the Ewing family of tumors (EWS). They published a dataset with 2308 genes and 63 samples. The 63 training samples include 23 EWS, 8 BL, 12 NB and 20 RMS.

The ground-truth of the partition, which includes such information as how many samples belong to each class and the class label for each sample, is only used to evaluate the experimental results.

4.2 Effectiveness evaluation

4.2.1 Partition of the samples

The Rand Index (Rand, 1971) between the ground-truth of phenotype structure P of the samples and the partition result Q of an algorithm is adopted to evaluate the effectiveness of the algorithm. Let a represent the number of pairs of samples that are in the same cluster in P and in the same cluster in Q, b represent the number of pairs of samples that are in the same cluster in P but not in the same cluster in Q, c be the number of pairs of samples that are in the same cluster in Q but not in the same cluster in P, and d be the number of pairs of samples that are in different clusters in P and in different clusters in Q. The Rand Index (Rand, 1971) is RI = (a + d)/(a + b + c + d). The Rand Index lies between 0 and 1. Higher values of the Rand Index indicate better performance of the algorithm.

To evaluate the performance of the proposed ESPD model, we first compare with some related approaches on detecting macroscopic phenotypes of samples. Table 3 provides the results obtained by applying our model and the related algorithms. All these algorithms were applied to the matrices after data normalization. The normalization formula is: w′_i,j = (w_i,j − w̄_i)/σ_i, where w′_i,j denotes the normalized value for gene i of sample j, w_i,j represents the original value, w̄_i is the mean of the values for gene i over all samples, and σ_i is the SD of the ith gene.

Table 3.

The average Rand Index values reached by applying different methods

Dataset	MS-IFN	MS versus controls	Leukemia-G1	Leukemia-G2	Breast	SRBCT
Data size	4132 × 28	4132 × 30	7129 × 38	7129 × 34	3226 × 22	2308 × 63
	2	2	2	2	3	4
J-express	0.482	0.485	0.510	0.497	0.411	0.655
CLUTO	0.482	0.483	0.578	0.487	0.636	0.731
CIT	0.484	0.485	0.659	0.492	0.584	0.563
CLUSFAVOR	0.524	0.540	0.510	0.492	0.584	0.578
δ-cluster	0.490	0.485	0.501	0.454	0.472	0.686
ESPD model	0.805	0.623	0.976	0.709	0.864	0.923

The tools J-Express (Rhodes et al., 2001), CIT (Dysvik and Jonassen, 2001) and CLUSFAVOR (Peterson, 2002) all provide multiple analysis methods such as hierarchical clustering, k-means, self-organizing maps. We tried every method for each tool. Some tools (Rhodes et al., 2001; Peterson, 2002) also provide the dimensionality reduction technique called principal component analysis (PCA) to reduce the gene dimension before clustering the samples. For these tools, we applied each clustering algorithm after running PCA on each dataset. For CLUTO, the clustering method we applied is the graph-partitioning-based algorithm (Schloegel and Karypis, 2000). The partition based clustering methods provided by the above tools, δ-cluster method, and our iterative adjustment approach are heuristic rather than deterministic, the results might be different in different executions. Thus for each tool or approach, we run the experiments multiple times using all different methods and different parameters and calculate the average Rand Index values. Therefore, the results shown in Table 3 are all average values.

Table 3 indicates that the ESPD model proposed in this paper consistently achieve clearly better pattern detection results than the previously proposed methods. We analyze the results briefly as follows (more discussion will be provide in Section 5.1). In clustering methods such as hierarchical clustering, k-means, self-organizing maps, objects are partitioned based on the full dimensional genes, the high percentage of irrelevant genes largely lower the performance. As indicated by Yeung and Ruzzo (2000), the principal components in PCA do not necessarily capture the class structure of the data. Therefore, the methods assisted by PCA can not guarantee to improve the clustering results. The central idea of subspace clustering is different from our empirical sample pattern detection. It is not surprising therefore that the δ-cluster algorithm is not effective in identifying the sample pattern.

4.2.2 Selection of the informative genes

In the following, we evaluate the informative genes identified by our approach on the Leukemia-G1 dataset and the SRBCT dataset.

Usually, there is no commonly accepted ground-truth on the informative genes. Even for the dataset Leukemia-G1 which often serves as the benchmark for microarray analysis methods (Siedow, 2001), different researchers identified different informative genes. Golub et al. (1999) applied a supervised method, named neighborhood analysis, to select top 50 genes to distinguish between ALL and AML classes. Thomas et al. (2001) used a statistical regression modeling approach to identify another set of 50 informative genes within the same dataset. Among these two 50-gene sets, 29 genes are overlapped.

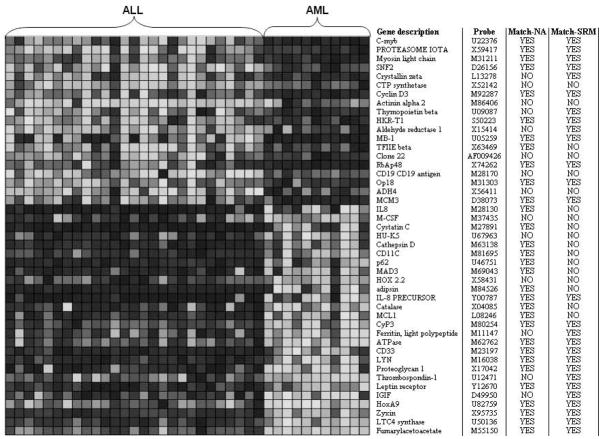
Figure 5 shows the pattern detection result of Leukemia-G1 dataset by our model. The algorithm selected 45 informative genes. In Figure 5, each column represents a sample, while each row corresponds to an informative gene. Different grey degrees in the matrix indicates the different expression levels. First 27 samples belong to ALL group while the rest 11 samples belong to AML group which agree with the ground-truth of the sample partition. Figure 5 shows that the top 19 genes distinguish ALL-AML phenotypes according to ‘on-off’ pattern while the rest 26 genes follow ‘off-on’ pattern. Abbreviated gene description and accession numbers for the probes on the array are provided on the first two columns on the right.

Fig. 5.

An empirical sample pattern detection result of Leukemia-G1 dataset.

We also compare this result with the above two extensively accepted supervised methods (Golub et al., 1999; Thomas et al., 2001). The column labeled as ‘match-NA’ in Figure 5 indicates whether the corresponding gene is also identified by the neighborhood analysis method. ‘YES’ means match while ‘NO’ means not match. The column labeled as ‘match-SRM’ indicates whether the corresponding gene is identified by the statistical regression modeling approach. Interestingly, as shown in Figure 5, 31 out of the 45 informative genes identified by our model match the neighborhood analysis method and 27 genes match the statistical regression modeling approach.

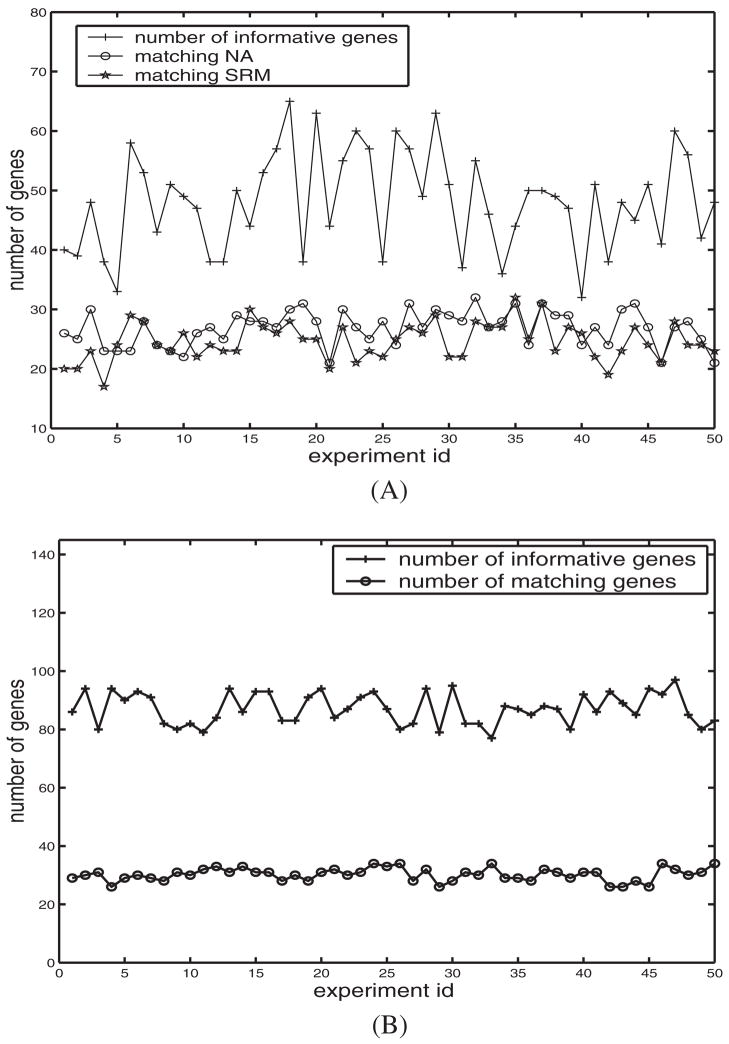
Figure 6 shows the pattern detection results on Leukemia-G1 dataset of 50 experiments by our method. In Figure 6A, the upper polyline shows the number of informative genes output of each experiment. The polyline marked as ‘matching NA’ means the number of informative genes that are also identified by the neighborhood analysis method. The polyline marked as ‘matching SRM’ means the number of informative genes that are identified by the statistical regression modeling approach. On the average, about 57% of them match that of the neighborhood analysis method and 52% of them match that of the statistical regression modeling. As mentioned in Section 1, unsupervised approaches are more complex than supervised methods. Similar percentage of matching informative genes with the above supervised methods therefore indicates that, even without supervision, the ESPD model learns well from the real-world datasets.

Fig. 6.

Informative genes identified by 50 executions of the algorithm on (A) the Leukemia-G1 dataset and (B) the SRBCT dataset.

4.2.3 Multi-class experiments

Given the promising results using ESPD model on 2-class datasets, we investigated the multi-class Breast Cancer and SRBCT datasets which have 3 and 4 classes of samples, and 3226 and 2308 genes, respectively. The accuracy of class discovery using the ESPD model was 0.864 for the Breast Cancer data and 0.923 for the SRBCT data. On average, the informative gene sets from ESPD contained 66 genes for the Breast cancer dataset and 86 genes for the SRBCT data.

We also assessed the overlap between the informative genes identified by ESPD model and those of the original authors. The informative gene sets identified by Hedenfalk et al. and Khan et al. contained 51 and 96 genes, respectively, Hedenfalk et al. (2001) and Khan et al. (2001). In the Breast cancer dataset, the overlap ranged from 30 to 33 genes whereas for the SRBCT dataset the overlap ranged from 26 to 34 across the executions of the ESPD algorithm. Figure 6B shows the results on the SRBCT dataset of 50 experiments by the ESPD model. The upper polyline shows the number of informative genes output of each execution. The lower polyline means the number of informative genes that are also identified by the supervised method reported in Khan et al. (2001). Figure 6B indicates that among 76–97 informative genes, about 27.7–44.2% of them match that of the method reported in Khan et al. (2001).

The extent of overlap is quite good given that ESPD model is unsupervised and uses no information regarding class labels. The mismatches between the informative gene set may be caused, in part, by the differences on the underlying approaches taken for identifying informative genes. Importantly, the ESPD model uses a graded or quantitative informative gene criterion whereas Khan et al. (2001) applied an ‘on-off’ binary informative gene scheme.

We also conducted two-way classifications by applying our method on the SRBCT dataset four times to identify the informative genes for each sample class, i.e. identifying informative genes that discriminate RMS samples from the rest samples using k = 2, and then identifying informative genes distinguishing BL class from the rest and so on. The overall informative genes identified matched 40–45 genes from Khan et al. (2001).

4.3 Efficiency evaluation

Table 4 reports the average number of iterations and the response time (in s) of the gene expression datasets. The algorithm was run 50 times with different parameters. The algorithm is implemented with MATLAB package and is executed on SUN Ultra 80 workstation with 450 MHz CPU and 256 MB main memory. The number of iterations is dominated by the simulate annealing function we used. We used a slow simulate annealing function for effectiveness of the approaches. Table 4 indicates that an experiment can be finished within several minutes; because the number of genes in the human genome is about 30,000–50,000, efficiency is not a major concern.

Table 4.

Average number of iterations and response time (in s) with respect to the matrix size

Data	Data size	# of iterations	runtime (s)
MS-IFN	4132 × 28	96	63
MS vs. controls	4132 × 30	102	68
Leukemia_G1	7129 × 38	116	158
Leukemia_G2	7129 × 34	117	155
Breast cancer	3226 × 22	94	57
SRBCT	2309 × 63	88	71

5 DISCUSSION

5.1 Why existing methods may not work well

5.1.1 Various bioinformatics applications

For biological applications, several array data analysis tools are available for seeking phenotypes of samples, e.g. CLUSFAVOR (Peterson, 2002), J-Express (Rhodes et al., 2001), CIT (Dysvik and Jonassen, 2001), and CLUTO (Schloegel and Karypis, 2000). In these approaches, samples are partitioned by K-means (Tavazoie et al., 1999), self-organizing maps (SOM) (Golub et al., 1999), hierarchical clustering (HC) (Eisen et al., 1998), or graph based clustering algorithms (Xing and Karp, 2001; Ding, 2002). However, these traditional clustering techniques may not be effective for detecting empirical sample pattern because the similarity measures used in these methods are based on the full gene space and cannot handle the noise in the gene expression data.

Although some approaches (Xing and Karp, 2001; Ding, 2002; Peterson, 2002) reduce gene dimension or filter genes for clustering samples, the genes filtering processes are noninvertible. The deterministic filtering causes the samples to be grouped based on the local decisions and some can only be applied on gene expression matrices with two phenotypes. In general, biologists are interested in methods applicable to any number of phenotypes of samples. Methods using PCA can reduce the number of genes involved in the datasets, but the results largely depend on the data distribution, and do not necessarily capture real phenotype structures (Yeung and Ruzzo, 2000).

5.1.2 Subspace clustering methods

Recent efforts on data mining and bioinformatics have studied methods for discovering clusters embedded in subspaces of a dataset (Agrawal et al., 1998; Getz et al., 2000; Cheng and Church, 2000; Yang et al., 2002). The main objective of subspace clustering is to find subsets of objects such that the objects appear as a cluster in a subspace formed by a subset of the attributes. Although, the subspace clustering problem may appear similar to the empirical sample pattern detection problem, there are significant differences.

• In subspace clustering, the gene subsets for different sub-space clusters are different while our goal is to find a unique set of genes to manifest a partition of all samples.

• Two subspace clusters can share some common samples and genes. Some samples may not belong to any subspace cluster. In EPSD, the sample partition is exclusive and exhaustive.

• The pattern similarity measurements (e.g. residue) of the subspace clustering algorithms which focus on gene expression data analysis (Yang et al., 2002; Cheng and Church, 2000; Getz et al., 2000) are not adequate for empirical sample pattern detection. Figure 2 shows two sets of genes over six samples. In Figure 2A, the genes all exhibit similar patterns. They will be considered as a subspace cluster by methods proposed by Cheng and Church (2000), Getz et al. (2000), and Yang et al. (2002). But we require the genes not only have similar pattern but also show steady signals within each base (as shown in Fig. 2B).

• The subspace clustering algorithms only detect local correlated genes and samples, they do not consider distribution over full gene dimension. But in our applications, the genes selected must both present high pattern similarity within one base and show large dissimilarity between different bases.

5.2 Conclusions of our model

In this paper, we have described the problem of detecting empirical pattern of sparse high-dimensional datasets. We also have presented a new ESPD model which includes a series of statistics-based metrics and an iterative adjustment approach to solve the problem.

The research is motivated by the needs of emerging high-dimensional array gene expression data analyzing applications and is designed to improve the unsupervised empirical pattern detecting performance for gene expression datasets. Our results show that without sample phenotypes as training information, our method can detect the empirical sample patterns and select informative genes from the array data-sets. The ESPD model takes the number of phenotypes as the input parameters and iteratively detect significant patterns within samples while dynamically selecting informative genes which manifest the empirical interest. We demonstrated the performance of proposed approach by extensive experiments on various real-world gene expression datasets. The empirical evaluation shows that our approach is effective for unsupervised analysis of sparse high-dimensional gene expression datasets.