Synaptic Ribbon Enables Temporal Precision of Hair Cell Afferent Synapse by Increasing the Number of Readily Releasable Vesicles: A Modeling Study

Abstract

Synaptic ribbons are classically associated with mediating indefatigable neurotransmitter release by sensory neurons that encode persistent stimuli. Yet when hair cells lack anchored ribbons, the temporal precision of vesicle fusion and auditory nerve discharges are degraded. A rarified statistical model predicted increasing precision of first-exocytosis latency with the number of readily releasable vesicles. We developed an experimentally constrained biophysical model to test the hypothesis that ribbons enable temporally precise exocytosis by increasing the readily releasable pool size. Simulations of calcium influx, buffered calcium diffusion, and synaptic vesicle exocytosis were stochastic (Monte Carlo) and yielded spatiotemporal distributions of vesicle fusion consistent with experimental measurements of exocytosis magnitude and first-spike latency of nerve fibers. No single vesicle could drive the auditory nerve with requisite precision, indicating a requirement for multiple readily releasable vesicles. However, plasmalemma-docked vesicles alone did not account for the nerve's precision—the synaptic ribbon was required to retain a pool of readily releasable vesicles sufficiently large to statistically ensure first-exocytosis latency was both short and reproducible. The model predicted that at least 16 readily releasable vesicles were necessary to match the nerve's precision and provided insight into interspecies differences in synaptic anatomy and physiology. We confirmed that ribbon-associated vesicles were required in disparate calcium buffer conditions, irrespective of the number of vesicles required to trigger an action potential. We conclude that one of the simplest functions ascribable to the ribbon—the ability to hold docked vesicles at an active zone—accounts for the synapse's temporal precision.

INTRODUCTION

Synaptic ribbons are found in photoreceptors and bipolar cells in the retina, and mechanosensory hair cells in the cochlea and vestibular end organs—all cells that encode sensory stimuli with a graded receptor potential instead of action potentials, or spikes (reviewed in Sterling and Matthews 2005). Ribbon synapses are characterized by an enigmatic electron-dense structure anchored to the presynaptic density and surrounded by a halo of tens to hundreds of synaptic vesicles. Although these cells can exocytose a large readily releasable pool of vesicles within tens of milliseconds, they also maintain high rates of sustained exocytosis for seconds (reviewed in Nouvian et al. 2006). Surprisingly, the sustained component of exocytosis was unaffected in goldfish retinal bipolar cells when ribbons were dissociated from active zones during the diurnal cycle, although rapid exocytosis was compromised (Hull et al. 2006). Furthermore, both rapid exocytosis and precise spike timing in the auditory nerve were degraded in a mouse mutant lacking anchored hair cell ribbons (Khimich et al. 2005), leading to the hypothesis that the ribbon stabilizes a large readily releasable pool, thereby enabling the temporal precision of auditory coding (Moser et al. 2006).

The hair cell ribbon synapse's temporal precision is revealed by the spike timing of eighth nerve fibers. Cat auditory-nerve fibers encode the onset of sound with a precisely timed first spike; the latency of this first spike decreases with increasing stimulus intensity and the fibers' minimum latencies range from 1 to 3 ms with SD (or jitter) as low as 0.1 ms (Heil and Irvine 1997). First-spike latency of frog nerve fibers are also precise, with jitter as low as 0.3 ms (estimated from data in Feng 1982; Ronken et al. 1993). These measures are based on spike timing and are notable compared with the 0.5- to 0.8-ms jitter of postsynaptic currents in cortical synapses (Jonas et al. 1993; Markram et al. 1997), where any temporal variation caused by fluctuations in action potential generation are absent.

The ribbon's molecular composition is largely unknown (Lenzi and von Gersdorff 2001) and provides limited clues to its role in precise spike timing. Several possibilities have been suggested. It might facilitate precisely timed exocytosis by colocalizing specialized proteins within the active zone (Hibino et al. 2002) or increasing calcium levels by restricting calcium diffusion (Roberts 1994). Perhaps it enables a precisely timed postsynaptic response by facilitating concurrent fusion of multiple vesicles (Glowatzki and Fuchs 2002) to rapidly depolarize the afferent fiber (Parsons and Sterling 2003); or the ribbon might facilitate rapid signaling despite slow exocytosis kinetics by simply increasing the number of available vesicles (Almers 1994).

We tested the hypothesis that the synaptic ribbon enables precise first-spike latency simply by increasing the size of the readily releasable pool. We derived a statistical model relating the number of readily releasable vesicles to the precision of first latency, assuming a single vesicle could trigger an action potential. As vesicle count increased latency became more precise. To examine the ribbon's role in this relationship, we created a biophysical model of the hair cell ribbon synapse with synaptic vesicles distributed according to detailed anatomical measurements. The temporal precision of simulated first-exocytosis latency was sufficient to account for observed first-spike latency—only when ribbon-associated vesicles contributed to the readily releasable pool. The dependence on ribbon-associated vesicles held for a variety of perturbations including stimulus intensity, calcium buffer conditions, and the number of vesicles required to trigger a spike. Thus our results are applicable to hair cell ribbon synapses in multiple species, as well as other synapses that drive precisely timed spikes with the synchronous fusion of multiple synaptic vesicles.

METHODS

Statistical model of first latency

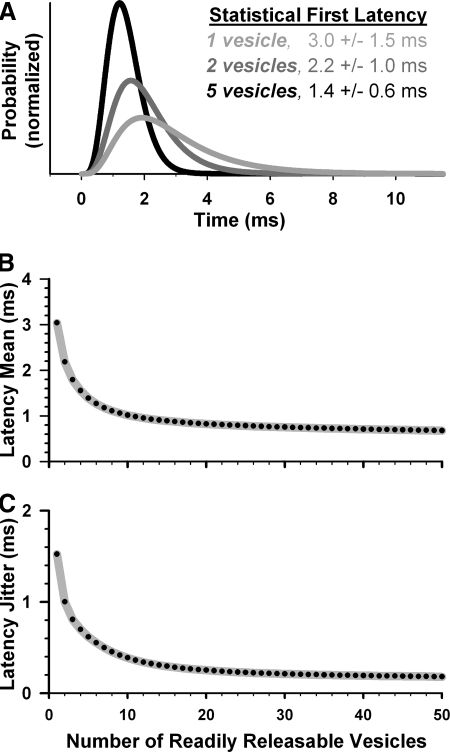
We defined the exocytic latency of a single vesicle as a random variable L with the probability density function f_L and cumulative distribution function F_L. Initially, we estimated f_L by integrating the kinetic equations describing calcium-dependent exocytosis (Beutner et al. 2001) during a step in calcium concentration from 0 to 50 μM (Fig. 1 A, light gray trace) using a fifth-order Runge–Kutta algorithm with a variable time step (Press et al. 1992). Subsequently, we estimated f_L by smoothing the simulated latency distribution of a single vesicle with a three-point moving average (Fig. 6A, blue trace). Random variables representing the exocytic latency of N readily releasable vesicles made the set [L₁, L₂, …, L_N], each drawn from the distribution f_L. First-exocytosis latency was the random variable T, where T = minimum [L₁, L₂, …, L_N]. The cumulative first latency distribution F_T, as a function of the number of readily releasable vesicles, was

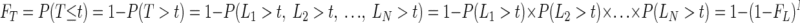(1)

FIG. 1.

Statistical model predicts inverse relationship between readily releasable pool size and first-exocytosis latency. A: latency histogram for a single synaptic vesicle subjected to a step increase in calcium concentration to 50 μM (light gray line). Statistical estimate of first-exocytosis latency distributions if 2 (dark gray) or 5 (black) vesicles sampled the single-vesicle distribution. B and C: first-exocytosis latency mean and jitter values calculated across a range of readily releasable vesicles (black points).

FIG. 6.

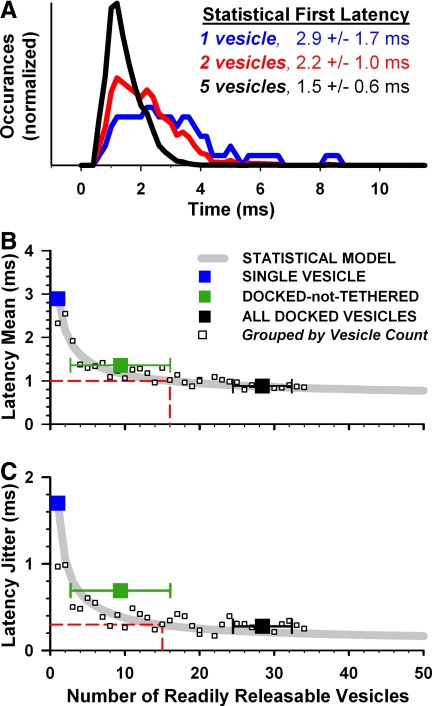
Exocytosis simulations validate the statistical model. A: latency histogram for a single colocalized vesicle (from Fig. 4D) smoothed with a 3-point triangle filter (blue line). Statistical estimate of first-exocytosis latency distributions if 2 (red) or 5 (black) vesicles sampled the single-vesicle distribution. B and C: first latency mean and jitter. Gray lines are statistical model predictions updated with biophysical model results. Large squares are stimulation results from Figs. 4 and 5, where the number of readily releasable vesicles equals the number of vesicles colocalized with channels. Small squares are simulation results divided into groups with the same number of readily releasable vesicles. Only groups with ≥5 trials were included (mean 13 trials/group). Horizontal dashed lines are minimum values observed in frog nerve fibers. Vertical dashed lines are the corresponding number of predicted vesicles.

The mean and jitter of T were equal to its expected value and the square root of its variance, respectively. To compare how vesicle populations with different kinetics contributed to first latency, we modified the final equation to include additional latency distributions.

Simulated active-zone exocytosis

We simulated calcium influx, buffered diffusion, and synaptic vesicle exocytosis following the Monte Carlo model of frog neuromuscular junction of Bennett and colleagues (2000). Their model accounted for mobile (diffusible) calcium buffers without resorting to the computationally intense approach of tracking diffusion and interaction of multiple species of molecules (e.g., Shahrezaei and Delaney 2004). This sacrifice in spatiotemporal accuracy for computational efficiency was essential for our analysis of variability between trials. Here we briefly describe the efficient Monte Carlo implementation and then focus on our adaptations to the ribbon synapse in leopard frog (Rana pipiens) saccular hair cells, particularly the distribution of synaptic vesicles and gating of calcium channels.

The model developed by Bennett and colleagues (2000) combined spatially resolved diffusion of individual calcium ions with coarse buffer molecule locations discretized into three-dimensional grids of volume elements. Each time step, ions probabilistically entered through open calcium channels, attempted to bind or unbind buffer molecules in their local volume element, and diffused. Ions bound to mobile buffers diffused according to the buffer's diffusion coefficient, whereas ions bound to fixed buffers or vesicle calcium sensors did not diffuse. Ions reflected from the edges of the simulated volume but diffused freely through synaptic vesicles and the synaptic ribbon. Background levels of calcium and occupied buffer molecules were removed from the simulation. This simplification had minimal impact on our mobile buffer concentration (3.1% decrement in total concentration) or synaptic vesicle calcium loading (only 0.3% of all sites would be occupied at background calcium levels). The modeling approach and assumptions were validated (Bennett et al. 2000), although a subsequent computationally intensive synapse model has been used to explore how synaptic vesicles themselves can act as calcium diffusion barriers (Shahrezaei and Delaney 2004).

We adapted the model proposed by Bennet and colleagues to the anatomy and physiology of the hair cell by modifying parameters to match published data (Table 1). We solved buffered diffusion with a 0.1-μs time step. Every time step, diffusing calcium ions jumped an average of 5.3 nm in each coordinate (compared with 14.5 nm in Bennett et al. 2000 and 1.7 nm in Shahrezaei and Delaney 2004). The frog's endogenous mobile buffer, calretinin, has at least five binding sites, four of which are high affinity and are likely cooperative. In the absence of detailed measurements of calretinin's cooperativity, we implemented a simplified model with a single high-affinity binding site at fourfold the measured concentration of the protein (see similar implementation in Roberts 1994). We used (40 nm)³ volume elements for fixed and mobile buffers, which were distributed uniformly throughout the cytosol, and (10 nm)³ elements for synaptic vesicle calcium sensors. Exocytosis required the cooperative binding of five calcium ions. We did not include calcium extrusion mechanisms due to the brevity of our stimuli (10 ms) and the size of our simulated volume (1.6 × 1.6 × 0.8 μm). The active-zone center was in the middle of the 1.6 × 1.6-μm surface representing the plasmalemma; the synaptic ribbon was centered above this point and 84 calcium channels were distributed ≤160 nm from this point to match freeze-fracture analysis of the presynaptic membrane (Roberts 1994; Roberts et al. 1990).

TABLE 1.

Active-zone simulation parameters

Parameter	Value	Reference
Calcium current
Channel count	84 channels	Roberts et al. 1990
Channel locations	Fig. 2E	Replicate location of presumed calcium channels in Roberts 1994
Channel conductance	2.1 pS	Rodriguez-Contreras et al. 2002
Maximum open probability	0.4	Rodriguez-Contreras and Yamoah 2001
Reversal potential	41.7 mV	Fit to Armstrong and Roberts 1998
Kinetic model states	3 closed, 1 open	Hudspeth and Lewis 1988
Kinetic model rate constants	Supplemental Fig. S1	Fit to Armstrong and Roberts 1998; Rodriguez-Contreras and Yamoah 2001
Calcium
Duffusion coefficient	223 μm2 s−1	Allbritton et al. 1992
Resting concentration	48 nM	Lumpkin and Hudspeth 1998
Fixed buffer
kon	1,357 μM−1 s−1	Lumpkin and Hudspeth 1998
KD	200 nM	Lumpkin and Hudspeth 1998
Concentration	0.610 mM	Lumpkin and Hudspeth 1998
Calretinin
Diffusion coefficient	32 μm2 s−1	Falke et al. 1994*
kon	100 μM−1 s−1	Dong et al. 1996**
KD	1.5 μM (high affinity)	Schwaller et al. 1997
	0.5 mM (low affinity)
Binding sites	4 (high affinity)	Schwaller et al. 1997
	1 (low affinity)
Protein concentration	1.2 mM	Edmonds et al. 2000
EGTA
Diffusion coefficient	113 μm2 s−1	Tsien 1980
kon	2.5 μM−1 s−1	Naraghi and Neher 1997
KD	180 nM	Naraghi and Neher 1997
Concentration	1 mM	Moser and Beutner 2000
Vesicle distribution
Location-dependent packing densities	***	Lenzi et al. 2002, inhibited values
Ribbon diameter	395 nm	Lenzi et al. 2002
Ribbon anchor	50 nm	***
Vesicle diameter	40 nm	***
Tether length	20 nm	***
Excytosis kinetics
Kinetic model states	0–5 ions bound, fused	Beutner et al. 2001
Binding rate	27.6 μM−1 s−1	Beutner et al. 2001
Unbinding rate	2,150 s−1	Beutner et al. 2001
Cooperativity constant	0.4	Beutner et al. 2001
Calcium-independent fusion rate	1,695 s−1	Beutner et al. 2001

List of values and citations used to parameterize the stochastic model.

^*Estimated from calmodulin, a comparably sized calcium buffer.

^**Estimated in Edmonds et al. (2000) from cardiac cell calretinin.

^***Estimated from Lenzi et al. (2002).

Synaptic vesicles were distributed randomly according to vesicle packing densities measured in isolated frog hair cells after 30 min of continuous inhibition with zero external calcium (Lenzi et al. 2002). We converted density per spatial unit (either volume or area) to vesicle count mean and SD, then drew Gaussian random deviates to find the number of vesicles per spatial unit each trial. Docked vesicles within a spatial unit that contained calcium channels (i.e., ≤200 nm from the active-zone center) were preferentially colocalized with those channels based on the possibility of their physical coupling (Hibino et al. 2002), given similar findings at other synapses (Rettig et al. 1996; Sheng et al. 1996). Otherwise, vesicle locations were randomly chosen within each spatial unit assuming uniform density. Locations were discretized into (10 nm)³ volume elements. We restricted overlap of docked vesicles by assuming each occupied a 3 × 3 × 3 cube of volume elements, slightly underestimating their 40-nm diameter. Nondocked vesicles required a smaller 2 × 2 × 2 cube for successful placement of all vesicles. We first placed all docked-not-tethered vesicles, then docked-and-tethered, then tethered, then outlier (see Fig. 2). Vesicle membranes contain multiple copies of calcium-sensing proteins thought to trigger exocytosis (Takamori et al. 2006), and we assumed the copy responsible for exocytosis sampled the volume element at the vesicle's plasmalemma-facing pole (see alternatives in Shahrezaei and Delaney 2004, 2005). One side of this volume element was the plasmalemma for docked vesicles. Colocalized vesicles contained a calcium channel within that 10 × 10-nm swath of plasmalemma. Therefore the center of a colocalized vesicle's calcium sensor was between 5 and 8 nm from its nearest calcium channel, within the range of values estimated experimentally in rat inner hair cells (∼3 and 23 nm; Goutman and Glowatzki 2007).

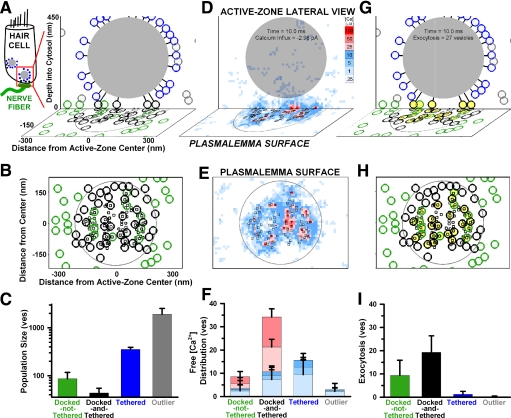
FIG. 2.

Spatial distribution of synaptic vesicles, free calcium, and exocytosis. Top row contains cross sections of the active zone (see diagram on left) with synaptic ribbon in gray and skewed representation of the plasmalemma surface below to indicate depth. Middle row contains full views of the plasmalemma surface. Top and middle rows are from a single trial of a 10 ms depolarization to −20 mV; bottom row is the mean ± SD of 250 trials. A–C: distribution of synaptic vesicles (circles), color coded into 4 morphologically distinct populations indicated in C. D and E: free calcium concentration averaged in (10 nm)³ volume elements during the last 0.1 ms of a 10-ms depolarization to −20 mV. Calcium channels are open squares. Color coding indicates concentration is equal to or greater than value indicated in legend (D, inset). F: the number of vesicles that sampled the calcium concentrations indicated in the color-coded legend above, where each vesicle's sampled concentration was averaged across the entire 10-ms depolarization. G and H: vesicles that exocytosed by the end of the stimulation are filled with yellow, averages in I.

Docked-and-tethered vesicles were colocalized more frequently than docked-not-tethered in our model because experimental evidence demonstrates that there are more docked-and-tethered vesicles in the region of the active zone where calcium channels are located (Lenzi et al. 2002; Roberts et al. 1990). Our model's vesicle distributions included 50 ± 13 docked vesicles within 200 nm of the active-zone center. In this area, docked-and-tethered vesicles outnumbered docked-not-tethered vesicles about 4:1. On average, 21 ± 7 vesicles in this area were not colocalized to channels despite the relative excess of channels, in part because most channels were within 20 nm of their nearest neighbor, such that if one was colocalized with a vesicle a second vesicle could not physically fit above the neighboring channel. Rather than randomly choosing vesicles to colocalize among the two populations, we attempted to increase the functional efficacy of docked-not-tethered vesicles by preferentially colocalizing them. As a result, 95% of docked-not-tethered vesicles within 200 nm of the active-zone center were colocalized and the ratio of colocalized docked-and-tethered to docked-not-tethered was about 2:1 in our simulations.

Calcium channel gating kinetics were based on a combination of single-channel (Rodriguez-Contreras and Yamoah 2001) and whole cell (Armstrong and Roberts 1998) current analysis. Opening and closing rate constants were derived assuming a four-state Markov model, with three independent closed states and an open state. We computed a sigmoid conductance–voltage curve from whole cell currents and then scaled it by the maximum open probability of a single channel to create an open probability–voltage curve. This and the activation time constant of whole cell currents were used to find voltage-dependent rate constants (Supplemental Fig. S1).1 Each channel was initialized in the fully closed state, then state transitions were evaluated probabilistically every 1 μs, subdividing when necessary to ensure all transition probabilities remained <0.1 (Gil et al. 2000). This method yielded realistic whole cell current kinetics and single-channel open probabilities. In contrast, whole cell current magnitudes estimated by scaling our single active-zone current by 19 (Roberts et al. 1990) was one fourth of the experimentally observed value (−83 vs. −363 pA in Armstrong and Roberts 1998), suggesting a significant number of calcium channels are extrasynaptic (see Rodriguez-Contreras and Yamoah 2001), an underestimate of the number of channels within each active zone, heterogeneity in calcium channel properties, or a discrepancy in single-channel conductance between preparations.

Three sets of source data were estimated from published graphical data: the location of calcium channels (Roberts 1994), the spatial distribution of synaptic vesicle densities (Lenzi et al. 2002), and the voltage dependence of calcium current (Armstrong and Roberts 1998). For each of these data sets, we imported digital copies of published images into a graphics program (Photoshop, Adobe), and then manually converted the graphical information into numeric values.

RESULTS

Statistical model of multiple released vesicles

As a first step in understanding the ribbon's role in precise spike timing, we sought to identify a mathematical relationship between the number of readily releasable vesicles and precision of auditory nerve spikes. Hair cell ribbon synapses are characterized by multiple readily releasable synaptic vesicles that exocytose in response to a few milliseconds of depolarization (Goutman and Glowatzki 2007; Keen and Hudspeth 2006; Moser and Beutner 2000), although a single vesicle may be sufficient to trigger an action potential in eighth nerve fibers (Geisler 1997). We hypothesized that the postsynaptic fiber responds to the first of several vesicles to yield a precise first-spike latency.

We estimated the latency of a single synaptic vesicle by integrating a kinetic model of calcium-dependent exocytosis in hair cells (Beutner et al. 2001). We assumed the vesicle was subject to a step increase to 50 μM calcium concentration based on physiological estimates from frog hair cells (Roberts 1993), although estimates from other ribbon synapses range from tens to hundreds of micromolar (Beutner et al. 2001; Heidelberger 2001). The stimulus caused a rapid onset of release probability that peaked 1.9 ms after the concentration change (Fig. 1A, light gray trace). A single vesicle's mean exocytic latency was 3.05 ms and its latency jitter (SD) was 1.52 ms.

INVERSE RELATIONSHIP BETWEEN LATENCY AND THE NUMBER OF READILY RELEASABLE VESICLES.

A mathematical relationship between exocytic latency of a single vesicle and the first-exocytosis latency of multiple vesicles can be derived from the statistics of random variables (see methods). A similar mathematical formalism was used to model how postsynaptic inputs contribute to spike-timing precision in the auditory brain stem (Xu-Friedman and Regehr 2005b). Synaptic vesicle exocytosis is quantal; therefore a vesicle's exocytic latency on any one trial could be represented by a random variable that sampled the smooth release probability. With two readily releasable vesicles, the first-latency distribution had a higher peak and shorter tail than that of a single vesicle because the probability that both vesicles exocytosed late in the same trial was low (Fig. 1A, dark gray trace). With five vesicles, first-latency distribution had an even higher peak and truncated tail and was thus even more precise (black trace).

The statistical model predicted a monotonic decrease in latency mean and jitter with increasing number of readily releasable vesicles (Fig. 1, B and C). Both first-latency mean and jitter decreased rapidly with the first few vesicles added and tapered off with increasing vesicle counts. Similar relationships were found when the calcium level sampled by each vesicle was either lower or higher than that estimated for frog (Supplemental Fig. S2). Although these inverse relationships lend mathematical justification to the intuitive hypothesis put forth previously by others (Almers 1994; Moser et al. 2006), several simplifying assumptions required further investigation. For instance, the model assumed a step increase in calcium concentration that stayed fixed throughout the stimulus. However, the time course of calcium concentration should fluctuate due to the stochastic nature of calcium influx and diffusion. Furthermore, the actual concentration sensed by synaptic vesicles should depend on many factors, including their distance from calcium channels and properties of the endogenous calcium buffer. The model also assumed all vesicles sampled the same release probability, whereas variation in vesicle-channel distances could cause drastic differences in the underlying release probability of each vesicle.

To investigate the validity of these simplifying assumptions, we developed a stochastic (Monte Carlo) computational model of the hair cell ribbon synapse that tracked individual calcium channels, ions, and synaptic vesicles during stimulation. This approach enabled us to distinguish the contribution of distinct vesicle populations at a ribbon synapse. We modeled the ribbon synapse with the most thorough anatomical characterization to date—the hair cell afferent synapse from the leopard frog (Rana pipiens) sacculus. In addition to the anatomical characterization of this synapse, the temporal precision of its afferent fiber has been extensively documented and provided a means of validating both our statistical and computational models.

Properties of simulated active-zone exocytosis

Three-dimensional reconstructions of this ribbon synapse revealed the distribution of synaptic vesicles in the active zone (Lenzi et al. 2002). The ribbon is spherical, about 400 nm across, and is surrounded by a halo of approximately 400 synaptic vesicles either touching or tethered to it by filaments. Additionally, a significant number of vesicles in the active zone are not associated with the ribbon and are either floating in the cytosol or docked to the plasmalemma. The location-dependent densities of four morphologically distinct populations of synaptic vesicles were reported (see Table 2): docked vesicles not associated with the ribbon (docked-not-tethered), docked vesicles associated with the ribbon (docked-and-tethered), nondocked vesicles associated with the ribbon (tethered), and nondocked vesicles floating freely in the cytosol (outliers). Our model active zone matched the reported spatial distribution of vesicles from each population (Fig. 2, A–C).

TABLE 2.

Distribution of synaptic vesicles and exocytosis by population

	Docked-not-Tethered	Docked-and-Tethered	Tethered	Outlier
Experimental vesicle counts	81 ± 37	43 ± 8	357 ± 42	1,997 ± 320
Simulated vesicle counts	91 ± 31	39 ± 11	361 ± 38	1,914 ± 615
Colocalized with channels	9 ± 6	19 ± 7	0	0
Simulated exocytosis
Vesicles	9.3 ± 6.4	19.8 ± 6.9	1.3 ± 1.4	0.1 ± 0.4
% of population	10 ± 7	52 ± 18	0.39 ± 0.46	0.01 ± 0.02
% of colocalized	98 ± 5	98 ± 3

All values are means ± SD of 250 trials, except experimental vesicle count variations, which are SE. Experimental vesicle counts from Lenzi et al. (2002), where they used the nomenclature: Outlying, docked; Synaptic body associated, docked; Synaptic body associated, not docked; Outlying, not docked. We modified their anatomical nomenclature in an effort to better reflect each group's functional significance in our active-zone simulations, specifically contrasting the two groups that dominate exocytosis: docked-not-tethered versus docked-and-tethered vesicles. Colocalized vesicles were 5–8 nm from the nearest calcium channel (see methods). Simulated exocytosis was driven by 10 ms of maximal calcium influx. Percentage exocytosis computed on a trial-by-trial basis then averaged across trials.

SPATIOTEMPORAL MODELING OF INTRACELLULAR CALCIUM DYNAMICS.

To drive exocytosis, we simulated calcium influx through 84 L-type calcium channels whose number, locations, and physiology were inferred from experimental observations (see methods and Table 1). The channels were distributed in the plasmalemma directly below the synaptic ribbon, within 160 nm of the active-zone center (Fig. 2B, squares are calcium channels). Most channels were <20 nm from their nearest neighbor. Synaptic vesicles docked near the active-zone center were preferentially colocalized to calcium channels such that their calcium sensors were within 5 to 8 nm of a channel (Fig. 2B, circles surrounding squares) based on the possibility of their physical coupling (Hibino et al. 2002) and physiological estimates of their spacing in hair cells (∼3 and 23 nm; Goutman and Glowatzki 2007). Maximal calcium influx was achieved with a voltage step to −20 mV, which drove about 13,000 ions/ms into the active zone, distributed among the flickering channels.

As calcium ions entered the active zone they diffused freely and were bound by a combination of fixed and mobile (diffusible) calcium buffers. The experimentally identified endogenous mobile buffer included in our model, calretinin (Edmonds et al. 2000), should be kinetically equivalent to a millimolar of the fast exogenous buffer BAPTA according to in vitro buffer titration experiments (Roberts 1993). Previous modeling studies predicted that such a buffer limits free calcium ions to within 50 nm of open calcium channels, with a theoretical space constant of about 20 nm (Roberts 1994). Our probabilistic model of calcium influx and diffusion agreed with these predictions; free calcium levels were >50 μM only within 20 nm of the open channels (Fig. 2, D and E, red and pink squares are 10 × 10 nm). A few calcium ions diffused deeper into the cytosol, leading to isolated volume elements with calcium concentrations ≤10 μM as far as 400 nm from the calcium channel array (Fig. 2, D and E, blue squares). Calcium buffers sequestered >99% of the calcium ions after they entered the cell, such that at the end of a 10-ms stimulus only 110 ions remained free in the cytosol.

We quantified the calcium concentrations sampled by morphologically distinct vesicle populations during a 10-ms step to −20 mV (Fig. 2F). On average, each population contained at least three vesicles per trial that were exposed to calcium concentrations ≥1 μM, with the docked-and-tethered population having the most and the outlier population having the fewest. Only vesicles colocalized with calcium channels sampled concentrations in excess of 25 μM, as expected from the location of calcium peaks in Fig. 2E. One tenth of docked-not-tethered vesicles are found within 200 nm of the active-zone center (Lenzi et al. 2002) and could thus colocalize with calcium channels (see methods); therefore most of these vesicles were too far from the source of influx to experience calcium levels as moderate as 0.25 μM. Overall, the distribution of calcium sampled by each population quantifies the extent that docked vesicles (docked-not-tethered and docked-and-tethered populations) sampled higher calcium concentrations than nondocked vesicles (tethered and outlier populations), despite the fact that a majority of the vesicles in the active zone were nondocked (Fig. 2C).

VESICLES COLOCALIZED WITH CALCIUM CHANNELS DOMINATE EXOCYTOSIS.

Our model is the first to combine vesicle location with the spatiotemporal distribution of calcium to predict the spatial distribution of exocytosis at the hair cell active zone (see Supplemental Movies S1 and S2). Previous models of other active zones have combined these computations (e.g., Bennett et al. 2000; Gil et al. 2000; Shahrezaei and Delaney 2004), although they lacked the unique three-dimensional distribution of vesicles found at ribbon synapses. Previous hair cell models either computed spatially detailed calcium dynamics without exocytosis (e.g., Roberts 1994), averaged calcium levels throughout the active zone (e.g., Sumner et al. 2002), computed exocytosis without considering calcium dependencies (Schnee et al. 2005), or embedded this step within a phenomenological model of signal transduction (e.g., Zhang et al. 2001).

We probabilistically simulated calcium-dependent exocytosis according to a kinetic model derived from mouse inner hair cell capacitance measurements (Beutner et al. 2001). Molecular mechanisms of regulated secretion are conserved across species (Bennett and Scheller 1993); therefore we assumed the rate constants derived from mouse cells in vitro at room temperature approximated those expected in vivo in the poikilothermic frog. Capacitance data suggest that vesicles not morphologically docked to the membrane can rapidly fuse when subjected to elevated calcium levels (Beutner et al. 2001). We therefore assumed all synaptic vesicles in our model were capable of calcium-dependent exocytosis, irrespective of their location. In our simulations, an average of 30 synaptic vesicles exocytosed by the end of the stimulus (Fig. 2, G and H, yellow-filled vesicles reveal a representative trial). This amount of exocytosis was within the range observed experimentally with capacitance measurements of hair cells from the frog sacculus after normalizing for differences in whole cell calcium current (Edmonds et al. 2004; Rutherford and Roberts 2006).

Each morphologically distinct population contributed a different number of vesicles to the overall response of the active zone (Fig. 2I). On average, most exocytosed vesicles originated from either the docked-not-tethered or docked-and-tethered populations (9.4 and 19.3 vesicles/trial, respectively). The tethered and outlier populations contributed little to the active zone's response (1.2 and 0.1 vesicles/trial). The minimal contribution of vesicles not docked at the active zone suggests that multiquantal release in the frog synapse (Keen and Hudspeth 2006) is supported by parallel release of multiple docked vesicles rather than the compound or cumulative fusion of vesicles tethered along the ribbon (Edmonds et al. 2004; Parsons and Sterling 2003). The distribution of exocytosed vesicles among each population resembled the distribution of vesicles that sampled elevated calcium concentrations in Fig. 2F. Ninety-one percent of all exocytosed vesicles were colocalized with calcium channels and, of the vesicles colocalized with calcium channels, 98% exocytosed (Table 2). Based on this reliability of fusion in the presence of the endogenous buffer, we defined the colocalized vesicles as readily releasable.

TEMPORAL PRECISION OF SYNAPTIC VESICLE EXOCYTOSIS.

Our simulations predicted the time course of synaptic vesicle exocytosis at the hair cell ribbon synapse with sub-millisecond resolution (Fig. 3 A). Each trial yielded a slightly different temporal pattern and number of exocytosed vesicles. After the stimulus onset there was a brief delay before any vesicle exocytosed, followed by an onslaught of vesicle fusions that subsided within 5 ms. Sometimes a vesicle fused before the stimulus started due to random channel openings at the −80-mV holding potential. The stochastic nature of synaptic vesicle exocytosis was captured by our probabilistic modeling technique and the exocytosis times from any one trial were qualitatively similar to the limited examples of postsynaptic current onsets measured in frog hair cell afferents (Keen and Hudspeth 2006).

FIG. 3.

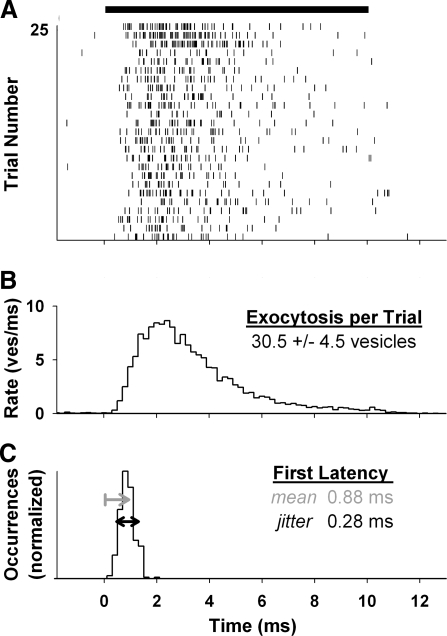
Active-zone exocytosis is temporally precise. Top: stimulus bar indicates step to −20 mV from −80 mV. A: exocytosis raster from 25 trials. Each mark represents the exocytosis of a single synaptic vesicle. B: average exocytosis rate from 250 trials. C: histogram of first-exocytosis latency after the stimulus onset. Arrows indicate latency mean (gray) and jitter (black). Histograms binned at 0.2 ms.

We computed the average exocytosis rate by combining the results from 250 trials of depolarization (Fig. 3B). It peaked at about 9 vesicles/ms within 3 ms of stimulus onset and rapidly declined during the stimulus. This decline, or adaptation, was due to the depletion of readily releasable vesicles. The half-width of the peak at half-height was <2 ms. Thus the time course closely resembled measurements from afferent fibers from immature rat inner hair cells (Goutman and Glowatzki 2007), which had a peak rate of about one excitatory postsynaptic current/ms. Furthermore, the time course was qualitatively similar to the initial time course of exocytosis rate measured with postsynaptic recordings during step depolarization of retinal ribbon synapses (Borges et al. 1995) and nonribbon synapses with multiple contributing active zones (Sakaba and Neher 2001; Stevens and Tsujimoto 1995). However, the peak in exocytosis rate was an order of magnitude less precise than the first-spike latency of frog nerve fibers.

FIRST-EXOCYTOSIS LATENCY ACCOUNTS FOR OBSERVED FIRST-SPIKE LATENCY OF FROG AFFERENT FIBERS.

The latency histogram of first-exocytosed vesicles from 250 trials was precisely timed, with a mean latency of 0.88 ms and jitter (SD) of 0.28 ms (Fig. 3C). Reported first-spike latency of acoustically driven leopard frog nerve fibers can have mean values as low as 1 ms (Feng 1982). Although jitter was not directly reported, our lowest estimate from published data of several individual fibers was 0.3 ms (Feng 1982; Ronken et al. 1993). Thus our simulations predicted that the temporal precision of first-exocytosis latency was sufficient to account for the observed first-spike latency of frog nerve fibers.

The hair cell is a nonspiking neuron; its synapses are driven by a graded receptor potential proportional to the intensity of an acoustic stimulus (Crawford and Fettiplace 1980). We simulated the synapse's response to voltage steps ranging from −65 to +25 mV that elicited calcium currents between 10 and 100% of the maximum. First-exocytosis latency was sufficiently precise to account for frog's minimum first-spike latency with steps between −35 and +5 mV, when calcium current was as low as 80% of the maximum (Supplemental Fig. S3). Given the robustness of our results, we limited our remaining analyses to exocytosis elicited during maximal calcium influx.

Anatomical basis of precise first latency

We attempted to identify which vesicle(s) were required for precise first-exocytosis latency. We first compared the nerve's spike latency to exocytosis latency of a single vesicle, then increased the readily releasable pool to include docked vesicles not associated with the ribbon (docked-not-tethered), and finally docked vesicles that were ribbon associated (docked-and-tethered). We then used our simulation results to update our statistical model relating the number of readily releasable vesicles to the precision of first-exocytosis latency. With the updated model, we predicted the minimum number of readily releasable vesicles required to account for the temporal precision of frog nerve fibers.

COLOCALIZED VESICLE TRACKS CALCIUM CHANNEL GATING.

Perhaps the temporal precision of first-exocytosis latency was conferred by a single vesicle that exocytosed rapidly. To test this hypothesis, we evaluated the latency of a single vesicle in the middle of the calcium channel array that was colocalized within 8 nm of one channel and <20 nm from a second channel. Previous theoretical studies predicted that calcium concentration increases rapidly and to high levels near open calcium channels (e.g., Roberts 1994). Therefore a vesicle located within a few nanometers of one or more open calcium channels should rapidly undergo calcium-dependent exocytosis and likely contributes to the temporal precision of the synapse (Brandt et al. 2005), although the advantages of colocalization may be diminished by the calcium channel's tendency to flicker open and closed.

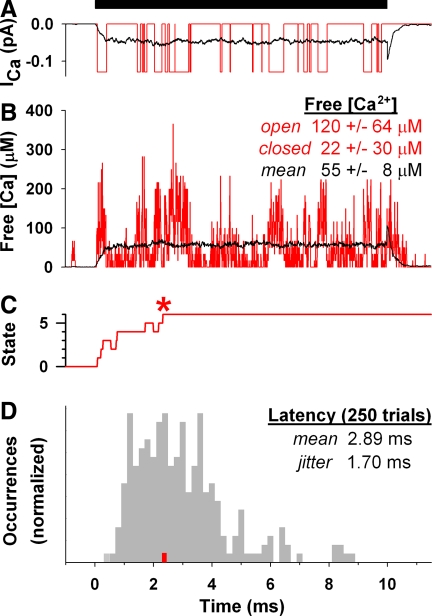
During a representative single trial, the closest channel opened soon after the stimulus onset, then went through a series of open and closed states (Fig. 4 A, red trace). Across 250 trials, the average single-channel current increased to its steady-state value in <0.5 ms, remained relatively constant throughout the duration of the stimulus, and exhibited a brief tail current on repolarization (Fig. 4A, black trace). The subunity maximum open probability of hair cell calcium channels (Rodriguez-Contreras and Yamoah 2001) caused frequent channel closures and resulted in an average steady-state current significantly less than that through an open channel (−0.05 vs. −0.13 pA).

FIG. 4.

Individual vesicle exocytosis is not temporally precise. Top: stimulus bar indicates step to −20 mV from −80 mV. A–C: compare the results from a single trial (red lines) to the average of 250 trials (black lines in A and B; gray bars in D). A: influx through a single channel. B: calcium concentration within a (10 nm)³ volume element sampled by a colocalized vesicle, averaged every 10 μs. Mean ± SD calcium concentration of this single trial during channel open or closed times during the 10-ms stimulation, and the average concentration during stimulation of 250 trials. C: state transitions as vesicle bound 5 calcium ions (states 1–5) and exocytosed (state 6, *). Initially the vesicle has no bound ions (state 0). D: distribution of exocytosis times, binned at 0.2 ms.

The calcium concentration within a few nanometers of the flickering channel peaked rapidly when the channel was open and decayed rapidly when the channel was closed (Fig. 4B, red trace). The single trial of channel gating in Fig. 4A yielded a similar (albeit noisier) time series of local calcium concentration, with peaks in the calcium concentration coinciding with when the channel was open and dips coinciding with when the channel was closed (compare red traces in Fig. 4, A and B). When the channel was open, calcium concentration in a (10 nm)³ volume of cytoplasm containing the channel was 120 μM, equivalent to a single free ion in the volume 7.2% of the time. When it was closed, concentration dropped to 22 μΜ, equivalent to an ion in the volume 1.3% of the time. The concentration was nonzero when the channel was closed due to diffusion of calcium from neighboring open channels and release of calcium from buffer molecules. The average calcium concentration mirrored the kinetics of the average single-channel current and had a steady-state value of 55 μM (Fig. 4B, black trace), a concentration sufficient to elicit rapid exocytosis in mouse inner hair cells (Beutner et al. 2001).

SINGLE VESICLE IS INSUFFICIENT FOR TEMPORAL PRECISION.

In most trials, the vesicle exocytosed during the stimulus, although on one trial it fused 5 ms before the stimulus started due to spontaneous channel openings at the holding potential (data not shown). We evaluated the binding and unbinding of calcium ions that lead to vesicle exocytosis in a single trial (Fig. 4C, * marks vesicle fusion). The vesicle bound ions rapidly when the channel was open, but less frequently when the channel was closed, and sometimes released ions. During the initial channel opening the vesicle bound three calcium ions, one of which was released once the channel closed. After a series of binding and unbinding ions, the vesicle eventually regained a fifth ion and fused 0.14 ms later. The single-vesicle latency distribution had a mean and jitter of 2.89 and 1.70 ms (Fig. 4D, gray bars) and was thus substantially slower and less precise than the first-spike latency of frog eighth nerve fibers (Feng 1982). Therefore a single vesicle was incapable of accounting for the nerve's temporal precision.

The transition from five bound ions to exocytosis (Fig. 4C) was governed by the rate constant of the calcium-independent step in hair cell exocytosis. In theory, a vesicle subject to an instantaneous increase to infinitely high calcium levels would be limited only by this rate constant and exocytose with a latency mean and jitter of 0.7 ms, which is still less precise than the first-spike latency of eighth nerve fibers. Thus the evolution of calcium binding during channel openings and unbinding during channel closures significantly prolonged the latency of exocytosis compared with the theoretical minimum. This highlights the detrimental effect of low maximum open probability on exocytic latency. These findings portend the need for more than one readily releasable vesicle to precisely encode acoustic transients.

RIBBON-ASSOCIATED VESICLES ARE REQUIRED FOR TEMPORAL PRECISION.

We tested the hypothesis that synaptic ribbons confer precise timing by increasing the number of readily releasable vesicles. We simulated the absence of an anchored synaptic ribbon by evaluating exocytosis of only the docked-not-tethered population, such that all vesicles normally associated with the ribbon were absent, including both the docked-and-tethered and tethered populations. On average, 91 docked vesicles remained in our simulations, 9 of which were colocalized with calcium channels (Table 2). Anatomically, this amounted to a 30% reduction in the number of docked vesicles in our simulations, which was comparable to the 33% reduction in docked vesicle count measured at hair cell afferent synapses lacking ribbons (Khimich et al. 2005). We did not add vesicles to the cytosol normally occupied by the ribbon because our simulations of the intact synapse indicated that few nondocked vesicles exocytosed (Fig. 2I); we thus likely underestimated the number of cytosolic vesicles in the ribbon-free active zone.

In the absence of a synaptic ribbon, exocytosis rate resembled a scaled version of the response of the intact active zone (Fig. 5 A, compare solid histogram and black trace). Both peaked within 3 ms of the stimulus onset, but magnitude decreased by approximately 66% without the ribbon-associated vesicles, as might be predicted from the relative contribution of the docked-and-tethered population to exocytosis in Fig. 2I. This decrease in response magnitude was comparable to the observed 75% reduction in readily releasable pool size in mice lacking anchored ribbons (Khimich et al. 2005). This decrease also matched a nearly 66% reduction in the fast component of exocytosis at active zones temporarily lacking anchored ribbons in goldfish bipolar cells, which we estimated from published data (Hull et al. 2006) assuming that exocytosis at intact synapses was unchanged (i.e., Khimich et al. 2005) and extrasynaptic exocytosis was negligible (Zenisek et al. 2003). Our ability to model the absence of a synaptic ribbon was essential to our analysis of its function and the congruence between both anatomical and physiological measures of these specialized synapses when they lack ribbons validated our approach.

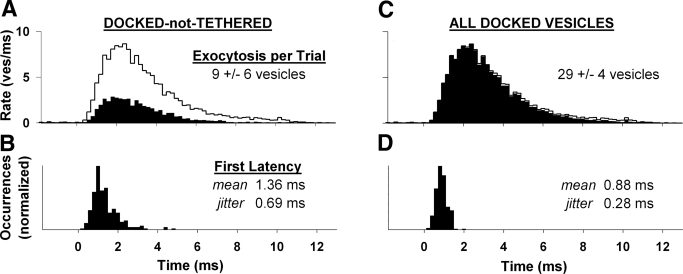
FIG. 5.

Ribbon-associated vesicles are required for temporal precision. Comparison of exocytosis rate (top) and first-exocytosis latency histograms (bottom) for different populations of vesicles. A and B: solid histograms from the docked-not-tethered population or (C, D) all docked vesicles, which include docked-not-tethered and docked-and-tethered populations. Black traces in A and C indicate exocytosis rate of the intact active zone (all vesicles), from Fig. 3B.

First-exocytosis latency was slower and less precise than predicted for the intact active zone, with a mean and jitter of 1.36 and 0.69 ms (Fig. 5B). Although the first-latency histogram had a peak near 1 ms, several trials yielded first-exocytosis latencies between 2 and 5 ms, thereby increasing latency mean and jitter. We concluded that a readily releasable pool consisting solely of docked-not-tethered vesicles was insufficient for achieving the observed spike-timing precision of frog nerve fibers.

The synapse's temporal precision was regained when our analysis also included docked vesicles associated with the ribbon (Fig. 5, C and D). The exocytosis rate of all docked vesicles (docked-not-tethered and docked-and-tethered) was almost identical to that of the intact active zone (Fig. 5C, compare solid histogram and black trace). The histograms differed slightly only after the stimulus had been on for >3 ms, arising from the limited contribution of tethered and outlier populations. First-exocytosis latency with all docked vesicles matched that of the intact active zone, with a mean and jitter of 0.88 and 0.28 ms (compare Figs. 5D and 3C). The addition of ribbon-associated vesicles reduced first-exocytosis latency by increasing the likelihood of an early first fusion and eliminating late first fusions. We concluded that docked vesicles associated with the synaptic ribbon must contribute to the readily releasable vesicle pool to account for first-spike latency precision of frog nerve fibers.

COMPARISON OF STATISTICAL MODEL AND BIOPHYSICAL SIMULATIONS.

Our simulations of active-zone exocytosis predicted a reduction in first-exocytosis latency mean and jitter as the size of the readily releasable vesicle pool increased. This result was in accordance with our preliminary statistical model that assumed all vesicles were subject to a step increase of 50 μM calcium concentration (Fig. 1). Using the results of our exocytosis simulations, we updated our statistical model to more accurately reflect the stochasticity of the underlying biophysical processes. The statistical model requires a single-vesicle latency distribution and the number of vesicles sampling that distribution; we replaced the single-vesicle latency distribution estimated for a constant step to 50 μM with the distribution resulting from biophysical simulations of a single colocalized vesicle in the frog active zone (Fig. 6A, blue trace smoothed histogram from Fig. 4D).

As with the preliminary statistical model, when two or five readily releasable vesicles sampled the latency distribution of a colocalized vesicle, the resultant first-latency distributions had increasingly higher peaks and shorter tails—latency mean and jitter decreased (Fig. 6A, red and blue traces). The inverse relationships between latency and the number of readily releasable vesicles (Fig. 6, B and C, gray lines) were very similar to those predicted with a calcium step (i.e., Fig. 1, B and C) because the average calcium concentration sampled by the colocalized vesicle was 55 μM. We estimated the number of vesicles required to match frog nerve fiber data with the updated statistical model (red dashed lines). At least 15 and 16 vesicles were required to match the precision of first-spike latency mean and jitter, respectively.

We compared the statistical model's predictions to exocytosis simulations. We first considered the simulated latency of a single available vesicle, just docked-not-tethered vesicles, and all docked vesicles, again defining the vesicles colocalized with calcium channels as readily releasable (Fig. 6, B and C, large squares). The number of readily releasable vesicles was always one during the single vesicle simulations but was variable in the docked-not-tethered and all docked simulations. The simulation results followed the trends of the statistical model's predictions. However, the latency jitter of the docked-not-tethered population was markedly higher than predicted (Fig. 6C, compare green square and gray line).

To understand this apparent discrepancy, we refined our analysis by subdividing the original categories of vesicle populations into groups of trials with the same number of readily releasable vesicles (Fig. 6, B and C, small squares). For example, we identified 7 of 250 trials with exactly 16 docked-not-tethered vesicles and computed the latency of those 7 trials to be 1.02 ± 0.35 ms. In these limited trials where there were sufficient numbers of docked-not-tethered vesicles in the active zone, latency and jitter nearly matched the performance of the nerve. The redefined groups of trials exquisitely tracked the statistical model's predictions and support our hypothesis that first-exocytosis latency can be reasonably inferred from the latency distribution of a single readily releasable vesicle and the number of readily releasable vesicles. This highlights the point that ribbon-associated vesicles did not constitute a physiologically unique pool of release-ready synaptic vesicles; ribbon-associated vesicles increased the size of a physiologically homogeneous pool so it was consistently large enough for precision.

RIBBON STATISTICALLY ENSURES PRECISE TIMING.

Simulations with and without ribbon-associated docked vesicles straddled the theoretical minimum number of vesicles required to match the nerve's latency precision (Fig. 6, B and C), substantiating the ribbon's role in increasing the number of readily releasable vesicles to drive precisely timed auditory nerve spikes. Variance in the number of docked vesicles not associated with the ribbon (docked-not-tethered) made this population susceptible to elevated latency (mean and jitter) from trials with few readily releasable vesicles. Adding ribbon-associated docked vesicles shifted the hair cell synapse away from the steep part of the theoretical curves, such that variability in the number of all docked vesicles had little effect on the synapse's latency. Therefore ribbon-associated vesicles enhanced the precision of first-exocytosis latency not just by increasing the mean number of releasable vesicles, but also by reducing sensitivity to variance in the readily releasable vesicle count.

RIBBON-ASSOCIATED VESICLES ARE ESSENTIAL FOR TEMPORAL PRECISION EVEN IF MORE THAN ONE VESICLE IS REQUIRED TO TRIGGER AN ACTION POTENTIAL.

Physiological measurements support our assumption that a single vesicle was sufficient to elicit an action potential in the afferent (Glowatzki and Fuchs 2002; Siegel 1992). However, multiquantal release is an emerging characteristic of the hair cell synapse (Glowatzki and Fuchs 2002; Keen and Hudspeth 2006) that might enable precise spike timing by rapidly depolarizing the postsynaptic fiber with neurotransmitter from multiple vesicles (Parsons and Sterling 2003). Accordingly, we examined temporal precision when more than one vesicle was required to elicit a spike. An analogous relationship between first-spike latency and the number of converging synaptic inputs, rather than the number of converging synaptic vesicles, was examined in neurons that respond to the temporal coincidence of two or more inputs (Xu-Friedman and Regehr 2005a). These coincidence-detecting neurons behave like ideal integrators on short timescales, responding to the precise timing of the Nth input when exactly N inputs were required to elicit a spike.

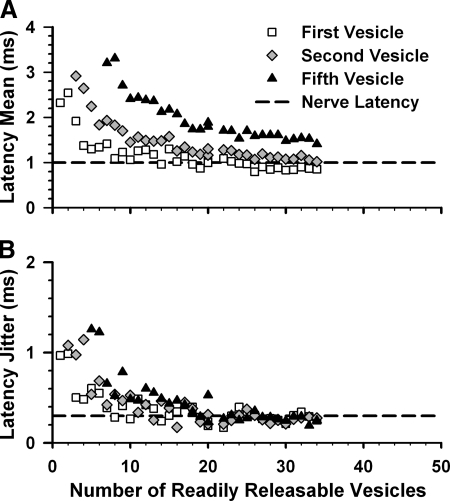
We reevaluated our active-zone simulations assuming two or more vesicles were required to elicit a spike. The temporal precision of the second or fifth exocytosed vesicle also improved with increasing readily releasable pool size. Increasing the number of vesicles required to trigger a spike increased latency mean (Fig. 7 A). In contrast, latency jitter was largely independent of coincident vesicle fusion requirements, especially when the readily releasable pool was ≳15 vesicles (Fig. 7B). Thus a large readily releasable pool was necessary for precise spike timing even when the afferent was a coincidence detector. We concluded that ribbon-associated vesicles were essential for exceeding first-spike latency precision of frog nerve fibers, irrespective of the number of vesicles required to trigger a spike.

FIG. 7.

Ribbon-associated vesicles are required for temporal precision during coincidence detection. Comparison of the latency mean (A) and jitter (B) of 1st exocytosed vesicle, 2nd vesicle, and 5th vesicle. Each point estimated from small groups of simulations with the same number of readily releasable vesicles as in Fig. 6. Dashed lines are minimum reported frog values.

RIBBON-ASSOCIATED VESICLES ENHANCE TEMPORAL PRECISION EVEN WITH A SLOW CALCIUM BUFFER.

A salient difference between hair cells for different species is the endogenous calcium buffer. In frog, turtle, and chicken hair cells, millimolar concentrations of the fast-binding buffer, BAPTA, were required to match the endogenous buffer's effect on calcium-dependent physiological processes (e.g., Roberts 1993). In contrast, the endogenous calcium buffer in mouse hair cells was matched with about 1 mM of the slow-binding buffer EGTA (Moser and Beutner 2000). Replacing the endogenous frog buffer with EGTA drastically increased the distribution of free calcium in the active zone, such that vesicles as far as 200 nm from the calcium channels exocytosed (Supplemental Fig. S4, Supplemental Movies S3 and S4). Vesicles close to calcium channels exocytosed more rapidly due to higher average calcium levels (Supplemental Fig. S5), whereas the more distant vesicles had slower kinetics. The contents of these more distant vesicles could in theory reach the synaptic cleft via calcium-dependent mechanisms of multiquantal exocytosis such as cumulative or compound fusion (Neef et al. 2007; Parsons and Sterling 2003).

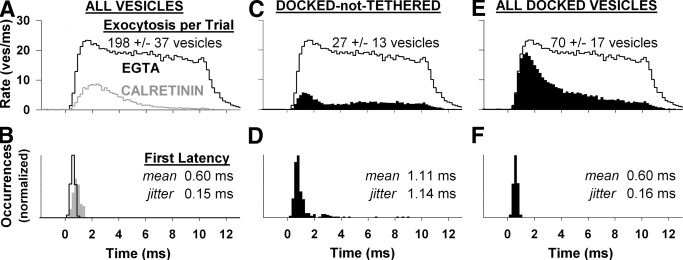
The time course of synaptic vesicle exocytosis in our simulations was dramatically different when EGTA replaced the frog's endogenous buffer (Fig. 8 A). The peak exocytosis rate with EGTA was more than twofold greater and transpired almost a millisecond before the peak with calretinin. The high exocytosis rate was maintained throughout the stimulus and exhibited little adaptation; the average exocytosis rate during the last 2 ms of the stimulus was 70% of the peak rate, compared to 5% with calretinin. After the stimulus ceased, the synapse exocytosed 20 vesicles per trial with EGTA, compared with 0.3 vesicle with calretinin. First-exocytosis latency mean and jitter were 0.6 and 0.15 ms, 30% faster and more precise than with calretinin (Fig. 8B), albeit at the expense of continued exocytosis after the stimulus terminated.

FIG. 8.

Ribbon-associated vesicles are required for temporal precision with a slow calcium buffer. A and B: comparison of exocytosis rate and first-exocytosis latency with the standard buffer, calretinin (gray), and the slow buffer EGTA (black). Simulations otherwise identical. C–F: replicates Fig. 5, but with EGTA.

As with calretinin, we evaluated the anatomical basis of temporally precise exocytosis by examining the contribution of different vesicle populations. With EGTA, docked-not-tethered vesicles alone resulted in the exocytosis of 27 docked-not-tethered vesicles (Fig. 8C) and a first-exocytosis latency mean and jitter of 1.11 and 1.14 ms (Fig. 8D). The EGTA buffered synapse recovered its temporal precision when the docked-and-tethered population was included (Fig. 8, E and F). The exocytosis rate of all docked vesicles had a prominent peak between 1 and 2 ms then adapted to a low level. The difference between exocytosis rate of all docked vesicles and the intact active zone demonstrated that tethered and outlier populations exocytosed late, thereby limiting adaptation. First-exocytosis latency of all docked vesicles matched the intact synapse, with a mean and jitter of 0.60 and 0.16 ms (compare Fig. 8, B and F). We concluded that ribbon-associated vesicles also enhanced the precision of first-exocytosis latency with EGTA.

DISCUSSION

The spike-timing jitter of leopard frog eighth nerve fibers can be as low as 0.3 ms (estimated from data in Feng 1982 and Ronken et al. 1993). Surprisingly, the theoretical lower bound of exocytic jitter for an individual vesicle is 0.7 ms. Jitter increases to 1.7 ms in simulations accounting for calcium channel gating and buffered diffusion (Fig. 4). Thus no single vesicle is capable of driving the nerve with requisite precision. The hair cell ribbon synapse compensates for the imprecise timing of individual vesicle fusions by encoding stimulus onset with the precisely timed fusion of the first of many readily releasable vesicles (Fig. 3). The synaptic ribbon is required to retain a pool of readily releasable vesicles sufficiently large to statistically ensure first-exocytosis latency is both short and reproducible (Fig. 6).

Validating the computational model

We carefully selected an experimental species and stimulus paradigm to minimize complications when juxtaposing simulation results derived from in vitro data to auditory-nerve responses recorded in vivo. In particular, we chose the frog not only because its ribbon synapse is well characterized, but because analyzing data collected at room temperature from a poikilothermic species obviated the need for temperature compensation between preparations. Furthermore, we limited our analysis to minimum first-spike latencies because the high-intensity acoustic transients that drive such responses could be reasonably simulated with a brief square-pulse voltage step. To allay concern about the physiological relevance of our test voltages, we confirmed that the model could match the nerve's minimum latency jitter for a range of simulated receptor potentials (Supplemental Fig. S3). Our selection of species and stimulus minimized the model's free parameters, although our conclusions are drawn from computational results and, as such, can only be as strong as the assumptions in the model.

One key assumption was that removing a synaptic ribbon could simply be modeled by removing all ribbon-associated vesicles from our analysis. Possibly, the ribbon acts as a calcium diffusion barrier that increases local calcium concentration near the channels (Roberts 1994). In our simulations, calcium ions rarely diffused >20 nm from open channels due to the frog's endogenous calcium buffer (Fig. 2, D and E); thus the ribbon's effect on local calcium levels should be negligible. Furthermore, simply removing ribbon-associated vesicles from our analysis was sufficient to account for experimentally observed reduction in both the number of docked vesicles (Khimich et al. 2005) and size of the readily releasable pool (Hull et al. 2006; Khimich et al. 2005). This validated our computational approach to removing the synaptic ribbon, thereby enabling us to make conclusions about its role in hair cells.

Another key assumption was the colocalization of synaptic vesicles and calcium channels, in that we defined these vesicles as readily releasable. There is no direct measure of the distance between vesicles and channels; we placed colocalized vesicles' calcium sensors 5 to 8 nm from a channel, which was between two experimental estimates from rat inner hair cells (∼3 and 23 nm; Goutman and Glowatzki 2007). Variation in this distance can significantly affect release probability due to the short space constant of calcium decay in frog hair cells (∼20 nm; Roberts 1993). For example, in additional simulations where docked vesicles were not explicitly colocalized with channels, such that on average 28 vesicles were between 5 to 30 nm of their nearest channel, exocytosis magnitude decreased by >40% and first-exocytosis latency mean and jitter more than doubled (data not shown). Furthermore, when vesicles act as calcium diffusion barriers, release probability depends on the specific location of the sensor on the vesicle's surface (Shahrezaei and Delaney 2004). Without more precise experimental measurements of the spacing between vesicles and calcium channels or the location of calcium sensors on a vesicle, our estimate of these parameters was necessarily approximate. The overall agreement between our standard simulations and multiple experimental results argues that our model was sufficiently accurate to support the hypothesis that ribbon-associated vesicles are essential for precise spike timing.

A ribbon synapse lacking a synaptic ribbon is not equivalent to a conventional synapse

It is important to distinguish the difference between a hair cell active zone lacking a synaptic ribbon and a conventional (non-ribbon) synapse. Some conventional active zones have many more docked vesicles than are found at an intact ribbon synapse (e.g., Gustafsson et al. 2002). Increasing vesicle count alone is insufficient to cause a reduction in first-exocytosis latency; our statistical model relates the number of physiologically active (readily releasable) vesicles to temporal precision. A ubiquitous characteristic of ribbon synapses is the exorbitant speed and quantity of synaptic vesicle exocytosis during brief stimuli (Edmonds et al. 2004; Moser and Beutner 2000; von Gersdorff et al. 1996) relative to most conventional synapses. These physiological measures indicate that ribbon synapses have higher numbers of readily releasable vesicles than most conventional synapses and perhaps are specialized to exocytose a greater proportion of anatomically docked vesicles (Moser et al. 2006).

First- versus coincident-exocytosis detection

Although a single vesicle likely triggers a spike in the postsynaptic afferent fiber (Geisler 1997), unitary postsynaptic current amplitudes measured at hair cell afferents are variable (Glowatzki and Fuchs 2002; Keen and Hudspeth 2006) and some may trigger a spike, whereas others may not. Specialized neurons in the auditory system detect the coincidence of multiple small postsynaptic currents to precisely encode acoustic transients (e.g., Oertel et al. 2000). In our simulations, latency jitter can be equally precise if more than one vesicle is required to trigger a spike (Fig. 7B), suggesting the afferent fiber could detect the coincident exocytosis of synaptic vesicles to establish temporal precision. Other features of the afferent fiber's response may provide clues to whether it detects first- or coincident-exocytosis events. Based on analogous studies of an auditory brain stem neuron (Rothman and Young 1996), a first-exocytosis detector should have a shorter mean latency, a higher spontaneous rate, and higher interspike interval variance than those of a coincident-exocytosis detector.

Slow buffer improves temporal precision of first-exocytosis latency

Replacing the endogenous calcium buffer in our simulations with a slow-binding surrogate causes a dramatic increase in the magnitude and temporal precision of active-zone exocytosis. With calretinin, vesicles colocalized to calcium channels dominate the exocytic response to a 10-ms stimulus. With EGTA, in addition to colocalized vesicles, many other vesicles exocytose. One possible explanation for increased temporal precision with EGTA is a functional increase in number of readily releasable vesicles. However, there are distinct kinetic components comprising active-zone exocytosis in the presence of EGTA (i.e., Fig. 8C). Docked vesicles within 200 nm of the active-zone center constitute the fastest kinetic component, whereas vesicles further out sample lower concentrations of calcium and have slower kinetics. Slightly modifying our statistical model of first-exocytosis latency to analyze the impact of vesicle populations residing different distances from the active-zone center, we found that those with the fastest kinetics almost exclusively determine the first-exocytosis latency distribution (data not shown). Therefore the improvement of first-exocytosis latency with EGTA was due primarily to faster exocytosis kinetics of colocalized vesicles that sampled higher calcium concentrations (Supplemental Fig. S4).

Rapid replenishment of the readily releasable pool for precise timing

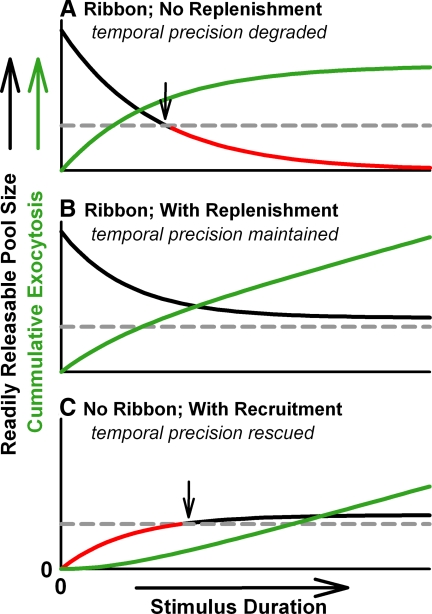
The predicted relationship between readily releasable pool size and temporal precision has several important implications for auditory-nerve function. Release-ready vesicles in hair cells are hypothesized to be transiently depleted during stimulation that results in neural adaptation (Furukawa et al. 1982; Goutman and Glowatzki 2007; Moser and Beutner 2000; Spassova et al. 2004). If temporal precision of the hair cell synapse depends on the size of the readily releasable pool, then pool depletion should degrade temporal precision (Fig. 9 A). However, chick auditory-nerve fibers maintain temporal precision during adaptation (Avissar et al. 2007). If the readily releasable pool is depleted sufficiently during stimulation to cause neural adaptation, but is replenished rapidly enough to maintain the pool size above a critical threshold, then temporal precision of ongoing tonal stimuli could be maintained (Fig. 9B). Our predictions of an asymptotic relationship between temporal precision and readily releasable pool size (Figs. 1C and 6C) suggests that reducing the pool size from its maximum value could reduce firing rate without sacrificing timing. Perhaps the rapid refilling of the hair cell's readily releasable pool compared with other ribbon synapses (Edmonds et al. 2004; Moser and Beutner 2000; Spassova et al. 2004) is essential not only to support bouts of sustained transmitter release (Griesinger et al. 2005), but also to maintain its temporal fidelity.

FIG. 9.

Readily releasable pool depletion and temporal precision of the auditory nerve. A: readily releasable pool depletion degrades temporal precision during prolonged stimuli. Cumulative synaptic vesicle exocytosis (green line) increases during stimulation as readily releasable vesicles (black and red line) exocytose without replenishment. At stimulus onset the large readily releasable pool (black line) exceeds the minimum size required for temporal precision (gray dashed line), as defined in Fig. 6C. During prolonged stimuli the readily releasable pool is depleted below this critical size (arrow), such that it is no longer large enough to support precise timing (red line). B: rapid replenishment of the readily releasable pool curtails depletion so temporal precision is maintained. C: in the absence of a synaptic ribbon, the readily releasable pool is initially small and temporal precision is poor (red line). Stimulus-induced recruitment of vesicles to the active zone increases the size of the readily releasable pool so it is sufficiently large (arrow) to enable temporally precise responses to prolonged stimuli (black line). All traces are based on a 3-state kinetic model describing the number of readily releasable vesicles, V_rr, where V_rr is irreversibly replenished and depleted with rate constants k_r and k_d, respectively, and has the initial value V_rr: [1/(k_r + k_d)] × (dV_rr/dt) + V_rr = V_rr × k_r/(k_r + k_d).

We have argued that the ribbon is important for maintaining a large readily releasable pool that ensures a rapid and reliable release event at sound onset (Figs. 5 and 8). Auditory-nerve fibers from mice lacking anchored synaptic ribbons exhibit increased first-latency jitter, which is consistent with our predictions. However, it has recently been reported in abstract form (Strenzke et al. 2008) that these fibers phase-lock to transposed tones with the same temporal precision as fibers from mice with anchored ribbons. We propose that during stimulation, rapid recruitment of synaptic vesicles to the active zone could sufficiently increase the readily releasable pool size to encode prolonged acoustic stimuli with temporal precision (Fig. 9C). This proposition is bolstered by observations that readily releasable pool refilling is calcium dependent (Moser and Beutner 2000; Spassova et al. 2004) and that the sustained component of release, often interpreted as the mobilization of synaptic vesicles to the readily releasable pool, is normal in mice lacking anchored ribbons (Khimich et al. 2005).

Thus we hypothesize that one important function of synaptic ribbons in hair cells is to catch and hold vesicles that are mobilized to the active zone during refilling. The ribbon could function as a depot to retain a sufficiently large number of mobilized vesicles to statistically ensure that first-spike latency is both short and reproducible at times when refilling is not active—such as at stimulus onset.

Spike-rate adaptation in the frog auditory nerve

One prominent feature of our simulations is the decrease in exocytosis rate during stimulation due to the exhaustion of the readily releasable pool (Figs. 3 and 5). Such exhaustion has been proposed to underlie rate adaptation of eighth nerve fibers (Furukawa et al. 1982; Goutman and Glowatzki 2007; Moser and Beutner 2000; Spassova et al. 2004). Thus it is interesting to consider how the extent and time course of exocytosis-rate adaptation in our model compares to spike-rate adaptation of frog nerve fibers. Unlike mammalian auditory-nerve fibers, which often share a stereotyped adaptation profile, frog fibers vary widely in their degree and time course of adaptation (Lewis 1986; Megela and Capranica 1981; Ronken 1990), depending on which end organ the fiber innervates (reviewed in Smotherman and Narins 2000).

In contrast to our simulations of hair cell exocytosis, the fibers innervating saccular hair cells often exhibit no adaptation at all (Lewis 1986; Smotherman and Narins 2000). This apparent discrepancy might be explained by a postsynaptic mechanism that blunts the onset response of the fibers, such as neurotransmitter receptor saturation or refractoriness of the spike generator. Instead we favor the idea that rapid replenishment of the readily releasable pool in vivo counteracts exocytosis-rate adaptation (i.e., Fig. 9B) and would thus limit neural adaptation. Furthermore, our simulations with a slow-binding calcium buffer exhibited significantly less adaptation than those with the endogenous buffer (Fig. 8A). Thus the differences in neural adaptation observed across the end organs and between fibers in frog auditory nerve might result from different endogenous buffering properties or different rates of vesicle replenishment in the hair cells that innervate them.

Strategies for reducing synaptic jitter

Our analysis of exocytic latency facilitates interpretation of how other synapses might be configured to achieve precise spike timing. Essentially there are two ways to improve timing: increasing the number of readily releasable vesicles (Fig. 6) or decreasing latency of each individual vesicle via faster exocytosis kinetics (Fig. 4 vs. Supplemental Fig. S5). The former could be achieved by increasing the size of the synaptic ribbon, or perhaps by combining readily releasable vesicles from separate active zones. Afferent fibers in amphibians and avians receive inputs from several synaptic ribbons (Fischer 1992; Simmons et al. 1992). Perhaps the barn owl, whose auditory-nerve fibers are among the most precisely timed (Koppl et al. 1993), detects first-exocytosis events across many active zones in its basilar papilla's fovea (Fischer 1994). Another example where multiple active zones might combine their outputs to increase the number of readily releasable vesicles is in the calyx of Held, where a single presynaptic terminal contains ≤600 active zones (Satzler et al. 2002) and drives postsynaptic currents with a jitter of 0.02 ms (Borst et al. 1995).

The other means of improving timing is to increase the rate of exocytosis for each readily releasable vesicle. Hair cells may increase exocytosis kinetics relative to conventional synapses with specialized proteins, such as oterferlin, the putative hair cell-specific calcium sensor (Roux et al. 2006). Another means of increasing exocytosis rate is to increase local calcium concentration by reducing the binding kinetics of the endogenous calcium buffer (Fig. 8). Calcium levels can also be increased by increasing the conductance of each calcium channel, increasing the number of channels, increasing the open probability of each channel, decreasing the distance between channels and vesicles, or creating local regions of high calcium with diffusion barriers such as the ribbon (Roberts 1994) or vesicles themselves (Shahrezaei and Delaney 2004). Furthermore, hair cell exocytosis kinetics increase with temperature (Nouvian 2007). Thus the possibility of slow calcium buffers (Beutner et al. 2001) in combination with elevated body temperature is consistent with the remarkably precise first-spike latencies recorded from mammalian afferents (Heil and Irvine 1997).

GRANTS

This work was supported by the National Institute on Deafness and Other Communication Disorders Grants T32 DC-005363 to J. H. Wittig and R01 DC-003783 to T. D. Parsons, and a Pennsylvania Lions Hearing Research Foundation grant to T. D. Parsons.